第四讲热学部分..(可编辑修改word版)
- 格式：docx
- 大小：228.38 KB
- 文档页数：14
下载文档原格式
合集下载
热学教程
dN ＝∫ f (v)dv N v1
v2
∫
N
0
∞ dN = ∫ f (v)dv = 1 0 N
归一化条件
13
应注意的问题: 应注意的问题: 分布函数是一个统计结果， 分布函数是一个统计结果，以上各种讨论都是建立在众多分子微 观运动基础上的，分子的数目越大，结论越正确。所以： 观运动基础上的，分子的数目越大，结论越正确。所以： 1）少数分子谈不上概率分布 偶然事件少了，或分子数少了，就不能表现出稳定的统计特性。 偶然事件少了，或分子数少了，就不能表现出稳定的统计特性。 例如，抛两分的硬币，抛的次数越多，币制和国徽朝上的次数才 例如，抛两分的硬币，抛的次数越多， 更加接近相等，否者将有很大差异。 更加接近相等，否者将有很大差异。 2）统计规律表现出涨落 所谓涨落就是对稳定的统计结果的偏差， 所谓涨落就是对稳定的统计结果的偏差，统计规律必然伴随着涨 例如，在某一速率v附近dv间隔内求出的比值dN/N dv间隔内求出的比值dN/N是 06， 落。例如，在某一速率v附近dv间隔内求出的比值dN/N是0.06， 表示有6 的分子，它们的速率取值分布在（ v+dv） 表示有6%的分子，它们的速率取值分布在（v，v+dv）内，但并 不 是 说 ， 每 时 每 刻 就 一 定 是 0.06 ， 也 有 可 能 是 0.05998 ， 0601， 等等 但长时间的平均值仍是0 06。 等等， 0.0601，…等等，但长时间的平均值仍是0.06。 14
3
复 习
气体动理论的基本观点 气体动理论的基本观点 理想气体的微观模型 理想气体的微观模型 理想气体压强公式 理想气体压强公式
p=
理想气体的温度 理想气体的温度
2 2 1 n( 2 mv ) = 2 n k 3 3
大学物理热学
表达式
ΔU=Q+W，其中ΔU表示系统内能的增量，Q表示外界对系统传递的热量，W表示外界对系统做的功。
热力学第二定律
内容
不可能把热从低温物体传到高温物体而不产生其他影响，或不可能从单一热源 取热使之完全转换为有用的功而不产生其他影响，或不可逆热力过程中熵的微 增量总是大于零。
表达式
对于可逆过程，有dS=(dQ/T)；对于不可逆过程，有dS>(dQ/T)，其中S表示熵， T表示热力学温度。
02
辐射传热特点
不需要介质，可在真空中传播；伴 随能量形式的转换；辐射强度与物
体温度的四次方成正比。
04
应用
太阳能利用、红外遥感测温、激光 器等。
复合传热过程分析
复合传热 分析方法 影响因素
应用
实际传热过程中往往同时存在热传导、对流和辐射三种传热方式。 根据具体传热条件，建立物理模型，综合运用热传导、对流和辐 射的传热规律进行分析计算。
02
理想气体性质及应用
理想气体状态方程
01
理想气体状态方程
pV = nRT，其中p为压强，V为 体积，n为物质的量，R为气体常 数，T为热力学温度。
02
理想气体状态方程 的适用条件
适用于稀薄气体，即气体分子间 距离较大，相互作用力可忽略不 计。
03
理想气体状态方程 的应用
可用于计算气体的压强、体积、 温度等物理量，以及进行气体状 态变化的分析。
热力学在其他领域应用
化学工业
制冷与空调
新能源领域
在化学工业中，热力学原理被广泛应用 于化学反应过程的分析和优化。通过热 力学计算和分析，可以确定化学反应的 条件、反应热、反应平衡常数等关键参 数，为化学工业的生产提供理论指导。
ΔU=Q+W，其中ΔU表示系统内能的增量，Q表示外界对系统传递的热量，W表示外界对系统做的功。
热力学第二定律
内容
不可能把热从低温物体传到高温物体而不产生其他影响，或不可能从单一热源 取热使之完全转换为有用的功而不产生其他影响，或不可逆热力过程中熵的微 增量总是大于零。
表达式
对于可逆过程，有dS=(dQ/T)；对于不可逆过程，有dS>(dQ/T)，其中S表示熵， T表示热力学温度。
02
辐射传热特点
不需要介质，可在真空中传播；伴 随能量形式的转换；辐射强度与物
体温度的四次方成正比。
04
应用
太阳能利用、红外遥感测温、激光 器等。
复合传热过程分析
复合传热 分析方法 影响因素
应用
实际传热过程中往往同时存在热传导、对流和辐射三种传热方式。 根据具体传热条件，建立物理模型，综合运用热传导、对流和辐 射的传热规律进行分析计算。
02
理想气体性质及应用
理想气体状态方程
01
理想气体状态方程
pV = nRT，其中p为压强，V为 体积，n为物质的量，R为气体常 数，T为热力学温度。
02
理想气体状态方程 的适用条件
适用于稀薄气体，即气体分子间 距离较大，相互作用力可忽略不 计。
03
理想气体状态方程 的应用
可用于计算气体的压强、体积、 温度等物理量，以及进行气体状 态变化的分析。
热力学在其他领域应用
化学工业
制冷与空调
新能源领域
在化学工业中，热力学原理被广泛应用 于化学反应过程的分析和优化。通过热 力学计算和分析，可以确定化学反应的 条件、反应热、反应平衡常数等关键参 数，为化学工业的生产提供理论指导。
热学课件
v cV
dN
1
N dx
1
N 0e
x
dx
N 0 个 分 子 中 自 由 程 大 于 的 分 子 数 ：N N 0 个 分 子 中 自 由 程 小 于 的 分 子 数 ：N
N 0e
1
0 .3 7 N 0
N 0 N 0.63 N 0
[例] 已知： O2，d 3.6×10-10m，
( t r 2 s ) kT B
每交换一对分子，沿z轴正方向输运的能量为： 1 1 ( t r 2 s ) kT A ( t r 2 s ) kT B 2 2
dt时间内通过dS面输运的总能量,即沿z轴正方向传递的热量为：
dQ
1 6
n vd S d t
(t r 2 s ) 2
现象、热传导、扩散过程，这些过程都可归结为某种物理
量的迁移和输运，统称为输运过程。
模型：
• • • 气体是处于接近平衡态的非平衡态，故可认为每个局部区域 麦克斯韦速率分布率及分子平均速率公式仍适用。 输运过程是通过分子无规则热运动和碰撞实现的。描述这三 处于平衡态，可用温度、压强等状态参量表示。
种输运过程要用到分子自由程、碰撞频率等概念。
v z
：
气体分子在相邻两次碰撞间飞行的平均路程。
二. 平均碰撞频率 理想气体，在平衡态下，并假定： （1）只有一种分子； （2）分子可视作直径为 d 的刚球； （3）被考虑的分子以平均相对速率 u 运动， 其余的分子静止。
2d d
中心在 扫过的柱体内的分子都能碰撞
π d
单原子分子气体 双原子分子气体
t r 2 s 3, C V ， m
热学第四讲§12.1准静态过程§12.2 热力学第一定律
热学第四讲：第12章 热力学基础研究热现象中物态变化和能量守恒及转换定律及应用的学科。
§12.1准静态过程一、准静态过程：始末平衡态之间的一系列中间态，都可近似看成是平衡态的状态，称为准静态过程。
只有准静态过程才能在PV 图中表示出来，而非准静态过程是无法在PV 图中表示出来。
二、内能、功和热量1、内能：表示热力学系统状态的物理量，是态函数。
① 理想气体的内能：()T E E= 是温度的单值函数，仅与始末位置有关。
② 一般气体的内能：()V T E E ，= RT2i E =2、功：系统对准静态过程是由于体积变化而做的功 ① 微功：V P PS F W ∆=∆=∆=∆ P d V dW =② 总功：∑∑∆=∆=V P w W⎰⎰==PdV dwW0W气体体积膨胀，系统对外界做正功；外界对系统做负功。
0W气体体积收缩，系统对外界做负功；外界对系统做正功3、热量：由于外界系统之间存在温度差而传递的能量摩尔热容：是1mol 物质在微小升温dT 过程中所吸收的热量。
()dTdQ C mm =§12.2 热力学第一定律一、 热力学第一定律：系统从外界吸收的热量，一部分用来改变系统的内能；另一部分用来对外做功。
是能量守恒定律在热学中的具体表现。
1、 表达式：()WE E W E Q12+-=+∆=2、 微分式：dW dE dQ+= 微小的变化过程3、 积分式：⎰⎰⎰⎰+-=⇒+==21121122E E QdE dQQ V V V V PdV E E Q PdV4、 第一类永动机是不可能造成的！是违背热力学第一定律的。
第一类永动机是指少耗能多做功；甚至是不消耗能量而做功。
热力学第一定律告诉我们对外做功是以消耗热能为代价的，不消耗能量就可以也要不断的对外做功的机器是不可能制造出来的。
二、 热力学第一定律对理想气体平衡过程的应用 1、 等体过程：12E E dQC V-=−−→−=⎰热一系统所吸收的热量全部用来增加系统的内能。
热学_课件_第4章_热力学第一定律
2.可逆过程还必须满足无耗散条件
只要某一过程不满足上述一种或几种，则这样的过程 就是不可逆过程。这四种不可逆因素即：力学、热 学、化学及耗散不可逆因素。
只有无耗散的准静态过程才是可逆过程。 教材在P194给出了以下不可逆过程的解释： 1.气体向真空自由膨胀及流体无抑制的膨胀的过程。 （在这一过程中始终不满足力学条件，即系统不是 处处压强相等）。 2.物体在有限温度差下热传导过程。（始终不满足热 学平衡条件）
定义
准静态过程是一个进行得无限缓慢，以致系统连 续不断地经历着一系列平衡态的过程。 显然，准静态过程是不可能达到的理想过程，但我 们可尽量趋近它。 对于实际的物理操作，我们只要求准静态过程的状 态变化足够缓慢就可， 而缓慢是否足够的标准是驰豫时间。 教材举例说明非准静态过程与准静态过程的区别。
[例1] 从活塞上移走砝码的实验。有两种方法:
电介质电容器工作时发热等。
只有无耗散的准静态过程才是可逆过程。 注意：两个条件缺一不可，同时满足才是可逆过程。 可见，可逆过程必须同时满足四个条件： 1.可逆过程必须是准静态过程，而准静态过程中系统 应始终满足：
（1） 力学平衡条件(可理解为压强处处相等)；
（2) 热学平衡条件(温度处处相等)； （3) 化学平衡条件(同一组元在各处的浓度处处相等)。
3.扩散、溶解、渗透及很能多的化学反应过程。（始 终不满足化学平衡条件，同一成分的浓度不是处处 相等）
§4.2 功和热量
§4.2.1 功是力学相互作用下的能量转移
力学知识点：外力作用下，物体运动状态发生改变的同时，将 伴随有能量的转移，这个转移的能量就是功。 热力学系统达到平衡态的条件是同时满足力学、热学和化学平 衡条件。力学平衡条件被破坏时所产生的对系统状态的影 响称为力学相互作用。 如图，从(I)变为( Ⅲ)的过程中，由于气 体施予活塞方向向上的压力始终比外界 向下的压力大一点儿，气体就能克服重 力及大气压强作功而准静态地膨胀。 功是力学相互作用过程中系统和外界之间转移的能量。
热学讲义
热学1、物质是由大量分子组成的（注意分子体积和分子所占据空间的区别） 对于分子（单原子分子）间距的计算，气体和液体可直接用3分子占据的空间，对固体，则与分子的空间排列（晶体的点阵）有关【例题1】如图6-1所示，食盐（N a Cl ）的晶体是由钠离子（图中的白色圆点表示）和氯离子（图中的黑色圆点表示）组成的，离子键两两垂直且键长相等。
已知食盐的摩尔质量为58.5×10－3kg/mol ，密度为2.2×103kg/m 3，阿伏加德罗常数为 6.0×1023mol －1，求食盐晶体中两个距离最近的钠离子中心之间的距离。
2、物质内的分子永不停息地作无规则运动固体分子在平衡位置附近做微小振动（振幅数量级为0.1A 0），少数可以脱离平衡位置运动。
液体分子的运动则可以用“长时间的定居（振动）和短时间的迁移”来概括，这是由于液体分子间距较固体大的结果。
气体分子基本“居无定所”，不停地迁移（常温下，速率数量级为102m/s ）。
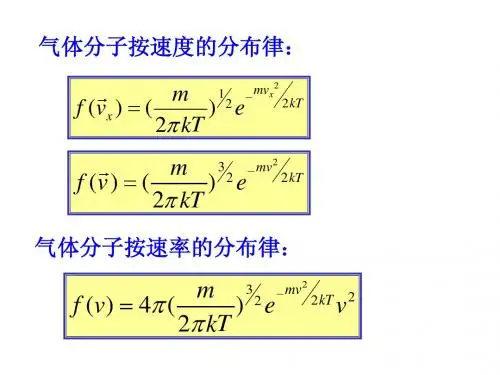
无论是振动还是迁移，都具备两个特点：a 、偶然无序（杂乱无章）和统计有序（分子数比率和速率对应一定的规律——如麦克斯韦速率分布函数，如图6-2所示）；b 、剧烈程度和温度相关。
气体分子的三种速率。
最可几速率v P ：f(v) =NN ∆（其中ΔN 表示v 到v +Δv 内分子数，N 表示分子总数）极大时的速率，v P =μRT 2=mk T 2 ；平均速率v ：所有分子速率的算术平均值，v =πμRT 8=mk T 8π；方均根速率2v ：与分子平均动能密切相关的一个速率，2v =μRT 3=mk T 3〔其中R 为普适气体恒量，R = 8.31J/(mol.K)。
k 为玻耳兹曼常量，k = AN R = 1.38×10－23J/K 〕【例题2】证明理想气体的压强P = 32n K ε，其中n 为分子数密度，K ε为气体分子平均动能。
3、分子间存在相互作用力（注意分子斥力和气体分子碰撞作用力的区别），而且引力和斥力同时存在，宏观上感受到的是其合效果。
物理热学(打印)资料.
合作深化
1气缸长为L=1m，固定在水平面上，气缸中有横截面积为 S=100cm2的光滑活塞，活塞封闭了一定质量的理想气体 ，当温度为t=27℃，大气压强为P0=1×105Pa时，气柱长 度为l=90cm，气缸和活塞的厚度均可忽略不计．求： ①如果温度保持不变，将活塞缓慢拉 至气缸右端口，此时水平拉力F的大 小是多少？ ②如果气缸内气体温度缓慢升高，使 活塞移至气缸右端口时，气体温度为 多少摄氏度？
出h＝6cm为止。求此时左、右两管中气体的压强。
已知大气压强p0＝76cmHg,温度不变。
左
l0
提示：这是两个研究对 象的问题，左、右两管
右
内的封闭气体都遵从玻 意耳定律，它们之间的 几何关系和压强关系是 解决问题的桥梁。
分析与解答：
左 76cmHg
右
l0 =10cm
左 x =? h1
右 h2 6cm
联立
，解得 p2’＝95cmHg x 6.5 cm
h1 ＝
如图，一固定的竖直气缸有一大一小两个同轴圆筒组成，
两圆筒中各有一个活塞，已知大活塞的质量为 m1 2.50kg ， 横截面积为 s1 80.0cm2，小活塞的质量为 m2 1.50kg ，横截 面积为 s2 40.0cm2；两活塞用刚性轻杆连接，间距保持为
)Pa
V2 V1
T3 360K p3 p2
V3 64 40 ΔV
气体从状态1到状态2为等容过程：
p1 p2 T1 T2代入数Fra bibliotek得 m=4kg
气体从状态2到状态3为等压过程：
代入数据得
ΔV 640cm3
V2 V3 T2 T3
练习2、如图所示，气缸内封闭有一定质量的理想气体，当时温
热学-（ＰＤＦ）
问题： 麦克斯韦速率分布律是关于无外力场时，气体分子 的速率分布（平衡态）。此时，分子在空间的分布 是均匀的，n p T 处处一致。 若有外力场存在，分子数密度如何分布呢？
一. 重力场中粒子数按高度的分布
在重力场中
分子热运动使分子在空间趋于均匀分布 重力作用使分子趋向地面降落
当二种作用共存达到平衡态时，分子在空间形成一种 非均匀的稳定分布：
从统计规律看：粒子总是优先占据低能量状态
ε ↘ ，dN ↗
18
出现的几率最大） ，最大多数分子所具有的速率。
从极值条件 d dv
f (v) = 0 求出：vp
f (v) = 4π (
μ
3
)2
− μv2
⋅ e 2kT
⋅v2
2π kT
vp =
2kT =
μ
2kN0T =
μ N0
2RT M mol
= 1.41 RT M mol
T
与
有关
Mmol （气体种类）
9
从 vp 的物理意义来分析分布曲线和 T、μ 的关系：
这是粒子关于位置的分布的规律. 常称为玻耳兹曼分布律。 它表明，在势场中的分子总是优先占据势能较低的状态。
17
三. 麦克斯韦–玻耳兹曼分布律
平衡态下温度为 T 的气体中，位置在 x~x+dx， y~y+dy， z~z+dz 中, 且速度在 vx ~ vx+dvx ， vy ~ vy+dvy ，vz ~ vz+dvz 区间的分子数为
2
v
而不是：ε = 1 μv 2
2
12
3. 讨论 1。说出下列各式的物理意义 f (v) 在速率v 处，单位速率区间内的分子数占总分子数的百分比
一. 重力场中粒子数按高度的分布
在重力场中
分子热运动使分子在空间趋于均匀分布 重力作用使分子趋向地面降落
当二种作用共存达到平衡态时，分子在空间形成一种 非均匀的稳定分布：
从统计规律看：粒子总是优先占据低能量状态
ε ↘ ，dN ↗
18
出现的几率最大） ，最大多数分子所具有的速率。
从极值条件 d dv
f (v) = 0 求出：vp
f (v) = 4π (
μ
3
)2
− μv2
⋅ e 2kT
⋅v2
2π kT
vp =
2kT =
μ
2kN0T =
μ N0
2RT M mol
= 1.41 RT M mol
T
与
有关
Mmol （气体种类）
9
从 vp 的物理意义来分析分布曲线和 T、μ 的关系：
这是粒子关于位置的分布的规律. 常称为玻耳兹曼分布律。 它表明，在势场中的分子总是优先占据势能较低的状态。
17
三. 麦克斯韦–玻耳兹曼分布律
平衡态下温度为 T 的气体中，位置在 x~x+dx， y~y+dy， z~z+dz 中, 且速度在 vx ~ vx+dvx ， vy ~ vy+dvy ，vz ~ vz+dvz 区间的分子数为
2
v
而不是：ε = 1 μv 2
2
12
3. 讨论 1。说出下列各式的物理意义 f (v) 在速率v 处，单位速率区间内的分子数占总分子数的百分比
热学第4章_热力学第一定律
§4.3 热力学第一定律
一、能量守恒与转换定律
能量守恒和转化定律的内容是：自然界一切物体都具 有能量，能量有各种不同形式，它能从一种形式转化
为另一种形式，从一个物体传递给另一个物体，在转 化和传递中能量的数值不变。
●这一定律也被表示为，第一类永动机(perpetual motion machine of the first kind)(不消耗任何形式的能量而能对外 作功的机械)是不能制作出来的。
Conservation of energy principle states that energy can be neither created nor destroyed; it can only change from one form to another but the total amount of energy remains constant.
力学相互作用：力学平衡条件被破坏时所产生的对系统状 态的影响。
在力学相互作用过程中系统和外界之间转移的能量就是功。
注意：
1）、只有在系统状态变化过程中才有能量转移。
2）、只有在广义力（如压强、电动势等）作用下 产生了广义位移（如体积变化、电量迁移等）后 才作了功。 3）、在非准静态过程中很难计算系统对外作的功。
判断 条件
•系统回到初态
•对外界也不产生任 何影响
f i
***只有无耗散的准静态过程才是可逆过程。
耗散过程：机械功、电磁功等自发转化为热量的过程。
注意：
不可逆过程并不是逆过程不能实现的过程，只是其实 现必然要引起外界的变化。
可逆过程必须同时满足四个条件：
（1）力学平衡条件； （2） 热学平衡条件； （3） 化学平衡条件; （4）满足无耗散条件。
《第四章传热》PPT课件
gradt dt dx
2. 傅立叶定律 傅立叶定律是热传导的基本定律，它表示热传导的速率与温度 梯度和垂直于热流方向的导热面积成正比。
Q S t 或：q t
n
n
热传导中，Q S，Q t n
Q——传热速率，W；
λ——导热系数，W/（m·K） 或W/（m·℃）；
S——导热面积，垂直于热流方向的截面积，m2；
946℃。试求：
(1)单位面积的热损失；(2)保温砖与建筑砖之间界面的温度；
(3)建筑砖外侧温度。
解 t3为保温砖与建筑砖的界面温度，t4为建筑砖的外侧温度。
（1）热损失q
q=
Q A
1
b1
t1
t2
1.06 0.15
(1000-946)
=381.6W/m2
(2) 保温砖与建筑砖的界面温度t3 由于是稳态热传导，所以 q1=q2=q3=q
典型换热设备： 间壁式换热器（冷、热流体间的换热设备） 例：列管式换热器 3、本章研究的主要问题 1）三种传热机理（传热速率计算） 2）换热器计算 3）换热设备简介
4.1.1传热的基本方式
根据传热机理不同，传热的基本方式有三种： 热传导、热对流和热辐射。
1．热传导 热传导（导热）：物体各部分之间不发生相对位移，依靠原子、 分子、自由电子等微观粒子的热流运动而引 起的热量传递。
t t'∞
t∞
u
tw-t=
t' t
tw
图4-13 流体流过平壁被加热时的温度边界
2、热边界层的厚度
tw t 0.99(tw t )
3、热边界层内（近壁处） 认为：集中全部的温差和热阻
dt 0 dy
热边界层外（流体主体）
2. 傅立叶定律 傅立叶定律是热传导的基本定律，它表示热传导的速率与温度 梯度和垂直于热流方向的导热面积成正比。
Q S t 或：q t
n
n
热传导中，Q S，Q t n
Q——传热速率，W；
λ——导热系数，W/（m·K） 或W/（m·℃）；
S——导热面积，垂直于热流方向的截面积，m2；
946℃。试求：
(1)单位面积的热损失；(2)保温砖与建筑砖之间界面的温度；
(3)建筑砖外侧温度。
解 t3为保温砖与建筑砖的界面温度，t4为建筑砖的外侧温度。
（1）热损失q
q=
Q A
1
b1
t1
t2
1.06 0.15
(1000-946)
=381.6W/m2
(2) 保温砖与建筑砖的界面温度t3 由于是稳态热传导，所以 q1=q2=q3=q
典型换热设备： 间壁式换热器（冷、热流体间的换热设备） 例：列管式换热器 3、本章研究的主要问题 1）三种传热机理（传热速率计算） 2）换热器计算 3）换热设备简介
4.1.1传热的基本方式
根据传热机理不同，传热的基本方式有三种： 热传导、热对流和热辐射。
1．热传导 热传导（导热）：物体各部分之间不发生相对位移，依靠原子、 分子、自由电子等微观粒子的热流运动而引 起的热量传递。
t t'∞
t∞
u
tw-t=
t' t
tw
图4-13 流体流过平壁被加热时的温度边界
2、热边界层的厚度
tw t 0.99(tw t )
3、热边界层内（近壁处） 认为：集中全部的温差和热阻
dt 0 dy
热边界层外（流体主体）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
8kTmv 2 l l一． 基础知识第四讲 热 学 部 分1. 分子运动论的基本内容2. 物态的微观解释3. 理想气体的压强设任意分子 a 的速度为 v ，在 x 、y 、z 三个方向的分量为 v x 、v y 、v z ，所以分子 a 在单位时间里与左右壁碰撞的冲量为：v mv 2I = f ⋅ ∆t = 2mv ⋅ x = x 2l 1 l 1mv 2 mv 2 m N F = I + I + = 1x + 2x+ = ∑v 2 1 2 1 1 1 ix i =1FmNmN v 2 + v 2 + v 2 + v 2 mNP = = ∑v 2 = ⋅ 1x 2 x 3x Nx = ⋅ v 2 = nmv 2l 2l 3 l 1l 2l 3 ix i =1 l 1l 2l 3 N l 1l 2l 3v 2 + v 2 + v 2 = v 2∴ v 2 = 1v 2 x y z x3∴ P = 2 n ⋅ 1 mv 2 = 2 neA3 2 3 k 4. 分子平均动能：PV = RT ⇒ e = 3P = 3RT= 3RT= 3RT= 3kT (k =R/N A ,为玻尔兹曼常数)k2n 2nV 2N 2N A 25. 阿伏伽德罗定律： P = nkT (n 为单位体积的分子数)① 分子的平均速率： v == ② 分子的方均根速率： =(μ为 mol 质量，可分子平均自由程推导)= 二． 物体的内能1.自由度：即确定一个物体的位置所需要的独立坐标参数，如自由运动的质点 需要三个独立坐标来描述其运动，故它有三个自由度。
2. 例：He 三个平动自由度 H 2 三个平动自由度，二个转动自由度CO 2 三个平动自由度，二个转动自由度，一个振动自由度。
3.理想气体的内能：E = N i kT = m 2 M ⋅ i RT (i =3 或 i =5) 2 4.物体的势能8RT 3kT m 3RT1 xl A x xV ∆TPVPVPV PV三． 外界对气体做功的计算1． 微元功：W = PS ∆x = P ∆V2．等压过程的功：W = P (V 2 - V 1 ) = R (T 2 - T 1 )3. 等温过程的功：W = ∑ P ∆V =RT ∑ ∆V= RT ln V 2V 14.一般情况下，外界对气体做功，就先画 P —V 图，再根据图象求功等温过程 绝热过程等压过程等容过程四． 热量的计算：(1) 热容、比热容、摩尔热容A. 热容 C 表示系统升高单位温度吸收的热量：C = lim ∆Q∆T →0B. 单位质量的物质的热容称为物质在该过程的比热容，即(m 为质量)c = Cm C. 1mol 物质的热容称为物质在该过程中的摩尔热容，即(为摩尔数)C = C mD. 系统热容与变化过程有关，同一系统从同一状态出发按不同过程变化，其热容不同。
但对固体、液体而言，一般认为定压热容与定容热容相等，统一用比热容表示。
而对气体，其定压摩尔热容 C p 与定容摩尔热容 C V 则不相等，可以证明：C p = C V + R(2) 热量的计算在定容过程中，摩尔气体温度变化(T 2-T 1)所需的热量为：Q = C V (T 2 - T 1 )在定压过程中，摩尔气体温度变化(T 2-T 1)所需的热量为：Q = C p (T 2 - T 1 )质量为 m 的固体、液体变化(T 2-T 1)所需的热量为：Q = mc (T 2 - T 1 )五． 热力学第一定律1. 定律内容： ∆E = W + Q2.热力学第一定律对理想气体特殊变化过程的分析 ① 等温过程： PV = C ② 等容过程：∆E = 0 Q = -W ，P = C∆V = 0W = 0 ∆E = Q = C (T - T )C= iR TV21V2③ 等压过程：V = C W = -P (V - V )= -R (T - T )Q = C (T - T )T∆E = ⋅ iR (T - T )2 2 121Cp2= ( i + 1)R 21p21④ 绝热过程： Q = 0,W = ∆E = ⋅ iR (T - T )2 2 1⑤ 循 环 过 程 (热 机 工 作过程)：六． 例题分析：例1． 使装着理想单原子气体的箱子骤然以速度 v 运动起来，求气体温度的变化。
已知一个气体原子的质量为 m 0，箱子的热容量和导热忽略不计。
∆E = 0, Q 吸 > Q 放， Q 吸 - Q 放 = W= W= 1 - Q 放 < 1， 被称作热机工作效率。
Q 吸 Q 吸例2．水平放置一个边长为l =10cm 的正方形扁盒子，在盒内不规则地放着N=1000 个很小的钢球，每个钢球的质量m=0.5mg，盒子以恒定的速度v0=10m/s 沿水平方向运动，经一段时间后，假定这些钢球的运动变得杂乱无章，与气体分子的运动相似。
(1)以地球为参照系，试计算这些球的平均能量为多少？(2)估算钢球作用到侧壁的力多大？设钢球与盒壁及钢球之间的碰撞是完全弹性的。
例3．一密闭容器内盛有水(未满)处于平衡状态，已知水在140C 时的饱和蒸汽压为12mmHg，设水蒸汽分子碰到水面时都变成水，气体分子的平均速率与气体的热力学温度T 的平方根成正比，试近似计算在1000C 和140C 时，单位时间内通过单位面积水面的蒸发变为水蒸汽的分子数之比n100/n14等于多少？x l lⅢⅡⅠl例4． 横截面积为 S 和αS(α>1)，长度相同的两圆柱形“对接”的容器内盛有理想气体，每个圆筒中间位置有一个用硬质相连的活塞，如图所示。
这时舱Ⅰ内气体的压强为 P 1，舱Ⅲ内气体的压强为βP 1，活塞处于平衡状态，整个系统吸收 热量 Q ，温度上升，使各舱温度相同。
试求舱Ⅰ内气体压强的变化。
1mol 气体内能为 CT(C 是气体摩尔热容量)圆筒和活塞热容量很小，摩擦不计。
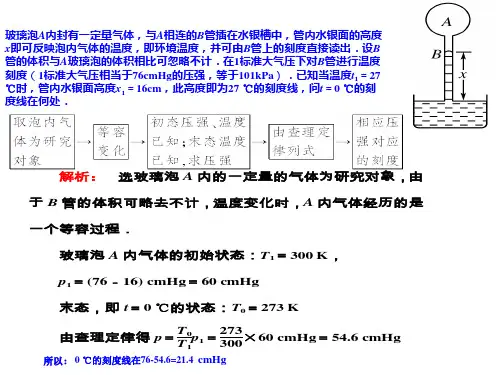
例5． （17 届复）如图所示，在一个大水银槽中竖直插有一根玻璃管，管的上端封闭，下端开口，已知槽中水银液面以上的哪部分玻璃管的长度为 l =76cm ，管内封闭有μ=1.0×10－3mol 的空气。
保持水银槽与玻璃管都 不动，而设法使玻璃管内空气的温度缓慢地降低 100C ， 问在此过程中空气放出的热量为多少？已知管外大气压为 76cmHg 水银柱，每摩尔空气的内能 U=C V T ，其中 T 为绝对温度，常量 C V =20.5J/mol ·K ，普适气体恒量 R=8.31J/mol ·K 。
2ln 、Tn 、T例6． 绝热容器 A 经一阀门与另一容积比 A 的容积大很多的绝热容器 B 相连，开始时阀门关闭，两容器中盛有同一种理想气体，温度均为 300C ，B 中气体压强为 A 中的两倍，现将阀门缓慢打开，直至压强相等时关闭，问此时容器 A 气 体的温度为多少？假设从打开到关闭阀门过程中处在 A 中的气体与 B 中的气体之间无热交换，已知每摩尔该气体的内能为 U = 5RT ，式中 R 为普适气体2恒量，T 为热力学温度。
例7． 长度为 2l 的水平圆柱形容器，被不导热的薄活塞分成相等的两部分，每个部分内盛有温度为 T 的μmol 单原子理想气体。
用两根劲度系数均为 K 未形变弹簧将活塞与容器两头相连，如图所示。
右边部分气体吸收了热量 Q ，结果使活 塞向左移动距离 x=l/2。
试求在温度 T 下传给恒温器的热量为 Q ＇，左边部分气体与恒温器始终保持热接触。
QA B例8． 如图所示的循环中，V 2=2V 1，1→2 为等压，气体与外界交换热量 104J ，做功 7×103J ；2→3 为等容过程，气体与外界交换热量 4×103J ；3→4 过程为等压过程，4→1 为等过程。
试求： (1) 在图上标明各过程吸、放热的热量 (2) 该循环的热效率是多少？p p 12例9． 0.1mol 的理想气体，历经如图所示的过程由初状态 A 沿直线段 AB 膨胀到 B 状态。
求这一过程中：(1) 气体达到最高温度在何处？(2) 气体从外界吸收的(不包括放出的)热量是多少？已知 C V =1.5R ，R=8.31J/mol ·K 。
1.51.00.5-3m 3)A B C第 19 届预赛四、（20 分）如图预 19-4 所示，三个绝热的、容积相同的球状容器 A 、B 、C ，用带有阀门 K 1、K 2 的绝热细管连通，相邻两球球心的高度差 h = 1.00 m ．初始时，阀门是关闭的，A 中装有 1mol 的氦 （He ）,B 中装有 1mol 的氪（Kr ）,C 中装有lmol 的氙（Xe ），三者的温度和压强都相同．气体均可视为理想气体．现打开阀门 K 1、K 2， 三种气体相互混合，最终每一种气体在整个容器中均匀分布，三个容器中气体的温度相同．求气体温度的改变量．已知三种气体的摩尔质量分别为He = 4.003⨯10-3kg ⋅ mol -1Kr = 83.8⨯10-3kg ⋅ mol -1Xe =131.3⨯10-3kg ⋅ mol -1 在体积不变时，这三种气体任何一种每摩尔温度升高 1K ，所吸收的热量均为 3R / 2 ， R 为普适气体常量．第 20 届复赛二、（15 分）U 形管的两支管 A 、B 和水平管 C 都是由内径均匀的细玻璃管做成的，它们的内径与管长相比都可忽略不计．己知三部分的截面积分别为S = 1.0 ⨯10-2 cm 2，S = 3.0 ⨯10-2 cm 2， S = 2.0 ⨯10-2 cm 2，在 C 管中有一段空气柱，两侧被水银封闭．当温度为t 1 = 27 ℃时，空气柱长为l ＝30 cm （如图所示），C 中气柱两侧的水银柱长分别为 a ＝2.0cm ， b ＝3.0cm ，A 、B 两支管都很长，其中的水银柱高均为h ＝12 cm ．大气压 强保持为 p 0 ＝76 cmHg 不变．不考虑温度变化时管和水银的热膨胀．试求气柱中空气 温度缓慢升高到 t ＝97℃时空气的体积．zhangli P (105N/m 2) 4 B3C2D V (10-3m 3)A成都七中嘉祥外国语学校物理竞赛 ng例10．(1)已知每摩尔单原子理想气体温度升高 1K 时，内能增加 1.5R ，现有 2.00mol8.31的单原子理想气体，经历 ABCDA 循环过程，在 P —V 图上是一个圆。
① 循环过程中哪一点的温度最高，温度是多少？② 从 C 到 D ，气体内能的增加量、外界对气体所做的功、气体吸收的热量各为多少？(2) 可否设计一个过程，使 nmol 单原子理想气体从图(2)的初态 A (P A 、V A 、TA )到 终态 B (P B = P A 、V B = 2V A 、T B )气体净吸热刚好等于内能的增量。