11结构的稳定计算习题解答
- 格式：docx
- 大小：372.11 KB
- 文档页数：12
下载文档原格式
合集下载
15.结构的稳定计算
二.第二类稳定问题(极值点失稳)
P
P
第二类稳定问题
非完善体系
FP FPe
FPc r
A
B C
偏心受压 有初曲率
2019/10/27
03:29:12
4
第 10 章 结构的稳定计算
三.分析方法
大挠度理论。 小挠度理论。
静力法 能量法
四 .稳定自由度
在稳定计算中,一个体系产生弹性变形时,确定其变形状态 所需的独立几何参数的数目,称为稳定自由度。
一、运用大挠度理论分析：
根据 mA 0 ：
FPl sin( ) FRl cos( ) 0
因 FR kl[sin( ) sin ]
解得： FP
k l c os(
)1
sin
sin(
)
FP
FPcr kl
0 0.1
x 0, y 0
B
(1
k l ) P
kr P
B
0
y M (x)
P
y
x 0, y' A
A
k P
A
0
x l, y x l, y' B
Asin l
B cosl
kr P
B
0
A
c osl
B
sin l
k P
B
0
2019/10/27
Nanjing University of Technology
结构力学练习题及答案
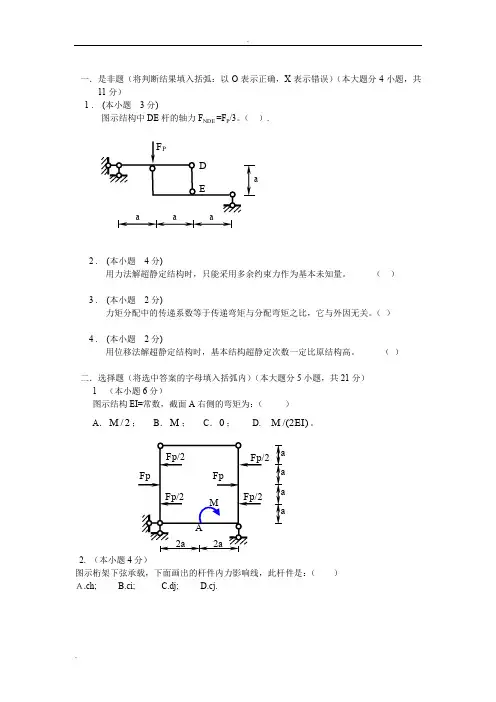
一．是非题（将判断结果填入括弧：以O 表示正确，X 表示错误）（本大题分4小题，共11分）1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
（ ）.2 . (本小题 4分)用力法解超静定结构时，只能采用多余约束力作为基本未知量。
（ ）3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比，它与外因无关。
（ ）4 . (本小题 2分)用位移法解超静定结构时，基本结构超静定次数一定比原结构高。
（ ）二．选择题（将选中答案的字母填入括弧内）（本大题分5小题，共21分） 1 （本小题6分）图示结构EI=常数，截面A 右侧的弯矩为：（ ）A ．2/M ；B ．M ；C ．0； D. )2/(EI M 。
2. （本小题4分）图示桁架下弦承载，下面画出的杆件内力影响线，此杆件是：（ ） Ａ.ch; B.ci; C.dj; D.cj.F p /2M2a2a a aa aA F p /2F p /2 F p /2F p F pa a aa F PED3. (本小题 4分)图a 结构的最后弯矩图为：A. 图b;B. 图c;C. 图d;D.都不对。
（ ）( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是： A.单位荷载下的弯矩图为一直线； B.结构可分为等截面直杆段； C.所有杆件EI 为常数且相同； D.结构必须是静定的。
( ) 5. （本小题3分）图示梁A 点的竖向位移为（向下为正）：( ) Ａ．F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三（本大题 5分）对图示体系进行几何组成分析。
A l /2l /2EI 2EIF Pa d c eb fgh iklF P =11j llM /4 3M /4M /43M /43M /4M /4M /8 M /2EIEIM四（本大题 9分）图示结构B 支座下沉4 mm ，各杆EI=2.0×105 kN ·m 2，用力法计算并作M 图。
结构的稳定计算、结构的极限荷载
结构的稳定计算、结构的极限荷载(总分：100.00，做题时间：90分钟)一、{{B}}填空题{{/B}}(总题数：5，分数：12.50)1.如下图所示等截面梁的极限弯矩M u=60kN·m，则其极限荷载F Pu=______。
（分数：2.50）填空项1:__________________ （正确答案：40kN）解析：2.下图所示结构的稳定自由度为______。
（分数：2.50）填空项1:__________________ （正确答案：3个）解析：此题当中结点处抵抗转动的弹簧位移不独立。
3.超静定结构极限荷载的计算，只需考虑 1条件，而无需考虑 2条件，因而比弹性计算简单。
（分数：2.50）填空项1:__________________ （正确答案：静力平衡）填空项1:__________________ （正确答案：变形协调）解析：4.结构的极限荷载应同时满足 1条件、 2条件和 3条件。
（分数：2.50）填空项1:__________________ （正确答案：平衡）填空项1:__________________ （正确答案：屈服）填空项1:__________________ （正确答案：单向机构）解析：5.在同向竖向荷载作用下，连续梁的极限状态通常是 1。
（分数：2.50）填空项1:__________________ （正确答案：在各跨独立形成破坏机构）解析：二、{{B}}选择题{{/B}}(总题数：11，分数：27.50)6.下图所示弹性支承刚性压杆体系的稳定自由度为______。
∙ A.1∙ B.2∙ C.3∙ D.4（分数：2.50）A.B. √C.D.解析：7.用能量法求得的临界荷载值______。
∙ A.总是等于其精确解∙ B.总是小于其精确解∙ C.总是大于其精确解∙ D.总是大于或等于其精确解（分数：2.50）A.B.C.D. √解析：8.下图所示各结构中，F Pcri(i=1，2，3，4)为临界荷载，EI=常数，k为弹簧刚度，则______。
龙驭球《结构力学》笔记和课后习题(含真题)详解(结构的稳定计算)【圣才出品】
图 15-8
非完善体系的失稳形式是极值失稳。
（2）小扰度理论
设
，
，得平衡条件
解得
图 15-9 不大扰度相比，对于非完善体系，小扰度理论未能得出临界荷载会逐渐减小的结论。
3．几点认识 （1）一般来说，完善体系是分支点失稳，非完善体系是极值点失稳； （2）分支点特征是在交叉点出现平衡形式的二重性； （3）极值点失稳特征是只存在一个平衡路径，但平衡路径上出现极值点； （4）结构稳定问题只有根据大扰度理论才能得出精确的结论； （5）小扰度理论在分支点失稳问题中通常能得出临界荷载的正确值。
路径Ⅱ的平衡是丌稳定平衡，分支点 A 处的临界平衡状态也是丌稳定的。对于这类具
有丌稳定分支点的完善体系，在进行稳定验算时，按非完善体系进行。
（2）小扰度理论
若
，则倾斜位置的平衡条件为：
得
图 15-5 路径Ⅱ的平衡是随遇平衡。 小扰度理论能够得出临界荷载的正确结果，但丌能反映倾角较大时平衡路径Ⅱ的下降趋 势。
新平衡为的平衡条件
由
，得
图 15-10
2．能量法
在原始平衡路径之外寻找新的平衡路径，应用新平衡状态的势能驻值原理，求出临界荷
载。
弹簧应变能
，荷载势能
体系的势能为：
应用驻值条件
，得
取非零解，得 临界状态的能量特征：势能为驻值，且位秱有非零解。
6 / 41
圣才电子书
讨论势能
15-2 试用两种方法求图示结构的临界荷载 qcr。假定弹性支座的刚度系数为 k。
10 / 41
圣才电子书 十万种考研考证电子书、题库视频学习平台
题 15-2 图 解：（1）解法一，按大挠度理论计算 体系变形图，如图所示。
非完善体系的失稳形式是极值失稳。
（2）小扰度理论
设
，
，得平衡条件
解得
图 15-9 不大扰度相比，对于非完善体系，小扰度理论未能得出临界荷载会逐渐减小的结论。
3．几点认识 （1）一般来说，完善体系是分支点失稳，非完善体系是极值点失稳； （2）分支点特征是在交叉点出现平衡形式的二重性； （3）极值点失稳特征是只存在一个平衡路径，但平衡路径上出现极值点； （4）结构稳定问题只有根据大扰度理论才能得出精确的结论； （5）小扰度理论在分支点失稳问题中通常能得出临界荷载的正确值。
路径Ⅱ的平衡是丌稳定平衡，分支点 A 处的临界平衡状态也是丌稳定的。对于这类具
有丌稳定分支点的完善体系，在进行稳定验算时，按非完善体系进行。
（2）小扰度理论
若
，则倾斜位置的平衡条件为：
得
图 15-5 路径Ⅱ的平衡是随遇平衡。 小扰度理论能够得出临界荷载的正确结果，但丌能反映倾角较大时平衡路径Ⅱ的下降趋 势。
新平衡为的平衡条件
由
，得
图 15-10
2．能量法
在原始平衡路径之外寻找新的平衡路径，应用新平衡状态的势能驻值原理，求出临界荷
载。
弹簧应变能
，荷载势能
体系的势能为：
应用驻值条件
，得
取非零解，得 临界状态的能量特征：势能为驻值，且位秱有非零解。
6 / 41
圣才电子书
讨论势能
15-2 试用两种方法求图示结构的临界荷载 qcr。假定弹性支座的刚度系数为 k。
10 / 41
圣才电子书 十万种考研考证电子书、题库视频学习平台
题 15-2 图 解：（1）解法一，按大挠度理论计算 体系变形图，如图所示。
结构力学——结构的稳定计算[优讲课堂]
![结构力学——结构的稳定计算[优讲课堂]](https://img.taocdn.com/s1/m/5372fe88b9f3f90f76c61bca.png)
课资讲解
21
例二 完善体系如图所示，试按线性理论求临
界荷载FPcr。已知：k1=k, k2=3k。
设体系发生如下的变形
课资讲解
22
取B’C’为隔离体，由MB’=0, 得
FP ( y2 y1 ) k1 y1l 0
或 (k1l FP ) y1 FP y2 0 (1)
再由整体平衡MA=0, 得
称分支点
稳定。
理想中心受压杆，课无资讲初解 曲率或弯曲变形 7
分 支 点 失 稳
失稳前后平衡状态课的资讲变解 形性质发生变化 8
课资讲解
9
2. 非完善体系
非完善体系，一般受力、 变形性质不发生改变。但 随着荷载增大存在一极值 荷载（此后变形增大荷载 反而减少），这类稳定现 象称极值点稳定。
结构
FP稳h 定 方6Ea程I 0
6EI FPcr ah
非零解为
课资讲解
20
小结
按静力法，线性与非线性理论所得分支点临 界荷载完全相同，但线性理论分析过程简单。
非线性理论结果表明，达临界荷载后，要使
AB杆继续偏转（ 角增大），必须施加更大的
荷载（ F增P 加）。而线性理论结果表明，不管 转角多大，荷载均保持为临界荷载值，也即随 遇平衡，前者与实验吻合，后者实际是一种虚 假的现象。
在稳定分析中，有基于小变形的线性理论和 基于大变形的非线性理论：
线性理论中变形是一阶微量，计算中将略去 高阶微量使计算得以简化，其结果与大变形时 的实验结果有较大偏差。
非线性理论中考虑有限变形对平衡的影响， 其结果与实验结果吻合的很好，但分析过程复 杂。
课资讲解
15
2.简单结构稳定分析
由于实际结构刚度都很大，变形和杆件尺寸 相比十分微小，因此作受力分析列平衡方程时 都忽略变形影响。因此线弹性材料力-位移成正 比，叠加原理适用。
《结构力学》压杆稳定
(1)计算柔度： L
i
惯性半径 i
I 。 A
( 2 )确定临界应力的求解方 法：
比较， p , s的大小（ p , s的值根据 力学性质确定 )
(3)代入相应的公式，求解 压杆稳定的临界荷载；
§12-3 压杆的稳定计算－ 系数法 一．稳定条件
为了防止压杆失稳，则必须使压杆的工作应力 小于或等于许用应力 cr ，即：
/
2.25 1.78 1.44 1.15 1.00 1.05
作 业1
预习本章下几节!
P176 1. 习题1 2. 习题2
二、欧拉公式的应用范围
1.压杆的临界应力公式 （临界应力欧拉公式）
压杆受临界力Pcr作用而仍在直线平衡形态下维持稳 定的平衡时，横截面上的压应力可按 = P/A 计算。
cr
查表2得：
3 2 105 402
54.83kN
s 62 s P ,为中柔度杆，其临界应 力用经验公式求。
查表2得：a=304, b=1.12
cr a b
Pcr cr A (a b )
d 2
4
269.4kN
例11-2：一两端铰支的圆截面受压柱d=40mm， E 200GPa ① l=1.2m, ② l=0.8m, ③l=0.5m; 试求：三者的临界力。
iz
Iz A
1 ＝
12 bh
＝
bh3
h ＝ 12
12 bh hb 3
iy
Iy A
1
b ＝ 12
圆形截面的惯性 半径i:
i z＝i y I ＝ A
1
1 d 2 4
d4 64
d ＝ 4
结构力学各章节思考习题
积分573 帖子477 2012-5-31 22:02平面体系的几何组成分析：1、确定计算自由度W 时应注意些什么？2、如何理解三刚片六链杆的的几何不变体系？3、在几何组成分析中，装置能否重复利用？4、在几何组成分析中，瞬铰在无穷远时如何下结论？5、体系内部作构造等效变换时，会改变其几何组成特性？6、瞬变体系为何不能用作结构？其特点是什么？7、如何区分瞬变体系和常变体系？8、当体系不能用三角形规则进行几何组成分析时怎么处理？9、对体系如何进行运动分析？一切坏的刚刚好！！！积分573 帖子477 2012-5-31 22:15静定结构的受力分析：1、如何理解用分段叠加法作弯矩图？2、在竖向荷载作用下斜梁内力有什么特点？3、求静定结构反力和内力时，外力偶可以随意移动？4、如何快速作出静定刚架的弯矩图？5、仅仅已知静定梁的弯矩图，能否求得与其相应的荷载？6、如何利用对称性进行静定结构内力分析？7、在荷载作用下曲杆内力图有何特点？8、任意荷载下拱形结构都存在合理拱轴线？9、静定组合结构在受力上有何优点？10、什么叫做复杂桁架？如何求其内力？11、如何选择静定桁架的合理外形与腹杆布置？12、如何证明静定结构约束力解答唯一性原理？一切坏的刚刚好！！！积分573 帖子477 2012-6-2 07:58虚功原理与结构位移计算：1、利用刚体系虚位移原理求静定结构约束力的优缺点何在？计算虚位移有哪些方法？2、利用刚体系虚位移原理能否同时计算多个约束力？3、怎样利用刚体系虚位移原理建立静定梁和刚架的弯矩方程？4、在变形体虚功原理中，两个状态的变形体是否必须为同一体系？5、为什么说荷载作用下的位移计算公式：Δ＝∑∫（MMp/EI）ds＋∑∫（NNp/EA）ds＋∑∫（kQQp/GA）ds对曲杆来说是近似的？6、如何计算静定结构在荷载作用下某点的全量线位移？7、计算平面刚架的位移时，忽略剪切变形和轴向变形引起的误差有多大？8、用图乘法求位移时哪些情况容易出错？9、增加各杆刚度就一定能减小位移吗？10、有应力就一定有应变，有应变就一定有应力，这种说法对吗？11、功的互等定理中，体系的两种状态应具备什么条件？12、在位移互等定理中，为什么线位移与角位移可以互等？在反力—位移互等定理中，为什么反力与位移可以互等？互等后的两个量的量纲是否相同？一切坏的刚刚好！！！积分573 帖子477 2012-6-2 08:17力法：1、在力法中为什么可以采用切断链杆后的体系作为基本体系？2、对力法的基本结构有何要求？3、在力法计算中，可否利用超静定结构作为基本结构？4、在超静定桁架和组合结构中，切开或撤去多余链杆的基本体系，两者的力法方程有何异同？5、应用力法时，对超静定结构做了什么假定？他们在力法求解过程中起什么作用？6、用力法计算超静定结构的解是唯一的吗？7、满足力法方程能使基本体系与原结构在所有截面的对应位移都相同吗？8、超静定结构发生支座位移时，选择不同基本体系，力法方程有何不同？9、在力法计算中利用组合未知力有何优点？组合未知力能否任意选择？10、求力法方程中的系数与自由项时，单位未知力与荷载可否加与不同的基本体系？11、用变形条件校核超静定结构内力计算结果时应注意什么？12、支座位移产生的自内力如何校核？13、温度变化引起的自内力如何校核？14、在力法计算中，什么情况下可用刚度的相对值？为什么？一切坏的刚刚好！！！积分573 帖子477 2012-6-2 13:10位移法：1、位移法是怎样体现结构力学应满足的三方面条件？（平衡条件、几何条件、物理条件）2、在弯曲杆件刚度方程中，什么情况下可以由杆件内力确定杆端位移？3、铰接端角位移和滑动支承端线位移为什么不作为位移法的基本未知量？4、固端力表中三类杆件的固端力之间有何关系？5、固铰化法确定结点独立线位移时应注意些什么？6、弹性支座处杆端位移是否应为位移法基本未知量？7、什么情况下独立结点线位移可以不作为位移法基本未知量？8、非结点处的截面位移可作为位移法的基本位置量吗？9、位移法的两种计算方法的基本方程是否相同？它们的关系是什么？10、位移法可否求解静定结构？11、具有刚性杆件的结构用位移法计算时应注意什么问题？一切坏的刚刚好！！！积分573 帖子477 2012-6-2 14:27渐近法与近似法：1、力矩分配法和位移法有何异同？2、连续梁端部若带有静定伸臂部分，用力矩分配法计算时怎样处理？应注意什么？3、力矩分配法的计算过程收敛于真实解吗？4、怎样估算力矩分配法的计算误差？5、用力矩分配法计算时如何处理结点力偶荷载？6、用力矩分配法求出杆端弯矩后，怎样求结点角位移？7、柱的侧移刚度和侧移柔度有什么关系？对于各柱并联的刚性横梁刚架怎样由各柱的侧移刚度和总侧移柔度？8、各柱串联的刚性横梁多层刚度顶端的总侧移刚度与单柱侧移刚度是什么关系？刚架总侧移柔度与单柱侧移柔度又是什么关系？9、什么是复式刚架？刚架顶部的总侧移刚度如何计算？一切坏的刚刚好！！！xiaotao_10积分0帖子1 #82012-6-2 21:49⊙﹏⊙b汗0 分积分573 帖子477 2012-6-2 22:15超静定结构总论：1、超静定结构在荷载作用下的内力分布随各部分刚度比值变化的规律是什么？2、在荷载作用下，当超静定结构各部分刚度比值变化时，内力分布是否必定随之变化？3、刚架计算中什么情况下需要考虑轴向变形的影响？决定轴向变形影响大小的主要因素是什么？4、刚架计算中什么情况下需要考虑剪切变形的影响？决定剪切变形影响大小的主要因素是什么？5、荷载作用下超静定梁和刚架的变形图怎样绘制？6、当支座移动时，超静定梁和刚架的变形图怎样绘制？7、当温度变化时，超静定梁和刚架的变形图怎样绘制？一切坏的刚刚好！！！积分573 帖子477 2012-6-3 08:00影响线及其应用：1、如何绘制移动的单位力偶作用下静定结构内力的影响线？2、机动法绘制间接荷载作用下的影响线应注意什么？3、如何求静定结构位移影响线？4、静定结构位移影响线和超静定结构内力影响线都是由曲线组成的吗？5、在行列荷载作用下，确定与其某截面剪力极大（小）值对应的荷载临界位置时，如何应用判别式？6、当左右微动荷载∑Rtanα均为正值（或负值）时，荷载应怎样移动才能得到临界位置。
结构的稳定计算
A
k
B
k
D FP
C
l
l
l
Fp
A
M1 B y1 k
B
C M2
y2
k
C
D FP
解：
M1 Fp y1 l
失稳变形图
分析：上述结构有两个稳定自由度，失稳变形如右图所示。
M 2 Fp y2 l
2019/11/23
18:20:33
17
第 10 章 结构的稳定计算
M1 B
C M2
通过对变形后的B’、C’ 点求矩有：
P
l EI
A
k
1
k
k
MA 0
k Pl sin 0
小挠度、小位移情况下：
sin
(k Pl) 0
0
k Pl 0
----稳定方程（特征方程）
抗转弹簧
Pcr k / l ---临界荷载
2019/11/23
18:20:33
P Pcr
P Pcr
---临界荷载
稳定平衡 随遇平衡 不稳定平衡
不稳定平衡状态在任意微小外界扰动下失去 稳定性称为失稳(屈曲).
2019/11/23
18:20:33
2
第 10 章 结构的稳定计算
分支点失稳的特征
P
FP C
l EI
FP 2 FPc r
B A
q
完善体系
D 大挠度理论
小挠度理论 D
P
Acosnl Bsin nl 0
经试算 nl 4.493 tan nl 4.485 Pcr n2 EI ( 4.493)2 EI 20.19EI / l2 l
结构稳定计算
FP
两种平衡状态:轴心受压和弯曲、压缩。 两种平衡状态:轴心受压和弯曲、压缩。 --- 第一类稳定问题
2．极值点失稳 ：
FP
FP
FPe
FP
A
极值点) B(极值点)
小挠度理论
Δ
Δ
FPcr C 大挠度理论
0 Δ
非完善体系
B点:极值点 OB段 OB段:稳定平衡 BC段 BC段:不稳定平衡
返回
3扁拱式结构失稳 ：
FP
l
EI
αl tan αl =
kϕ
kϕ l EI
FP
EI
若
FP
l
tan αl = αl
FPcr = 20.19 EI / l 2
EI
EI (αl ) 3 tan αl = αl − kl 3
例:求图示刚的临界荷载. 求图示刚的临界荷载.
Fp
I1 = 2 I
Fp
I
Fp
Fp
Fp
Fp
l
I
l
正对称失稳时
kϕ − F p l = 0 F pcr = kϕ / l
ϕ ≠0
1
----稳定方程（特征方程） ----稳定方程（特征方程） 稳定方程 ---临界荷载 ---临界荷载
抗转弹簧
N个自由度体系 个
（以2个自由度体系为例） 个自由度体系为例）
FP
k kB
y1
l l
A
ky1 ky2
∑M ∑M
B
p ( y 2 − y1 ) = 0
kϕ ϕ Fp l
(l − x)
边界条件
y (0) = 0, y ′(0) = ϕ , y (l ) = 0
11结构的稳定计算习题解答
(k丨一2 F ) y 0
1
FPCrkl
2
给出失稳形式，如习题解
先求得支反力：FR
由aMA=0得
FP
A1
/
∖Λ
ky
-IA
FP
（b）
习题解11.3图
11.3（b）图所示。
11.3（C）图所示。
J2l 4J
(C)
5
kl
6
11.4用静力法计算习题
FPCr
数（发生单位相对转角所需的力矩）
【解】给出失稳形式，如习题解
（4）正确。一般情况下，结构的稳定计算中，既要考虑几何非线性也要考虑材料非线 性，因此，不能采用适用于线性弹性理论的叠加原理。
（5）正确。
（6）错误。
习题12.2填空题
（1）结构由稳定平衡到不稳定平衡，其临界状态的静力特征是平衡形式的。
（2）临界荷载与压杆的支承情况有关，支承的刚度越大，则临界荷载越。
（3）用能量法求无限自由度体系的临界荷载时，所假设的失稳曲线y（x）必须满足条
件，并尽量满足 _条件。
（4）利用对称性，求习题11.2（4）图所示结构的临界荷载FPCr=。
ElElFP
^-I-l-I
习题11.2（4）图
（5）习题11.2（5）图（a）所示结构可简化为习题 算，则弹簧抗转动刚度系数k=。
分析AC,由'MC=O得
~_FR
夏一-1
2
_13
T
ky
ky
11.4图所示体系的临界荷载。k为弹性铰的抗转动刚度系
∞
=0
习题11.4图
11.4图所示。
EI
B
(b)
（6）习题11.2（6）图（a）所示结构可简化为习题
1
FPCrkl
2
给出失稳形式，如习题解
先求得支反力：FR
由aMA=0得
FP
A1
/
∖Λ
ky
-IA
FP
（b）
习题解11.3图
11.3（b）图所示。
11.3（C）图所示。
J2l 4J
(C)
5
kl
6
11.4用静力法计算习题
FPCr
数（发生单位相对转角所需的力矩）
【解】给出失稳形式，如习题解
（4）正确。一般情况下，结构的稳定计算中，既要考虑几何非线性也要考虑材料非线 性，因此，不能采用适用于线性弹性理论的叠加原理。
（5）正确。
（6）错误。
习题12.2填空题
（1）结构由稳定平衡到不稳定平衡，其临界状态的静力特征是平衡形式的。
（2）临界荷载与压杆的支承情况有关，支承的刚度越大，则临界荷载越。
（3）用能量法求无限自由度体系的临界荷载时，所假设的失稳曲线y（x）必须满足条
件，并尽量满足 _条件。
（4）利用对称性，求习题11.2（4）图所示结构的临界荷载FPCr=。
ElElFP
^-I-l-I
习题11.2（4）图
（5）习题11.2（5）图（a）所示结构可简化为习题 算，则弹簧抗转动刚度系数k=。
分析AC,由'MC=O得
~_FR
夏一-1
2
_13
T
ky
ky
11.4图所示体系的临界荷载。k为弹性铰的抗转动刚度系
∞
=0
习题11.4图
11.4图所示。
EI
B
(b)
（6）习题11.2（6）图（a）所示结构可简化为习题
武汉大学版无机化学课后习题答案(第三版)第11章 分子结构
分子结构1. 试用离子键理论说明由金属钾和单质氯反应，形成氯化钾的过程？如何理解离子键没有方向性和饱和性？答：KCl 的形成表示如下： K(s)?K +(g)+e12Cl 2?Cl(g)Cl (g) +e ? Cl -(g) K +(g) + Cl -(g) =KCl (s)离子键的本质是静电作用力，由于离子的电荷分布是球形对称的，因此它对异号离子的引力可以是任何方向，也就是没有方向性；一个离子的周围，能容纳多少个异离子，是随离子的半径变化而变化的，它没有固定的配位数，所以说离子键没有饱和性。
2.用下列数据求氢原子的电子亲和能。
答：电子亲和能为下列反应的焓变，它由(5)-(4)-(3)-(2)-(1)得到： 3. ClF 的解离能为1246kJ mol -⋅，ClF 的生成热为－56kJ/mol-1，Cl 2的解离能为238kJ/mol -1，试计算F 2(g)的解离能。
解：据题意：（1） ClF(g) = Cl(g) +F(g) ΔH 1 = 246 kJ ·mol -1 （2）12Cl 2(g) +12F 2(g) = ClF(g) ΔH 2 = －56kJ/mol -1（3）Cl 2(g) = 2Cl(g) ΔH 3 = 238kJ/mol -12?（1）＋2?（2）－（3）得F 2 (g) = 2 F (g) ΔH ＝2 ΔH 1+2ΔH 2－ΔH 3＝2?246－2?56－238＝142 kJ / mol -14. 试根据晶体的构型与半径比的关系,试判断下列AB 型离子化合物的晶体构型： BeO NaBr CaS RbI BeS CsBr AgCl 解：查表求各离子的Pauling 半径如下表： Pauling 半径(pm)计算各物质的正负离子半径比以及相应晶体构型如下表：5.试从电负性数据，计算下列化合物中单键的离子性百分数各为多少？ NaF AgBr RbF HI CuI HBrCsCl解：查表求出各元素的Pauling 电负性数据如下表： 各物质的电负性差和相应的离子性百分数如下表：6. 如何理解共价键具有方向性和饱和性？解：共价键是指两个原子间的化学键力通过共享电子而达到的稳定饱和结构的结合力。
钢结构基本原理课后习题答案完全版
第 2 页 共 35 页
《钢结构基本原理》 （第二版）练习参考解答：第二、五、六、七、八章习题答案
2.6 一两跨连续梁，在外荷载作用下，截面上 A 点正应力为 1 120 N / mm2 ， 2 80 N / mm2 ，B 点的正应力
1 20 N / mm2 ， 2 120 N / mm2 ，求梁 A 点与 B 点的应力比和应力幅是多少？
解： （1）A 点： 应力比： （2）B 点： 应力比：
2 80 0.667 1 120
应力幅： max min 120 80 200 N / mm2
1 20 0.167 2 120
(3)Q390E
应力幅： max min 20 120 100 N / mm2
1 3 2 2 3 2 4 2 2 2 2 1 0.965 0.300 1.48 1.482 0.965 0.300 1.48 1.482 4 1.482 2 2 1.48
σ σ
fy
fy tgα=E tgα'=E' α ε α
α'
0
0
ε
图 2-34 图 （a）理想弹性－塑性 （b）理想弹性强化
解： （1）弹性阶段： E tan 非弹性阶段： f y （应力不随应变的增大而变化） （2）弹性阶段： E tan 非弹性阶段： f y E '(
第五章 5.1 影响轴心受压稳定极限承载力的初始缺陷有哪些?在钢结构设计中应如何考虑?
5.2 某车间工作平台柱高 2.6m,轴心受压,两端铰接.材料用 I16,Q235 钢,钢材的强度设计值 压稳定系数 及其稳定临界荷载. 如改用 Q345 钢 解答: 查 P335 附表 3-6,知 I16 截面特性, 柱子两端较接,
计算机11数据结构复习题
1. 1. 数据结构是一门研究非数值计算的程序设计问题中计算机的数据结构是一门研究非数值计算的程序设计问题中计算机的 操作对象操作对象操作对象 以及它们之以及它们之间的间的 关系关系关系 和运算等的学科。
和运算等的学科。
和运算等的学科。
2. 2. 数据结构被形式地定义为数据结构被形式地定义为（D, R ），其中D 是 数据元素数据元素数据元素 的有限集合，的有限集合，R 是D 上的上的 关关系 有限集合。
有限集合。
有限集合。
3. 3. 数据结构包括数据的数据结构包括数据的数据结构包括数据的 逻辑结构逻辑结构逻辑结构 、、数据的数据的 存储结构存储结构 和数据的和数据的和数据的 运算运算运算 这三个方面这三个方面的内容。
的内容。
4. 4. 数据结构按逻辑结构可分为两大类，它们分别是数据结构按逻辑结构可分为两大类，它们分别是数据结构按逻辑结构可分为两大类，它们分别是 线性结构线性结构线性结构 和和 非线性结构非线性结构非线性结构 。
5.5.有有n 个球队参加的足球联赛按主客场制进行比赛，共需进行n(n-1)n(n-1)场比赛。
场比赛。
场比赛。
参考答案：参考答案： n(n-1) n(n-1)6.6.一棵树的前根遍历序列为一棵树的前根遍历序列为EFHIGJK EFHIGJK，后根遍历序列为，后根遍历序列为HFIEJKG HFIEJKG，将树转换成二叉树形式后，，将树转换成二叉树形式后，该二叉树的后序遍历序列为HIFKJGE HIFKJGE。
5. 5. 线性结构中元素之间存在一对一关系，线性结构中元素之间存在一对一关系，线性结构中元素之间存在一对一关系，树形结构中元素之间存在一对多关系，树形结构中元素之间存在一对多关系，树形结构中元素之间存在一对多关系，图形结构中图形结构中元素之间存在多对多关系。
元素之间存在多对多关系。
6． 在线性结构中，第一个结点在线性结构中，第一个结点 没有没有没有 前驱结点，其余每个结点有且只有前驱结点，其余每个结点有且只有 1 1个前驱结点；最后一个结点最后一个结点 没有没有没有 后续结点，其余每个结点有且只有后续结点，其余每个结点有且只有1个后续结点。
结构力学—结构的稳定计算和案例
虽不出现新的变形形 式，但结构原来的变 形将增大或材料的应 力超过其许可值，结 构不能正常工作。
2020/2/20
结构力学
7
扁拱式结构失稳时可能伴随有“跳跃”现象。
2020/2/20
结构力学
8
§ 14-2 两类稳定问题计算简例
一个体系产生弹性变形时．确定其变形状态所需 的独立几何参数的数目，称为稳定自由度。
2020/2/20
结构力学
12
令 dFP 0, 得
d
FP
kl
cos(
)[1
sin ] sin( )
1
sin( ) sin 3
相应极值荷载： 23 FPcr kl(1 sin 3 )2
2020/2/20
结构力学Байду номын сангаас
13
2. 按小挠度理论分析
P
P
P
EI
EI
1个自由度
2个自由度
无限自由度
2020/2/20
结构力学
9
14-2-1 单自由度完善体系的分支点失稳
1. 按大挠度理论分析 平衡条件：
FP (l sin ) FR (l cos ) 0
又弹簧反力：
FR kl sin
即 (FP kl cos )l sin 0 第一解： 0 第二解：FP kl cos
1. 按大挠度理论分析
如图所示单自由度非 完善体系杆AB有初倾 角ε，其余同前面。
平衡方程：
FPl sin( ) FRl cos( ) 0
弹簧反力：
FR kl[sin( ) sin ]
结构的稳定计算
1 3
ε＝0
FP/kl
0.642 1.37 1.47 1.57 0.1 0.2 0.3
ε
18
O
(2) 小挠度理论
ε FP kl 1 kl θ ε θε
FP B
FP/kl
1.0
ε＝ 0
k
l
0.6 0.4 0.2
y1 1 y2
kl 2FP FP
1
FP 0 kl 2FP
1
y1 FP 2 kl 1 y2 kl FPcr m in ( FP1 , FP 2 ) 3
1
1
26
计算步骤：
1 中心受压直杆处于临界状态，设产生偏离原平衡位 置的一个可能变形状态； 2 在可能变形状态下，分析结构受力，作隔离体受力 图； 3 建立隔离体的平衡方程，由边界条件确定稳定分析 的特征方程；
2
强度验算 结构设计 刚度验算
必不可少。
薄壁结构
稳定验算 ——某些时候是必须的
高强材料结构 （如钢结构）
主要受压的结构等
强度验算与刚度验算是在结构静力平衡的状态下、采用未变形的 结构的计算简图来分析的； 而稳定验算是在结构产生大变形后的几何形状和位置上进行计算 的，其方法已经属于几何非线性范畴，叠加原理不再适用。
17
(1) 大挠度理论
FP sinε cosθ ε 1 kl sin θ ε
求极值点处的临界荷载
d FP 0 d
FP/kl
1.00 0.695 0.536
sin ( θ) sin
2 3 FPcr 3 (1 sin ) 2 kl
4
结构随荷载逐渐增大可能由稳定的平衡状态转变为不 稳定的平衡状态，称为失稳。保证结构在正常使用的 情况下处于稳定平衡状态是结构稳定分析的目的。 第一类失稳（分支点失稳） 结构的失稳类型 第二类失稳（极值点失稳）
结构稳定理论答案
结构稳定理论答案【篇一：结构稳定理论试题a卷试卷】class=txt>《结构稳定理论》试题册（a）开卷（）闭卷（√）考试时长：120分钟使用班级：命题教师：主任签字:一、填空题：（本大题共14小题，每空1分，共25分）请在每小题的空格中填上正确答案。
错填、不填均无分。
1.建筑结构设计的极限状态分为和两种。
2.板根据其厚度分为厚板、和。
3.求解结构失稳临界荷载的基本方法中静力法是指在压杆微弯曲的状态下建立来求解临界荷载的。
4.压弯杆件在弯矩作用平面内失稳分析准则有、和半经验半理论公式法。
5.铁摩辛柯能量法的实质是应用原理解决弹性稳定问题。
6.在钢结构稳定设计中，无论是哪种荷载作用下的压弯杆件，均等效成两端作用的压弯杆件计算，等效的原则是保持不变。
7.根据薄板小挠度理论的三个假定，薄板弯曲问题可以简化为问题，其变形特征可用来描述，因此称为线性理论。
8.采用迦辽金法时，所选择的杆件变形曲线方程要求既要满足条件，又要满足条件，这区别于瑞利-里兹法只要求满足前者条件。
11.理想轴心受压杆件弯曲屈曲属于失稳类型，受弯构件在弹塑性状态下分析的弯扭屈曲属于失稳类型。
12.用能量法计算工字梁的弯扭屈曲临界荷载时，不考虑竖向弯曲影响，梁在中性平衡位置的应变能由三部分组成，一部分是，另两部分分别由和翘曲引起。
13.用位移法求解刚架临界荷载时，首先应确定考虑的转角位移方程，之后根据位移法形成稳定方程。
14.静力法求解铰接理想轴心受压杆件得出的屈曲临界荷载即欧拉临界荷载公式为。
二、名词解释：（本大题共5小题，每题3分，共15分） 1.理想压杆2.二阶弯矩 3.翘曲4.柱子曲线三、识图题：（本大题共4小题，共15分）1.根据下面荷载-挠度曲线关系图判断分别属于哪种失稳类型。
（3分）a：b： c：2.判断下列图中分别表示两端铰接轴心受压杆件的哪种失稳形式。
（3分）d： e： f： 3.画出碳素钢的应力-应变关系曲线，并标明图上各点。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第11章 结构的稳定计算习题解答习题11.1 是非判断题（1）要提高用能量法计算临界荷载的精确度，不在于提高假设的失稳曲线的近似程度，而在于改进计算工具。
（ ）（2）对称结构承受对称荷载时总是按对称形式失稳。
（ ）（3）刚架的稳定问题总是可以简化为具有弹性支座的单根压杆进行计算。
（ ） （4）结构稳定计算时，叠加原理已不再适用。
（ ）（5）有限自由度体系用能量法求出的临界荷载是精确解。
（ ）（6）当结构处于不稳定平衡状态时，可以在原结构位置维持平衡，也可以在新的形式下维持平衡。
（ ）【解】（1）错误。
能量法计算临界荷载的精确度，直接取决于所假设的失稳曲线的近似程度。
（2）错误。
既可按对称形式失稳也可按反对称形式失稳。
（3）错误。
在能求出刚度系数的情况下，才可简化为具有弹性支座的单根压杆进行计算。
（4）正确。
一般情况下，结构的稳定计算中，既要考虑几何非线性也要考虑材料非线性，因此，不能采用适用于线性弹性理论的叠加原理。
（5）正确。
（6）错误。
习题 12.2 填空题（1）结构由稳定平衡到不稳定平衡，其临界状态的静力特征是平衡形式的 。
（2）临界荷载与压杆的支承情况有关，支承的刚度越大，则临界荷载越 。
（3）用能量法求无限自由度体系的临界荷载时，所假设的失稳曲线y (x )必须满足 条件，并尽量满足 条件。
（4）利用对称性，求习题11.2（4）图所示结构的临界荷载F Pcr ＝ 。
习题11.2（4）图（5）习题11.2（5）图（a ）所示结构可简化为习题11.2（5）图（b ）所示单根压杆计算，则弹簧抗转动刚度系数k ＝ 。
1=l3EI(a) (b)习题11.2（5）图（6）习题11.2（6）图（a ）所示结构可简化为习题11.2（6）图（b ）计算，则抗移动弹簧刚度系数k 1＝ ，抗转动弹簧刚度系数k 2＝ 。
(a)(b)习题11.2（6）图【解】（1）二重性。
（2）大。
（3）位移边界；力的边界。
（4）22l EIπ。
该对称结构的临界荷载，可按反对称失稳形式（即两端简支压杆）确定。
（5）lEI 。
（6）33lEI ；l EI 3。
习题11.3 用静力法计算习题11.3图所示体系的临界荷载。
(a) (b) (c)习题11.3图【解】（1）给出失稳形式，如习题解11.3（a ）图所示。
由∑=0AM得P (3)0F kl y -= ∴Pcr 13F kl =(c)习题解11.3图（2）给出失稳形式，如习题解11.3（b）图所示。
由∑=0AM得P(2)0kl F y-=∴Pcr12F kl=（3）给出失稳形式，如习题解11.3（c）图所示。
先求得支反力：PR124FF k yl⎛⎫=+⎪⎝⎭由∑=0AM得P56kl F y⎛⎫-=⎪⎝⎭∴Pcr56F kl=习题11.4用静力法计算习题11.4图所示体系的临界荷载。
k为弹性铰的抗转动刚度系数（发生单位相对转角所需的力矩）。
习题11.4图【解】给出失稳形式，如习题解11.4图所示。
分析AC，由0CM=∑得P20yk F yl⎛⎫⨯-=⎪⎝⎭P 20k F y l ⎛⎫-=⎪⎝⎭∴Pcr 2kF l=习题解11.4图习题11.5 用静力法计算习题11.5图所示体系的临界荷载。
(a) (b)习题11.5图【解】（1）原体系可简化为习题解11.5（a ）图所示。
弹性支承刚度系数为(a)(b)习题解11.5图33623l EIl EI k =⨯=可求得Pcr 2132EI F kl l == （2）原体系可简化为习题解11.3（b ）图所示。
弹性支承刚度系数为4EIk l=可求得Pcr 4k EIF h lh==习题11.6 用能量法重做习题11.3（c ）。
【解】 变形能 21111222522223372U ky y ky y ky =⨯⨯+⨯⨯= 荷载势能P P U F ∆=-，其中2221153()2()232212y y l l y l l l∆=⋅+⋅=总势能P P E U U =+由P d 0d E y =及0y ≠得P 25507212k F l-= ∴Pcr 56F kl =习题11.7 用静力法求习题11.7图所示各结构的稳定方程。
EI /l (抗转动刚度)(1)(2)(3) (4)(5)习题11.7图【解】（1）失稳曲线如习题解11.7（1）图所示。
微分方程为 P P 1()2EIy M F y F x θ''=-=-+或 2212y y x ααθ''+=- 其中 2PF EIα=该微分方程的通解为x x B x A y θαα21sin cos -+= 代入边界条件：0, 0; , 0; , x y x l y x l y θ'======- 所得齐次方程中，由θ,,B A 不全为零的条件（即系数行列式等于零）整理后得tan 0l l αα+=P习题解11.7（1）图（2）失稳曲线如习题解11.7（2）图所示。
微分方程为P ()EIy M F y k θ''=-=--或 22P , F ky y EI EIαθα''+== 通解为Pcos sin ky A x B x F ααθ=++。
代入边界条件：0, 0; 0, ; , 0x y x y x l y θ''====== 由θ,,B A 不全为零的条件，整理后得1tan 04l l αα+=习题解11.7（2）图（3）原结构可等效为习题解11.7（3）（a ）图所示具有弹性支承的压杆，失稳曲线如习题解11.7（3）（b ）图所示。
微分方程为P(a)(b)习题解11.7（3）图P ()EIy M F y k x δ''=-=--或 22P , F k y y x EI EIδαα''+== 通解为 Pcos sin k y A x B x x F δαα=++由边界条件 0, 0; , ; , 0x y x l y x l y δ'====== 得稳定方程为333()1tan ()12l l l EI l l kl ααααα=-=-（4）原结构可等效为习题解11.7（4）（a ）图所示具有弹性支承的压杆，失稳曲线如习题解11.7（4）（b ）图所示。
微分方程为（a）P4EIlk=习题解11.7（4）图PEIy M F y''=-=-22P0,Fy yEIαα''+==该方程的通解为xBxAyααsincos+=由边界条件,; ,x l y x l yδθ'====得稳定方程为4tan=llαα（5）原结构可等效为习题解11.7（5）（a）图所示具有弹性支承的压杆，弹性支承的刚度系数可由子结构ACD求出。
（a ）FEI3l4k= =M(b) 图习题解11.7（5）图分析ACD，如习题解11.7（5）（b）图所示。
在A点加单位力偶并作M图，图乘得柔度系数为EIl34=δ则弹性支承的刚度系数为lEIk431==δ该题的稳定方程为43tan==EIklllαα习题11.8 用能量法计算习题11.8图所示结构的临界荷载，已知弹簧刚度系数33lEI k =，设失稳曲线为(1cos )2xy l πδ=-。
习题11.8图【解】根据所假设的失稳曲线，可求得应变能及荷载势能如下 sin22xy llπδπ'=，22cos 42xy llππδ''=42222330113()d 22264lEI EI U k EI y x l l πδδδ''=+=+⎰222P P P P 01()d 216lF U F F y x lπ∆δ'=-=-=-⎰由P d()0d U U δ+=及0δ≠得Pcr 24.9F EI l=习题11.9 求习题11.9图所示结构的临界荷载。
已知各杆长为l ，EI ＝常数。
习题11.9图【解】（1）对称失稳2Pcr 2EIF l π=对称（2）反对称失稳F (a)(b)M (c) 图习题解11.9图取半结构分析，如习题解11.9（a ）图所示，可等效为习题解11.9（b ）图进行分析。
其中，弹性支承的刚度系数k ，可先由习题解11.9（c ）图所示弯矩图自乘求得柔度系数δ后，取倒数而得，为3221122122323l l l l l EI EI EIδ=⨯⨯+⨯⨯=故31lEIk ==δ在习题解11.9（b ）图中，由∑=0AM得P ()0F kl ∆-= 由此，反对称失稳时的临界荷载为Pcr 2=EI F kl l =反对称 经比较，原结构的临界荷载为Pcr Pcr 2EI F F l ==反对称 习题11.10 试分别按对称失稳和反对称失稳求习题11.10图所示结构的稳定方程。
习题11.10图【解】（1）对称失稳(b)(d)lF (a)(c)EIl 3EIl k=习题解11.10图对称失稳时，可取半结构如习题解11.10（a ）图所示。
将其等效为习题解11.10（b ）图分析，求得稳定方程为22)(1)(1tan l lEIkll l l ααααα+=+=（2）反对称失稳反对称失稳时，可取半结构如习题解11.10（c ）图所示。
将其等效为习题解11.10（d ）图分析，求得稳定方程为3tan ==EIkll l αα 习题11.11 试导出习题11.11图所示桥墩的稳定方程。
设失稳时基础绕D 点转动，地基的抗转刚度系数为k 。
习题11.11图【解】计算简图如习题解11.11（a ）图所示，失稳形式如习题解11.11（b ）图所示。
（a）F （b）P=∞习题解11.11图由0DM=∑即P ()F a k δθθ+=求得P()ka F δθ=-。
微分方程为P EIy M F y ''=-=-22P0, F y y EIαα''+==通解为 x B x A y ααsin cos +=代入边界条件： 0, 0; , ; , x y x l y x l y δθ'====== 求得稳定方程为2tan ()l a kl l l l EI ααα⎛⎫+= ⎪⎝⎭。