对数函数应用-求值域

函数值域求法基本初等函数的值域：1、一次函数y=kx+b （k ≠0）的值域为R ；2、二次函数y=ax 2+bx+c （a ≠0）的值域：当a ＞0时，值域为[ab ac 442-，﹢∞）；当a ＜0时，值域为（-∞，ab ac 442-]。

3、反比列函数y=xk（k ≠0，x ≠0）的值域为：{y|y ≠0，y ∈R} 4、指数函数y=a x（a ＞0且a ≠1）的值域为：R +5、对数函数y=㏒a x （a ＞0，且a ≠1）的值域R6、正、余弦函数的值域为：[-1，+1]，正、余切函数的值域为R函数值域求法观察法对于一些比较简单的函数，其值域可结合不等式的性质、图象通过观察得到。

如利用|x|≥0，2x ≥0，x ≥0等，直接得出它的值域．例1、 求下列函数的值域⑴ y ＝1x ． ⑵ y ＝25x +． 解：⑴ 由x ∈R ，且x ≠0，易知y ∈R 且x ≠0．所以函数的值域为{ y|y ∈R 且y ≠0}．⑵ ∵ x2≥0，∴25x +≥5．∴ 函数的值域为{ y| y ≥5}．例2、求函数x3y -=的值域。

解：∵x≥0 ∴- x ≤0 3—x ≤3。

故函数的值域是：（ —∞，3 ]例3、求函数[]2,1,211∈-=x xy 的值域。

解：由21≤≤x 得1213-≤-≤-x ，312111-≤-≤-x ，故函数的值域是⎥⎦⎤⎢⎣⎡--31,1.例4、求函数111y x =++的值域。

分析：首先由1x +≥0，得1x ++1≥1，然后在求其倒数即得答案。

解：1x +≥0∴1x ++1≥1，∴０＜111x ++≤１，∴函数的值域为（０，１]．例5、求242-+-=x y 的值域。

由绝对值函数知识及二次函数值域的求法易得：)[)[∞+-∈∞+∈-+-=,2,,024)(2y x x g 所以 例6、求函数y =211x +的值域 解：Θ 22111,011x x +≥∴<≤+ 显然函数的值域是：(]0,1配方法当所给函数是二次函数或可化为二次函数的复合函数时，可利用配方法求值域 例1、求下列函数的值域：⑴ y ＝－2x －4x ＋1，x ∈[－3，3]；⑵y ＝4x ＋41x －1．解：⑴配方，得y ＝－(x ＋2)2＋5，又x ∈[－3，3]，结合图象，知 函数的值域是{ y │－20≤y ＜5}⑵ ∵y ＝4x ＋41x －1＝2221x x ⎛⎫- ⎪⎝⎭＋1≥1， 当且仅当221x x -＝0，即x ＝±1时取等号，∴ 函数y ＝x4＋41x －1的值域为[1，＋∞)．例2、求函数y=2x —2x+5，x ∈[-1，2]的值域。

对数函数的定义与性质1. 定义对数函数是指可以将正实数映射到实数集上的函数。

常用的对数函数有自然对数函数和常用对数函数。

自然对数函数以数学常数e为底的对数函数，通常以ln(x)表示，其中x为正实数。

常用对数函数以10为底的对数函数，通常以log(x)表示，其中x为正实数。

2. 性质2.1 对数函数的定义域和值域自然对数函数ln(x)的定义域是正实数集(0, +∞)，值域是实数集(-∞, +∞)。

常用对数函数log(x)的定义域是正实数集(0, +∞)，值域是实数集(-∞, +∞)。

2.2 对数函数的性质（1）对数函数的图像：自然对数函数ln(x)和常用对数函数log(x)的图像都是单调递增的曲线。

（2）基本性质：对数函数具有以下基本性质：•ln(1) = 0，即自然对数函数ln(x)在x=1处的函数值为0。

•ln(e) = 1，即自然对数函数ln(x)在x=e处的函数值为1。

•log(1) = 0，即常用对数函数log(x)在x=1处的函数值为0。

•log(10) = 1，即常用对数函数log(x)在x=10处的函数值为1。

（3）对数函数的性质：对数函数具有以下性质：•ln(x y) = ln(x) + ln(y)，即自然对数函数ln(x y)等于自然对数函数ln(x)和ln(y)的和。

•ln(x/y) = ln(x) - ln(y)，即自然对数函数ln(x/y)等于自然对数函数ln(x)和ln(y)的差。

•ln(x^n) = n * ln(x)，即自然对数函数ln(x^n)等于n乘以自然对数函数ln(x)。

•log(x y) = log(x) + log(y)，即常用对数函数log(x y)等于常用对数函数log(x)和log(y)的和。

•log(x/y) = log(x) - log(y)，即常用对数函数log(x/y)等于常用对数函数log(x)和log(y)的差。

•log(x^n) = n * log(x)，即常用对数函数log(x^n)等于n乘以常用对数函数log(x)。

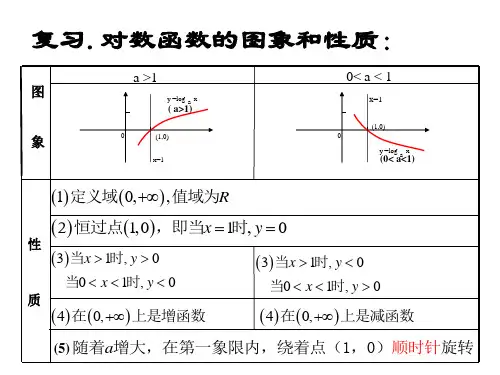
对数函数及其应用对数函数的性质与应用对数函数是数学中常见的一类函数，具有广泛的应用价值。

本文将介绍对数函数的性质和应用，并探讨其在实际问题中的具体运用。

一、对数函数的性质对数函数是以常数e（欧拉数）为底的指数函数的逆运算。

对数函数的一些基本性质如下：1. 定义域和值域：对数函数的定义域为正实数集，值域为实数集。

2. 对数函数与指数函数的互为反函数关系：对数函数与指数函数是互为反函数的关系，即$log_a(a^x)=x$，$a^{log_a(x)}=x$。

3. 对数函数的增减性：对数函数是递增函数，即$log_a(x)<log_a(y)$成立当且仅当$x<y$。

4. 对数函数的图像：对数函数的图像通常为一条上升曲线，随着自变量的增大，函数值也相应增大，但增长速度逐渐减缓。

二、对数函数的应用对数函数在各个领域都有重要的应用，在以下几个方面具有特别的价值：1. 指数增长和衰减模型：对数函数可以描述许多具有指数增长和衰减的现象，例如人口增长、物种繁殖、放射性衰变等。

通过对数函数的分析，可以预测和控制这些现象的发展趋势。

2. 财务和利息计算：对数函数在金融领域中有广泛的应用，例如计算复利、评估投资回报率等。

对数函数可以帮助我们理解时间价值的概念，为财务决策提供重要的依据。

3. 数据压缩和编码：对数函数可以用于数据的压缩和编码，减少存储空间的占用和传输成本。

常见的压缩算法中就包括对数函数的运算，例如对数编码、哈夫曼编码等。

4. 检测与测量：对数函数在物理测量和数据处理中有广泛应用，例如声音强度的测量（分贝）、地震强度的测量（里氏震级）等。

对数函数使得我们能够更好地处理海量的测量数据，提高数据处理的效率和准确性。

结论对数函数是数学中的重要内容，具有广泛的应用领域。

通过对对数函数的性质和应用的了解，我们可以更好地理解和运用数学知识，解决实际问题。

对数函数的应用远不止以上几个方面，不同领域中还有许多其他实际问题可以通过对数函数的运算和分析来解决。

求函数值域的几种常见方法函数的值域可以定义为函数的输出或结果的集合。

确定一个函数的值域有几种常见的方法，包括图像法、符号法和算法法。

下面将详细介绍这些方法。

一、图像法图像法是通过绘制函数的图像来确定函数的值域。

要使用图像法确定函数的值域，需要遵循以下步骤：1.根据函数的定义确定函数的自变量的取值范围。

通常需要考虑定义域和边界条件。

2.绘制函数的图像。

可以使用图表、软件或手工绘制。

3.根据图像确定函数的值域。

值域是函数图像上所有可能的输出值的集合。

可以观察图像找出最大值、最小值和其他可能的取值。

注意：图像法仅适用于可视化的函数。

对于复杂函数，可能需要使用其他方法来确定值域。

二、符号法符号法是利用函数的数学特性和符号来确定函数的值域。

符号法可以分为以下几种情况：1.对于代数函数，可以通过感性地观察含有未知数的表达式中的符号来确定函数的值域。

例如，对于一个二次函数，通过观察二次项系数的符号可以确定函数的开口方向和最值的取值。

2.对于三角函数，可以使用周期性和界限来确定函数的值域。

例如，对于正弦函数，它的值域在[-1,1]之间。

3.对于指数函数和对数函数，可以使用指数和对数的性质来确定函数的值域。

例如，指数函数的值域在(0,+∞)，对数函数的值域在(-∞,+∞)。

三、算法法算法法是通过算法或计算来确定函数的值域。

算法法常用于分段函数、复合函数和隐函数等情况。

以下是一些常见的算法法：1.对于分段函数，可以将定义域分成若干个区间，然后通过分析每个区间的函数表达式来确定函数的值域。

2.对于复合函数，可以从内层函数开始，将结果代入外层函数，逐步计算并确定函数的值域。

3.对于隐函数，可以通过假设一组函数值，然后解方程组，将解代入隐函数表达式来确定函数的值域。

注意：算法法可能需要进行大量的计算和推理，适用于复杂函数，但可能会带来较高的计算复杂性。

同时，算法法可能无法找到确切的值域，只能给出一个估计或范围。

总结：函数的值域可以通过图像法、符号法和算法法来确定。

求函数值域的方法1500字函数的值域（range）是函数所有可能的输出（或称为函数的“结果”）的集合。

值域是由函数的定义域（domain）决定的。

一、确定函数的定义域和值域的基本方法：1. 找到函数的定义域：函数的定义域是指函数输入的所有可能取值的集合。

它可以通过函数的表达式、图像或其它方式确定。

2. 找到函数在定义域上的取值范围：通过对函数进行分析和计算，确定函数在定义域上的取值范围。

这可以通过求导、化简、求极值等数学方法进行计算。

二、求常数函数的值域：常数函数的值域即为函数的常数值。

三、求幂函数的值域：幂函数的值域取决于幂指数的奇偶性。

1. 当幂指数为奇数时，幂函数的值域是整个实数集。

2. 当幂指数为偶数时，幂函数的值域取决于底数的正负和定义域的取值范围。

四、求指数函数的值域：指数函数一般具有如下形式：f(x) = a^x，其中a为常数且a>0。

具体求解方法如下：1. 当a>1时，值域是(0, +∞)；2. 当0<a<1时，值域是(0, 1)；3. 当a=1时，值域是{1}；4. 当a<0时，指数函数的值域不是实数集，因为负数的幂是复数。

这时，可以考虑扩展值域为复数集。

五、求对数函数的值域：对数函数一般具有如下形式：f(x) = loga(x)，其中a为常数且a>0且a≠1。

具体求解方法如下：1. 当a>1时，值域是(-∞, +∞)；2. 当0<a<1时，值域是(-∞, 0)；3. 当a=1时，对数函数的值域不存在；4. 当a<0时，对数函数的值域不是实数集，因为负数的对数是复数。

六、求三角函数的值域：三角函数的值域取决于函数的周期和定义域的取值范围。

1. 正弦函数和余弦函数的值域是[-1, 1]；2. 正切函数在定义域的各个区间上具有不同的值域，可以通过观察和计算来确定。

七、求复合函数的值域：复合函数是多个函数的组合。

求复合函数的值域通常需要先求出每个函数的值域，然后根据复合的关系来确定最终的值域。

对数函数值域的求法观察法通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。

例1求函数y=3+√(2-3x)的值域。

二.反函数法当函数的反函数存在时，则其反函数的定义域就是原函数的值域。

例2求函数y=(x+1)/(x+2)的值域。

三.配方法当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域例3：求函数y=√(-x2+x+2)的值域。

四.判别式法若可化为关于某变量的二次方程的分式函数或无理函数,可用判别式法求函数的值域。

例4求函数y=(2x2-2x+3)/(x2-x+1)的值域。

五.最值法对于闭区间[a,b]上的连续函数y=f(x),可求出y=f(x)在区间[a,b]内的极值,并与边界值f(a).f(b)作比较,求出函数的最值,可得到函数y的值域。

例5已知(2x2-x-3)/(3x2+x+1)≤0,且满足x+y=1,求函数z=xy+3x的值域。

六.图象法通过观察函数的图象，运用数形结合的方法得到函数的值域。

例6求函数y=∣x+1∣+√(x-2)2的值域。

点拨：根据绝对值的意义，去掉符号后转化为分段函数，作出其图象。

七.单调法利用函数在给定的区间上的单调递增或单调递减求值域。

例7求函数y=4x-√1-3x(x≤1/3)的值域。

八.换元法以新变量代替函数式中的某些量，使函数转化为以新变量为自变量的函数形式，进而求出值域。

例8求函数y=x-3+√2x+1的值域。

九.构造法根据函数的结构特征，赋予几何图形，数形结合。

例9求函数y=√x2+4x+5+√x2-4x+8的值域。

十.比例法对于一类含条件的函数的值域的求法，可将条件转化为比例式，代入目标函数，进而求出原函数的值域。

例10已知x,y∈R，且3x-4y-5=0,求函数z=x2+y2的值域。

十一.利用多项式的除法例11求函数y=(3x+2)/(x+1)的值域。

十二.不等式法例12求函数Y=3x/(3x+1)的值域。

对数函数求值域的方法在数学中，对数（logarithm）函数是一类特殊的函数，用来把乘法问题转换成加法问题。

它有一个别名叫“对数关系”，指的是一个数是另一个数的多少次方。

它可以用来求 log N，即以 N 为底数的对数值。

此外，它还可以用来求值域，即在特定的区间内的值的范围。

一般来说，求值域的方法可以分两类：一类是给定对数函数的值，求对数函数的定义域；另一类是给定对数函数的定义域，求对数函数的值。

具体来说，求一个对数函数的值域，可以用下面四步简单的步骤来实现：第一步：设定一个想要求的值域x，它的区间为[a, b]（a < b）。

第二步：把x的定义域映射到定义域中x的取值，使得对数函数取值y在[a, b]之间。

第三步：求出x的定义域中x的取值集合。

第四步：将x的取值集合映射到值域[a, b]之间，即求出x的值域。

具体来说，假如给定一个值域x，它的区间为[a, b]，且已知原函数可以表示成y=f（x），那么根据上面的定义，对数函数可以表示成y=logf（x），因此，只要把x的定义域映射成适当的取值集合，便可以求出x的值域。

例如，已知f（x）=2^x，值域x的定义域为[0,3]，则可以将[0,3]映射到x的取值集合{0,1,2,3}；这四个取值都可以被2^x映射，因此，x的值域可以表示成[log2^0, log2^3]，即[0,3]。

这样，我们就可以求出x值域为[0,3]的对数函数求值域的方法了。

此外，还有另一种求值域的方法，即给定对数函数的定义域，求对数函数的值。

具体来说，假如给定一个定义域[a, b]，且已知函数可以表示成y=f（x），那么根据上面的定义，对数函数可以表示成y=logf（x），则可以求出定义域[a, b]之间的对数函数值。

例如，已知f（x）=2^x，定义域x的定义域为[1,4]，则可以将[1,4]映射到x的取值集合{1,2,3,4}；这四个取值都可以被2^x映射，因此，x的值域可以表示成[log2^1, log2^4]，即[1,4]。

函数值域的求法大全值域为R（注意判别式）；对数函数y=logax(a>0,a≠1)的定义域为R+，值域为R；指数函数y=ax(a>0,a≠1)的定义域为R，值域为(0,+∞)；三角函数y=sin x，y=cos x的值域均为[-1,1]；反三角函数y=arcsin x的定义域为[-1,1]，值域为[-π/2,π/2]；y=arccos x的定义域为[-1,1]，值域为[0,π]；y=arctan x的定义域为R，值域为(-π/2,π/2)。

利用函数的单调性来求值域对于单调递增函数f(x)，其值域为[f(a),f(b)]；对于单调递减函数f(x)，其值域为[f(b),f(a)]。

利用反函数来求值域设函数f(x)的反函数为g(x)，则f(x)的值域等于g(x)的定义域，即f(x)的值域为{x|g(x)∈R}。

利用配方法来求值域对于形如y=f(x)=ax2+bx+c(a>0)的二次函数，可通过配方法将其化为y=a(x+p)2+q的形式，其中a>0，(p,q)为顶点坐标，此时，y的值域为[q,+∞)或(−∞,q]。

利用不等式来求值域对于形如y=f(x)=ax2+bx+c(a>0)的二次函数，可通过求解不等式ax2+bx+c≥0来确定其值域。

以上是常见的求值域的方法，不同的函数类型可能需要不同的方法来求值域。

在解题过程中，要根据具体情况选择合适的方法，结合图像、单调性、反函数等性质进行分析，才能得出正确的结果。

剔除下面文章的格式错误，删除明显有问题的段落，然后再小幅度的改写每段话。

求函数值域是数学中常见的问题。

下面介绍两种常用的方法：单调性法和换元法。

单调性法是指利用函数的单调性来确定函数的值域。

具体来说，可以先找到函数在给定区间内的单调区间，然后比较区间两端点的函数值，从而确定函数的最大值或最小值。

当顶点横坐标是字母时，需要根据其对应区间特别是区间两端点的位置关系进行讨论。

求函数值域的12种方法函数是中学数学的重要的基本概念之一，它与代数式、方程、不等式、三角函数、微积分等内容有着密切的联系，应用十分广泛。

函数的基础性强、概念多，其中函数的定义域、值域、奇偶性等是难点之一，是高考的常见的题型。

下面就函数的值域的求法，举例说如下。

一．观察法通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。

例1求函数y=3+√(2－3x)的值域。

点拨：根据算术平方根的性质，先求出√(2－3x)的值域。

解：由算术平方根的性质，知√(2－3x)≥0，故3+√(2－3x)≥3。

∴函数的知域为.点评：算术平方根具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性。

本题通过直接观察算术平方根的性质而获解，这种方法对于一类函数的值域的求法，简捷明了，不失为一种巧法。

练习：求函数y=[x](0≤x≤5)的值域。

（答案：值域为：｛0，1，2，3，4，5｝）二．反函数法当函数的反函数存在时，则其反函数的定义域就是原函数的值域。

例2求函数y=(x+1)/(x+2)的值域。

点拨：先求出原函数的反函数，再求出其定义域。

解：显然函数y=(x+1)/(x+2)的反函数为:x=(1－2y)/（y－1）,其定义域为y≠1的实数,故函数y的值域为｛y∣y≠1,y∈R｝。

点评：利用反函数法求原函数的定义域的前提条件是原函数存在反函数。

这种方法体现逆向思维的思想，是数学解题的重要方法之一。

练习：求函数y=(10x+10-x)/(10x－10-x)的值域。

（答案：函数的值域为｛y∣y<－1或y>1｝）三．配方法当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域例3：求函数y=√(－x2+x+2)的值域。

点拨：将被开方数配方成完全平方数，利用二次函数的最值求。

解：由－x2+x+2≥0,可知函数的定义域为x∈[－1，2]。

此时－x2+x+2=－（x－1/2）2＋9/4∈[0，9/4]∴0≤√－x2+x+2≤3/2,函数的值域是[0,3/2]点评：求函数的值域不但要重视对应关系的应用,而且要特别注意定义域对值域的制约作用。

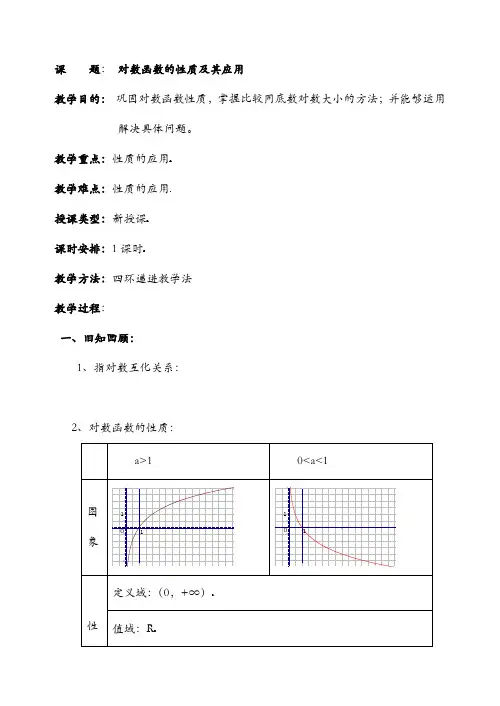
课题：对数函数的性质及其应用教学目的：巩固对数函数性质，掌握比较同底数对数大小的方法；并能够运用解决具体问题。

教学重点：性质的应用教学难点：性质的应用.授课类型：新授课课时安排：1课时教学方法：四环递进教学法教学过程：一、旧知回顾：1、指对数互化关系：2、对数函数的性质：二、巩固运用：1、比较下列各组数中两个值的大小：⑴5.8log ,4.3log 22； ⑵7.2log ,8.1log 3.03.0；⑶1,0(9.5log ,1.5log ≠>a a a a小结：两个同底数的对数比较大小的一般步骤：①确定所要考查的对数函数；②根据对数底数判断对数函数增减性；③比较真数大小，然后利用对数函数的增减性判断两对数值的大小④分类讨论的思想：对数函数的单调性取决于对数的底数是大于1还是小于1。

而已知条件并未指明，因此需要对底数a 进行讨论，体现了分类讨论的思想，要逐步掌握2、比较下列各组中两个值的大小：⑴6log 7log 76与； ⑵.0log log 23与小结：引入中间变量比较大小：利用对数函数的增减性比较两个对数的大小，当不能直接比较时，经常在两个对数中间插入1或0等，间接比较两个对数的3、设有一种放射性物质经过衰变，一年后残留量为原来的84%，设每年的衰变速度不变，问该物质经过多少年后的残留量为原来的50%？（结果保留整数）4、碳-14的半衰期为5730年，古董市场有一幅达.芬奇（1452-1519）的绘画，测得其碳-14的含量为原来的94.1%，根据这个信息，请你从时间上判断这幅画是不是赝品？三、延伸拓展：1、比较大小⑴3.0log 7.0log 4.03.0与，⑵8.0log 7.0log 6.04.3与，⑶1.0log 1.0log 2.03.0与2、求下列函数的定义域、值域： ⑴41212-=--x y ⑵)52(log 22++=x x y ⑶)54(log 231++-=x x y ⑷)(log 2x x y a --=10(<<a四、课堂小结 本节课学习了以下内容：比较对数大小的方法，两种情况，求函数定义值域的方法五、作业测评：1．比较2log 0.7与31log 0.8两值大小2．已知下列不等式，比较正数m 、n 的大小：（1）3log m ＜3log n (2) 3.0log m ＞3.0log n(3) a log m ＜a log n(0＜a ＜1) (4)a log m ＞a log n(a ＞1) 六、板书设计七、课后记：。

对数函数专题——含参对数函数完整版题型汇总一、定义与性质1. 对数函数的定义对数函数是指定义域在正数集合上的函数，它的函数值是指数函数的反函数。

通常用符号 $\log$ 表示对数函数。

2. 对数函数的性质- 对数函数的图像是一条倾斜的曲线，与指数函数的图像关于直线 $y = x$ 对称。

- 对数函数具有单调递增性质，即随着自变量的增加，函数值也会增加。

- 对数函数的定义域是正数集合，值域是实数集合。

二、常见题型1. 对数运算题型例题：计算 $\log_3 27$。

解析：由于 $3^3 = 27$，所以 $\log_3 27 = 3$。

2. 对数方程题型例题：求解方程 $2^x = 8$。

解析：将 $8$ 表示成 $2$ 的幂次形式得到 $8 = 2^3$，所以$2^x = 2^3$，即 $x = 3$。

3. 对数不等式题型例题：求解不等式 $\log_2 \left( \frac{x}{3} \right) \geq 2$。

解析：根据对数定义，$\log_2 \left( \frac{x}{3} \right) \geq2$ 可转化为 $\frac{x}{3} \geq 2^2$，即 $\frac{x}{3} \geq 4$。

解得$x \geq 12$。

三、注意事项1. 在计算对数函数的值时，要注意指数与对数的关系，充分运用指数函数和对数函数的定义和性质。

2. 在解对数方程和不等式时，要注意将题目中的式子转化为指数形式，再进行相应的运算。

以上是对数函数专题中含参对数函数完整版题型汇总的简要内容。

对数函数作为数学中常见的函数之一，在应用中具有广泛的用途。

掌握对数函数的基本定义、性质和解题方法，有助于提高数学问题的解决能力。

对数函数性质的应用一．对数函数的定义域、值域例1、求函数)35(log 21-=x y 的定义域。

解：由题意，得0)35(log 21≥-x ，结合对数函数的图像与性质，得1350≤-<x ， 解得5443≤<x ，所以函数)35(log 21-=x y 的定义域为}.5443|{≤<x x 点评：本题的易错点是注意了被开方数要大于等于0，却忽略了对数函数本身的定义域。

求解对数型复合函数的问题时，应该首先保证对数的真数大于0.二．对数函数的单调性对数函数的单调性受底数a 的制约，所以当题目中关于对数函数的底数的条件仅仅是“a>0且1≠a ”时，就要注意对底数进行分类讨论。

例2、)1(log )(++=x a x f a x 在[0，1]上的最大值与最小值之和为a ，则a 的值是（ ）A 、41B 、21 C 、2 D 、4 解：（1）当a>1时，2log )1()(max a a f x f +==，11log )0()(0min =+==a a f x f ，所以a a a =++12log ，所以a ＝21，不合题意，舍去； （2）当0<a<1时，11log )0()(0max =+==a a f x f ，2log )1()(min a a f x f +==，所以a a a =++12log ，所以a ＝21，故选B. 点评：对于对数函数的底数，要根据单调性的不同，分a>1和0<a<1两种情况讨论。

三．对数函数的图像过定点（1，0）根据01log =a （a>0且1≠a ）可知，对数函数的图像经过定点（1，0）例3、若函数112log -+=x x y a（a>0且1≠a ）的图像过定点P ，则点P 的坐标为________. 解：当1112=-+x x ，即x ＝－2时，y ＝0，故点P 的坐标为（－2，0）. 点评：对复合函数112log -+=x x y a （a>0且1≠a ），内层函数112-+=x x μ就是外层函数μa y log =的自变量，因为外层函数的图像过定点（1，0），所以令1=μ，得x 的值，从而得复合函数经过的定点。

求函数值域的12种方法函数是中学数学的重要的基本概念之一，它与代数式、方程、不等式、三角函数、微积分等内容有着密切的联系，应用十分广泛。

函数的基础性强、概念多，其中函数的定义域、值域、奇偶性等是难点之一，是高考的常见的题型。

下面就函数的值域的求法，举例说如下。

一．观察法通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。

例1求函数y=3+√(2－3x)的值域。

点拨：根据算术平方根的性质，先求出√(2－3x)的值域。

解：由算术平方根的性质，知√(2－3x)≥0，故3+√(2－3x)≥3。

∴函数的知域为.点评：算术平方根具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性。

本题通过直接观察算术平方根的性质而获解，这种方法对于一类函数的值域的求法，简捷明了，不失为一种巧法。

练习：求函数y=[x](0≤x≤5)的值域。

（答案：值域为：｛0，1，2，3，4，5｝）二．反函数法当函数的反函数存在时，则其反函数的定义域就是原函数的值域。

例2求函数y=(x+1)/(x+2)的值域。

点拨：先求出原函数的反函数，再求出其定义域。

解：显然函数y=(x+1)/(x+2)的反函数为:x=(1－2y)/（y－1）,其定义域为y≠1的实数,故函数y的值域为｛y∣y≠1,y∈R｝。

点评：利用反函数法求原函数的定义域的前提条件是原函数存在反函数。

这种方法体现逆向思维的思想，是数学解题的重要方法之一。

练习：求函数y=(10x+10-x)/(10x－10-x)的值域。

（答案：函数的值域为｛y∣y<－1或y>1｝）三．配方法当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域例3：求函数y=√(－x2+x+2)的值域。

点拨：将被开方数配方成完全平方数，利用二次函数的最值求。

解：由－x2+x+2≥0,可知函数的定义域为x∈[－1，2]。

此时－x2+x+2=－（x－1/2）2＋9/4∈[0，9/4]∴0≤√－x2+x+2≤3/2,函数的值域是[0,3/2]点评：求函数的值域不但要重视对应关系的应用,而且要特别注意定义域对值域的制约作用。

指数函数、对数函数求值域【学习目标】1.掌握指数、对数型复合函数求值域的方法2.掌握二次型函数求值域的方法3.理解双变量问题中任意、存在的含义,确定值域间的关系【学习重难点】1.在指数、对数型复合函数求值域过程中换元法的应用2.在底数范围不确定情况下应用分类讨论思想解决问题【知识精讲】1.指数、对数复合型函数求值域求指数、对数函数与其他函数复合而成的函数的值域问题,一般要借助换元法,令内层函数为u ,先求u 的取值范围,再把u 看成自变量,求对应指数或对数函数的值域即可. 2.二次型函数求值域此类问题将指数、对数函数与二次函数综合考察,仍然借助换元法,换元后本质是二次函数,再借助二次函数的图像和性质来解决问题. 3.底数含参讨论在指数、对数函数底数a 范围不确定的情况下需按011a a <<>和分类讨论 4.双变量综合问题此类问题考察两个函数值域间的关系,借助函数图像理解“任意”“存在”的含义,从而确定值域间的关系.【经典例题】例1. 求下列函数的值域： (1)22()2xxf x +=(2)212()log (617)f x x x =-+【答案】(1) 1[,)2+∞;(2) (,3]-∞-【解析】(1)由222(1)11u x x x =+=+-≥-,所以函数()2u f x =的值域为1[,)2+∞(2)由22617(3)88u x x x =-+=-+≥,所以函数12()log f x u =的值域为(,3]-∞-【变式】求下列函数的值域：(1)|1|1()()2x f x +=(2)22()log (1)log (62)f x x x =++- 【答案】（1）(0,1] ;（2）(,3]-∞【解析】（1）由|1|0u x =+≥,所以函数1()()2u f x =的值域为(0,1]（2）由10620x x +>⎧⎨->⎩知函数()f x 的定义域为(1,3)-,由对数的运算法则知2()log (1)(62)f x x x =+-,令(1)(62)u x x =+-,所以08u <≤,所以函数2()log f x u =的值域为(,3]-∞例2. 已知函数223()3axx f x ++=,若()f x 的值域是(0,)+∞,求实数a 的取值范围及()f x 的定义域．【答案】0a =;定义域为R【解析】令223u ax x =++,因为()f x 的值域是(0,)+∞,所以u 取遍所有的实数,故0a =;因为对任意实数x ,()f x 都有意义,所以定义域为R例3. 已知函数2()lg(21)f x ax x =++(1)若()f x 的定义域是R ,求实数a 的取值范围及()f x 的值域; (2)若()f x 的值域是R ,求实数a 的取值范围及()f x 的定义域． 【答案】见解析【解析】（１）因为()f x 的定义域为R ,所以2210ax x ++> 对一切x R ∈成立;由此得0440a a >⎧⎨∆=-<⎩解得1a >．又因为2211121()11ax x a x a a a ++=++-≥-,所以21()lg(21)lg(1)f x ax x a =++≥-,故实数a 的取值范围是(1,)+∞,()f x 的值域为1[lg(1),)a -+∞;（２）令221u ax x =++,因为()f x 的值域为R ,所以u 取遍全体正数,当0a =时,符合要求;当0a ≠,需满足440a a >⎧⎨∆=-≥⎩ ,解得01a <≤ ,所以a 的取值范围是[0,1];要使函数()f x 有意义,则2210ax x ++>①,则由上面知方程221=0ax x ++有两个实根：1x =,2x =所以不等式①的解是12(,)(,)x x -∞⋃+∞,故a 的取值范围是[0,1],()f x 的定义域为12(,)(,)x x -∞⋃+∞.【变式】已知函数22()log (1)f x mx mx =-+的值域是R ,则m 的取值范围是( ) A.04m <≤ B.01m ≤≤ C.4m ≥ D.04m ≤≤ 【答案】A ．【解析】当0m =时,()0f x =,不合题意; 当0m ≠时,令2()1g x mx mx =-+, 只需240m m m >⎧⎨∆=-≥⎩, 解得：4m ≥故选：A ．例4. （1）设02x ≤≤,求函数124325x x y -=-⨯+的值域_______．（2）函数2()log 5log 6f x x x =-+的值域为_______．【变式】求函数11()()142x x y =-+在[3,2]-上的值域．【答案】3[,57]4【解析】令11(),[,8]24x t t =∈,得22131()24y t t t =-+=-+,∴当12t =,即1x =时,y 得最小值为34;当8t =,即3x =-时,y 的最大值为57.∴函数11()()142x x y =-+在[3,2]-上的值域为3[,57]4例5. (1)已知指数函数21()(),[1,1][()]2()3()3x f x x y f x af x g a =∈-=-+当时，求函数的最小值(2)已知对数函数2131()log ,[,3][()]2()3()3f x x x y f x af x h a =∈=-+当时，求函数的最大值【解析】（1）当[1,1]x ∈-时,11()()[,3]33x t f x ==∈,所以22223()3y t at t a a =-+=--+.当13a <时,228()39g a a =-+, 当133a ≤≤时,2()3g a a =-+, 当3a >时,()126g a a =-, 综上所述,22281,3931()3,33126,3a a g a a a a a ⎧-+<⎪⎪⎪=-+≤≤⎨⎪⎪->⎪⎩（2）当1[,3]3x ∈时,13()log [1,1]t f x x ==∈- 所以22223()3y t at t a a =-+=--+当0a ≤时,函数y 在1t =处取得最大值,()42h a a =-; 当0a >时,函数y 在1t =-处取得最大值,()24h a a =+;综上所述,42,0()24,0a a h a a a -≤⎧=⎨+>⎩例6. 若函数()(0,1)x f x a a a =>≠在[1,2]-上的最大值为4,最小值为m ,且函数()(14g x m =-在[0,)+∞上是例7. 若定义域为D 的函数()f x 满足：（1）()f x 在D 内是单调函数;（2）存在[,]a b D ⊆,使得()f x 在[,]a b 上的值域为[,]22a b,则称函数()f x 为“半值函数”.已知函数()log ()(0,1)x c h x c t c c =+>≠是“半值函数”,则实数t 的取值范围是（ ）A.(0,)+∞B.1(,)4-∞ C.1(,)4+∞ D.1(0,)4【答案】D【解析】因为当1c >或01c <<时,()log ()x c h x c t =+都是R 上的增函数, ∴()2()2a h a b h b ⎧=⎪⎪⎨⎪=⎪⎩,即log ()2x c x c t +=即2x x c t c +=有两个不等实根,令1(0)x c m m =>例8. 已知函数2()log ,()2x f x x g x a ==+,若对任意11[,2],2x ∈都存在2[1,3]x ∈,使得121()(),2f xg x =则实数a 的取值范围是________. 【答案】[6,4]--【解析】由题意12()[2,2]f x ∈-, 故只需2()g x 的值域包含[2,2]-, 故32222a a +≤-⎧⎨+≥⎩,解得：64a -≤≤-,故答案为：[6,4]--.【变式】 已知函数1()lg ,()2(0,1),1x xf xg x a a a x -==->≠+若存在12,[0,1),x x ∈使得12()()f x g x =成立,求实数a 的取值范围. 【答案】(2,)+∞【解析】由题意知,当[0,1)x ∈时,()f x 与()g x 的值域有交集.[0,1)x ∈时,2()lg(1)1f x x =-++是减函数, ∴()(,0]f x ∈-∞;当1a >时,()g x 单调递减, ∴()(2,1]g x a ∈-, ∴20a -< ∴2a >当01a <<时,()g x 单调递增()[1,2)g x a ∈-,不合题意. 综上：a 的取值范围为(2,)+∞【课后练习】1.函数|1|1()()2x f x +=的值域为__________．2.函数6()log (61)x f x =+的值域 ( )A. (0,1]B. (0,+∞)C. [1,+∞)D. [2,+∞)３．已知22()log ()f x x mx m =--．若函数()f x 的值域为R ,求实数m 的取值范围;【课后练习答案】１．【答案】(0,1] 【解析】∵ |1|1x +≥,∴ 010()()12f x <≤=即函数|1|1()()2x f x +=的值域是(0,1]．故答案为：(0,1]．２．【答案】B 【解析】∵611x t =+>, ∴62()log (61)log 0x f x t =+=>, 即函数的值域是(0,)+∞． 故选：B ．３．【答案】0m ≥或4m ≤- 【解析】令2()g x x mx m =--,则()g x 取遍所有的正数, 即2=40m m ∆+≥, ∴0m ≥或4m ≤- 故答案为：0m ≥或4m ≤-。