大学物理角动量守恒定律55页PPT

L

r

P

Lx
ˆx

Ly
ˆy

Lz
ˆz
M

r

F

M x ˆx

M y ˆy

M z ˆz
Lx ：质点对x轴的角动量
M
：质点对
x
x轴的力矩
某一方向的分量怎么求呢？由定义出发：
L (xxˆ yyˆ zzˆ) (Px xˆ Py yˆ Pz zˆ) M (xxˆ yyˆ zzˆ) (Fx xˆ Fy yˆ Fz zˆ)
v v oro 1 rr
星球所需向心力： 可近似认为引力：
v2 1
F向 m r r 3
F引

1 r2
引力使r到一定程度
F引 F向 ，r 就不变了，
引力不能再使 r 减小 。
但在z 轴方向却无此限制，
可以在引力作用下不断收缩。
比较 动量定理

dP
F
t2
dt

Fdt ΔP
[C]
2.质量为 m 的小球，以水平速度 v 与固
定的竖直壁作弹性碰撞，设指向壁内的方 向为正方向，则由于此碰撞，小球的动量 变化为
（A）mv
（B）0
（C）2mv （D）2mv
[D]
3.(本题3分)0063 P17-1
质量为m的质点,以同一速率V沿图中正三角形ABC 的水平光滑轨道运动,质点越过A角时,轨道作用于质 点的冲量的大小为
ds dt
const
行星对太阳的矢径在相等的时间内扫过相等的面积。
▲ 星云具有盘形结构：

数学补充知识：
点积
abba
aaa2
叉积
a b b a
a a 0
c ( a b ) a ( b c ) b ( a c )
点积的微商 叉积的微商
c ( a b ) a ( b c ) b ( c a )
d(a b )a db da b
L
Or v
（对圆心的）角动量：
m
L r p r ( m v ) m r v (r v )
大小：
L mrv
方向：满足右手关系，向上。
2.行星在绕太阳公转时的椭圆轨道运动
对定点（太阳）的角动量：
v
L r p m (r v)
大小： Lmvsrin
v
r
r
Sun
方向： 满足右手关系，向上。
L dm trv m ( a c o ti s b si t jn )
( asit in bco t j) s
m m ( a a k c bb (2 恒矢o t k 量 ) a ss b 2 i t k ) n
M
dL
0
!
dt
或由 M rF 直接计算力矩
r a co ti s b sit j n
(1)对C点的角动量是否守恒？
(2)对O点的角动量是否守恒？
C T
O
mg C'
(3)对竖直轴CC'的角动量是否守恒？
请同学思考！
质点系的角动量定理和角动量守恒定律
1.一对作用力、反作用力对定点（定轴）的合力
矩等于零。
证明：
M 1r1f1
M 2r2f2
r2
f2
r
M 1 M 2 r 1 f 1 r 2 f 2

未来对于角动量守恒定律的研究和应用，将会推动物理学和科技领域的 不断发展，为人类社会的进步提供更加坚实的理论基础和技术支持。
05
角动量守恒定律的拓展学习
与角动量相关的其他定律
角动量定理
描述角动量随时间变化的 规律，即角动量定理。
拉格朗日定理
与角动量守恒定律相关的 另一个重要定理，它描述 了系统在保守力作用下的 运动规律。
公式
L=r×p，其中L表示角动量，r表 示位置矢量，p表示动量。
Байду номын сангаас
角动量守恒的条件
无外力矩作用
系统内力的力矩相互抵消，或者系统受到的外力矩为零。
孤立系统
系统与外界没有能量交换或相互作用，即系统处于孤立状态 。
角动量守恒定律的应用场景
01
02
03
天体运动
行星绕太阳的旋转运动、 卫星绕地球的运动等都遵 循角动量守恒定律。
哈密顿原理
一个描述系统在保守力作 用下最短路径的原理，与 角动量守恒定律有密切联 系。
角动量守恒定律的深入学习资源
《经典力学》教材
深入探讨角动量守恒定律的理论 基础和应用，包括数学推导和实
例分析。
网络公开课
一些在线教育平台提供关于角动量 守恒定律的深入学习课程，可以作 为辅助学习资料。
学术论文
查阅相关学术论文，了解角动量守 恒定律在前沿科学研究中的应用和 最新研究成果。
们更好地设计和控制卫星轨道。
分子运动实例
总结词
分子转动是微观领域中角动量守恒的实例，对于理解化学反应机理和分子结构具有重要意义。
详细描述
分子转动是指分子中的原子或基团绕分子轴线的旋转运动。在分子转动过程中，分子的角动量是守恒的。这是因 为分子内部没有摩擦力矩，从而保证了角动量的守恒。了解和利用角动量守恒定律，可以帮助我们更好地理解和 预测化学反应机理和分子结构。

1 2 r gt , p mv mgt 2
r
v
2.4 角动量守恒定律
o
若以O为参考点，质点在任 意时刻的角动量为：
R
A
r
r
v
R
L0 r P ( R r ) p R mgt .
rmgt ; 方向垂直纸面向里
2.4 角动量守恒定律
• 若质点作匀速直线运动，以 O点为参考点，质点的角动 量为：
L0 r mv r mv const
L0 r mv sin r mv
• 注意：对不同的参考点有不同的角动量
开普勒第二定律 对于任一行星，由太阳 到行星的矢径在相等的 时间内扫过相等的面积
2.4 角动量守恒定律
3、质点系的角动量定理及守恒定律
质点系角动量对时间的变化率等 于质点系所受合外力矩，而与内 力矩无关。
写成积分式
dL 即： M 外 dt
L0

t
t0
L Mdt dL L L0 L
t0 L0
L Li ri pi ri mi vi
质点系的角动量守恒
当 M 外 0 时，L 恒矢量
2.4 角动量守恒定律 例1 一半径为 R 的光滑圆环置于竖直平面内.一质 量为 m 的小球穿在圆环上, 并可在圆环上滑动. 小球开始 时静止于圆环上的点 A (该点在通过环心 O 的水平面上), 然后从 A 点开始下滑.设小球与圆环间的摩擦略去不计.求 小球滑到点 B 时对环心 O 的角动量和角速度. 解 小球受重力和支持 力作用, 支持力的力矩为零, 重力矩垂直纸面向里

只要整个系统受到的合外力矩为0，则系统 只要整个系统受到的合外力矩为 ， 的总角动量守恒， 的总角动量守恒，即： 恒量 比如：当研究质点与刚体的碰撞问题 质点与刚体的碰撞问题时 比如：当研究质点与刚体的碰撞问题时，可以把质 点和刚体看成一个系统，在碰撞过程中， 点和刚体看成一个系统，在碰撞过程中，系统所受 的合外力矩为零，所以系统的角动量守恒 系统的角动量守恒。 的合外力矩为零，所以系统的角动量守恒。
刚体定轴转动的角动量定理 三、刚体定轴转动的角动量守恒定律 若 ，则
当刚体受到的合外力矩为0 时，其角动量保持不变。 其角动量保持不变。 当刚体受到的合外力矩为 讨论 Ø 内力矩不改变系统的角动量。 内力矩不改变系统的角动量。 Ø 在冲击等问题中 冲击等问题中 常量
Ø 角动量守恒定律是自然界的一个基本定律。 角动量守恒定律是自然界的一个基本定律。
可得：质点系的角动量守恒定律： 可得：质点系的角动量守恒定律： 若： 则： 或：
当质点系所受的合外力矩为零时，其角动量守恒。 当质点系所受的合外力矩为零时，其角动量守恒。
二、刚体定轴转动的角动量定理角动量守恒定律 刚体定轴转动的角动量定理角动量守恒定律 质点对点的角动量： 质点对点的角动量： 作圆周运动的质点的角动量： 作圆周运动的质点的角动量： 1、刚体定轴转动的角动量
（ 海豚 Ⅱ ）
（支奴干 CH47)
装置反向转动的双旋翼产生 反向角动量而相互抵消
用两个对转的顶浆
自然界中存在多种守恒定律 2 动量守恒定律 2 能量守恒定律 2 角动量守恒定律 2 电荷守恒定律 2 质量守恒定律 2 宇称守恒定律等
例：人与转盘的转动惯量J0，伸臂时 人与转盘的转动惯量 ， 臂长为 l1，收臂时臂长为 l2。人站在 ， 。 不计摩擦的自由转动的圆盘中心上， 不计摩擦的自由转动的圆盘中心上， 的哑铃。 每只手抓有质量为 m的哑铃。伸臂时 的哑铃 转动角速度为 1， ， 求：收臂时的角速度 2 。 解：整个过程合外力矩为0， 整个过程合外力矩为 ， 角动量守恒， 角动量守恒，

M M1 M2 M3
（2）刚体内作用力和反作用力的力矩互相抵消．
M ij
rj
j

O
d ri
i Fji
Fij
Mij M ji
M ji
（3）力矩必须明确是对哪个点（或轴） 8
三、角动量定理 角动量守恒
1.质点的角动量定理
将角动量 L r p 两边对时间求导
14
角动量守恒定律是一条普遍的规律，存在
于很多自然现象中，例如，行星受恒星引力作
用作椭圆轨道运动，引力的作用线始终通过恒
星中心，这样的力称为有心力。由于有心力对
力心的力矩恒为零，因此，受有心力作用的质
点对力心的角动量守恒。 掠面速度
·m
f
r
dS 1 r v dt 2
o r
vdt
12
将角动量定理的微分形式 M dL 两边乘以
dt 并积分得
t
dt
0 M dt L L0
t
0 M
dt :
质点或质点系的合外力矩的冲量矩；
L0 与L 分别是质点或质点系始末状态的角动量。
在一段时间内，质点（系）角动量的增量
等于作用于质点（系）的合外力矩的冲量
矩——质点（系）角动量定理的积分形式
Lrp
(xi yj zk ) (pxi py j pzk )
各坐标轴的分量
Lx ypz zpy Ly zpx xpz Lz xpy ypx
分别称为对 x、y 、z 轴的角动量
2
例 质点L沿某r一 p方向r作 m直v线运动，对O点的角动量 角动量大小为
L rm vsin m v d

角动量守恒定律
一、角动量定理
由转动定律
4-3 角动量守恒定律
M dL dt
Mdt dL
L L t2 Mdt L2 dL
t1
L1
21
系统所受合外力矩的冲量矩等于系统 角动量的增量。
4-3 角动量守恒定律
二、角动量守恒定律
由角动量定理：
t2 t1
M
d
t
L2
L1
若 M 0，则 L J =恒矢量
4-3 角动量守恒定律
一、角动量定理：
t2 tL1
二、角动量守恒定律：
若 M 0，则 L J =恒量
1、刚体： J不变， 也不变（大小、方向） 2、非刚体： J变， 变 → J ，；J ，
课后思考：
4-3 角动量守恒定律
试分析为什么直升机要安装尾翼螺旋桨呢？
4-3 角动量守恒定律
内容：当系统所受合外力矩为零时，则 系统的总角动量保持不变。
应用：
4-3 角动量守恒定律
1、刚体： J不变， 也不变 （大小、方向）
应用：
4-3 角动量守恒定律
2、非刚体： J变， 变 → J ，；J ，
4-3 角动量守恒定律
2、非刚体： J变， 变 → J ，；J ，
J ，
J ，
小结：

若转轴不动，称定轴转动。 O
1. 定轴转动特征
(1) 刚体上各点都在垂直于固定轴的平面内(转动平面) 做圆周运动.其圆心都在一条固定不动的直线(转轴)上.
(2) 刚体上各点到转轴的垂直线在同样的时间内所转过 的角度都相同。因而用角量描述刚体的运动.
www. ******.com
3.3 刚体的运动
2. 定轴转动的描述
解：
N

R
T
Mg
T' M.
a R
mg
m
www. ******.com
3.4 刚体的角动量 转动定律 转动惯量
根据转动定律 根据牛顿第二定律
TR=Jβ
1 MR2
2
mg-T=ma
因绳与滑轮间无滑动，所以 a=Rβ
解以上三式得
a mg mM /2
a
mg
R R( m M / 2 )
rF
www. ******.com
3.1 质点的角动量 力矩
3.1.2 质点的角动量定理
力矩定义：
M rF
力矩大小：
M r F sinθ 式中 rsinθ d 为力臂，则
M Fd
因 Fsin θ F ，即合力切向分量，所以：
M r F
www. ******.com
3.2 质点的角动量守恒定律
(1) 角坐标 称角位置或角坐标。
规定逆时针转向 为正。

p x
O
刚体定轴转动的运动学方程
= (t) (2) 角位移
为 t时间内刚体所转过的角度。
p x O
www. ******.com
3.3 刚体的运动
(3) 角速度 角速度 lim Δ d Δt0 Δt dt 在定轴转动中，转向只可能有

得 所以
d r v v v 0 dt
d r F r m v dt
质点的角动量定理：作用于
dl M＝ dt
质点的合力对某参考点的力矩， 等于质点对同一参考点的角动 量随时间的变化率。 12 成立条件：惯性系
这样,
M
d l dt
将上式两边同乘以dt再积分得
大学物理
1
第四章 角动量守恒定律
• §4-1 力矩 • §4-2 质点角动量守恒定律
2
补充：矢量
1、矢量的加法和减法 平行四边形法则、三角形法则 2、矢量的数乘
B mA
3、矢量的标积（点积） 4、矢量的矢积（叉积）
A F s Fs cos
i C A B Ax Bx j Ay By k Az Bz
MrF r(F F 1 F 2 n) rF rF 1 rF 2 n M M 1 M 2 n
则：
即：合力对某参考点O的力矩等于各分力对同一 点力矩的矢量之和。
7
三、力对转轴的力矩 力对O点的力矩在通过O点的轴上的投影称为力 对转轴的力矩。 在以参考点O为原点的直角坐标系中，将力矩矢
L
11
二、质点的角动量定理
设质点的质量为m，在合力F 的作用下，运动方程 m v d dm v r F r F dt dt
考虑到
d r d d r m v r m v m v dt dt dt
1r 22 1 2 2 3 2 2 A m () mr mr 0 0 22 2 2
18
例题4-3 在一光滑的水平面上，有一轻弹簧,倔强 系数为k=100N/m,一端固定于o点，另一端连接一质 量为m=1kg的滑块，如图所示。设开始时，弹簧的 长度为l0=0.2m(自然长度), 滑块速度0=5m/s, 方向与 弹簧垂直。当弹簧转过900时，其长度l=0.5m，求此 时滑块速度 的大小和方向。 解 对滑块运动有影响的力只有弹性力，故角动量 和机械能都守恒： l m0l0=m lsin o m 1 2 1 2 1 2 m k ( l l ) 0 m 0 d l0 2 2 2 解得: =4m/s, =300。

(练习二，17)
解 设猴子、重物对地面的速度分别为
。
由猴、重物组成的系统角动量守恒，得
v1、v 2
v1 v2
R
∵ v1 v猴绳 v绳-地 v v绳-地
v1
v2
而 v绳地 v物地 v2 , 则 v1 v v2
∴
v2
v 2
第23页/共29页
机械能不守恒
力物的猴拉加，力由速于上和轻爬相绳过等各程m，处中1又g张，因力绳为相对猴等猴和，的物所拉相以力同在大质另于量一猴，端的绳重对重T1
[ C]
第9页/共29页
第五章 角动量、角动量守恒定律
本章主要阐述三个问题：
1）角动量。 2）角动量守恒定律。 3）有心力与角动量守恒定律。 3）有心力与角动量守恒定律。
第10页/共29页
5-3 有心力与角动量守恒定律
自然界中有些力具有这样的性质：力的方向始终通过某一固定点，力的 大小仅依赖于质点与这个点之间的距离。我们称这样的力为有心力，相应的 固定点称为力心。例如，万有引力是有心力；静电作用力也是有心力。
作半径为 的m圆轨道运动。取圆周上 点R为参考点，如图所示，试求：①质P点
在图中点1处所受的力矩 和质点的角动量
的力矩 和质点的角动量 。
；②质m点
在图中点2处所受
M1
L1
m
M2
L2
解 ① 力矩 M 1
2
在点1处， 所m受引力指向 点，故 P M 1 0
角动量 L1
由 m作圆周运动的动力学方程，可得速度
A 另离一端系向一右质，运量绳O动子，处到于达松位的弛置物状体态时。。物开O现体始A在速时使度，物的物体方m体以向位与与于0绳.位5d垂k置垂g直直0。处.的2试，5初求m速物度间体的在距 处

dt M 外i riFi外
f2 1
2
m2
质点系总角动量的时间变化率等于质点系所受
外力矩的矢量和 (合外力矩 )
dL
dt M 外i riFi外
注意： 合外力矩 M是外质点系所受各外力矩的矢
量和，而非合力的力矩。
注意：质点系内力矩的作用
不能改变质点系总角动量，但是影响总角动量 在系内各质点间的分配。
L r c m i v ir i m i v c r i m i v i
第三项：
i
i
i
与 i 有关
rimivi 各质点相对于质心角动量的矢量和
i
反映质点系绕质心的旋转运动，与参考点O的选择无关，
描述系统的内禀性质： L自 旋
L自 旋
L轨 道
于是：
∑
L=rc×Mvc+
本讲内容：三个基本概念
1.角动量
质点
L r p r m v
质点系 L r c M v c r i m iv i L 轨 L 自 道
i
定轴刚体 Lz ri2mi J
i
2. 转动惯量
J ri2mi J r2dm i
3.力矩
M rF M zrF
Mi内0
i
上讲 §5.1 角动量 转动惯量
动量对参考点（或轴）求矩
1.质点的角动量
定义 ： L = r× p = r× m v r
m θ
p p
r
大小： L=rmvs inθ
o
=r p⊥= pr⊥
z
方向：
垂直r于 和p组
成
L
的平面o，
服从右手定则。
x
r
r m

v M 外 dt
d J
dt
v L1 v L2
v L1
dL v
dL
J d
dt
L2 v L2
L1 v L1
积分
M轴 dt Jd J2 J1
当 M 轴合外 0 时
t1
1
J2 J1 恒量
定轴转动刚体 角动量守恒
若转动惯量有变化，则有：J22 J11 恒量 19
5.5 定轴转动刚体的转动定律 转动中的功和能
Jz Jc mh2
式中:
J
关于通过质心轴的转动惯量
c
m 是刚体质量, h 是 c 到 z 的距离
h Cz
J z 是对平行于质心轴的一个轴的转动惯量
23
2） 转动惯量叠加，如图
z B
Jz JA JB JC
A
C
式中:J A 是A球对z轴的转动惯量
JB 是B棒对z轴的转动惯量
J c 是C球对z轴的转动惯量
点的角动量
有 r
1 2
g
t
2
LA
r
p
1 2
mpt3gmvg
mgt 0
o
r
RA r
（2） 对 O 点的角动量
m
mv
r r R
LO r p (R r) p R p R mgt
Rg
LO Rmgt
4
2. 质点的角动量定理
角动量的时间变化率
dL
d
(r
v
r
O
B S
A r
[证明] (1) 行星对太阳O的角动量的大小为
L r p rmvsin
其中 是径矢 r 与行星的动量 p 或速度 v 之间的夹角.

L v
四、角动量守恒定律
dL M dt

·
F
m
r // F
r
（中心力）
O

角动量守恒定律是物 本定律之一，
理学的基
宏观、微观，高速、低速范围 均适用。
质点只受有心力作用， 角动量守恒！
五、角动量守恒定律的应用
例
r // F M r F 0 rmv sin const
i
d d Li （ L） （M i 外 M i内 ） i dt i i dt i L Li dL i M外 M内 质点系的角动量 dt
i j i
dLi Mi dt
于是有：
M外
dL dt
— 质点系角动量定理
的右手螺旋方向。 p （ p L垂直于 和 r确定的平面）
A
（d —“距”）
单位: Kg· m2/s, J· s
在圆周运动中
r v
O
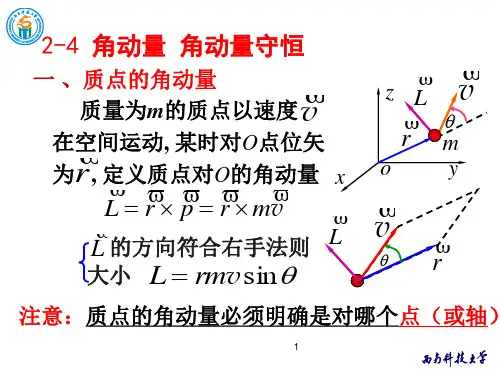
L v m r
Lr p
·
L rmv
方向：垂直于圆周平面。
二、同样的方式定义力矩
M
od
M r F
3.(本题3分)0063 P17-1
质量为m的质点,以同一速率V沿图中正三角形ABC 的水平光滑轨道运动,质点越过A角时,轨道作用于质 点的冲量的大小为 (A) mV (B) 2m V (C) 3m V (D) 2mV B C A
4.(本题5分)5259
t 未能推动木 一人用力 推地上的木箱,经历时间 箱,此推力的冲量等于多少?木箱既然受了力 的冲 F 量,为什么它的动量没有改变?
Fdt ΔP t1 F 0 P 0

大学物理
1
第四章 角动量守恒定律
• §4-1 力矩 • §4-2 质点角动量守恒定律
2
补充：矢量
1、矢量的加法和减法 平行四边形法则、三角形法则 2、矢量的数乘
B mA
3、矢量的标积（点积） 4、矢量的矢积（叉积）
A F s Fs cos
i C A B Ax Bx j Ay By k Az Bz
3
5、矢量函数的导数（只介绍一元函数）
d d A dB (1). ( A B ) dt dt dt d dA (2).当C是常数， (C A) C dt dt (3).当f (t )是t的可微函数，则 d dA [ f (t ) A] f (t ) f (t ) A dt dt
16
例题4-1 一质点的质量为m，位矢为： r =acos t i+bsin t j (式中a、b、 均为常量); 求质点的角动量及它所受的力矩。
解
dr a sin ti b cos tj dt
j k i l r (m ) m a cos t b sin t 0 a sin t b cos t 0 =mabk
23
第四章习题
1，4，7，8，9
24

即
t2
t1
M 外dt l2 l1
根据上式,如果合外力矩零(即M外=0),则l1=l2 ,
l=常矢量 这就是说,对一固定点o,质点所受的合外力矩为 零,则此质点的角动量矢量保持不变。这一结论 叫做质点角动量守恒定律。
对比： 角动量守恒定律是：M外=0，则l=常矢量。 动量守恒定律是： F外=0 ，则p=常矢量。
1 r 2 2 1 2 2 3 2 2 A m( ) mr 0 mr 0 2 2 2 2

dt 12
dt
考虑到 t
dr g cost 7lg cos(12v0 t)
dt 2
24 v0
7l
37
例6 一杂技演员M由距水平跷板高为h 处 自由下落到跷板的一端A，并把跷板另一端 的演员N弹了起来．问演员N可弹起多高?
M
h
N
C
A
B
l/2
l
38
设跷板是匀质的，长度为l，质量为m'，
6mv0
(M 3m)l
v0 m
31
例3 摩擦离合器 飞轮1：J1、 w1 摩擦轮2： J2 静止，两轮沿轴向结合，结合后两轮达到 的共同角速度。 解：两轮对共同转轴的角动量守恒
21
试与下例的齿轮啮合过程比较。
32
例4 两圆盘形齿轮半径r1 、 r2 ，对通过盘心
垂轮直以于0 盘转面动转，轴然的后转两动轮惯正量交为啮J1合、，J2求，啮开合始后1
点o的矢径为 r ，动量为 p ，如下图。在计算其
角动量时，注意有两个特点：
(1) o点到 p 方向的垂直距离 r sin 不变;
(2) L 方向不变;
p2
假如 p 的大小也不变， 显然L 的大小不变。这表
明，自由质点对任意参考 点的角动量保持不变。
p1
1 r1

2
r2
r sin o
5
1.5.2 质点角动量定理
必须指明是对哪个点而言的
注意两点：
(1) 质点的角动量是相对某一参考点而言的，因此
对不同的参考点，角动量 L 不同;
(2) L 的大小在0~ rp 之间变化，如果把动量分解
为径向分量 pcos 和横向分量 psin ，则仅横