流程图、程序的三种基本结构、语句、顺序结构
- 格式:ppt
- 大小:206.00 KB
- 文档页数:6





第2课流程图及算法结构⑴—顺序结构教学目标:1.掌握程流程图的概念,会用通用的图形符号表示算法,了解算法的三个基本逻辑结构:顺序结构、选择结构、循环结构;2.掌握画流程图的基本规则,了解流程图基本结构;3.掌握算法的顺序结构的概念,能熟练画出顺序结构的流程图;教学重点:重点是流程图的基本概念、基本图形符号;对算法的三个基本逻辑结构中的顺序结构的理解及应用教学难点:难点是能综合运用这些知识正确地画出流程图。
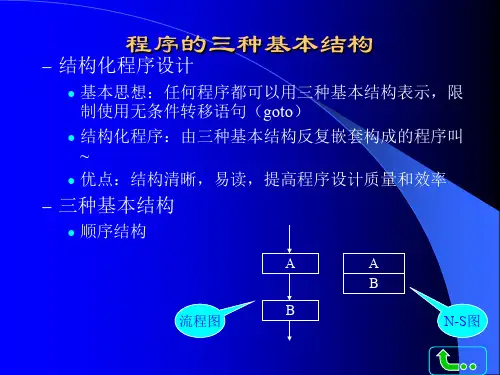
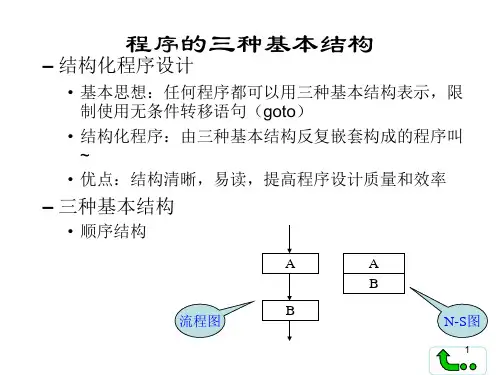
教学过程一、问题情境在研究函数时,由于我们要解决抽象的数量关系问题,而引入了直观的图形——函数图象.利用图象,利用数形结合思想,解决了很多较难解决的问题,并使得解题过程显得简捷.思考在用自然语言表述算法时,因为一些语句太长,看起来显得较为麻烦,那我们能否也象在研究函数时一样,引入一个图呢?并进而借用图的直观性,方便地表述算法呢?请设计求满足1+2+3+…+n>2004的最小正整数n 的一种算法.S1 取n=1;S2 计算n(n+1)2;S3 若n(n+1)2的值大于2004,那么n的值即为所求;否则让n的值增加1转到S2重复操作.为了将设计好的算形式法清晰直观地描述出来,我们可用流程图的形式来表达。
二、建构数学 1.流程图 流程图基本概念:(1)流程图的概念:流程图是由一些图框和带箭头的流线组成的,其中图框表示各种操作的类型,图框中的文字和符号表示操作的内容,带箭头的流线表示操作的先后次序. 说明:①一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明。
②流程图直观、清晰、易懂,便于检查及修改.(2)构成程序框的图形符号及其作用进行的,有些需要选择进行,有些则要循环进行.⑶算法的三种基本逻辑结构:顺序结构、选择结构、循环结构.2.顺序结构依次进行多个处理的结构称为顺序结构.如右图2所示,虚线框内是一个顺序结构,其中A和B两个框是依次执行的.顺序结构是一种最简单、最基本的结构.图2三、数学应用例1 已知两个单元分别存放了变量x 和变量y 的值,试交换这两个变量的值.例2 半径为r 的圆的面积公式为S=πr 2,当r =10时, 写出计算圆的面积的算法,画出流程图. 课堂练习: 1.课本P9EX. 2.补充练习⑴ 计算下列梯形的面积:上底为3,下底为7,高为6.试设计该问题的算法并画出流程图. ⑵ 写出将△ABC 面积五等分的一个算法. ⑶求下列二次函数的最小值:y =x 2+4x +3.试写出其算法并画出流程图.⑷(⑶的引伸)求下列二次函数的最值:y =ax 2+bx +c (a ≠0)⑴解 算法如下:S1 输入a ,b ,h ;S2 S ←1()2a b h +;S3 输出S .图3算法流程图如图3所示.⑵解:S1 过点B任作以B为端点的射线l;S2 在l上依次截取BM=MN=NP=PQ=QR;S3 连结CR;S4 分别过点M、N、P、Q作RC的平行线,交BC 于点D、E、F、G,则点D、E、F、G就是线段BC 的五等分点;S5 分别连结AD、AE、AF、AG,则它们将△ABC的面积五等分.图形如图4所示.AFED C BPGNMQR l图4⑶解 算法为: S1 输入a ,b ,c ;S2 m ←244a c ba -;S3 输出m .其流程图如图2所示.⑷解:算法: S1 输入a ,b ,cS2m←244ac b a-;S3 判断a >0? 是,输出最大值为否,输出最小值为流程图为:课外巩固练习:图51.下列图形符号中,表示判断框的是( )A .B .C .D .2.以下关于流程图(符号)的几种说法: ①任何一个流程图都必须有起止框;②输入框只能放在开始框后,输出框只能放在结束框前; ③判断框是唯一具有超过一个退出点的符号. 其中正确说法的个数是( )A .1B .2C .3D .03.下列所画流程图是已知直角三角形两条直角边a 、b 求斜边的算法,其中正确的是A .B .C .D .4.如图的流程图,其运行结果为.5.画出由球的半径R求其体积的流程图.6.设计一个算法计算正整数的前n项和,并画出流程图.第4题图。

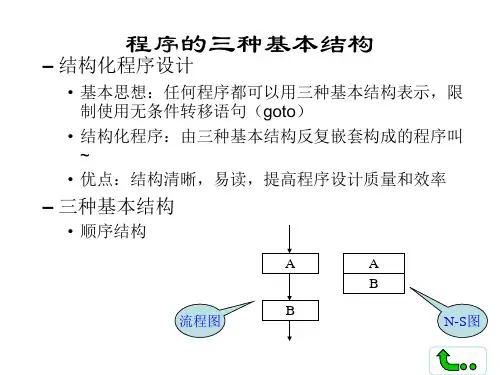
程序的三种基本结构;
【学习者分析】
通过整章的学习,学生对程序设计有了一定的了解,对程序的结构、算法流程都有了一定的了解,本节通过实例加深学生对程序三种基本结构的理解。
【教材内容分析】
・本节的主要内容及在本章中的地位:
本节是对本章知识的小结、整理和提升。
本节总结归纳了程序的三种基本结构,分析三种基本结构的执行过程及特点,为学生进一步学习算法与程序设计打下基础。
・教学重点:
程序的三种基本结构的执行过程。
・教学难点:
程序的三种基本结构的执行过程。
・课时安排:1课时。
【教学目标】
・知识与技能:
了解程序的三种基本结构的执行过程,并能画出它们的流程图。
・过程与方法:
通过教学实例的分析,让学生体验利用程序的三种基本结构编写计算机程序,解决实际问题。
・情感态度价值观:
培养学生的逻辑思维能力。
【教学理念和方法】
通过教学实例的讲练,以教师为主导,学生主动,体验思考,讲练结合,以任务驱动等方式来完成教学内容。
【教学过程设计】
・教学内容的组织与呈现方式:
以实例分析深入展开,小结归纳,将程序的三种基本结构的执行过程和特点一一呈现,通过不同的练习,让学生从中慢慢理解并掌握程序的三种基本结构的执行过程,最后完成课堂自评。
・教学过程:
教学环节
教师教学
学生活动
设计意图
复习引入
我们学习了“求圆面积”的程序,请看程序段(演示),程序中语句的执行是如何的?。
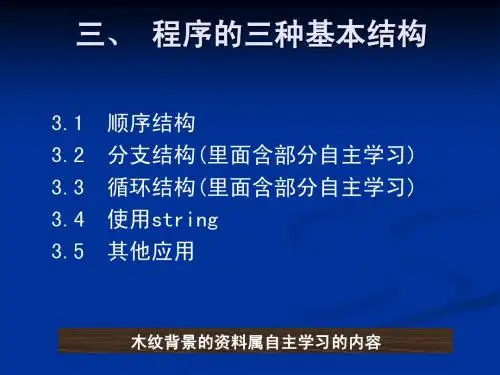
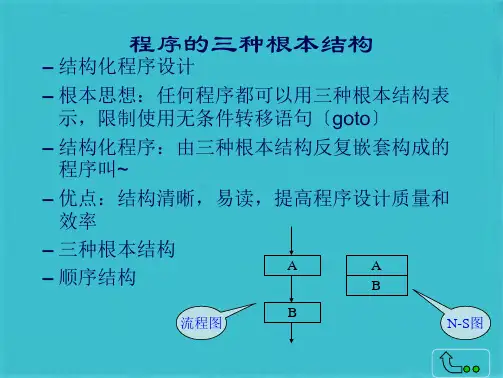
程序化设计的三种结构
程序化设计的三种基本结构分别是:顺序结构、选择结构和循环结构。
1. 顺序结构:顺序结构是一种线性、有序的结构,它按照程序语句执行的
自然顺序,一条语句接一条语句地执行程序。
2. 选择结构:选择结构是根据条件成立与否选择程序执行的通路。
它通过
对一定条件进行判断,根据判断结果选择执行不同的代码块。
选择结构可以分为简单选择和多分支选择。
3. 循环结构:循环结构是重复执行一个或几个模块,直到满足某一条件为
止。
在循环结构中,可以根据需要设置循环次数或使用无限制循环。
循环结构可以帮助简化程序,提高代码的可读性和可维护性。
这三种结构可以单独使用,也可以相互组合使用,以实现更复杂的程序逻辑。
在实际编程中,根据需求灵活运用这三种结构,可以使程序更加清晰、简洁、易于理解和维护。