Matlab机械优化设计实例教程

化设计hl4HU©0⑥ 3 hlu 凹内r d X1州fci-rU-fFF卢F ♦ 忡下¥为+1 —*— S-ll-« F41：Si —MATLABoftiHMirjirCfiffliiiiJ PHI■1**■ 温不平?」11,・—喜M - 〜FT 文词一时y 片 34ml 3F*L9TR0i. Jill!-LkftLgWf 1S1CSI掰f 1 ■ >A A A »W I % ：k Dnfl w I ■ J k^lXMprfaMk tjn nn Alflhw初选 x0=[1,1] 程序：Step 1: Write an Mfle objfunl.m.function f1=objfun1(x)f1=x(1)人2+2*x(2)入2-2*x(1)*x(2)-4*x(1);Step 2: Invoke one of the unconstrained optimization routinesx0=[1,1]；>> options = 0Ptimset('LargeScale','off);>> [x,fval,exitflag,output] = fminunc(@objfun1,x0,options)运行结果： x =4.0000 2.0000 fval = -8.0000exitflag =1 output = iterations: 3 funcCount: 12 stepsize: 1 firstorderopt: 2.3842e-007algorithm: 'medium-scale: Quasi-Newton line search message: [1x85 char]非线性有约束优化1. Min f(x)=3 x ： + x 2+2 x 1-3 x 2+5 Subject to:g 2(x)=5 X 1-3 X 2 -25 < 0 g (x)=13 X -41 X 2 < 0 3 12g 4(x)=14 < X 1 < 130无约束优化 min f(x)=X 2 + x 2-2 x 1 x 2-4 x 1g5 (x)=2 < X 2 < 57初选x0=[10,10]Step 1: Write an M-file objfun2.mfunction f2=objfun2(x)f2=3*x(1)人2+x(2)人2+2*x(1)-3*x(2)+5;Step 2: Write an M-file confunl.m for the constraints. function [c,ceq]=confun1(x) % Nonlinear inequality constraints c=[x(1)+x(2)+18;5*x(1)-3*x(2)-25;13*x(1)-41*x(2)人2;14-x(1);x(1)-130;2-x(2);x(2)-57];% Nonlinear inequality constraints ceq=[];Step 3: Invoke constrained optimization routinex0=[10,10]; % Make a starting guess at the solution>> options = optimset('LargeScale','off);>> [x, fval]=...fmincon(@objfun2,x0,[],[],[],[],[],[],@confun1,options)运行结果：x =3.6755 -7.0744 fval =124.14952.min f (x) =4x2 + 5x2s.t. g 1(x) = 2X] + 3x2- 6 < 0g (x) = x x +1 > 0初选x0=[1,1]Step 1: Write an M-file objfun3.m function f=objfun3(x) f=4*x(1)人2 + 5*x(2)人2Step 2: Write an M-file confun3.m for the constraints. function [c,ceq]=confun3(x) %Nonlinear inequality constraints c=[2*x(1)+3*x(2)-6;-x(1)*x(2)-1];% Nonlinear equality constraints ceq口；Step 3: Invoke constrained optimization routinex0=[1,1];% Make a starting guess at the solution>> options = optimset('LargeScale','off);>> [x, fval]=...fmincon(@objfun,x0,[],[],[],[],[],[],@confun,options)运行结果：Optimization terminated: no feasible solution found. Magnitude of search direction less than2*options.TolX but constraints are not satisfied.x =11fval =-13实例：螺栓连接的优化设计图示为一压气机气缸与缸盖连接的示意图。

机械优化设计matlab优化设计程序学校：班级：学号：姓名：指导老师：一．进退法求最优点所在区间1．算例：函数：f=x(1)^3+x(2)^2-10*x(1)*x(2)+1;初始参数：x0=0,step=0.01,st=[0,0],sd=[1,1];2．编程代码：function [lb,ub]=jintuifa(x0,step0,st,sd)% lb为区间下限，up为区间上限% x0初始探测点，step0是初始探测步长，st初始搜索点，sd是初始搜索方向step=step0;f0=jintui(x0,st,sd);x1=x0+step0;f1=jintui(x1,st,sd);if f1<=f0while truestep=2*step;x2=x1+step;f2=jintui(x2,st,sd);if f1<=f2lb=x0;ub=x2;break;elsex0=x1;x1=x2;f0=f1;f1=f2;endendelsewhile truestep=2*step;x2=x0-step;f2=jintui(x2,st,sd);if f0<=f2lb=x2;ub=x1;break;elsex1=x0;x0=x2;f1=f0;f0=f2;endendendend%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=jintui(a,st,sd)f=objfun(st+a.*sd);end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=objfun(x)f=x(1)^3+x(2)^2-10*x(1)*x(2)+1;end3.运行结果二．黄金分割法求最求最优值1.eg：函数：f=x^2+2*x;初始参数：a=-3,b=5,e=0.0001;2.编程代码：function [ans,sp]=golden(a,b,e)%[a,b]初始区间，e为最小区间长度要求%ans为最优解，sp为所需迭代次数a(1)=a;b(1)=b;L=e;t(1)=a(1)+0.382*(b(1)-a(1));u(1)=a(1)+0.618*(b(1)-a(1));k=1;m(1)=feval('f1',t(1));n(1)=feval('f1',u(1));while(b(k)-a(k)>L)if(m(k)>n(k))a(k+1)=t(k);b(k+1)=b(k);t(k+1)=u(k);u(k+1)=a(k+1)+0.618*(b(k+1)-a(k+1));elsea(k+1)=a(k);b(k+1)=u(k);u(k+1)=t(k);t(k+1)=a(k+1)+0.382*(b(k+1)-a(k+1));endm(k+1)=feval('f1',t(k+1));n(k+1)=feval('f1',u(k+1));ans=feval('f1',t(k+1));k=k+1;endans=(a(k)+b(k))/2;sp=k-1;end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function y=f1(x)y=x^2+2*x;end3.运行结果三．无约束优化方法——坐标轮换法1.eg：函数：min f(x)=4*(x(1)-5)^2+(x(2)-6)^2;初始参数：初始点x为[8,9];2.编程代码：function [x,f]=lunhuan(x0)%输入初始点x0[8,9]%输出最优解点x,与最优解值fp=1;h=0.000001;x=x0;while(p>h)%做精度比较w=x(1);q=x(2);d1=[1,0];a1=golden('objfun',x,d1);%黄金分割法求最佳步长 x=x+a1*d1;d2=[0,1];a2=golden('objfun',x,d2);x=x+a2*d2;p=sqrt((x(1)-w)^2+(x(2)-q)^2);endf=objfun(x);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=objfun(x)%函数名f=4*(x(1)-5)^2+(x(2)-6)^2;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [lb,ub]=jintuifa(st,sd)%进退法函数x0=0;step0=0.000001;step=step0;f0=jintui(x0,st,sd);x1=x0+step0;f1=jintui(x1,st,sd);if f1<=f0while truestep=2*step;x2=x1+step;f2=jintui(x2,st,sd);if f1<=f2lb=x0;ub=x2;break;elsex0=x1;x1=x2;f0=f1;f1=f2;endendelsewhile truestep=2*step;x2=x0-step;f2=jintui(x2,st,sd);if f0<=f2lb=x2;ub=x1;break;elsex1=x0;x0=x2;f1=f0;f0=f2;endendendend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=jintui(a,st,sd)f=objfun(st+a.*sd);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function ans=golden(f_name,st,sd)[a,b]=jintuifa(st,sd); %进退法求最佳步长区间a(1)=a;b(1)=b;L=0.1;t(1)=a(1)+0.382*(b(1)-a(1));u(1)=a(1)+0.618*(b(1)-a(1));k=1;p=st+t(1)*sd;q=st+u(1)*sd;m(1)=feval(f_name,p);n(1)=feval(f_name,q);while(b(k)-a(k)>L)if(m(k)>n(k))a(k+1)=t(k);b(k+1)=b(k);t(k+1)=u(k);u(k+1)=a(k+1)+0.618*(b(k+1)-a(k+1));elsea(k+1)=a(k);b(k+1)=u(k);u(k+1)=t(k);t(k+1)=a(k+1)+0.382*(b(k+1)-a(k+1));endw=st+t(k+1)*sd;z=st+u(k+1)*sd;m(k+1)=feval(f_name,w);n(k+1)=feval(f_name,z);ans=feval(f_name,w);k=k+1;endt(k)=0;u(k)=0;m(k)=0;n(k)=0;p=[a',b',t',u',m',n'];ans=(a(k)+b(k))/2;end3.运行结果四．无约束优化方法——鲍威尔法1.eg：函数：min f(x)=4*(x(1)-5)^2+(x(2)-6)^2;初始参数：初始点x为[8,9]，初始搜索方向[0,1],[1,0];2.编程代码：function [x,f]=powill(x0,d1,d2)%输入x0为初始点，d1,d2为两个线性无关向量for k=1:2w=x0(1);q=x0(2);a1=golden('objfun',x0,d1);x1=x0+a1*d1;a2=golden('objfun',x1,d2);x2=x1+a2*d2;d1=d2;d2=x2-x0;a3=golden('objfun',x2,d2);x3=x2+a3*d2;x0=x3;endx=x0;f=objfun(x);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=objfun(x)f=4*(x(1)-5)^2+(x(2)-6)^2;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [lb,ub]=jintuifa(st,sd)x0=0;step0=0.0001;step=step0;f0=jintui(x0,st,sd);x1=x0+step0;f1=jintui(x1,st,sd);if f1<=f0while truestep=2*step;x2=x1+step;f2=jintui(x2,st,sd);if f1<=f2lb=x0;ub=x2;break;elsex0=x1;x1=x2;f0=f1;f1=f2;endendelsewhile truestep=2*step;x2=x0-step;f2=jintui(x2,st,sd);if f0<=f2lb=x2;ub=x1;break;elsex1=x0;x0=x2;f1=f0;f0=f2;endendend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=jintui(a,st,sd)f=objfun(st+a.*sd);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function ans=golden(f_name,st,sd)[a,b]=jintuifa(st,sd);a(1)=a;b(1)=b;L=0.1;t(1)=a(1)+0.382*(b(1)-a(1));u(1)=a(1)+0.618*(b(1)-a(1));k=1;p=st+t(1)*sd;q=st+u(1)*sd;m(1)=feval(f_name,p);n(1)=feval(f_name,q);while(b(k)-a(k)>L)if(m(k)>n(k))a(k+1)=t(k);b(k+1)=b(k);t(k+1)=u(k);u(k+1)=a(k+1)+0.618*(b(k+1)-a(k+1));elsea(k+1)=a(k);b(k+1)=u(k);u(k+1)=t(k);t(k+1)=a(k+1)+0.382*(b(k+1)-a(k+1));endw=st+t(k+1)*sd;z=st+u(k+1)*sd;m(k+1)=feval(f_name,w);n(k+1)=feval(f_name,z);ans=feval(f_name,w);k=k+1;endend3.运行结果五．有约束优化方法——复合形法1.eg：函数：min f(x)=x1^2+x2^2-x1*x2-10*x1-4*x2+60 St:g1(x)=-x1≤0g2(x)=-x2≤0g3(x)=x1-6≤0g4(x)=x2-8≤0g5(x)=x1+x2-11≤02.编程代码：function fuhexing(n,b,h,xb1,xb2)%元素数n,初始可行点b,精度h，xb1横坐标上下界，xb2为纵坐标上下界if (rem(n,2)==0)k=n+n/2;elsek=n+(n+1)/2;end%取k值A=kexingdian(k,xb1,xb2,b');%确定可行点A=mubiao(A,n,k,h);%求出目标函数并排序比较，得出最优解End %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function A=mubiao(A,n,k,h)for i=1:kA(3,i)=objfun(A(:,i));endB=A';%根据目标函数值排序A=sortrows(B,3)';p=0;for j=1:kx=(objfun(A(:,j))-objfun(A(:,1)))^2;p=p+x;endo=sqrt(p/(k-1));%收敛条件if(o<h)%判断所求点是否为最优点disp('最优点为')xz(1)=A(1,1);xz(2)=A(2,1);disp(xz);disp('其函数值为')f=A(3,1);disp(f);elsexr=Xcpanduan(A,k,n,h,1.3);endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function A=kexingdian(k,xb1,xb2,b)A=zeros(3,k);A(1,1)=b(1);A(2,1)=b(2);for i=2:kA(1,i)=xb1(1)+rand(1)*(xb1(2)-xb1(1));A(2,i)=xb2(1)+rand(1)*(xb2(2)-xb2(1));%产生j个顶点endt=0;for j=1:kif(A(1,j)+A(2,j)<=11&&A(1,j)<=6&&A(2,j)<=8)%判断是否有不可行点t=t+1;T(:,t)=A(:,j);endendif(t<k)%计算出可行点的中心位置xcxc=zhongxindian(T,t);endt=0;for j=1:k%利用中心点将原不可行点逼近为可行点while(A(1,j)+A(2,j)>11||A(1,j)>6||A(2,j)>8)A(:,j)=xc+0.5*(A(:,j)-xc);endendendx=x0;f=objfun(x);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function f=objfun(x)f= x1^2+x2^2-x1*x2-10*x1-4*x2+60;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function xc=Xcpanduan(A,k,n,h,a)for i=1:k-1T(:,i)=A(:,i);endxc=zhongxindian(T,k-1);%计算除最坏点以外的可行点中心坐标if(xc(1)+xc(2)<=11&&xc(1)<=6&&xc(2)<=8)%判断xc是否可行xr=Xrpanduan(xc,A,a,n,k,h);A(:,k)=xr;else%不可行时，即重新确定初始可行点fuhexing(n,h,A(:,1),xr);endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function xc=zhongxindian(T,t)xc=[0;0;0];for i=1:txc=xc+T(:,i);endxc=xc/t;%求解中心点end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function xr=Xrpanduan(xc,A,a,n,k,h)xr=xc+a*(xc-A(:,k));while(xr(1)+xr(2)>11||xr(1)>6||xr(2)>8)%判断xr 是否可行若不可行，则持续迭代a=0.5*a;xr=xc+a*(xc-A(:,k));endxr=ercipanduan(a,xr,A(:,k),A,n,k,xc,h,xr);%可行时进入下一判断end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function xr=ercipanduan(a,p,b,A,n,k,xc,h,t)if(objfun(p)>=objfun(b))%判断反射点和最坏点函数值的大小if(a<=1e-10)A(:,k)=A(:,k-1);xr=Xcpanduan(A,k,n,h,a);disp(xr);elsea=0.5*a;xr=Xrpanduan(xc,A,a,n,k,h);%返回中心点判断，持续迭代endelseA(:,k)=p;%以反射点取代最坏点进行循环mubiao(A,n,k,h);xr=t;endend3.运行结果五．有约束优化方法——混合惩罚法1.eg:函数：min f(x)=(x(4)-x(1))^2+(x(5)-x(2))^2+(x(6)-x(3))^2;St:g1=x(1)^2+x(2)^2+x(3)^2-5;g2=(x(4)-3)^2+x(5)^2-1;g3=x(6)-8;g4=4-x(6);2.编程代码function [x,f]=hunhechengfa(x0,r0,c,h1,h2)k=1;z=0;A(:,1)=x0;r(1)=r0;while (z==0)k=k+1;x=lunhuan(x0,r(k-1));A(:,k)=x;r(k)=c*r(k-1);z=shoulian(A,r,h1,h2,k);if(z==1)break;endx0=x;enddisp('最优解点x=');disp(x);disp('最优值=');f=fhanshu(x);disp(f);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function z=shoulian(A,r,h1,h2,k)%判断收敛条件U=abs(objfun(A(:,k),r(k))-objfun(A(:,k-1),r(k-1))/obj fun(A(:,k-1),r(k-1)));V=0;for i=2:kV=V+(A(1,k)-A(1,k-1))^2;endV=sqrt(V);if(U<=h1&&V<=h2)z=1;elsez=0;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function p=objfun(x,r)%φ函数g1=x(1)^2+x(2)^2+x(3)^2-5;g2=(x(4)-3)^2+x(5)^2-1;g3=x(6)-8;g4=4-x(6);j=sqrt(r);u=r*(1/g1+1/g2+1/g3+1/g4);v=(g1^2+g2^2+g3^2+g4^2)/j;p=fhanshu(x)-u+v;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function f=fhanshu(x)%目标函数f=(x(4)-x(1))^2+(x(5)-x(2))^2+(x(6)-x(3))^2;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function x=lunhuan(x0,r)%轮换法p=1;h=0.01;d=zeros(6,6);a=zeros(6,1);x=x0;for i=1:6for j=1:6if(i==j)d(i,j)=1;endendendwhile(p>h)t=x;v=0;for k=1:6a(k)=golden(x,d(:,k),r);c=d(:,k);x=x-a(k)*c';v=v+(x(k)-t(k))^2;endp=sqrt(v);endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function ans=golden(st,sd,r)%黄金分割法求最佳步长 [g,h]=jintuifa(st,sd,r);a(1)=g;b(1)=h;L=0.01;t(1)=a(1)+0.382*(b(1)-a(1));u(1)=a(1)+0.618*(b(1)-a(1));k=1;p=st+t(1)*sd';q=st+u(1)*sd';m(1)=objfun(p,r);n(1)=objfun(q,r);while(b(k)-a(k)>L)if(m(k)>n(k))a(k+1)=t(k);b(k+1)=b(k);t(k+1)=u(k);u(k+1)=a(k+1)+0.618*(b(k+1)-a(k+1));elsea(k+1)=a(k);b(k+1)=u(k);u(k+1)=t(k);t(k+1)=a(k+1)+0.382*(b(k+1)-a(k+1));endw=st+t(k+1)*sd';z=st+u(k+1)*sd';m(k+1)=objfun(w,r);n(k+1)=objfun(z,r);k=k+1;endans=(a(k)+b(k))/2;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=jintui(a,st,sd,r)%代入步长f=objfun(st+a.*sd',r);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [lb,ub]=jintuifa(st,sd,r)%进退法求最佳步长区间x0=0;step0=0.001;step=step0;f0=jintui(x0,st,sd,r);x1=x0+step0;f1=jintui(x1,st,sd,r);if f1<=f0while truestep=2*step;x2=x1+step;f2=jintui(x2,st,sd,r);if f1<=f2lb=x0;ub=x2;break;elsex0=x1;x1=x2;f0=f1;f1=f2;endendelsewhile truestep=2*step;x2=x0-step;f2=jintui(x2,st,sd,r);if f0<=f2lb=x2;ub=x1;break;elsex1=x0;x0=x2; f1=f0; f0=f2;endendend3.运行结果。

利用MATLAB求解机械设计优化问题的分析周婷婷(能源与动力学院,油气0701>摘要：MATLAB是目前国际上最流行的科学与工程计算的软件工具,它具有强大的数值分析、矩阵运算、信号处理、图形显示、模拟仿真和最优化设计等功能。

本文浅谈MATLAB在机械设计优化问题的几点应用。

关键词：MATLAB 约束条件机械设计优化引言：在线性规划和非线性规划等领域经常遇到求函数极值等最优化问题，当函数或约束条件复杂到一定程度时就无法求解，而只能求助于极值分析算法，如果借助计算器进行手工计算的话，计算量会很大，如果要求遇到求解极值问题的每个人都去用BASIC,C和FORTRAN之类的高级语言编写一套程序的话，那是非一朝一日可以解决的，但如用MATLAB语言实现极值问题的数值解算，就可以避免计算量过大和编程难的两大难题，可以轻松高效地得到极值问题的数值解，而且可以达到足够的精度。

1无约束条件的极值问题的解算方法设有Rosenbrock函数如下：f(X1,X2>=100(X2-X1*X1>2+(1-X1>2求向量X取何值时，F(x>的值最小及最小值是多少？先用MATLAB语言的编辑器编写求解该问题的程序如下：%把函数写成MATLAB语言表达式fun=’100*(X(2>-X(1>*X(1>2+(1-X(1>>2%猜自变量的初值X0=[-1 2]。

%所有选项取默认值options=[ ]；%调用最优化函数进行计算。

%函数最小值存放在数组元素options(8>中%与极值点对应的自变量值存放在向量X里%计算步数存放在数组元素options(10>中[X,options]=fmins(fun,X0,options>；%显示与极值点对应的自变向量X的值。

%显示函数最小值options(8>%显示函数计算步数options(10>把上面这段程序保存为m文件，然后用“Tools”菜单中的“Run”命令行这段程序，就可以轻松的得到如下结果：X=9.999908938395383e-0019.99982742178110e-001ans=1.706171071794760e-001ans=195显然，计算结果与理论结果的误差小到e-10级,这里调用了MATLAB的最优化函数fmins(>,它采用Nelder-Mead的单纯形算法，就是因为这个函数的采用，使最小值问题的解算变得非常简单。

3．机械优化设计应用实例机械优化设计把数学规划理论与数值方法应用于设计中，用计算机从大量可行方案中找出最优化设计方案，从而大大提高设计质量和设计效率。

MATLAB 具有解决线性规划和非线性规划、约束优化和无约束优化问题的内部函数，因而可以完成这一功能。

现举一例：螺栓组联结的优化设计如图4所示的压力容器螺栓组联接中，已知D 1= 400mm,D 2 =250mm ，缸内工作压力为p=1.5 MPa ，螺栓材料为35号钢，σs =320Mpa,安全系数S=3,取残余预紧力Q ’p =1.6F,采用铜皮石棉密封垫片。

现从安全、可靠、经济的角度来选择螺栓的个数n 和螺栓的直径d 。

3．1 设计问题分析若从经济性考虑，螺栓数量尽量少些、尺寸小些，但这会使降低联结的强度和密封性，不能保证安全可靠的工作；若从安全、可靠度考虑，螺栓数量应多一些、尺寸大一些为好，显然经济性差，甚至造成安装扳手空间过小，操作困难。

为此，该问题的设计思想是：在追求螺栓组联结经济成本最小化的同时，还要保证联结工作安全、可靠。

3 ．2 设计变量 目标函数 约束条件3．2 .1 设计变量 选取螺栓的个数n 和直径d(mm)为设计变量:T 21T ]x [x ]d [n X ==3．2 .2 目标函数 追求螺栓组联结经济成本C n 最小为目标。

而当螺栓的长度、材料和加工条件一定时，螺栓的总成本与nd 值成正比，所以本问题优化设计的目标函数为min F(X) = C n = n d = x 1x 2① 强度约束条件 为了保证安全可靠地工作，螺栓组联结必须满足强度条件][32.521σπσ≤=d Qca ； 其中Mpa S s 106.3320][===σσ； n n p n D F F F F Q Q p πππ6093742505.16.246.26.26.1222'=⨯=⨯==+=+= N ；对于粗牙普通螺纹：由文献[3]推荐，小径 d 1=0.85d 所以，强度约束条件为：0106146192106146192106105624)(2212211≤-=-=-=x x nd nd X g ② 密封约束条件 为了保证密封安全，螺栓间距应小于10d ，所以，密封约束条件为：01040010)(2112≤-=-=x x d n D X g ππ ③ 安装扳手空间约束条件 为了保证足够的扳手空间，螺栓间距应大于5d ，所以，安装约束条件为：040055)(1213≤-=-=x x n D d X g ππ ④ 边界约束条件 0)(14≤-=x X g ；0)(25≤-=x X g3．3 ．3 建立数学模型综上所述，本问题的数学模型可表达为：设计变量：T 21]x [x X =目标函数：min F(X) = x 1x 2约束条件： s.t. 0)(≤X g i ( i = 1, 2, 3, 4, 5,)现运用MATLAB 的优化函数进行求解 :先编写M 文件function [c,ceq]=mynas(x)c(1)=/(x(1)*x(2)^2)-106; % 非线性不等式约束c(2)=400*pi/x(1)-10*x(2);c(3)=-400*pi/x(1)+5*x(2);ceq=[]; % 非线性等式约束在MATLAB 命令窗口输入:fun='x(1)*x(2)'; % 目标函数x0=[4,6]; % 设计变量初始值A=[-1,0;0,-1]; % 线性不等式约束矩阵b=[0;0];Aeq=[]; % 线性等式约束矩阵beq=[];lb=[]; % 边界约束矩阵ub=[];[x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,@mynlsub) % 调用有约束优化函数运行结果如下:x = 11.4499 10.9751fval = 125.6637所以，该问题优化结果为：n =11.4499 ,d = 10.9751，目标函数最小值：F(X)= 125.6637。

MATLAB在机械设计与动力学仿真中的应用实例1. 引言机械设计与动力学仿真是现代工程领域非常重要的一个环节。

通过仿真软件可以在设计前对机械系统进行全面的分析和验证，大大减少了实际试制的时间和成本。

而MATLAB作为一种功能强大的科学计算软件，被广泛应用于机械设计与动力学仿真中。

本文将通过几个实际应用例子来展示MATLAB在这一领域的应用。

2. 机械结构分析机械结构的分析是机械设计的基础。

MATLAB提供了各种方法和工具，可以帮助工程师对机械结构进行静力学和动力学分析。

例如，可以利用MATLAB的有限元分析工具对机械结构进行强度校核。

通过输入结构的几何参数和材料性质，MATLAB可以计算出结构的应力和变形情况，从而判断是否满足设计要求。

此外，还可以利用MATLAB的多体动力学分析工具对机械结构的振动和冲击响应进行模拟和优化，以确保结构的安全性和可靠性。

3. 机械传动系统分析机械传动系统是机械设备中的重要组成部分，对于许多机械设备的运转效果和精度起着至关重要的作用。

MATLAB可以对不同类型的机械传动系统进行仿真分析，从而帮助工程师优化设计参数和减小误差。

例如，可以利用MATLAB的信号处理工具箱对传动系统中的振动和噪音进行分析和消除，提高系统的稳定性和准确性。

此外，还可以利用MATLAB的优化工具箱对传动系统的传动比、齿轮模数等参数进行优化，以满足设计要求。

4. 机械控制系统仿真机械控制系统在现代机械设备中起着至关重要的作用。

MATLAB提供了强大的控制系统设计和仿真工具，可以帮助工程师进行各种机械控制系统的仿真分析和优化设计。

例如，可以利用MATLAB的控制系统工具箱对机械控制系统的稳定性和性能进行评估和改进。

此外，还可以利用MATLAB的仿真工具对机械控制系统进行实时仿真，通过改变输入信号，观察输出响应，从而优化控制算法和参数。

5. 系统性能优化在机械设计与动力学仿真中，系统性能优化是一个重要的目标。

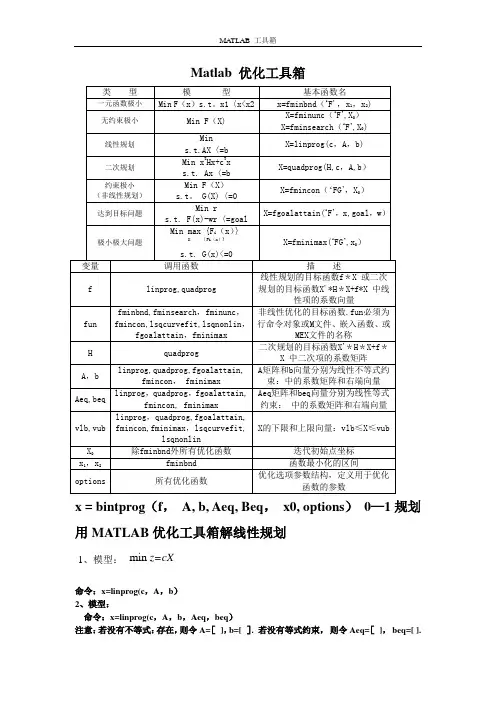
Matlab 优化工具箱x = bintprog （f ， A, b, Aeq, Beq ， x0, options ） 0—1规划 用MATLAB 优化工具箱解线性规划命令：x=linprog(c ，A ，b ） 2、模型：命令：x=linprog(c ，A ，b ，Aeq ，beq ） 注意：若没有不等式：存在，则令A=［ ]，b=[ ］. 若没有等式约束， 则令Aeq=［ ]， beq=[ ].min z=cX1、模型：3、模型：命令：［1］x=linprog（c，A，b，Aeq，beq，VLB，VUB）[2］x=linprog（c，A，b，Aeq,beq，VLB，VUB, X0）注意：［1] 若没有等式约束，则令Aeq=[ ］，beq=［]. [2]其中X0表示初始点4、命令:［x,fval]=linprog（…）返回最优解ｘ及ｘ处的目标函数值fval.例1 max解编写M文件小xxgh1。

m如下：c=［-0.4 —0。

28 —0.32 —0.72 -0.64 -0。

6］；A=[0。

01 0.01 0.01 0.03 0。

03 0.03;0。

02 0 0 0。

05 0 0;0 0。

02 0 0 0。

05 0;0 0 0.03 0 0 0。

08］；b=[850；700；100;900]；Aeq=[]; beq=［];vlb=[0；0；0;0;0;0]；vub=[］；[x，fval］=linprog(c,A，b，Aeq，beq,vlb,vub)例2解: 编写M文件xxgh2.m如下：c=[6 3 4］；A=[0 1 0]；b=[50];Aeq=［1 1 1］；beq=［120];vlb=[30,0,20］;vub=［];［x，fval]=linprog（c,A,b,Aeq，beq,vlb，vub例3 (任务分配问题）某车间有甲、乙两台机床，可用于加工三种工件。

假定这两台车床的可用台时数分别为800和900，三种工件的数量分别为400、600和500，且已知用三种不同车床加工单位数量不同工件所需的台时数和加工费用如下表.问怎样分配车床的加工任务，才能既满足加工工件的要求,又使加工费用最低？解设在甲车床上加工工件1、2、3的数量分别为x1、x2、x3，在乙车床上加工工件1、2、3的数量分别为x4、x5、x6。

机械优化设计MATLAB程序
1.建立目标函数和约束条件
在机械优化设计中，目标函数是需要最小化或最大化的量，可以是机械结构的重量、成本、应力等。

约束条件是指机械结构必须满足的条件，例如最大应力、最小挠度等。

在MATLAB中通过函数来定义目标函数和约束函数。

2.选择优化算法
MATLAB提供了多种优化算法，例如遗传算法、粒子群算法、模拟退火算法等。

根据实际情况选择合适的优化算法。

3.设计参数和变量范围
机械结构的优化设计通常涉及到多个参数和变量，如尺寸、材料等。

在MATLAB中通过定义参数和变量范围来限制优化过程中的空间。

4.编写优化程序
在MATLAB中，可以使用优化工具箱的相关函数来编写机械优化设计程序。

程序的基本结构包括定义目标函数、约束函数、参数和变量范围，并选择合适的优化算法进行求解。

5.运行优化程序
在编写完成程序后，可以通过运行程序来开始优化过程。

MATLAB会根据设定的目标函数和约束条件进行，并最终得到最优解。

6.分析优化结果
优化程序运行完成后，可以通过MATLAB提供的分析工具对优化结果进行评估。

可以通过绘制图表、计算相关指标等方式对结果进行分析和比较。

7.进一步优化和改进
根据优化结果，可以对机械结构进行进一步优化和改进。

可以调整参数和变量范围，重新运行优化程序，直到得到满意的结果。

总之，以上是一种用MATLAB编写机械优化设计程序的基本流程。

通过合理地利用MATLAB提供的工具和函数，可以帮助工程师进行机械结构的优化设计，提高设计效率和准确性。

机械优化设计MATLAB程序机械优化设计MATLAB程序引言机械优化设计是现代工程领域中的重要课题，通过采用数值方法和优化算法，可以实现对机械产品设计的自动化和优化。

MATLAB 作为一种功能强大的科学计算软件，为机械优化设计提供了丰富的工具和函数。

本文将介绍如何使用MATLAB编写机械优化设计程序，并讨论如何应用MATLAB进行机械优化设计。

MATLAB的优势与其他科学计算软件相比，MATLAB具有许多优势：1. 丰富的工具箱：MATLAB包含了各种各样的工具箱，涵盖了数值计算、优化、曲线拟合、数据可视化等领域，这些工具箱为机械优化设计提供了强大的支持。

2. 简单易用的编程语言：MATLAB使用的编程语言是一种高级语言，语法简单易懂，对于初学者而言非常友好。

即使没有编程经验，用户也能够快速上手。

3. 丰富的函数库：MATLAB拥有丰富的函数库，用户可以直接调用这些函数来完成各种任务，无需从零开始编写代码。

4. 广泛的应用领域：MATLAB在工程、科学、金融等领域得到了广泛的应用，拥有一个庞大的用户社区。

用户可以通过查看官方文档、参与用户社区等途径获取帮助和支持。

机械优化设计的步骤机械优化设计一般包括以下几个步骤：1. 建立数学模型：首先需要建立机械系统的数学模型，该模型可以基于物理原理或实验数据。

通过建立数学模型，可以将机械系统的性能指标与设计变量进行数学描述。

2. 确定优化目标：根据机械系统的需求和限制条件，确定优化目标。

优化目标可以是多个，如最小化能量损失、最小化材料使用量等。

3. 选择优化算法：基于问题的性质选择合适的优化算法。

常用的优化算法包括遗传算法、粒子群算法、梯度下降算法等。

4. 编写MATLAB代码：根据以上步骤，编写MATLAB代码实现机械优化设计。

MATLAB提供了丰富的工具箱和函数来辅助编写优化算法的代码。

编写机械优化设计MATLAB程序的步骤以下是编写机械优化设计MATLAB程序的一般步骤：1. 导入必要的工具箱和函数库：```% 导入优化工具箱import optim.% 导入其他必要的函数库import matlab.```2. 建立数学模型：根据机械系统的特点和要求，建立相应的数学模型。

matlab在机械优化设计中的应用一、引言随着科技的不断发展，机械优化设计在工程领域中得到了广泛的应用。

而在机械优化设计中，matlab作为一款强大的数学软件，在优化算法的实现和结果分析等方面具有很大的优势。

本文将探讨matlab在机械优化设计中的应用。

二、matlab在机械优化设计中的基础知识1. matlab基础知识Matlab是一种交互式数值计算环境和编程语言，可用于科学计算、数据分析和可视化等多个领域。

Matlab有着丰富的函数库和工具箱，可进行各种数学运算、统计分析、图像处理、信号处理等操作。

2. 机械优化设计基础知识机械优化设计是指通过运用数学模型和计算方法对机械结构进行全面分析和综合考虑，以达到最佳性能指标或最小成本等目标。

其中包括了多目标规划、遗传算法、神经网络等多种方法。

三、matlab在机械优化设计中的应用1. 优化算法实现Matlab提供了各种常见的数值计算方法和最优化方法，如线性规划、非线性规划、遗传算法等。

通过Matlab的函数库和工具箱，可以轻松地实现各种优化算法，并且可以根据具体需求进行自定义编程。

2. 结果分析Matlab在结果分析方面也有很大的优势。

通过Matlab的图形界面，可以绘制各种图表，如散点图、折线图、柱状图等。

同时，Matlab还提供了多种统计分析方法，如方差分析、回归分析等，可以对优化结果进行全面的统计分析。

3. 机械结构设计Matlab还可以用于机械结构设计。

通过建立机械结构模型，并运用Matlab中的有限元分析工具箱进行模拟计算，可以得到机械结构在不同载荷下的应力和变形情况。

这些数据可以进一步用于优化设计和结构改进。

4. 案例应用以一台压缩机为例，利用Matlab进行机械优化设计。

首先建立压缩机的数学模型，并根据实际需求设置相关参数和目标函数。

然后采用遗传算法对压缩机进行优化设计，并得到最佳设计方案。

最后利用Matlab中的有限元分析工具箱对最佳设计方案进行模拟计算，并得到应力和变形等数据。

机械优化设计MATLAB程序正文：⒈前言⑴研究背景机械优化设计是一种在机械工程领域中被广泛应用的方法，旨在通过使用数学模型和优化算法来改进机械系统的性能。

MATLAB是一种强大的数值计算和编程工具，可以用于开发机械优化设计程序。

⑵目的和范围⒉问题描述⑴设计需求在开始编写机械优化设计程序之前，需要明确设计需求，即需要实现的机械系统的性能指标或目标。

这些需求可以包括系统的功率、效率、噪声、振动等方面。

⑵优化目标根据设计需求，确定最终优化目标。

例如，通过调整机械系统的参数来最大化系统的效率、最小化系统的振动等。

⒊数学模型⑴设计变量设计变量是机械系统中可以调整的参数。

需要对设计变量进行定义和范围设定，以确保优化算法能够在合理的范围内搜索最优解。

⑵约束条件约束条件是在进行优化时必须满足的条件。

这些条件可以包括设计变量的边界条件、约束函数等。

在编写MATLAB程序时，需要将这些约束条件作为输入参数。

⒋算法选择与实现⑴优化算法选择根据优化目标和系统的特点，选择合适的优化算法。

常见的优化算法包括遗传算法、粒子群优化算法、模拟退火算法等。

⑵优化算法实现根据选择的优化算法，编写MATLAB程序实现优化过程。

程序应包括目标函数的定义、算法的参数设置、迭代过程和终止条件等。

⒌算法验证与结果分析⑴数据采集与处理在进行机械优化设计实验时，需要采集相应的实验数据，并对数据进行处理。

这些数据可以包括设计变量的调整情况、系统性能指标的变化等。

⑵结果分析基于采集到的数据，分析和比较不同优化算法的性能。

可以绘制图表展示优化过程和结果的变化，以便于进一步分析和优化。

⒍结论与展望总结机械优化设计MATLAB程序的设计过程和结果，对实验结果进行分析，并提出未来改进和研究的方向。

1、本文档涉及附件：附件1：MATLAB程序代码示例附件2：数据采集记录表2、本文所涉及的法律名词及注释：机械优化设计：指利用数学模型和优化算法改善机械系统性能的方法。

轴承优化算法 matlab 程序轴承优化算法的Matlab程序在机械领域中，轴承是一种用于减少摩擦和支撑转动运动的重要元件。

轴承的性能直接影响到机械设备的运行效率和寿命。

为了提高轴承的性能，并解决实际工程问题，优化算法是一种常用的工具。

本文将介绍一种使用Matlab编写的轴承优化算法程序。

轴承优化算法的设计目标是通过调整设计参数以达到最佳性能。

优化算法基于数学模型和计算机算法，通过迭代寻找最佳的解。

对于轴承而言，常见的设计参数包括几何尺寸、材料、润滑方式等。

首先，我们需要创建一个Matlab函数来定义轴承的数学模型。

例如，我们可以使用Reynolds方程来描述轴承的润滑情况。

根据Reynolds方程，轴承的载荷和润滑剂的粘度将影响到摩擦和热平衡。

函数的输入参数可以包括轴承的几何参数、载荷、转速和润滑剂的粘度等。

接下来，我们可以选择一个适当的优化算法来解决轴承的优化问题。

常见的优化算法包括遗传算法、粒子群算法、模拟退火算法等。

对于大规模优化问题，遗传算法通常是较好的选择。

在Matlab中，可以使用Global Optimization Toolbox来实现这些算法。

以遗传算法为例，需要定义目标函数、约束条件和遗传算法的参数。

然后，我们可以使用Matlab编写主程序来调用上述的函数和算法。

主程序负责设置优化问题的目标函数和约束条件，以及调用遗传算法进行求解。

在每次迭代之后，程序将输出当前的最佳解以及对应的目标函数值。

在轴承优化算法程序中，还可以加入一些其他的功能和模块，以提高其实用性和可扩展性。

例如，可以添加一个用户界面模块，使用户可以方便地输入轴承的参数和运行优化算法。

还可以添加一个结果分析模块，用于评估不同参数组合的性能，并提供可视化的结果展示。

最后，需要对程序进行验证和优化。

可以通过比较优化算法的结果和现有的经验数据来验证程序的正确性。

如果发现程序存在性能问题，可以通过调整参数或改进算法来进行优化。

一维无约束优化算法——二次插值法二次插值法亦是用于一元函数在确定的初始区间内搜索极小点的一种方法。

它属于曲线拟合方法的范畴。

一、基本原理在求解一元函数的极小点时，常常利用一个低次插值多项式来逼近原目标函数，然后求该多项式的极小点(低次多项式的极小点比较容易计算)，并以此作为目标函数的近似极小点。

如果其近似的程度尚未达到所要求的精度时，可以反复使用此法，逐次拟合，直到满足给定的精度时为止。

常用的插值多项式为二次或三次多项式，分别称为二次插值法和三次插值法。

这里我们主要介绍二次插值法的计算公式。

假定目标函数在初始搜索区间中有三点、和，其函数值分别为、和(图1}，且满足，，即满足函数值为两头大中间小的性质。

利用这三点及相应的函数值作一条二次曲线，其函数为一个二次多项式，式中、、为待定系数。

图1根据插值条件，插值函数与原函数在插值结点、、处函数值相等，得（2）为求插值多项式的极小点，可令其一阶导数为零，即（3）解式(3)即求得插值函数的极小点（4）式(4)中要确定的系数可在方程组(2)中利用相邻两个方程消去而得:（5）（6）将式(5)、(6)代入式(4)便得插值函数极小值点的计算公式：（7）把取作区间内的另一个计算点，比较与两点函数值的大小，在保持两头大中间小的前提下缩短搜索区间，从而构成新的三点搜索区间，再继续按上述方法进行三点二次插值运算，直到满足规定的精度要求为止，把得到的最后的作为的近似极小值点。

上述求极值点的方法称为三点二次插值法。

为便于计算，可将式(7)改写为（8）式中：（9）（10）二．程序框图)/()(3211212212131a a c a a y y c a a y y c ----←--←)/(5.02131c c a a a p -+←)(p p a f y ←?22ε<-y y y p?0)(2>-h a a p ?2p y y <pp y y a a ←←**2*2*y y a a ←←结束?2p y y <?2p y y ≥pp y y a a y y a a ←←←←222121pp y y a a ←←33pp y y a a y y a a ←←←←222323pp y y a a ←←11否否否否否是 是是 是是给定hy y y a a a ,,,,,,313,212ε开始三．例题及其程序代码1.用二次差值法求f(α)=sinα在4≤α≤5上的极小值2.程序(1) function y=f(x)y=sin(x); …………………….%定义f文件（2）c1=(y3-y1)/(x3-x1);c2=((y2-y1)/(x2-x1)-c1)/(x2-x3);ap=0.5*(x1+x3-c1/c2);yp=f(ap);……………………%定义f1文件（3）x1=4;x2=4.5;x3=5;e=0.001;y1=f(x1);y2=f(x2);y3=f(x3); ………………%确定初始差值节点h=0.1;c1=(y3-y1)/(x3-x1);c2=((y2-y1)/(x2-x1)-c1)/(x2-x3);ap=0.5*(x1+x3-c1/c2);yp=f(ap);…% 计算二次插值函数极小点while (abs((y2-yp)/y2)<e)....%判断迭代终止if ((ap-x2)*h>0) 条件if(y2>=yp)x1=x2;y1=y2;x2=ap;y2=yp;f1;elsex3=ap;y3=yp;f1;endelseif (y2>=yp)x3=x2;y3=y2;x2=ap;y2=yp;f1;elsex1=ap;y1=yp;f1;…………………..%缩短搜索区间endendif (y2<yp)xo=x2;yo=y2;elsexo=ap;yo=yp;endxoyo二次插值法四结果分析经过MA TLAB运算，结果如上，与解析法运算结果相同，说明二次差值的效果很好。

优化设计Matlab实例解析MATLAB是一种基于矩阵运算的高级编程语言和环境，被广泛应用于各个领域的科学计算和工程问题。

在实际应用中，我们经常面临优化设计的任务，即在给定的限制条件下，寻找最优的解决方案。

优化设计可以应用于诸如控制系统设计、信号处理、图像处理、机器学习等问题中。

下面我们以一个简单的例子来说明如何使用MATLAB进行优化设计。

假设我们有一个矩形花园，每边有一定的长度，我们希望找到一个长和宽使得花园的面积最大化。

令矩形花园的长和宽分别为x和y，由于边长有限制条件，即x的范围为0到20，y的范围为0到10，同时花园的长度之和不得超过30。

我们的目标是找到一组合适的x和y，使得面积A 最大。

在MATLAB中，我们可以使用优化工具箱中的函数fmincon来求解这个问题。

以下是具体的实现步骤：1.创建目标函数首先，我们需要定义一个目标函数来评估每组x和y的解决方案。

在这个例子中，我们的目标是最大化矩形花园的面积，因此我们的目标函数可以简单地定义为A=x*y。

```matlabfunction A = objective(x)A=-x(1)*x(2);%最大化面积，取负号end```2.设置限制条件接下来，我们需要定义限制条件。

在这个例子中，我们需要考虑两个限制条件，即x和y的范围以及长度之和的限制。

我们可以使用函数fmincon提供的constr函数来定义这些限制条件。

```matlabfunction [c, ceq] = constr(x)c=[x(1)-20;%x的上限x(2)-10;%y的上限x(1)+x(2)-30];%长度之和的限制ceq = []; % 无等式限制end```3.求解问题有了目标函数和限制条件，我们可以使用fmincon函数来求解问题。

```matlabx0=[10,5];%初始猜测lb = [0, 0]; % x和y的下限ub = [20, 10]; % x和y的上限options = optimoptions('fmincon', 'Display', 'iter'); % 设置选项```在这里，我们使用了初始猜测x0、x和y的上下限lb和ub以及其他选项。