功角特性的计算公式

2020.01目录二发电机功角特性的表达形式三发电机迟相、进相运行特性一、发电机功角特性的定义功角特性的常用术语电机带上对称负载后，电枢绕组（定子线圈）有电流通过，产生电枢磁动势及相应电枢磁场，其基波在气隙中使气隙磁势的分布发生变化，从而使气隙磁场和感应电势发生变化，这种影响称为电枢反应。

实际上是坐标轴，而不是实际的轴，在永磁同步电机控制中，为了能够得到类似直流电机的控制特性，在电机转子上建立了一个坐标系，此坐标系与转子同步转动，取转子磁场方向为d 轴（直轴），垂直于转子磁场方向为q 轴（交轴）。

由励磁电流产生的磁场而在定子绕组中单独产生的电动势，为非合成电动势。

功角特性的常用术语直轴同步电抗包含漏抗和直轴电枢反应电抗X ad 。

表示了漏抗和直轴电枢反应对气隙磁场的影响作用大小。

对应同步电机交轴磁阻的交轴电枢反应电抗X aq 与定子漏抗之和。

指的是当电枢磁势F a 的轴线既不和直轴又不和交轴重合时，可以把电枢磁势F a 分解成直轴分量F ad 和交轴分量F aq ，然后分别求出直轴和交轴磁势的电枢反应，最后再把它们的效果叠加起来。

是励磁电动势领先于机端电压的角，是表征同步发电机运行状态和判别电力系统稳定性的重要参量。

功角特性发电机电抗(X d、X q)、励磁电动势(E0)和机端电压(U)一定的情况下，发电机的有功功率(P)和功角(θ)的关系特性，即P em = f (θ)显示电机内部电磁关系的电磁功率表达式，确定稳态运行时发电机所能发出的最大的电磁功率。

1、表示E0和U这两个时间相量之间的时间相位差角；2、表示产生E0的主磁极磁势F f与产生端电压U的定子合成磁势F u之间的空间相位角。

二、发电机功角特性的表达形式发电机的负载运行根据双反应理论，凸极同步发电机不饱和运行时的基本电磁关系为：转子励磁电流I f 磁动势F f 磁通Φ0励磁电动势E 0定子三相电流I磁动势F ad 磁通Φad 直轴电动势E ad 磁动势F aq 磁通Φaq交轴电动势E aq 交轴分量I q 直轴分量I d漏磁通Φσ电动势E δ电动势E σI d 轴E 0q 轴I d I q 发电机的负载运行根据凸极同步发电机不饱和运行时的基本电磁关系，可做出对应的相量图，如下所示：根据相量图，可以写出凸极同步发电机电动势平衡方程为：∑E=E 0+E ad +E aq +E σ =U+IR a （2.1）E ad E aq E σIR a UΦ0Φaq Φad Φσ不计饱和时，有如下关系式：将电动势E 写成负电抗压降的形式，则有如下表达式：θ ψ发电机的负载运行将负电抗压降表达式带入式2.1，可改写如下：E 0=U+IR a –E ad – E aq – E σ =U+IR a +jI d （X ad +X σ）+jI q （X aq +X σ） =U+IR a +jI d X d + jI q X q E 0jI d X djI q X qIR a Ud 轴q 轴Φ0Φaq I Φad I d I qΦσ其中： X d = X ad +X σ X q = X aq +X σ重新绘制相量图，可做出如右图所示：机组运行过程中，由于定子绕组电阻R a 远远小于交轴同步电抗X q 和直轴同步电抗X d ，故可忽略定子绕组铜耗，重新绘制相量图，如下所示：忽略铜耗之后，发电机电磁功率与输出功率可认为近似相等，则：P em =P 2=mUIcos =mUIcos （ ψ -θ） =mUI （cos ψ cos θ +sin ψ sin θ ） =mU I q cos θ+mUI d sin θ由凸极同步发电机相量图中可知：负载运行下的功率计算E 0jI d X djI q X qU d 轴q 轴Φ0Φaq I Φad I dI qΦσθ ψ功角特性的一般表达式E 0jI d X djI q X qUd 轴q 轴Φ0Φaq I Φad I d I qΦσ机组运行过程中，由于定子绕组电阻远远小于交轴同步电抗和直轴同步电抗，故可忽略定子绕组铜耗，重新绘制相量图，如下所示：在保持E 0不变（即I f 不变），而电网电压U 和频率f 可视为恒定，故可做出如图所示的曲线功角特性的一般表达式对于隐极发电机，转子磁极不论哪个角度都是圆的,所以电抗只有一个值，由式2.1可得隐极机的电动势表达式为：E0=U+IR a+jI X a + jI X σ=U+IR a+jIX t其中X t= X a+ X σ令X d=X q=X t，可得隐极机的功角特性表达式：P em = E0USinθ/X t三、发电机进相、迟相运行特性无功功率调节与V形曲线当发电机带感性负载时，电枢反应具有去磁作用，这时为了维持发电机机端电压恒定，就必须增大励磁电流，以补偿电枢反应的影响。

所示。

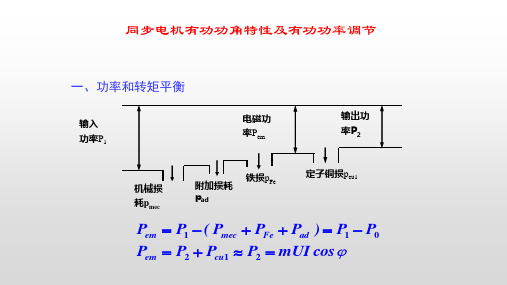
为自原动机向发动部分与空气的摩擦及通风设备的损耗，总计为机械损耗,为通过电磁感应作用转变为定子绕组上的电功率，如果是负载运行，定子绕组中还存在定子铜耗，＝－就是发电机的输出功率。

磁电势和端电压之间相角差。

功角认为≈+，对应于转子磁势，对应于电枢磁势，所以可近似认为端电压由合成磁势=+所感应。

和之间的空间相角差即为和之间的时行时，为电网电压，其大小和频率不变，对应的合成磁势总是以同步速度旋转，因此功角的大小只能由转子磁势的角速稳定运行时，和之间无相对运动，功角特性指的是电磁功率随功角系曲线=f(令可以求出对应于最大电磁功率的功角,一般来说凸极电机的在90之间。

功角特性=f(率决定，恒等于同步转速，即，发电机的电磁转矩和电磁功率之间成正比关系：电磁转矩与原动机提供的动力转矩相平衡其中为空载转矩因摩擦、风阻等引起的阻力转矩）。

到范围内时，随着的增大，亦增大，同步发电机在这一区间能够稳定运行。

δ >时，的增大，反而减小，电磁功率无法与输入的机械功率相平衡，发电机转速越来越大，发电机将失去同步，故在这的有功功率的极限是。

当<时发电机可以稳定运行；<发电机不能稳定运行。

无功功率的调节▴接在电网上运行的负载类型很多，多数负载除了消耗有功功率外，还要消耗电感性无功功率，如接在电网上运行的异步电机、变压器、电抗器等。

所以电网除了供应有功功率外，还要供应大量滞后性的无功功率。

▴电网所供给的全部无功功率一般由并网的发电机分担。

▴电网的电压和频率不会因为一台发电机运行情况的改变而改变，即并网发电机的电压和频率将维持常数。

▴如果保持原动机的拖动转矩不变(即不调节原动机的汽门、油门或水门)，那么发电机输出的有功功率亦将保持不变。

▴图17.11给出了有功功率不变而空载电势变化时，隐极发电机的电势相量图，和的矢端必须落在直线AB和CD上。

①如果在某一励磁电流时，正好与平行，此时无功功率为零,发电机输出的全部是有功功率，发电机正常励磁。

发电机功角特性同步发电机的功角特性是指发电机的有功功率(P)、无功功率(Q)与发电机电抗(Xd、Xq)、内电动势(Ed)、机端电压(U)和功角(δ)的关系特性。

(1) 发电机功角特性。

1)有功特性：发电机输出的有功功率为：P = Ed*U*Sinδ/Xd + U2*Sin2δ*(1/Xq – 1/Xd)/22)无功特性：发电机输出的无功功率为Q = Ed*U*Cosδ/Xd + U2*Cos2δ*(1/Xq – 1/Xd)/2 - U2*(1/Xq + 1/Xd)/2(2)隐极发电机功角特性。

对于隐极发电机，取Xd = Xq。

1) 有功特性：发电机输出的有功功率为P = Ed*U*Sinδ/XdP代表发电机输出的有功功率，对发电机产生制动的电磁转矩。

在一定的电压和励磁电流下，发电机的有功功率P与功角多是函数关系。

2) 无功特性：发电机输出的无功功率为Q = Ed*U*Cosδ/Xd + U2/Xd式中第一项与Ed和δ有关，它表示由转子励磁经电磁感应传递到定子的无功功率，值随δ角的余弦而改变。

由于U*Cosδ = Ed – Id*Xd，则上式第一项可改写为Ed2/Xd – Ed*Id第二项与Ed和δ无关，它代表发电机维持一定端电压U所需励磁的无功功率。

因为Ed = U*Costδ + Id*Xd，故Q = Ed*Id – Id2*Xd，即供给电网的无功功率等于主磁通转换的无功功率减去电枢绕组电感的无功损耗。

由此可见，增加发电机的励磁电流(即加大Ed)，便可增大发电机的无功输出。

对于隐极发电机，取Xd = Xq。

此时发电机输出的有功功率为P = Ed*U*Sinδ/Xd但当δ = 90°时，P为最大功率（即极限功率）。

功角特性是同步发电机的基本特性之一。

通过功角特性，可以确定稳态运行时发电机所能发出的最大电磁功率。

功角特性还是研究同步发电机并联运行时经常应用的重要特性。

功角的物理含义功角有两重含义：一是表示E和U这两个时间相量之间的时间相位差角；二是表示产生E0的主磁极磁势Ff与产生端电压U的定子合成磁势Fu之间的空间相位角，即转子磁极轴线与定子合成等效磁极轴线之间的空间夹角(电角度)。

发电机功角的实时计算方法1、发电机的功角根据电机学原理，在忽略电机电枢电阻情况下，隐极发电机的有功功率和无功功率可分别表示为：（1）P=E q Ux d sinδ (2)Q=E q Ux dcosδ+U2x dP x d=E q U sinδQ x d= E q U cosδ+U2Q x d−U2=E q U cosδSo tanδ= P x d/( Q x d−U2)其中，U为发电机的端电压，E q为发电机的感应电势，x d为发电机的同步电抗，δ为感应电势与端电压间的相位夹角（称为发电机的功率角或功角），P为有功功率，Q为无功功率。

当感应电势和电压恒定时，传输的有功功率是功角δ的正弦函数。

功角δ在电力系统稳定中占据十分重要的地位，为保证发电机的静态稳定性，应使功率增量ΔP和角度增量Δδ的比值为正，即静态稳定性的判据为ΔP/Δδ>0。

当电力系统受扰动，发电机定子磁场与转子发生相对运动，发电机的功角δ发生变化，若功角经过振荡后能稳定在某一个数值，则表明发电机重新恢复了同步运行，系统具有瞬时稳定性；若电力系统受大扰动，发电机功角不断增大，发电机不再保持同步，则系统失去瞬时稳定。

因此，可用电力系统受大扰动后功角随时间变化的特性δ=f(t)作为瞬时稳定的判据，记录实时功角信息，显示功角的变化，对功角摆动超过设定界限进行报警，以便于及时处理可能发生的不稳定情况。

发电机的功角δ反映发电机转子的相对运动，是判断发电机是否同步运行的依据。

要确定发电机功角δ，有两种方法1、直接测量法（1-5）；2、计算法（6-9）。

1.1直接测量法，直接测量法是指根据功角δ所表征的物理意义，直接测量发电机转子的位置信号，进而得到功角δ值。

如图1所示，功角δ具有双重物理意义：发电机的感应电势E0和端电压U之间的时间相角；主极磁场F f和气隙合成磁场Fδ之间的空间夹角。

在转子轴上确定一个固定的机械位置，如d（与d轴的相角为β），则d可间接代表E0的方向，E0与d间相角差为δ0=90°+β（δ为定相位角差）。

发电机功角公式在咱们探索发电机功角公式这个奇妙的世界之前，我先跟您讲讲我之前的一个小经历。

有一次，我去参观一个小型的发电厂，那里面各种设备轰隆隆地运转着，巨大的发电机让人不禁感叹科技的力量。

我站在一旁，看着技术人员认真地监测着各种数据，心中充满了好奇。

就在这时，一位老师傅注意到了我好奇的目光，走过来跟我聊起了天。

他指着那台正在稳定运行的发电机，笑着说：“这玩意儿可藏着不少学问呢！”咱先来说说发电机功角。

简单来讲，它就是发电机内电势和端电压之间的夹角。

那这个功角有啥用呢？它可是关系到发电机的稳定性、传输功率等重要指标的关键因素。

发电机功角公式，一般表示为：P = E * U * sinδ / X 。

这里的 P 代表发电机输出的有功功率，E 是发电机的内电势，U 是端电压，δ就是咱们说的功角，X 则是同步电抗。

这个公式看起来可能有点复杂，但咱们一点点来拆解。

就拿同步电抗 X 来说，它反映了发电机内部的电磁特性，就像是发电机的“个性标签”。

而内电势 E 和端电压 U 呢，它们的大小和相对位置决定了功角δ 的大小，进而影响着输出的有功功率 P 。

比如说，当功角δ 增大时，sinδ 的值也会增大，从而使输出的有功功率 P 增加。

但可别以为功角能无限增大，要是超过了一定限度，发电机就可能会失去稳定，出现各种问题。

在实际应用中，理解和运用这个公式可不简单。

就像在那个发电厂里，技术人员得时刻根据各种运行参数，结合这个公式来判断发电机的工作状态，及时调整和优化，以确保电力的稳定供应。

想象一下，如果不能准确掌握发电机功角公式，那电力系统可能就会像没头的苍蝇一样，乱了套。

家里的电灯可能会忽明忽暗，工厂的机器可能会突然停工，那可就麻烦大了！所以说，这个小小的公式，虽然看起来不起眼，但在电力世界里，它可是起着至关重要的作用。

咱们得好好琢磨，才能让发电机乖乖地为我们服务，源源不断地提供稳定可靠的电力。

总之，发电机功角公式虽然有点复杂，但只要咱们耐心去理解，就能发现它背后隐藏的神奇规律，为我们的生活带来更多的光明和便利。

发电机功角计算公式发电机功角是同步发电机运行中的一个重要概念，它在电力系统的稳定性分析和运行控制中起着关键作用。

那咱就来好好聊聊发电机功角的计算公式。

咱先来说说啥是发电机功角。

简单来讲，功角就是发电机内电势与端电压之间的相位差。

这个相位差可不得了，它能反映出发电机输出功率的大小和稳定性。

发电机功角的计算公式通常涉及到一些复杂的电学参数。

一般来说，功角δ可以通过以下公式计算：δ = arctan（Q*Xd - P*Xq）/（E*U）。

这里面，P 是有功功率，Q 是无功功率，E 是发电机内电势，U 是端电压，Xd 是直轴电抗，Xq 是交轴电抗。

要说理解这个公式，还真得费点脑筋。

就好比我之前在一个电力系统的实验课上，老师让我们通过实际操作去理解这个公式。

当时我们小组面对着一堆复杂的仪器和线路，头都大了。

我们小心翼翼地调整着各种参数，记录下每一次的数据变化。

特别是在计算功角的时候，那真是一个数字一个数字地仔细核对，就怕出错。

有个同学因为粗心把一个数据写错了，结果整个计算都错了，大家不得不重新再来。

经过好一番折腾，我们终于算出了功角，那一刻的成就感真是无法形容。

再回到这个公式，其中有功功率 P 就像是发电机在努力工作输出的“实际成果”，无功功率 Q 则像是在为系统提供“后勤保障”。

而内电势E 和端电压 U 就像是两个在拔河的队伍，它们之间的较量通过功角δ体现出来。

直轴电抗 Xd 和交轴电抗 Xq 则反映了发电机内部的电磁特性，就好像是发电机自身的“性格特点”。

不同型号的发电机，这两个参数也会有所不同。

在实际的电力系统运行中，准确计算发电机功角非常重要。

它能帮助工程师们判断系统的稳定性，提前发现可能存在的问题，并采取相应的措施来保障电力的稳定供应。

总之，发电机功角计算公式虽然看起来复杂，但只要我们深入理解其中每个参数的含义，再结合实际的操作和应用，就能更好地掌握它，为电力系统的稳定运行贡献一份力量。

希望通过我的这番讲解，能让您对发电机功角计算公式有更清晰的认识。

高三物理功的知识点一、引言考生们，即将迎来高考物理考试，本文将为大家系统地介绍高三物理中与功相关的知识点。

希望通过学习和掌握这些知识点，能够在考试中取得好成绩。

二、功的基本概念1. 功的定义：功是力沿着力的方向作用于物体时所做的功。

2. 功的计算公式：功 = 力 ×距离× cosθ。

其中，力的单位为牛顿（N），距离的单位为米（m），角度θ的单位为弧度（rad）。

三、功的性质1. 正功与负功：当力和物体位移方向相同时，所做的功为正功；当力和物体位移方向相反时，所做的功为负功。

2. 功的巧算法则：a) 多次相同力的作用：总功等于各个力分别所做功的矢量和。

b) 多次作用的力的方向不同：总功等于各个力分别所做功的代数和。

c) 一物体受到多个力的作用：总功等于各个力分别作用于物体时所做功的矢量和。

四、功的特殊情况1. 重力做功：当物体在重力方向上运动时，重力会对物体做功，计算公式为：功 = 重力 ×上升或下降的高度。

2. 弹力做功：当弹簧或弹性物体发生形变时，弹力会对物体做功，功的大小等于形变时的弹力与位移的乘积。

3. 摩擦力做功：当物体受到摩擦力时，摩擦力会对物体做功，计算公式为：功 = 摩擦力 ×物体的位移。

4. 常用功的单位：国际单位制中，功的单位为焦耳（J），可用千焦（kJ）、兆焦（MJ）等较大单位表示。

五、功与能的关系1. 功与能的区别：功是对物体的描述，是一种物理量；而能是物体所具有的能够做功的能力，是一种性质。

2. 功与能的转化：根据能量守恒定律，功可以导致物体的能量转化。

例如，重力做的功可以使物体的重力势能或动能发生变化。

六、常见问题解析1. 什么情况下物体的功为零？当力和物体位移方向垂直时，力所做的功为零，即cosθ = 0。

2. 功与功率有何区别？功是对物体在力作用下移动的描述，是一个物理量；而功率是指在单位时间内所做的功，是功的时间变化率，单位为瓦特（W）。