不规则立体图形的表面积和体积

加油！有志者事竟成答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好! 经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！1五年级数学下册典型例题系列之期中专项练习：求不规则立体图形的表面积与体积（解析版）1．计算下面图形的表面积和体积。

【解析】（1）（10×6＋10×4＋6×4）×2＝（60＋40＋24）×2＝124×2＝248（cm2）10×4×6＝40×6＝240（cm3）（2）556⨯⨯＝25×6＝150（dm2）⨯⨯555＝25×5＝125（dm3）2．求下面图形的表面积和体积。

不规则立体图形的分类和计算一、不规则立体图形的定义及特点不规则立体图形是指那些没有规则几何形状的立体图形，它们由不规则的多边形组成。

不规则立体图形在生活中广泛存在，如天然石块、树枝、果实的形状等。

不规则立体图形的特点是形状复杂、无规律，但可以通过数学方法进行分类和计算。

二、不规则立体图形的分类1.根据组成元素分类：（1）单体不规则立体图形：由一个不规则的多边形组成，如天然石块、树枝等。

（2）组合不规则立体图形：由多个不规则多边形组成，如拼图、建筑物的外观等。

2.根据空间结构分类：（1）一维不规则立体图形：如线段、曲线等。

（2）二维不规则立体图形：如平面上的不规则多边形等。

（3）三维不规则立体图形：如立体拼图、建筑物等。

三、不规则立体图形的计算方法1.单体不规则立体图形的计算：（1）体积计算：通过排水法、溢水法等实验方法测量不规则立体图形的体积。

（2）表面积计算：将不规则立体图形切割成多个规则几何图形，计算每个规则图形的面积，再求和。

2.组合不规则立体图形的计算：（1）体积计算：分别计算每个单体不规则立体图形的体积，再求和。

（2）表面积计算：分别计算每个单体不规则立体图形的表面积，再求和。

四、不规则立体图形的实际应用1.建筑设计：建筑师利用不规则立体图形设计独特的建筑物，提高建筑物的美观性和实用性。

2.工业制造：在不规则立体图形的基础上，设计生产各种形状的零件、产品，满足工业生产的需求。

3.艺术创作：艺术家利用不规则立体图形进行绘画、雕塑等艺术创作，展现个性和创意。

4.自然科学研究：科学家通过研究不规则立体图形，探索自然界中的规律和奥秘。

总结：不规则立体图形的分类和计算是中学数学的重要内容，通过对不规则立体图形的认识和计算，可以提高学生的空间想象能力、创新思维能力和实际应用能力。

习题及方法：1.习题一：计算下列不规则立体图形的体积。

一个天然石块，测量其排水体积为200cm³。

答案：200cm³解题思路：根据题目所给的排水体积，直接得出天然石块的体积。

教育学科教师辅导讲义学员编号： 年 级： 课 时 数： 学员姓名： 辅导科目： 学科教师： 授课 类型T (立体图形相关知识点) C （典型例题试题讲解） T （拓展提高）授课日期时段教学内容知识点一：表面积1、长方体表面积=长x 宽× 2+ 宽× 高× 2+ 长×高× 2 字母公式：S=ax b× 2+ a× c× 2+ b×c× 2 或者：长方体的表面积 =( 长×宽 + 长×高 + 宽×高 ) × 2 。

字母公式：S=(ax b+ a× c+ b×c)× 22、正方体的表面积 =棱长×棱长×6。

字母公式：S=a ×a× 63、圆柱体的表面积：圆柱表面积=上底+下底+侧面（侧面面积=底面圆的周长×圆柱的高） 用字母表示：22s r ch π=+注：侧面积的求法：已知底面半径和高，rh π侧2s = 已知底面直径和高，dh π侧=s知识点二：体积1、长方体体积：长方体体积= ① 长×宽×高 （Ｖ＝ａｂｈ）② 底面积×高=横截面积×长 （V =sh ） 2、正方体的体积：正方体体积＝棱长×棱长×棱长检测题1：把一个圆柱的侧面展开，得到一个正方形．已知这个圆柱的高是10厘米，它的侧面积是（ ）平方厘米．A ．50B ．100C ．50πD ．100π答案：B检测题2．把一个棱长4厘米的正方体分割成两个长方体，表面积增加了______平方厘米．答案：64检测题3 一个正方体的棱长之和是48厘米，它的棱长是______厘米，表面积是______平方厘米，体积是______立方厘米． 答案：2 24 8检测题4 把两个棱长5厘米的正方体拼成一个长方体，这个长方体的表面积是______平方厘米．答案：250检测题5．一个练功房铺设了1600块长50厘米，宽10厘米，厚3厘米的木地板，这个练功房的面积有______平方米．答案：这个练功房的面积有80平方米．检测题6．圆柱的底面半径扩大2倍，高缩小到原来的21，它的体积就（ ）答案：扩大2倍检测题7．做一个圆柱体，侧面积是9.42平方厘米，高是3厘米，它的底面半径是______．答案：1.57cm一、专题精讲例1.如图是高为10厘米的圆柱，如果它的高增加4 厘米，那么它表面积就增加125.6平方厘米。

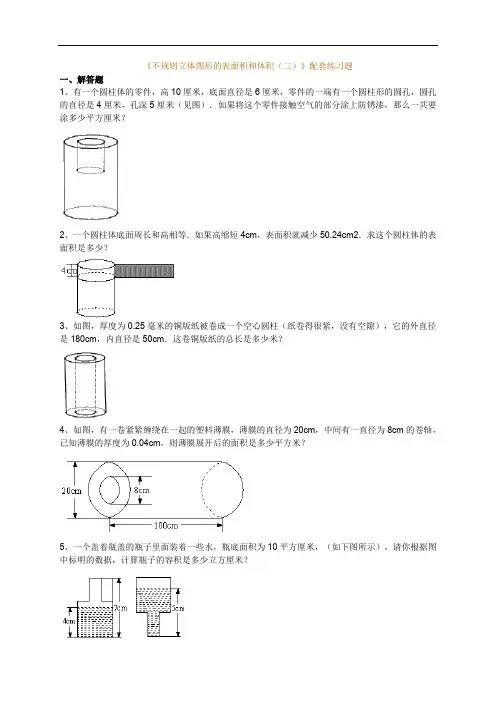
《不规则立体图形的表面积和体积（二）》配套练习题一、解答题1、有一个圆柱体的零件，高10厘米，底面直径是6厘米，零件的一端有一个圆柱形的圆孔，圆孔的直径是4厘米，孔深5厘米（见图）．如果将这个零件接触空气的部分涂上防锈漆，那么一共要涂多少平方厘米？2、一个圆柱体底面周长和高相等．如果高缩短4cm，表面积就减少50.24cm2．求这个圆柱体的表面积是多少？3、如图，厚度为0.25毫米的铜版纸被卷成一个空心圆柱（纸卷得很紧，没有空隙），它的外直径是180cm，内直径是50cm．这卷铜版纸的总长是多少米？4、如图，有一卷紧紧缠绕在一起的塑料薄膜，薄膜的直径为20cm，中间有一直径为8cm的卷轴，已知薄膜的厚度为0.04cm，则薄膜展开后的面积是多少平方米？5、一个盖着瓶盖的瓶子里面装着一些水，瓶底面积为10平方厘米，（如下图所示），请你根据图中标明的数据，计算瓶子的容积是多少立方厘米？6、一个酒精瓶，它的瓶身呈圆柱形（不包括瓶颈），如图．已知它的容积为26.4π立方厘米．当瓶子正放时，瓶内的酒精的液面高为6厘米．瓶子倒放时，空余部分的高为2厘米．问：瓶内酒精的体积是多少立方厘米？合多少升？7、铁路油罐车由两个半球面和一个圆柱面钢板焊接而成，尺寸如图所示．问：该油罐车的容积是多少立方米？(π=3.14)8、如图所示，一个5×5×5的立方体，在一个方向上开有1×1×5的孔，在另一个方向上开有2×1×5的孔，在第三个方向上开有3×1×5的孔，剩余部分的体积是多少？表面积为多少？9、如图，原来的大正方体是由125个小正方体所构成的．其中有些小正方体已经被挖除，图中涂黑色的部分就是贯穿整个大正方体的挖除部分．请问剩下的部分共有多少个小正方体？10、如图，ABCD是矩形，BC＝6cm，AB＝10cm，对角线AC、BD相交O．E、F分别是AD与BC的中点，图中的阴影部分以EF为轴旋转一周，则白色部分扫出的立体图形的体积是多少立方厘米？（π取3）答案部分一、解答题1、【正确答案】307.72【答案解析】涂漆的面积等于大圆柱表面积与小圆柱侧面积之和，为6π×10＋π×（6÷2）2×2＋4π×5＝60π＋18π＋20π＝98π＝307.72（平方厘米）．【答疑编号10299065】2、【正确答案】182.8736【答案解析】圆柱体底面周长和高相等，说明圆柱体侧面展开是一个正方形．高缩短4cm，表面积就减少50.24cm2．阴影部分的面积为圆柱体表面积减少部分，值是50.24cm2，所以底面周长是50.24÷4＝12.56（cm），侧面积是：12.56×12.56＝157.7536（cm2），两个底面积是：3.14×（12.56÷3.14÷2）2×2＝25.12（cm2）．所以表面积为：157.7536＋25.12＝182.8736（cm2）．【答疑编号10299073】3、【正确答案】9388.6【答案解析】卷在一起时铜版纸的横截面的面积为（cm2），如果将其展开，展开后横截面的面积不变，形状为一个长方形，宽为0.25mm（即0.025cm），所以长为7475π÷0.025＝938860cm＝9388.6m．所以这卷铜版纸的总长是9388.6米．【答疑编号10299080】4、【正确答案】65.94【答案解析】缠绕在一起时塑料薄膜的体积为：[π×（20÷2）2－π×（8÷2）2]×100＝8400π（cm3）薄膜展开后为一个长方体，体积保持不变，而厚度为0.04cm，所以薄膜展开后的面积为：8400π÷0.04＝659400cm2＝65.94平方米【答疑编号10299082】5、【正确答案】60【答案解析】由已知条件知，第二个图上部空白部分的高为7－5＝2cm，从而水与空着的部分的比为4∶2＝2∶1，由左图知水的体积为10×4，所以总的容积为40÷2×（2＋1）＝60立方厘米．【答疑编号10299088】6、【正确答案】62.172；0.062172【答案解析】6÷2＝326.4π÷（3＋1）×3＝62.172（立方厘米）62.172立方厘米＝62.172毫升＝0.062172升．答：酒精的体积是62.172立方厘米，合0.062172升．【答疑编号10299090】7、【正确答案】41.9【答案解析】（立方米）【答疑编号10299093】8、【正确答案】100；204【答案解析】求体积：开了3×1×5的孔，挖去3×1×5＝15，开了1×1×5的孔，挖去1×1×5－1＝4；开了2×1×5的孔，挖去2×1×5－（2＋2）＝6，剩余部分的体积是：5×5×5－（15＋4＋6）＝100．（另解）将整个图形切片，如果切面平行于纸面，那么五个切片分别如图：得到总体积为：22×4＋12＝100．求表面积：表面积可以看成外部和内部两部分．外部的表面积为5×5×6－12＝138，内部的面积可以分为前后、左右、上下三个方向，面积分别为2×（2×5＋1×5－1×2－1×3）＝202×（1×5＋3×5－1×3－1）＝322×（1×5＋1×5－1×1－2）＝14所以总的表面积为：138＋20＋32＋14＝204．【答疑编号10299104】9、【正确答案】72【答案解析】对于这一类从立体图形中间挖掉一部分后再求体积（或小正方体数目）的题目一般可以采用“切片法”来做，所谓“切片法”，就是把整个立体图形切成一片一片的（或一层一层的），然后分别计算每一片或每一层的体积或小正方体数目，最后再把它们相加．采用切片法，俯视第一层到第五层的图形依次如下，其中黑色部分表示挖除掉的部分．从图中可以看出，第1、2、3、4、5层剩下的小正方体分别有22个、11个、11个、6个、22个，所以总共还剩下22＋11＋11＋6＋22＝72（个）小正方体．【答疑编号10299107】10、【正确答案】180【答案解析】扫出的图形如图所示，白色部分实际上是一个圆柱减去两个圆锥后所形成的图形．两个圆锥的体积之和为（立方厘米）；圆柱的体积为π×32×10＝270（立方厘米），所以白色部分扫出的体积为270－90＝180（立方厘米）．【答疑编号10299110】。

第28讲表面积与体积（二）一、知识要点解答立体图形的体积问题时，要注意以下几点：（1）物体沉入水中，水面上升部分的体积等于物体的体积。

把物体从水中取出，水面下降部分的体积等于物体的体积。

这是物体全部浸没在水中的情况。

如果物体不全部浸在水中，那么派开水的体积就等于浸在水中的那部分物体的体积。

（2）把一种形状的物体变为另一种形状的物体后，形状变了，但它的体积保持不变。

（3）求一些不规则形体体积时，可以通过变形的方法求体积。

（4）求与体积相关的最大、最小值时，要大胆想象，多思考、多尝试，防止思维定。

二、精讲精练【例题1】有大、中、小三个正方体水池，它们的内边长分别为6米、3米、2米。

把两堆碎石分别沉在中、小水池里，两个水池水面分别升高了6厘米和4厘米。

如果将这两堆碎石都沉在大水池里，大水池的水面升高多少厘米？中、小水池升高部分是一个长方体，它的体积就等同于碎石的体积。

两个水池水面分别升高了6厘米和4厘米，两堆碎石的体积就是3×3×0.06+2×2×0.04=0.7（立方米）。

把它沉到大水池里，水面升高部分的体积也就是0.7立方米，再除以它的底面积就能求得升高了多少厘米。

3×3×0.06+2×2×0.04=0.7（立方米）0.7÷6的平方=7/360（米）=1又17/18（厘米）答：大水池的水面升高了1又17/18厘米。

练习1：1、有大、中、小三个正方体水池，它们的内边长分别为4米、3米、2米。

把两堆碎石分别沉没在中、小水池的水中，两个水池的水面分别升高了4厘米和11厘米，如果将这两堆碎石都沉没在大水池中，那么大水池水面将升高多少厘米？2、用直径为20厘米的圆钢，锻造成长、宽、高分别为30厘米、20厘米、5厘米的长方体钢板，应截取圆钢多长（精确到0.1厘米）？3、将表面积为54平方厘米、96平方厘米、150平方厘米的三个铁质正方体熔铸成一个大正方体（不计损耗），求这个大正方体的体积。

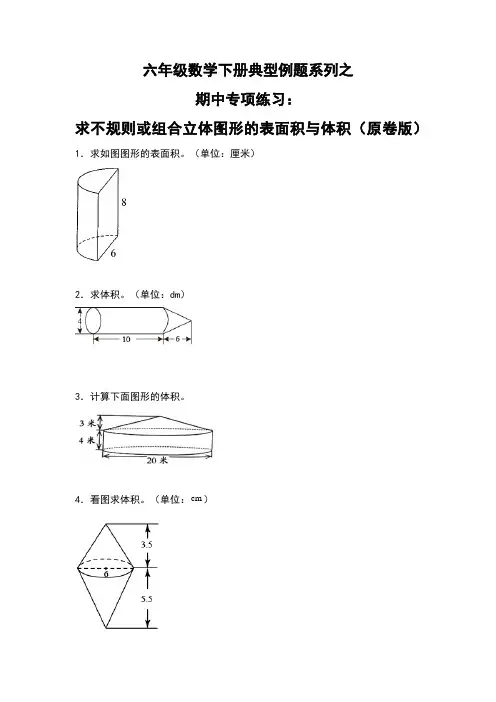
六年级数学下册典型例题系列之期中专项练习：求不规则或组合立体图形的表面积与体积（原卷版）1．求如图图形的表面积。

（单位：厘米）2．求体积。

（单位：dm）3．计算下面图形的体积。

4．看图求体积。

（单位：cm）5．计算下图的表面积与体积。

（单位：厘米）6．计算下面模具（由正方体与圆柱体组成）的表面积与体积。

（单位：厘米）7．下图中圆柱的底面周长是6.28厘米，高是3厘米，求阴影部分的体积。

8．求下面图形的体积。

9．求下面面图形的表面积。

10．如下图，求一个直角梯形以AB为轴旋转一周后形成的立体图形的体积。

（单位：厘米）11．计算下面物体的体积。

（单位：cm）12．求下面图形的表面积和体积。

（单位：cm）13．计算下图（按45°斜切）的体积（单位：厘米）。

14．计算下面图形的体积。

（半圆柱的底面直径是10cm）15．下图是一块长方形铁皮，利用图中的阴影部分，刚好能做成一个圆柱形油桶（接头忽略不计），求这个油桶的体积。

16．右图是一个底面半径为3厘米的圆柱木块被削去一半后的形状，请你计算出它的体积。

17．如图，一个圆柱体零件，高10厘米，底面直径6厘米，零件的一端有一个圆柱形的圆孔，圆孔的直径是4厘米，孔深5厘米。

（1）这个零件的体积是多少立方厘米？（2）如果将这个零件接触空气的部分涂上防锈漆，那么一共要涂多少平方厘米？18．下图ABCD是直角梯形，以AB为轴并将梯形绕这个轴旋转一周，得到一个旋转体，它的体积是多少立方厘米？（除不尽的保留两位小数）19．如图，卫生纸的高度是10cm，中间硬纸轴的直径是4 cm。

制作100个这样的硬纸轴，至少需要多少平方米的硬纸皮？学习与生活的苦，每一个人必须选择一个。

不管你选择了哪一个，都应该尽最大的努力做到最好，只有做到最好，人生才会在不留遗憾。

老一辈教育我们，书山有路勤为径，学海无涯苦作舟；吃得人中苦，方为人上人；吃亏是福，在学习的年龄不要贪图享乐；认认真真听课，勤勤恳恳学习，美好的未来可以值得可期。

名校真题测试卷3 （几何篇二）时间：15分钟满分5分姓名_________ 测试成绩_________1 （05年101中学考题）求下图中阴影部分的面积：2 （06年清华附中考题）从一个长为8厘米，宽为7厘米，高为6厘米的长方体中截下一个最大的正方体，剩下的几何体的表面积是_________平方厘米.3 （06年三帆中学考试题）有一个棱长为1米的立方体，沿长、宽、高分别切二刀、三刀、四刀后，成为60个小长方体(见左下图).这60个小长方体的表面积总和是______平方米.4 （06年西城八中考题）右上图中每个小圆的半径是1厘米，阴影部分的周长是_______厘米.（ ＝3.14）5 (05年首师附中考题)一千个体积为1立方厘米的小正方体合在一起成为一个边长为10厘米的大正方体，大正方体表面涂油漆后再分开为原来的小正方体，这些小正方体至少有一面被油漆涂过的数目是多少个？【附答案】1 【解】如左下图所示，将左下角的阴影部分分为两部分，然后按照右下图所示，将这两部分分别拼补在阴影位置。

可以看出，原题图的阴影部分等于右下图中AB弧所形成的弓形，其面积等于扇形OAB与三角形OAB的面积之差。

所以阴影面积：π×4×4÷4-4×4÷2=4.56。

2 【解】最大正方体的边长为6，这样剩下表面积就是少了两个面积为6×6的，所以现在的面积为(8×7+8×6+7×6) ×2-6×6×2=220.3 【解】原正方体表面积：1×1×6＝6（平方米），一共切了2＋3＋4＝9（次），每切一次增加2个面：2平方米。

所以表面积： 6＋2×9＝24（平方米）．4 【解】可见大圆的半径是小圆的3倍，所以半径为3，那么阴影部分的周长就等于7的小圆的周长加上1个大圆的周长，即7×π×2+π×6=20π。

小学数学精讲(9)几何（三） 立体图形一、知识地图⎧⇒⎧⎪⎪⎧⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎩⎪⎪⎪⇒⎩⎪⎪⇒⎨⎪⎧⎪⎨⎪⎩⎪⎪⎪⎪⎪⎩3“一个思想”不规则化为规则阳光照面求图形体积表面积“三个方法”看变化规律整体切片“一个模式”整体思考最短路线与展开图形状以点定线，以线定面n 边小正方形染色规律染色问题欧拉公式 二、基础知识万丈高楼平地起。

我们可以这样说：把平面图形从平面拎到空间，让平面图形在空间上产生高度就形成了这一讲我们要研究的立体图形。

在现阶段，我们主要研究的立体图形有以下几种：立体图形 表面积体积26S a =正方体 3V a =正方体2S ab bc ac =++长方体（） V abc =长方体2222S rh r ππ=+=+圆柱侧面积个底面积 2V r h π=圆柱22S l r ππ=++圆锥n侧面积底面积=360 注：l 是母线，即从顶点到底面圆上的线段长。

213V r h π=圆锥体24S r π=球体343V r π=球体特别的：关于球体还有这样一个结论：如果一个球体的直径与一个圆柱的直径与高都相等，那么：球体的体积等于以球大圆为底球的直径为高的圆柱体积的三分之二； 球体的表面积等于以球大圆为底球的直径为高的圆柱的侧面积；球体的体积还等于以球大圆为底，球的半径为高的圆锥的体积的4倍。

这个图就是有名的阿基米德圆柱容球。

二、求立体图形的表面积和体积规则立体图形的表面积和体积我们可以直接应用公式进行计算。

不规则的立体图形的表面积和体积，一方面，我们可以应用和平面图形相同思考的方法来考虑把它转化为规则的立体图形进行计算；而另一方面，我们更注重的是观察图形从规则变为不规则的变化过程，通常这个过程我们需要以图形整体考虑为出发点。

这也就是我们求解此类问题常用方法的思想基础：、 方法一：阳光照面阳光照面法从图形整体考虑出发，观察图形表面积特点。

方法二：与时俱进图形的变化，是从整体的变到不变的过程，找到变化的规律，注意图形的变化过程，观察求解，与时俱进，就是解决问题的秘籍宝典。

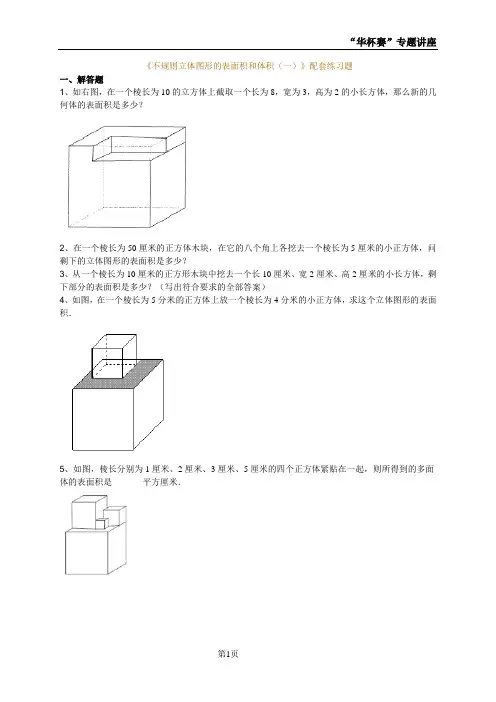
《不规则立体图形的表面积和体积（一）》配套练习题一、解答题1、如右图，在一个棱长为10的立方体上截取一个长为8，宽为3，高为2的小长方体，那么新的几何体的表面积是多少？2、在一个棱长为50厘米的正方体木块，在它的八个角上各挖去一个棱长为5厘米的小正方体，问剩下的立体图形的表面积是多少？3、从一个棱长为10厘米的正方形木块中挖去一个长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？（写出符合要求的全部答案）4、如图，在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体，求这个立体图形的表面积．5、如图，棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起，则所得到的多面体的表面积是_______平方厘米．6、用棱长是1厘米的立方块拼成如右图所示的立体图形，问该图形的表面积是多少平方厘米？7、有30个边长为1米的正方体，在地面上摆成如图的形状，然后把露出的表面涂成红色．求被涂成红色的表面积．8、右图是一个零件的直观图．下部是一个棱长为40cm的正方体，上部是圆柱体的一半．求这个零件的表面积和体积（π＝3.14）．9、用铁皮做一个如图（单位：cm）所示的管道工件，需用铁皮多少平方厘米（π＝3.14）？10、如图所示，三个圆柱堆放在一起，求这个立体图形的表面积和体积（单位：米）（π＝3.14）．答案部分一、解答题1、【正确答案】600【答案解析】我们从三个方向（前后、左右、上下）考虑，新几何体的表面积仍为原立方体的表面积：10×10×6＝600．【答疑编号10296776】2、【正确答案】15000【答案解析】对于和长方体相关的立体图形表面积，一般从上下、左右、前后3个方向考虑．变化前后的表面积不变：50×50×6＝15000（平方厘米）．【答疑编号10296777】3、【正确答案】592平方厘米；632平方厘米；648平方厘米；672平方厘米【答案解析】按图1所示沿一条棱挖，为592平方厘米；按图2所示在某一面上挖，为632平方厘米；按图3所示在某面上斜着挖，为648平方厘米；按图4所示挖通两个对面，为672平方厘米．【答疑编号10296778】4、【正确答案】214平方分米【答案解析】我们把上面的小正方体想象成是可以向下“压缩”的，“压缩”后我们发现：小正方体的上面与大正方体上面中的阴影部分合在一起，正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分：上下方向：大正方体的两个底面；四周方向（左右、前后方向）：小正方体的四个侧面，大正方体的四个侧面．上下方向：5×5×2＝50（平方分米）；侧面：5×5×4＝100（平方分米），4×4×4＝64（平方分米）．这个立体图形的表面积为：50＋100＋64＝214（平方分米）．【答疑编号10296779】5、【正确答案】194【答案解析】（法1）四个正方体的表面积之和为：（12＋22＋32＋52）×6＝39×6＝234（平方厘米），重叠部分的面积为：12×3＋（22×2＋12）＋（32＋22＋12）＋（32＋22＋12）＝3＋9＋14＋14＝40（平方厘米），所以，所得到的多面体的表面积为：234－40＝194（平方厘米）．（法2）三视图法．从前后面观察到的面积为52＋32＋22＝38平方厘米,从左右两个面观察到的面积为52＋32＝34平方厘米，从上下能观察到的面积为52＝25平方厘米．表面积为（38＋34＋25）×2＝194（平方厘米）．【答疑编号10296780】6、【正确答案】46【答案解析】该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成．该图形的表面积等于（9＋7＋7）×2＝46个小正方形的面积，所以该图形表面积为46平方厘米．【答疑编号10296781】7、【正确答案】56【答案解析】4×4＋（1＋2＋3＋4）×4＝56（平方米）．【答疑编号10296782】8、【正确答案】11768cm2，89120cm3【答案解析】表面积＝40×40×5＋3.14×40×40÷2＋3.14×（40÷2）2÷2×2＝8000＋2512＋1256＝11768cm2，体积＝40×40×40＋3.14×（40÷2）2×40÷2＝64000＋25120＝89120cm3．【答疑编号10296783】9、【正确答案】2355cm2【答案解析】将两个同样的工件可拼成下图的圆柱体，所以一个工件需铁皮3.14×15×（46＋54）÷2＝2355（cm2）【答疑编号10296784】10、【正确答案】262.19平方米；240.995立方米【答案解析】表面积：［3.14×（5÷2）2×2＋3.14×5×10］＋3.14×3×5＋3.14×2×3 ＝3.14×12.5＋3.14×50＋3.14×15＋3.14×6＝3.14×83.5＝262.19（平方米）体积：3.14×（5÷2）2×10＋3.14×（3÷2）2×5＋3.14×（2÷2）2×3＝3.14×62.5＋3.14×11.25＋3.14×3＝3.14×76.75＝240.995（立方米）【答疑编号10296785】。

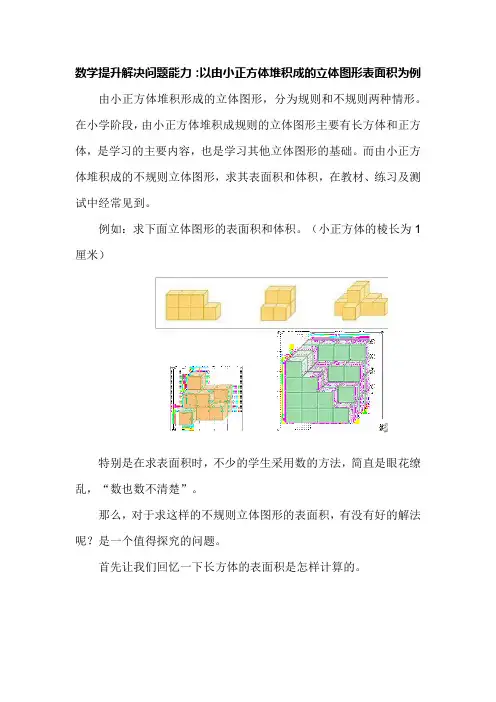
数学提升解决问题能力：以由小正方体堆积成的立体图形表面积为例由小正方体堆积形成的立体图形，分为规则和不规则两种情形。

在小学阶段，由小正方体堆积成规则的立体图形主要有长方体和正方体，是学习的主要内容，也是学习其他立体图形的基础。

而由小正方体堆积成的不规则立体图形，求其表面积和体积，在教材、练习及测试中经常见到。

例如：求下面立体图形的表面积和体积。

（小正方体的棱长为1厘米）特别是在求表面积时，不少的学生采用数的方法，简直是眼花缭乱，“数也数不清楚”。

那么，对于求这样的不规则立体图形的表面积，有没有好的解法呢？是一个值得探究的问题。

首先让我们回忆一下长方体的表面积是怎样计算的。

长方体的表面积是六个面的和，而前面与后面相同、左面与右面相同、上面与下面相同，因此只要把前面、左面、上面三个面相加，用得到的和乘2即可。

如图：长方体的表面积也可以理解为是从六个方向（前后左右上下）所能看到的小正方体的面数之和。

而前面与后面、上面与下面、左面与右面所能看到的小正方形面数分别相同，所以只要用相邻三个面的小正方形面数之和乘2就可以了。

那么，这种想法能否应用在这些不规则的立体图形中呢？立体图形①：从前面看有7个小正方形面，从后面看也有7个小正方形面；从上面看有4个小正方形面，从下面看也有4个小正方形面；从左面看有2个小正方形面，从右面看也有2个小正方形面。

那么这个立体图形的表面积就可以用（7+4+2）×2=26个小正方形面来求得。

立体图形②：从前面看有4个小正方形面，从后面看也有4个小正方形面；从上面看有4个小正方形面，从下面看也有4个小正方形面；从左面看有3个小正方形面，从右面看也有3个小正方形面。

那么这个立体图形的表面积也可以用（4+4+3）×2=22个小正方形面来求得。

立体图形③：从前面看有5个小正方形面，从后面看也有5个小正方形面；从上面看有8个小正方形面，从下面看也有8个小正方形面；从左面看有5个小正方形面，从右面看也有5个小正方形面。

高三空间几何知识点空间几何是数学的一个重要分支，也是高中数学中的重点内容之一。

在高三阶段，学生需要掌握一系列的空间几何知识点，本文将对一些重要的知识进行介绍和总结。

一、立体图形的性质和计算1.平行四边形棱柱：平行四边形棱柱是一种特殊的棱柱，它的底面是一个平行四边形，侧面是一系列平行于底面的平行四边形。

它的体积可以通过底面积乘以高来计算，表达式为V=底面积×高。

2.正方体与立方体：正方体是一种特殊的长方体，六个面都是正方形。

立方体是一种特殊的长方体，六个面都是正方形，且长、宽、高相等。

它们的体积可以通过边长的立方来计算，表达式为V=边长³。

3.圆锥与直角圆锥：圆锥是一种侧面由一个封闭曲线和封闭点构成的几何体，封闭曲线称为母线，封闭点称为顶点。

直角圆锥是一种特殊的圆锥，它的底面是一个圆，顶点到底面的垂直距离等于半径的一半。

圆锥的体积可以通过底面积乘以高再除以3来计算，表达式为V=底面积×高÷3。

4.圆柱与直角圆柱：圆柱是一种侧面由一个封闭曲线和两个平行线段构成的几何体。

直角圆柱是一种特殊的圆柱，它的底面是一个圆，侧面与底面垂直。

圆柱的体积可以通过底面积乘以高来计算，表达式为V=底面积×高。

5.球与球的体积：球是一种所有点到球心的距离都相等的几何体。

球的体积可以通过4/3乘以π乘以半径的立方来计算，表达式为V=4/3πr³。

二、空间几何的相关性质1.平面与直线的关系：平面与直线可以有三种关系，即相交、平行和重合。

平面与直线相交于一点时，称为交点；平面与直线平行时，它们在空间中没有交点；平面与直线重合时，它们在空间中完全重合。

2.平面与平面的关系：平面与平面可以有四种关系，即相交、平行、互相垂直和重合。

平面与平面相交于一条直线时，称为交线；平面与平面平行时，它们在空间中没有交线；平面与平面互相垂直时，它们的法向量互相垂直；平面与平面重合时，它们在空间中完全重合。

专题四 立体几何第一讲 空间几何体的表面积与体积——小题备考微专题1 空间几何体的表面积和体积常考常用结论1．柱体、锥体、台体、球的表面积公式： ①圆柱的表面积S ＝2πr (r ＋l )； ②圆锥的表面积 S ＝πr (r ＋l )；③圆台的表面积S ＝π(r ′2＋r 2＋r ′l ＋rl )； ④球的表面积S ＝4πR 2.2．柱体、锥体和球的体积公式： ①V 柱体＝Sh (S 为底面面积，h 为高)； ②V 锥体＝13Sh (S 为底面面积，h 为高)；③V 球＝43πR 3.保 分 题1.[2022·山东枣庄三模]若圆锥的母线长为2，侧面积为2π，则其体积为( ) A ．√6π B ．√3π C ．√63π D ．√33π2．[2022·河北保定一模]圆柱的底面直径与高都等于球的直径，则球的表面积与圆柱的侧面积的比值为( )A ．1∶1B ．1∶2C ．2∶1D ．2∶33．[2022·湖北武汉二模]如图，在棱长为2的正方体中，以其各面中心为顶点构成的多面体为正八面体，则该正八面体的体积为( )A ．2√23B ．43 C ．4√23D ．83提分题例1 (1)[2022·河北张家口三模]如图，在三棱柱ABC­ A1B1C1中，过A1B1的截面与AC交于点D，与BC交于点E，该截面将三棱柱分成体积相等的两部分，则CDAC＝()A．13B．12C．2−√32D．√3−12(2)[2022·湖南雅礼中学二模]某圆锥高为1，底面半径为√3，则过该圆锥顶点的平面截此圆锥所得截面面积的最大值为()A．2 B．√3C．√2D．1听课笔记：【技法领悟】1．求几何体的表面积及体积问题，可以多角度、多方位地考虑，熟记公式是关键．求三棱锥的体积，等体积转化是常用的方法，转化原则是其高易求，底面放在已知几何体的某一面上．2．求不规则几何体的体积，常用分割或补形的方法，将不规则几何体转化为规则几何体，易于求解．巩固训练11.[2022·山东菏泽一模]如图1，在高为h的直三棱柱容器ABC ­ A1B1C1中，AB＝AC＝2，AB⊥AC.现往该容器内灌进一些水，水深为2，然后固定容器底面的一边AB于地面上，再将容器倾斜，当倾斜到某一位置时，水面恰好为A 1B 1C (如图2)，则容器的高h 为( )A ．3B ．4C ．4√2D ．62．[2022·福建福州三模]已知AB ，CD 分别是圆柱上、下底面圆的直径，且AB ⊥CD ，O 1，O 分别为上、下底面的圆心，若圆柱的底面圆半径与母线长相等，且三棱锥A ­ BCD 的体积为18，则该圆柱的侧面积为( )A ．9πB ．12πC ．16πD ．18π微专题2 与球有关的切、接问题常考常用结论1．球的表面积S ＝4πR 2，体积V ＝43πR 3.2．长方体、正方体的体对角线等于其外接球的直径． 3．n 面体的表面积为S ，体积为V ，则内切球的半径r ＝3VS .4．直三棱柱的外接球半径：R ＝√r 2+(L2)2，其中r 为底面三角形的外接圆半径，L 为侧棱长，如果直三棱柱有内切球，则内切球半径R ′＝L2.5．正四面体中，外接球和内切球的球心重合，且球心在高对应的线段上，它是高的四等分点，球心到顶点的距离为外接球的半径R ＝√64a (a 为正四面体的棱长)，球心到底面的距离为内切球的半径r ＝√612a ，因此R ∶r ＝3∶1.保 分 题1.[2022·广东深圳二模]已知一个球的表面积在数值上是它的体积的√3倍，则这个球的半径是( )A ．2B ．√2C ．3D ．√32．已知正四棱锥P ­ ABCD 中，AB ＝√6，P A ＝2√3，则该棱锥外接球的体积为( )A．4π B．32π3C．16π D．16π33．[2022·天津红桥一模]一个长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为1、√2、3，则此球的体积为________．提分题例2 (1)[2022·江苏苏州三模]《九章算术》卷第五《商功》中，有“贾令刍童，上广一尺，袤二尺，下广三尺，袤四尺，高一尺．”，意思是：“假设一个刍童，上底面宽1尺，长2尺；下底面宽3尺，长4尺，高1尺．”(注：刍童为上下底面为相互平行的不相似长方形，两底面的中心连线与底面垂直的几何体)，若该几何体所有顶点在一球体的表面上，则该球体的体积为()立方尺A．√41πB．41π3D．3√41πC．41√41π6(2)[2022·山东泰安三模]如图，已知三棱柱ABC ­ A1B1C1的底面是等腰直角三角形，AA1⊥底面ABC，AC＝BC＝2，AA1＝4，点D在上底面A1B1C1(包括边界)上运动，则三棱锥D ­ ABC 的外接球表面积的最大值为()π B．24πA．814C．243π D．8√6π16听课笔记：【技法领悟】1．确定球心的位置，弄清球的半径(直径)与几何体的位置和数量关系．2．求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．3．补成正方体、长方体、正四面体、正棱柱、圆柱等规则几何体．巩固训练21.已知圆柱的轴截面为正方形，其外接球为球O，球O的表面积为8π，则该圆柱的体积为()A．√22π B．√2πC．2π D．2√2π2．[2022·广东潮州二模]已知△ABC是边长为3的等边三角形，三棱锥P ­ ABC全部顶点都在表面积为16π的球O的球面上，则三棱锥P ­ ABC的体积的最大值为()A．√3B．3√32C．9√34D．√32专题四 立体几何第一讲 空间几何体的表面积与体积微专题1 空间几何体的表面积和体积保分题1．解析：设圆锥的底面半径为r ，高为h ，则πr ×2＝2π，可得r ＝1，则h ＝√22−r 2＝√3，因此，该圆锥的体积为V ＝13πr 2h ＝13π×12×√3＝√33π. 答案：D2．解析：设球的半径为r ，依题意圆柱的底面半径也是r ，高是2r ， 圆柱的侧面积＝2πr ·2r ＝4πr 2 ，球的表面积为4πr 2 ， 其比例为1∶1. 答案：A3．解析：该正八面体是由两个同底的正四棱锥组成，且正四棱锥的底面是边长为√2的正方形，棱锥的高为1，所以该正八面体的体积为2×13×√2×√2×1＝43.答案：B提分题[例1] 解析：(1)由题可知平面A 1B 1ED 与棱柱上、下底面分别交于A 1B 1，ED ， 则A 1B 1∥ED ，ED ∥AB ， 显然CDE - C 1A 1B 1是三棱台，设△ABC 的面积为1，△CDE 的面积为S ，三棱柱的高为h ， ∴12·1·h ＝13h (1＋S ＋√S )， 解得√S ＝√3−12，由△CDE ∽△CAB ，可得CD AC ＝√S√1＝√3−12. (2)如图，截面为△P AB ，设C 为AB 中点，设OC ＝x ，x ∈[0，√3)，则AB ＝2√3−x 2，PC ＝√x 2+1，则截面面积S ＝12×2√3−x 2×√x 2+1＝√−(x 2−1)2+4，则当x 2＝1时，截面面积取得最大值为2. 答案：(1)D (2)A[巩固训练1]1．解析：在图1中V 水＝12×2×2×2＝4，在图2中，V 水＝V ABC − A 1B 1C 1− V C − A 1B 1C 1＝12×2×2×h －13×12×2×2×h ＝43h ， ∴43h ＝4，∴h ＝3.答案：A2．解析：分别过A ，B 作圆柱的母线AE ，BF ，连接CE ，DE ，CF ，DF ，设圆柱的底面半径为r ，则三棱锥A - BCD 的体积为两个全等四棱锥C - ABFE 减去两个全等三棱锥A - CDE ， 即2×13×r ×2r ×r －2×13×r ×12×2r ×r ＝23r 3＝18，则r ＝3，圆柱的侧面积为2πr ×r ＝18π答案：D微专题2 与球有关的切、接问题保分题1．解析：设球的半径为R ，则根据球的表面积公式和体积公式， 可得，4πR 2＝43πR 3×√3，化简得R ＝√3. 答案：D2．解析：正方形ABCD 的对角线长√6+6＝2√3，正四棱锥的高为 √(2√3)2−(2√32)2＝3，设外接球的半径为R ，则(3－R )2＋(2√32)2＝R 2⇒R ＝2， 所以外接球的体积为4π3×23＝32π3.答案：B3．解析：长方体外接球的直径为√12+(√2)2+32＝2√3，所以外接球半径为√3，所以球的体积为4π3×(√3)3＝4√3π.答案：4√3π提分题[例2] 解析：(1)作出图象如图所示：由已知得球心在几何体的外部， 设球心到几何体下底面的距离为x ， 则R 2＝x 2＋(52)2＝(x ＋1)2＋(√52)2，解得x ＝2，∴R 2＝414， ∴该球体的体积V ＝4π3×(√412)3＝41√41π6.(2)因为△ABC 为等腰直角三角形，AC ＝BC ＝2，所以△ABC 的外接圆的圆心为AB 的中点O 1, 且AO 1＝√2，连接O 1与A 1B 1的中点E ，则O 1E ∥AA 1，所以O 1E ⊥平面ABC ， 设球的球心为O ，由球的截面性质可得O 在O 1E 上， 设OO 1＝x ，DE ＝t (0≤t ≤√2)，半径为R ， 因为OA ＝OD ＝R ，所以√2+x 2＝√(4−x )2+t 2， 所以t 2＝8x －14，又0≤t ≤√2， 所以74≤x ≤2，因为R 2＝2＋x 2，所以8116≤R 2≤6，所以三棱锥D －ABC 的外接球表面积的最大值为24π. 答案：(1)C (2)B [巩固训练2]1．解析：设外接球的半径为R ，圆柱底面圆的半径为r ，因为圆柱的轴截面为正方形，所以圆柱的高h ＝2r ，由球O 的表面积S ＝4πR 2＝8π，得R ＝√2，又R ＝ √(h2)2+r 2＝√2r ，得r ＝1，所以圆柱的体积V ＝πr 2·2r ＝2πr 3＝2π.答案：C2．解析：球O 的半径为R ，则4πR 2＝16π，解得：R ＝2，由已知可得：S △ABC ＝√34×32＝9√34，其中AE ＝23AD ＝√3，球心O 到平面ABC 的距离为√R 2−(√3)2＝1， 故三棱锥P - ABC 的高的最大值为3， 体积最大值为13S △ABC ·3＝9√34.答案：C。

1.掌握立体图形的体积计算常用公式．2.掌握求不规则立体图形体积的常用方法．本讲立体图形的体积计算，与第七讲的立体图形的表面积，是姐妹篇．对于小学几何而言，立体图形的体积计算，既可以很好地考查学生的空间想象能力，又可以具体考查学生在公式应用中处理相关数据的能力，所以，很多重要考试(比如仁华的入学考试，几乎每年必考)都很重视对立体图形的考查．其中，尤其要以“不规则立体图形的体积”为考查重点．立体图形的体积计算常用公式：立体图形示例体积公式相关要素长方体V abh=V Sh=三要素：a、b、h二要素：S、h正方体3V a=V Sh=一要素：a二要素：S、h 立体图形的体积圆柱体V=Sh二要素：S (或r 、d 、C ) 和h圆锥体V=13Sh 二要素：S 、h不规则形体的体积常用方法：一、 化虚为实法 二、 切片转化法 三、 先补后去法 四、 实际操作法 五、 画图建模法【例 1】 (第五届《小数报》数学竞赛决赛)一个长方体的宽和高相等，并且都等于长的一半(如图)．将这个长方体切成12个小长方体，这些小长方体的表面之和为600平方分米．求这个大长方体的体积．【分析】 设大长方体的宽(高)为a 分米，则长为2a ，右(左)面积为2a ，其余面的面积为22a ，根据题意， 22222862600a a a ⨯++⨯= 所以225a =，5a =． 大长方体的体积2555250=⨯⨯⨯=(立方分米)．［铺垫］ (第十五届“迎春杯”决赛)把一根长2.4米的长方体木料锯成5段(如图)，表面积比原来增加了96平方厘米．这根木料原来的体积是_____立方厘米．2.4米［分析］ 96812÷=(平方厘米)，122402880⨯=(立方厘米)．所以这根木料原来的体积为2880立方厘米．【例 2】 (第九届“祖冲之杯”数学邀请赛)有一个长方体的盒子，从里面量长40厘米，宽12厘米，高7厘米，在这个盒子里放长5厘米，宽4厘米，高3厘米的长方体木块．最多可放 块．【分析】 下图表明34⨯的长方形可以填满712⨯的长方形．于是534⨯⨯的长方体可以填满40712⨯⨯的长方体，即盒子中最多可放这种长方体规则立体图形体积的计算44443333340712(534)56⨯⨯÷⨯⨯=(个)．［巩固］ (第九届“迎春杯”数学竞赛决赛)把1个棱长是3厘米的正方体分割成若干个小的正方体，这些小正方体的棱长必须是整厘米数．如果这些小正方体的体积不要求都相等，那么最少可分割 成 个小正方体．［分析］ 因为小正方体的棱长只可能是2厘米或1厘米．必须分割出棱长是2厘米的小正方体才能使数量减少．显然，棱长是3厘米的正方体只能切割出一个棱长为2厘米的小正方体，剩余部分再切割出33322227819⨯⨯-⨯⨯=-=个棱长是1厘米的小正方体，这样总共可以分割成11920+=(个)小正方体．现有一张长40厘米、宽20厘米的 长方形铁皮，请你用它做一只深是 5厘米的长方体无盖铁皮盒(焊接处 及铁皮厚度不计，容积越大越好)， 你做出的铁皮盒容积是多少立方厘 米?【分析】 如图，在4020⨯的长方形铁皮的四角截去边1030长5厘米的正方形铁皮，然后焊接成长方形无盖 铁皮盒．这个铁皮盒的长405530=--=(厘米)．宽205510=--=(厘米)，高5=(厘米)． 体积301051500=⨯⨯=(立方厘米)．如图，在4020⨯长方形铁皮的左侧两角上割下 边长5厘米的正方形(二块)，紧密焊接到右侧的中间部分，这样做成的无盖铁皮盒的长40535=-=(厘米)，宽205510=--=(厘米)， 高5=(厘米)，体积351051750=⨯⨯=(立方厘米)．如图，在4020⨯的长方形铁皮的左右两侧各割 下一条宽为5厘米的长方形铁皮(共二块)，分 别焊到上、下的中间部分，这样做成的无盖铁 皮盒的长40555520=----=(厘米)， 宽20=(厘米)，高5=(厘米)，体积202052000=⨯⨯=(立方厘米)． 因此，最后一种容积最大．［铺垫］ (第三届“华杯赛”复赛)如图从长为13厘米，宽为9厘米的长方形硬纸板的四角去掉边长2厘米的正方形，然后，沿虚线折叠成长方体容器．这个容器的体积是多少立方厘米？［分析］ 容器的底面积是(134)(94)45-⨯-=(平方厘米)，高为2厘米，所以容器的体积是，45290⨯=(立方厘米)．【例 3】 (第七届“华杯赛”决赛)用大小相等的无色透明玻璃小正方体和红色玻璃小正方体拼成一个大正方体1111ABCD A B C D -(如图)，大正方体内的对角线1AC ，1BD ，1CA ，1DB 所穿的小正方体都是红D 1C 1B 1A 1DC焊上焊上103520焊上焊上1392色玻璃小正方体，其它部分都是无色透明玻璃小正方体，小红正方体共用了401个，问：无色透明小正方体用了多少个?【分析】 1AC 、1BD ，1CA ，1DB ，四条对角线都穿过在正中央的那个小正方体．除此而外，每条对角线穿过相同的小正方体，所以每条对角线穿过401111014-+=个小正方体这就表明大正方体的每条边由101个小正方体组成．因此大正方体由3101个小正方体组成，其中无色透明的小正方体有310140110303014011029900-=-=． 即用了1029900个无色透明的小正方体．【例 4】 小明用若干个大小相同的正方体木块堆成一个几何体，这个几何体从正面看如下图左,从上面看如下图右．那么这个几何体至少用了 块木块．【分析】 这道题很多同学认为答案是26块．这是受思维定势的影响，认为右图中每一格都要至少放一块．其实，有些格不放，看起来也是这样的．如右图，带阴影的3块不放时，小正方体块数最少，为23块．［拓展］ 右图是由22个小正方体组成的立体图形，其中共有多少个大大小小的正方体？由两个小正方体组成的长方体有多少个？［分析］ 正方体只可能有两种：由1个小正方体构成的正方体，有22个；由8个小正方体构成的222⨯⨯的正方体，有4个． 所以共有正方体22426+=(个)． 由两个小正方体组成的长方体，根据摆放的方向可分为下图所示的上下位、左右位、前后位三种，其中上下位有13个，左右位有13个，前后位有14个，共有13131440++=(个)．【例 5】 有黑白两种颜色的正方体积木，把它摆成右图所示的形状，已知相邻(有公共面)的积木颜色不同，标A 的为黑色，图中共有黑色积木多少块？【分析】 分层来看，如下图(切面平行于纸面)共有黑色积木17块.A不规则立体图形体积的计算［拓展］ 这个图形，是否能够由112⨯⨯的长方体搭构而成？ ［分析］ 每一个112⨯⨯的长方体无论怎么放，都包含了一个黑色正方体和一个白色正方体，而黑色积木有17块，白色积木有15块，所以该图形不能够由112⨯⨯的长方体搭构而成.【例 6】 一个酒瓶里面深30cm ，底面内直径是10cm ，瓶里酒深15cm ．把酒瓶塞紧后使其瓶口向下倒立这时酒深25cm ．酒瓶的容积是多少？(π取3)253015【分析】 观察前后，酒瓶中酒的总量没变，即瓶中液体体积不变．当酒瓶倒过来时酒深25cm ，因为酒瓶深30cm ，这样所剩空间为高5cm 的圆柱，再加上原来15cm 高的酒即为酒瓶的容积．酒的体积：101015π375π22⨯⨯=瓶中剩余空间的体积1010(3025)π125π22-⨯⨯=酒瓶容积：375π125π500π1500(ml)+==［巩固］ 输液100毫升，每分钟输2.5毫升．如图，请你观察第12分钟时图中的数据，问：整个吊瓶的容积是多少毫升？［分析］ 100毫升的吊瓶在正放时，液体在100毫升线下方，上方是空的，容积是多少不好算．但倒过来后，变成圆柱体，根据标示的格子就可以算出来．由于每分钟输2.5毫升，12分钟已输液2.51230⨯=(毫升)，因此开始输液时液面应与50毫升的格线平齐，上面空的部分是50毫升的容积．所以整个吊瓶的容积是 10050150+=(毫升)．【例 7】 一只装有水的圆柱形玻璃杯，底面积是80平方厘米，高是15厘米，水深10厘米．现将一个底面积是16平方厘米，高为12厘米的长方体铁块竖放在水中后．现在水深多少厘米?【分析】 8010(8016)12.5⨯÷-=，因为12.512>，所以此时水已淹没过铁块，8010(8016)1232⨯--⨯=，32800.4÷=，所以现在水深为120.412.4+=厘米［铺垫］ 一只装有水的圆柱形玻璃杯，底面积是80平方厘米，高是15厘米，水深8厘米．现将一个底面积是16平方厘米，高为12厘米的长方体铁块竖放在水中后．现在水深多少厘米?［分析］ 根据等积变化原理：用水的体积除以水的底面积就是水的高度．(法1)：808(8016)6406410⨯÷-=÷=(厘米)；(法2)：设水面上升了x 厘米．根据上升部分的体积=浸入水中铁块的体积列方程为：8016(8)x x =+，解得：2x =，8210+=(厘米)． (提问“圆柱高是15厘米”，和“高为12厘米的长方体铁块”这两个条件给的是否多余？)［拓展］ 一只装有水的圆柱形玻璃杯，底面积是80平方厘米，高是15厘米，水深13厘米．现将一个底面积是16平方厘米，高为12厘米的长方体铁块竖放在水中后．现在水深多少厘米?【分析】 玻璃杯剩余部分的体积为80(1513)160⨯-=立方厘米，铁块体积为1612192⨯=立方厘米，因为160192<，所以水会溢出玻璃杯，所以现在水深就为玻璃杯的高度15厘米总结铁块放入玻璃杯会出现三种情况①放入铁块后，水深不及铁块高.②放入铁块后，水深比铁块高但未溢出玻璃杯，③水有溢出玻璃杯.小故事 教师可以在此穿插一个关于阿基米德测量黄金头冠的体积的故事．一天国王让工匠做了一顶黄金的头冠，不知道工匠有没有掺假，必须知道黄金头冠的体积是多少，可是又没有办法来测量．(如果知道体积，就可以称一下纯黄金相应体积的重量，再称一下黄金头冠的重量，就能知道是否掺假的结果了)于是，国王就把测量头冠体积的任务交给他的大臣阿基米德．(小朋友们，你们能帮阿基米德解决难题吗？)阿基米德苦思冥想不得其解，就连晚上沐浴时还在思考这个问题． 当他坐进水桶里，看到水在往外满溢时，突然灵感迸发，大叫一声：“我找到方法了……”，就急忙跑出去告诉别人，大家看到了一个还光着身子的阿基米德．他的方法是：把水桶装满水，当把黄金头冠放进水桶，浸没在水中时，所收集的溢出来的水的体积正是头冠的体积．【例 8】 (武汉明心杯数学挑战赛)如图所示，一个555⨯⨯的立方体，在一个方向上开有115⨯⨯的孔，在另一个方向上开有215⨯⨯的孔，在第三个方向上开有315⨯⨯的孔，剩余部分的体积是多少？表面积为多少？【分析】 求体积：开了315⨯⨯的孔，挖去31515⨯⨯=，开了115⨯⨯的孔， 挖去11514⨯⨯-=；开了215⨯⨯的孔， 挖去215(22)6⨯⨯-+=，剩余部分的体积是：555(1546)100⨯⨯-++=．(另解)将整个图形切片，如果切面平行于纸面，那么五个切片分别如图：得到总体积为：22412100⨯+=． 求表面积：表面积可以看成外部和内部两部分．外部的表面积为55612138⨯⨯-=，内部的面积可以分为前 后、左右、上下三个方向，面积分别为()22515121320⨯⨯+⨯-⨯-⨯=、 ()2153513132⨯⨯+⨯-⨯-=、()2151511214⨯⨯+⨯-⨯-=，所以总的表面积为 138203214204+++=．(另解)运用类似于三视图的方法，记录每一方向上的不同位置上的裸露正方形个数： 前后方向：32上下方向：30 左右方向：40112211121222211211221122112111111222111111211211211222222222221121122总表面积为()2323040204⨯++=．［巩固］ 一个由125个同样的小正方体组成的大正方体，从这个大正方体中抽出若干个小正方体，把大正方体中相对的两面打通，右图就是抽空的状态．右图中剩下的小正方体有多少个？［分析］ 解法一：(用“容斥原理”来解)由正面图形抽出的小正方体有5525⨯=个，由侧面图形抽出的小正方体有5525⨯=个，由底面图形抽出的小正方体有4520⨯=个，正面图形和侧面图形重合抽出的小正方体有1221228⨯+⨯+⨯=个，正面图形和底面图形重合抽出的小正方体有13227⨯+⨯=个，底面图形和侧面图形重合抽出的小正方体有1211227⨯+⨯+⨯=个，三个面的图形共同重合抽出的小正方体有4个．根据容斥原理，252520877452++---+=，所以共抽出了52个小正方体．1255273-=，所以右图中剩下的小正方体有73个．注意这里的三者共同抽出的小正方体是4个，必须知道是哪4块，这是最让人头疼的事． 但你可以先构造空的两个方向上共同部分的模型，再由第三个方向来穿过“花墙”． 这里，化虚为实的思想方法很重要． 解法二：(用“切片法”来解) 可以从上到下切五层，得： （1） 从上到下五层，如图：（2） 或者，从右到左五片，如图：请注意这里的挖空的技巧是：先认一种方向．比如：从上到下的每一层，首先都应该有第一层的空四块的情况，即——如果挖第二层：第(1)步，把中间这些位置的四块挖走如图：第(2)步，把从右向左的两块成线地挖走．(请注意挖通的效果就是成线挖去)，如图：第(3)步，把从前向后的一块(请注意跟第二层有关的只是一块！)挖成线！如图：总结一下“切片法”： 全面打洞(例如本题，五层一样)挖块成线(例如本题，在前一次的基层上，一条线一条线地挖)． 这里体现的思想方法是：化整为零，有序思考！【例10】 如图,已知A 、B 、C 分别是相邻的三条棱的中点．沿三个中点连成一个正三角形，把原来的立方体切掉一角．如果原来的立方体棱长为8，求：⑴切掉的小部分的体积是多少？⑵剩下的大部分的体积是多少？【分析】 本题应用相关体积公式．⑴2111244103323V Sh ==⨯⨯⨯=锥⑵3185013V V =-=剩锥⑴教师可以沿三个不相邻的顶点再切一下，求小的图形与大的图形的体积各是多少？小的是：21118885323⨯⨯⨯=;大的是：24263.⑵教师可以提问：去掉一个角上的部分后，它的体积是原立方体体积的几分之几？【例11】 如图，是一个正方体，将正方体的A 、C 、B '、D '四个顶点两两连接就构成一个正四面体，已知正方体的边长为3，求正四面体的体积.D′C′B′A′DC BA【分析】 这个正四面体可以看作由正方体切掉A '、C '、B 、D 四个角后得到的，如图所示：B C AD′D′D′D′C′B′B′B′B′A′D CCB AA AA所以正四面体的体积1133343332718932⎛⎫=⨯⨯-⨯⨯⨯⨯⨯=-=⎪⎝⎭.【例12】如图是一个四棱锥的展开图，该展开图由正三角形和正方形构成，其中正方形的面积为8平方厘米，那么该四棱锥的体积为多少？【分析】知道四棱锥的底面面积，只要知道四棱锥的高就能求得四棱锥的体积．将四棱锥沿对角线和顶点构成的平面剖开，剖面是一个三角形.该三角形的斜边等于正方形的对角线，直角边等于正方形和等边三角形的边长，所以三角形是一个等腰直角三角形，它的高等于对角线的一半，根据对称性，这条高也等于四棱锥的高.本题，我们要想知道四棱锥的高，如果仅仅通过操作法，可能无法准确得知．我们隆重推出“画图建模法”，比如：请注意在一个正方体中如何作等边三角形，这一经验，会让我们“类比联想”到，如何让四个等边三角形围绕一个正方形，得到四棱锥．另外，这个四棱锥的高正好等于原正方体棱长的一半．根据小正方形面积是8推得，大正方形面积是小正方形的2倍，所以大正方形面积是16，所以大正方体的边长是4．所以小正方体的棱长为2．即四棱锥的高度为2．四棱锥的体积为168233⨯÷=立方厘米．1.(第十一届“迎春杯”)有一个长方体，长是宽的2倍，宽是高的3倍；长的12与高的13之和比宽多1厘米．这个长方体的体积是 立方厘米．【分析】 长的12即宽，所以高的13就是1厘米，高是3厘米，宽是339⨯=厘米，长是9218⨯=厘米，体积是3918486⨯⨯=(立方厘米)．2. (第六届“华杯赛”决赛口试)某工人用薄木板钉成一个长方体的邮件包装箱，并用尼龙编织条(如图所示)在三个方向上的加固．所用尼龙编织条分别为365厘米，405厘米，485厘米．若每个尼龙加固时接头重叠都是5厘米．问这个长方体包装箱的体积是多少立方米?【分析】 长方体中高+宽1(3655)1802=-=， ⑴高+长1(4055)2002=-=， ⑵长+宽1(4855)2402=-=， ⑶⑵-⑴：长-宽20=， ⑷ ⑷+⑶：长130=，从而宽110=， 代入⑴得高70=． 所以长方体体积为701101301001000⨯⨯=(立方厘米) 1.001=(立方米)3. 有三个大小一样的正方体，将接触的面用胶粘接在一起成图示的形状，表面积比原来减少了16平方厘米.求所成形体的体积.【分析】 三个小正方体拼接成图中的样子，减少了小正方体的4个侧面正方形的面积，表面积减少了16平方厘米，每个正方形侧面为1644÷=平方厘米，每个正方体棱长为2厘米，三个小正方体体积(即所成形体的体积)是33224⨯=立方厘米.4. 一个盖着瓶盖的瓶子里面装着一些水，瓶底面积为10平方厘米，(如下图所示)，请你根据图中标明的数据，计算瓶子的容积是＿＿＿＿＿＿． 7cm4cm5cm【分析】 由已知条件知，第二个图上部空白部分的高为752cm -=，从而水与空着的部分的比为4:22:1=，由图1知水的体积为104⨯，所以总的容积为()4022160÷⨯+=立方厘米．5. 有许多相同的立方体，每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻，再将写着3的立方体写着2的立方体相邻(见左下图)．依这样构成右下图所示的立方体，它的六个面上的所有数字之和是多少?高宽长33223323322323111111【分析】 第一层如下图，第二层、第三层依次比上面一层每格都多1(见下图)．765434565第三层654323454第二层第一层343212345上面的9个数之和是27，由对称性知，上面、前面、右面的所有数之和都是27．同理，下面的9个数之和是45，下面、左面、后面的所有数之和都是45．所以六个面上所有数之和是(2745)3216+⨯=．6.把一个长方体形状的木料分割成3小块，使这3小块的体积相等．已知这长方体的长为15厘米，宽为12厘米，高为9厘米．分割时要求只能锯两次，如图1就是一种分割线的图．除这种分割的方法外，还可有其他不同的分割方法，请把分割线分别画在图2的各图中．图1图2【分析】 分割方法很多，如图3，给出以下9种分割方法：图3。

学科培优 数学立体几何综合学生姓名 授课日期 教师姓名授课时长知识定位本讲复习已经学过的立体图形的相关知识和解题技巧，主要有:长方体、立方体、圆柱、圆锥的体积及表面积求解，立体几何计数及多面体顶点与棱以及表面的关系。

重难点在于：1．不规则立体图形的表面积或体积求解2．多面体的顶点与棱数计数 3．体积的等量代换主要的考点：1．规则立体图形的表面积（侧面积）与体积计算2．不规则立体图形的表面积与体积计算 3．染色问题4．立体图形的三视图与展开图知识梳理主要知识点 立体几何⑴规则立体图形的表面积和体积公式长方体：体积：长宽高 表面积：（长宽+宽高+长高） 立方体：体积：棱长的立方 表面积：棱长的平方6 圆柱： 体积：2r h π 侧面积：2rh π 圆锥： 体积：213r h π⑵不规则立体图形的表面积整体观照法⑶体积的等积变形①水中浸放物体：V 升水=V 物 ②测啤酒瓶容积：V=V 空气+V 水⑷三视图与展开图最短线路与展开图形状问题⑸染色问题几面染色的块数与“芯”、棱长、顶点、面数的关系。

例题精讲【试题来源】【题目】一个长方体的表面积是33.66平方分米，其中一个面的长是2.3分米，宽是2.1分米，它的体积是_____立方分米.【试题来源】 【题目】右图是一个棱长为2厘米的正方体，在正方体上面的正中向下挖一个棱长为1厘米的正方形小洞；接着在小洞的底面正中再挖一个棱长为21厘米的小洞；第三个小洞的挖法与前两个相同，棱长为41厘米．那么最后得到的立体图形的表面积是 平方厘米【试题来源】【题目】把一个长25厘米，宽10厘米，高4厘米的长方体木块锯成若干个大小相等的正方体，然后拼成一个大的正方体．这个大正方体的表面积是_____平方厘米。

【试题来源】【题目】右图是3层没有缝隙的小立方块组成的．如果它的外表面(包括底面)全都被涂成红色，那么把它们再分开成一个个小立方块时，有多少个小立方块恰有三面是红色的?【试题来源】【题目】一个正方体木块，棱长是15．从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体．这个木块剩下部分的表面积最少是( )．【试题来源】【题目】把一根长2．4米的长方体木料锯成5段(如图)，表面积比原来增加了96平方厘米．这根木料原来的体积是_____立方厘米．【试题来源】【题目】用棱长是1厘米的立方体拼成右图所示的立体图形．求这个立体图形的表面积．【试题来源】【题目】把1个棱长是3厘米的正方体分割成若干个小的正方体，这些小正方体的棱长必须是整厘米数．如果这些小正方体的体积不要求都相等，那么最少可分割成个小正方体．【试题来源】【题目】用10块长7厘米，宽5厘米，高3厘米的长方体积木堆成一个长方体，这个长方体的表面积最小是多少?【试题来源】【题目】一个盛有水的圆柱形容器，底面内半径为5厘米，深20厘米，水深15厘米．今将一个底面半径为2厘米，高为17厘米的铁圆柱垂直放人容器中．求这时容器的水深是多少厘米?【试题来源】【题目】有甲、乙两只圆柱形玻璃杯，其内直径依次是10厘米、20厘米，杯中盛有适量的水．甲杯中沉没着一铁块，当取出此铁块后，甲杯中的水位下降了2厘米；然后将铁块沉没于乙杯，且乙杯中的水未外溢．问：这时乙杯中的水位上升了多少厘米?【试题来源】【题目】将高都是1米，底面半径分别为1．5米、1米和0．5米的三个圆柱组成一个物体．求这个物体的表面积．【试题来源】【题目】这里有一个圆柱和一个圆锥(下图)，它们的高和底面直径都标在图上，单位是厘米．请回答：圆锥体积与圆柱体积的比是多少?【试题来源】【题目】一个长、宽、高分别为21厘米、15厘米、12厘米的长方体．现从它的上面尽可能大的切下一个正方体．然后从剩余的部分再尽可能大的切下一个正方体．最后再从第二次剩余的部分尽可能大的切下一个正方体．剩下的体积是平方厘米．【试题来源】【题目】一个圆柱形玻璃杯内盛有水，水面高2．5厘米，玻璃杯内侧的底面积是72平方厘米．在这个杯中放进棱长6厘米的正方体铁块后，水面没有淹没铁块．这时水面高多少厘米?【试题来源】【题目】图1是下面的表面展开图①甲正方体；②乙正方体；③丙正方体；④甲正方体或丙正方体．【试题来源】【题目】如图，剪一块硬纸片可以做成一个多面体的纸模型(沿虚线折，沿实线粘)．这个多面体的面数、顶点数和棱数的总和是多少?【试题来源】【题目】下面是一辆汽车模型纸工平面展开图，中轴线上面的一半标出了尺寸．将该图剪下折叠粘合(相同字母标记处粘合在一起)做成汽车模型的体积为V ．请回答：①403<v<445②473<V<500，哪一个正确，为什么?【试题来源】【题目】现有一张长40厘米、宽20厘米的长方形铁皮，请你用它做一只深是5厘米的长方体无盖铁皮盒(焊接处及铁皮厚度不计，容积越大越好)，你做出的铁皮盒容积是多少立方厘米?【试题来源】【题目】如图，在一个立方体的两对侧面的中心各打通一个长方体的洞在上下侧面的中心打通一个圆柱形的洞，已知立方体边长为10厘米，侧面上的洞口是边长为4厘米的正方形，上下侧面的洞口是直径为4厘米的圆，求该立方体的表面积和体积(取 =3．14)．【试题来源】【题目】用大小相等的无色透明玻璃小正方体和红色玻璃小正方体拼成一个大正方体ABCD —1A 1B 1C 1D (如图)，大正方体内的对角线A 1C ，B 1D ，C 1A ，D 1B 所穿的小正方体都是红色玻璃小正方体，其它部分都是无色透明玻璃小正方体，小红正方体共用了401个，问：无色透明小正方体用了多少个?习题演练【试题来源】【题目】一个长方体的各条棱长的和是48厘米，并且它的长是宽的2倍，高与宽相等，那么这个长方体的体积是______ 立方厘米【试题来源】【题目】右图是一个表面被涂上红色的棱长为lO厘米的正方体木块，如果把它沿虚线切成8个正方体，这些小正方体中没有被涂上红色的所有表面的面积和是_____平方厘米【试题来源】【题目】张大爷去年用长2米、宽1米的长方形苇席围成容积最大的圆柱形粮囤．今年改用了长3米、宽2米的长方形苇席围成容积最大的圆柱形粮囤．问：今年粮囤的容积是去年粮囤容积的多少倍?【试题来源】【题目】把一个大长方体木块表面上涂满红色后，分割成若干个同样大小的小长方体，其中只有两个面涂上红色的小长方体恰好是12块．那么至少要把这个大长方体分割成个小长方体．【试题来源】【题目】六个立方体A、B、C、D、E、F的可见部分如下图，下边是其中一个立体的侧面展开图，那么它是立方体____的侧面展开图．2。

立体几何专题不规则立体图形的表面积和体积　基础知识：规则立体图形的表面积和体积　表面积体积正方体（棱长为a）6a2a3长方体（边长a、b、c）2（ab+bc+ca）abc圆柱体（底面半径r，高h）2πr2+2πr·hπr2·h圆锥体（底面半径r，高h）πr2+πr·l 例1.把19个边长为2厘米的正方体重叠起来，作成如图那样的组合形体，求这个组合形体的体积和表面积。

[答疑编号505787490101]【答案】体积是152立方厘米；表面积是216平方厘米。

【解答】体积：19×23＝152（立方厘米） 上下看：3×3＝9 左右看：4＋3＋1＝8 前后看：4＋4＋3＝10 （9＋8＋10）×2×22＝216（平方厘米） 进一步思考： （1）对于由小正方体搭起来的组合形体，其表面积总是等于三个方向看到的面积之和的两倍？ [答疑编号505787490102]【答案】不是 （2）如果挪动最上面那个小正方体，将它移动到其他位置，那么所得到的新的组合形体的表面积最少是多少？ [答疑编号505787490103]【答案】200平方厘米【解答】找盖住的面最多的位置，最多可以盖住3个面。

例2.如图，用高都是1米，底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体。

问这个物体的表面积是多少平方米？（π取3.14。

） [答疑编号505787490104]【答案】32.97平方米【解答】结合例1的方法，我们将这个物体的表面积分为上下底的面积和侧面积两部分，不难看出这种叠放并不影响上下底的面积。

解：上底面积与下底面积相等，都是π×1.52=2.25π（平方米）； 侧面积就是三个圆柱体的侧面积之和，等于2π×（1.5+1+0.5）×1=6π（平方米）； 这个物体的表面积是2.25π×2+6π=10.5π=32.97（平方米）。