角平分线的解题模型

专题01 角平分线的五种模型模型一、角平分线垂两边例1.如图，AD是△ABC的角平分线，且AB：AC＝3：2，则△ABD与△ACD的面积之比为（）A．3：2B．6：4C．2：3D．不能确定【答案】A【详解】过点D作DE⊥AB于E，DF⊥AC于F．∵AD为∠BAC的平分线，∴DE=DF，又AB：AC=3：2，∴S△ABD：S△ACD=（12AB•DE）：（12AC•DF）=AB：AC=3：2．故选A．例2.如图，∠AOP＝∠BOP＝15°，PC//OA，PD⊥OA，若PC＝4，则PD的长为___．【答案】2【详解】解：过P作PE⊥OB，交OB与点E，∵∠AOP＝∠BOP，PD⊥OA，PE⊥OB，∴PD＝PE，∵PC//OA，∴∠CPO＝∠POD，又∠AOP＝∠BOP＝15°，∴∠CPO＝∠BOP＝15°，又∠ECP为△OCP的外角，∴∠ECP＝∠COP＋∠CPO ＝30°，在直角三角形CEP 中，∠ECP ＝30°，PC ＝4，∴PE ＝12PC ＝2，则PD ＝PE ＝2．故答案为：2． 【变式训练1】如图所示，在四边形ABCD 中，DC //AB ，∠DAB =90°，AC ⊥BC ，AC =BC ，∠ABC 的平分线交A D ，AC 于点E 、F ，则BFEF的值是___________.11221BCBC BC ==--【详解】解：如图，作FG ⊥AB 于点G ，∠DAB -90°，∴FG /AD ，∴BF EF =BGAGAC ⊥BC ，∴∠ACB =90° 又BF 平分∠ABC ，∴FG =FC 在Rt △BGF 和Rt △BCF 中BF BFCF GF=⎧⎨=⎩ ∴△BGF ≌△BCF （HL ），∴BC =BGAC =BC ，∴∠CBA =45°，∴AB =2BC1BF BG BC EF AG AB BG ∴====- 【变式训练2】如图，BD 平分ABC 的外角∠ABP ，DA =DC ，DE ⊥BP 于点E ，若AB =5，BC =3，求BE 的长．【答案】1【详解】解：过点D 作BA 的垂线交AB 于点H ，∵BD平分△ABC的外角∠ABP，DH⊥AB，∴DE＝DH，在Rt△DEB和Rt△DHB中，DE DHDB DB=⎧⎨=⎩，∴Rt△DEB≌Rt△DHB（HL），∴BE＝BH，在Rt△DEC和Rt△DHA中，DE DHDC DA=⎧⎨=⎩，∴Rt△DEC≌Rt△DHA（HL），∴AH＝CE，由图易知：AH＝AB−BH，CE＝BE＋BC，∴AB−BH＝BE＋BC，∴BE＋BH＝AB−BC＝5−3＝2，而BE＝BH，∴2BE＝2，故BE＝1．【变式训练3，的平分线相交于点E，过点E作交AC于点F，则EF的长为.【答案】【解析】延长FE交AB于点D G H，如图所示：四边形BDEG是矩形，平分CE平分，四边形BDEG是正，，设，则，，，解得，，即，解得，.模型二、角平分线垂中间例．如图，已知，90,,BAC AB AC BD ∠=︒=是ABC ∠的平分线，且CE BD ⊥交BD 的延长线于点E ．求证：2BD CE =． 【答案】见解析【详解】证明：如图，延长CE 与BA 的延长线相交于点F ，∵90,90EBF F ACF F ∠+∠=︒∠+∠=︒，∴EBF ACF ∠=∠，在ABD △和ACF 中，EBF ACF AB AC BAC CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()ABD ACF ASA △≌△，∴BD CF =，∵BD 是ABC ∠的平分线，∴EBC EBF ∠=∠．在BCE ∆和BFE ∆中，EBC EBF BE BE CEB FEB ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()BCE BFE ASA ≌△△， ∴CE EF =，∴2CF CE =， ∴2BD CF CE ==．【变式训练1】如图，已知△ABC ，∠BAC ＝45°，在△ABC 的高BD 上取点E ，使AE ＝BC ． （1）求证：CD ＝DE ；（2）试判断AE 与BC 的位置关系？请说明理由；【答案】（1）见解析；（2）AE BC ⊥，理由见解析；（3）【详解】（1）证明：∵BD AC ⊥，45BAC ∠=︒，∴90,45EDA BDC ABD BAD ∠=∠=︒∠=∠=︒，∴AD BD =，在Rt ADE △和Rt BDC 中，∵AD BDAE BC =⎧⎨=⎩ ∴()Rt ADE Rt BDC HL ≅，∴CD ＝DE ； （2）AE BC ⊥，理由如下：如图，延长AE ，交BC 于点F ， 由（1）得,90EAD EBF EAD AED ∠=∠∠+∠=︒，∵AED AEF ∠=∠，∴90BEF EBF ∠+∠=︒，∴90EFB =︒，即AE BC ⊥；【变式训练2】如图，D 是△ABC 的BC 边的中点，AE 平分∠BAC ，AE ⊥CE 于点E ，且AB =10，AC =16，则DE 的长度为________【答案】3【解答】解：如图，延长CE ，AB 交于点F .AE 平分∠BAC ，AE ⊥EC ，∴∠F AE =∠CAE ，∠AEF =∠AEC =90°在△AFE 和△ACE 中，EAF EAC AE AE AEF AEC =⎧⎪=⎨⎪=⎩∠∠∠∠，∴△AFE ≌ACE （ASA ），∴AF =AC =16，EF =EC ，∴B F =6又D 是BC 的中点，∴BD =CD ，∴DE 是△CBF 的中位线，∴DE =12BF =3，故答案为：3. 【变式训练3】如图，在ABC ∆中，CD 是ACB ∠的平分线，AD CD ⊥于点D ,DE //BC 交AB 于点E ，求证:EA EB =.【答案】见解析【解答】证明：延长AD 交BC 于点F .CD 平分ACF ∠, ACD FCD ∴∠=∠.又,,AD CD CD CD ⊥=ADC ∴∆≌FDC ∆,AD FD ∴=. 又DE ∥BC ,EA EB ∴=.模型三、角平分线+平行线构造等腰三角形例.如图所示，在△ABC 中，BC =6，E 、F 分别是AB 、AC 的中点，动点P 在射线EF 上，BP 交CE 于D，∠CBP 的平分线交CE 于Q ，当CQ =13CE 时，EP +BP =________.【答案】12【解答】解：如图，延长BQ 交射线EF 于点M .E 、F 分别是AB 、AC 的中点，∴EF //BC ，∴∠CBM =∠EMBBM 平分∠ABC ，∴∠ABM =∠CBM ，∴∠EMB =∠EBM ，∴EB =EM ，∴EP +BP =EP +PM =EM CQ =13CE ，∴EQ =2CQ由EF //BC 得，△EMQ ∽△CBQ∴2 212 12EM EQEM BC EP BP BC CQ==∴==∴+=【变式训练1】如图，平分于点C ，，求OC 的长？【解析】如图所示：过点D 作交OA 于点E ，则，平分，，中，，.【变式训练2C=90°，AD平分∠CAB，BE平分∠ABC，AD、BE相交于点F，且，则AC=．【解析】过点E于G，连接CF，如图所示：分别是，CF是的平分线，，，由勾股定理可得.模型四、利用角平分线作对称例.平分.【答案】见解析【解析】证明：在AB上截取，连接DE，如图所示：.【变式训练】AD是△ABC的角平分线，过点D作DE⊥AB于点E，且DE＝3，S△ABC＝20．（1）如图1，若AB＝AC，求AC的长；（2）如图2，若AB＝5，请直接写出AC的长．【答案】（1）203；（2）253【详解】解：（1）如图1，作DF⊥AC于F，∵AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，∴DF ＝DE ＝3， 由题意得，12×AB ×3＋12×AC ×3＝20，解得，AC ＝AB ＝203； （2）如图2，作DF ⊥AC 于F ，∵AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，∴DF ＝DE ＝3， 由题意得，12×5×3＋12×AC ×3＝20，解得，AC ＝253． 模型五、内外模型例.如图，在△ABC 中，AB=AC ，∠A=30°，E 为BC 延长线上一点，∠ABC 与∠AC E 的平分线相交于点D ，则∠D 的度数为（ ）A ．15°B ．17.5°C ．20°D ．22.5°【答案】A4321DA【解析】∵∠ABC与∠AC E的平分线相交于点D，∴∠DCE=∠DCA，∠CBD=∠ABD，即.的外角的平分线CP与内角BP交于点P，若，则.【解析】平分平分又，过点P的延长线，垂足分别为点E、F、G，如图所示：由角平分线的性质可得，AP是.课后训练1．如图，BD是ABC的外角∠ABP的角平分线，DA＝DC，DE⊥BP于点E，若AB＝5，BC＝3，则BE 的长为（）A ．2B ．1.5C ．1D ．0【答案】C【详解】解：如图，过点D 作DF AB ⊥于F ，BD 是ABP ∠的角平分线，DF AB ⊥，DE ⊥BP ，DE DF ∴=，在Rt BDE 和Rt BDF 中，BD BDDE DF =⎧⎨=⎩，()Rt BDE Rt BDF HL ∴△≌△，BE BF ∴=，在Rt ADF 和Rt CDE △中，DA DCDE DF=⎧⎨=⎩，()Rt ADF Rt CDE HL ∴△≌△，AF CE ∴=，AF AB BF =-，CE BC BE =+，AB BF BC BE ∴-=+，2BE AB BC ∴=-，5AB =，3BC =，2532BE ∴=-=，解得：1BE =．故选：C ．2．如图，AD 是ABC 中BAC ∠的平分线，DE AB ⊥交AB 于点E ，DF AC ⊥交AC 于点F ，若7ABC S =△，32=DE ，5AB =，则AC 的长为（ ）A ．133B ．4C ．5D ．6【答案】A【详解】∵AD 是ABC ∆中BAC ∠的平分线，DE AB ⊥于点E ，DF AC ⊥交AC 于点F ，∴32DF DE ==． 又∵ABCABD ACDSSS=+，5AB =，∴1313752222AC =⨯⨯+⨯⨯，∴133AC =．故选：A ． 3．如图，在Rt △ABC 中，∠C ＝90°，∠BAC 的平分线交BC 于点D ，CD ＝2，BD ＝3，Q 为AB 上一动点，则DQ 的最小值为（ ）A．1B．2C．2.5D【答案】B【详解】解：作DH⊥AB于H，如图，∵AD平分∠BAC，DH⊥AB，DC⊥AC，∴DH=DC=2，∵Q为AB上一动点，∴DQ的最小值为DH的长，即DQ的最小值为2．故选：B．4．如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC＝9，CD＝4，则四边形ABCD 的面积是______．【答案】30【详解】过D作DE⊥AB，交BA的延长线于E，则∠E＝∠C＝90°，∵∠BCD＝90°，BD平分∠ABC，∴DE＝DC=4，∴四边形ABCD的面积S＝S△BCD＋S△BAD＝12×BC×CD＋12×AB×DE＝12×9×4＋12×6×4＝30，故答案为：30．5．如图，在△ABC中，AD为△ABC的角平分线，DE⊥AB，垂足为E，DF⊥AC，垂足为F，若AB=5，AC=3，DF=2，则△ABC的面积为______．【答案】8【详解】解：∵AD为△ABC的角平分线，DE⊥AB，DF⊥AC，∴DE=DF=2，∴△ABC的面积=12×5×2+12×3×2=8，故答案侍：8．6．在△ABC中，∠ABC＝62°，∠ACB＝50°，∠ACD是△ABC的外角∠ACD和∠ABC的平分线交于点E，则∠AEB＝_____︒【答案】25【详解】解：如图示：过点E ，分别作EF BD ⊥交BD 于点E ，EG AC ⊥交AC 于点G ，EH AB ⊥，交AB 延长线于点H ， ∵BE 平分ABC ∠，CE 平分ACD ∠，∴EH EF =，EG EF =，∴EH EG =，∴AE 平分HAC ∠， ∵62ABC ∠=︒，50∠=°ACB ，∴6250112HAC ABC ACB ∠=∠+∠=︒+︒=︒，∴111125622EAO HAC ∠=∠=⨯︒=︒， ∵BE 平分ABC ∠，62ABC ∠=︒∴11623122EBC ABC ∠=∠=⨯︒=︒ 在AOE △和BOC 中，OBC OCB OAE AEB ∠+∠=∠+∠∴31505625AEB OBC OCB OAE ∠=∠+∠-∠=︒+︒-︒=︒，故答案是：25． 7．如图，DE ⊥AB 于E ，DF ⊥AC 于F ，若BD =CD ，BE =CF ．（1）求证：AD 平分∠BAC ：（2）已知AC =18，BE =4，求AB 的长． 【答案】（1）见解析；（2）10AB =．【详解】（1）证明：DE AB ∵⊥，DF AC ⊥，90E DFC ∴∠=∠=︒，在Rt BED 和Rt CFD △中，BD CD BE CF =⎧⎨=⎩，∴Rt BED Rt CFD ≅()HL ，DE DF ∴=，DE AB ∵⊥，DF AC ⊥，AD ∴平分BAC ∠；（2）解：DE DF =，AD AD =，Rt ADE Rt ADF ∴≅()HL ，AE AF ∴=，AB AE BE AF BE AC CF BE =-=-=--，184410AB ∴=--=．8．如图1，在平面直角坐标系中，△ABC 的顶点A （-4，0），B （0，4），AD ⊥BC 交BC 于D 点，交y 轴正半轴于点E （0，t ）（1）当t=1时，点C 的坐标为 ； （2）如图2，求∠ADO 的度数；（3）如图3，已知点P （0，3），若PQ ⊥PC ，PQ=PC ，求Q 的坐标（用含t 的式子表示）． 【答案】（1）点C 坐标（1，0）；（2）∠ADO =45°；（3）Q （-3，3-t ）． 【详解】（1）如图1，当t =1时，点E （0，1）， ∵AD ⊥BC ， ∴∠EAO +∠BCO =90°， ∵∠CBO +∠BCO =90°，∴∠EAO =∠CBO ，在△AOE 和△BOC 中，∵90EAO CBOAO BO AOE BOC ∠=∠⎧⎪=⎨⎪∠=∠︒⎩＝，∴△AOE ≌△BOC （ASA ），∴OE =OC =1，∴点C 坐标（1，0）． 故答案为：（1，0）；（2）如图2，过点O 作OM ⊥AD 于点M ，作ON ⊥BC 于点N ，∵△AOE ≌△BOC ，∴S △AOE =S △BOC ，且AE =BC ， ∵OM ⊥AE ，ON ⊥BC ，∴OM =ON ，∴OD 平分∠ADC ；AD ⊥BC ，90ADC ∴∠=︒∴∠ADO =1452ADC ∠=︒；（3）如图3，过P 作GH ∥x 轴，过C 作CG ⊥GH 于G ，过Q 作QH ⊥GH 于H ，交x 轴于F ，∵P （0，3），C （t ，0），∴CG =FH =3，PG =OC =t ， ∵∠QPC =90°，∴∠CPG +∠QPH =90°， ∵∠QPH +∠HQP =90°，∴∠CPG =∠HQP ，∵∠QHP=∠G=90°，PQ=PC，∴△PCG≌△QPH，∴CG=PH=3，PG=QH=t，∴Q（-3，3-t）．。

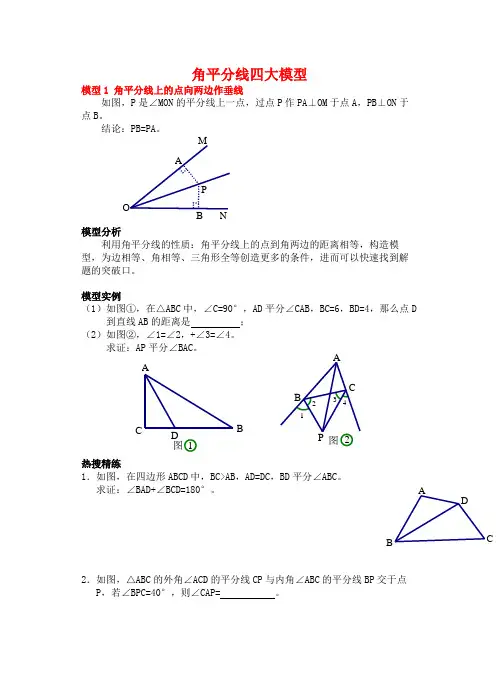
角平分线四大模型模型1 角平分线上的点向两边作垂线如图，P 是∠MON 的平分线上一点，过点P 作PA ⊥OM 于点A ，PB ⊥ON 于点B 。

结论：PB=PA 。

模型分析利用角平分线的性质：角平分线上的点到角两边的距离相等，构造模型，为边相等、角相等、三角形全等创造更多的条件，进而可以快速找到解题的突破口。

模型实例（1）如图①，在△ABC 中，∠C=90°，AD 平分∠CAB ，BC=6，BD=4，那么点D到直线AB 的距离是 ； （2）如图②，∠1=∠2，+∠3=∠4。

求证：AP 平分∠BAC 。

热搜精练1．如图，在四边形ABCD 中，BC>AB ，AD=DC ，BD 平分∠ABC 。

求证：∠BAD+∠BCD=180°。

2．如图，△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点 P ，若∠BPC=40°，则∠CAP= 。

N M OAB P 2图4321A CP B D AB C图1A B DC模型2 截取构造对称全等如图，P 是∠MON 的平分线上一点，点A 是射线OM 上任意一点，在ON 上截取OB=OA ，连接PB 。

结论：△OPB ≌△OPA 。

模型分析利用角平分线图形的对称性，在角的两边构造对称全等三角形，可以得到对应边、对应角相等。

利用对称性把一些线段或角进行转移，这是经常使用的一种解题技巧。

模型实例（1）如图①所示，在△ABC 中，AD 是△ABC 的外角平分线，P 是AD 上异于点A 的任意一点，试比较PB+PC 与AB+AC 的大小，并说明理由；（2）如图②所示， AD 是△ABC 的内角平分线，其他条件不变，试比较 PC-PB 与AC-AB 的大小，并说明理由。

热搜精练1．已知，在△ABC 中，∠A=2∠B ，CD 是∠ACB 的平分线，AC=16，AD=8。

求线段BC 的长。

A B DCPP O N M B A 图2DP AB C D C 1图P B A ABCD2．已知，在△ABC 中，AB=AC ，∠A=108°，BD 平分∠ABC 。

⾓平分线四⼤模型总结+习题+解析（最全版）⾓平分线四⼤辅助线模型⾓平分线的性质为证明线段或⾓相等开辟了新的途径，同时也是全等三⾓形知识的延续，⼜为后⾯⾓平分线的判定定理的学习奠定了基础．涉及到⾓平分线的考点主要是性质、判定以及四⼤辅助线模型，在初⼆上期中、期末考试中都是经常考察的⽅向。

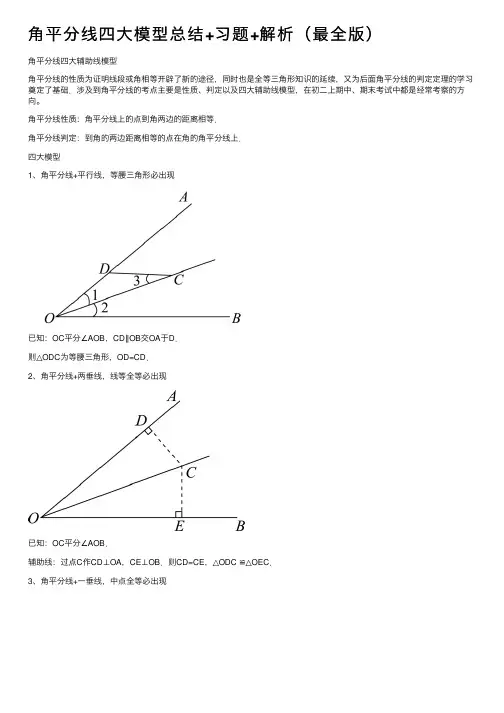
⾓平分线性质：⾓平分线上的点到⾓两边的距离相等．⾓平分线判定：到⾓的两边距离相等的点在⾓的⾓平分线上．四⼤模型1、⾓平分线+平⾏线，等腰三⾓形必出现已知：OC平分∠AOB，CD∥OB交OA于D．则△ODC为等腰三⾓形，OD=CD．2、⾓平分线+两垂线，线等全等必出现已知：OC平分∠AOB．辅助线：过点C作CD⊥OA，CE⊥OB．则CD=CE，△ODC ≌△OEC．3、⾓平分线+⼀垂线，中点全等必出现已知：OC平分∠AOB，DC垂直OC于点C．辅助线：延长DC交OB于点E．则C是DE的中点，△ODC ≌△OEC．4、⾓平分线+截长补短线，对称全等必出现已知：OC平分∠AOB,截取OE=OD，连接CD、CE．则△ODC和△OCE关于OC对称，即△ODC ≌△OEC．【核⼼考点⼀】⾓平分线的性质与判定1．（2016?张家界模拟）如图，OP 平分MON ∠，PA ON ⊥于点A ，点Q 是射线OM 上⼀个动点，若3PA =，则PQ 的最⼩值为( )A B ．2C ．3D ．2．（2016秋?抚宁县期末）如图，在ABC ?中，AD 是它的⾓平分线，8AB cm =，6AC cm =，则:(ABD ACD S S ??= )A ．3:4B ．4:3C ．16:9D ．9:163．（2017春?崇仁县校级⽉考）如图，在ABC ?中，90ACB ∠=?，BE 平分ABC ∠，DE AB ⊥于点D ，如果3AC cm =，那么AE DE +等于( )A ．2cmB ．3cmC ．4cmD ．5cm4．（2018春?⼤东区期中）如图，在Rt ABC ?中，90C ∠=?，BD 是⾓平分线，若CD m =，2AB n =，则ABD ?的⾯积是( )A ．mnB ．5mnC ．7mnD ．6mn5．（2019秋?樊城区期末）⼩明同学在学习了全等三⾓形的相关知识后发现，只⽤两把完全相同的长⽅形直尺就可以作出⼀个⾓的平分线．如图：⼀把直尺压住射线OB ，另⼀把直尺压住射线OA 并且与第⼀把直尺交于点P ，⼩明说：“射线OP 就是BOA ∠的⾓平分线．”他这样做的依据是( )A ．⾓的内部到⾓的两边的距离相等的点在⾓的平分线上B ．⾓平分线上的点到这个⾓两边的距离相等C ．三⾓形三条⾓平分线的交点到三条边的距离相等D ．以上均不正确6．（2019秋?梁平区期末）如图，若BD AE ⊥于B ，DC AF ⊥于C ，且DB DC =，40BAC ∠=?，130ADG ∠=?，则DGF ∠=．7．（2018春?开江县期末）如图，在Rt ABC ?中，90C ∠=?，以顶点A 为圆⼼，适当长为半径画弧，分别交AB 、AC 于点M 、N ，再分别以点M 、N 为圆⼼，⼤于12MN 的长为半径画弧，两弧交于点P ，射线AP 交边BC 于点D ．下列说法错误的是( ) A ．CAD BAD ∠=∠B ．若2CD =，则点D 到AB 的距离为2C ．若30B ∠=?，则CDA CAB ∠=∠D ．2ABD ACD S S ??=8．（2014秋?西城区校级期中）如图，点E 是AOB ∠的平分线上⼀点，EC OA ⊥，ED OB ⊥，垂⾜分别是C ，D ．下列结论中正确的有( )（1）ED EC =；（2）OD OC =；（3）ECD EDC ∠=∠；（4）EO 平分DEC ∠；（5）OE CD ⊥；（6）直线OE 是线段CD 的垂直平分线．A ．3个B ．4个C ．5个D ．6个9．（2019春?杜尔伯特县期末）如图：在ABC ?中，90C ∠=?，AD 是BAC ∠的平分线，DE AB ⊥于E ，F 在AC 上，BD DF =，证明：（1）CF EB =．（2）2AB AF EB =+．10．（2019秋?垦利区期中）如图，ABC⊥⊥且平分BC，DE AB中，AD平分BAC∠，DG BC于E，DF AC⊥于F．（1）判断BE与CF的数量关系，并说明理由；（2）如果8AB=，6AC=，求AE、BE的长．11．（2017秋?遂宁期末）某地区要在区域S内（即COD∠内部）建⼀个超市M，如图所⽰，按照要求，超市M到两个新建的居民⼩区A，B的距离相等，到两条公路OC，OD的距离也相等．这个超市应该建在何处？（要求：尺规作图，不写作法，保留作图痕迹）【核⼼考点⼆】⾓平分线+⾓两边垂线12．（2019秋?肥城市期末）如图，//AB CD ，BP 和CP 分别平分ABC ∠和DCB ∠，AD 过点P ，且与AB 垂直，垂⾜为A ，交CD 于D ，若8AD =，则点P 到BC 的距离是．13．（2015?湖州）如图，已知在ABC ?中，CD 是AB 边上的⾼线，BE 平分ABC ∠，交CD 于点E ，5BC =，2DE =，则BCE ?的⾯积等于( )A ．10B ．7C ．5D ．414．（2010秋?涵江区期末）如图所⽰，在Rt ABC ?中，90C ∠=?，BC AC =，AD 平分BAC ∠交BC 于D ，求证：AB AC CD =+．15．（2012秋?蓬江区校级期末）如图，已知90∠=∠=?，M是BC的中点，DM平分B C∠．求证：ADC（1）AM平分DAB∠；（2）DM AM⊥．16．（2016秋?西城区校级期中）已知：如图，12∠=∠，P为BN上的⼀点，PF BC⊥于F，=，PA PC（1）求证：180∠+∠=?；PCB BAP（2）线段BF、线段BC、线段AB之间有何数量关系？写出你的猜想及证明思路．【核⼼考点三】⾓平分线+垂线17．（2017秋?和平区校级⽉考）如图．在ABC ?中，BE 是⾓平分线，AD BE ⊥，垂⾜为D ，求证：21C ∠=∠+∠．18．（2013秋?昌平区期末）已知：如图，在ABC ?中，AD 平分BAC ∠，CD AD ⊥于点D ，DCB B ∠=∠，若10AC =，6AD=，求AB 的长．19．如图所⽰，ABC ?中，ACB ABC ∠>∠，AE 平分BAC ∠，CD AE ⊥于D ，求证：ACD B ∠>∠．20．已知：如图，在ABC ?中，3ABC C ∠=∠，12∠=∠，BE AE ⊥．求证：2AC AB BE -=．21．（2019秋?下陆区期中）如图，BD 是ABC ∠的⾓平分线，AD BD ⊥，垂⾜为D ，20DAC ∠=?，38C ∠=?，则BAD ∠=．22．（2019秋?曲⾩市校级⽉考）如图，在ABC ?中，AB AC =，90BAC ∠=?，BD 平分ABC ∠交AC 于D ，过C 作CE BD ⊥交BD 延长线于E ．求证：12CE BD =．23．（2019?沂源县⼀模）（1）如图（a）所⽰，BD、CE分别是ABC的外⾓平分线，过点A作AD BD⊥，AE CE⊥，垂⾜分别为D、E，连接DE，求证：1() 2DE AB BC AC=++；（2）如图（b）所⽰，BD、CE分别是ABC的内⾓平分线，其他条件不变，DE与ABC三边有怎样的数量关系？并证明这个数量关系；（3）如图（c）所⽰，BD为ABC的内⾓平分线，CE为ABC的外⾓平分线，其他条件不变，DE与ABC三边⼜有怎样的数量关系？并证明这个数量关系．24．（2017秋?夏⾢县期中）如图，在ABC ?中，ABC ∠、ACB ∠的平分线相交于F ，过F 作//DE BC ，交AB 于D ，交AC 于E ，那么下列结论：①BDF ?、CEF ?都是等腰三⾓形；②DE DB CE =+；③AD DE AE AB AC ++=+；④BF CF =．正确的有．25．（2019秋?垦利区期末）如图，平⾏四边形ABCD 中，3AB cm =，5BC cm =；，BE 平分ABC ∠，交AD 于点E ，交CD 延长线于点F ，则DE DF +的长度为．26．（2010秋?海淀区期末）如图，BD 是ABC ?的⾓平分线，//DE BC ，DE 交AB 于E ，若AB BC =，则下列结论中错误的是( )A ．BD AC ⊥B ．A EDA ∠=∠C ．2AD BC =D ．BE ED =27．如图，若BD 、CD 分别平分ABC ∠和ACB ∠，过D 作//DE AB 交BC 于E ，作//DF AC 交BC 于F ，求证：BC 的长等于DEF ?的周长．28．（2018秋?邳州市期中）如图，在四边形ABCD中，对⾓线AC平分BAD >，∠，AB AD 下列结论正确的是()A．AB AD CB CD->-B．AB AD CB CD-=-C．AB AD CB CD-<-D．AB AD-与CB CD-的⼤⼩关系不确定29．（2012?⿇城市校级模拟）在ABC∠的外⾓平分线，P是AD上的任意中，AD是BAC⼀点，试⽐较PB PC+与AB AC+的⼤⼩，并说明理由．30．（2018秋?万州区期中）已知：如图，在四边形ABCD中，AC平分BAD ∠，CE AB⊥于=+．E，且180B D∠+∠=?，求证：AE AD BE31．（2017秋?海淀区期中）如图，已知AD是BAC∠=?，C=+，31的⾓平分线，AC AB BD 求B∠的度数．32．（2019秋?平⼭县期中）如图，90∠=?，OM平分AOB∠，将直⾓三⾓板的顶点PAOB在射线OM上移动，两直⾓边分别与OA、OB相交于点C、D，问PC与PD相等吗？试说明理由．33．（2016秋?丰宁县期中）如图，在ABC ?中，100A ∠=?，40ABC ∠=?，BD 是ABC ∠的平分线，延长BD ⾄E ，使DE AD =．求证：BC AB CE =+．34．（2018秋?丰城市期中）在ABC ?中，2ACB B ∠=∠，（1）如图1，当90C ∠=?，AD 为BAC ∠的⾓平分线时，在AB 上截取AE AC =，连接DE ，求证：AB AC CD =+；（2）如图2，当90C ∠≠?，AD 为BAC ∠的⾓平分线时，线段AB 、AC 、CD ⼜有怎样的数量关系？请直接写出你的结论，不需要证明；（3）如图3，当AD 为ABC ?的外⾓平分线时，线段AB 、AC 、CD ⼜有怎样的数量关系？请写出你的猜想，并说明理由．35．（2019春?利津县期末）如图，在ABC∠平分线，AD的垂直平分线分中，AD是BAC别交AB、BC延长线于F、E．求证：（1）EAD EDA∠=∠；（2）//DF AC；（3）EAC B∠=∠．36．（2014?西城区⼆模）在ABC>，AD平分BAC∠交BC于点∠为锐⾓，AB AC，BACD．（1）如图1，若ABC是等腰直⾓三⾓形，直接写出线段AC，CD，AB之间的数量关系；（2）BC的垂直平分线交AD延长线于点E，交BC于点F．①如图2，若60∠=?，判断AC，CE，AB之间有怎样的数量关系并加以证明；ABE②如图3，若AC AB+，求BAC∠的度数．⾓平分线四⼤辅助线模型--解析⼀．⾓平分线的性质与判定（共11⼩题）1．（2016?张家界模拟）如图，OP 平分MON ∠，PA ON ⊥于点A ，点Q 是射线OM 上⼀个动点，若3PA =，则PQ 的最⼩值为( )A B ．2C ．3D ．【分析】⾸先过点P 作PB OM ⊥于B ，由OP 平分MON ∠，PA ON ⊥，3PA =，根据⾓平分线的性质，即可求得PB 的值，⼜由垂线段最短，可求得PQ 的最⼩值．【解答】解：过点P 作PB OM ⊥于B ， OP 平分MON ∠，PA ON ⊥，3PA =，3PB PA ∴==，PQ ∴的最⼩值为3．故选：C ．2．（2016秋?抚宁县期末）如图，在ABC ?中，AD 是它的⾓平分线，8AB cm =，6AC cm =，则:(ABD ACD S S ??= )A ．3:4B ．4:3C ．16:9D ．9:16【分析】利⽤⾓平分线的性质，可得出ABD ?的边AB 上的⾼与ACD ?的AC 上的⾼相等，估计三⾓形的⾯积公式，即可得出ABD ?与ACD ?的⾯积之⽐等于对应边之⽐．【解答】解：AD 是ABC ?的⾓平分线，∴设ABD ?的边AB 上的⾼与ACD ?的AC 上的⾼分别为1h ，2h ，12h h ∴=，ABD ∴?与ACD ?的⾯积之⽐:8:64:3AB AC ===，故选：B ．3．（2017春?崇仁县校级⽉考）如图，在ABC ?中，90ACB ∠=?，BE 平分ABC ∠，DE AB ⊥于点D ，如果3AC cm =，那么AE DE +等于( )A ．2cmB ．3cmC ．4cmD ．5cm【分析】根据⾓平分线的性质得到ED EC =，计算即可．【解答】解：BE 平分ABC ∠，DE AB ⊥，90ACB ∠=?， ED EC ∴=，3AE DE AE EC AC cm ∴+=+==，故选：B ．4．（2018春?⼤东区期中）如图，在Rt ABC ?中，90C ∠=?，BD 是⾓平分线，若CD m =，2AB n =，则ABD ?的⾯积是( )A ．mnB ．5mnC ．7mnD ．6mn【分析】过点D 作DE AB ⊥于E ，根据⾓平分线上的点到⾓的两边距离相等可得DE CD =，然后根据三⾓形的⾯积公式即可得到结论．【解答】解：如图，过点D 作DE AB ⊥于E ，BD 是ABC ∠的平分线，90C ∠=?，DE CD m ∴==，ABD ∴?的⾯积122n m mn =??=，故选：A．5．（2019秋?樊城区期末）⼩明同学在学习了全等三⾓形的相关知识后发现，只⽤两把完全相同的长⽅形直尺就可以作出⼀个⾓的平分线．如图：⼀把直尺压住射线OB，另⼀把直尺压住射线OA并且与第⼀把直尺交于点P，⼩明说：“射线OP就是BOA∠的⾓平分线．”他这样做的依据是()A．⾓的内部到⾓的两边的距离相等的点在⾓的平分线上B．⾓平分线上的点到这个⾓两边的距离相等C．三⾓形三条⾓平分线的交点到三条边的距离相等D．以上均不正确【分析】过两把直尺的交点C作CE AO=，再根据⾓⊥，CF BO⊥，根据题意可得CE CF的内部到⾓的两边的距离相等的点在这个⾓的平分线上可得OP平分AOB∠；【解答】解：（1）如图所⽰：过两把直尺的交点P作PE AO⊥，⊥，PF BO两把完全相同的长⽅形直尺，PE PF∴=，∠（⾓的内部到⾓的两边的距离相等的点在这个⾓的平分线上），OP∴平分AOB故选：A．。

N M O A B PPO N M B A专题01 角平分线四大模型在三角形中的应用（知识解读）【专题说明】角平分线在几何中占有重要地位，是解决许多问题的桥梁和纽带，角平分线把一个角分成相等的两个部分，其“轴承对称功能”衍生出“角平分线上的点到角两边的距离相等”以及“等腰三角形三线合一”、“三角形的内心到三边的距离相等”等性质，而角平分线与平行线相结合构造出等腰三角形，也常在解题中给我们带来帮助，本专题介绍四种常考解题方法。

【方法技巧】模型1 角平分线上的点向两边作垂线如图，P 是∠MON 的平分线上一点，过点P 作PA ⊥OM 于点A ，PB ⊥ON 于点B 。

结论：PB=PA 。

【模型分析】利用角平分线的性质：角平分线上的点到角两边的距离相等，构造模型，为边相等、角相等、三角形全等创造更多的条件，进而可以快速找到解题的突破口。

模型2 截取构造对称全等如图，P 是∠MON 的平分线上一点，点A 是射线OM 上任意一点，在ON 上截取OB=OA ，连接PB 。

结论：△OPB ≌△OPA 。

P O N M B AQP O N M 【模型分析】利用角平分线图形的对称性，在角的两边构造对称全等三角形，可以得到对应边、对应角相等。

利用对称性把一些线段或角进行转移，这是经常使用的一种解题技巧。

模型3 角平分线+垂线构造等腰三角形如图，P 是∠MO 的平分线上一点，AP⊥OP 于P 点，延长AP 于点B 。

结论：△AOB 是等腰三角形。

【模型分析】构造此模型可以利用等腰三角形的“三线合一”，也可以得到两个全等的直角三角形，进而得到对应边、对应角相等。

这个模型巧妙地把角平分线和三线合一联系了起来。

模型4 角平分线+平行线如图，P 是∠MO 的平分线上一点，过点P 作PQ ∥ON ，交OM 于点Q 。

结论：△POQ 是等腰三角形。

【模型分析】有角平分线时，常过角平分线上一点作角的一边的平行线，构造等腰三角形，为证明结论提供更多的条件，体现了角平分线与等腰三角形之间的密切关系。

初中数学 ︵ 角平分线模型 ︶培优篇角平分线在中考数学中都占据着重要的地位，角平分线常作为压轴题中的常考知识点，需要掌握其各类模型及相应的辅助线作法，且辅助线是大部分学生学习几何内容中的弱点，本专题就角平分线的几类全等模型作相应的总结，需反复掌握．【模型解读与图示】条件：如图1，OC 为AOB 的角平分线、CA OA 于点A 时，过点C 作CA OB ．结论：CA CB 、OAC ≌OBC ．图1常见模型1（直角三角形型）条件：如图2，在ABC 中，90C ，AD 为CAB 的角平分线，过点D 作DE AB ．结论：DC DE 、DAC ≌DAE ．（当ABC 是等腰直角三角形时，还有AB AC CD ）图2初中数学 ︵ 角平分线模型 ︶培优篇常见模型2（邻等对补型）条件：如图3，OC 是∠COB 的角平分线，AC =BC ，过点C 作CD ⊥OA 、CE ⊥OB 。

结论：①180BOA ACB ；②AD BE ；③2OA OB AD ．图3A ．4 例2．如图，已知BF ，垂足分别为①CP 平分ACF ； ② APM CPN APC S S ．其中结论正确的是（ A ．①②③B ．①②③④初中数学 ︵ 角平分线模型 ︶培优篇 例3．如图所示，90BC ，E 是BC 的中点，DE 平分ADC ． （1）求证：AE 是DAB 的平分线； （2）若2cm,BAD=60CD ，求AD 的长．例4．已知，OA 平分MON ，点P 在射线OA 上，点B 在射线OM 上，点C 在直线ON 上，连接PB ，PC ，且180MON BPC ．（1）如图1，当90MON 时，PB 与PC 的数量关系是______．（2）如图2，当MON 是钝角时，（1）中的结论是否成立？如果成立，请证明；如果不成立，请说明理由；（3）当120MON 时，若6OP ，2OC ，请直接写出OBP 与OCP △的面积的比值．初中数学 ︵ 角平分线模型 ︶培优篇【模型解读与图示】条件：如图1，OC 为AOB 的角平分线，AB OC ．结论：△AOC ≌△BOC ，OAB 是等腰三角形、OC 是三线合一等．图1 图2 图3 条件：如图2，BE 为ABC 的角平分线，BE EC ，延长BA ，CE 交于点F ． 结论：△BEC ≌△BEF ，BFC 是等腰三角形、BE 是三线合一等。

模型1：角平分线上的点向两边作垂线这个模型的基本思想是过角平分线上一点 P 作角两边的垂线。

如图中 PA⊥OA，PB⊥OB。

容易通过全等得到 PA=PB（角平分线性质）。

注意：题目一般只有一条垂线，需要自行补出另一条垂线。

甚至只给你一条角平分线，自行添加两条垂线。

模型1：角平分线上的点向两边作垂线模型分析利用角平分线的性质：角平分线上的点到角两边的距离相等，构造模型，为边相等、角相等、三角形全等创造更多的条件，进而可以快速找到解题的突破口。

模型2：截取构造对称全等这个模型的基础是在角的两边分别截取 OA=OB，然后在对角线上取任意一点 P，连接 AP，BP。

容易证得△APO≌△BPO。

注意：一般这样的模型最容易被孩子忽略，因为这个模型里没有的角度，因而对于孩子而言添出 PB 这条辅助线是有难度的。

添加这条辅助线的基本思想是在 ON 上截取 OB，使得 AP=BP。

从而构造出一个轴对称。

这样的模型一般会出现在截长补短里。

模型2：截取构造对称全等模型分析利用角平分线图形的对称性，在角的两边构造对称全等三角形，可以得到对应边、对应角相等。

利用对称性把一些线段或角进行转移，这是经常使用的一种解题技巧。

模型3：角平分线+垂线构造等腰三角形这个模型的基础是，在角平分线上任意找一点 P，过点 P 作角平分线的垂线交角的两条边与A、B。

这样就构造出了一个等腰三角形AOB，即 OA=OB。

这个模型还可以得到P是AB 中点。

注意：这个模型与一之间的区别在于垂直的位置。

并且辅助线的添加方法一般是延长一段与角平分线垂直的线段。

如图中的 PB。

模型3：角平分线+垂线构造等腰三角形模型分析构造此模型可以利用等腰三角形的“三线合一”，也可以得到两个全等的直角三角形，进而得到对应边、对应角相等。

这个模型巧妙地把角平分线和三线合一联系了起来。

模型4：角平分线+平行线这个模型是在角平分线上任意找一个点 P。

分别过点 P 作 ON，OM 的平行线 PA， PB。

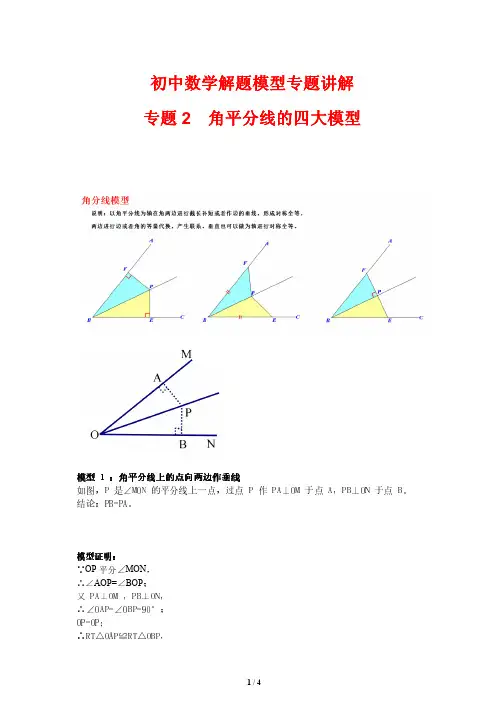
初中数专题2模型模型 1 1 ：：角平分线上的点向如图，P 是∠MON 的平分线上结论：PB=PA。

模型证明模型证明：：∵OP平分∠MON，∴∠AOP=∠BOP；又 PA⊥OM ，PB⊥ON，∴∠OAP=∠OBP=90°；OP=OP；∴RT△OAP≌RT△OBP,初中数学解题模型专题讲解2 角平分线的四大模型的点向两边作垂线的点向两边作垂线分线上一点，过点 P 作 PA⊥OM 于点 A，PB⊥ONON 于点 B。

∴PB=PA。

模型分析利用角平分线的性质：角平分为边相等、角相等、三角形全突破口。

模型实例模型实例（1）如图①，在△ABC 中到直线 AB 的距离是_____（2）如图②，∠1=∠2，∠求证：AP 平分∠BAC。

解析解析：（：（1）由角平分线模型知（2）如图分别做AB ∴AP 平分∠BAC角平分线上的点到角两边的距离相等，构造模型角形全等创造更多的条件，进而可以快速找到解题中，∠C=90°，AD 平分∠CAB，BC=6，BD=4，那么___；∠3=∠4。

模型知模型知，，D 到AB 的距离等于DC=2AB 、BC 、AC 三边的高三边的高，，由题意易得三边高相等由题意易得三边高相等，，模型， 到解题的 那么点 D ，模型练习1．如图，在四边形 ABCD 求证：∠BAD+∠BCD=180°证明证明：：如图延长BA ，过D 作DE 、DF ∵BD 平分∠ABC∴DE=DF,又AD=DC∴RT△DEA≌RT△DFC ∴∠DAE=∠BCD∴∠BAD+∠BCD=180°2．如图，△ABC 的外角∠P，若∠BPC=40°，则∠CAP=CD 中，BC>AB，AD=DC，BD 平分∠ABC。

°。

垂直BA 延长线延长线、、BC 于E 、F 两点两点，， DFC°∠ACD 的平分线 CP 与内角∠ABC 的平分线 BP CAP= 。

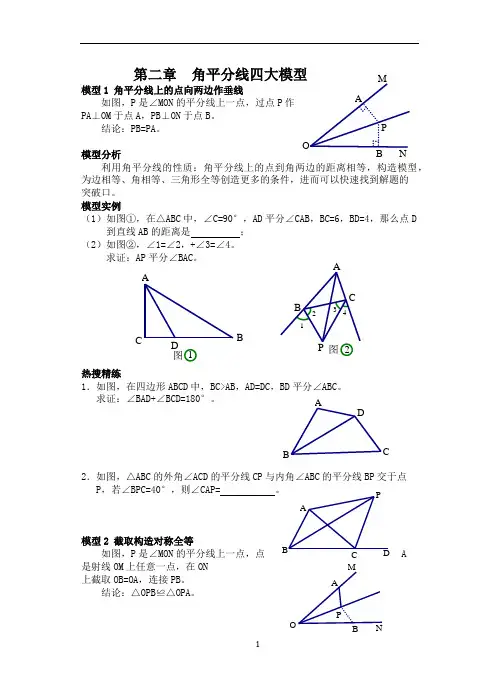
N MOA B P 2图4321A CP B D AB C图1A B D C AB D CPP ONM BA 第二章 角平分线四大模型模型1 角平分线上的点向两边作垂线如图，P 是∠MON 的平分线上一点，过点P 作PA ⊥OM 于点A ，PB ⊥ON 于点B 。

结论：PB=PA 。

模型分析利用角平分线的性质：角平分线上的点到角两边的距离相等，构造模型，为边相等、角相等、三角形全等创造更多的条件，进而可以快速找到解题的突破口。

模型实例（1）如图①，在△ABC 中，∠C=90°，AD 平分∠CAB ，BC=6，BD=4，那么点D到直线AB 的距离是 ； （2）如图②，∠1=∠2，+∠3=∠4。

求证：AP 平分∠BAC 。

热搜精练1．如图，在四边形ABCD 中，BC>AB ，AD=DC ，BD 平分∠ABC 。

求证：∠BAD+∠BCD=180°。

2．如图，△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点 P ，若∠BPC=40°，则∠CAP= 。

模型2 截取构造对称全等如图，P 是∠MON 的平分线上一点，点A 是射线OM 上任意一点，在ON 上截取OB=OA ，连接PB 。

结论：△OPB ≌△OPA 。

图2DP AB C D C 1图P B A ABC DA BC DE DC B AP ONM B A 模型分析利用角平分线图形的对称性，在角的两边构造对称全等三角形，可以得到对应边、对应角相等。

利用对称性把一些线段或角进行转移，这是经常使用的一种解题技巧。

模型实例（1）如图①所示，在△ABC 中，AD 是△ABC 的外角平分线，P 是AD 上异于点A 的任意一点，试比较PB+PC 与AB+AC 的大小，并说明理由；（2）如图②所示， AD 是△ABC 的内角平分线，其他条件不变，试比较 PC-PB 与AC-AB 的大小，并说明理由。

角平分线四大模型口诀
角平分线是指将一个角分成两个相等的部分的线段。

根据不同的角度和图形特征，我们可以将角平分线分为四种不同的模型，它们分别是：
1. 垂直平分线模型：当一个角的平分线和角的两边垂直相交时，我们称之为垂直平分线模型。

垂直平分线将角分成两个相等的部分，并且平分线和角的两边垂直相交。

2. 边平分线模型：当一个角的平分线与角的一条边重合时，我们称之为边平分线模型。

边平分线将角分成两个相等的部分，并且平分线与角的一条边重合。

3. 内角平分线模型：当一个角的平分线在角的内部，并且和角的两边相交时，我们称之为内角平分线模型。

内角平分线将角分成两个相等的部分，并且平分线在角的内部。

4. 外角平分线模型：当一个角的平分线在角的外部，并且与角的一条边相交时，我们称之为外角平分线模型。

外角平分线将角分成两个相等的部分，并且平分线在角的外部。

这些角平分线模型在几何学和三角学中经常被使用，可以帮助我们研
究角的性质和定理。

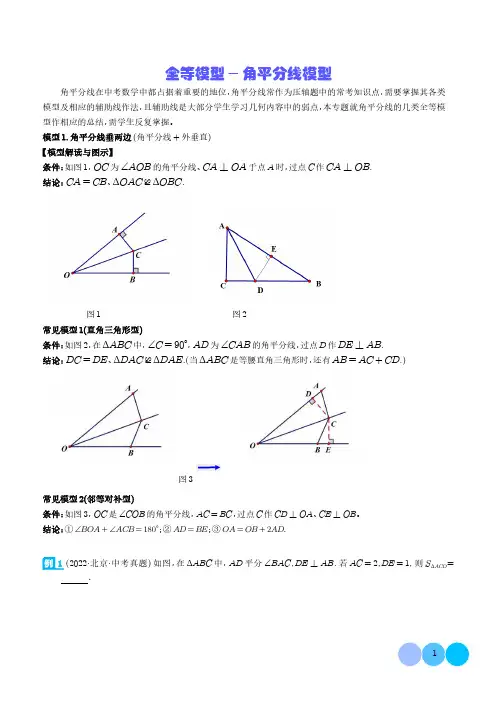
全等模型-角平分线模型角平分线在中考数学中都占据着重要的地位，角平分线常作为压轴题中的常考知识点，需要掌握其各类模型及相应的辅助线作法，且辅助线是大部分学生学习几何内容中的弱点，本专题就角平分线的几类全等模型作相应的总结，需学生反复掌握。

模型1.角平分线垂两边(角平分线+外垂直)【模型解读与图示】条件：如图1，OC为∠AOB的角平分线、CA⊥OA于点A时，过点C作CA⊥OB.结论：CA=CB、ΔOAC≌ΔOBC.图1图2常见模型1(直角三角形型)条件：如图2，在ΔABC中，∠C=90°，AD为∠CAB的角平分线，过点D作DE⊥AB.结论：DC=DE、ΔDAC≌ΔDAE.(当ΔABC是等腰直角三角形时，还有AB=AC+CD.)图3常见模型2(邻等对补型)条件：如图3，OC是∠COB的角平分线，AC=BC，过点C作CD⊥OA、CE⊥OB。

结论：①∠BOA+∠ACB=180°；②AD=BE；③OA=OB+2AD.1(2022·北京·中考真题)如图，在ΔABC中，AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则SΔACD=．2(2022·山东泰安·中考真题)如图，△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P，若∠BPC=40°，则∠CAP=()A.40°B.45°C.50°D.60°3(2023·广东中山·八年级校联考期中)如图，△ABC中，∠ABC、∠EAC的角平分线BP、AP交于点P，延长BA、BC，PM⊥BE，PN⊥BF，则①CP平分∠ACF；②∠ABC+2∠APC=180°；③∠ACB= 2∠APB；④S△PAC=S△MAP+S△NCP．上述结论中正确的是()A.①②B.①③C.②③④D.①②③④4(2023秋·浙江·八年级专题练习)如图，四边形ABDC中，∠D=∠ABD=90°，点O为BD的中点，且OA 平分∠BAC．(1)求证：OC平分∠ACD；(2)求证：OA⊥OC；(3)求证：AB+CD=AC．5(2022·河北·九年级专题练习)已知OP平分∠AOB，∠DCE的顶点C在射线OP上，射线CD交射线OA于点F，射线CE交射线OB于点G．(1)如图1，若CD⊥OA，CE⊥OB，请直接写出线段CF与CG的数量关系；(2)如图2，若∠AOB=120°，∠DCE=∠AOC，试判断线段CF与CG的数量关系，并说明理由．模型2.角平分线垂中间(角平分线+内垂直)【模型解读与图示】条件：如图1，OC为∠AOB的角平分线，AB⊥OC，结论：△AOC≌△BOC，ΔOAB是等腰三角形、OC是三线合一等。

角平分线四大模型模型一：角平分线上的点向两边作垂线如图，P是∠MON的平分线上一点，过点P作PA⊥OM于点A,PB⊥ON于点B,则PB=PA.模型分析：利用角平分线的性质：角平分线上的点到角两边的距离相等，构造模型，为边相等、角相等、三角形全等创造更多的条件，进而可以快速找到解题的突破口。

例1：（1）如图①，在△ABC,∠C=90°，AD平分∠CAB，BC=6cm，BD=4cm，那么点D到AB的距离是___cm(2)如图②，已知∠1=∠2，∠3=∠4，求证：AP平分∠BAC.练习1 如图，在四边形ABCD中，BC>BA，AD=DC，BD平分∠ABC.求证：∠BAD+∠C=180°练习2 如图，△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P，若∠BPC=40°，则∠CAP=（）模型二：截取构造对称全等如图，P是∠MON的平分线上一点，点A是射线OM上任意一点，在ON上截取OB=OA，连接PB，则△OPB≅△OPA.模型分析：利用角平分线图形的对称性，在角的两边构造对称全等三角形，可以得到对应边、对应角相等、利用对称性把一些线段或角进行转移，这是经常使用的一种解题技巧。

例2：(1)如图①所示，在△ABC中，AD是△BAC的外角平分线，P是AD上异于点A的任意一点，试比较PB+PC与AB+AC的大小，并说明理由．(2)如图②所示．AD是△ABC的内角平分线，其他条件不变，试比较PC -PB与AC-AB的大小，并说明理由．练习 3 已知：△ABC中，∠A=2∠B，CD是∠ACB的平分线，AC=16，AD=8，求线段BC的长。

练习4 已知,如图AB=AC,∠A=108°，BD平分∠ABC交AC于D，求证：BC=AB+CD.练习5 如图,在△ABC中,∠A=100°,∠ABC=40°，BD是∠ABC的平分线，延长BD至E，使DE=AD.求证：BC=AB+CE.模型三：角平分线+垂线构造等腰三角形如图，P是∠MON的平分线上一点，AP⊥OP于P点，延长AP交ON于点B,则△AOB是等腰三角形。

一、常见模型 1. 角度计算：（1）角平分线＋高线：如图，AD 平分∠BAC ，AE ⊥BC ， 则∠DAE ＝12B C ∠-∠ （2）角平分线的夹角模型（内心和旁心）： 如图①，点I 是△ABC 的内心，则∠I ＝90°＋12A ∠；如图②，点P 是△ABC 的一个旁心，则∠P ＝12A ∠；如图③，点Q 是△ABC 的一个旁心，则∠Q ＝90°－12A ∠.2. 角平分线＋平行线→等腰三角形3.角平分线＋高线（中线）：构造等腰三角形4.角平分线＋对角互补四边形： 如图，∠A ＋∠C ＝180°，BD 是∠ABC 的平分线，则AD ＝C D ．5.双角平分线＋梯形：如图，AD ∥BC ,AE 平分∠BAD ，BE 平分∠ABC ，则 ①DE ＝CE ；②AB ＝AD ＋BC ；③AE ⊥BE .构造轴对称图形．．．．．．．截长补短 补形法（构造法） ：作另一边垂线ABC 中AD 平分∠BAC ，AE ⊥BC 于E ，若 B ＝40°，∠C ＝70°，求∠DAE.3.如图，△ABC的外角平分线AP，CP交于点P.（1）求证：BP平分∠ABC；（2）若∠B＝50°，求∠APC；（3）若∠ACE＝110°，求∠AP B.6. 条件同上题，猜测∠A，∠C，∠P的关系，并证明.2. 【面积问题】1.如图，AD是△ABC的角平分线，DE⊥AB，若AB＝14cm，AC＝10cm，DE＝3cm，求△ABC的面积.2.如图，点I是△ABC的内心，ID⊥BC于点D，△ABC 周长为18cm,ID＝3cm，求△ABC的面积.3.【角平分线＋平行线→等腰三角形】1. 如图，在△ABC中，∠B、∠C的平分线交于点O，过点O作EF∥BC分别交AB、AC于点E、F.若EF＝6,BE＝4,则CF＝.4. 5.2.如图，在△ABC中，∠B、∠C的平分线交于点I，过点I作MN∥BC分别交AB、AC于点M、N.若AB＝14cm,AC＝10cm,求△AMN的周长.3. 已知：如图所示△ABC，∠ACB＝90°，D为BC延长线上一点，E是AB上一点，EM垂直平分BD，M为垂足，DE交AC于F，求证：E在AF的垂直平分线上.4.【角平分线＋角平分线的垂线】补形法2. 如图，△ABC中，∠A＝90°，AB＝AC，CE平分∠ACB交AB于点D，BE垂直CE于E.求证：CD＝2BE.5.【角平分线＋一边的垂线】1. 如图，AD∥BC，AE平分∠BAD，BE平分∠AB C.求证：①DE＝CE；②AB＝AD＋BC；③AE⊥BE.B 1.2．如图，BD是∠ABC的平分线，BC＞AB,AD＝C D.若DE⊥BC于点E，求证：2BE＝BA＋B C.6.【截长补短】1．如图，BD是∠ABC的平分线，BC＞A B.（1）若∠A＋∠C＝180°，求证：AD＝CD；（2）若AD＝CD，求证：∠A＋∠C＝180°．2. 如图，AD∥BC，AE平分∠BAD，BE平分∠AB C.求证：①DE＝CE；②AB＝AD＋BC；③AE⊥BE.3. 已知：如图，在△ABC中，∠ABC＝60°，△ABC的角平分线AD，CE交于点O．（1）求∠AOC；（2）求证：OD＝OE；（3）求证：AC＝AE＋C D．。

专题06全等模型-角平分线模型角平分线在中考数学中都占据着重要的地位，角平分线常作为压轴题中的常考知识点，需要掌握其各类模型及相应的辅助线作法，且辅助线是大部分学生学习几何内容中的弱点，本专题就角平分线的几类全等模型作相应的总结，需学生反复掌握。

模型1.角平分线垂两边（角平分线+外垂直）【模型解读与图示】条件：如图1，OC 为AOB ∠的角平分线、CA OA ⊥于点A 时，过点C 作CA OB ⊥.结论：CA CB =、OAC ∆≌OBC ∆.图1图2常见模型1（直角三角形型）条件：如图2，在ABC ∆中，90C ∠=︒，AD 为CAB ∠的角平分线，过点D 作DE AB ⊥.结论：DC DE =、DAC ∆≌DAE ∆.（当ABC ∆是等腰直角三角形时，还有AB AC CD =+.）图3常见模型2（邻等对补型）条件：如图3，OC 是∠COB 的角平分线，AC =BC ，过点C 作CD ⊥O A 、CE ⊥OB 。

结论：①180BOA ACB ∠+∠=︒；②AD BE =；③2OA OB AD =+.例1．（2022·北京·中考真题）如图，在ABC ∆中，AD 平分,.BAC DE AB ∠⊥若2,1,AC DE ==则ACD S ∆=____．【答案】1【分析】作DF AC ⊥于点F ，由角平分线的性质推出1DF DE ==，再利用三角形面积公式求解即可．【详解】解：如图，作DF AC ⊥于点F ，∵AD 平分BAC ∠，DE AB ⊥，DF AC ⊥，∴1DF DE ==，∴1121122ACD S AC DF ∆=⋅=⨯⨯=．故答案为：1．【点睛】本题考查角平分线的性质，通过作辅助线求出三角形ACD 中AC 边的高是解题的关键．例2．（2022·山东泰安·中考真题）如图，△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ，若∠BPC ＝40°，则∠CAP ＝（）A ．40°B ．45°C ．50°D ．60°【答案】C 【分析】根据外角与内角性质得出∠BAC 的度数，再利用角平分线的性质以及直角三角形全等的判定，得出∠CAP ＝∠FAP ，即可得出答案.【详解】解：延长BA ，作PN ⊥BD ，PF ⊥BA ，PM ⊥AC ，设∠PCD ＝x °，∵CP 平分∠ACD ，∴∠ACP ＝∠PCD ＝x °，PM ＝PN ，∵BP 平分∠ABC ，∴∠ABP ＝∠PBC ，PF ＝PN ，∴PF ＝PM ，∵∠BPC ＝40°，∴∠ABP ＝∠PBC ＝∠PCD ﹣∠BPC ＝（x ﹣40）°，∴∠BAC＝∠ACD﹣∠ABC＝2x°﹣（x°﹣40°）﹣（x°﹣40°）＝80°，∴∠CAF＝100°，在Rt△PFA和Rt△PMA中，{PA PA PM PF==，∴Rt△PFA≌Rt△PMA（HL），∴∠FAP＝∠PAC＝50°．故选C．【点睛】本题考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识，根据角平分线的性质得出PM＝PN＝PF是解题的关键．例3．（2023·山东·七年级专题练习）如图，∠D＝∠C＝90°，点E是DC的中点，AE平分∠DAB，∠DEA ＝28°，求∠ABE的大小．【答案】28°【分析】过点E作EF⊥AB于F，根据角平分线上的点到角的两边距离相等可得DE=EF，根据线段中点的定义可得DE=CE，然后求出CE=EF，再根据到角的两边距离相等的点在角的平分线上证明即可得出BE平分∠ABC，即可求得∠ABE的度数．【详解】如图，过点E作EF⊥AB于F，∵∠D=∠C=90°，AE平分∠DAB，∴DE=EF，∵E是DC的中点，∴DE=CE，∴CE=EF，又∵∠C=90°，∴点E在∠ABC的平分线上，∴BE平分∠ABC，又∵AD∥BC，∴∠ABC+∠BAD=180°，∴∠AEB=90°，(1)填空：角平分线的性质定理：角平分线上的点到．符号语言：∵如图1，OP 为COD ∠上的平分线，且，∴．(2)解答：已知：如图2，60AOB ∠=︒，OP 为AOB ∠的平分线，以点P 为顶点的CPD ∠与角的两边相交于点C 、D ，且120CPD ∠=︒．求证：PC PD =．(3)作图：根据以上种情况，再次寻找其它情况，点P P 为AOB ∠的平分线上的点，请你用尺规作图作PE OA ⊥于E ，作PF OB ⊥于F ，90PEC PFD PEO PFO ∴∠=∠=∠=∠=︒，OP 平分AOB ∠，PE PF ∴=，在四边形EOFP 中，60AOB ∠=︒，90PEO PFO ∠=∠=︒，36060290120EPF ∴∠=︒-︒-⨯︒=︒，120CPD ∠=︒ ，CPD EPF ∴∠=∠，CPD EPD EPF EPD ∴∠-∠=∠-∠，CPE DPF ∴∠=∠，PEC PFD ∴≅ （ASA ）PC PD ∴=；（3）证明：如图2，作射线PC ，交OA 于C ，作PCN AOB ∠=∠，反向延长NP ，交OB 于D ，则PC PD =；,（4）解：如图3，当ODP ∠和OCP ∠互补时，PC PD =，理由如下：作PE OA ⊥于E ，作PF OB ⊥于F ，90PEC PFD PEO PFO ∴∠=∠=∠=∠=︒，OP 平分AOB ∠，PE PF ∴=，在四边形EOFP 中，90PEO PFO ∠=∠=︒，360290180EPF AOB ∴∠+∠=︒-⨯︒=︒，180CPD AOB ∠+∠=︒ ，CPD EPF ∴∠=∠，CPD EPD EPF EPD ∴∠-∠=∠-∠，CPE DPF ∴∠=∠，PEC PFD ∴≅ (ASA)PC PD ∴=．【点睛】本题考查全等三角形的判定，角平分线的性质等知识，解决问题的关键是熟练掌握有关基础知识．模型2.角平分线垂中间（角平分线+内垂直）【模型解读与图示】条件：如图1，OC 为AOB ∠的角平分线，AB OC ⊥，结论：△AOC ≌△BOC ，OAB ∆是等腰三角形、OC 是三线合一等。

角平分线四大模型模型1 角平分线的点向两边作垂线如图，P是∠MON的平分线上一点，过点P作PA⊥OM于点A，PB⊥ON于点B，则PB＝PA模型分析利用角平分线的性质：角平分线上的点到角两边的距离相等，构造模型，为边相等、角相等、三角形全等创造更多的条件，进而可以快速找到解题的突破口模型实例（1）如图①，在△ABC中，∠C＝90°，AD平分∠CAB，BC＝6,BD＝4,那么点D到直线AB的距离是解答：如图，过点D作DE⊥AB于点E，∵AD平分∠CAB,∴CD＝DE.∵CB＝6,BD＝4,∴DE＝CD＝2，即点D到直线AB的距离是2.（2）如图②，∠1＝∠2，∠3＝∠4，求证：AP平分∠BAC证明：如图，过点P作PD⊥AB于点D，PE⊥BC于点E，PF⊥AC于点F，∵∠1＝∠2，∴PD＝PE,∵∠3＝∠4, ∴PE＝PF，∴PD＝PF又∵PD⊥AB，PF⊥AC，∴AP平分∠BAC（角平分线的判定）练习1、如图，在四边形ABCD中，BC＞AB，AD＝DC,BD平分∠ABC ，求证：∠BAD＋∠BCD＝180°证明：作DE⊥BC于E，作DF⊥BA的延长线于F，∴∠F＝∠DEC＝90°,∵BD平分∠ABC,∴DF＝DE，又∵AD＝DC，∴△DFA≌DEC,∴∠FAD＝∠C∵∠FAD＋∠BAD＝180°，∴∠BAD＋∠BCD＝180°2.如图，△ABC的外角∠ACD∠的平分线CP与内角∠ABC的平分线BP相交于点P，若∠BPC＝40°，则∠CAP＝.解答：如图所示，作PN⊥BD于N，作PF⊥BA，交BA延长线于F，作PM⊥AC于M∵BP、CP分别是∠CBA和∠DCA的角平分线，∴∠ABP＝∠CBP,∠DCP＝∠ACP，PF＝PN＝PM，∵∠BAC＝∠ACD－∠ABC，∠BPC＝∠PCD－∠PBC(外角性质)∴∠BAC＝2∠PCD－2∠PBC＝2(∠PCD－∠PBC)＝2∠BPC＝80°∴∠CAF＝180°－∠BAC＝100°，∵PF＝PM∴AP是∠FAC的角平分线，∴∠CAP＝∠PAF＝50°模型2 截取构造对称全等如图，P是∠MON的平分线上的一点，点A是射线OM上任意一点，在ON上截取OB＝OA,连接PB，则△OPB≌△OPA模型分析利用角平分线图形的对称性，在铁的两边构造对称全等三角形，可以得到对应边，对应角相等，利用对称性把一些线段或角进行转移，这是经常使用的一种解题技巧模型实例（1）如图①所示，在△ABC中，AD是△BAC的外角平分线，P是AD上异于点A的任意一点，试比较PB＋PC与AB＋AC的大小，并说明理由解题：PB+PC＞AB+AC证明：在BA的延长线上取点E,使AE＝AB,连接PE，∵AD平分∠CAE∴∠CAD＝∠EAD，在△AEP与△ACP中，∵AE＝AB，∠CAD＝∠EAD,AP＝AP，∴△AEP≌△ACP （SAS），∴PE＝PC∵在△PBE中：PB+PE＞BE,BE＝AB+AE＝AB+AC，∴PB+PC＞AB+AC（2）如图②所示，AD是△ABC的内角平分线，其它条件不变，试比较PC－PB与AC－AB的大小，并说明理由解答：AC-AB>PC-PB证明:在△ABC中, 在AC上取一点E,使AE=AB ，∴AC-AE=AB-AC=BE ∵AD平分∠BAC ，∴∠EAP=∠BAP ，在△AEP和△ACP中∴△AEP≌△ABP (SAS) ，∴PE=PB ，∵在△CPE中CE>CP-PE ，∴AC-AB>PC-PB练习1.已知，在△ABC中，∠A＝2∠B,CD是∠ACB的平分线，AC＝16,AD＝8,求线段BC的长解：如图在BC边上截取CE＝AC，连结DE，在△ACD和△ECD中⎪⎩⎪⎨⎧=∠=∠=CDCDECDACDECAC∴△ACD≌△ECD(SAS)∴AD＝DE ，∠A＝∠1 ，∵∠A＝2∠B，∴∠1＝2∠B，∵∠1＝∠B＋∠EDB ，∴∠B＝∠EDB，∴EBB＝ED ，∴EB＝DA＝8，BC＝EC＋BE＝AC＋DA＝16＋8＝242.在△ABC中，AB＝AC,∠A＝108°,BD平分∠ABC，求证：BC＝AB＋CD证明：在BC上截取BE＝BA，连结DE，∵BD平分∠ABC,BE＝AB,BD＝BD∴△ABD≌△EBD(SAS)，∴∠DEB＝∠A＝108°，∴∠DEC＝180°－108°＝72°∵AB＝AC，∴∠C＝∠ABC＝12(180°－108°)＝36°，∴∠EDC＝72°，∴∠DEC＝∠EDC，∴CE＝CD ，∴BE＋CE＝AB＋CD，∴BC＝AB＋CD3.如图所示，在△ABC中，∠A＝100°,∠ABC＝40°,BD是∠ABC的平分线，延长BD至E，使DE ＝AD，求证：BC＝AB＋CE证明：在CB上取点F，使得BF＝AB,连结DF，∵BD平分∠ABC，BD＝BD∴△ABD≌△FBD，∴DF＝AD＝DE,∠ADB＝∠FDB，∴BD平分∠ABC∴∠ABD＝20°,则∠ADB＝180°－20°－100°＝60°＝∠CDE∠CDF＝180°－∠ADB－∠FDB＝60°，∴∠CDF＝∠CDE，在△CDE和△CDF中⎪⎩⎪⎨⎧=∠=∠=CDCDCDECDFDFDE∴△CDE≌CDF，∴CE＝CF，∴BC＝BF＋FC＝AB＋CE模型3 角平分线+垂线构造等腰三角形如图，P是∠MON的平分线上一点，AP丄OP于P点，延长AP交ON于点.B,则△AOB是等腰三角形.模型分析构造此模型可以利用等腰三角形的"三线合一”，也可以得到两个全等的直角三角形.进而得到对应边.对应角相等.这个模型巧妙地把角平分线和三线合一联系了起来.模型实例如图.己知等腰直角三角形ABC中，∠A=90°, AB=AC, BD平分∠ABC, C£丄BD.垂足为E.求证：BD=2C£.解答：如图，延长CE、BA交于点F,∵CE丄BD于E, ∠BAC=90°，∴∠BAD=∠CED.∴∠ABD=∠ACF.又∵AB=AC, ∠BAD=∠CAF=90°, ∴△ABD≌△ACF.∴ BD=CF.∵BD平分∠ABC, ∴∠CBE=∠FBE. 又BE=BE,∴△BCE≌△BFE.∴CE=EF. ∴BD=2CE.练习1.如图.在△ABC中.BE是角平分线.AD丄BE.垂足为D.求证：∠2=∠1+∠C.证明：延长AD交BC于F,∵AD⊥BE, ∴∠ADB=∠BDF=90°, ∵∠ABD=∠FBD,∴∠2=∠BFD. ∵∠BFD=∠1+∠C,∴∠2=∠1+∠C.2.如图.在△ABC中. ∠ABC=3∠C,AD是∠BAC的平分线, BE丄AD于点E.求证:1()2BE AC AB =-.(2)证明:延长BE 交AC 于点F.∵AD 为∠BAC 的角平分线,∴∠BAD=∠CAD.∵AE=AE, ∴∠BAE=∠FAE,则△AEB ≌△AEF ，∴AB=AF, BE=EF, ∠ 2=∠3.∴AC-AB=AC-AF=FC. ∵∠ABC=3∠C,∴∠2+∠1=∠3+∠1=∠1+∠C+∠1=3∠C.∴2∠1=2∠C 即∠1=∠C ∴BF=FO=2BE.∴()1122BE FC AC AB ==-模型4 角平分线+平行线模型分析有角平分线时.常过角平分线上一点作角的一边的平行线. 构造等腰三角形.为证明结论提供更多的条件.体现了用平分线与等腰三角形之间的密切关系.模型实例 解答下列问题：(1)如图①.△ABC 中，EF ∥BC,点D 在EF 上,BD 、CD 分别平分∠ABC 、∠ACB.写出线段EF 与BE 、CF 有什么数量关系？(2)如图②，BD平分∠ABC,CD平分外角∠ACG. DE//BC交AB于点E,交AC于点F，线段EF与BE、CF有什么数量关系？并说明理由.(3)如图③，BD、CD为外角∠CBM、∠BCN的平分线，DE//BC交AB延长线于点E.交AC延长线于点F,直接写出线段EF与BE、CF有什么数关系？解答：(1) ∵EF//BC,∴∠EDB=∠DBC.∴BD平分∠EBC，∴∠EBD=∠DBC=EDB. ∴EB=ED.同理：DF=FC. ∴EF=ED+DF=BE+CF.(2)图②中有EF=BE=CF，BD平分∠BAC,∴∠ABD=∠DBC.又DE//BC、∴∠EDB=∠DBC.∴DE=EB.同理可证：CF=DF ∴EF=DE-DF=BE-CF.(3) EF=BE+CF.练习1.如图. 在△ABC中,∠ABC和∠ACB的平分线交于点E.过点E作MN∥BC交AB于M点. 交AC 于N点.若BM+CN=9，则线段MN的长为.解答：∵∠ABC、∠ACB的平分线相交于点E,∴MBE=∠EBC，∠ECN=∠ECB.∵MN//BC,∴∠EBC=∠MEB, ∠NEC=∠ECB. ∴∠MBE-∠MEB, ∠NEO=∠ECN.∴BM=ME, EN=CN.∴MN=ME+EN,即MN=BM+CN.∵BM+CN=9,∴MN=9.2. 如图. 在△ABC中,AD平分∠BAC.点E、F分別在BD，AD上,EF∥AB.且DE=CD,求证：EF=AC.证明：如图，过点C作CM∥AB交AD的延长线于点M,∵AB∥EF,∴CM∥EF.∴∠3=∠4.∵DE=CD, ∠5=∠6, ∴△DEF≌△DCM.∴EF=CM. ∵AB//CM,∴∠2=∠4. ∵∠1=∠2,∴∠1=∠4.∴CM=AC.∴EF=AC3.如图.梯形ABCD中,AD∥BC,点E在CD上,且AE平分∠BAD.BE平分∠ABC.求证：AD=AB-BC.证明：延长AD、BE交于点F.∵AD∥BC,∴∠2=∠F. ∵∠1=∠2,∴∠1=∠F.∴AB=AF.∵AE平分∠BAD∴BE=EF. ∵∠DEF=∠CEB, ∴△DEF≌△CEB.∴DF=BC.∴AD=AF-DF=AB-BC.。

第四讲角平分线性质定理判定定理及四大模型一、性质定理、判定定理1．角平分线的性质：角平分线上的点到角两边的距离相等．如图，∵OP平分∠AOB，PE⊥OA，PF⊥OB，∴PE=PF．2．角平分线的判定：角内部到角两边的距离相等的点在角的平分线上．如图，∵PE⊥OA，PF⊥OB，PE=PF，∴OP平分∠AOB．二、角分线四大模型1.角分线+平行线，等腰三角形必呈现；基本图形：已知，OP平分∠AOB，若过点P作PE//OB交OA于点E，如上图，可以得到等腰三角形EOP，其中EP=EO. 例1：如图，在△ABC中，BD、CD分别平分∠ABC和∠ACB，DE//AB，FD//AC，BC=6，求△DEF的周长.练1：如图，在△ABC中，∠ABC与∠ACB的角平分线相交于点F，过点F作DF//BC，交AB于点D，交AC于点E，若BD+CE=9，则线段DE的长为.练2：（1）如图，在△ABC中，BD平分∠ABC，CD平分外角∠ACG，DE//BC交AB于点E，交AC于点F，线段EF、BE、CF有什么关系？请说明理由.（2）如图，BD、CD分别为∠ABC、∠ACB外角的角平分线，DE//BC交AB的延长线于点E，交AC的延长线于点F，直接写出线段EF、BE、CF的数量关系.2.点垂线，垂两边，线等全等都出现；基本图形：已知，OP 平分∠AOB ，若PE ⊥OA ，则过点P 作PF ⊥OB ，则PE=PF ，OE=OF ，△EOP ≌△FOP .例1：如图，在△ABC 中，∠C =90°，AD 平分∠CAB ，BC =6，BD =4，则点D 到直线AB 的距离是 .例2：如图，∠1=∠2，∠3=∠4，求证AP 平分∠BAC .练1：如图，四边形ABCD 中，∠B+∠D =180°，BC=CD ，求证AC 平分∠BAD .练2：如图，在RT △ABC 中，∠ACB =90°，CD ⊥AB ，垂足为D ，AF 平分∠CAB ，交CD 于点E ，交CB 于点F ，（1）求证：CE=CF .（2）将图中的△ADE 沿AB 向右平移到三角形A’D’E’的位置，使点E’落在BC 边上，其它条件不变，试猜想BE’于CF 有怎样的数量关系？请证明你的结论.3.角分线+垂线，中点全等必可见；基本图形：已知，OP 平分∠AOB ，E 为OA 上一点，EP ⊥OP ，延长EP 交OB 于点F ，则EP=FP ，△EOP ≌△FOP .ED F CB A E'D'A'A BCFDE例1：已知等腰直角△ABC中，∠A=90°，AB=AC，BD平分∠ABC，CE⊥BD，垂足为点E，求证：BD=2CE.练1：如图，在△ABC中，∠ABC＝3∠C，AD是∠BAC的平分线，BE⊥AD于点E，求证：BE＝12（AC－AB）．4.角分线，分两边，对称全等要记全.基本图形：已知，OP平分∠AOB，E为OA上一点，可在OB上取一点F，使得OF=OE，则有△EOP≌△FOP.例1：如图，已知△ABC中，AB=AC，∠A=108°，BD平分∠ABC，求证：BC=AB+CD.例2：（1）在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE 相交于点F，请判断FE与FD之间的数量关系；（2）在△ABC中，如果∠ACB不是直角，而（1）中其它条件不变，那么（1）中结论是否仍然成立？若成立，请证明；若不成立，请说明理由.练1：如图，四边形ABCD中，AD>AB，AC平分∠BAD.，BC=CD，求证∠B+∠D=180°三、课后练习1. 如图，在△ABC 中，∠A ＝60°，∠AB C ．∠ACB 的角平分线B D ．CE 交于点O ． 求证：（1）BC ＝BE ＋CD ；（2）OE ＝O D ．2. 如图，点C 是∠MAN 的平分线上一点，AD ≠AB ，∠DAB ＋∠DCB ＝180°．求证：CD ＝C B3. 如图，等腰Rt △ABC 中，∠C ＝90°，CA ＝CB ，BD 平分∠ABC ，AE ⊥BD ，垂足为E ．（1）求证：BD ＝2AE ；（2）连EC ，求∠CEB 的度数．4. 如图，已知，在△ABC 中，AD 是∠BAC 的平分线，AC ＝16，AB ＝10，BD ＝7．求线段CD 的长．5. （1）如图1，在△ABC 中，∠C ≠90°，AD 平分∠CAB ，AC ＝6，BC ＝9，AB ＝10，求C D ．（2）如图2，在△ABC 中，∠ACB ≠90°，AD 平分∠CAB 的外角交BC 延长线于点D ，AC ＝6，BC ＝9，AB ＝10，求CD ．图1 图26. 如图，在△ABC 中，∠CAB ＝120°，∠C ＝40°，BE 是△ABC 的内角平分线，点D 在BC 上，且∠CAD＝60°，求∠ADE 的度数．O EDCB AP N MD CB AE D CAD CB AD B C A D BC AOE D C B A7. 如图，△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ．若∠BPC ＝40°，求∠CAP .8. 如图，△AOB 为等腰直角三角形，点P 为动点，P A ⊥PB ．（1）如图，P 点为在第一象限时，求∠OP A ；（2）如图，P 点为在第四象限时，求∠OP A ．9. 如图所示，点A 为∠MON 的角平分线上一点，过A 任作一直线分别与∠MON 的两边交于B ．C ．P 为BC 的中点，过P 作BC 的垂线交OA 于点D.（1）若∠MON ＝ 90°，如图1，则∠BDC ＝；（2）若∠MON ＝ 60°，如图2，则∠BDC ＝；（3）若∠MON ＝ ，如图3，∠BDC ＝，请给予证明．PD C B AN C D P A O B M M B O A P D C N P D C ABN MO。

专题07 角平分线的重要模型（一）全等类角平分线在中考数学中都占据着重要的地位，角平分线常作为压轴题中的常考知识点，需要掌握其各大模型及相应的辅助线作法，且辅助线是大部分学生学习几何内容中的弱点，本专题就角平分线的全等类模型作相应的总结，需学生反复掌握。

模型1.角平分线构造轴对称模型（角平分线+截线段等）【模型解读与图示】已知如图1，OP为AOB∠的角平分线、PM不具备特殊位置时，辅助线的作法大都为在OB上截取ON OM=，连结PN即可.即有OMP∆≌ONP∆，利用相关结论解决问题.图1 图21．（2022·湖北十堰·九年级期末）在△ABC中，△ACB＝2△B，如图①，当△C＝90°，AD为△BAC 的角平分线时，在AB上截取AE＝AC，连结DE，易证AB＝AC＋CD．（1）如图②，当△C≠90°，AD为△BAC的角平分线时，线段AB，AC，CD又有怎样的数量关系？不需要证明，请直接写出你的猜想；（2）如图③，当AD为△ABC的外角平分线时，线段AB，AC，CD又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明．【答案】（1）AB AC CD=+；证明见解析；（2）AB AC CD+=；证明见解析．【分析】（1）首先在AB上截取AE＝AC，连接DE，易证△ADE△△ADC（SAS），则可得△AED＝△C，ED＝CD，又由△AED＝△ACB，△ACB＝2△B，所以△AED＝2△B，即△B＝△BDE，易证DE＝CD，则可求得AB＝AC＋CD；（2）首先在BA的延长线上截取AE＝AC，连接ED，易证△EAD△△CAD，可得ED＝CD，△AED ＝△ACD，又由△ACB＝2△B，易证DE＝EB，则可求得AC＋AB＝CD．【详解】（1）猜想：AB AC CD=+．AB∥CD⇒AB+CD=BCFDEBAC证明：如图②，在AB 上截取AE AC =，连结DE ，△AD 为ABC 的角平分线时，△BAD CAD ∠=∠，△AD AD =，△()SAS ADE ADC ≌△△， △AED C ∠=∠，ED CD =，△2ACB B ∠=∠，△2AED B ∠=∠．△B EDB ∠=∠，△EB ED =，△EB CD =，△AB AE DE AC CD =+=+．（2）猜想：AB AC CD +=．证明：在BA 的延长线上截取AE AC =，连结ED ．△AD 平分FAC ∠，△EAD CAD ∠=∠．在EAD 与CAD 中，AE AC =，EAD CAD ∠=∠，AD AD =，△EAD CAD ≌△△．△ED CD =，AED ACD ∠=∠．△FED ACB ∠=∠．又2ACB B ∠=∠，FED B EDB ∠=∠+∠，EDB B ∠=∠．△EB ED =．△EA AB EB ED CD +===．△AC AB CD +=．【点睛】此题考查三角形综合题、全等三角形的判定与性质、等腰三角形的判定、角平分线的定义等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．2．（2022·山东烟台·九年级期末）已知在ABC 中，满足2ACB B ∠=∠，(1)【问题解决】如图1，当90C ∠=︒，AD 为BAC ∠的角平分线时，在AB 上取一点E 使得AE AC =，连接DE ，求证：AB AC CD =+．(2)【问题拓展】如图2，当90C ∠≠︒，AD 为BAC ∠的角平分线时，在AB 上取一点E 使得AE AC =，连接DE ，（1）中的结论还成立吗？若成立，请你证明：若不成立，请说明理由．(3)【猜想证明】如图3，当AD 为ABC 的外角平分线时，在BA 的延长线上取一点E 使得AE AC =，连接DE ，线段AB 、AC 、CD 又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明． 【答案】(1)证明见解析(2)成立，证明见解析 (3)猜想AB AC CD +=，证明见解析【分析】（1）先根据SAS 定理证出AED ACD ≅，根据全等三角形的性质可得ED CD =，AED ACD ∠=∠，再根据三角形的外角性质可得45B BDE ∠=∠=︒，然后根据等腰三角形的判定可得EB ED =，从而可得EB CD =，最后根据线段和差、等量代换即可得证； （2）先根据SAS 定理证出AED ACD ≅，根据全等三角形的性质可得ED CD =，AED C ∠=∠，再根据三角形的外角性质可得B BDE ∠=∠，然后根据等腰三角形的判定可得EB ED =，从而可得EB CD =，最后根据线段和差、等量代换即可得证；（3）先根据SAS 定理证出AED ACD ≅，根据全等三角形的性质可得ED CD =，AED ACD ∠=∠，从而可得FED ACB ∠=∠，再根据三角形的外角性质可得B BDE ∠=∠，然后根据等腰三角形的判定可得EB ED =，从而可得EB CD =，最后根据线段和差、等量代换即可得证．（1）证明：△AD 为BAC ∠的角平分线，△EAD CAD ∠=∠，在AED 与ACD △中，AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩，△()AED ACD SAS ≅，△ED CD =，AED ACD ∠=∠，又△90ACB ∠=︒，2ACB B ∠=∠，△45B ∠=︒，90AED ∠=︒，△45AED BDE B ∠=∠=∠-︒，△B BDE ∠=∠，△EB ED =，△EB CD =，△AB AE EB AC CD =+=+．（2）解：（1）中的结论还成立，证明如下：△AD 为BAC ∠的角平分线时，△EAD CAD ∠=∠，在AED 与ACD △中，AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩，△()AED ACD SAS ≅，△AED C ∠=∠，ED CD =，△2ACB B ∠=∠，△2AED B ∠=∠，又△AED B EDB ∠=∠+∠，△B EDB ∠=∠，△EB ED =，△EB CD =，△AB AE EB AC CD =+=+．（3）解：猜想AB AC CD +=，证明如下：△AD 平分EAC ∠，△EAD CAD ∠=∠，在AED 与ACD △中,AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩，△()AED ACD SAS ≅，△ED CD =，AED ACD ∠=∠，如图，△180180AED ACD ︒-∠=︒-∠，即FED ACB ∠=∠，△2ACB B ∠=∠，△2∠=∠，FED B又△FED B EDB∠=∠+∠，△EDB B∠=∠，△EB ED=，+===，△AB AE EB ED CD△AB AC CD+=．【点睛】本题主要考查了三角形全等的判定与性质、等腰三角形的判定，熟练掌握三角形全等的判定方法是解题关键．3．（2022·浙江·九年级期中）（1）如图1，在△ABC中，△ACB＝2△B，△C＝90°，AD为△BAC 的平分线交BC于D，求证：AB＝AC＋CD．（提示：在AB上截取AE＝AC，连接DE）（2）如图2，当△C≠90°时，其他条件不变，线段AB、AC、CD又有怎样的数量关系，直接写出结果，不需要证明．（3）如图3，当△ACB≠90°，△ACB＝2△B ，AD为△ABC的外角△CAF的平分线，交BC的延长线于点D，则线段AB、AC、CD又有怎样的数量关系？写出你的猜想，并加以证明．【答案】（1）见解析；（2）AB＝AC＋CD；（3）AB＝CD﹣AC【分析】（1）在AB上截取AE=AC，连接DE，根据角平分线的定义得到△1=△2．推出△ACD△△AED （SAS）．根据全等三角形的性质得到△AED=△C=90，CD=ED，根据已知条件得到△B=45°．求得△EDB=△B=45°．得到DE=BE，等量代换得到CD=BE．即可得到结论；（2）在AC取一点E使AB=AE，连接DE，易证△ABD△△AED，所以△B=△AED，BD=DE，又因为△B=2△C，所以△AED=2△C，因为△AED是△EDC的外角，所以△EDC=△C，所以ED=EC，BD=EC，进而可证明AB+BD=AE+EC=AC；（3）在AB的延长线AF上取一点E，使得AE=AC，连接DE．证明△ACD△△AED，根据全等三角形的性质得到DE=BE，BE=CD，即可得出结论．【详解】（1）证明：在AB上取一点E，使AE=AC△AD为△BAC的平分线△△BAD=△CAD．在△ACD和△AED中，AE ACBAD CADAD AD=⎧⎪∠=∠⎨⎪=⎩△△ACD△△AED（SAS）．△△AED=△C=90°，CD=ED，又△△ACB=2△B，△C=90°，△△B=45°．△△EDB=△B=45°．△DE=BE，△CD=BE．△AB=AE＋BE，△AB=AC＋CD．（2）证明：在AB取一点E使AC=AE，在△ACD和△AED中，AC AEBAD EADAD AD＝＝＝⎧⎪∠∠⎨⎪⎩,△△ACD△△AED，△△C=△AED，CD=DE，又△△C=2△B，△△AED=2△B，△△AED是△EDC的外角，△△EDB=△B，△ED=EB，△CD=EB，△AB=AC+CD；（3）猜想：AB=CD﹣AC证明：在BA的延长线上取一点E，使得AE=AC，连接DE，在△ACD和△AED中，AC AECAD EADAD AD=⎧⎪∠=∠⎨⎪=⎩，△△ACD△△AED（SAS），△△ACD=△AED，CD=DE，△△ACB=△FED，又△△ACB=2△B△△FED=2△B，又△△FED=△B＋△EDB，△△EDB=△B，△DE=BE，△BE=CD，△AB=BE-AE△AB=CD﹣AC．【点睛】本题考查全等三角形的判定和性质，关于线段和差关系的证明，通常采用截长补短法.4．（2022·北京九年级专题练习）在四边形ABDE中，C是BD边的中点．（1）如图（1），若AC 平分BAE ∠，90ACE ∠=︒，则线段AE 、AB 、DE 的长度满足的数量关系为______；（直接写出答案）（2）如图（2），AC 平分BAE ∠，EC 平分AED ∠，若120ACE ∠=︒，则线段AB 、BD 、DE 、AE 的长度满足怎样的数量关系？写出结论并证明．【答案】（1）AE ＝AB ＋DE ；（2）AE ＝AB ＋DE ＋12BD ，证明见解析．【分析】（1）在AE 上取一点F ，使AF ＝AB ，由三角形全等的判定可证得△ACB ≌△ACF ，根据全等三角形的性质可得BC ＝FC ，∠ACB ＝∠ACF ，根据三角形全等的判定证得△CEF ≌△CED ，得到EF ＝ED ，再由线段的和差可以得出结论；（2）在AE 上取点F ，使AF ＝AB ，连结CF ，在AE 上取点G ，使EG ＝ED ，连结CG ，根据全等三角形的判定证得△ACB ≌△ACF 和△ECD ≌△ECG ，由全等三角形的性质证得CF ＝CG ，进而证得△CFG 是等边三角形，就有FG ＝CG ＝12BD ，从而可证得结论．【详解】解：（1）如图（1），在AE 上取一点F ，使AF ＝AB ．∵AC 平分∠BAE ，∴∠BAC ＝∠FAC ．在△ACB 和△ACF 中，AB AF BAC FAC AC AC ⎧⎪∠∠⎨⎪⎩＝＝＝∴△ACB ≌△ACF （SAS ）．∴BC ＝FC ，∠ACB ＝∠ACF ．∵C 是BD 边的中点，∴BC ＝CD ．∴CF ＝CD ．∵∠ACE ＝90°，∴∠ACB ＋∠DCE ＝90°，∠ACF ＋∠ECF ＝90°．∴∠ECF ＝∠ECD ．在△CEF 和△CED 中，CF CD ECF ECD CE CE ⎧⎪∠∠⎨⎪⎩＝＝＝∴△CEF ≌△CED （SAS ）．∴EF ＝ED ．∵AE ＝AF ＋EF ，∴AE ＝AB ＋DE ．故答案为：AE ＝AB ＋DE ；（2）AE ＝AB ＋DE ＋12BD ．证明：如图（2），在AE 上取点F ，使AF ＝AB ，连结CF ，在AE 上取点G ，使EG ＝ED ，连结CG ．∵C 是BD 边的中点，∴CB ＝CD ＝12BD ．∵AC 平分∠BAE ，∴∠BAC ＝∠FAC ． 在△ACB 和△ACF 中，AB AF BAC FAC AC AC ⎧⎪∠∠⎨⎪⎩＝＝＝∴△ACB ≌△ACF （SAS ）．∴CF ＝CB ，∠BCA ＝∠FCA ．同理可证：△ECD ≌△ECG ∴CD ＝CG ，∠DCE ＝∠GCE ．∵CB ＝CD ，∴CG ＝CF ．∵∠ACE ＝120°，∴∠BCA ＋∠DCE ＝180°−120°＝60°．∴∠FCA ＋∠GCE ＝60°．∴∠FCG ＝60°．∴△FGC 是等边三角形．∴FG ＝FC ＝12BD ．∵AE ＝AF ＋EG ＋FG ，∴AE ＝AB ＋DE ＋12BD ．【点睛】本题主要考查了全等三角形的判定与性质的运用，能熟练应用三角形全等的判定和性质是解决问题的关键．模型2.角平分线垂两边（角平分线+外垂直）【模型解读与图示】已知如图1，OP 为OAB ∠的角平分线、PM OA ⊥于点M 时，辅助线的作法大都为过点P 作PN OB ⊥即可.即有PM PN =、OMP ∆≌ONP ∆等，利用相关结论解决问题. 图1图2图3D B邻等对补模型：已知如图2，AP 是∠CAB 的角平分线，EP =DP辅助线：过点P 作PG ⊥AC 、PF ⊥AB结论：①︒=∠+∠180EPD BAC （D P E A 、、、四点共圆）；②EG DF =；③DF AE AD 2+=1．（2022·北京·中考真题）如图，在ABC ∆中，AD 平分,.BAC DE AB ∠⊥若2,1,AC DE ==则ACD S ∆=____．【答案】1【分析】作DF AC ⊥于点F ，由角平分线的性质推出1DF DE ==，再利用三角形面积公式求解即可．【详解】解：如图，作DF AC ⊥于点F ，△AD 平分BAC ∠，DE AB ⊥，DF AC ⊥，△1DF DE ==， △1121122ACD S AC DF ∆=⋅=⨯⨯=．故答案为：1． 【点睛】本题考查角平分线的性质，通过作辅助线求出三角形ACD 中AC 边的高是解题的关键．2．（2022·山东泰安·中考真题）如图，△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ，若∠BPC ＝40°，则∠CAP ＝（ ）A ．40°B ．45°C ．50°D ．60°【答案】C【分析】根据外角与内角性质得出∠BAC 的度数，再利用角平分线的性质以及直角三角形全等的判定，得出∠CAP ＝∠FAP ，即可得出答案.【详解】解：延长BA ，作PN ⊥BD ，PF ⊥BA ，PM ⊥AC ，设∠PCD ＝x °，∵CP 平分∠ACD ，∴∠ACP ＝∠PCD ＝x °，PM ＝PN ，∵BP 平分∠ABC ，∴∠ABP ＝∠PBC ，PF ＝PN ，∴PF ＝PM ，∵∠BPC ＝40°，∴∠ABP ＝∠PBC ＝∠PCD ﹣∠BPC ＝（x ﹣40）°，∴∠BAC ＝∠ACD ﹣∠ABC ＝2x °﹣（x °﹣40°）﹣（x °﹣40°）＝80°，∴∠CAF ＝100°， 在Rt △PFA 和Rt △PMA 中，{PA PAPM PF ==，∴Rt △PFA ≌Rt △PMA （HL ），∴∠FAP ＝∠PAC ＝50°．故选C ．【点睛】本题考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识，根据角平分线的性质得出PM ＝PN ＝PF 是解题的关键．3．（2022·江苏扬州·中考真题）如图，在ABCD 中，BE 、DG 分别平分ABC ADC ∠∠、，交AC 于点E G 、．(1)求证：,BE DG BE DG =∥；(2)过点E 作EF AB ⊥，垂足为F ．若ABCD 的周长为56，6EF =，求ABC ∆的面积． 【答案】(1)见详解(2)84【分析】（1）由平行四边形的性质证()ABE CDG ASA ∆≅∆即可求证；（2）作EQ BC ⊥，由ΔΔΔABC ABE EBC S S S =+即可求解；（1）证明：在ABCD 中，△//AB CD ，△BAE DCG ∠=∠，△ABCD 的周长为56，AB BC +=BE 平分∠EQ EF ==ABC S S ∆∆=【点睛】本题主要考查平行四边形的性质、三角形的全等、角平分线的性质，掌握相关知识CD 交射线OA 于点F ，射线CE 交射线OB 于点G ．（1）如图1，若CD △OA ，CE △OB ，请直接写出线段CF 与CG 的数量关系；（2）如图2，若△AOB =120°，△DCE =△AOC ，试判断线段CF 与CG 的数量关系，并说明理由．【答案】（1）CF=CG；（2）CF=CG，见解析【分析】（1）结论CF=CG，由角平分线性质定理即可判断．（2）结论：CF=CG，作CM△OA于M，CN△OB于N，证明△CMF△△CNG，利用全等三角形的性质即可解决问题．【详解】解：（1）结论：CF=CG；证明：△OP平分△AOB，CF△OA，CG△OB，△CF=CG（角平分线上的点到角两边的距离相等）；（2）CF=CG．理由如下：如图，过点C作CM△OA，CN△OB，△OP平分△AOB，CM△OA，CN△OB，△AOB=120°，△CM=CN（角平分线上的点到角两边的距离相等），△△AOC=△BOC=60°（角平分线的性质），△△DCE=△AOC，△△AOC=△BOC=△DCE=60°，△△MCO=90°-60° =30°，△NCO=90°-60° =30°，△△MCN=30°+30°=60°，△△MCN=△DCE，△△MCF=△MCN-△DCN，△NCG=△DCE-△DCN，△△MCF=△NCG，在△MCF和△NCG中，CMF CNG CM CNMCF NCG ∠=∠⎧⎪=⎨⎪∠=∠⎩△△MCF △△NCG （ASA ），△CF =CG （全等三角形对应边相等）．【点睛】本题考查三角形综合题、角平分线的性质、全等三角形的判定和性质，解题的关键是掌握角平分线的性质的应用，熟练证明三角形全等．模型3.角平分线垂中间（角平分线+内垂直）【模型解读与图示】已知如图1，OP 为AOB ∠的角平分线，PM OP ⊥于点P 时，辅助线的作法大都为延长MP 交OB 于点N 即可。