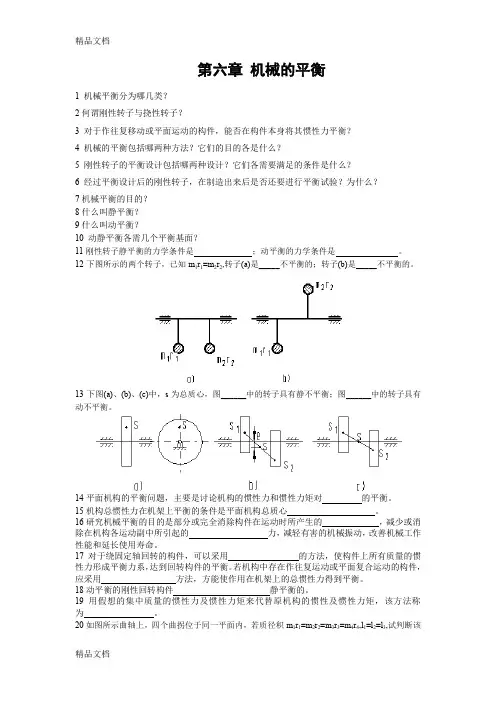
第六章机械的平衡1 机械平衡分为哪几类？2何谓刚性转子与挠性转子？3 对于作往复移动或平面运动的构件，能否在构件本身将其惯性力平衡？4 机械的平衡包括哪两种方法？它们的目的各是什么？5 刚性转子的平衡设计包括哪两种设计？它们各需要满足的条件是什么？6 经过平衡设计后的刚性转子，在制造出来后是否还要进行平衡试验？为什么？7机械平衡的目的？8什么叫静平衡？9什么叫动平衡？10 动静平衡各需几个平衡基面？11刚性转子静平衡的力学条件是；动平衡的力学条件是。
12下图所示的两个转子，已知m1r1=m2r2,转子(a)是_____不平衡的；转子(b)是_____不平衡的。
13下图(a)、(b)、(c)中，s为总质心，图______中的转子具有静不平衡；图______中的转子具有动不平衡。
14平面机构的平衡问题，主要是讨论机构的惯性力和惯性力矩对的平衡。
15机构总惯性力在机架上平衡的条件是平面机构总质心。
16研究机械平衡的目的是部分或完全消除构件在运动时所产生的，减少或消除在机构各运动副中所引起的力，减轻有害的机械振动，改善机械工作性能和延长使用寿命。
17对于绕固定轴回转的构件，可以采用的方法，使构件上所有质量的惯性力形成平衡力系，达到回转构件的平衡。
若机构中存在作往复运动或平面复合运动的构件，应采用方法，方能使作用在机架上的总惯性力得到平衡。
18动平衡的刚性回转构件静平衡的。
19用假想的集中质量的惯性力及惯性力矩来代替原机构的惯性及惯性力矩，该方法称为。
20如图所示曲轴上，四个曲拐位于同一平面内，若质径积m1r1=m2r2=m3r3=m4r4,l1=l2=l3,试判断该曲轴是否符合动平衡条件？为什么？21图示一盘形回转体，其上有四个不平衡质量，它们的大小及质心到回转轴线的距离分别为：m 110=kg ，214kg m =，316kg m =，420kg m =，1200mm r =，r 2400=mm ，3300mm r =，4140mm r =，欲使该回转体满足静平衡条件，试求需加平衡质径积m r b b 的大小和方位。
22 图示一钢质圆盘。
盘厚20mm δ=，在向径1100mm r =处有一直径50mm d =的通孔，向径2200mm r =处有一重量为2N 的重块，为使圆盘满足静平衡条件，拟在向径200mm r =的圆周上再钻一通孔，试求此通孔的直径和方位(钢的重度5106.7-⨯=γ3N/mm )。
23 一转子上有两个不平衡质量kg 2001=m ，kg 1002=m ，m m 501=r ， 402=r mm ，选定平面Ⅰ、Ⅱ为平衡校正面，若两个平面内平衡质量的回转半径为mm 60bII bI ==r r ，求平衡质量bI m 、bII m 的大小及方位。
24 图示一双缸发动机的曲轴，两曲拐在同一平面内，相隔180︒，每一曲拐的质量为50 kg ，离轴线距离为200mm ，A 、B 两支承间距离为900mm ，工作转速n =3000r/min 。
试求：（1）支承A 、B 处的动反力大小；（2）欲使此曲轴符合动平衡条件，以两端的飞轮平面作为平衡平面，在回转半径为500mm 处应加平衡质量的大小和方向。
25 为了平衡曲柄滑块机构ABC 中滑块C 的往复惯性力，在原机构上附加一滑块机构ABC '，设曲柄和连杆的质量不计,滑块C 和C '质量都为m ，连杆长度l l BC BC ='，试证明机构的第二级惯性力(即惯性力中具有曲柄转动频率两倍的频率分量)将获得完全平衡。
26 图示盘形回转件上存在三个偏置质量，已知m110= kg ，m 215= kg ，m 310= kg ，r 150= mm ，r 2100= mm ，r 370= mm ，设所有不平衡质量分布在同一回转平面内，问应在什么方位上加多大的平衡质径积才能达到平衡？27图示盘状转子上有两个不平衡质量：m115=.k g ，m 208=.kg ，r 1140= mm ，r 2180= mm ，相位如图。
现用去重法来平衡，求所需挖去的质量的大小和相位(设挖去质量处的半径r =140mm )。
28 高速水泵的凸轮轴系由三个互相错开120︒的偏心轮组成，每一偏心轮的质量为m ，其偏心距为r ，设在平衡平面A 和B 上各装一个平衡质量m A 和m B ，其回转半径为2r ，其他尺寸如图示。
试求m A 和m B 的大小和方向(可用图解法)。
29一回转体上有三质量：1 3 kg m =，2 1 kg m =，3 4 kg m =，绕z 轴等角速度旋转，160 mm r =，2140 mm r =，390 mm r =，其余尺寸如图示，试用图解法求应在平面Ⅰ和Ⅱ处各加多大平衡质量才能得到动平衡(设平衡质量bI m 和bII m 离转动轴线的距离bI r 、bII r 为bI bII 100 mm r r ==)。
30图示为V形发动机机构。
设每一活塞部件的质量都为m，今在曲柄延长线上与曲柄销B 对称的点D处加上一平衡质量m，则该发动机的所有第一级惯性力(即惯性力上具有与曲柄转动频率相同的频率分量)将被完全平衡。
试证明之(连杆、曲柄质量不计)。
提示：曲柄滑块机构中滑块的加速度变化规律为2cos cos2Nra rlωϕϕ⎛⎫≈-+⎪⎝⎭第六章 机械的平衡11刚性转子静平衡的力学条件是 不平衡惯性力的矢量和为零 ；动平衡的力学条件是 1)其惯性力的矢量和等于零，即∑P=0 ;(2)其惯性力矩的矢量和也等于零，即∑M=0 12子(a)是 静 不平衡的；转子(b)是 动 不平衡的。
13 a),b) 中的转子具有静不平衡；图 c) 中的转子具有动不平衡。
14 机座 15 静止不动 16 惯性力；动压17 静平衡或动平衡；完全平衡或部分平衡 18一定是 19 质量代换法20该曲轴符合动平衡条件21 m kg 22.01011⋅=⨯=r m (方向向上);m kg 6.54.01422⋅=⨯=r m (方向向右);m kg 8.43.01633⋅=⨯=r m (方向向下);m kg 8.214.02044⋅=⨯=r m (方向向左)。
m /m mkg 1.0⋅=mr μ0b b 44332211=++++r m r m r m r m r m ρρρρρ由图量得mkg 96.3b b ⋅=r m 方向量得与水平夹角即与44r m ρ夹角为45o。
或用计算法求得：2442221133)()(r m r m r m r m r m b b -+-=96.38.28.222=+=kg m ⋅ ︒=135b θ，与m r 22夹角22向径r 1处挖去通孔的质量kg3.08.9/4211=⨯⨯=γδπd m质径积m m kg 301003.011⋅=⨯=r m静平衡条件：0b b 2211=++-r m r m r m ρρρ 作矢量多边形，质径积m m kg 8.408.9/200222⋅=⨯=r m 得：m mkg 6.36b b ⋅=r m︒=82.74ϕ应在︒=18.255θ处去重，孔径为d b6.362008.9/42b b b =⨯⎪⎭⎫⎝⎛=δγπd r m6.15022b =d 76.38b =d mm23mm kg 5000502002 1 1⋅=⨯=''l lr mmm kg 5000502002"1"1⋅=⨯=l lr m mmkg 4000401002222⋅-=⨯-=''l l r m mmkg 80004010024"2"2⋅=⨯=l l r m m m kg 640020320 b b ⋅=⨯=''r mmm kg 940020470"b "b ⋅=⨯=r mkg 67.10660/6400bI ==m kg 67.15660/9400bII ==m方向θ¡'方向θ"24 (1) 不平衡质径积引发的离心力偶矩为m N 600000100060060230001000200502⋅=⨯⎪⎭⎫ ⎝⎛⨯⨯⨯π(2) A 、B 处附加动反力R 为6670006000009.0==⨯R R N(3) 为满足动平衡条件，在飞轮处应加平衡质量m b10 2.06.0505.02.1b b =⨯⨯=⨯⨯m m kg左端飞轮，平衡质量在下方。
右端飞轮，平衡质量在上方。
25 曲柄滑块机构中滑块的加速度变化规律为⎪⎭⎫⎝⎛+-≈ϕϕω2cos cos 2l r r a Nϕω=t ω---曲柄角速度由提示得滑块的第二级惯性力ϕω2cos 2I l rmr P =正号表示沿x 轴方向。
设曲柄AB 处在α角位置，活塞C 的第二级惯性力αω2cos 2I BCBABA C l ml P =方向为A 指向C 。
活塞的第二级惯性力()αω-=1802cos22I BC BA BA C l ml P =ml l BA BA BC 222ωα'cos方向为A 指向B 。
显然，活塞C 和系统的第二级惯性力获得完全平衡。
26 111050500 kg mm m r =⨯=⋅22151001500 kg mm m r =⨯=⋅ 331070700 kg mm m r =⨯=⋅1r 与3r 共线，可代数相加得图3311700500200 kg mm m r m r -=-=⋅方向同3r r平衡条件：b b1122330m r m r m r m r +++=r r r r 所以依次作矢量()331122,m r m r m r +r r r，封闭矢量b b m r r即所求，如图示。
b b 1513.275 kg mm m r ==⋅0200270arctg277.5951500θ=+=︒b b27 不平衡质径积 11210 kg mm m r =⋅22144 kg mm m r =⋅静平衡条件1122b b 0m r m r m r ++=r r r 解得b b 140 kg mm m r =⋅ 例6-2图 应加平衡质量b 140/140 1 kg m ==挖去的质量应在b b m r r矢量的反方向，140mm 处挖去1kg 质量。
28 偏心轮的不平衡质径积C C D D E E m r m r m r mr ===分别分解到平衡平面A 和B()5/4250/200mr mr r m A C C ==()5/250/50mr mr r m B C C ==()2/250/125mr mr r m A D D ==()2/250/125mr mr r m B D D ==()5/250/50mr mr r m A E E ==()5/4250/200mr mr r m BE E ==动平衡条件()()()()0b b =+++A E E A D D A C C A r m r m r m r m ρρρρ ()()()()0b b =+++BE E B D D B C C B r m r m r m r m ρρρρ解得：()2/b b mr r m A =因为 b 2r r =，所以()m m m A A 25.0b ==， ()2/b b mr r m B=因为r r b =2，所以()m m m B B 25.0b ==方向如图示。
