中考经典题目训练
- 格式:docx
- 大小:98.69 KB
- 文档页数:10

1、如图所示,用滑轮组拉着重600N的物体A沿水平方向匀速移动,在40s内物体移动了8m,拉力F做的功为1280J。
(不计绳重及机械内部摩擦)求:(1)拉力F的大小及拉力的功率;(2)若动滑轮的重为12N,计算滑轮组的机械效率.2、小文的体重为600 N,当他使用如图所示的滑轮组匀速提升水中的体积为0.01m3的重物A时(重物始终未出水面),他对地面的压强为8.75×103Pa。
已知小文与地面的接触面积为400cm2。
当他用此滑轮组在空气中匀速提升重物B时,滑轮组的机械效率是80%。
已知重物A重物B所受重力之比G A︰G B=5︰12,若不计绳重和摩擦,g=10N/kg。
求:(1)提升重物A时小文对地面的压力。
(2)物体A的密度。
(3)在水中提升重物A时滑轮组的机械效率。
(4)重物A完全出水面后,以0.2m/s的速度匀速上升,小文拉绳的功率P。
3、如图所示,是利用器械提升重物的示意图。
当某人自由站在水平地面上时,他对地面的压强P0=2×104Pa;当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P1=2.375×104Pa;当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P2=5.75×104Pa。
假设这个人用的力和绳端B用的力始终沿竖直方向,加挂重物前后他对杠杆A端施加的举力分别为F1、F2,已知F2=1500N。
(杠杆、绳重和机械间摩擦忽略不计,g取10N/kg)求:(1)F1与F2之比;(2)人的质量m人;(3)当重物G被匀速提升过程中,滑轮组的机械效率η;(4)已知重物G的密度与水的密度比为9:1,将重物完全浸没在水中匀速上升时的速度为0.1m/s,若此时已知动滑轮重为100N,那么绳端B的拉力F’做功的功率P’为多大?5、体重为510N的人,站在水平地面上对地面的压强为P1, 如图所示,用滑轮组拉物体A沿水平方向做匀速运动,此时人对地面的压强为P2,压强变化了2750pa。

初二中考语文练习题一、阅读理解阅读下面的短文,然后根据短文内容选择正确答案。
(1)鲁迅曾说:一个民族不能没有英雄,就像一本书不能没有插图。
英雄对于我们的作用真的很大,他们的精神激励着一代又一代的人。
我国历史上有很多伟大的英雄人物,下面我就给大家介绍三位。
1.孔子孔子是古代中国的伟大思想家、教育家和政治家,他的学说成为了中国古代文化的代表,对后世影响深远。
他提倡“仁爱之道”,主张君子庙堂之上,义之所在。
他的思想对于中国的教育、道德和人际关系有着重要的指导作用。
2.岳飞岳飞是南宋时期的抗金名将,他以勇猛的战斗精神和忠诚于国家的品质而闻名于世。
他与金兵浴血奋战,直到壮烈牺牲,成为民族英雄,他的精神激励着无数后来者。
3.邓稼先邓稼先是中国现代航天事业的奠基人之一,他是我国第一颗原子弹和第一颗氢弹的总设计师。
他以顽强的毅力和无私的奉献精神,为国家的科技进步做出了巨大贡献,被誉为“钢铁院士”。
根据短文内容,选择最佳答案。
1. 孔子对中国有着哪些重要的影响?A. 科技进步B. 国家安全C. 教育、道德、人际关系D. 军事战争2. 岳飞以何种品质而闻名于世?A. 勇猛战斗精神B. 谦逊和善良C. 学识渊博D. 聪明才智3. 下列人物是中国现代航天事业的奠基人之一的是:A. 孔子B. 岳飞C. 邓稼先D. 鲁迅(2)近代中国有很多英雄人物,他们为国家和民族做出了巨大贡献。
下面是其中三位的简要介绍。
1.林则徐林则徐是清朝末年的政治家和思想家,他积极参与反对鸦片战争,曾任福建巡抚,坚决主张取缔鸦片贸易。
他领导“福建洋务”,提出了许多改革措施,为中国近代化进程做出了重要贡献。
2.孙中山孙中山是中国近代民主革命的伟大先行者,被誉为“中国民主革命的伟大导师”。
他创建了中国同盟会,推翻了满清王朝,成立了中华民国。
他提出了“三民主义”,对中国影响深远。
3.毛泽东毛泽东是中国共产党的创始人之一,中国革命和建设的伟大领导者。
他领导了中国人民的抗日战争和解放战争,建立了中华人民共和国。

【中考数学】有理数解答题训练经典题目(附答案)一、解答题1.点A、O、B、C从左向右依次在数轴上的位置如图所示,点O在原点,点A、B、C表示的数分别是a、b、c .(1)若a=﹣2,b=4,c=8,D为AB中点,F为BC中点,求DF的长.(2)若点A到原点的距离为3,B为AC的中点.①用b的代数式表示c;②数轴上B、C两点之间有一动点M,点M表示的数为x,无论点M运动到何处,代数式|x﹣c|﹣5|x﹣a|+bx+cx 的值都不变,求b的值.2.已知表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离请试着探索:(1)找出所有符合条件的整数,使,这样的整数是________;(2)利用数轴找出,当时,的值是________;(3)利用数轴找出,当取最小值时,的范围是________.3.已知有理数a,b,c在数轴上的位置如图所示:解答下列式子:(1)比较a,,c的大小(用“<”连接);(2)若,试化简等式的右边;(3)在(2)的条件下,求的值.4.如图,点、、是数轴上三点,点表示的数为,, .(1)写出数轴上点、表示的数:________,________.(2)动点,同时从,出发,点以每秒个单位长度的速度沿数轴向右匀速运动,点以个单位长度的速度沿数向左匀速运动,设运动时间为秒.①求数轴上点,表示的数(用含的式子表示);② 为何值时,点,相距个单位长度.5.如图,数轴上点A,B分别对应数a,b.其中a<0,b>0.(1)当a=﹣2,b=6时,求a-b=________,线段AB的中点对应的数是________;(直接填结果)(2)若该数轴上另有一点M对应着数m.①当a=﹣4,b=8,点M在A,B之间,且AM=3BM时,求m的值.②当m=2,b>2,且AM=2BM时,求代数式a+2b+20的值.6.同学们都知道,|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.试探索:(1)求|5-(-2)|=________.(2)找出所有符合条件的整数x,使得|x+5|+|x-2|=7这样的整数是________.(3)由以上探索猜想对于任何有理数x,|x-3|+|x-6|是否有最小值?如果有写出最小值,如果没有说明理由.7.观察下列等式,,,以上三个等式两边分别相加得:(1)猜想并写出: ________(2)计算: ________(3)探究并计算:8.(1)阅读下面材料:点、在数轴上分别表示实数,,、两点之间的距高表示为当、两点中有一点在原点时,不妨设点在原点,如图1,;当、都不在原点时,①如图2,点、都在原点的右侧,;②如图3,点、都在原点的左侧,;③如图4,点、在原点的两侧,;(1)回答下列问题:①数轴上表示2和5的两点间的距离是________,数轴上表示-2和-5的两点之间的距离是________,数轴上表示1和-3的两点之间的距离是________;②数轴上表示和-1的两点和之间的距离是________,如果,那么为________;③当代数式取最小值时,相应的的取值范围是________;④求的最小值,提示:.9.点A在数轴上对应的数为3,点B对应的数为b,其中A、B两点之间的距离为5 (1)求b的值(2)当B在A左侧时,一点D从原点O出发以每秒2个单位的速度向左运动,请问D运动多少时间,可以使得D到A、B两点的距离之和为8?(3)当B在A的左侧时,一点D从O出发以每秒2个单位的速度向左运动,同时点M从B出发,以每秒1个单位的速度向左运动,点N从A出发,以每秒4个单位的速度向右运动;在运动过程中,MN的中点为P,OD的中点为Q,请问MN-2PQ的值是否会发生变化?若发生变化,请说明理由;如果没有变化,请求出这个值.10.已知数轴上,点A和点B分别位于原点O两侧,AB=14,点A对应的数为a,点B对应的数为b.(1)若b=-4,则a的值为________.(2)若OA=3OB,求a的值.(3)点C为数轴上一点,对应的数为c.若O为AC的中点,OB=3BC,直接写出所有满足条件的c的值.11.如图,数轴上两点分别表示有理数-2和5,我们用来表示两点之间的距离.(1)直接写出的值=________;(2)若数轴上一点表示有理数m,则的值是________;(3)当代数式∣n +2∣+∣n -5∣的值取最小值时,写出表示n的点所在的位置;(4)若点分别以每秒2个单位长度和每秒3个单位长度的速度同时向数轴负方向运动,求经过多少秒后,点到原点的距离是点到原点的距离的2倍.12.阅读材料:如图①,若点B把线段分成两条长度相等的线段AB和BC,则点B叫做线段AC的中点.回答问题:(1)如图②,在数轴上,点A所表示的数是﹣2,点B所表示的数是0,点C所表示的数是3.①若A是线段DB的中点,则点D表示的数是________;②若E是线段AC的中点,求点E表示的数________.(2)在数轴上,若点M表示的数是m,点N所表示的数是n,点P是线段MN的中点.①若点P表示的数是1,则m、n可能的值是________(填写符合要求的序号);(i)m=0,n=2;(ii)m=﹣5,n=7;(iii)m=0.5,n=1.5;(iv)m=﹣1,n=2②直接用含m、n的代数式表示点P表示的数________.13.数轴上点A表示的数为10,点M,N分别以每秒a个单位长度,每秒b个单位长度的速度沿数轴运动,a,b满足|a-5|+(b-6)2=0.(1)请真接与出a=________,b=________;(2)如图1,点M从A出发沿数轴向左运动,到达原点后立即返回向右运动:同时点N从原点0出发沿数轴向左运动,运动时间为t,点P为线段ON的中点若MP=MA,求t的值: (3)如图2,若点M从原点向右运动,同时点N从原点向左运动,运动时间为t时M运动到点A的右侧,若此时以M,N,O,A为端点的所有线段的长度和为142,求此时点M对应的数.14.我们知道,|a|表示数a在数轴上的对应点与原点的距离.如:|5|表示5在数轴上的对应点到原点的距离。
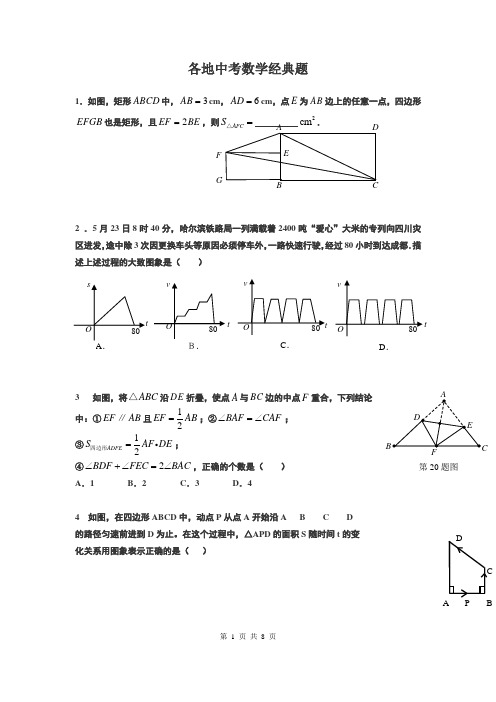
各地中考数学经典题1.如图,矩形ABCD 中,3AB =cm ,6AD =cm ,点E 为AB 边上的任意一点,四边形EFGB 也是矩形,且2EF BE =,则AFC S =△ 2cm .2 .5月23日8时40分,哈尔滨铁路局一列满载着2400吨“爱心”大米的专列向四川灾区进发,途中除3次因更换车头等原因必须停车外,一路快速行驶,经过80小时到达成都.描述上述过程的大致图象是( )3 如图,将ABC △沿DE 折叠,使点A 与BC 边的中点F 重合,下列结论中:①EF AB ∥且12EF AB =;②BAF CAF ∠=∠; ③12ADFE S AF DE =四边形; ④2BDF FEC BAC ∠+∠=∠,正确的个数是( )A .1B .2C .3D .44 如图,在四边形ABCD 中,动点P 从点A开始沿A B C D 的路径匀速前进到D 为止。
在这个过程中,△APD 的面积S 随时间t 的变 化关系用图象表示正确的是( )ADCEF GBtB.C .D .第20题图OG F BDACE5如图,在正方形纸片ABCD 中,对角线AC 、BD 交于点O ,折叠正方形纸片ABCD ,使AD 落在BD 上,点A 恰好与BD 上的点F 重合.展开后,折痕DE 分别交AB 、AC 于点E 、G .连接GF.下列结论:①∠AGD=112.5°;②tan ∠AED=2;③S △AGD=S △OGD ;④四边形AEFG 是菱形;⑤BE=2OG .其中正确结论的序号是 .6 福娃们在一起探讨研究下面的题目:参考下面福娃们的讨论,请你解该题,你选择的答案是( )贝贝:我注意到当 0x =时,0y m =>. 晶晶:我发现图象的对 称轴为12x =.欢欢:我判断出12x a x <<.迎迎:我认为关键要判断1a -的符号. 妮妮:m 可以取一个特殊的值.7 正方形ABCD 中,E 是BC 边上一点,以E 为圆心、EC 为半径的半圆与以A 为圆心,AB 为半径的圆弧外切,则sin EAB ∠的值为( )A .43B .34 C .45D .35s tOAs tOBs tOCstOD函数2y x x m =-+(m 为常数)的图象如左图, 如果x a =时,0y <;那么1x a =-时,函数值( ) A .0y < B .0y m << C .y m > D .y m =x yO x 1x 28 一个函数的图象如图,给出以下结论: ①当0x =时,函数值最大;②当02x <<时,函数y 随x 的增大而减小; ③存在001x <<,当0x x =时,函数值为0. 其中正确的结论是( )A .①②B .①③C .②③D .①②③9.函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是 ( )10 如图,水平地面上有一面积为230cm π的扇形AOB ,半径OA=6cm ,且OA 与地面垂直.在没有滑动的情况下,将扇形向右滚动至OB 与地面垂直为止,则O 点移动的距离为( )A 、20cm B 、24cm C 、10cm π D 、30cm π11 在Rt △ABC 内有边长分别为,,a b c 的三个正方形,则,,a b c 满足的关系式是( ) A 、b a c =+ B 、b ac =C 、222b ac =+ D 、22b a c ==12 古尔邦节,6位朋友均匀地围坐在圆桌旁共度佳节.圆桌半径为60cm ,每人离圆桌的距离均为10cm ,现又来了两名客人,每人向后挪动了相同的距离,再左右调整位置,使8人都坐下,并且8人之间的距离与原来6人之间的距离(即在圆周上两人之间的圆弧的长)相等.设每人向后挪动的距离为x ,根据题意,可列方程( )A .2π(6010)2π(6010)68x +++=B .2π(60)2π6086x +⨯=C .2π(6010)62π(60)8x +⨯=+⨯D .2π(60)82π(60)6x x -⨯=+⨯13 如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm 2, 则该半圆的半径为( ).A . (45)+ cmB . 9 cmC . 45cmD . 62cm14 如图,A B C D ,,,为O 的四等分点,动点P 从圆心O 出发,沿O C D O ---路线作匀速运动,设运动时间为t (s ).()APB y =∠,则下列图象中表示y 与t 之间函数关系最恰当的是( )15 如图,边长为a 的正ABC △内有一边长为b 的内接正DEF △,则AEF △的内切圆半径为.A B C DOP B .ty 045 90 D .t y 045 90 A .ty45 90 C .ty 045 9016 如图,⊙O 的半径为2,点A 的坐标为(2,32),直线AB 为⊙O 的切线, B 为切点.则B 点的坐标为A .⎪⎪⎭⎫ ⎝⎛-5823, B .()13,- C .⎪⎭⎫ ⎝⎛-5954, D .()31,-17 如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次,点P 依次落在点12P P ,,的横坐标为 .18 如图①,1O ,2O ,3O ,4O 为四个等圆的圆心,A ,B ,C ,D 为切点,请你在图中画出一条直线,将这四个圆分成面积相等的两部分,并说明这条直线经过的两个点是 ;如图②,1O ,2O ,3O ,4O ,5O 为五个等圆的圆心,A ,B ,C ,D ,E 为切点,请你在图中画出一条直线,将这五个圆...分成面积相等的两部分,并说明这条直线经过的两个点是 .19 课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那(第19题)第(18)题图① 第(18)题图②(第19题)么标号为100的微生物会出现在( ) A .第3天B .第4天C .第5天D .第6天20如图所示,AB 是⊙O 的直径,AD =DE ,AE 与BD 交于点C ,则图中与∠BCE 相等的角有 A .2个 B .3个 C .4个 D .5 个21.有一个附有进出水管的容器,每单位时间进、出的水量都是一定的.设从某一时刻开始5分钟内只进水不出水,在接着的2分钟内只出水不进水,又在随后的15分钟内既进水又出水,刚好将该容器注满.已知容器中的水量y 升与时间x 分之间的函数关系如图所示.则在第7分钟时,容器内的水量为 升.A.15 B.16 C.17 D.1821.如图,⊙O 1、⊙O 2内切于P 点,连心线和⊙O 1、⊙O 2分别交于A 、B 两点,过P 点的直线与⊙O 1、⊙O 2分别交于C 、D 两点,若∠BPC=60º,AB=2,则CD= . A.1 B.2 C.21 D.41 22.已知:如图所示,抛物线y=ax 2+bx+c 的对称轴为x=-1,与x 轴交于A 、B 两点,交y 轴于点C ,且OB=OC ,则下列结论正确的个数是 . ①b=2a ②a-b+c>-1 ③0<b 2-4ac<4 ④ac+1=b A.1个 B.2个 C.3个 D.4个23.已知:如图,∠ACB=90º,以AC 为直径的⊙O 交AB 于D 点,过D 作⊙O 的切线交BC 于E 点,EF ⊥AB 于F 点,连OE 交DC 于P ,则下列结论:其中正确的有 .①BC=2DE ; ②OE ∥AB; ③DE=2PD ; ④AC•DF =DE•CD . A.①②③ B.①③④ C.①②④ D.①②③④PBEDACO24 已知:如图,直线MN 切⊙O 于点C ,AB 为⊙O 的直径, 延长BA 交直线MN 于M 点,AE ⊥MN ,BF ⊥MN ,E 、F 分别为垂足,BF 交⊙O 于G ,连结AC 、BC ,过点C 作 CD ⊥AB ,D 为垂足,连结OC 、CG. 下列结论:其中正确的有 . ①CD=CF=CE ; ②EF 2=4AE •BF; ③AD •DB=FG •FB ; ④MC •CF=MA •BF. A.①②③ B.②③④ C.①③④ D.①②③④25 如图,M 为⊙O 上的一点,⊙M 与⊙O 相交于A 、 B 两点,P 为⊙O 上任意一点,直线PA 、PB 分别交 ⊙M 于C 、D 两点,直线CD 交⊙O 于E 、F 两点,连 结PE 、PF 、BC ,下列结论:其中正确的有 . ①PE=PF ; ②PE 2=PA ·PC; ③EA ·EB=EC ·ED ; ④rRBC PB =(其中R 、r 分别为⊙O 、⊙M 的半径). A.①②③ B.①②④ C.②④ D.①②③④1 如图,菱形OABC 中,120A =∠,1OA =,将菱形OABC绕点O 按顺时针方向旋转90,则图中由BB ',B A '',A C ',CB 围成的阴影部分的面积是 .•ACDFBP O E•MABF OGC DE N··BADPO FM E C'(第18题)答 案1 9 2D 3B 4B 5(1,4,5) 6 C 7D 8 C 9 C 10 C 11 A 12 A 13C 14 C 15)a b - 16D 17 2008 18 18.1O ,3O ,如图① (提示:答案不惟一,过31O O 与42O O 交点O 的任意直线都能将四个圆分成面积相等的两部分);5O ,O ,如图② (提示:答案不惟一,如4AO ,3DO ,2EO ,1CO 等均可).19 C20 D 25 2π3-第(18)题图②。

【中考数学】二元一次方程组易错压轴解答题训练经典题目(附答案)一、二元一次方程组易错压轴解答题1.某商场经销A,B两款商品,若买20件A商品和10件B商品用了360元;买30件A 商品和5件B商品用了500元.(1)求A、B两款商品的单价;(2)若对A、B两款商品按相同折扣进行销售,某顾客发现用640元购买A商品的数量比用224元购买B商品的数量少20件,求对A、B两款商品进行了几折销售?(3)若对A商品进行5折销售,B商品进行8折销售,某顾客同时购买A、B两种商品若干件,正好用完49.6元,问该顾客同时购买A、B两款商品各几件?2.已知关于x,y的方程(m,n为实数)(1)若m+4n=5,试探究方程组的解x,y之间的关系(2)若方程组的解满足2x+3y=0,求分式的值.3.已知关于、的方程组(1)若是方程组的解时,求的值;(2)当时,若方程组的解满足为非正数,为负数,化简:.4.我们用表示不大于x的最大整数,例如请解决下列问题:(1) =________. =________.(其中为圆周率);(2)已知x,y满足方程组求x,y的取值范围.5.如图,已知和的度数满足方程组,且 .(1)分别求和的度数;(2)请判断与的位置关系,并说明理由;(3)求的度数。
6.在直角坐标系中,已知点A,B的坐标是(a,0),(b,0).a,b满足方程组,C为y轴正半轴上一点,且S△ABC=6.(1)求A,B,C三点的坐标;(2)是否存在点P(t,t),使S△PAB= S△ABC?若存在,请求出P点的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,长方形ABCD的边AB在y轴正半轴上,顶点A的坐标为(0,2),设顶点C的坐标为(a,b).(1)顶点B的坐标为________,顶点D的坐标为________(用a或b表示);(2)如果将一个点的横坐标作为x的值,纵坐标作为y的值,代入方程2x+3y=12成立,就说这个点的坐标是方程2x+3y=12的解.已知顶点B和D的坐标都是方程2x+3y=12的解,求a,b的值;(3)在(2)的条件下,平移长方形ABCD,使点B移动到点D,得到新的长方形EDFG,这次平移可以看成是先将长方形ABCD向右平移________个单位长度,再向下平移________个单位长度的两次平移;(4)若点P(m,n)是对角线BD上的一点,且点P的坐标是方程2x+3y=12的解,试说明平移后点P的对应点P′的坐标也是方程2x+3y=12的解.8.如果A,B都是由几个不同整数构成的集合,由属于A又属于B的所有整数构成的集合叫做A,B的交集,记作A∩B.例如:若A={1,2,3},B={3,4,5},则A∩B={3};若A={0,﹣62,37,2},B={2,﹣1,37,﹣5,0,19},则A∩B={37,0,2}.(1)已知C={4,3},D={4,5,6},则C∩D={________};(2)已知E={1,m, 2},F={6,7},且E∩F={m},则m=________;(3)已知P={2m+1,2m﹣1},Q={n,n+2,n+4},且P∩Q={m,n},如果关于x的不等式组,恰好有2019个整数解,求a的取值范围.9.小红用110根长短相同的小木棍按照如图所示的方式,连续摆正方形或六边形,要求相邻的图形只有一条公共边.(1)小红首先用根小木棍摆出了个小正方形,请你用等式表示之间的关系:________;(2)小红用剩下的小木棍摆出了一些六边形,且没有木棍剩余.已知他摆出的正方形比六边形多4个,请你求出摆放的正方形和六边形各多少个?(3)小红重新用50根小木棍,摆出了排,共个小正方形.其中每排至少含有1个小正方形,每排含有的小正方形的个数可以不同.请你用等式表示之间的关系,并写出所有可能的取值.10.如图,在平面直角坐标系中,把一个点的横、纵坐标都乘以同一个实数,然后将得到的点先向右平移个单位,再向上平移个单位,得到点(1)若,,,,则点坐标是________;(2)对正方形及其内部的每个点进行上述操作,得到正方形及其内部的点,其中点的对应点分别为.求;(3)在(2)的条件下,己知正方形内部的一个点经过上述操作后得到的对应点与点重合,求点的坐标.11.水果商贩老徐上水果批发市场进货,他了解到草莓的批发价格是每箱60元,苹果的批发价格是每箱40元. 老徐购得草莓和苹果共60箱,刚好花费3100元.(1)问草莓、苹果各购买了多少箱?(2)老徐有甲、乙两家店铺,每售出一箱草莓或苹果,甲店分别获利15元和20元,乙店分别获利12元和16元. 设老徐将购进的60箱水果分配给甲店草莓箱,苹果箱,其余均分配给乙店.由于他口碑良好,两家店都很快卖完了这批水果.①若老徐在甲店获利600元,则他在乙店获利多少元?________②若老徐希望获得总利润为1000元,则 =________.(直接写出答案)12.某公园的门票价格如下表所示:购票人数1~50人51~100人100人以上每人门票价20元17元14元1)班人数较少,不足50人,(2)班人数较多,超过50人,但是不超过100人.如果两个班都以班为单位分别购票,则一共应付1912元;如果两个班联合起来,作为个团体购票,则只需付1456元(1)列方程或方程组求出两个班各有多少学生?(2)若(1)班全员参加,(2)班有20人不参加此次活动,请你设计一种最省钱方式来帮他们买票,并说明理由.(3)你认为是否存在这样的可能:51到100人之间买票的钱数与100人以上买票的钱数相等?如果有,是多少人与多少人买票钱数相等?(直接写结果)【参考答案】***试卷处理标记,请不要删除一、二元一次方程组易错压轴解答题1.(1)解:设A商品单价为x元,B商品单价为y元.根据题意,得: {20x+10y=36030x+5y=500解得 {x=16y=4所以A商品的单价是16元,B商品的单价是4元.解析:(1)解:设A商品单价为x元,B商品单价为y元.根据题意,得:解得所以A商品的单价是16元,B商品的单价是4元.(2)解:设打折后A、B两款商品进的价格分别为16a和4a,则解得a=0.8经检验,a=0.8为原方程的解且符合题意所以A、B两款商品进行了8折销售(3)解:设顾客购买A商品m件,B商品n件.则∵m、n都为正整数∴①m=1,n=13②m=3,n=8③m=5,n=3所以顾客购买A商品1件,B商品13件;或A商品3件,B商品8件;A商品5件,B商品3件.【解析】【分析】(1)设A商品单价为x元,B商品单价为y元,根据题中“买20件A商品和10件B商品用了360元;买30件A商品和5件B商品用了500元”可列出关于x,y 的二元一次方程组,求解即可;(2)设打折后A、B两款商品进的价格分别为16a和4a,根据题中“用640元购买A商品的数量比用224元购买B商品的数量少20件”可列出关于a的分式方程,求解即可;(3)设顾客购买A商品m件,B商品n件,根据“同时购买A、B两种商品若干件,正好用完49.6元”可得关于m,n的二元一次方程,由m,n都为正整数讨论其所有可能性即可.2.(1)解:方程组由①-2×②得:3m+12n=-3x+3y+15,即m+4n=-x+y+5,将m+4n=5代入得:y=x,∴方程组的解x,y之间的关系为y=x;(2)解: =解析:(1)解:方程组由①-2×②得:3m+12n=-3x+3y+15,即m+4n=-x+y+5,将m+4n=5代入得:y=x,∴方程组的解x,y之间的关系为y=x;(2)解: = ,①+②得:3x=3m-6n+9,即:x=m-2n+3,将x=m-2n+3代入①中,得:y=2m+2n-2,∵2x+3y=0,∴2(m-2n+3)+3(2m+2n-2)=0∴n=-4m,∴原式= ,【解析】【分析】(1)由由①-2×②将方程组变形整理得:3m+12n=-3x+3y+15,即m+4n=-x+y+5,将m+4n=5代入即可得到x、y之间的关系式;(2)先化简分式,再解方程组,将用m、n、表示的x、y代入2x+3y=0中,得到m、n的关系式,然后代入化简式子中求解即可.3.(1)把 {x=2y=1 代入方程组,得 {-7-n=3n+3m=1解得 {n=-103m=11∴3m+n=11-10=1(2)当n=-2时,解方程组得解得;解析:(1)把代入方程组,得解得∴3m+n=11-10=1(2)当n=-2时,解方程组得解得;【解析】【分析】(1)将x=2,y=1代入方程组,即可得到m和n的值,计算得到3m+n 的值即可;(2)将n=-2代入方程组,用含m的代数式表示x和y,根据x为非正数,y为负数表示出其范围,即可得到m的取值范围,继而化简得到答案即可。

专题训练——论证过程一、《专注》⑤专注催化成功。
现实中,人们并不缺乏雄心壮志以及奋斗毅力,但最终无所建树,因为他们没有始终专注于一个目标并为之奋斗。
我的一位同学,大学毕业后先在一所农村中学教书,他对这份工作并不热心,于是报考了研究生,惜乎名落孙山。
又去搞律师证,苦熬几年终于拿到了证书,然后到一家律师事务所实习。
因为刚入行,没名气,接不到案子,所以没过多久,他又跑到一个亲戚开的装潢公司做事去了。
最近听说他又回到那所中学。
我这位同学奋斗多年最终又回到起点,糟就糟在没有专注在一个点上,空耗了半生的光阴和精力。
而世界首富比尔·盖茨有着可以投资房地产、金融业等其它行业的多种选择,但他始终专注于操作系统和软件的开发,从而使微软事业长盛不衰,不仅获得了巨大财富,更赢得了崇高声誉。
请你简要分析第⑤段的论证过程。
二、《从容面对挫折》③有些挫折可能让人致命,却也可能成为成功的垫脚石。
生活中,挫折是难免的,农民会遇到自然灾害而颗粒无收,工人会因为企业经营困难而下岗,机关干部也会面临精简机构而裁员。
但是,也可能是幸运的。
“宝剑锋从磨砺出,梅花香自苦寒来。
”困难只能吓倒懦夫,而胜利永远属于敢于攀登高峰的人。
历史上一帆风顺而又大有成就的人实在少见。
真正出类拔萃的人,大多数是那些历尽艰辛,在挫折中磨炼出坚强的意志,在逆境中不懈地奋斗的人。
孔子从小生活贫寒,但他孜孜不倦地求学,最终成为著名的思想家;司马迁因李陵事件而蒙受人生灾祸,忍辱著《史记》,留下了一部宏伟巨著。
还有屈原、贝多芬、邓小平、张海迪等,无不经历了种种坎坷、磨难和挫折。
艰难的环境确实会使很多人意志消沉,丧失斗志,但在积极进取的人面前,艰难的环境却使他们抖擞精神,发奋努力。
这就是所谓的挫折不一定是一件坏事,它也有助于我们获得成功。
简要分析第③段的论证过程。
三、《微笑》⑤把微笑留给伤害我们的人,是一种人际关系的艺术,是一种生存智慧。
它一方面解放了自己,使自己不至于因别人的伤害而耿耿于怀,黯然神伤。
【中考数学】有理数解答题训练经典题目(附答案)一、解答题1.如图,在数轴上A点表示的数是-8,B点表示的数是2。
动线段CD=4(点D在点C的右侧),从点C与点A重合的位置出发,以每秒2个单位的速度向右运动,运动时间为t 秒。
(1)①已知点C表示的数是-6,试求点D表示的数;②用含有t的代数式表示点D表示的数。
(2)当AC=2BD时,求t的值。
(3)试问当线段CD在什么位置时,AD+BC或AD-BC的值始终保持不变?请求出它的值并说明此时线段CD的位置。
2.在数轴上,点A,点B分别表示数,则线段AB的长度可以用表示.例如:在数轴上点A表示5,点B表示2,则线段AB的长表示为 .(1)若线段AB的长表示为6, ,则ab的值等于________;(2)已知数轴上的任意一点P表示的数是x,且的最小值是4,若,则b=________;(3)已知点A在点B的右边,且,若,,试判断的符号,说明理由.3.已知数轴上有A.B. C三点,分别表示有理数−26,−10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒。
(1)PA=________,PC=________(用含t的代数式表示)(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,当点P运动到点C时,P、Q两点运动停止,①当P、Q两点运动停止时,求点P和点Q的距离;②求当t为何值时P、Q两点恰好在途中相遇.4.已知多项式,次数是b,3a与b互为相反数,在数轴上,点A表示数a,点B表示数b.(1)数轴上A、B之间的距离记作,定义:设点C在数轴上对应的数为x,当时,直接写出x的值.(2)有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度按照如此规律不断地左右运动,当运动了2019次时,求点P所对应的有理数.(3)若小蚂蚁甲从点A处以1个单位长度秒的速度向左运动,同时小蚂蚁乙从点B处以2单位长度秒的速度也向左运动,一同学观察两只小蚂蚁运动,在它们刚开始运动时,在原点O处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒,求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t.5.已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是________;(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.6.(1)阅读下面材料:点、在数轴上分别表示实数,,、两点之间的距高表示为当、两点中有一点在原点时,不妨设点在原点,如图1,;当、都不在原点时,①如图2,点、都在原点的右侧,;②如图3,点、都在原点的左侧,;③如图4,点、在原点的两侧,;(1)回答下列问题:①数轴上表示2和5的两点间的距离是________,数轴上表示-2和-5的两点之间的距离是________,数轴上表示1和-3的两点之间的距离是________;②数轴上表示和-1的两点和之间的距离是________,如果,那么为________;③当代数式取最小值时,相应的的取值范围是________;④求的最小值,提示:.7.阅读理解:若A,B,C为数轴上的三点,且点C到点A的距离是点C到点B的距离的2倍,我们就称点C是【A,B】的好点。
【部编版中考语文】现代文阅读训练经典题目(附答案)一、现代文阅读1.现代文阅读阅读下面文章,完成后面小题向大海也能要“药〃刘诗瑶①前不久,由中国海洋大学、中国科学院上海药物研究所和上海绿谷制药联合研发的治疗阿尔茨海默症新药“甘露寡糖二酸〃(GV—971)顺利完成临床印期试验,在新药研制上迈过了最关键的一步。
该药物是从海藻中提取的海洋寡糖类分子,其新颖的作用模式与独特的多靶作用特征,为阿尔茨海默症药物研发开辟了新路径。
②海洋约占地球表面积的71%,是巨大的生物资源库。
以海洋生物和海洋矿物中的有效成分为基础开发的药物就是海洋药物。
据中国海洋大学、青岛海洋科学与技术试点国家实验室学委会主任管华诗院士介绍,目前认识和开发的海洋药物主要来自海洋生物资源。
③人类主要生活在陆地上,所研发的药物主要来源于陆地,但使用多了,就有可能产生耐药性。
于是,人们将目光转向了浩瀚深邃的海洋。
④除了够新,海洋药物还够“奇〃。
据管华诗介绍,为了适应在深海环境中的生存、繁衍、防御等活动,深海生物进化出了独特的基因,耐寒耐热耐高压等,能够产生结构奇特、活性多样显著的海洋天然产物,它们为现代创新药物研发提供了重要结构信息,是肿瘤、心脑血管疾病、免疫性疾病、神经系统疾病等人类重大疾病药物先导化合物发现的重要源泉。
⑤半个多世纪以来,全球共有13个海洋创新药物被批准上市,其中管华诗院士1985年开发上市的我国首个海洋新药藻酸双酯钠(PSS)就是其中之一。
进入21世纪后,海洋药物的开发和上市速度明显加快,十几年间,先后有8个海洋药物被美国FDA (食品药品监督管理局)或欧盟EMEA (欧洲药品评估局)批准上市。
到2016年,海洋药物的全球市场达到86亿美元,已成为蓝色经济发展中的重要一极。
⑥据了解,世界各国尤其是美国、日本及欧盟等国家纷纷制订相应计划,斥巨资开发海洋生物资源,海洋药物已经成为国际医药领域竞争的热点。
⑦但向大海要“药〃,并不容易。
一、选择题1.如图,在平面直角坐标系中,菱形ABCD 的顶点A ,B 在反比例函数ky x=(0k >,0x >)的图象上,横坐标分别为1,4,对角线BD x ∥轴.若菱形ABCD 的面积为452,则k 的值为( )A .54B .154C .4D .52.下列二次根式中,与3是同类二次根式的是( ) A .18B .13C .24D .0.33.“绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x 万平方米,则下面所列方程中正确的是( ) A .606030(125%)x x-=+ B .606030(125%)x x-=+C .60(125%)6030x x ⨯+-=D .6060(125%)30x x⨯+-= 4.如图,直线//AB CD ,AG 平分BAE ∠,40EFC ∠=,则GAF ∠的度数为( )A .110B .115C .125D .1305.某公司计划新建一个容积V(m 3)一定的长方体污水处理池,池的底面积S(m 2)与其深度h (m )之间的函数关系式为()0S Vh h=≠,这个函数的图象大致是( )A .B .C .D .6.已知直线y =kx ﹣2经过点(3,1),则这条直线还经过下面哪个点( ) A .(2,0)B .(0,2)C .(1,3)D .(3,﹣1)7.如果√(2a −1)2=1−2a ,则a 的取值范围是( ) A .a <12 B .a ≤12 C .a >12 D .a ≥128.甲种蔬菜保鲜适宜的温度是1℃~5℃,乙种蔬菜保鲜适宜的温度是3℃~8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是( ) A .1℃~3℃B .3℃~5℃C .5℃~8℃D .1℃~8℃9.将一个矩形纸片按如图所示折叠,若∠1=40°,则∠2的度数是( )A .40°B .50°C .60°D .70°10.将一块直角三角板ABC 按如图方式放置,其中∠ABC =30°,A 、B 两点分别落在直线m 、n 上,∠1=20°,添加下列哪一个条件可使直线m ∥n( )A .∠2=20°B .∠2=30°C .∠2=45°D .∠2=50°11.如图,在矩形ABCD 中,AD=3,M 是CD 上的一点,将△ADM 沿直线AM 对折得到△ANM ,若AN 平分∠MAB ,则折痕AM 的长为( )A.3 B.23C.32D.612.如图,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草,如果使草坪部分的总面积为112m2,设小路的宽为xm,那么x满足的方程是()A.2x2-25x+16=0B.x2-25x+32=0C.x2-17x+16=0D.x2-17x-16=0 13.甲、乙二人做某种机械零件,已知每小时甲比乙少做8个,甲做120个所用的时间与乙做150个所用的时间相等,设甲每小时做x个零件,下列方程正确的是()A.1201508x x=-B.1201508x x=+C.1201508x x=-D.1201508x x=+14.如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是()A.B.C.D.15.如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为()A.66°B.104°C.114°D.124°16.肥皂泡的泡壁厚度大约是0.0007mm,0.0007用科学记数法表示为()A.0.7×10﹣3B.7×10﹣3C.7×10﹣4D.7×10﹣5 17.等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为()A.12 B.15 C.12或15 D.1818.下列图形是轴对称图形的有()A.2个B.3个C.4个D.5个19.老师设计了接力游戏,用合作的方式完成分式化简,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:接力中,自己负责的一步出现错误的是()A.只有乙B.甲和丁C.乙和丙D.乙和丁20.如图,⊙O的半径为5,AB为弦,点C为AB的中点,若∠ABC=30°,则弦AB的长为()A.12B.5C.532D.5321.将一副三角板和一张对边平行的纸条按如图摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是()A.15°B.22.5°C.30°D.45°22.如图所示,已知A(12,y1),B(2,y2)为反比例函数1yx图像上的两点,动点P(x,0)在x正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是()A.(12,0)B.(1,0)C.(32,0)D.(52,0)23.已知一个正多边形的内角是140°,则这个正多边形的边数是()A.9B.8C.7D.624.下列四个实数中,比1-小的数是( ) A .2-B .0C .1D .225.若直线1l 经过点()0,4,直线2l 经过点()3,2,且1l 与2l 关于x 轴对称,则1l 与2l 的交点坐标为( ) A .()6,0- B .()6,0 C .()2,0- D .()2,026.在数轴上,与表示6的点距离最近的整数点所表示的数是( ) A .1B .2C .3D .427.如图是由5个相同大小的正方体搭成的几何体,则它的俯视图是( )A .B .C .D .28.下列几何体中,其侧面展开图为扇形的是( )A .B .C .D .29.如图,在直角坐标系中,矩形OABC 的顶点O 在坐标原点,边OA 在x 轴上, OC 在y 轴上,如果矩形OA′B′C′与矩形OABC 关于点O 位似,且矩形OA′B′C′的面积等于矩形OABC 面积的14,那么点B′的坐标是( )A .(-2,3)B .(2,-3)C .(3,-2)或(-2,3)D .(-2,3)或(2,-3)30.如图,⊙C 过原点,且与两坐标轴分别交于点A 、点B ,点A 的坐标为(0,3),M 是第三象限内OB 上一点,∠BMO=120°,则⊙C 的半径长为( )A.6 B.5 C.3 D.32【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1.D2.B3.C4.A5.C6.A7.B8.B9.D10.D11.B12.C13.D14.B15.C16.C17.B18.C19.D20.D21.A22.D23.A24.A25.D26.B27.B28.C29.D30.C2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1.D解析:D【解析】【分析】设A(1,m),B(4,n),连接AC交BD于点M,BM=4-1=3,AM=m-n,由菱形的面积可推得m-n=154,再根据反比例函数系数的特性可知m=4n,从而可求出n的值,即可得到k的值.【详解】设A(1,m),B(4,n),连接AC交BD于点M,则有BM=4-1=3,AM=m-n,∴S菱形ABCD=4×12 BM•AM,∵S菱形ABCD=452,∴4×12×3(m-n)=452,∴m-n=154,又∵点A,B在反比例函数kyx ,∴k=m=4n,∴n=54,∴k=4n=5,故选D.【点睛】本题考查了反比例函数k的几何意义、菱形的性质、菱形的面积等,熟记菱形的对角线互相垂直平分是解题的关键.2.B解析:B【解析】【分析】【详解】ABC =D 故选B .3.C解析:C 【解析】分析:设实际工作时每天绿化的面积为x 万平方米,根据工作时间=工作总量÷工作效率结合提前 30 天完成任务,即可得出关于x 的分式方程.详解:设实际工作时每天绿化的面积为x 万平方米,则原来每天绿化的面积为125%x+万平方米,依题意得:606030125%x x-=+,即()60125%6030x x⨯+-=. 故选C .点睛:考查了由实际问题抽象出分式方程.找到关键描述语,找到合适的等量关系是解决问题的关键.4.A解析:A 【解析】 【分析】依据AB//CD ,EFC 40∠=,即可得到BAF 40∠=,BAE 140∠=,再根据AG 平分BAF ∠,可得BAG 70∠=,进而得出GAF 7040110∠=+=. 【详解】 解:AB//CD ,EFC 40∠=,BAF 40∠∴=, BAE 140∠∴=,又AG 平分BAF ∠,BAG 70∠∴=,GAF 7040110∠∴=+=,故选:A . 【点睛】本题考查的是平行线的性质和角平分线的定义,理解两直线平行,内错角相等是解题的关键.5.C解析:C 【解析】 【分析】 【详解】解:由题意可知:00v h >>, , ∴ (0)v s h h=≠中,当v 的值一定时,s 是h 的反比例函数, ∴函数 (0)v s h h=≠的图象当00v h >>,时是:“双曲线”在第一象限的分支. 故选C.6.A解析:A 【解析】 【分析】把点(3,1)代入直线y =kx ﹣2,得出k 值,然后逐个点代入,找出满足条件的答案. 【详解】把点(3,1)代入直线y =kx ﹣2,得1=3k ﹣2, 解得k =1, ∴y =x ﹣2,把(2,0),(0,2),(1,3),(3,﹣1)代入y =x ﹣2中,只有(2,0)满足条件. 故选A . 【点睛】本题考查了一次函数图象上点的坐标特点,熟悉一次函数图象上点的特点是解此题的关键.7.B解析:B 【解析】试题分析:根据二次根式的性质1可知:√(2a −1)2=|2a −1|=1−2a ,即2a −1≤0故答案为B.a ≤12.考点:二次根式的性质.8.B解析:B 【解析】 【分析】根据“1℃~5℃”,“3℃~8℃”组成不等式组,解不等式组即可求解.【详解】解:设温度为x ℃,根据题意可知1538x x x x ≥⎧⎪≤⎪⎨≥⎪⎪≤⎩ 解得35x ≤≤.故选:B .【点睛】本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.9.D解析:D【解析】【分析】根据折叠的知识和直线平行判定即可解答.【详解】解:如图可知折叠后的图案∠ABC=∠EBC ,又因为矩形对边平行,根据直线平行内错角相等可得∠2=∠DBC ,又因为∠2+∠ABC=180°,所以∠EBC+∠2=180°,即∠DBC+∠2=2∠2=180°-∠1=140°.可求出∠2=70°.【点睛】掌握折叠图形的过程中有些角度是对称相等的是解答本题的关键.10.D解析:D【解析】【分析】根据平行线的性质即可得到∠2=∠ABC+∠1,即可得出结论.【详解】∵直线EF ∥GH ,∴∠2=∠ABC+∠1=30°+20°=50°,故选D.【点睛】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.11.B解析:B【解析】【分析】根据折叠的性质可得∠MAN=∠DAM,再由AN平分∠MAB,得出∠DAM=∠MAN=∠NAB,最后利用三角函数解答即可.【详解】由折叠性质得:△ANM≌△ADM,∴∠MAN=∠DAM,∵AN平分∠MAB,∠MAN=∠NAB,∴∠DAM=∠MAN=∠NAB,∵四边形ABCD是矩形,∴∠DAB=90°,∴∠DAM=30°,==∴故选:B.【点睛】本题考查了矩形的性质及折叠的性质,解题的关键是利用折叠的性质求得∠MAN=∠DAM, 12.C解析:C【解析】解:设小路的宽度为xm,那么草坪的总长度和总宽度应该为(16-2x)m,(9-x)m;根据题意即可得出方程为:(16-2x)(9-x)=112,整理得:x2-17x+16=0.故选C.点睛:本题考查了一元二次方程的运用,弄清“草坪的总长度和总宽度”是解决本题的关键.13.D解析:D【解析】【分析】首先用x表示甲和乙每小时做的零件个数,再根据甲做120个所用的时间与乙做150个所用的时间相等即可列出一元一次方程.【详解】解:∵甲每小时做x个零件,∴乙每小时做(x+8)个零件,∵甲做120个所用的时间与乙做150个所用的时间相等,∴1201508x x=+,故选D.【点睛】本题考查了分式方程的实际应用,熟练掌握是解题的关键.14.B解析:B【解析】试题分析:从左面看易得第一层有2个正方形,第二层最左边有一个正方形.故选B.考点:简单组合体的三视图.15.C解析:C【解析】【分析】根据平行四边形性质和折叠性质得∠BAC=∠ACD=∠B′AC=12∠1,再根据三角形内角和定理可得.【详解】∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ACD=∠BAC,由折叠的性质得:∠BAC=∠B′AC,∴∠BAC=∠ACD=∠B′AC=12∠1=22°∴∠B=180°-∠2-∠BAC=180°-44°-22°=114°;故选C.【点睛】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质,求出∠BAC的度数是解决问题的关键.16.C解析:C【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:0.0007=7×10﹣4故选C.【点睛】本题考查科学计数法,难度不大.17.B解析:B【解析】试题分析:根据题意,要分情况讨论:①、3是腰;②、3是底.必须符合三角形三边的关系,任意两边之和大于第三边.解:①若3是腰,则另一腰也是3,底是6,但是3+3=6,∴不构成三角形,舍去.②若3是底,则腰是6,6.3+6>6,符合条件.成立.∴C=3+6+6=15.故选B.考点:等腰三角形的性质.18.C解析:C【解析】试题分析:根据轴对称图形的概念:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.据此对图中的图形进行判断.解:图(1)有一条对称轴,是轴对称图形,符合题意;图(2)不是轴对称图形,因为找不到任何这样的一条直线,使它沿这条直线折叠后,直线两旁的部分能够重合,即不满足轴对称图形的定义.不符合题意;图(3)有二条对称轴,是轴对称图形,符合题意;图(3)有五条对称轴,是轴对称图形,符合题意;图(3)有一条对称轴,是轴对称图形,符合题意.故轴对称图形有4个.故选C.考点:轴对称图形.19.D解析:D【解析】【分析】根据分式的乘除运算步骤和运算法则逐一计算即可判断.【详解】∵22211x x x x x -÷--=2221·1x x x x x ---=() 2212·1xx xx x----=()()221·1x x xx x----=()2xx --=2xx-,∴出现错误是在乙和丁,故选D.【点睛】本题考查了分式的乘除法,熟练掌握分式乘除法的运算法则是解题的关键. 20.D解析:D【解析】【分析】连接OC、OA,利用圆周角定理得出∠AOC=60°,再利用垂径定理得出AB即可.【详解】连接OC、OA,∵∠ABC=30°,∴∠AOC=60°,∵AB为弦,点C为AB的中点,∴OC⊥AB,在Rt△OAE中,53∴AB=53,故选D.【点睛】此题考查圆周角定理,关键是利用圆周角定理得出∠AOC=60°.21.A解析:A【解析】试题分析:如图,过A点作AB∥a,∴∠1=∠2,∵a∥b,∴AB∥b,∴∠3=∠4=30°,而∠2+∠3=45°,∴∠2=15°,∴∠1=15°.故选A.考点:平行线的性质.22.D解析:D【解析】【分析】求出AB 的坐标,设直线AB 的解析式是y=kx+b ,把A 、B 的坐标代入求出直线AB 的解析式,根据三角形的三边关系定理得出在△ABP 中,|AP-BP|<AB ,延长AB 交x 轴于P′,当P 在P′点时,PA-PB=AB ,此时线段AP 与线段BP 之差达到最大,求出直线AB 于x 轴的交点坐标即可.【详解】∵把A (12,y 1),B (2,y 2)代入反比例函数y=1x 得:y 1=2,y 2=12, ∴A (12,2),B (2,12), ∵在△ABP 中,由三角形的三边关系定理得:|AP-BP|<AB ,∴延长AB 交x 轴于P′,当P 在P′点时,PA-PB=AB ,即此时线段AP 与线段BP 之差达到最大,设直线AB 的解析式是y=kx+b ,把A 、B 的坐标代入得:122122k b k b ⎧+⎪⎪⎨⎪+⎪⎩==, 解得:k=-1,b=52, ∴直线AB 的解析式是y=-x+52, 当y=0时,x=52,即P(52,0),故选D.【点睛】本题考查了三角形的三边关系定理和用待定系数法求一次函数的解析式的应用,解此题的关键是确定P点的位置,题目比较好,但有一定的难度.23.A解析:A【解析】分析:根据多边形的内角和公式计算即可.详解:.答:这个正多边形的边数是9.故选A.点睛:本题考查了多边形,熟练掌握多边形的内角和公式是解答本题的关键.24.A解析:A【解析】试题分析:A.﹣2<﹣1,故正确;B.0>﹣1,故本选项错误;C.1>﹣1,故本选项错误;D.2>﹣1,故本选项错误;故选A.考点:有理数大小比较.25.D解析:D【解析】【分析】根据1l与2l关于x轴对称,可知2l必经过(0,-4),1l必经过点(3,-2),然后根据待定系数法分别求出1l、2l的解析式后,再联立解方程组即可求得1l与2l的交点坐标.【详解】∵直线1l经过点(0,4),2l经过点(3,2),且1l与2l关于x轴对称,∴直线1l经过点(3,﹣2),2l经过点(0,﹣4),设直线1l的解析式y=kx+b,把(0,4)和(3,﹣2)代入直线1l的解析式y=kx+b,则4342 bk=⎧⎨+=-⎩,解得:24kb=-⎧⎨=⎩,故直线1l的解析式为:y=﹣2x+4,设l2的解析式为y=mx+n,把(0,﹣4)和(3,2)代入直线2l的解析式y=mx+n,则324m nn+=⎧⎨=-⎩,解得m2n4=⎧⎨=-⎩,∴直线2l的解析式为:y=2x﹣4,联立2424y xy x=-+⎧⎨=-⎩,解得:2xy=⎧⎨=⎩即1l与2l的交点坐标为(2,0).故选D.【点睛】本题考查了关于x轴对称的点的坐标特征、待定系数法求一次函数的解析式即两直线的交点坐标问题,熟练应用相关知识解题是关键.26.B解析:B【解析】【分析】的大小,即可得到结果.【详解】46 6.25<<,2 2.5∴<<,的点距离最近的整数点所表示的数是2,故选:B.【点睛】此题考查了实数与数轴,以及算术平方根,熟练掌握各自的性质是解本题的关键.27.B解析:B【解析】【分析】根据从上边看得到的图形是俯视图,可得答案.【详解】从上边看第一列是一个小正方形,第二列是一个小正方形,第三列是两个小正方形,故选:B.【点睛】本题考查了简单几何体的三视图,从上边看上边看得到的图形是俯视图.28.C解析:C【解析】【分析】根据特殊几何体的展开图逐一进行分析判断即可得答案.【详解】A、圆柱的侧面展开图是矩形,故A错误;B、三棱柱的侧面展开图是矩形,故B错误;C、圆锥的侧面展开图是扇形,故C正确;D、三棱锥的侧面展开图是三个三角形拼成的图形,故D错误,故选C.【点睛】本题考查了几何体的展开图,熟记特殊几何体的侧面展开图是解题关键.29.D解析:D【解析】如果两个图形不仅是相似图形,而且每组对应点的连线交于一点,对应边互相平行或在一条直线上,那么这两个图形叫做位似图形。
2015年重点、难点、易错题集训101、如图,Rt △ABC 在平面直角坐标系中,顶点A 在x 轴上,∠ACB=90°,CB ∥x 轴,双曲线xk y =(k ≠0)经过C 点及AB 的三等分点D (BD=2AD ),S △BCD =6,则k 的值为( )A.3B.6C.-3D.-62、如图,一次函数b x y +=的图象与x 轴交于点A ,与y 轴交于点B ,反比例函数x y 2=交于点C (2,m ),则点B 到OC 的距离是( ) A.2 B.5 C.25 D.5523、如图,矩形OABC 的顶点A 、C 分别在x 、y 轴的正半轴上,点D 为对角线OB 的中点,反比例函数xk y =(k ﹥0)在第一象限内的图象经过点D ,且与AB 、BC 分别交于E 、F 两点,四边形BEDF 的面积为4.5,则k 的值为( )A.3B.4C.5D.64、如图,在正方形ABCD 中,AB=4,将△ADC 绕点A 顺时针旋转α°(0<α<45),记旋转后的三角形为△AD ′C ′,过点B 作BE ⊥AC ′于点E ,延长BE 交射线AD ′于点F ,连接DF ,取AB 的中点H ,连接HE ,在旋转过程中,当HE ⊥BD 时,()2DF BE +的值为5、如图,矩形ABCD 中,AB=6,BC=8,将△ACD 沿对角线AC 翻折得△ACE.AE 交BC 于点F ,将△CEF 绕点C 逆时针旋转α角(0°<α<180°)得△CE ′F ′,点E 、F 的对应点分别为E ′、F ′,旋转过程中直线CF ′、E ′F ′分别交直线AE 于点M 、N ,当△F ′NM 是等腰三角形,且MN=MF ′时,则MN=6、如图,△ABC 中,点D 在AC 上,点E 在BC 上,且DE ∥AB ,将△CDE 绕点C 按顺时针方向旋转得到△CD ′E ′(使∠BCE ′<180°),连接AD ′、BE ′,设直线BE ′与AC 、AD ′分别交于点O 、F ,若△ABC 满足∠ACB=3,BC=2,且E 为BC 的中点,则△OBC 面积的最大值是 .7、从-1、0、1、3、4这五个数中任选一个数,记为a ,则使二次函数()1222-+--=a ax x a y 的顶点在第四象限,且双曲线xa y 27-=在第一、三象限的概率是8、从-2、-1、-32、0、1这五个数中,随机抽取一个数,记为a ,则使得关于x 的方程132=-+x ax 的解为非负数,且满足关于x 的不等式组⎩⎨⎧≤+--1230x a x φ有三个整数解的概率是 9、如图,每个小方格都是边长为1个单位长度的小正方形,将左图8×1的矩形随机沿方格竖线剪成三个小矩形(含正方形,三个面积相等的算作同一种剪法,如面积1、3、4和面积为4、3、1算同一种剪法,且长、宽均为正整数),补在右图上,恰好能将右图补成一个 4×4的正方形的概率是10、解方程:x x x +=⎪⎭⎫ ⎝⎛++814522111、已知:∠D=∠E ,AD=AE ,∠1=∠2.求证:BD=CE12、化简下列各式⑴ ()()()()y x y y x x y y x 222222--+-+- ⑵ 222⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-++-a b a ab b a b ab b 13、先化简,再求值⎪⎭⎫ ⎝⎛+--÷++-2122216822m m m m m m .其中m 是方程5221+=-m m 的解 14、先化简,再求值22211212a a a a a a a --+-÷⎪⎭⎫ ⎝⎛+-,其中a 是方程0272=--x x 的解15、商场经营某品牌服装,去年11月份的销量为100件,为了扩大销量,12月份商场对这种服装打九折销售,结果销量增加了50%,销售额增加了28000元.⑴ 求该服装去年11月份的销售单价和销售额各是多少?⑵ 若去年11月份销售这种服装获利20000元,今年1月份全月商场为迎新年进行促销,此服装在去年11月份的基础上一律打8折销售,若该服装成本不变,则销量至少为多少件,才能保证今年1月份的利润比去年11月份利润至少增加25%16、每年的3月15日是“国际消费者权益日”,许多商家都会利用这个契机进行打折促销活动.甲卖家的A商品成本为500元,在标价800元的基础上打9折销售.⑴现在甲卖家欲继续降价吸引买主,问最多降价多少元?才能使利润率不低于10%⑵据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售A商品,成本、标价与甲卖家一致,以前每周可售出50件,为扩大销量,尽快减少库存,他决定打折促销.但他先将标价提高3m%,再大幅降价26m元,使得A商品在3月15日那一12m%,这样一天的利润达天卖出的数量比原来一周卖出的数量增加了5到了20000元,求m的值17、为了尽快的适应中招体考项目,现某校初二⑴班班委会准备筹集1800元购买A、B两种类型跳绳供班集体使用.⑴班委会决定,购买A种跳绳的资金不少于B种跳绳资金的2倍,问最多用多少资金购买B种跳绳?⑵经初步统计,初二⑴班有25人自愿参与购买,那么平均每生需交72元.初三⑴班了解情况后,把体考后闲置的跳绳赠送了若干给初二⑴班,这样只需班级共筹集1350元.经初二⑴班班委会进一步宣传,自愿参与购买的学生在25人的基础上增加了2a%.则每生平均交费在72元基础上减少了1.25a%,求a的值18、如图所示,成渝高铁全长308km,计划于2015年10月1日通车营运,成渝两地迈入1小时经济圈.经测量,森林保护区中心M在成都的南偏东80°和重庆的南偏西53°的方向上.已知森林保护区的范围在以M 为圆心,40km 为半径的圆形区域内.⑴ 请问:成渝高铁会不会穿越保护区?为什么?⑵ 求重庆到森林保护区中心BM 的距离.(精确到0.1)(tan80°≈5.67,tan53°≈1.33,cos53°≈0.60,sin53°≈0.8)19、重庆市是着名的山城,许多美丽的建筑建在山上,如图,刘老师为了测量小山顶一建筑物DE 的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的A 处测得建筑物顶端D 的仰角为53°,山坡AE 的坡度i=1:5,潘老师在B 处测得建筑物顶端D 的仰角为45°,若此时刘老师与潘老师的距离AB=200米,求建筑物DE 的高度. (sin53°≈54,cos53°≈53,tan53°≈34,结果精确到0.1米)20、如图,一艘渔船位于小岛M 的北偏东45°方向,距离小岛180海里的A 处. 渔船从A 处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B 处.⑴ 求渔船从A 到B 的航行过程中与小岛M 之间的最小距离(结果用根号表示)⑵ 若渔船以20海里/小时的速度从B 沿BM 方向行驶,求渔船从B 到达小岛M 的航行时间(结果精确到0.1小时)(参考数据:2≈1.41,3≈1.73,6≈2.45) 21、阅读材料:如图,在平面直角坐标系中,O 是坐标原点,对于任意两点A (x?,y?),B (x?,y?),由勾股定理得:()()2222112y x y x AB -+-=,我们把()()221221y y x x -+-叫做A 、B 两点之间的距离,记作AB=()()221221y y x x -+-.例题:在平面直角坐标系中,O 为坐标原点,设点P (x ,0). ① A (0,2),B (3,-2),则AB= ;PA= ;解:由定义有AB=()()()5223022=--+-;PA=()()4203222+=-+-x x . ② ()412+-x 表示的几何意义是 ;()92122+-++x x 表示的几何意义是 ;解:因为()412+-x =()()22201-+-x ,所以()412+-x 表示的几何意义是点P (x ,0)到点(1,2)的距离;同理可得()92122+-++x x 表示的几何意义是点P (x ,0)到点(0,1)和点(2,3)的距离之和. 根据以上阅读材料,解决下列问题:⑴ 如图,已知直线82+-=x y 与反比例函数xy 6=(x ﹥0)的图象交于A (x?,y?),B (x?,y?)两点,则点A 、B 的坐标分别为A ( , ),B ( , ),AB=⑵ 在⑴的条件下,设点P (x ,0),则()()22222121y x x y x x +-++-表示的几何意义是 ;试求()()22222121y x x y x x +-++-的最小值,以及取得最小值时点P 的坐标.22、定义:任何一个一次函数q px y +=,取出它的一次项系数p 和常数项q ,有序数组[]q p ,为其特征数,例如:52+=x y 的特征数是[]5,2,同理[]c b a ,,为二次函数c bx ax y ++=2的特征数.⑴ 直接写出二次函数x x y 52-=的特征数是: ;⑵ 若特征数是[]1,2+m 的一次函数为正比例函数,求m 的值; ⑶ 以y 轴为对称轴的二次函数c bx ax y ++=2的图象经过点A (2,m ),B (n ,1)两点,(其中m ﹥0,n <0),连接OA 、OB 、AB ,得到OA ⊥OB ,S △AOB =10,求二次函数c bx ax y ++=2的特征数.23、先阅读下列材料,然后回答后面问题:将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法,能分组分解的多项式通常有四项或六项.一般的分组分解有四种形式,即“2+2”分法、“3+1”分法,“3+2”分法及“3+3”分法等.如“2+2”分法:by bx ay ax +++ 如“3+1”分法: =()()by bx ay ax +++ 2212x y xy +-+ =()()y x b y x a +++ =1222-++y xy x =()()b a y x ++ =()12-+y x=()()11-+++y x y x请你仿造以上方法,探究并解决下列问题:⑴ 分解因式:y x y x ---22 ⑵ 分解因式 2225202045ay axy ax am -+-⑶ 分解因式:1444422+---+ab b b a a a24、在△ABC 中,AC=BC ,D 是边AB 上一点,E 是线段CD 上一点,且 ∠AED=∠ACB=2∠BED.⑴ 如图1,若∠BED=45°,点E 是CD 的中点,AD=2,求线段BD 的长度;⑵ 如图1,若∠ACB=90°,求证:AE=2BE ;⑶ 如图2,若∠ACB=60°,猜想AE 与BE 的数量关系,并证明你的结论.25、如图1,在□ABCD 中,AE ⊥BC 于E ,AE=AD ,EG ⊥AB 于G ,延长GE 、DC 交于点F ,连接AF.⑴ 若BE=2EC ,AB=13,求AD 的长;⑵ 求证:EG=BG+FC ;⑶ 如图2,若AF=52,EF=2,点M 是线段AG 上的一个动点,连接ME ,将△GME 沿ME 翻折得△G ′ME ,连接DG ′,试求当DG ′取得最小值时GM 的长.26、两个全等的Rt △ABC 和Rt △EDA 如图放置,点B 、A 、D 在同一条直线上,其中∠ABC 的平分线BF ,过点D 作DF ⊥BF ,垂足为F ,连接CE. ⑴ 求证:BF ⊥CE ;⑵ 求证:BF=21CE27、如图,抛物线42-+=bx ax y 与x 轴交于A 、B 两点,与y 轴交于点C ,对称轴是直线x=25,直线421-=x y 经过B 、C 两点.⑴ 求抛物线的解析式;⑵ 若在对称轴右侧的抛物线上有一点P ,过点P 作PD ⊥直线BC ,垂足为D ,当∠PBD=∠ACO 时,求出点P 的坐标;⑶ 如图2,过点C 作CE ∥x 轴交抛物线于点E ,连接AE ,点F 是线段CE上的动点,过点F作FG⊥x轴,交AE于H,垂足为点G,将△EFH沿直线AE翻折,得到△EMH,连接GM.是否存在这样的点F,使△GHM是等腰三角形?若存在,求出对应的EF的长度;若不存在,请说明理由28、已知抛物线c-3与x轴交于点A(1,0)、B(3,0),=2+bxxy+与y轴相交于点C,抛物线的顶点为D.⑴求b、c的值及顶点D的坐标;⑵如图1,点E是线段BC上的一点,且BC=3BE,点F(0,m)是y 轴正半轴上一点,连接BF、EF,EF交线段OB于点G,OF:OG=2:3,求△FEB的面积;⑶如图2,P为线段BC上一动点,连接DP,将△DBP绕点D顺时针旋转60°得△DB′P′,(点B的对应点是B′,点P的对应点是P′),DP′交y 轴于点M,N为MP′的中点,连接PP′、NO,延长NO交BC于点Q,1,求线段BP的长. 连接QP′,若△PP′Q的面积是△BOC面积的929、如图①所示,抛物线cy+=2过A、D、C三点,其中D(0,+axbx2)、3C(6,32),已知CB⊥AB,AD⊥DB,点P是边BC上的动点(点P不与点B、C重合),过点P作直线PQ∥BD,交CD边于点Q,再把△PQC沿着直线PQ对折,点C的对应点为R.⑴求抛物线的解析式及R落在BD上时CP的长;⑵当点R刚好落在线段AB上时,如图②,若此时将△所得的点R在线段AB上移动,问在移动过程中是否存在某一时刻,使得△ADR为等腰三角形?若存在,求出AR的长度;若不存在,请说明理由;⑶当点R落在BD上时(如图③),点M为BC边上一动点,连接QM,将△CQM绕点Q顺时针旋转60°,得到△RQH.延长HR交直线CB于点3.求CM的长.K.若△HMK的面积等于2。