寻找三个纳什均衡

1.纳什均衡：给出对方的策略，你所选的是最优的（至少不比其它策略差），如果每个局中人都是这样，那么所构成的策略组合（对局），就称为纳什均衡。

2.效用：消费者偏好与收入之间的相互作用导致人们做出消费选择，效用则是人们从这种消费选择中所获得的愉悦或满足。

3.边际产量：当其他要素不变时，可变要素增加一个单位所带来的总产量的增加量。

4.生产成本：经营一个企业，为达到利润最大化，必须支付一些资金来维持运营，如建造厂房，采购机器及原料，雇用员工等支出都可视为厂家的生产成本。

5.帕累托标准：如果一种变化可以改善某些人的处境，同时对其他人都没有伤害。

则这种变化是好事，应该给予实行。

6.恩格尔系数：是食品支出总额占个人消费支出总额的比重。

一个家庭收入越少，家庭收入中或者家庭总支出中用来购买食物的支出所占的比例就越大，随着家庭收入的增加，家庭收入中或者家庭支出中用来购买食物的支出将会下降。

恩格尔系数是用来衡量家庭富足程度的重要指标。

7.效用：消费者偏好与收入之间的相互作用导致人们做出消费选择，效用则是人们从这种消费选择中所获得的愉悦或满足。

8.价格管制：是指政府对新药定价以及上市药品价格上涨实施严格的管制，企业不能自由定价，而是由政府和制药企业谈判决定新药的价格。

9.软着陆：当一个国家经过强劲的经济增长后，仍维持缓和的增长，并未因此转入衰退，即使“软着陆”。

10.硬着陆：一个国家的经济在高速增长的同时伴随着高度通货膨胀，使得经济迅速从增高长直接走入低增长甚至衰退。

11.通货膨胀：平均物价水平持续上扬的状态，通货膨胀率通常是以消费者物价指数（CPI）的变化率来表示。

指数上升→物价上升，货币购买力下降。

12.再贴现率：一般商业银行可以直接向中央银行借贷的利率。

所谓“贴现”：通过一定的方式把发生在未来（或不同时间）的费用和效益转化为现值的方式就叫贴现。

13.机会成本：在资源一定的情况下，多生产一个单位的某种产品，就要以少生产若干单位的另一种产品为代价。

不会令人后悔的均衡在纳什均衡中，你不一定满意其他的策略，但你的策略是回馈对手招数的最佳策略。

从囚徒困境中我们会发现，作为博弈各方的行动就是针对对方行动而确定的最佳对策，而一旦知道对方在做什么，就没人愿意改变自己的做法。

博弈论学把这么一个结果称为均衡。

这个概念是有普林斯顿大学数学家约翰·纳什提出的，因此被称为纳什均衡。

诺贝尔经济学奖获得者萨缪尔森有句名言，你可以将一只鹦鹉训练成经济学家，因为它所需要学习的只有两个词，供给与需求。

博弈论专家坎多瑞引申说：“要成为现代经济学家，这只鹦鹉必须再多学一个词，这个词就是纳什均衡”。

1950年，还是一名研究生的纳什写了一篇论文，题为《n人博弈的均衡问题》，该文只有短短一页纸，可就这短短一页纸成了博弈论的经典文献。

纳什的贡献是，他证明了在这一类的竞争中，在很广泛的条件下是有稳定解存在的，只要是别人的行为确定下来，竞争者就可以有最佳的策略。

那么，什么纳什均衡呢？简单说，就是一策略组合中，所有的参与者面临这样的一种情况：给定你的策略，我的策略是我最好的策略。

给定我的策略，你的策略也是你最好的策略，即双方在对方给定的策略下不愿意调整自己的策略。

纳什均衡从此成为经济学家用来分析商业竞争到贸易谈判现象的有力工具，所以纳什均衡是对冯诺依曼和摩根斯坦的合作博弈论的重大发展，甚至说是一场革命。

纳什均衡首先对亚当斯密“看不见的手”的原理提出挑战，按照斯密的理论，在市场经济中，每一个人都从利己的目的出发，而最终全社会达到利他的效果，从纳什均衡引出一个悖论：从利己的目的触发，结果损人不利己。

“囚徒困境”就是如此，从这个意义说，纳什均衡提出的悖论实际上动摇了西方经济学的基石。

纳什的想法成为我们指导“同时行动博弈”的最后一个法则的基础。

这个法则如下：走完寻找优势策略和剔除劣势策略的捷径之后，下一步就是寻找这个博弈的均衡。

所谓博弈均衡，它是一稳定的博弈结果。

均衡是博弈的一结果，但不是说博弈的结果都能成为均衡。

纳什均衡的数学定义哎呀呀，啥是纳什均衡呀？对于我这个小学生（初中生）来说，一开始听到这四个字，简直就像听到了外星语言一样，完全摸不着头脑！咱们先来说说啥叫均衡。

就好比玩跷跷板，两边重量差不多，谁也压不下去谁，这就叫均衡。

那纳什均衡又是啥呢？假设咱们班组织了一场拔河比赛，分成两队，每队都想赢。

如果我们队使足了劲儿，对方没使多大劲儿，那我们可能一下子就把对方拉过来了，这就不均衡。

可要是我们两队都使出了差不多的力气，谁也拉不过谁，这是不是就有点像均衡啦？这其实就有点像纳什均衡的意思。

再打个比方，就像两个商家在卖同样的东西。

如果一家拼命降价，另一家不降价，那降价的那家可能生意就特别好，这不均衡。

但要是两家价格都差不多，谁也没法通过降价或者涨价来获得更多的顾客，这是不是就均衡啦？想象一下，在一个小镇上有两家超市，一家叫小红超市，一家叫小蓝超市。

小红超市的老板想：“我要是把价格降得特别低，那大家不都来我这买东西啦？”可他又一想：“不行呀，如果我降价，小蓝超市也跟着降价，那最后大家都赚不到钱，这可咋办？”小蓝超市的老板也在琢磨呢：“我要是涨价，会不会大家都去小红超市买东西啦？”这时候，纳什均衡就出现啦！两家超市的价格都差不多，服务也差不多，谁也不敢轻易变动，因为一旦变动，可能自己的利益就受损啦。

这就好像两个人在走钢丝，谁要是乱动，就可能掉下去。

所以他们都小心翼翼地保持着平衡，不敢轻易打破这个状态。

你说这纳什均衡神奇不神奇？它好像无处不在，影响着我们的生活。

比如说交通，大家都遵守交通规则，不抢行，这不就是一种纳什均衡嘛。

反正我觉得吧，纳什均衡虽然听起来挺复杂，但仔细想想，在我们身边到处都能看到它的影子。

它让这个世界变得好像有规律可循，大家都在一种平衡的状态里寻找着自己的利益。

我觉得吧，了解纳什均衡能让我们更明白这个世界是怎么运转的，能让我们在做决定的时候多想想，可太有用啦！。

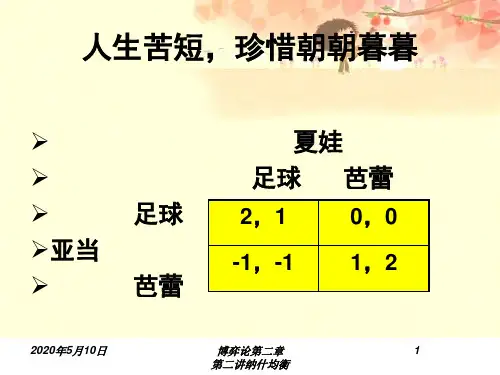
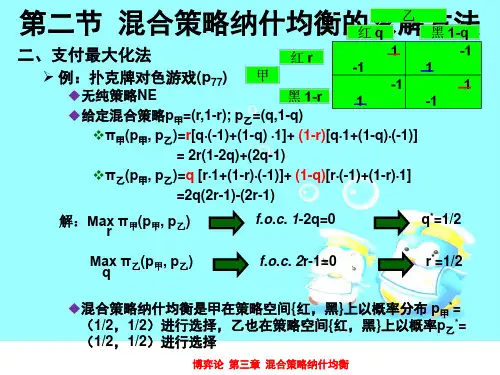
囚徒困境和纳什均衡当对手知道了你的决定之后，就能做出对自己最有利的决定------普林斯顿大学数学家约翰·纳什囚徒困境著名的“囚徒困境”，是纳什均衡理论的经典案例。

警方逮捕甲、乙两名嫌疑犯，但没有足够证据指控二人入罪。

于是警方分开囚禁嫌疑犯，分别和二人见面，并向双方提供一下相同的选择：若有一人认罪并作证检控对方（背叛对方）而对方保持沉默，此人将立即获释，沉默者将判监禁十年。

若两人都保持沉默(互相合作）则两人同时被判监禁半年。

若两人都互相检举（互相背叛）则两人同时监禁两年。

如同博弈论的其他论证，囚徒困境假设每个囚徒都是利己的，激斗寻求自己的最大利益。

囚徒到底应该选择哪一项策略，才能将自己的刑期缩至最短？两名囚徒由于相互隔离监禁，并不知道对方的选择。

试想困境中两名理性的囚徒会如何选择：若对方沉默，背叛会让我获释，所以对方会选择背叛。

若对方背叛我，我也要指控对方才能得到较低的刑期，所以也是这样会选择背叛。

二人面对的情况一样，所以二人的理想思考会得到相同的答案----选择背叛。

背叛是两种策略之间的支配性策略。

因此这场博弈中唯一可能达到的纳什均衡就是两人选择同时背叛对方，结果两人同时服刑两年。

这场博弈的纳什均衡，显然不是最优的解决方案。

如果两人都选择沉默，两人都只会被判刑半年。

但根据以上假设，两人均为理性的个人，均衡状况回事两个囚徒都选择背叛。

这就是“困境”所在。

寻找“纳什均衡点”在现实生活中，纳什均衡理论影响着人们的行为。

比如，在有些国家，报亭既无管理人员也不上锁，买报纸的人在自行放下前后拿走报纸。

当然某些人可能取走报纸却不付钱（背叛）但由于大家意识到如果每个人都偷窃报纸（共同背叛）会造成以后不方便的有害结果，这种情形很少发生。

在商业活动中，也会出现各种各样的囚徒困境的例子。

两个公司相互竞争，他们的广告互相影响，即一公司的广告较被顾客接受则会夺取对方的部分收入。

但若二者同时期发出质量类似的广告，收入增加很少但成本增加。

纳什均衡纯策略求解算法
纳什均衡是博弈论中非常重要的一个概念，在许多领域都有广泛的应用。

纳什均衡指的是博弈中每个参与者的策略都是最优的，即在其他参与者的策略下，自己的策略是最好的选择。

在博弈中，有时会出现多个纳什均衡，这时需要找到其中一个最好的纳什均衡，这个最好的纳什均衡被称为最优纳什均衡。

纳什均衡纯策略求解算法是一种求解博弈中纳什均衡的方法。

该算法主要分为以下几个步骤：
1.列出参与者的策略空间：首先需要列出每个参与者的所有可能策略，这些策略构成了参与者的策略空间。

2.列出每个参与者的收益函数：接下来需要列出每个参与者在每种策略下的收益函数，收益函数可以根据实际问题进行定义。

3.构建博弈矩阵：将每个参与者的策略空间组合起来，得到一个博弈矩阵，矩阵中每个元素表示每个参与者在对应策略组合下的收益。

4.寻找纳什均衡：通过对博弈矩阵进行分析，可以找到博弈中的纳什均衡。

其中，纳什均衡是指没有参与者可以通过单方面改变自己的策略来获得更好的收益的策略组合。

5.确定最优纳什均衡：在找到多个纳什均衡的情况下，需要通过一定的方法来确定最优纳什均衡。

纳什均衡纯策略求解算法是一种比较常用的博弈求解方法，在实际问题中也有广泛的应用。

- 1 -。

纳什均衡概念嘿，朋友！咱今天来聊聊纳什均衡这个有点神秘又超级有趣的概念。

你知道吗，纳什均衡就好像是一场拔河比赛。

两边的队伍都使足了劲儿，谁也没法一下子把对方拉过来，就这么僵持着，形成了一种稳定的状态。

这就跟纳什均衡很像，在某个局面里，参与的各方都选了对自己最优的策略，谁也不愿意单独改变，因为一旦改变可能就会吃亏。

比如说，在市场竞争中，两家公司都在考虑要不要降价来吸引更多的顾客。

如果一家降了，另一家不降，那降价的那家可能会抢走很多生意；可要是两家都降，虽然能吸引更多顾客，但利润可能都降低了。

最后，他们都选择了一个价格，谁也不再变动，这就是一种纳什均衡。

再想象一下，两个学生在考试前商量要不要一起作弊。

如果一个作弊一个不作弊，作弊的那个可能会拿到高分；但要是都作弊，被抓到的风险就大大增加；如果都不作弊，那就公平竞争。

最后他们达成了一个共识，都不作弊，这也是一种纳什均衡。

纳什均衡可不只是在商业和学校里出现哦。

在恋爱关系中也有它的影子。

比如情侣之间商量周末怎么度过，一方想去看电影，一方想去逛街。

要是都坚持自己的想法，可能会闹得不愉快；要是能找到一个双方都能接受的活动，比如先逛街再看电影，或者反过来，这就形成了一种平衡，也是纳什均衡。

还有啊，在国际政治中也能看到纳什均衡。

两个国家在贸易上互相设置关税，你加我也加，大家都不好过；你不加我也不加，大家都受益。

最后找到一个双方都能接受的关税水平，这就是纳什均衡在发挥作用。

你看，纳什均衡在我们的生活中无处不在，它影响着我们的决策和行为。

它让我们明白，在很多情况下，我们的选择不仅仅取决于自己，还受到其他人选择的影响。

所以啊，了解纳什均衡能让我们更聪明地做出决策，在各种复杂的局面中找到那个稳定的平衡点。

朋友，你是不是也觉得纳什均衡很有意思呢？是不是开始在自己的生活中寻找它的踪迹啦？。

数学博弈中的纳什均衡：寻找最优策略的迷宫探险在数学这座神秘的殿堂中，有一个充满智慧与策略的角落，那便是博弈论。

而在这个领域中，一个闪耀着耀眼光芒的明珠，便是纳什均衡。

它似乎拥有一种神奇的力量，能够指引我们在复杂的博弈中找到那条通往最优策略的道路。

那么，纳什均衡究竟隐藏在哪里呢？让我们踏上这场寻找最优策略的迷宫探险之旅吧！一、初识纳什均衡：一场心智的较量在博弈论的世界里，参与者们总是在不断地进行策略选择，试图在这场心智的较量中占据上风。

而纳什均衡，就是这样一种策略组合，使得每个参与者在其他参与者策略不变的情况下，都无法通过改变自身策略而获得更大的利益。

换句话说，纳什均衡就是一种稳定的策略状态，任何人都没有动机去打破它。

想象一下，在一个迷宫中，你和对手都在寻找出口。

你们可以选择合作，共同寻找出口；也可以选择竞争，试图抢先找到出口。

而纳什均衡，就是这样一个策略点，让你们在选择合作与竞争之间达到了一种平衡状态，既不会因过度竞争而两败俱伤，也不会因缺乏合作而错失良机。

二、寻找纳什均衡：探索最优策略的迷宫要找到纳什均衡，首先需要了解博弈的基本结构。

在一个博弈中，参与者、策略、收益是三个核心要素。

参与者是博弈的决策主体；策略是参与者在博弈中可以选择的行动方案；收益则是参与者在不同策略组合下获得的利益。

在了解了博弈的基本结构后，我们就可以开始探索最优策略的迷宫了。

这个过程需要运用数学工具和逻辑思维，对博弈进行深入分析。

我们需要考虑每个参与者的可能策略以及这些策略组合下的收益情况。

通过对比不同策略组合下的收益，我们可以逐步缩小搜索范围，最终找到那个让所有人都无法通过改变策略而获得更大收益的纳什均衡点。

当然，这个过程并不总是一帆风顺的。

有时候，我们可能会遇到多个纳什均衡点的情况，这时就需要根据具体情况进行判断和选择。

有时候，我们甚至可能会陷入一种看似无解的死循环中，这时就需要运用一些高级的数学方法或者调整博弈规则来打破僵局。

微观经济学纳什均衡微观经济学纳什均衡是一种重要的博弈论方法，以解决多个参与者在竞争中达成最优策略的问题。

纳什均衡在经济学、政治学和社会学等领域广泛应用，为决策者提供了优化交互的理论基础。

在这篇文章中，我们将探讨纳什均衡的基本概念、应用范围和实际案例。

什么是纳什均衡？纳什均衡是指一个博弈中所有参与者做出最优策略的状态。

博弈表示多个参与者面临不同的选项，根据其他参与者的行为做出决策，并在最终结果中获得利益或损失。

纳什均衡是在假设所有参与者都知道其他人的战略和最终结果的情况下得出的，通过寻找参与者最大化利益的策略来确定最终状态。

纳什均衡的概念描述了一个节点，称为均衡点。

在均衡点上，每个参与者的策略形成了一种稳定的状态，使得任何人采取不同策略都会使其利益有所减少。

纳什均衡不一定是最优策略或最优结果，但对于所有参与者来说，选择这个策略就是最合理的。

纳什均衡的应用范围纳什均衡可以用于解决一系列经济和社会问题，例如市场竞争、资本博弈、国际贸易和环境政策等。

在市场竞争中，企业、供应商和消费者都会对价格和数量做出决策，纳什均衡可以帮助我们预测市场价格和数量的稳定状态。

在资本博弈中，银行、交易商和投资者参与多重游戏，纳什均衡可以测量资本流动方向与趋势。

在国际贸易中，不同国家参与进出口贸易会影响市场价值和公平分配，纳什均衡可以帮助我们确定进出口关税和贸易协议的最优方案。

在环境政策中，制定人员需要考虑经济效益和环境保护之间的平衡，纳什均衡可以帮助我们制定环保监管和税收政策。

实际应用案例在经济学中，纳什均衡在实际应用中具有重要的作用。

以下是几个应用案例：1. OPEC石油产量协调。

在20世纪70年代，石油输出国组织（OPEC）协调其成员国的石油产量，以提高全球价格。

使用纳什均衡模型，我们可以预测OPEC成员国的产量分配和全球石油价格的愈合点。

2. 拍卖策略的分析。

在拍卖过程中，竞拍者必须根据所有其他竞拍者的行为做出决策。

纯策略纳什均衡和混合策略纳什均衡简单来说，纯策略纳什均衡指的是，参与人选择的策略是确定的。

比如，在性别之战中，我们通过每个参与人的最优反应确定了该博弈的两种纯策略，即（拳击，拳击）和（芭蕾，芭蕾）。

在纯策略纳什均衡的情况下，我们只能知道具体的纳什均衡下每个参与人的收益，并无法求得参与人进行该博弈的整个的期望收益。

（暂且称为期望收益吧），因为在参与人做选择时，并不知道对方会做出什么样的选择。

假设我们自己为参与人1，我们就会开始想，现在我也不知道对方（参与人2）会做什么样的选择，我先假设他选择芭蕾的概率为p 吧，那么他选择拳击的概率就是1-p，那么这个时候，我们自己在两种策略下的收益为，我们就会选择芭蕾，如果我们就会选择拳击。

我们可以画出参与人1的最优反应曲线E1是双方都百分百选择拳击，E2是双方都百分百选择芭蕾，也就是我们之前求出的纯策略纳什均衡，而E3就是我们要算的混合策略纳什均衡。

在该点U1=4/3由于博弈是对称的，U2=4/3由于参与人1在（拳击，拳击）时的收益1比选择（芭蕾，芭蕾）时的E3的收益4/3低，所以参与人1是肯定不会百分百选择E1作为均衡点的，同理，参与人2也不会百分百选择E2作为均衡点。

既然参与人都可以自主选择自己的概率，那么只有在混合策略纳什均衡点E3这一个均衡。

即参与人1分别以2/3和1/3的概率选择芭蕾和拳击，参与人2以1/3和2/3的概率选择芭蕾和拳击。

所以在这个博弈里，只有一个混合策略纳什均衡，也就是E3点所代表的均衡。

只要偏离这个点的概率，那么博弈的结果就会变为E1或者E2，这时总会有一个参与人不愿选择这样的结果，博弈无法达到均衡。

所以最终寻找这个严格混合策略纳什均衡点的过程可以陈述为，给定其他参与人的混合策略，目标参与人在可行行动中的任意随机选择都是无差异的。

即令2p=1-p，q=2（1-q），这就是寻找混合策略纳什均衡的解题方式。

也可以通过同时假设两个参与人的概率，写出每个参与人在假设概率下的效用，通过让双方同时效用最大化求解。

纳什均衡的划线法口诀
纳什均衡是博弈论中的重要概念，指的是在一个博弈中，每个参与者都选择了最佳策略，无法通过改变自己的策略来获得更大的收益。

在寻找纳什均衡时，可以使用划线法来辅助求解。

划线法是一种用于解决二人零和博弈的方法，其中的零和表示两个参与者的利益完全相反，即一个人的获得是另一个人的损失。

划线法通过画线标记来找到纳什均衡。

以下是一个简单的划线法口诀，有助于我们更好地理解和应用纳什均衡的概念：
1. 画出博弈矩阵：首先，绘制一个表格，将参与者的可选策略列在
左侧，将对应的收益写在矩阵中的相应位置。

2. 找出最大值：对于每个参与者，在其选择的策略下找到获得最高
收益的结果，并在该结果上方或左侧画一条线。

3. 找出最小值：对于每个参与者，找到获得最低收益的结果，在该
结果所在的行或列上画一条线。

4. 交叉点：在博弈矩阵中找到所有线的交叉点。

5. 确定纳什均衡：如果交叉点处只有一条线，则该点为纳什均衡点，表示两个参与者选择了最佳策略。

如果有多个交叉点，则所有交叉点都是潜在的纳什均衡点。

划线法的口诀可以帮助我们在求解纳什均衡时，更加系统和有条理地进行分析。

通过确定纳什均衡，参与者可以在博弈中做出最优决策，最大化自己的利益。

然而，需要注意的是，划线法是一种简化的方法，可能无法涵盖复杂博弈中的所有情况，因此在实际应用中需要结合其他方法进行综合分析。