大作业题解

国家开放大学《中国近现代史纲要》形考任务：大作业（论述题一）国家开放大学《中国近现代史纲要》形考任务：大作业（论述题一）学号：姓名：论述题：历史是最好的教科书。

在对历史的深入思考中，激荡着走向未来的智慧和力量。

党的百年历史，蕴含着丰富的政治营养和精神瑰宝。

请同学们分析为什么说“没有共产党，就没有新中国”？中国革命取得胜利的基本经验是什么？（30 分）一、为什么说“没有共产党，就没有新中国”？答：今年是中华人民共和国成立 72 周年,中国共产党成立 100 周年。

中华人民共和国的成立，是中国共产党领导、团结中国人民，同帝国主义、封建主义、官僚资本主义三大敌人进行 28 年浴血奋战取得的伟大胜利！没有共产党就没有新中国。

通过《中国近代史纲要》和《中国共产党党史》的学习，中国近代史、中国共产党历史证明：没有共产党，就没有新中国中国是世界上几大文明古国之一，有着五千多年文明史，一直延续下来。

但到了近代欧洲经过文艺复兴、工业革命后进入资本主义社会，而中国仍停在封建社会轨道上，仍停留在农耕社会，在制度上、科学文化技术、生产力发展水平等各个方面都落后于资本主义社会。

落后必然挨打。

1840 年鸦片战争失败，中国沦为半殖民地半封建社会。

到 1921 年，中国人民同帝国主义、封建主义进行了长达 80 年的反抗斗争，但都失败了，根本原因是没有共产党领导。

1917 年俄国十月革命胜利，在人类历史上，工农第一次掌握了政权。

俄国十月革命一声炮响，把马克思列宁主义送到了中国。

1919 年中国爆发了“五四”爱国主义运动，工人阶级走上历史舞台。

五四运动是中国旧民主主义革命和新民主主义革命的分水岭。

新旧民主主义革命的根本区别，就在于领导权不同。

旧民主主义革命是民族资产阶级领导，新民主主义革命是是共产党领导的，无产阶级领导的。

马克思列宁主义与工人运动相结合，产生了中国共产党。

1921 年中国共产党的成立，是中国开天辟地的大事。

自从有了中国共产党领导，中国革命就焕然一新了。

1313 波动班号 学号 姓名 成绩一、选择题（在下列各题中，均给出了4个~5个答案，其中有的只有1个是正确答案，有的则有几个是正确答案，请把正确答案的英文字母序号填在题后的括号内）1. 在下列关于机械波的表述中，不正确的是：A. 机械波实际上就是在波的传播方向上，介质中各质元的集体受迫振动；B. 在波的传播方向上，相位差为2π 的两质元之间的距离称为波长；C. 振动状态在介质中传播时，波线上各质元均可视为新的子波波源；D. 波的振幅、频率、相位与波源相同；E. 波线上离波源越远的质元，相位越落后。

（D ） [知识点] 机械波的概念。

[分析与题解]平面简谐波在弹性介质中传播，介质中各质元都做受迫振动，各质元均可视为新的子波波源，因此，各质元的振幅、频率与波源是相同的，但各质元的相位是沿传播方向逐点落后的。

2. 平面简谐波波函数的一般表达式为])(cos[ϕω+=uxt A y ，则下列说法中不正确的是：A ．ux ω表示波线上任一质元落后于原点处质元的相位，或者说是波线上相距为x 的两质元的相位差；B ．ux表示波从x = 0 传到 x 处所需时间； C ．)(u x -中的负号表示相位落后；)(ux +中的正号表示相位超前；图13-1(a)图13-1(b)D ．ty∂∂是任一时刻波线上任一质元的振动速度v ，它并不等于波速u ； E ．ty∂∂表示波速u ，它与介质的性质有关。

（E ） [知识点] 波动方程中各物理量的意义。

[分析与题解]t y ∂∂表示波动某一质元的振动速度v ，它并不等于波速u 。

一般来说ty ∂∂是时间的函数并且与质元位置x 有关，而波速u 只与介质的性质有关。

3．在下列关于波的能量的表述中，正确的是： A ．波的能量2p k 21kA E E E =+=； B ．机械波在介质中传播时，任一质元的E k 和E P 均随时间t 变化，但相位相差2π； C ．由于E k 和E P 同时为零，又同时达到最大值，表明能量守恒定律在波动中不成立； D ．E k 和E P 同相位，表明波的传播是能量传播的过程。

数值计算大作业题目一、非线性方程求根1.题目假设人口随时间和当时人口数目成比例连续增长，在此假设下人口在短期内的增长建立数学模型。

（1）如果令()N t 表示在t 时刻的人口数目，β表示固定的人口出生率，则人口数目满足微分方程()()dN t N t dt β=，此方程的解为0()=tN t N e β； （2）如果允许移民移入且速率为恒定的v ，则微分方程变成()()dN t N t vdt β=+， 此方程的解为0()=+(1)t t vN t N e e βββ-；假设某地区初始有1000000人，在第一年有435000人移入，又假设在第一年年底该地区人口数量1564000人，试通过下面的方程确定人口出生率β，精确到410-；且通过这个数值来预测第二年年末的人口数，假设移民速度v 保持不变。

4350001564000=1000000(1)e e βββ+-2.数学原理采用牛顿迭代法，牛顿迭代法的数学原理是，对于方程0)(=x f ，如果)(x f 是线性函数，则它的求根是很容易的，牛顿迭代法实质上是一种线性化方法，其基本思想是将非线性方程0)(=x f 逐步归结为某种线性方程来求解。

设已知方程0)(=x f 有近似根k x (假定0)(≠'x f )，将函数)(x f 在点k x进行泰勒展开，有.))(()()(⋅⋅⋅+-'+≈k k k x x x f x f x f于是方程0)(=x f 可近似地表示为))(()(=-'+k k x x x f x f这是个线性方程，记其根为1k x +，则1k x +的计算公式为)()(1k k k k x f x f x x '-==+，,,2,1,0⋅⋅⋅=k这就是牛顿迭代法，简称牛顿法。

3.程序设计作出函数的图像，大概估计出根的位置fplot('1000*exp(x)+(435*x)*(exp(x)-1)-1564',[0 3]);grid大概估计出初始值x=0.5function [p1,err,k,y]=newton(f,df,p0,delta,max1) % f 是非线性系数 % df 是f 的微商 % p0是初始值% dalta 是给定允许误差 % max1是迭代的最大次数 % p1是牛顿法求得的方程近似解 % err 是p0误差估计 % k 是迭代次数 p0,feval('f',p0) for k=1:max1p1=p0-feval('f',p0)/feval('df',p0); err=abs(p1-p0); p0=p1;p1,err,k,y=feval('f',p1) if(err<delta)|(y==0), break,endp1,err,k,y=feval('f',p1) endfunction y=f(x)y=1000000*exp(x)+435000*(exp(x)-1)/x-1564000; function y=df(x)y=1000000*exp(x)+435000*(exp(x)/x-(exp(x)-1)/x^2);4.结果分析与讨论newton('f','df',1.2,10^(-4),10) 运行后得出结果 p0 =0.5000p1 =0.1679 err =0.3321 k =1 y =9.2415e+004 p1 =0.1031 err =0.0648 k =2 y =2.7701e+003 p1 =0.1010 err =0.0021 k =3 y =2.6953p1 =0.1010 err =2.0129e-006 k =4 y = 2.5576e-006 ans =0.1010运算后的结果为1010.0=β，通过这个数值来预测第二年年末的人口数，0.10100.1010435000f(t)=1000000(1)0.1010t te e +-t=2时候对于f ()2187945.865x =实践表明，当初始值难以确定时，迭代法就不一定收敛了，因此要根据问题实际背景或者二分法先得一个较好的初始值，然后再进行迭代；再者迭代函数选择不合适的话，采用不动点迭代法也有可能出现不收敛的情况；因此我采用的是牛顿法。

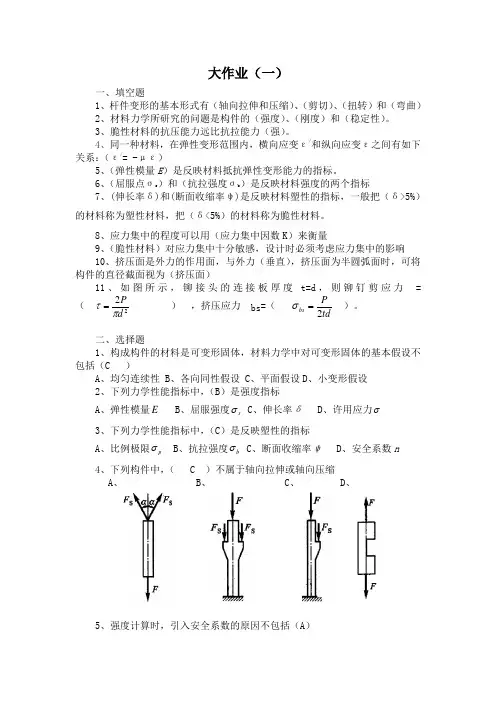
大作业（一）一、填空题1、杆件变形的基本形式有（轴向拉伸和压缩）、（剪切）、（扭转）和（弯曲）2、材料力学所研究的问题是构件的（强度）、（刚度）和（稳定性）。

3、脆性材料的抗压能力远比抗拉能力（强）。

4、同一种材料，在弹性变形范围内，横向应变ε/和纵向应变ε之间有如下关系：（ε/= -με）5、（弹性模量E ）是反映材料抵抗弹性变形能力的指标。

6、（屈服点σs ）和（抗拉强度σb ）是反映材料强度的两个指标7、(伸长率δ)和(断面收缩率ψ)是反映材料塑性的指标，一般把（δ>5%）的材料称为塑性材料，把（δ<5%）的材料称为脆性材料。

8、应力集中的程度可以用（应力集中因数K ）来衡量 9、（脆性材料）对应力集中十分敏感，设计时必须考虑应力集中的影响 10、挤压面是外力的作用面，与外力（垂直），挤压面为半圆弧面时，可将构件的直径截面视为（挤压面）11、如图所示，铆接头的连接板厚度t=d ，则铆钉剪应力=（ 22dP πτ= ） ，挤压应力bs =（ td Pbs 2=σ ）。

二、选择题1、构成构件的材料是可变形固体，材料力学中对可变形固体的基本假设不包括（C ）A 、均匀连续性B 、各向同性假设C 、平面假设D 、小变形假设 2、下列力学性能指标中，（B ）是强度指标A 、弹性模量EB 、屈服强度s σC 、伸长率δD 、许用应力σ 3、下列力学性能指标中，（C ）是反映塑性的指标A 、比例极限p σB 、抗拉强度b σC 、断面收缩率ψD 、安全系数n 4、下列构件中，（ C ）不属于轴向拉伸或轴向压缩 A 、 B 、 C 、 D 、5、强度计算时，引入安全系数的原因不包括（A ）A 、力学性能指标测定方法都不是太科学B 、对构件的结构、尺寸和受力等情况都作了一定程度的简化C 、加工工艺对构件强度的影响考虑的不全面D 、构件需有必要的强度储备6、一直杆受外力作用如图所示，此杆各段的轴力图为（C ）A 、B 、C 、D 、7、一直杆受外力作用如图所示，此杆各段的轴力为（A ）A 、+6（拉力），- 4（压力），4（拉力）B 、-6（压力），- 4（压力），4（拉力）C 、+6（拉力），+ 4（拉力），4（拉力）D 、-6（压力），+ 4（拉力），4（拉力）8、图所示为两端固定的杆。

第三题（思路）
多相流计算只考虑重力和摩擦损失，故井筒压力损失由重力损失和摩擦损失组成。

有题目1可知摩擦损失，进而可得摩擦梯度f
dp dL ⎛⎫ ⎪⎝⎭。

f
dp dL ⎛⎫ ⎪⎝⎭=1804.2612/1500=1.2028408 (1) f
dp dL ⎛⎫ ⎪⎝⎭=8196.8454/1500=5.4645636 (2) f
dp dL ⎛⎫ ⎪⎝⎭=11278.535/1500=7.519023333 (3)
f
dp dL ⎛⎫ ⎪⎝⎭=15074.400/1500=10.0496 (4)
以井口为求解节点，关系式为：
P 2=P 1+P 12f +P 12g
式中，P 12f 为摩擦损失，P 12g 为重力损失。

P 2=P wf ；
P 12f =f
dp h dL ⎛⎫⨯ ⎪⎝⎭； 12[(1)]g m o w w w P gh f f gh ρρρ==-+*0.7+ρg gh*0.3
1 2
把结果画到图2中得到曲线A
（曲线A 不一定是直线），与曲线B 的交点所对应的产量即为该井对应的最大产量。

若产量可观，则认为投产初期油藏能量充足，为充分利用地层能量，选择自喷生产，若产量不可观，选择气举生产。

1MPa P 1（MPa ）。

【大题】工科物理大作业04-刚体定轴转动 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN0404 刚体定轴转动班号 学号 姓名 成绩一、选择题（在下列各题中，均给出了4个~5个答案，其中有的只有1个是正确答案，有的则有几个是正确答案，请把正确答案的英文字母序号填在题后的括号内）1．某刚体绕定轴作匀变速转动，对刚体上距转轴为r 处的任一质元来说，在下列关于其法向加速度n a 和切向加速度τa 的表述中，正确的是：A ．n a 、τa 的大小均随时间变化；B ．n a 、τa 的大小均保持不变；C ．n a 的大小变化，τa 的大小保持恒定；D ．n a 的大小保持恒定，τa 大小变化。

（C ）[知识点］刚体匀变速定轴转动特征，角量与线量的关系。

[分析与题解] 刚体中任一质元的法向、切向加速度分别为 r a n 2ω=，r a τβ=当β = 恒量时，t βωω+=0 ，显然r t r a n 202)(βωω+==，其大小随时间而变，ra τβ=的大小恒定不变。

2. 两个均质圆盘A 和B ，密度分别为ρA 和ρB ，且B ρρ>A ，但两圆盘的质量和厚度相同。

若两盘对通过盘心且与盘面垂直的轴的转动惯量分别为A I 和B I ，则 A ．B I I >A； B. B I I <A ；C ．B I I =A ； D. 不能确定A I 和B I 的相对大小。

（B ）[知识点］转动惯量的计算。

[分析与题解] 设A 、B 两盘厚度为d ，半径分别为R A 和R B ，由题意，二者质量相等，即B B A A d R d R ρπρπ22=因为B A ρρ>， 所以22B A R R < 且转动惯量221mR I =，则B A I I <3．在下列关于刚体的表述中，不正确的是：A ．刚体作定轴转动时，其上各点的角速度相同，线速度不同；B ．刚体定轴转动的转动定律为βI M =，式中β,,I M 均对同一条固定轴而言的，否则该式不成立；C ．对给定的刚体而言，它的质量和形状是一定的，则其转动惯量也是唯一确定的；D ．刚体的转动动能等于刚体上各质元的动能之和。

大学英语（B）（本，2019春）A. Very well.B. By taking a course.C. In the libraryD. In the morning反馈【解析】根据问句中的疑问词How可知答语应该是某种方式，所以选B。

句意："---马克是怎样学西班牙的？----通过选课学习的。

”题目2正确获得3分中的3分2. --You know, I have three kids now.--___________________选择一项：A. That's terrific!B. Well, I've grown a mustache.C. Say, you've really changed your mind.D. Well, I gave up drinking.反馈【解析】此题可用排除法进行解题。

上文说"你知道吗，我现在有3个孩子”，这属于好事情，所以答语用That's terrific.（太好了）表示积极回应。

题目3正确获得3分中的3分3. --John, 回答B?--Oh, that's my father! And beside him, my mother.A. which is thatB. who's talking over thereC. what are they doingD. what is the person over there反馈【解析】根据下文回答"那是我爸爸”来判断，上文在问"某人是谁（Who's...?）”。

句意："----约翰，谁在那里说话？----哦，那是我爸爸，他旁边是我妈妈。

”题目4正确获得3分中的3分4. --How do you do? Glad to meet you.反馈【解析】此题考查如何回应问候。

针对问候语"How do you do”，只要回答"How do you do”就可以。

《数据库管理与应用》练习1答案二、填空题1．经过处理和加工提炼而用于决策或其他应用活动的数据称为_______。

2．数据管理技术经历了____________①、___________②和___________③三个阶段。

3．数据库系统一般是由______________①、______________②、______________③、______________④、______________⑤组成。

4．数据库是长期存储在计算机内、有____________①的、可___________②的数据集合。

5．DBMS是指_____________①，它是位于__________②和___________③之间的一层管理软件。

6．DBMS管理的是_____的数据。

7．由______________负责全面管理和控制数据库系统。

8．数据库系统与文件系统的本质区别在于______________________。

9．数据独立性又可分为______________①和______________②。

10．当数据的物理存储改变了，应用程序不变，而由DBMS处理这种改变，这是指数据的______________。

11．数据模型是由______________①、______________②和______________③三部分组成的。

12．按照数据结构的类型来命名，数据模型分为_____________①、______________②和_____________③。

13．______________①是对数据系统的静态特性的描述，______________②是对数据库系统的动态特性的描述。

14．以子模式为框架的数据库是______________①；以模式为框架的数据库是______________②；以物理模式为框架的数据库是______________③。

15．关系数据库是采用_____作为数据的组织方式。