2021届高三化学一轮大复习知识扫描——晶胞结构的分析与计算

晶体结构知识汇总及解题方法技巧一、晶胞中质点得占有率在一个晶胞结构中出现得多个原子,并不就是只为这一个晶胞所独立,而就是为多个晶胞共用,所以每一个晶胞只能按比例分摊。

分摊得根本原则:晶胞任意位置上得原子如果就是被n 个晶胞所共有,则每个晶胞只能分得这个原子得n 1。

立方晶胞,顶点上得粒子占 棱上得粒子占 面上得粒子占 体心得粒子占二、常见晶胞分析1. NaCl 型⑴每个晶胞占有 个Na+, 个Cl-,即 个NaCl 粒子⑵每个Na ＋周围有 个Cl －,每个Cl －周围有 个Na ＋,与一个Na ＋距离最近且相等得Cl－围成得空间构型为 。

每个Na ＋周围与其最近且距离相等得Na ＋有 个。

⑶0、585g NaCl 晶体(0、01mol)含有 个晶胞。

⑷若已知Na+与Cl-得最短距离为a cm,则NaCl 晶体得密度为 。

2. CsCl 型⑴在CsCl 晶体中,每个Cs+周围与之最接近得且距离相等得Cs+有 个,每个Cs+周围与之最接近得且距离相等得Cl-有 个。

⑵每个晶胞占有 个CsCl 粒子。

3. 干冰型在干冰晶体中,每个CO2分子周围与之最接近得且距离相等得CO2分子有 个。

每个晶胞中含有 个CO2分子。

4. 金刚石型金刚石得网状结构中,,每个碳原子与其她4个碳原子等距离紧邻,含有由共价键形成得碳原子环,其中最小得环上有6个碳原子,每个碳原子上得任意两个C—C键得夹角都就是109°28′,其中C原子个数:C—C个数= 。

5.石英晶体在二氧化硅晶体中,一个硅原子与4个氧原子形成4个共价键,1个氧原子与2个硅原子形成2个共价键,故Si原子与O原子数目之比为。

实际上,该晶体就是由硅原子与氧原子按1:2得比例组成得立体网状晶体,没有单个分子存在。

在晶体中最小得环为十二元环,每个环占有6个Si原子与6个O原子。

6.石墨晶体结构石墨晶体就是一种混合型晶体,层内存在共价键,层间以范德华力结合,兼具有原子晶体、分子晶体得特征与特性。

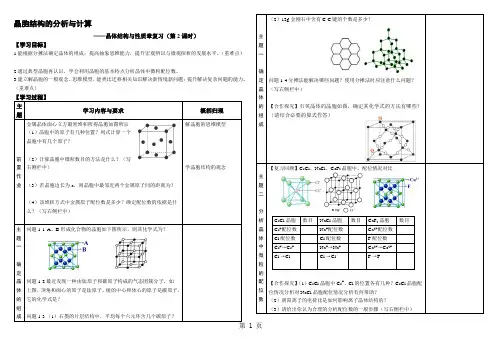
晶胞结构的分析与计算——晶体结构与性质章复习（第2课时）【学习目标】1.能根据分摊法确定晶体的组成；提高抽象思维能力，提升宏观辨识与微观探析的发展水平。

（重难点）2.通过典型晶胞再认识，学会利用晶胞的基本特点分析晶体中微粒配位数。

3.建立解晶胞的一般观念、思维模型，能类比迁移相关知识解决新情境新问题；提升解决复杂问题的能力。

（重难点），则晶胞中最邻近两个金属原子间的距离为？最近发现一种由钛原子和碳原子构成的气态团簇分子，如顶角和面心的原子是钛原子，棱的中心和体心的原子是碳原子，它的化学式是？分摊法能解决哪些问题？使用分摊法时应注意什么问题？石英晶体的晶胞如图，确定其化学式的方法有哪些？晶胞中，配位情况对比CsCl晶胞数目NaCl晶胞数目CaF2晶胞数目+Ca2+配位数1.有下列某晶体的空间结构示意图。

图中●和化学式中M分别代表阳离子，图中○和化学式中N分别代表阴离子，则化学式为MN2的晶体结构为（）A B C D2.下列说法正确的是（）（N A表示阿伏加德罗常数）A.1mol冰中含有氢键的个数为2 N AB.12g石墨中含有C-C键的个数为3N AC.二氧化硅晶体中存在四面体网状结构，O处于中心，Si处于4个顶点D.密置层在三维空间堆积可得体心立方堆积和面心立方最密堆积3.氮化碳结构如下图所示，其硬度超过金刚石，下列有关氮化碳的说法不正确的是（）A.氮化碳属于原子晶体B.氮化碳中碳显－4价，氮显＋3价C.氮化碳的化学式为C3N4D.每个碳原子与四个氮原子相连，每个氮原子与三个碳原子相连4.ZnS在荧光体、光导体材料、涂料、颜料等行业中应用广泛。

立方ZnS晶体结构如下图所示，其晶胞边长为540.0 pm．密度为（列式并计算），a位置S2－离子与b位置Zn2+离子之间的距离为pm（列示表示）5.晶胞有两个基本要素：①原子坐标参数，表示晶胞内部各原子的相对位置，下图为Ge单晶的晶胞，其中原子坐标参数A为（0，0，0）；B为（1/2，0，1/2）；C为（1/2，1/2，0）。

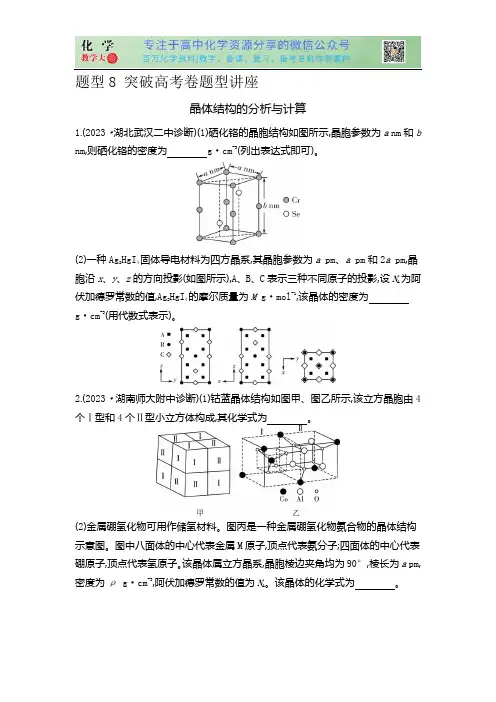
题型8 突破高考卷题型讲座晶体结构的分析与计算1.(2023·湖北武汉二中诊断)(1)硒化铬的晶胞结构如图所示,晶胞参数为a nm和b nm,则硒化铬的密度为g·cm-3(列出表达式即可)。

(2)一种Ag2HgI4固体导电材料为四方晶系,其晶胞参数为a pm、a pm和2a pm,晶胞沿x、y、z的方向投影(如图所示),A、B、C表示三种不同原子的投影,设N A为阿伏加德罗常数的值,Ag2HgI4的摩尔质量为M g·mol-1,该晶体的密度为g·cm-3(用代数式表示)。

2.(2023·湖南师大附中诊断)(1)钴蓝晶体结构如图甲、图乙所示,该立方晶胞由4个Ⅰ型和4个Ⅱ型小立方体构成,其化学式为。

(2)金属硼氢化物可用作储氢材料。

图丙是一种金属硼氢化物氨合物的晶体结构示意图。

图中八面体的中心代表金属M原子,顶点代表氨分子;四面体的中心代表硼原子,顶点代表氢原子。

该晶体属立方晶系,晶胞棱边夹角均为90°,棱长为a pm,密度为ρ g·cm-3,阿伏加德罗常数的值为N A。

该晶体的化学式为。

3.[2021·全国乙卷·35(4)]在金属材料中添加AlCr2颗粒,可以增强材料的耐腐蚀性、硬度和机械性能。

AlCr2具有体心四方结构,如图所示。

处于顶角位置的是原子。

设Cr和Al原子半径分别为r Cr和r Al,则金属原子空间占有率为%(列出计算表达式)。

4.(2021·湖北卷·10)某立方晶系的锑钾(Sb-K)合金可作为钾离子电池的电极材料,图a为该合金的晶胞结构图,图b表示晶胞的一部分。

下列说法正确的是( )。

A.该晶胞的体积为a3×10-36 cm3B.K和Sb原子数之比为3∶1C.与Sb最邻近的K原子数为4a pmD.K和Sb之间的最短距离为125.(2021·重庆卷·18节选)研究发现纳米CeO2可催化O2-分解。

高三化学知识点晶胞晶胞是固体中最基本的结构单元，通过晶胞的叠加形成了整个晶体的结构。

在高三化学中，晶胞是一个重要的知识点，其中包括晶体结构的分类、晶胞的构成和晶体的性质等内容。

本文将详细介绍高三化学知识点晶胞。

一、晶体结构的分类晶体结构根据晶体中原子、分子、离子等的空间排列方式，可以分为晶格和非晶态两类。

晶格是指具有规则排列的晶体，而非晶态则是指没有规则排列的晶体。

晶体结构的进一步分类包括简单晶体结构、复式晶体结构、过渡金属复合晶体结构等。

其中简单晶体结构指的是晶体中只有一个类型的晶胞，如简单立方晶体结构、面心立方晶体结构等。

复式晶体结构是指晶体中存在多种类型的晶胞，如锌铁矿晶体结构等。

过渡金属复合晶体结构则是指晶体中的晶胞由不同类型的过渡金属离子共同构成。

二、晶胞的构成晶胞是晶体中最基本的结构单位，它由晶体中的原子、离子、分子等构成。

具体来说，晶胞由一个或多个原子、离子、分子等围成，且晶胞的排列方式决定了晶体的结构。

晶胞的构成取决于晶体中的组成元素和它们的空间排列方式。

例如，在简单立方晶体结构中，晶胞由一个原子组成，而在面心立方晶体结构中，晶胞由四个原子构成。

这些原子的排列方式决定了晶格的类型和晶胞的形状。

三、晶体的性质晶体的性质受晶体结构的影响，晶体结构的不同导致晶体具有不同的物理、化学性质。

首先，晶体具有各向异性，即晶体在不同方向上的性质不同。

这是因为晶体中的晶胞具有规则的排列方式，导致晶体在不同方向上具有不同的结构和性质。

其次，晶体的硬度、导电性等性质与晶体结构有关。

例如，金刚石是一种具有非常高硬度的晶体，这是因为金刚石的晶格结构非常坚固。

另外，金属晶体由于电子的自由运动而具有良好的导电性。

最后，晶体的光学性质也与晶体结构密切相关。

根据晶体对光的透射性，可以将晶体分为各种光学类别，如各向同性晶体和各向异性晶体等。

总结：高三化学知识点晶胞是固体结构的基本单位，通过晶胞的叠加形成了整个晶体的结构。

高三化学一轮复习《晶体结构与性质》第1课时[考纲要求] 能根据晶胞确定晶体的组成并进行相关的计算考点一、 晶体与晶胞(1)概念 :描述晶体结构的__________。

(2)晶体中晶胞的排列——无隙并置常见题型1．确定晶体组成或晶胞中原子个数的计算的方法——均摊法均摊法：指每个晶胞平均拥有的粒子数目。

如：某个粒子为n 个晶胞所共有，则该粒子有1/n 属于一个晶胞。

(1)长方体形(正方体)晶胞中不同位置的粒子对晶胞的贡献注意：①处于顶点的粒子，同时为____个晶胞共有，每个粒子对晶胞的贡献为____。

②处于棱上的粒子，同时为____个晶胞共有，每个粒子对晶胞的贡献为____。

③处于面上的粒子，同时为____个晶胞共有，每个粒子对晶胞的贡献为____。

④处于体心的粒子，则完全属于该晶胞，对晶胞的贡献为____。

(2)在使用均摊法计算晶胞中微粒个数时，要注意晶胞的形状，不同形状的晶胞，应先分析任意位置上的一个粒子被几个晶胞所共有，非长方体形(正方体)晶胞中粒子对晶胞的贡献视具体情况而定。

如六棱柱晶胞中，顶点、侧棱、底面上的棱、面心依次被6、3、4、2个晶胞所共有。

如石墨晶胞每一层内6个碳原子排成六边形，其顶点的1个碳原子对六边形的贡献为1/3。

在计算晶胞中粒子个数的过程中，不是任何晶胞都可用均摊法。

练习1．科学家把C 60和K 掺杂在一起制造出的化合物具有超导性能，其晶胞如图所示。

该化合物中的K 原子和C 60分子的个数比为________。

练习2 Cu 元素与H 元素可形成一种红色化合物，其晶体结构单元如右图所示。

则该化合物的化学式为________。

练习3某晶体的一部分如图所示，这种晶体中A 、B 、C 三种粒子数之比是( )A ．3∶9∶4B ．1∶4∶2C ．2∶9∶4D ．3∶8∶4常见题型2．晶胞结构(强化记忆)练习4判断下列物质的晶胞结构，将对应序号填在线上。

(1)干冰晶体；(2)氯化钠晶体(3)金刚石；(4)碘晶体；(5)氟化钙；(6)钠；(7)冰晶体；(8)水合铜离子；(9)H3BO3晶体；(10)铜晶体。

课时65 晶体结构的分析与计算题型一 晶体结构的分析与方法【考必备·清单】 1．晶胞结构的分析(1)判断某种微粒周围等距且紧邻的微粒数目时，要注意运用三维想象法。

如NaCl 晶体中，Na ＋周围的Na ＋数目(Na ＋用“○”表示)：每个面上有4个，共计12个。

(2)记住常见晶体如干冰、冰、金刚石、SiO 2、石墨、CsCl 、NaCl 、K 、Cu 等的空间结构及结构特点。

当题中信息给出的某种晶胞空间结构与常见晶胞的空间结构相同时，可以直接套用该种结构。

2．晶胞中微粒数目的计算方法——均摊法(1)原则：晶胞中任意位置上的一个原子如果是被n 个晶胞所共有，那么，每个晶胞对这个原子分得的份额就是1n。

(2)方法长方体(包括立方体)晶胞中不同位置的粒子数的计算方法如图所示：3．“均摊法”在晶胞组成计算中的应用 (1)计算一个晶胞中粒子的数目非平行六面体形晶胞中粒子数目的计算同样可用“均摊法”，其关键仍是确定一个粒子为几个晶胞所共有。

例如，石墨晶胞：每一层内碳原子排成六边形，其顶点(1个碳原子)对六边形的贡献为13，那么一个六边形实际有6×13＝2个碳原子。

又如，六棱柱晶胞(MgB 2晶胞)中，顶点上的原子为6个晶胞(同层3个，上层或下层3个)共有，面上的原子为2个晶胞共有，因此镁原子个数为12×16＋2×12＝3个，硼原子个数为6。

(2)计算原子晶体中共价键的数目在金刚石晶体(如图所示)中，每个C 参与了4个C—C 键的形成，而在每条键中的贡献只有一半，因此，平均每一个碳原子形成共价键的数目为4×12＝2个，则1 mol 金刚石中碳碳键的数目为2N A 。

(3)计算化学式【探题源·规律】角度一：晶胞中微粒数目及晶体化学式的计算[例1] (1)(2019·全国卷Ⅱ)一种四方结构的超导化合物的晶胞如图1所示。

晶胞中Sm 和As 原子的投影位置如图2所示。

聚焦突破(三) 关于晶胞结构的分析与计算(2021·新高考山东卷)非金属氟化物在生产、生活和科研中应用广泛。

XeF 2晶体属四方晶系，晶胞参数如图所示，晶胞棱边夹角均为90°，该晶胞中有________个XeF 2分子。

以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置，称为原子的分数坐标，如A 点原子的分数坐标为(12 ，12 ，12 )。

已知Xe —F 键长为r pm ，则B 点原子的分数坐标为________；晶胞中A 、B 间距离d ＝______________pm 。

[解析] 图中大球的个数为8×18 ＋1＝2，小球的个数为8×14 ＋2＝4，根据XeF 2的原子个数比知大球是Xe 原子，小球是F 原子，该晶胞中有2个XeF 2分子；由A 点坐标知该原子位于晶胞的体心，且每个坐标系的单位长度都记为1，B 点在棱的r c 处，其坐标为(0，0，r c )；如图中y 是底面对角线的一半，则y ＝22 a pm ，x ＝⎝ ⎛⎭⎪⎫c 2－r pm ，所以d ＝ x 2＋y 2 ＝ 12a 2＋（c 2－r ）2 pm 。

[答案] 2 (0，0，r c ) 12a 2＋（c 2－r ）2 (2021·新高考河北卷)KH 2PO 4晶体具有优异的非线性光学性能。

我国科学工作者制备的超大KH 2PO 4晶体已应用于大功率固体激光器，填补了国家战略空白。

分别用○ 、● 表示H 2PO －4 和K ＋，KH 2PO 4晶体的四方晶胞如图(a)所示，图(b)、图(c)分别显示的是H 2PO －4 、K ＋在晶胞xz 面、yz 面上的位置：(1)若晶胞底边的边长均为a pm 、高为c pm ，阿伏加德罗常数的值为N A ，晶体的密度为__________g·cm －3(写出表达式)。

(2)晶胞在x 轴方向的投影图为________(填标号)。