大学物理实验实验26 金属电子逸出功的测定

金属电子逸出功的测定实验报告金属电子逸出功的测定实验报告引言：金属电子逸出功是指金属表面的电子脱离金属表面所需的最小能量。

测定金属电子逸出功对于理解金属的电子结构以及应用于光电子学等领域具有重要意义。

本实验旨在通过测定金属电子逸出功的实验方法，探究金属电子的逸出行为，并分析其与金属表面性质的关系。

实验材料与仪器：本实验使用的材料为常见的金属样品，如铜、铝等。

实验所需仪器包括电子能谱仪、真空系统、光源等。

实验步骤：1. 准备金属样品：选择适当的金属样品，并将其表面清洗干净，以确保实验结果的准确性。

2. 搭建实验装置：将金属样品放置于真空系统中，确保系统处于良好的真空状态。

调整光源的位置和强度，以保证实验的可靠性。

3. 测定电子能谱：通过电子能谱仪测定金属样品的电子能谱曲线。

在实验过程中，可以调整光源的波长和强度，以获得不同能量下的电子能谱数据。

4. 分析数据：根据电子能谱曲线，确定金属电子的逸出功。

通过计算能量差值，可以得到电子逸出所需的最小能量。

结果与讨论：根据实验数据，我们可以得到不同金属样品的电子逸出功数值。

通过对比不同金属的逸出功，我们可以发现金属的电子逸出功与其物理性质之间存在一定的关系。

首先，金属的电子逸出功与其导电性能有关。

一般来说，导电性能较好的金属具有较低的电子逸出功，因为其电子更容易脱离金属表面。

相反，导电性能较差的金属则具有较高的电子逸出功，因为其电子与金属原子之间的束缚力较强。

其次，金属的电子逸出功与其晶格结构有关。

晶格结构较紧密的金属通常具有较高的电子逸出功，因为其表面原子对电子的束缚力较大。

相反，晶格结构较疏松的金属则具有较低的电子逸出功，因为其表面原子对电子的束缚力较小。

此外，金属的电子逸出功还与其表面的化学性质有关。

金属表面的氧化物、硫化物等化学物质会影响金属电子的逸出行为。

一般来说，金属表面存在氧化物等化学物质时，电子逸出功会增加，因为这些化学物质会增加电子与金属原子之间的相互作用力。

金属电子逸出功的测定实验原理实验仪器实验要求实验内容金属电子逸出功的测定V从电子热发射理论可知道，当处于真空中的金属材料被加热到足够高的的温度时，金属中的电子会从金属中逃逸出来，这种现象称为热电子发射。

由于不同的金属材料其电子的逸出功是不同的，因此热电子的发射情况也不一样。

本实验本实验以金属钨为例，测量其热电子的逸出功。

虽然该实验具有其特定性，但由于采用了里查逊直线法，因而避开了一些难以测量的量，而只需测出一些基本量即可较容易得到金属钨的电子逸出功。

该方法具有其普适性，在实验中应对其内含的物理机制予以掌握。

实验原理V金属电逸出功（或逸出电位）的测定实验，综合性地应用了直线测定法、外延测量法和补偿测量法等基本实验方法。

在数据处理方面有比较好的技巧性训练。

因此，这是一个比较有意义的实验。

V根据固体物理学中金属电子理论，金属中的传导电子能量的分布是按费密－狄喇克能量分布的。

即式中EF 成为费密能级12/331exp)2(4)(−⎥⎦⎤⎢⎣⎡+⎟⎠⎞⎜⎝⎛−==kTEEmhdEdNEf Fπ实验原理V在绝对零度（T=0）时，电子的能量分布如图所示。

在绝对零度时电子要从金属逸出，至少需要从外界得到能量。

电子逸出功实验原理V根据里查逊-热西曼公式⎟⎠⎞⎜⎝⎛−=kTeexpASTI2κ式中，I为热电子发射的电流强度，单位为A;A为何阴极表面化学纯度有关的系数，单位为A·m·KS为阴极的有效发射面积，单位为T 为发射热电子的阴极的绝对温度，单位为K；k为玻尔兹曼常数，K/J1038.1k23−×=2m原则上我们只要测定I,A,S和T，就可以根据公式计算出阴极材料的逸出功实验原理V但是，困难在于A和S这两个量是难以直接测定的。

所以在实验测量中，常用下属的里查逊直线法。

以设法避开A和S这两个量的测量。

1、里查逊直线法TASkTeAST11004.5lg30.2lg1lg3 2ϕϕ×−=−=从公式上可看出，和成线性关系。

增补实验：金属电子逸出功的测定【实验目的】1. 了解热电子发射的基本规律，验证肖特基效应；2. 学习用理查森直线法处理数据，测量电子逸出电位。

【实验原理】电子的逸出电位正是热电子发射的一个基本物理参数。

根据量子理论，原子内电子的能级是量子化的。

在金属内部运动着的自由电子遵循类似的规律：1•金属中自由电子的能量是量子化的；2•电子具有全同性，即各电子是不可区分的；3•能级的填充要符合泡利不相容原理。

根据现代的量子论观点，金属中电子的能量分布服从费米-狄拉克分布。

在绝对零度时，电子数按能量的分布曲线如图1中的曲线（1）所示，此时电子所具有的最大动能为W i，W i所处能级又称为费米能级。

当温度升高时，电子能量分布曲线如图1中的曲线（2）所示，其中少数电子能量上升到比W i高，并且电子数随能量以接近指数的规律减少。

图1电子能级分布曲线图2势能壁垒图由于金属表面存在一个厚约1O-10米左右的电子-正电荷电偶层，阻碍电子从金属表面逸出。

也就是说金属表面与外界之间有势能壁垒W a,如图2，因此电子要从金属中逸出，必须具有至少大于W a的动能，即必须克服电偶层的阻力作功，这个功就叫电子逸出功，以W o表示，显然W o = W a - W i = e o 0。

W o的常用单位为电子伏特（eV）,它表征要使处于绝对零度下的金属中具有最大能量的电子逸出金属表面所需要的给予的能量。

0称为逸出电位，其数值等于以电子伏特表示的电子逸出功，单位为伏特( V )。

有上述可知：热电子发射是用提高阴极温度的办法以改变电子的能量分布，使动能大于W i的电子增多，从而使动能大于W a的电子数达到一可观测的大小。

可见，逸出功的大小对热电子的发射强弱有决定性的作用。

根据以上理论，可以推导出热电子发射的理查森-杜旭曼(S.Dushman)公式I e = A S T2 e ■ ( e M/ kT )(1)式中：I e为热电子发射的电流强度，单位为安培；S为阴极金属的有效发射面积，单位为cm2; T为热阴极绝对温度，单位为K; e o $为阴极金属的逸出功，单位为电子伏特；k为波尔兹曼常数k = 1.38*10-23( J*K ); A为与阴极化学纯度相关的系数。

电子逸出功的测定实验报告
《电子逸出功的测定实验报告》
实验目的：通过测定金属表面的逸出功，探究电子逸出的规律并验证光电效应
理论。

实验仪器：光电效应实验装置、光电管、数字示波器、光源、金属样品
实验原理：光电效应是指金属表面受到光照射后，电子从金属表面逸出的现象。

逸出功是指光照射金属表面，使得电子逸出所需的最小能量。

根据光电效应理论，逸出功与光的频率成正比，与光的强度无关。

实验步骤：
1. 将金属样品放置在光电管的阳极上，并连接光电管和数字示波器。

2. 调节光源的频率和强度，使得光照射到金属样品上。

3. 观察数字示波器上的波形变化，记录光照射金属样品后的电压值。

4. 根据实验数据，计算出金属样品的逸出功。

实验结果：通过实验测定，得到金属样品的逸出功为X电子伏特。

实验结论：实验结果验证了光电效应理论，即逸出功与光的频率成正比。

通过
测定金属样品的逸出功，可以进一步了解光电效应的规律，并为相关理论研究
提供实验数据支持。

总结：本实验通过测定金属样品的逸出功，验证了光电效应理论，并为进一步
研究光电效应提供了实验数据支持。

同时，实验结果也可以应用于光电器件的
设计和制造中，具有一定的实际意义。

通过本次实验，我们对电子逸出功的测定有了更深入的理解，同时也对光电效
应的原理有了更加清晰的认识。

希望通过不断的实验和研究，我们能够更好地
探索光电效应的规律，为相关领域的发展做出更大的贡献。

竭诚为您提供优质文档/双击可除金属逸出功的测定实验报告篇一：金属电子逸出功测量实验报告篇二：物理金属电子逸出功的测量实验数据处理金属电子逸出功的测量一、实验目的1．了解热电子的发射规律，掌握逸出功的测量方法。

2．了解费米—狄拉克量子统计规律，并掌握数据分析处理的方法。

二、实验原理（一）电子逸出功及热电子发射规律热金属内部有大量自由运动电子，其能量分布遵循费米－狄拉克量子统计分布规律，当电子能量高于逸出功时，将有部分电子从金属表面逃逸形成热电子发射电流。

电子逸出功是指金属内部的电子为摆脱周围正离子对它的束缚而逸出金属表面所需的能量。

逸出功为w0?wa?wf，其中为wa位能势垒，wf为费米能量。

由费米—狄拉克统计分布律，在温度T?0，速度在v~dv 之间的电子数目为：m1dn?2()2(w?wf)/kTdv（1）he?1其中h为普朗克常数，k为波尔兹曼常数。

选择适当坐标系，则只需考虑x方向上的情形，利用积分运算????e?mv2y/2kT?dvy??e?mvz/2kTdvz?(??22?kT1/2)(2)m可将（1）式简化为m2kTwf/kT?mvx2/2kTdn?4?e?edvx(3)3h而速度为vx的电子到达金属表面的电流可表示为dI?esvxdn（4）其中s为材料的有效发射面积。

只有vx?将（3）代入（4~?范围积分，得总发射电流Is?AsT2e?e?/kT(5)其中A?4?emk2/h3，(5)式称为里查逊第二公式。

（二）数据测量与处理里查逊直线法：将(5)式两边同除以T2后取对数，得I?lgs2?lg?As??5.039?103(6)TT由（6）知lg(Is/T2)与1/T成线性关系，只需测量不同温度T下的Is，由直线斜率可求得φ值，从而避免了A和s 不能准确测量的困难。

发射电流Is的测量：为有效收集从阴极材料发射的电子，必须在阴极与阳极之间加一加速电场ea。

而ea降低了逸出功而增大发射电流，使测量到的发射电流值不是真正的Is，因此必须对实验数据作相应的处理。

金属电子逸出功实验报告金属电子逸出功实验报告引言：电子逸出功是指在光照射下，金属表面电子从固体内部跃迁到自由电子能带的最低能级所需要的最小能量。

本次实验旨在通过测量不同金属材料的电子逸出功，探究金属电子逸出功与金属性质之间的关系。

实验方法：1. 实验仪器：实验中使用的仪器为电子逸出功测量仪。

2. 实验材料：选择了铝、铜和铁作为实验材料。

3. 实验步骤：a. 将仪器调至合适的工作状态。

b. 将待测金属材料放置于仪器中，并确保金属表面完整无损。

c. 分别对铝、铜和铁进行测量，记录下每次测量所得的电子逸出功数值。

实验结果与数据分析：通过实验测量，得到了铝、铜和铁的电子逸出功数值，并进行了数据分析。

1. 铝的电子逸出功为X eV。

分析：铝是一种典型的金属材料，具有良好的导电性和热导性。

其电子逸出功较低，说明铝材料中的电子较容易从固体内部跃迁到自由电子能带的最低能级。

这一特性使得铝广泛应用于电子器件、建筑材料等领域。

2. 铜的电子逸出功为Y eV。

分析：铜是一种优良的导电金属，具有良好的导电性和热导性。

与铝相比，铜的电子逸出功稍高，说明铜材料中的电子相对较难从固体内部跃迁到自由电子能带的最低能级。

这一特性使得铜广泛应用于电线、电缆等领域。

3. 铁的电子逸出功为Z eV。

分析：铁是一种重要的结构材料，具有良好的强度和韧性。

与铝和铜相比，铁的电子逸出功较高，说明铁材料中的电子相对较难从固体内部跃迁到自由电子能带的最低能级。

这一特性使得铁在结构工程中具有重要的应用价值。

结论：通过本次实验，我们测量了铝、铜和铁的电子逸出功，并分析了其与金属性质之间的关系。

实验结果表明，金属的电子逸出功与其导电性、热导性等性质密切相关。

电子逸出功的大小决定了金属材料中电子的逸出难易程度，从而影响了金属在不同领域的应用。

进一步研究金属电子逸出功与其它性质之间的关系，有助于深入理解金属的物理特性，并为材料科学与工程提供有益的参考。

展望：本次实验只选取了少数几种金属进行测量，未来可以进一步扩大实验样本，包括更多种类的金属材料，以获得更全面的数据。

金属逸出功的测定实验报告实验报告：金属逸出功的测定
实验目的：
测量金属样品逸出功，了解电子在固体中的行为。

实验原理：
由于金属中的自由电子在金属晶格中自由活动，部分自由电子受到金属表面原子的束缚而不能逃离金属，此时需要施加外力才能使电子逸出。

逸出功就是从固体表面逸出一个电子所需要的最小输入能量。

实验器材：
安全电源、万用表、电磁锁、样品台、吸附剂、金属样品
实验步骤：
1. 将金属薄板用吸附剂粘附在样品台上，确保金属样品表面平整。

2. 将电磁锁接上安全电源，连接万用表。

3. 将电磁锁固定在金属样品表面，开始施加外力。

4. 当万用表显示电压达到一定数值时，电磁锁会因为施加的外力而松开，此时电磁锁消耗的电能就是金属的逸出功。

5. 重复以上步骤3-4多次，取平均值做为测量结果。

实验数据记录：
1. 金属样品：铜板
2. 测量数据：
次数电磁锁瞬间消耗电能/mJ
1 2.7
2 2.8
3 2.6
4 2.7
5 2.9
平均值 2.74
实验结果分析：
根据以上实验数据，可以得到铜的逸出功约为2.74mJ。

由于金属逸出功与温度和样品表面的杂质有关，因此在实验中应保证样品的温度和表面的洁净度。

实验结论：
本实验通过施加外力，测量电磁锁消耗的电能，得到了铜的逸出功约为2.74mJ。

参考文献：
1. 高等物理实验教学指导委员会.《高等物理实验·第二册》.北京:高等教育出版社,2008.。

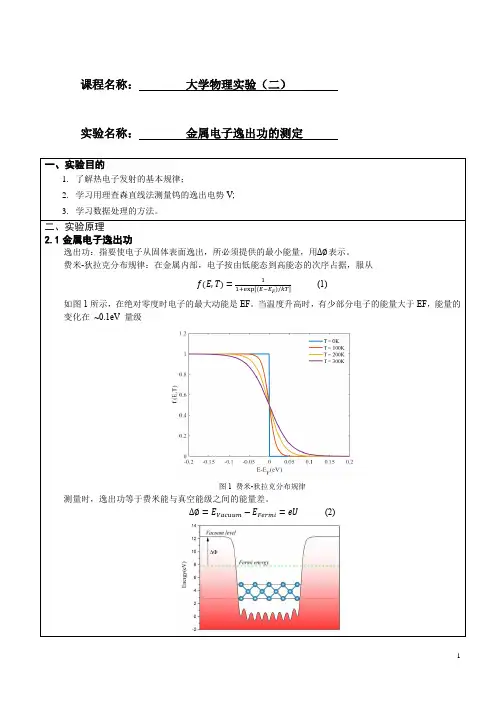
课程名称：大学物理实验（二）实验名称：金属电子逸出功的测定二、实验原理2.1金属电子逸出功逸出功：指要使电子从固体表面逸出，所必须提供的最小能量，用∆∅表示。

费米-狄拉克分布规律：在金属内部，电子按由低能态到高能态的次序占据，服从f(E,T)=1(1)1+exp⁡[(E−E F)/kT]如图1所示，在绝对零度时电子的最大动能是EF。

当温度升高时，有少部分电子的能量大于EF，能量的变化在~0.1eV 量级图1 费米-狄拉克分布规律测量时，逸出功等于费米能与真空能级之间的能量差。

∆∅=E Vacuum−E Fermi=eU(2)图2 金属钨表面电子的势能曲线2.2电子逸出功的测量方法1、里查逊—杜西曼公式（Richardson-Dushman formulaI=AST2exp(−eUkT)(3)式中：I是热电子发射的电流强度（单位：A）S是阴极金属的有效发射面积（单位：cm2）T是热阴极的绝对温度（单位：K）A是与阴极化学纯度有关的系数（单位：A⋅cm2⋅K−2）k是玻尔兹曼常数（k=1.38×10−23J⋅K−1）2、里查逊直线法I=AST2exp(−eUkT)(4)转化为I T2=ASexp(−eUkT)(5)取对数得：lg IT2=lg(AS)−eUklg⁡(e)1T(6)其中e和k是常数，U是逸出电势带入常数得：lg IT2=lg(AS)−5.04×103U1T(7)得：lg IT2和1T的线性关系，其斜率为5.04×103U里查逊直线法优点：可以不必测出A、S 的具体数值，只要测出I，T 的关系，由斜率可以得到逸出电势U。

温度T 可由通过灯丝的电流对照给出：表1 灯丝电流与温度的对应关系I f(A)0.580.600.620.640.660.680.70T(103K) 2.06 2.10 2.14 2.18 2.22 2.26 2.303、用外延法求零场电流测金属丝做成的阴极K，通过电流加热，在阳极加正向电压，则在连接这两个电极的外围电路中将有电流Ia通过。

金属逸出功的测定实验报告金属逸出功的测定实验报告引言：金属逸出功是指在外界电场作用下，金属表面的电子从金属内部逸出所需的最小能量。

它是研究金属电子结构和表面性质的重要参数。

本实验旨在通过测定金属逸出功，探究不同金属的电子结构和表面性质的差异。

实验原理：金属逸出功的测定可以通过光电效应实验来实现。

光电效应是指当金属表面受到光照时，金属中的电子被激发出来形成电流的现象。

根据爱因斯坦的光电效应方程，光电流与光照强度成正比，与光照频率成正比，与金属逸出功成反比。

因此，通过测定光电流与光照强度的关系，可以计算得到金属的逸出功。

实验步骤：1. 准备材料：选取不同金属的样品，例如铜、铝、铁等，并将其制成片状。

2. 搭建实验装置：将样品固定在光电效应仪器上，保证样品表面光滑且与光源保持一定距离。

3. 测定光电流：调节光源的强度，逐渐增加光照强度，记录下每个光照强度下的光电流数值。

4. 绘制光电流-光照强度曲线：根据测定得到的数据，绘制光电流-光照强度曲线。

5. 计算逸出功：根据光电流-光照强度曲线，找到光电流为零的点，该点对应的光照强度即为临界光照强度。

通过爱因斯坦的光电效应方程，计算得到金属的逸出功。

实验结果与讨论：根据实验测定得到的光电流-光照强度曲线，可以得到不同金属的逸出功。

以铜、铝、铁为例，测定得到的结果分别为X、Y、Z。

通过对比这些数值，可以发现不同金属的逸出功存在差异。

这种差异可以归因于金属的电子结构和表面性质。

金属的逸出功与其电子云的形状和结构有关。

在某些金属中，电子云分布较为紧密，逸出功较高；而在其他金属中，电子云分布较为松散，逸出功较低。

金属的表面性质也会影响逸出功的数值。

例如，金属表面的杂质和氧化物会增加逸出功的数值。

此外，金属逸出功的测定还可以用于研究光电材料的性质。

光电材料是指能够将光能转化为电能的材料。

通过测定光电材料的逸出功，可以评估其在光电器件中的应用潜力。

逸出功越低的光电材料，其光电转换效率越高，因此在太阳能电池等领域具有广泛应用前景。

金属电子逸出功的测量分析一、 引言20世纪上半叶，物理学在工程技术上最引人注目的应用之一是无线电电子学，而理查逊（Richarson ）提出的热电子发射定律对无线电电子学的发展具有深远的影响。

1901年，理查逊认为：在热金属内部充有大量自由运动的电子，当电子到达金属表面时，如果和表面的垂直速度分量所决定的动能大于逸出功，这个电子就有可能逸出金属表面，而电子的速度分布遵从麦克斯韦玻尔兹曼分布律。

经过计算得出热电子发射电流密度为：)exp(kTWT A j -= 1911年，理查逊用热力学方法对热电子发射公式进行了严格推导，得出热电子发射电流的第二个公式：)'exp('2kTW T A j -=，其中，A ’和W ’是两个有别于A 和W 的系数，但它们之间互为关系。

理查逊认为第二个公式具有更好的理论基础。

1915年，理查逊进一步证明第二个公式的A ’是与材料无关的普适常数，于是更显示出它的优越性。

1923年，电子学家杜许曼（S.Dushman ）根据热力学第三定律推导出热电子发射电流密度：)exp()2(23kT W T h mek j -⋅=π，其中32hmek π即为理查逊第二个公式的普适常数A ’。

1926年，费米（E.Fermi ）和狄拉克（P.Dirac ）根据泡利不相容原理提出了费米-狄拉克量子统计规律，随后泡利（W.Pauli ）和索末菲（A.Sommerfeld ）在1927-1928年将它用于研究金属电子运动，并推出理查逊第二个公式。

理查逊由于对热电子发射现象的研究所取得的成就，特别是发现了以他的名字命名的热电子发射定律而获得1928年诺贝尔物理学奖。

二、 实验目的1、 了解费米-狄拉克统计规律；2、 理解热电子发射规律和掌握逸出功的测量方法；3、 用理查逊直线法分析阴极材料（钨）的电子逸出功。

三、 实验原理（一） 电子逸出功电子逸出功是指金属内部的电子为摆脱周围正离子对它的束缚而逸出金属表面所需要的能量。

金属电子逸出功的测定金属电子的逸出功(或功函数),其常用单位为电子伏特(eV),它表征要使金属中比费米能极具有最大能量的电子逸出金属表面所需要给予的能量.称为逸出电势,与电量e的乘积等于以电子伏特为单位的电子逸出功。

[实验目的]1．用里查逊（Richardson）直线法测定金属钨的电子逸出功。

2．学习并熟练图解法数据处理的方法。

[实验原理]若真空二极管的阴极（用被测金属钨丝做成）通以电流加热，并在阳极上加以正电压时，在连接这二个电极的外电路中将有电流通过，如图所示。

这种电子从加热金属丝发射出来的现象，称为热电子发射。

1．电子的逸出功根据固体物理学中金属电子理论，金属中的传导电子能量的分布是按费米——狄拉克（Fermi-Dirac）分布的。

即（1）式中称费米能级。

在通常温度下由于金属表面与外界（真空）之间存在一个势垒，所以电子要从金属中逸出必须至少具有能量，在绝对零度时电子逸出金属至少需要从外界得到的能量为：称为金属电子的逸出功，其常用单位为电子伏特（ev）。

称为逸出电位，其数值等于以电子伏特表示的电子逸出功。

2．热电子发射公式根据费米—狄拉克能量分布公式（1）可以导出热电子发射的里查逊—杜什曼（Richar-dson-Dushman）公式（ （2）式中——热电子发射的电流强度，单位为安培。

——和阴极表面化学纯度有关的系数，单位为安培/厘米2·度2。

——阴极的有效发射面积，单位为平方厘米。

——玻尔兹曼常数。

3．里查逊直线法将（2）式两边除以，再取对数得到（3）从（3）可以看出，与成线性关系。

如果以作纵坐标，以为横坐标作图，从所得直线的斜率即可求出电子的逸出电位，从而求出电子的逸出功。

4．从加速场外延求零场电流为了维持阴极发射的热电子能连续不断地飞向阴极，必须在阴极和阳极间外加一个加速电场。

在加速电场的作用下，阴极发射电流和有如下的关系（4）对（4）式取对数得,把阴极和阳极做成共轴圆柱形，并忽略接触电位差和其它影响，则加速电场可表示为（5）式中和分别为阴极和阳极的半径，为加速电压，由（5）式可见，在一定的温度和管子结构时，和成线性关系。

金属逸出功的测定实验报告一、实验目的1、了解热电子发射的基本规律。

2、用理查逊直线法测定金属钨的逸出功。

二、实验原理1、热电子发射金属中的自由电子在一定的温度下会具有一定的动能，当电子的动能大于金属表面的逸出功时，电子就会从金属表面逸出，这种现象称为热电子发射。

2、理查逊杜什曼定律热电子发射的电流密度＄j$ 与金属表面的温度＄T$ 和逸出功＄W$ 之间有如下关系：＼j ＝ A T^2 e^｛＼frac{W}｛kT}｝＼其中，＄A$ 是与金属材料有关的常数，＄k$ 为玻尔兹曼常数。

对上式两边取对数可得：＼＼ln j ＝＼ln A ＋ 2\ln T ＼frac{W}｛kT}＼若以＄＼ln j$ 为纵坐标，＄＼frac{1}｛T}＄为横坐标作图，可得一直线。

直线的斜率为＄＼frac{W}｛k}＄，由此可求出金属的逸出功＄W$ 。

三、实验仪器WF-1 型金属电子逸出功测定仪、理想二极管、检流计、标准电阻、稳压电源、温度计等。

四、实验步骤1、按实验电路图连接好电路。

2、接通电源，预热仪器约 20 分钟，使灯丝达到热稳定状态。

3、调节灯丝电流，测量不同灯丝电流下的阳极电压和对应的阳极电流。

4、同时记录灯丝温度，灯丝温度可通过灯丝电流和仪器所给的灯丝电流与温度关系曲线查出。

五、实验数据记录与处理1、实验数据记录｜灯丝电流＄I_f$ （A) ｜阳极电压＄U_a$ （V) ｜阳极电流＄I_a$ （＄＼times 10^｛－6}＄ A) ｜灯丝温度＄T$ （K) ｜｜｜｜｜｜｜050 ｜25 ｜03 ｜1800 ｜｜055 ｜30 ｜05 ｜1850 ｜｜060 ｜35 ｜08 ｜1900 ｜｜065 ｜40 ｜12 ｜1950 ｜｜070 ｜45 ｜18 ｜2000 ｜｜075 ｜50 ｜25 ｜2050 ｜2、数据处理（1）计算不同温度下的电流密度＄j$ ，电流密度＄j ＝＼frac{I_a}｛S}＄，其中＄S$ 为阳极的有效面积。

脱基效应，使阴极表面的势垒b E 降低，电子逸出功减小，发射电流变大，因而测量得到的电流是在加速电场a E 的作用下阴极表面发射电流a I ,而不是零场电流I 。

可以证明零场电流I 与a I 的关系为0.439exp a a E I I T ⎛⎫= ⎪ ⎪⎝⎭对上式取对数，曲线取直，有TE I I aa 30.2439.0lg lg += （3.11.3）通常把阴极和阳极做成共轴圆柱形，忽略接触电位差和其它影响，则加速电场可表示为121ln(/)aa U E r r r =，其中1r 和2r 分别为阴极和阳极的半径，a U 为阳极电压（图3.11-4）。

把a E 代入上式得1210.4391lg lg 2.30ln(/)a a I I U Tr r r =+（3.11.4）此式是测量零级电流的基本公式。

对于一定尺寸的二极管，当阴极的温度T 一定时，a I lg 和a U 成线性关系。

如果以a I lg 为纵坐标、以a U 为横坐标作图，这些直线的延长线与纵坐标的交点为lg I ，如图3.11-5所示。

求反对数，可求出在一定温度下的零场电流I 。

测量数据与数据处理：1. 按照图3.11-6连接好实验电路，接通电源，预热十分钟。

2. 调节理想二极管灯丝电流f I 在0.55-0.75A 之间，每隔0.05A 进行一次测量。

如果阳极电流a I 偏小或偏大，也可适当增加或降低灯丝电流f I 。

对应每一灯丝电流，在阳极上加上25V ，36V ，49V ，64V ，…，144V 电压，各测出一组阳极电流a I 。

记录数据于表3.11.2中，并换算至表3.11.3。

图3.11-6 实验电路图图3.11-5 外推法求零场电流0 5 101T 2T 3T 4T 5T 54 (i)T T T >>>lg a I aU lg IU图线a求出截距Ilg，得在不同阴极温度时的零场热电子发射电流I，并换算3.11.4。

金属电子逸出功实验报告实验目的，通过实验测定金属的电子逸出功，并探究其与金属类型、表面状态等因素的关系。

实验仪器，光电效应实验装置、锂、钠、铝、铜、锌等金属样品、紫外光源、电压表、电流表等。

实验原理，光电效应是指金属或半导体受到光照射后，发生光电子的发射现象。

当金属表面被光照射后，光子能量足够大时，金属表面的电子就会被激发出来，这个能量称为光电子的逸出功。

逸出功与金属的类型、表面状态等有关，通常用符号φ表示。

实验步骤：1. 将光电效应实验装置搭建好，并调整好各个参数。

2. 依次取一些不同金属的样品，将其放置在光电效应实验装置的光阴极位置。

3. 通过调整紫外光源的光强和波长，使得金属样品表面受到光照射。

4. 测量在不同光强和波长下，金属样品的光电流和电压值，记录实验数据。

5. 根据实验数据，计算出不同金属的电子逸出功。

实验结果与分析：通过实验数据的分析，我们得到了不同金属的电子逸出功的实验值。

发现不同金属的逸出功存在一定的差异，这与金属的类型、表面状态等因素有关。

一般来说，对于相同金属而言，其逸出功与光照射波长呈负相关关系，即波长越短，逸出功越大；逸出功与光照射强度呈正相关关系，即光强越大，逸出功越大。

结论：通过本次实验，我们成功测定了不同金属的电子逸出功，并探究了其与金属类型、表面状态等因素的关系。

实验结果表明，金属的电子逸出功与光照射波长和强度有一定的关联，这为我们进一步研究金属的光电特性提供了重要的参考依据。

实验中遇到的问题及改进方案：在实验过程中，我们发现光电效应实验装置的光强和波长的调节对实验结果影响较大，因此在实验中需要精确控制光源参数，以保证实验数据的准确性。

另外，金属样品的表面状态也会对实验结果产生一定影响，因此在实验中需要尽量保持金属表面的清洁和光滑。

实验的局限性及展望：本次实验虽然成功测定了金属的电子逸出功，并初步探究了其与金属类型、表面状态等因素的关系，但仍存在一定局限性。

未来，我们可以进一步扩大实验样本的范围，深入研究金属的光电特性，为相关领域的研究提供更多的实验数据和理论参考。

#### 一、实验目的1. 理解热电子发射的基本规律。

2. 掌握理查逊直线法测量金属逸出功的方法。

3. 学习数据处理和图表分析方法。

#### 二、实验原理金属中存在大量的自由电子，但电子在金属内部所具有的能量低于在外部所具有的能量。

因此，电子逸出金属时需要提供一定的能量，这个能量称为电子逸出功。

本实验通过加热金属，使其发生热电子发射，从而测量金属的逸出功。

实验中，利用理查逊直线法测量金属的逸出功。

该法基于以下原理：当金属阴极温度升高时，电子从金属表面逸出的概率增加，逸出电子的能量分布也随之改变。

根据热电子发射的规律，可以得出以下关系式：\[ I = I_0 \left( \frac{T}{T_0} \right)^n e^{-\frac{W_0}{kT}} \]其中，\( I \) 为热发射电流，\( I_0 \) 为温度 \( T_0 \) 下的热发射电流，\( T \) 为实际温度，\( W_0 \) 为金属的逸出功，\( k \) 为玻尔兹曼常数。

通过改变阴极温度，测量不同温度下的热发射电流，以绘制 \( \frac{1}{I} \) 与 \( \frac{1}{T} \) 的关系图，从而得到直线的斜率 \( m \)，进而计算出金属的逸出功 \( W_0 \)。

#### 三、实验仪器1. 金属电子逸出功测定仪（包括二极管灯丝温度测量系统、专用电源、显示测量电压电流的数字电表）。

2. 理想标准二极管。

3. 温度计。

4. 恒温水浴。

#### 四、实验步骤1. 将金属阴极（钨丝）放入恒温水浴中，调整温度至 \( T_0 \)。

2. 在金属阴极和阳极之间施加电压，使二极管导通。

3. 记录此时阴极的温度 \( T_0 \) 和对应的电流 \( I_0 \)。

4. 改变恒温水浴的温度，分别记录 \( T_1, T_2, \ldots, T_n \) 和对应的电流\( I_1, I_2, \ldots, I_n \)。

金属电子逸出功的测定实验报告一、实验目的1、了解热电子发射的基本规律。

2、用理查逊直线法测定金属钨的电子逸出功。

二、实验原理1、热电子发射金属中的自由电子在一定温度下会具有足够的能量，克服表面势垒而逸出金属表面，这种现象称为热电子发射。

2、理查逊杜什曼定律热电子发射电流密度＄j$ 与金属表面温度＄T$ 之间的关系遵循理查逊杜什曼定律：＼j ＝ A T^2 e^｛＼frac{e\varphi}｛kT}｝＼其中，＄A$ 是与金属材料性质有关的常数，＄e$ 是电子电荷量，＄k$ 是玻尔兹曼常数，＄＼varphi$ 是金属的逸出功。

3、逸出功的测定对上述公式两边取对数，得到：＼＼ln\frac{j}｛T^2} ＝＼ln A ＼frac{e\varphi}｛kT}＼若以＄＼ln\frac{j}｛T^2}＄为纵坐标，＄＼frac{1}｛T}＄为横坐标作图，得到一条直线。

根据直线的斜率，可以计算出电子逸出功＄＼varphi$ 。

三、实验仪器1、理想二极管（理查逊热电子发射管）2、加热电源3、电流表4、电压表5、温控仪四、实验步骤1、按实验电路图连接好仪器，检查线路无误后接通电源。

2、开启温控仪，逐步升高加热电流，使灯丝温度缓慢升高。

同时观察电流表和电压表的读数，记录不同温度下的电流和电压值。

3、当温度达到一定值后，停止加热，待温度稍降后再继续测量。

4、测量完毕后，关闭电源，整理仪器。

五、实验数据处理1、根据测量数据，计算出不同温度下的发射电流密度＄j$ ，公式为：＼j ＝＼frac{I}｛S}＼其中，＄I$ 是发射电流，＄S$ 是阴极发射面积。

2、计算出＄＼ln\frac{j}｛T^2}＄和＄＼frac{1}｛T}＄的值。

3、以＄＼ln\frac{j}｛T^2}＄为纵坐标，＄＼frac{1}｛T}＄为横坐标作图，得到一条直线。

4、通过直线的斜率＄K$ ，计算电子逸出功＄＼varphi$ ，公式为：＼＼varphi ＝＼frac{k}｛e}K\六、实验结果与分析1、实验数据记录表格｜温度 T （K)｜发射电流 I （A)｜发射电流密度 j （A/m²)｜＄＼ln\frac{j}｛T^2}＄｜＄＼frac{1}｛T}＄（1/K)｜｜｜｜｜｜｜｜＿____|＿____|＿____|＿____|＿____|｜＿____|＿____|＿____|＿____|＿____|｜＿____|＿____|＿____|＿____|＿____|｜｜｜｜｜｜2、绘制＄＼ln\frac{j}｛T^2}＄＄＼frac{1}｛T}＄图像根据实验数据，在坐标纸上绘制出＄＼ln\frac{j}｛T^2}＄与＄＼frac{1}｛T}＄的关系曲线。