当前位置：文档之家 › 二次函数y=ax的图像

二次函数y=ax的图像

  • 格式：ppt
  • 大小：911.00 KB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

二次函数y=ax2图像和性质

二次函数y=ax2图像和性质
二次函数y=ax²图像和性质
欢迎来到我们的演示文稿！今天我们将深入探讨关于二次函数的图像和性质。 让我们一起来探索吧！
二次函数的定义和表达式
二次函数是一个形如 y = ax²+ bx + c 的函数，其中 a、b、c 为常数。 它的图像通常是一个平滑的弧线，可以呈现不同的形状和方向。
二次函数图像的基本形状
二次函数图像的对称性
二次函数的图像关于其顶点对称。 这意味着，如果顶点的坐标是 (h, k)，则对称轴是 x = h。
二次函数的顶点和轴
二次函数的顶点是抛物线的最高或最低点。 顶点坐标可以通过公式 (-b/2a, f(-b/2a)) 计算得出。 其中，f(x) 是二次函数的解析式。
二次函数的零点和解析式
通过二次函数来描述物体的运动轨迹，如抛 物线的飞行轨迹。
3 面积计算
二次函数图像下方的面积可以用于计算各种 形状的面积，如池塘或园艺项目。
4 信号处理和图像处理
二次函数的性质被广泛应用于数字信号处理 和图像处理算法中。
向上凹的抛物线
当 a 的值大于 0 时，抛物线开口向上。
向下凹的抛物线
当 a 的值小于 0 时，抛物线开口向下。
二次函数图像的平移和缩放
平移
通过增加或减小 c 的值可以改变抛物线在 y 轴上的位置。
缩放
通过改变 a 的值来控制抛物线的宽度和高度。
特殊情况
当 a 的绝对值很大时，抛物线会变得非常陡峭或扁平。
二次函数的零点，也称为根，是函数与 x 轴相交的点。 通过求解二次方程 ax²+ bx + c = 0，我们可以找到二次函数的零点。 解析式为 x = (-b ± √(b² - 4ac)) / (2a)。

二次函数 y=ax2的图象及其性质ppt课件

二次函数 y=ax2的图象及其性质ppt课件

x轴
______对称.
如果已知y=ax2 (a≠0)的图象，可通过
2的图象.
翻折
_________更方便地得到y=－ax
上
当a＞0时，抛物线开口向___；
当a＜0时，抛物线开口向___.
下
y
7
6
5
4
3
2
1
-5 -4 -3 -2 -1 O
-1
-2
-3
-4
-5
-6
y=2x2
1 2 3 4 5
x
y=-2x2
第1章 二次函数
1.2 二次函数的图象
第1课时 二次函数 y=ax²的图象及其性质
学习目标
知识与技能 ：能够利用描点法画函数y=ax2的图象。
过程与方法 ：
①经历二次函数y=ax2图象的作法。
②探索二次函数y=ax2性质，获得利用图象研究函数性质的经验。
重点：会画函数y=ax2的图象，并根据图象认识和理解二次函数y=ax2
0 时， y 随x 的增大而减小
当 x=0 时， y 最大值 =0
16
探究新知
例1 已知二次函数y=ax2 (a≠0)的图象经过点(－2，－3).
(1)求a的值，并写出这个二次函数的表达式.
解：把点(－2，－3)的坐标代入y=ax2 ，
得－3=a(－2)2，
解得 a=－

.

所以这个二次函数的表达式是y=－
0.5x2的图象，它们的共同特点是( D )
A．都关于x轴对称，抛物线开口向上
B．都关于原点对称，顶点都是原点
C．都关于y轴对称，抛物线开口向下
D．都关于y轴对称，顶点都是原点
24

二次函数y=ax2的图象和性质ppt课件

二次函数y=ax2的图象和性质ppt课件

例4 如图， 四个二次函数的图象分别对应 ① y=ax2 ；② y=bx2；
③ y=cx2；④ y=dx2，且①与③，②与④分别关于x 轴对称.
(1)比较a，b，c，d 的大小； (2)说明a 与c，b 与d 的数量关系.
解：(1)由抛物线的开口方向，知 a ＞ 0，b ＞ 0，c ＜ 0，d ＜ 0，
由抛物线的开口大小，知 |a| ＞ |b|，|c| ＞ |d|， 因此a ＞ b，c ＜ d. ∴ a ＞ b ＞ d ＞ c. (2)∵①与③，②与④分别关于x 轴对称，
∴①与③，②与④的开口大小相同，方向相反. ∴ a+c=0，b+d=0.
课堂练习
1、下列函数中，y总随x增大而减小的是( B )
归纳总结
位置开 开口向上,在x轴上方 开口向下,在x轴下方
口方向
a的绝对值越大，开口越小
对称性 顶点最值
关于y轴对称，对称轴方程是直线x＝0 顶点坐标是原点（0，0）
当x=0时，y最小值=0 当x=0时，y最大值=0
增减性
在对称轴左侧递减 在对称轴左侧递增 在对称轴右侧递增 在对称轴右侧递减
1、如右图，观察函数y=（ k-1）x2的图象, 则k的取值范围是 k>1 .
复习引入
1.二次函数的一般形式是怎样的？ y=ax²+bx+c(a,b,c是常数,a≠ 0)
2.下列函数中,哪些是二次函数？
①
②
③
④
⑤
3.一次函数的图象是一条 直线.
4.通常怎样画一个函数的图象？ 列表、描点、连线
那么，二次函数的图象会是什么样的图形呢？这节课我们 来学习最简单的二次函数y=ax2的图像
不同点： a的值越大，开口越小.

22.1.2二次函数y=ax2图像与性质

22.1.2二次函数y=ax2图像与性质

y=ax2+c (a≠0) 开口方向 顶点坐标 对称轴 增 减 性 极值
a>0 向上 (0 ,c) y轴
当x<0时， y随着x的增大而减小。 当x>0时， y随着x的增大而增大。
a<0 向下 (0 ,c) y轴
当x<0时, y随着x的增大而增大。 当x>0时， y随着x的增大而减小。
x=0时,y最小=c
x y = x2 · · · · · · －3 －2 －1 0 1 2 3 · · · · · ·
9
4
1
0
1
9
4
9
2. 根据表中x,y的数值在 坐标平面中描点（x,y） 3.连线 如图，再用平 滑曲线顺次连接各点， －3 2 就得到y = x 的图象．
y = x2
6
3 3
二次函数 y = x2的图象是一条曲线，它的形状类似 于投篮球时球在空中所经过的路线，只是这条曲线 开口向上，这条曲线叫做抛物线 y = x2 ， 二次函数的图象都是抛物线， 它们的开口或者向 上或者向下． 一般地，二次函数 y = ax2 + bx + c （a≠0）的图象叫做抛物线y = ax2 + bx + c y = x2
m2+m
解②得:m1=－2, m2=1 由①得:m>－1 ∴ m=1 此时,二次函数为: y=2x2,
x ….. y=x2 …… y=x2+1 ……
-2 4
-1 1
0 0
y
8
1 1
2 4
…… ……
5
2
0
2
5

y=x2+1
函数y=x2+1的图象与y=x2的 图象的位置有什么关系? 函数y=x2+1的图 象与y=x2的图象 的形状相同吗?

22.1.2 二次函数y=ax2的图象和性质

22.1.2 二次函数y=ax2的图象和性质

x
… -2 -1
0
1
y=2x2 …
y=2x2
…
(2)描点并连线:
2
…
…
…
【思路点拨】 首先列表求出函数图象上点的坐标,进而描点连线画出图象即可.注 意连线时一定要用平滑的实线连接.
解:(1)8 2 0 2 8 -8 -2 0 -2 -8 (2)
类型二:二次函数y=ax2图象的性质的应用
例2 已知函数y=ax2的图象过点(1, 1 ).
2
增大而减小.
(2)在其图象上有两点(x1,y1),(x2,y2),且x1>x2>0,比较y1,y2的大小.
【思路点拨】 (2)二次函数y=ax2的对称轴为y轴,由(1)知a<0,所以在其对称轴 的右侧y随x的增大而减小,又x1>x2>0,故y1<y2. 解:(2)因为x1>x2>0, 所以y1<y2.

(1)简述函数y=ax2的性质;
2
【思路点拨】 (1)把点(1, 1 )代入函数y=ax2的解析式求得a的值,即可判定函
数的性质.
2
解:由题意得 a=- 1 ,所以 y=- 1 x2.
2
2
(1)函数 y=- 1 x2,开口向下,在 y 轴左侧 y 随 x 的增大而增大,在 y 轴右侧 y 随 x 的
22.1.2 二次函数y=ax2的图象和性质
1.二次函数y=ax2的图象
二次函数y=ax2的图象是 抛物线 ,对称轴与抛物线的交点叫做 顶点 ,顶点是
(0,0) ,当a>0时,抛物线的开口 向上 ,顶点是抛物线的最 低 点;当a<0时, 抛物线的开口 向下 ,顶点是抛物线的最 高 点.对于y=ax2,|a|越 大 ,抛物 线的开口越小.

初中数学课件 2二次函数y=ax2的图象

初中数学课件 2二次函数y=ax2的图象
当x=0时,函数y的值最大,最大值是 0 ,
当x ≠ 0时,y<0.
活动三、应用迁移
例1.
（1）若抛物线y=(2-m)xm2-3有最低点,则m=---------------
（2）点A(-3,y1),B(-2,y2),C(-1,y3)在抛物线
y=ax （a<0）上,则y ,y ,y 的大小关系是 2
x>0时,y随x增大而增大 x>0时,y随x增大而减小
做一做
(1)抛物线y=5x 的顶点坐标是(0,0) ,开口 向上 2 -------------------------对称轴是 y轴 ,在对称轴 右 侧,y随着x的增大而增 大；在对称轴左 侧,y随着x的增大而减小,当x= 0 时,函数y的值最小,最小值是 0 ,抛物线y=5x2在x轴 的_上___方(除顶点外). (2)抛物线 y 2 x2 当x<0时,y随着x的 增大而增大 ； 3 当x >0 ,y随着x的增大而减小； ------------------
作业：金榜行动 P4第1-10题，选做P5第6、8题
活动三、应用迁移
例3.已知正方形周长为Ccm，面积为Scm2； （1）求S和C之间的函数关系式，并画出图像； （2）根据图像，求出S=1cm2时，正方形的周长； （3）根据图像，求出C取何值时，S≥4cm2 .
结束寄语
下课了!
只有不断的思考,才会 有新的发现;只有量的 变化,才会有质的进步.
∴x的值可取负数、零、正数
(2)为了计算和描点方便,x取整数.且以1为 间距取值,取有代表性的7对值
画函数y=x2的图象.
x … -3 -2 -1 0 1 2 3 …
y=x2 … 9 4 1 0 1 4 9 …

二次函数的图像及性质1


试一试：
1、函数y=2x2的图象的开口 ，对称轴 是 ，顶点是 ；在对称轴的左 侧，y随x的增大而 y随x的增大而 ； ，在对称轴的右侧，
2、函数y=-3x2的图象的开口 ，对称轴 是 ，顶点是 ；在对称轴的左 侧，y随x的增大而 y随x的增大而 ； ，在对称轴的右侧，
3、观察函数y=x2的图象，则下列判断中正确的是 （ A ） A 若a,b互为相反数，则x=a与x=b的函数值相等。 B 对于同一个自变量x，有两个函数值与它对应。
2
x （2）当 a 0 时，设自变量 x1， 2 的对应值分别为 y1 ，y 2 ， 当 x1 x2 0 时，必有 y1 y2 吗？为什么？
小结： １．函数y=ax2+bx+c(a,b,c是常数，a≠0) 叫做x的二次函数． ２．二次函数y=ax2的图象性质与特点：
（1） 顶点都在原点;对称轴是y轴
2、已知函数
y m 1x
m 2m2
2
m 2x
是二次函数，且开口向上。
求m的值及二次函数的解析式，并回答y随x的变化 规律
回顾练习及提高： ，对称轴是 ， 图像在 x 轴的 （顶点除外），开口方向向 ，当 x 时，y 随着 x 的增大而减小，当 时，y 随着 x 的增大而增大。
y x 2 的顶点坐标是 1、二次函数
y 3x 2，当 x 2、抛物线 时， y 随着 x 的增大而 减小，当 x 时，函数 y 有最 值，此时 y ＝ 。
3、根据二次函数 y ax 的图像的性质，回答下列问题： （1）如果点P(m, n) 在抛物线y ax2 上，那么点Q(m, n)也在 这条抛物线上吗？为什么？
（２）当a>0时，开口向上；当a<0时，开口 向下． （３）当a＞0时， 在对称轴的左恻:y随x的增大而减小； 在对称轴的右恻:y随x的增大而增大。 当a<0时， 在对称轴的左恻:y随x的 增大而增大； 在对称轴的右恻:y随x的增大而减小。

二次函数y=ax2的图象和性质


3.(2018湖北武汉硚口期中,16,★★☆)已知点M(2,3),F
0,
1 2
,点P(m,n)为
抛物线y= 1 x2上一动点,则用含m的式子表示PF为
2
;PF+PM的最
小值是
.
答案 1 (m2+1); 7
2
2
解析 ∵点P(m,n)为抛物线y=1 x2上一动点,∴n=1 m2,
2
2
∴点P的坐标为
2
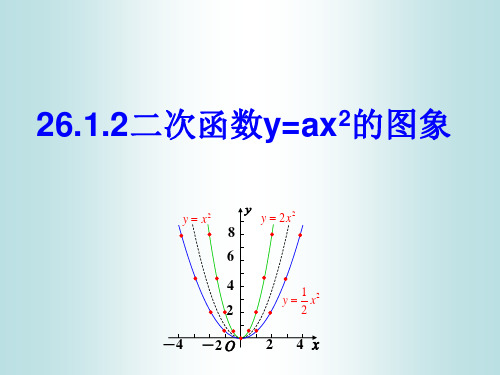
同性质:
.
答案 对称轴是y轴(或顶点是原点) 解析 ∵函数y= 1 x2的图象开口向上,对称轴为y轴,顶点坐标为(0,0);函
2
数y=x2的图象开口向上,对称轴为y轴,顶点坐标为(0,0);函数y=-x2的图象
开口向下,对称轴为y轴,顶点坐标为(0,0),∴三个函数的共同性质为:对
称轴是y轴,顶点是原点.
例 已知y=(k+1) xk22 是关于x的二次函数. (1)求满足条件的k的值; (2)k为何值时,抛物线有最低点?求出这个最低点.当x为何值时,y的值随x 值的增大而增大? (3)k为何值时,函数有最大值?最大值是多少?当x为何值时,y的值随x值 的增大而减小?
解析
(1)由题意,得
k
2
2
2,
解得k=±2.
k 1 0,
∴当k=±2时,原函数是二次函数.
(2)若抛物线有最低点,则抛物线的开口向上,
∴k+1>0,即k>-1,∴k=2.∴该抛物线的解析式为y=3x2,
∴抛物线的顶点坐标为(0,0),当x>0时,y随x的增大而增大.
(3)若函数有最大值,则抛物线的开口向下,∴k+1<0,∴k<-1,∴k=-2.∴抛

27.2.1二次函数y=ax^2的图象与性质课件

o x
a<o
(3)、增减性
当a＞0时， 在对称轴的左侧(x<0): y随x的增大而减小； 在对称轴的右侧(x>0): y随x的增大而增大。
a＞0
∴ 当 x=0 时, y最小值=o.
当a<0时 在对称轴的左侧(x<0): y随x的增大而增大。 在对称轴的右侧(x>0): y随x的增大而减小。
a<0
∴ 当 x=0 时, y最大值=o.
y ax 的图象与性质
2
二次函数的定义：
函数y=ax2+bx+c(a,b,c是常数，a≠0) 叫做x的二次函数
思考：你认为判断二次函数的关键是什么？
判断一个函数是否是二次函数的关键是：看 二次项的系数是否为0．
练习： 若函数y=(m2+3m-4)x2+(m+2)x+3m是x的二次函数，则m______
试一试：
1、函数y=2x2的图象的开口 ，对称轴 是 ，顶点是 ；在对称轴的左 侧，y随x的增大而 y随x的增大而 ； ，在对称轴的右侧，
2、函数y=-3x2的图象的开口 ，对称轴 是 ，顶点是 ；在对称轴的左 侧，y随x的增大而 y随x的增大而 ； ，在对称轴的右侧，
3、观察函数y=x2的图象，则下列判断中正确的是 （ A ） A 若a,b互为相反数，则x=a与x=b的函数值相等。 B 对于同一个自变量x，有两个函数值与它对应。
2
x （2）当 a 0 时，设自变量 x1， 2 的对应值分别为 y1 ，y 2 ， 当 x1 x2 0 时，必有 y1 y 2 吗？为什么？
小结： １．函数y=ax2+bx+c(a,b,c是常数，a≠0) 叫做x的二次函数． ２．二次函数y=ax2的图象性质与特点：

课件_人教版数学九年级二次函数y=ax的图像和性质PPT课件_优秀版

y -4 -2 0 2 4 x
-3 -6 -9
探究新知 知识点 2 二次函数y=ax2的图象性质
根据你以往学习函数图象性质的经验，说说二次函 数y=x2的图象有哪些性质，并与同伴交流.
1.y＝x2的图象是一条抛物线; 2.图象开口向上; 3.图象关于y轴对称; 4.顶点（ 0 ，0 ）; 5.图象有最低点．
···
-8
-4.5 -2
-0.5 0 -0.5 -2 -4.5 -8
···
x ··· －2 －1.5 －1 －0.5 0 0.5 1 1.5 2 ··· y 2x2 ··· -8 -4.5 －2 －0.5 0 －0.5 －2 －4.5 －8 ···
探究新知
【思考】二次函数 y 1 x2 , y x2 , y 2x2
y 9 6 3
-4 -2 o 2 4 x
探究新知
当取更多个点时，函数y=x2的图象如下：
解②得:m1=－2, m2=1
（1） 你们喜欢打篮球吗？
y
利用函数y=ax2的图像性质确定字母的值
顶点（ 0 ，0 ）;
9
连线：如图，再用平滑曲线顺次连接各点，就得到y = x2 的图象．
在已对知称 ：轴如的图左，侧直线, yy随＝x3的x增＋大4与而抛物线y＝, x2交于A、B两点，求出A6、B两点的坐标，并对求称出两轴交与点与抛原物点所线围的成的交三角形的面积．
（3）根据图象，求出当S=1cm2时，正方形的周长；
（4）根据图象，求出C取何值时，S ≥4cm2.
探究新知
解：（1）∵正方形的周长为Ccm，
∴正方形的边长为 C cm，
4
∴S与C之间的关系式为S
=
C2
；
16
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2 … y=x2
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
9
4
1
y 10 8 6 4 2
0
1
4
9
…
描点,连线
y= x2
-4
-3
-2
-1
0 -2
1
2
3
4
x
二次函数y=ax2的图象形如物体抛射时 所经过的路线，我们把它叫做抛物线。 函数y＝ax2的图象，以后叫做抛物线y＝ax2
观察图象,回答问题串
y
10
当x=
0 时，函数y的值最小，最小值是 0 ,抛
物线y=2x2在x轴的 上 __方（除顶点外）。
y 2x2
2
1、根据左边已画好的函数图象
2 2 y x 3
填空： 2 2 y x 3 （2）抛物线 在x轴的 下 方（除顶点外）， 增大而增大 ；
在对称轴的左侧，y随着x的
在对称轴的右侧，y随着x的 增大而减小，
二次函数y=ax² + bx+c（a ≠ 0）其图象又 是什么呢？ 还记得如何用描 我们先研究二次函数y=ax2的图像 点法画一个函数 的图象吗？ 你会画函数y=x2的图象吗？ 选择适当x值,并计算相应的y值,完成下表：
x … -3 9 -2 4 -1 1 0 0 1 1 2 4 3 9 … …
当x=0时，函数y的值最大，最大值是 0
，
当x 0时，y<0.
例1.已知 y =(m+1)x 是二次函数且其图象开 下,(1)求m的值和函数解析式;(2)x在何范围 口向上 内,y随x的增大而增大? y随x的增大而减小?
① m+1>0 ① m+1<0 解: (1) 依题意有: 2 m +m=2 ② m2+m=2 ② 解②得:m1=－2, m2=1 解②得:m1=－2, m2=1 由①得:m<－1 由①得:m>－1 ∴ m=－2 ∴ m=1 2 二次函数为 : y= － x 此时,二次函数为: y=2x2, (2) ∵ a=2>0, (2) ∵ a=－1<0, ∴抛物线 y=－x2开口向下, ∴抛物线 y=2x2开口向上, 当x<0时,y随x的增大而减小; 当x<0时,y随x的增大而增大; 当x>0时,y随x的增大而增大. 当x>0时,y随x的增大而减小.
2、已知a＜－1，点（a－1，y1）、（a，y2）、（a＋1， y3）都在函数y=x2的图象上，则（ C ）A．y1＜y2＜y3
B ．y 1＜y 3＜y 2 C ．y 3＜y 2＜y 1 D ．y 2＜y 1＜y 3
3 ．函数 y=x2 与 y= － x2 的图象关于 原点 对称，也 可以认为 y= － x2 ，是函数 y=x2 的图象绕 原点 旋 转 180°得到．
x
共同点： 1、开口向上；
函数y= x2,y=2x2的图像与函数y=x2(图中虚线图 形)的图像相比,有什么共同点和不同点? 2 1 2
10 9 8 7 6 5 4 3 2 1
1 2
y y y 2x
2
x
2、抛物线的对称轴是y轴； 3、顶点是原点；
4 、在对称轴的左侧， y随x的增大而减小； 在对称轴的右侧， y随x的增大而增大；
m2+m
1.填空：已知二次函数 9 3 2 x ;② y=15x2;③ y=-4x2;④y=① y= x 2; 5 10 2 2 ⑤ y=4x .⑥ y=-x ; ①②⑤ (1)其中开口向上的有__________( 填题号)； ④ 填题号)； (2)其中开口向下且开口最大的是____( (3)当自变量由小到大变化时，函数值先逐渐变大， 然后逐渐变小的有_____(④⑥ 填题号). 2、点A（1，b）是抛物线y=x2上的一点，则 b= 1 ；点A关于y轴的对称点B是 (-1,1) ，它 在 函数y=x2上；点A关于原点的对称点C ____ 是 (-1,-1) ，它 不在 ___函数y=x2上．
开口
对称性 顶点
增减性
顶点是最高点 顶点是最低点 在对称轴左侧递减 在对称轴左侧递增 在对称轴右侧递增 在对称轴右侧递减
y 2x2
2
2 2 y x 3
1、根据左边已画好的函 数图象填空： （1）抛物线y=2x2的 顶点坐标是 （0，0） _, 对称轴是 y轴 ___，
在 对称轴的右 侧，y随着x的增大而增大； 在 对称轴的左 侧，y随着x的增大而减小，
y x2
这条抛物线关于 y轴对称，y轴就 是它的对称轴.
对称轴与抛物 线的交点叫做 抛物线的顶点.
例1、在同一坐标系中作出函数y=1/2x2、y=x2和 y=2x2的图象
10 9 8 7 6 5 4 3 2 1
1 2 y x y y 2x2 2
-5 -4 -3 -2 -1 o 1 2 3 4 5
2 y= x
(1)图象是轴对称图形吗？如果是 ,它的对称轴 8 是什么?
(2)图象与对称轴有交点吗？如果有,交点坐标是 4 什么?
2 (3)当x取什么值时,y的值最小 ?最小值是什么？ 1 0 -4 时 -3 -2 x-1 1 ,y 2的值如何变化？ 3 4 x (4)当x<0 ,随着 的值增大 -2 当x>0呢？ 6
2
2、正方形的周长C(cm)，面积为S(cm2) ⑴求S与C之间的函数关系式 ⑵画出图象 ⑶根据图象，求出S=1cm2时，正方形的周长 ⑷根据图象若C＞ 1cm，S的取值范围是多少？ 再求出C取何值时，S≥4cm2
2
回顾知识:
一、正比例函数y=kx（k ≠ 0）的图象是什么?
正比例函数y=kx（k ≠ 0）的图象是一条经过原点的直线。 二、一次函数y=kx+b（k ≠ 0）的图象又是什么? 一次函数y=kx+b（k ≠ 0）的图象也是一条直线。
k 三、反比例函数 y x
（k ≠ 0）的图象又是什么?
k 反比例函数 y （k ≠ 0来自的图象是双曲线。 xY
（4）求S△ABO。
B P A 0 X
二次函数y=ax2的性质
y＝ax2 图象 开口向下 开口向上 a的绝对值越大，开口越小 关于y轴对称 顶点坐标是原点（0，0） 顶点是最高点 在对称轴左侧递减 在对称轴左侧递增 在对称轴右侧递增 在对称轴右侧递减 顶点是最低点 a>0 a<0
开口
对称性
顶点 增减性
x
2、抛物线的对称轴是y轴； 顶点是原点； 3、在对称轴的左侧， y随x的增大而增大； 在对称轴的右侧， y随x的增大而减小；
4、除顶点外，图象都在x轴的下方； 不同点： 开口大小不同;a越大开口越大。
二次函数y=ax2的性质
y＝ax2 图象 开口向下 开口向上 a的绝对值越大，开口越小 关于y轴对称 顶点坐标是原点（0，0） a>0 a<0
-5 -4 -3 -2 -1 o 1 2 3 4 5
x
5、除顶点外，图象都在x轴的上方； 不同点： 开口大小不同;a越大开口越小。
2 2 函数y=－x 与y=
和不同点?
共同点： 1、开口向下；
3
x2的图像相比,有什么共同点
1 y -5 -4 -3 -2 -1 o 1 2 3 4 5 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10
4、函数y＝ax2和函数y＝ax＋a的图象在同一坐标 系中大致是图中（ ）
5.已知抛物线y=ax2经过点A（-2，-8）. （1）求此抛物线的函数解析式； （2）判断点B（-1，- 4）是否在此抛物线上. （3）求出此抛物线上纵坐标为-6的点的坐标.
已知抛物线y=ax2与直线y=-2x+3交于点 A（1，b）与点B，直线与y轴交于点P。 求（1）求抛物线y=ax2的解析式， 并求顶点的坐标和对称轴。 （2）判断点C（-1， 4）是否在此抛物线上。 （3）求出此抛物线上纵坐标为6的点的坐标。