8.5几何选讲

8.5 怎样判定三角形相似（判定方法1、2）注沟中学 张子顺一：学习目标1、 理解并掌握判定三角形相似的方法1、方法22、 会选择恰当的方法判定两三角形是否相似3、 能够运用相似三角形的性质解决实际问题二：学习重点难点理解相似三角形的判定定理及重要结论，并能用其来解决有关问题。

三：教学工具及媒体课件、幻灯投影，利用多媒体动画展示角相等，验证结论的正确性。

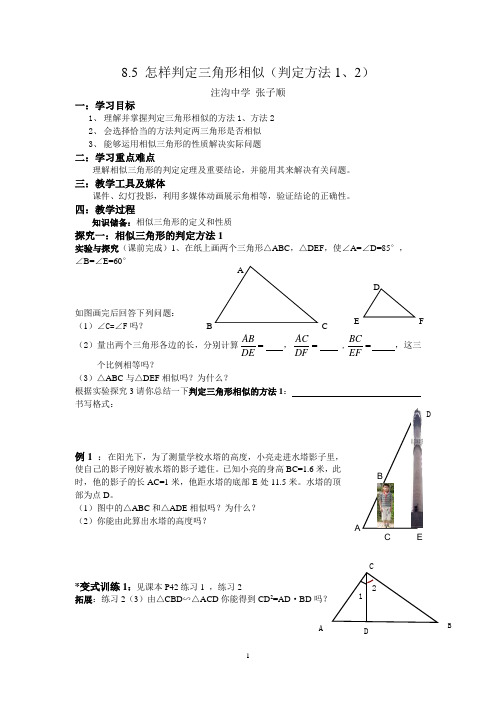
四：教学过程知识储备：相似三角形的定义和性质探究一：相似三角形的判定方法1实验与探究（课前完成）1、在纸上画两个三角形△ABC ，△DEF ，使∠A=∠D=85°， ∠B=∠E=60°如图画完后回答下列问题： （1）∠C=∠F 吗？（2）量出两个三角形各边的长，分别计算ABDE= ，AC DF = ,BC EF = ，这三个比例相等吗？（3）△ABC 与△DEF 相似吗？为什么？根据实验探究3请你总结一下判定三角形相似的方法1： 书写格式：例1 ：在阳光下，为了测量学校水塔的高度，小亮走进水塔影子里，使自己的影子刚好被水塔的影子遮住。

已知小亮的身高BC=1.6米，此时，他的影子的长AC=1米，他距水塔的底部E 处11.5米。

水塔的顶部为点D 。

（1）图中的△ABC 和△ADE 相似吗？为什么？ （2）你能由此算出水塔的高度吗？*变式训练1：见课本P42练习1 ，练习2拓展：练习2（3）由△CBD ∽△ACD 你能得到CD 2=AD ·BD吗？ A B CE FD ABD C EADBC 12探究二：相似三角形的判定方法2实验与探究（课前完成）2、请按下面的要求进行操作：用量角器、直尺在纸上画三角形，两人为一组，一位同学画△ABC，另一位同学画△DEF。

①△ABC：AB=4㎝, ∠B=50°,BC=6㎝; ②△DEF：DE=2㎝, ∠E=50°,EF=3㎝.通过观察你自己所画的三角形另一位同学的三角形进行比较,看看有什么发现？（1）检验∠C与∠F，∠A与∠D是否相等？（2）△ABC与△DEF相似吗？误区警示讨论：两边对应成比例并且其中一边的对角对应相等，这两个三角形相似吗？根据实验探究2请你总结一下判定三角形相似的方法2：书写格式：问题：（1）所有的正三角形都相似吗？（2）有一个锐角相等的两个直角三角形相似吗？例2 ：如右图AD=3,AE=4,BE=5, CD=9.△ADE和△ABC相似吗？变式训练2见课本P44 练习1,练习2五：本节小结这一节课同学们学习了那两种相似三角形判定的方法？你应该注意哪些问题？请你自己归纳一下！六：随堂检测1、判断题：(1)两个顶角相等的等腰三角形是相似的三角形。

第1章集合与常用逻辑用语§1.1 集合的概念及运算§1.2 命题及其关系、充分条件与必要条件§1.3 简单的逻辑联结词、全称量词与存在量词第二章函数§2.1 函数的概念及表示§2.2 函数的基本性质§2.3 二次函数与幂函数§2.4 指数与指数函数§2.5 对数与对数函数§2.6 函数的图象§2.7 函数与方程§2.8 函数的应用第三章导数及其应用§3.1 导数§3.2 导数的应用第四章三角函数§4.1 三角函数的概念、同角三角函数的关系及诱导公式§4.2 三角函数的图象和性质§4.3 三角函数的最值与综合应用§4.4 三角恒等变换第五章平面向量与解三角形§5.1 平面向量的概念及线性运算、平面向量的基本定理§5.2 平面向量的数量积及其应用§5.3 正、余弦定理及解三角形第六章数列§6.1 数列的概念及其表示§6.2 等差数列§6.3 等比数列§6.4 数列求和、数列的综合应用第七章不等式§7.1 不等式的概念、性质§7.2 不等式的解法§7.3 简单的线性规划§7.4 基本不等式§7.5 不等式的综合应用第八章立体几何§8.1 空间几何体的结构及其三视图和直观图§8.2 空间几何体的表面积和体积§8.3 空间点、直线、平面之间的关系§8.4 直线、平面平行的判定和性质§8.5 直线、平面垂直的判定和性质§8.6 空间直角坐标系第九章直线和圆的方程§9.1 直线方程和两直线的位置关系§9.2 圆的方程§9.3 直线与圆、圆与圆的位置关系第十章圆锥曲线§10.1 椭圆§10.2 双曲线§10.3 抛物线§10.4 直线与圆锥曲线的位置关系§10.5 圆锥曲线的综合问题第十一章概率与统计§11.1 古典概型与几何概型§11.2 统计第十二章统汁案例第十三章算法初步第十四章推理与证明§14.1 合情推理与演绎推理§14.2 直接证明与间接证明第十五章数系的扩充与复数的引入第十六章几何证明选讲第十七章坐标系与参数方程。

数学几何选讲试题答案及解析1.（本小题满分10分）选修4－1：几何证明选讲如图，圆O的半径OB垂直于直径AC,M为AO上一点，BM的延长线交圆O于N，点是线段延长线上一点，连接PN,且满足（Ⅰ）求证：是圆O的切线；(Ⅱ)若圆O的半径为，OA=OM，求MN的长.【答案】（Ⅰ）见解析(Ⅱ) 2【解析】（Ⅰ）证明：如图，连接ON，∵，则，……2分又，则.,∴，……4分∴，故是圆O的切线．……5分(Ⅱ) .在△BOM中，，,延长BO交圆O于点D，连接DN，由条件知△BOM∽△BND,于是,，即MN=BN-BM=6-4=2.……10分【考点】本题考查切线的判定定理、三角形相似等基础知识，意在考查学生推理证明和逻辑思维能力.2.如图，，是圆的两条弦，它们相交于的中点，若，，,求圆的半径.【答案】1【解析】解：由，,，得 5分又为中点，，， 10分【考点】本题考查圆的基本性质，相交弦定理等知识，意在考查推理论证能力.3.（本小题满分10分）选修4－1：几何证明选讲如图，Δ是内接于圆，,直线切于点，弦，与相交于点．（1）求证：≌；（2）若求．【答案】（1）见解析（2）【解析】（1）在ΔABE和ΔACD中，∵，∠ABE=∠ACD．又∠BAE=∠EDC，∵BD∥MN，∴∠EDC=∠DCN，∵直线是圆的切线，∴∠DCN=∠CAD，∴∠BAE=∠CAD，∴Δ≌Δ（角、边、角）． 5分（2）∵∠EBC=∠BCM，∠BCM=∠BDC，∴∠EBC=∠BDC=∠BAC，BC=CD=4，又∠BEC=∠BAC+∠ABE=∠EBC+∠ABE=∠ABC=∠ACB，∴BC=BE=4．设AE=，易证ΔABE∽ΔDEC，∴，从而.又，，∴，解得.因此. 10分【命题意图】本题考察弦切角定理、等腰三角形的性质、三角形相似等基础知识，意在考察学生推理证明和逻辑思维能力.4.如图，已知△ABC的两条角平分线AD和CE相交于H，∠B＝60°，F在AC上，且AE＝AF.（1）证明：B、D、H、E四点共圆；（2）证明：CE平分∠DEF.【答案】（1）见解析（2）见解析【解析】（1）在△ABC中，因为∠ABC＝60°，所以∠BAC＋∠BCA＝120°.因为AD、CE是角平分线，所以∠HAC＋∠HCA＝60°，故∠AHC＝120°，于是∠EHD＝∠AHC＝120°.因为∠EBD＋∠EHD＝180°，所以B、D、H、E四点共圆．（2）连结BH，则BH为∠ABC的平分线，得∠HBD＝30°.由（1）知B、D、H、E四点共圆，所以∠CED＝∠HBD＝30°.又∠AHE＝∠EBD＝60°，由已知可得EF⊥AD.可得∠CEF＝30°.所以CE平分∠DEF.【点评】熟记圆的切线性质、圆周角定理、切割线定理、相交弦定理，这些知识点是解决有关圆的问题的关键，要好好理解．5.如图, 弦AB与CD相交于内一点E, 过E作BC的平行线与AD的延长线相交于点P. 已知PD＝2DA＝2, 则PE＝ .【答案】【解析】本题考查平面几何证明，利用三角形相似即可求解，属于容易题。

《几何证明选讲》1.了解平行线截割定理，会证直角三角形射影定理.2.会证圆周角定理、圆的切线的判定定理及性质定理.3.会证相交弦定理、圆内接四边形的性质定理与判定定理、切割线定理.一、基础知识填空：看图并用式子表示定理和推论1.平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段_________.用式子表示为推论1: 经过三角形一边的中点与另一边平行的直线必______________.用式子表示为推论2: 经过梯形一腰的中点，且与底边平行的直线________________.用式子表示为2.平行线分线段成比例定理：三条平行线截两条直线，所得的________________成比例.用式子表示为推论：平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段___________.用式子表示为3.相似三角形的性质定理：相似三角形对应高的比、对应中线的比、对应角平分线的比都等于______；相似三角形周长的比、外接圆的直径比、外接圆的周长比都等于_________________；相似三角形面积的比、外接圆的面积比都等于____________________；用式子表示为4.直角三角形的射影定理：直角三角形斜边上的高是______________________ 的比例中项；两直角边分别是它们在斜边上_______ 与_________ 的比例中项.用式子表示为5.圆周角定理：圆上一条弧所对的圆周角等于它所对的____________ 的一半.用式子表示为圆心角定理：圆心角的度数等于______________ _的度数.推论1：同弧或等弧所对的圆周角_________等圆中，相等的圆周角所对的弧_______.用式子表示为推论2：半圆（或直径）所对的圆周角是____；90o的圆周角所对的弦是________.弦切角定理：弦切角等于它所夹的弧所对的______________.6.圆内接四边形的性质定理与判定定理：圆的内接四边形的对角______用式子表示为如果一个四边形的对角互补，那么这个四边形的四个顶点______；如果四边形的一个外角等于它的内角的对角，那么这个四边形的四个顶点_________.用式子表示为7.切线的性质定理：圆的切线垂直于经过切点的用式子表示为推论：经过圆心且垂直于切线的直线必经过_______过切点且垂直于切线的直线必经过______.用式子表示为切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的________.用式子表示为8.相交弦定理:圆内两条相交弦，用式子表示为割线定理:从圆外一点引圆的两条割线，的两条线段长的积相等.用式子表示为切割线定理:从圆外一点引圆的切线和割线，切线长是__________ 的比例中项用式子表示为切线长定理:从圆外一点引圆的两条切线，它们的切线长____ ；圆心和这点的连线平分_____ 的夹角.用式子表示为几何证明选讲二 、经典试题：1.如图所示，在四边形ABCD 中， EF//BC ，FG//AD ，则E F FG +=B CA D．2.在平行四边形ABCD 中，点E 在边AB 上，且AE ：EB=1：2，DE 与AC 交于点F ，若△AEF 的面积为3cm 2，则△DFC 的面积为cm 2． 3.已知：如图，在梯形ABCD 中，AD ∥BC ∥EF ， E 是AB 的中点，EF 交BD 于G ，交AC 于H. 若 AD=5，BC=7，则GH=________.4如图，在△ABC 中，D 是AC 的中点，E 是BD 的中点，AE 交BC于F ，则B F=FC .5、如图，圆O 上一点C 在直径AB 上的射影为D.AD=2，AC=52，则AB=____ __,CD=___ __.6、.如图，四边形ABCD 内接 于⊙O ，BC 是直径，MN 切⊙O 于A ，∠MAB=250，则∠D= ___ .A BCD E F GABCDEFG HBADEFB7.、如图：EB 、EC 是⊙O 的两条切线，B 、C 是切点，A 、D 是⊙O 上两点，如果∠E ＝460，∠DCF ＝320，则∠A 的度数是 .8、如图，AB 是圆O 的直径，直线CE 和圆O 相切于点C ，AD ⊥CE 于D ， 若AD=1，∠ABC=300，则圆O 的面积是______.9、等腰三角形ABC 的底边AC 长为6 ,其外接圆的半径长为5, 则三角形ABC 的面积是____． 10、如图所示, 圆的内接△ABC 的∠C 的平分线CD 延长后交圆于点E ，连接BE ，已知BD=3，CE=7，BC=5，则线段BE= .11、如图所示，圆O 的直径AB=6，C 圆周上一点，BC=3，过C 作圆的切线l ， 过A 作l 的垂线AD ，AD 分别与直线l 、圆交于点D 、E ，则∠DAC ＝ __，线段AE 的长为 __.12、如图，AB 、CD 是圆O 的两条弦， 且AB 是线段CD 的中垂线，已知AB=6，CD=52， 则线段AC 的长度为 ．BADCEABCD13、如图所示，从圆O 外一点P 作圆O 的割线PAB 、PCD ，AB 是圆若PA=4，PC=5，CD=3，则∠CBD= __.14、已知PA 是圆O 的切线，切点为A ，PA=2. AC 是圆O 的直径，PC 与圆则圆O 的半径R=_______.15、.如图所示，PC 切⊙O 于点C ，割线PAB 经过圆心O ，弦CD⊥AB 于点E ，PC=4，PB=8，则CD=________.16、如图所示，从圆O 外一点A 引圆的切线AD 和割线ABC ，已知AD=4AC=8，圆O 的半径为5，则圆心O 到AC 的距离为________.17、如图所示，圆O 是△ABC 的外接圆，过点C 的切线交AB 的延长线于点D ，CD=，AB=BC=3. 则BD 的长______，AC 的长_______．18、如图， ⊙O′和⊙O 相交于A 和B ， PQ 切⊙O 于P ， 交⊙O′于Q 和M ，交AB 的延长线于N ， MN=3，NQ=15，则 PN ＝______．19、如图，PA 是圆的切线，A 为切点，PBC 是圆的 割线，且1P B =B C 2，则P A P B的值是________.BC D O A P 20、.如图，⊙O 的割线PAB 交⊙O 于A 、B 两点，割线 PCD 经过圆心O ，PE 是⊙O 的切线。

数学分析专题选讲教案一、引言1.1 课程背景1.2 课程目标1.3 课程内容概述1.4 教学方法与手段二、函数极限与连续性2.1 函数极限的概念2.2 极限的性质与运算2.3 无穷小与无穷大2.4 函数的连续性2.5 连续函数的性质与应用三、导数与微分3.1 导数的概念3.2 导数的计算规则3.3 高阶导数3.4 隐函数与参数方程函数的导数3.5 微分学的基本定理与应用四、不定积分与定积分4.1 不定积分的基本概念与计算方法4.2 定积分的基本概念与计算方法4.3 定积分的性质与应用4.4 变限积分的导数4.5 定积分的推广与应用五、微分方程5.1 微分方程的基本概念5.2 常微分方程的解法5.3 线性微分方程5.4 微分方程的应用5.5 线性微分方程组六、级数6.1 级数的基本概念6.2 幂级数6.3 泰勒级数与麦克劳林级数6.4 级数的收敛性6.5 级数的应用七、多元函数微分学7.1 多元函数的基本概念7.2 多元函数的极限与连续性7.3 多元函数的偏导数7.4 全微分与高阶偏导数7.5 多元函数的极值及其判定八、重积分8.1 二重积分的基本概念与计算8.2 二重积分的性质与应用8.3 三重积分的基本概念与计算8.4 三重积分的性质与应用8.5 重积分的应用案例九、常微分方程组9.1 常微分方程组的概述9.2 常微分方程组的解法9.3 常微分方程组的解的存在性与唯一性9.4 常微分方程组的应用9.5 常微分方程组的数值解法十、泛函分析与线性空间10.1 泛函分析的基本概念10.2 线性空间与线性映射10.3 内积空间与正交关系10.4 希尔伯特空间与巴拿赫空间10.5 泛函分析在数学分析中的应用十一、微分几何11.1 微分几何基本概念11.2 曲线和曲面的切线与法线11.3 曲率、挠率和曲率张量11.4 测地线与测地线方程11.5 微分几何在物理学和工程学中的应用十二、偏微分方程12.1 偏微分方程的定义与分类12.2 偏微分方程的基本解法12.3 偏微分方程的解的存在性与唯一性12.4 偏微分方程的应用案例12.5 偏微分方程的数值解法十三、复变函数13.1 复数与复平面13.2 复变函数的基本概念13.3 复变函数的积分13.4 复变函数的级数13.5 复变函数在复平面上的应用十四、随机变量与概率积分14.1 随机变量及其分布14.2 随机变量的数字特征14.3 概率积分与变换14.4 随机过程的基本概念14.5 随机过程的应用十五、数值分析15.1 数值分析概述15.2 插值法与函数逼近15.3 数值微积分15.4 常微分方程的数值解法15.5 非线性方程与系统的数值解法重点和难点解析一、函数极限与连续性重点：函数极限的性质与运算，无穷小与无穷大的概念，函数的连续性及其性质。

高三数学一轮总结复习目录理科数学 -模拟试题分类目录1第一章会合与常用逻辑用语1.1 会合的观点与运算专题 1 会合的含义与表示、会合间的基本关系专题 2 会合的基本运算专题 3 与会合有关的新观点问题1.2 命题及其关系、充要条件专题 1 四种命题及其关系、命题真假的判断专题 2 充足条件和必需条件专题 3 充足、必需条件的应用与研究（利用关系或条件求解参数范围问题）1.3 简单的逻辑联络词、全称量词与存在量词专题 1 含有简单逻辑联络词的命题的真假专题 2 全称命题、特称命题的真假判断专题 3 含有一个量词的命题的否认专题 4 利用逻辑联络词求参数范围第二章函数2.1 函数及其表示专题 1 函数的定义域专题 2 函数的值域专题 3 函数的分析式专题 4 分段函数2.2 函数的单一性与最值专题 1 确立函数的单一性（或单一区间）专题 2 函数的最值专题 3 单一性的应用2.3 函数的奇偶性与周期性专题 1 奇偶性的判断专题 2 奇偶性的应用专题 3 周期性及其应用2.4 指数与指数函数专题 1 指数幂的运算专题 2 指数函数的图象及应用专题 3 指数函数的性质及应用2.5 对数与对数函数专题 1 对数的运算专题 2 对数函数的图象及应用专题 3 对数函数的性质及应用2.6 幂函数与二次函数专题 1 幂函数的图象与性质专题 2 二次函数的图象与性质2.7 函数的图像专题 1 函数图象的辨别专题 2 函数图象的变换专题 3 函数图象的应用2.8 函数与方程专题 1 函数零点所在区间的判断专题 2 函数零点、方程根的个数专题 3 函数零点的综合应用2.9 函数的应用专题 1 一次函数与二次函数模型专题 2 分段函数模型2专题 3 指数型、对数型函数模型第三章导数及其应用3.1 导数的观点及运算专题 1 导数的观点与几何意义专题 2 导数的运算3.2 导数与函数的单一性、极值、最值专题 1 导数与函数的单一性专题 2 导数与函数的极值专题 3 导数与函数的最值3.3 导数的综合应用专题 1 利用导数解决生活中的优化问题专题 2 利用导数研究函数的零点或方程的根专题 3 利用导数解决不等式的有关问题3.4 定积分与微积分基本定理专题 1 定积分的计算专题 2 利用定积分求平面图形的面积专题 4 定积分在物理中的应用第四章三角函数、解三角形4.1 三角函数的观点、同角三角函数的基本关系及引诱公式专题 1 三角函数的观点专题 2 同角三角函数的基本关系专题 3 引诱公式4.2 三角函数的图像与性质专题 1 三角函数的定义域、值域、最值专题 2 三角函数的单一性专题 3 三角函数的奇偶性、周期性和对称性4.3 函数 y = A sin(wx +j ) 的图像及应用专题 1 三角函数的图象与变换专题 2 函数 y=Asin( ωx+φ ) 图象及性质的应用4.4 两角和与差的正弦、余弦与正切公式专题 1 非特别角的三角函数式的化简、求值专题 2 含条件的求值、求角问题专题 3 两角和与差公式的应用4.5 三角恒等变换专题 1 三角函数式的化简、求值专题 2 给角求值与给值求角专题 3 三角变换的综合问题4.6 解三角形专题 1 利用正弦定理、余弦定理解三角形专题 2 判断三角形的形状专题 3 丈量距离、高度及角度问题专题 4 与平面向量、不等式等综合的三角形问题第五章平面向量5.1 平面向量的观点及线性运算专题 1 平面向量的线性运算及几何意义专题 2 向量共线定理及应用专题 3 平面向量基本定理的应用5.2 平面向量基本定理及向量的坐标表示专题 1 平面向量基本定理的应用3专题 2 平面向量的坐标运算专题 3 平面向量共线的坐标表示5.3 平面向量的数目积专题 1 平面向量数目积的运算专题 2 平面向量数目积的性质专题 3 平面向量数目积的应用5.4 平面向量的应用专题 1 平面向量在几何中的应用专题 2 平面向量在物理中的应用专题 3 平面向量在三角函数中的应用专题 4 平面向量在分析几何中的应用第六章数列6.1 数列的观点与表示专题 1 数列的观点专题 2 数列的通项公式6.2 等差数列及其前 n 项和专题 1 等差数列的观点与运算专题 2 等差数列的性质专题 3 等差数列前 n 项和公式与最值6.3 等比数列及其前 n 项和专题 1 等比数列的观点与运算专题 2 等比数列的性质专题 3 等比数列前 n 项和公式6.4 数列乞降专题 1 分组乞降与并项乞降专题 2 错位相减乞降专题 3 裂项相消乞降6.5 数列的综合应用专题 1 数列与不等式相联合问题专题 2 数列与函数相联合问题专题 3 数列中的研究性问题第七章不等式推理与证明7.1 不等关系与一元二次不等式专题 1 不等式的性质及应用专题 2 一元二次不等式的解法专题 3 一元二次不等式恒建立问题7.2 二元一次不等式（组）与简单的线性规划问题专题 1 二元一次不等式（组）表示的平面地区问题专题 2 与目标函数有关的最值问题专题 3 线性规划的实质应用7.3 基本不等式及其应用专题 1 利用基本不等式求最值专题 2 利用基本不等式证明不等式专题 3 基本不等式的实质应用7.4 合情推理与演绎推理专题 1 概括推理专题 2 类比推理专题 3 演绎推理7.5 直接证明与间接证明专题 1 综合法4专题 2 剖析法专题 3 反证法7.6 数学概括法专题 1 用数学概括法证明等式专题 2 用数学概括法证明不等式专题 3 概括－猜想－证明第八章立体几何8.1 空间几何体的构造及其三视图和直观图专题 1 空间几何体的构造专题 2 三视图与直观图8.2 空间几何体的表面积与体积专题 1 空间几何体的表面积专题 2 空间几何体的体积专题 3 组合体的“接”“切”综合问题8.3 空间点、直线、平面之间的地点关系专题 1 平面的基天性质及应用专题 2 空间两条直线的地点关系专题 3 异面直线所成的角8.4 直线、平面平行的判断与性质专题 1 线面平行、面面平行基本问题专题 2 直线与平面平行的判断与性质专题 3 平面与平面平行的判断与性质8.5 直线、平面垂直的判断与性质专题 1 垂直关系的基本问题专题 2 直线与平面垂直的判断与性质专题 3 平面与平面垂直的判断与性质专题 4 空间中的距离问题专题 5 平行与垂直的综合问题（折叠、研究类）8.6 空间向量及其运算专题 1 空间向量的线性运算专题 2 共线定理、共面定理的应用专题 3 空间向量的数目积及其应用8.7 空间几何中的向量方法专题 1 利用空间向量证明平行、垂直专题 2 利用空间向量解决研究性问题专题 3 利用空间向量求空间角第九章分析几何9.1 直线的倾斜角、斜率与直线的方程专题 1 直线的倾斜角与斜率专题 2 直线的方程9.2 点与直线、两条直线的地点关系专题 1 两条直线的平行与垂直专题 2 直线的交点问题专题 3 距离公式专题 4 对称问题9.3 圆的方程专题 1 求圆的方程专题 2 与圆有关的轨迹问题专题 3 与圆有关的最值问题59.4 直线与圆、圆与圆的地点关系专题 1 直线与圆的地点关系专题 2 圆与圆的地点关系专题 3 圆的切线与弦长问题专题 4 空间直角坐标系9.5 椭圆专题 1 椭圆的定义及标准方程专题 2 椭圆的几何性质专题 3 直线与椭圆的地点关系9.6 双曲线专题 1 双曲线的定义与标准方程专题 2 双曲线的几何性质9.7 抛物线专题 1 抛物线的定义与标准方程专题 2 抛物线的几何性质专题 3 直线与抛物线的地点关系9.8 直线与圆锥曲线专题 1 轨迹与轨迹方程专题 2 圆锥曲线中的范围、最值问题专题 3 圆锥曲线中的定值、定点问题专题 4 圆锥曲线中的存在、研究性问题第十章统计与统计事例10.1 随机抽样专题 1 简单随机抽样专题 2 系统抽样专题 3 分层抽样10.2 用样本预计整体专题 1 频次散布直方图专题 2 茎叶图专题 3 样本的数字特点专题 4 用样本预计整体10.3 变量间的有关关系、统计事例专题 1 有关关系的判断专题 2 回归方程的求法及回归剖析专题 3 独立性查验第十一章计数原理11.1 分类加法计数原理与分步乘法计数原理专题 1 分类加法计数原理专题 2 分步乘法计数原理专题 3 两个计数原理的综合应用11.2 摆列与组合专题 1 摆列问题专题 2 组合问题专题 3 摆列、组合的综合应用11.3 二项式定理专题 1 通项及其应用专题 2 二项式系数的性质与各项系数和专题 3 二项式定理的应用第十二章概率与统计612.1 随机事件的概率专题 1 事件的关系专题 2 随机事件的频次与概率专题 3 互斥事件、对峙事件12.2 古典概型与几何概型专题 1 古典概型的概率专题 2 古典概型与其余知识的交汇（平面向量、直线、圆、函数等）专题 3 几何概型在不一样测度中的概率专题 4 生活中的几何概型问题12.3 失散型随机变量及其散布列专题 1 失散型随机变量的散布列的性质专题 2 求失散型随机变量的散布列专题 3 超几何散布12.4 失散型随机变量的均值与方差专题 1 简单的均值、方差问题专题 2 失散型随机变量的均值与方差专题 3 均值与方差在决议中的应用12.5 二项散布与正态散布专题 1 条件概率专题 2 互相独立事件同时发生的概率专题 3 独立重复试验与二项散布专题 4 正态散布下的概率第十三章算法初步、复数13.1 算法与程序框图专题 1 次序构造专题 2 条件构造专题 3 循环构造13.2 基本算法语句专题 1 输入、输出和赋值语句专题 2 条件语句专题 3 循环语句13.3 复数专题 1 复数的有关观点专题 2 复数的几何意义专题 3 复数的代数运算第十四章选修模块14.1 几何证明选讲专题 1 平行线分线段成比率定理专题 2 相像三角形的判断与性质专题 3 直角三角形的射影定理专题 4 圆周角、弦切角及圆的切线专题 5 圆内接四边形的判断及性质专题 6 圆的切线的性质与判断专题 7 与圆有关的比率线段14.2 坐标系与参数方程专题 1 极坐标与直角坐标的互化专题 2 直角坐标方程与极坐标方程的互化专题 3 曲线的极坐标方程的求解专题 4 曲线的参数方程的求解专题 5 参数方程与一般方程的互化7专题 6 极坐标方程与参数方程的应用14.3 不等式选讲专题 1 含绝对值不等式的解法专题 2 绝对值三角不等式的应用专题 3 含绝对值不等式的问题专题 4 不等式的证明8。

绝密★启用前2008年普通高等学校招生全国统一考试（江苏卷）数 学本试卷分第I 卷（填空题）和第II 卷（解答题）两部分．考生作答时，将答案答在答题卡上，在本试卷上答题无效．考试结束后，将本试卷和答题卡一并交回． 注意事项： 1．答题前，考生先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的准考证号、姓名，并将条形码粘贴在指定位置上．2．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或炭素笔书写，字体工整，笔迹清楚． 3．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效． 4．保持卡面清洁，不折叠，不破损．5．作选考题时，考生按照题目要求作答，并用2B 铅笔在答题卡上把所选题目对应的标号涂黑．参考公式：样本数据1x ，2x ， ，n x 的标准差锥体体积公式s =13V Sh =其中x 为样本平均数 其中S 为底面面积、h 为高 柱体体积公式 球的表面积、体积公式V Sh =24πS R =，34π3V R =其中S 为底面面积，h 为高 其中R 为球的半径一、填空题：本大题共14小题，每小题5分，共70分． 1．)6cos()(πω-=x x f 最小正周期为5π，其中0>ω，则=ω ▲ 2．一个骰子连续投2次，点数和为4的概率 ▲3．),(11R b a bi a ii∈+-+表示为的形式，则b a += ▲ 4．{}73)1(2-<-=x x x A ，则集合A Z 中有 ▲ 个元素5．b a ,的夹角为120，1,3a b == ，则5a b -= ▲6．在平面直角坐标系xoy 中，设D 是横坐标与纵坐标的绝对值均不大于2的点构成的区域，E 是到原点的距离不大于1的点构成的区域，向D 中随机投一点，则落入E 中的概率 ▲7．某地区为了解70~80岁老人的日平均睡眠时间（单位：h ），现随机地选择50位老人做调查，下表是50位老人日睡眠时间频率分布表：则输出的S 的值为 ． 8．直线b x y +=21是曲线ln (0)y x x =>的一条切线，则实数b 的值为 ▲9．在平面直角坐标系中，设三角形ABC 的顶点分别为)0,(),0,(),,0(c C b B a A ，点P （0，p ）在线段AO 上（异于端点），设p c b a ,,,均为非零实数，直线CP BP ,分别交AB AC ,于点F E ,，一同学已正确算的OE 的方程：01111=⎪⎪⎭⎫⎝⎛-+⎪⎭⎫⎝⎛-y a p x c b ，请你求OF 的方程： ( ▲ )011=⎪⎪⎭⎫⎝⎛-+y a p x10．将全体正整数排成一个三角形数阵：1 2 3 4 5 6 7 8 9 10。

高三一轮第八章平面解析几何8。

5 椭圆【教学目标】1.掌握椭圆的定义、几何图形、标准方程及简单性质．2。

了解椭圆的简单应用．3.理解数形结合思想.【重点难点】1。

教学重点：掌握椭圆的定义、几何图形、标准方程及简单性质；2.教学难点：学会对知识进行整理达到系统化,提高分析问题和解决问题的能力；【教学策略与方法】自主学习、小组讨论法、师生互动法【教学过程】图形性质范围－a≤x≤a－b≤y≤b－b≤x≤b－a≤y≤a对称性对称轴：坐标轴;对称中心：原点顶点A1(－a,0），A2（a,0)B1（0,－b)，B2(0，b）A1(0，－a)，A2(0,a）B1（－b,0）,B2(b，0)离心率e＝错误!，且e∈（0，1)轴长轴A1A2的长为2a短轴B1B2的长为2b焦距|F1F2｜＝2ca，b，c的关系a2＝b2＋c21．必会结论；(1）点P（x0，y0)在解题中注意引导学生自主分析和解决问题,教师及时点拨从而提高学生的解题能力和兴趣。

教师引教师引导学生及时总结，以帮助学生形成完整的认知结构。

引导学生对所学的知识不妨设点B在第一象限,由AB⊥x轴，∴B错误!，A错误!.由于AB∥y轴，｜F1O｜＝｜OF2｜，∴点D为线段BF1的中点，则D错误!，由于AD⊥F1B，知错误!·错误!＝0,则错误!·错误!＝2c2－3b42a2＝0,即2ac＝错误!b2，∴2ac＝错误!（a2－c2),又e＝错误!，且e∈（0,1),∴错误!e2＋2e－错误!＝0，解得e＝错误!（e＝－错误!舍去）．【答案】错误!跟踪训练：1．设F1，F2分别是椭圆C:错误!＋错误!＝1（a〉b〉0)的左、右焦点,点P在椭圆C上，若线段PF1的中点在y轴上,∠PF1F2＝30°，则椭圆的离心率为（）A.错误!B。

错误!C.错误!D 。

错误!【解析】如图,设PF1的中点为M,连接PF2。

因为O为F1F2的中点,所以OM 为△PF1F2的中位线．所以OM∥PF2,所以∠PF2F1＝∠MOF1＝90°.因为∠PF1F2＝30°,所以|PF1｜＝2|PF2｜.由勾股定理得|F1F2｜＝错误!＝（1). (2014·安徽高考)设F1，F2分别是椭圆E：x2＋错误!＝1(0〈b<1）的左、右焦点,过点F1的直线交椭圆E于A，B两点．若｜AF1｜＝3｜F1B|,AF2⊥x轴，则椭圆E的方程为________．(2)（2015·陕西高考）已知椭圆E:错误!＋错误!＝1（a〉b>0）的半焦距为c，原点O到经过两点（c，0），（0,b）的直线的距离为12 c。