历年真题汇编试卷 参考答案及解析_4122
- 格式:pdf
- 大小:165.66 KB
- 文档页数:3

真题汇编(一)参考答案及解析一、单项选择题1.【答案】A。
解析:人类历史上最早、最完整论述教育问题的著作是我国的《学记》。
2.【答案】C。
解析:亚里士多德的和谐教育思想以灵魂论为基础、以培养优良的公民为目标、以德智体和谐发展为内容、以音乐陶冶为途径。
其最早根据儿童身心发展的特点提出按年龄划分教育阶段的主张。
3.【答案】A。
解析:“用一把钥匙开一把锁”意为用不同的方法解决不同的问题,在教学中教师要因材施教,有针对性地对学生进行个别指导。
4.【答案】C。
解析:奥苏贝尔指出,有意义学习过程的实质是将符号所代表的知识与学习者认知结构中已有知识的适当观念建立非人为的和实质性的联系。
5.【答案】B。
解析:“君子欲化民成俗,其必由学乎”出自《礼记•学记》,意思是君子如果要教化人民,形成良好的风俗习惯,一定要从教育入手。
表达了这样一种治学精神,即教育担负的最大责任不是传承知识,而是移风易俗。
“古之王者,建国君民,教学为先”意为古代的君王建立国家,治理民众,都把教育当作首要的事情。
都体现了社会本位论的教育目的观。
6.【答案】C。
解析:教师劳动的创造性主要表现在三个方面:因材施教、教育方法的不断更新和教育机智。
7.【答案】D。
解析:美国教育学家布鲁纳提出了结构教学理论和发现式学习法。
他认为学习是一个主动形成和发展认知结构的过程,是在内在动机的推动下,学习者主动对新知识加以选择、转换、储存和应用的过程。
8.【答案】D。
解析:刚能引起感觉的最小刺激量称为绝对感觉阈限,与之相应的感觉能力称为绝对感受性,二者在数值上成反比关系。
能觉察的刺激物的最小差异量称为差别感觉阈限或最小可觉差,与之相应的感受能力称为差别感受性,它与差别阈限在数值上成反比。
9.【答案】A。
解析:“入芝兰之室,久而不闻其香”在心理学中把这种现象称为感觉的适应。
适应现象指的是在同一刺激持续作用于同一感受器而产生的感受性提高或降低的变化。
10.【答案】A。
解析:有利于教育的原则是班级组织建构的首要原则。

历年全国卷高考政治真题汇编12.2012年,某县农民种植的土豆产量大增.但市场没有相应扩大.农民不得不低价销售收入不增反降。
图5的①②⑤④中,能够反映这种“丰产不丰收”经济现象的是A.①B.②C.③D.④13.中国H公司与美国某公司签订服装出口合同。
约定服装单价为2幸美元,一年后交货。
H公司生产一件服装的成本是144人民币元。
签订合同时汇率为1美元=6.32人民币元,交货时为1美元=6.27人民币元。
在不考虑其他条件的情况下,H公司交货时的利润率比签约时的利润率A.下降0.83%B.下降0.76%C.上升0.83%D.上升0.76%14.2012年3月,中国某集团公司收购了4个在美国的风电场。
美国政府于9月28日以安全为由签发行政命令禁止该项目的收购。
在多次申诉无效之后,该公司根据美国法律向美国联邦法院提起诉讼。
这一案例表明A.走出去的中国企业面临各种形式的贸易保护主义的挑战B.向投资国司法部门提起诉讼是投资者维护自身利益的最有效手段C.对外直接投资取代商品出口成为中国企业走出去的主要形式D.跨国并购是企业强强联合的主要表现形式15.2011年我国城乡居民人民币储蓄存款余额达35.2万亿元,人均储蓄25548元,分别比2010年增长16%和15.3%,高于同期GDP的增长速度。
根据上述事实可以推断出①社会保障体系不断健全增加了人们储蓄意愿②我国居民的储蓄率随GDP的增长而增长③我国居民投资理财的渠道比较狭窄、品种较少④我国城乡居民的恩格尔系数不断下降A.①②B.①③C.②④D.③④16.十一届全国人大第二十三次会议修改通过新的居民身份证法,规定在居民身份证登记项目中增加指纹信息,同时加大对泄露公民个人信息行为的惩罚力度。
身份证法的这些修改①扩大了对公民权利的保护范围②有利于提高社会管理和服务水平③体现了权利与义务相统一的原则④是坚持依法行政的必要保证A.①②B.①③C.②④D.③④17.2012年初,国务院下发《关于实行最严格水资源管理制度的意见》,明确了严格控制用水总量、用水效率、入河湖排污总量的“三条红线”,将水资源开发、利用、节约和保护的主要指标纳入地方经济社会发展综合评价体系,建立水资源管理责任和考核制度。

2012年4·21联考《申论》真题给定材料查看真题解析及参考答案查看材料收起解析(一)结合“给定材料6”简述动物福利立法有哪些现实意义。
(15分)要求:准确、全面、简明,不超过200字。
参考答案:动物福利是人类合理利用动物前提下保障动物权益的行为和提供的外部条件;福利立法是衡量社会文明程度的重要标志:1.保护生态环境、促进动物产业发展,确保国家、社会的可持续利益。
2.为反对贸易壁垒提供法律保障,确保动物产品产量与质量。
3.体现动物对于人类的精神价值,反映人类尊重生命的基本态度。
4.规范人与动物和谐关系,限制不文明、不合理虐待动物行为;5.维持物种内部、物种之间以及生态系统的多样性平衡。
查看材料收起解析(二)根据“给定材料1”,“活熊取胆”事件中存在的一些具体争议,请归纳争议的焦点问题并作简要说明。
(20分)要求:准确、全面、简明,不超过400字。
参考答案:争议的焦点是:活熊取胆存废与否?表现为:1.活熊取胆无痛还是虐待?支持者认为活熊取胆是无管引流,对熊无不良影响;反对者认为对熊危害巨大,手术风险大。
2.活熊取胆是否无法替代?支持者认为熊胆药物不可替代,为医药必需品,性能最佳;反对者认为熊胆药物可被替代,人工熊胆疗效.质量稳定性。
3.活熊取胆质量真的好吗?反对者认为活熊取胆会导致熊胆汁循环不足,引流口有生理变化,质量较差,甚至威胁消费者身体健康。
4.活熊取胆汁与天然熊胆质量一样吗?反对者认为活熊取胆汁与天然熊胆质量有很大差距,引流熊与天然熊的生活方式和饮食结构有很大差异。
5.活熊取胆应限制用途吗?目前活熊取胆汁多被用于保健品等礼品消费;反对者认为使用违反国家标准,应给与严格限制。
6.活熊有义务为人服务吗?支持者认为活熊有义务为人服务;反对者认为人有义务合理利用动物。
两方说法都有道理,但反对方的观点更合理,说服性更强。
查看材料收起解析(三)为了维护M县的声誉,挽回“虐猫事件”造成的负面影响,请以M县政府的名义就“虐猫事件”的处理情况写一份宣传稿,在县人民政府网站上公布。

第一部分言语理解与表达本部分包括表达与理解两方面的内容,请根据题目要求,在四个选项中选出一个最恰当的答案。
请开始答题:1.“诗是不可译的,中国古典诗歌更是不可译的。
”爱好古典诗歌的中国人,包括不少作家、学者、翻译家常常如是说,语气中带着七分三分。
然而,话说回来,如果没有翻译。
中国古典诗歌如何走出国门,走向世界呢?依此填入划横线部分最恰当的一项是()A.自豪遗憾B.无奈悲伤C.感伤埋怨D.骄傲惭愧2.茶艺与茶道精神是中国茶文化的核心,“艺”是指制茶、烹茶、品茶等艺茶之术,“道”是指艺茶过程中所的精神。
有道而无艺,那是的理论;有艺而无道,艺则无精、无神。
依此填入划横线部分最恰当的一项是()A.传达虚浮B.包涵虚无C.贯穿空洞D.体现枯燥3.从20世纪90年代“人类基因工程”计划启动之日起,美国,日本,欧洲等展开了一场激烈的基因专利争夺战,因为谁拥有专利,就意味着谁能在国籍上获得基因产业的“王牌”,谁就能拥有今后基因开发的庞大市场,为此,美国等少数发达国家大量地将阶段性研究成果申请了专利。
依此填入划横线部分最恰当的一项是()A.垄断抢先B.操作独立C.控制自发D.专营及时4.明代工艺品的名字大都先强调年号,然后再强调东西本身,但景泰蓝不是在景泰年间出现,而是在元代就出现了,到了景泰年间,皇家的重视使它,因此有了今天这样一个通俗易懂且带有文学色彩的名字──景泰蓝。
依此填入划横线部分最恰当的一项是()A.如日中天B.名声大噪C.声名鹊起D.享誉中外5.五四运动后,许多人追求真理。
追求人们开始用新的眼光看中国、看世界,从对各种社会思潮,政治主张和政治力量的中认真思考,逐步看到西方的种种社会,开始怀疑资产阶级共和国的救国方案。
依此填入划横线部分最恰当的一项是()A.识别通病B.甄别矛盾C.辨别现象D.鉴别弊端6.世界主要经济发展发达国家和地区目前已就发展低碳经济达成共识:以经济发展模式由“高碳”向“低碳”转型为,通过市场机制下的经济手段推动低碳经济的发展,以减缓人类活动对气候的破坏并逐渐达到一种互相的良性发展状态。

第一部分言语理解与表达(共40题,参考时限35分钟)本部分包括表达与理解两方面的内容,根据题目要求,在四个选项中选出一个最恰当的答案。
请开始答题:1.史学研究如果离开了哲学的——,不关注重大的历史事变和基本的理论问题,以繁琐考辨取代理论思维,以堆砌资料为——,以叠床架屋为——,拾芝麻以为玑珠,袭陈言而自诩多闻,见枯木以为树林,——,见小遗大,就注定要湮没在史料的汪洋之中,堕落为服务故纸堆的陈腐工具。
依次填入划横线部分最恰当的一项是:A.指引多强一孔见天B.引导广美窥斑见豹C.指导博精以偏概全D.指点全妙以管窥天2.克罗地亚在入欧盟的过程中,将国内仅有的数十家大型国企卖给了外国投资者,而很多工厂企业也在入欧盟改革中纷纷关闭,有人说这将使得克罗地亚的发展——。
但是,克罗地亚目前的经济水平比起欧盟中那些负债累累的国家来说还是要____。
现在看来,加入欧盟后克罗地亚将负担援助他国的义务才是大问题,这恐怕与克罗地亚人的预期——。
依次填入划横线部分最恰当的一项是:A.难以可期聊以自慰相差甚大B.难以实现稍胜一筹相去甚远C.难以为继略胜一筹相差甚远D.难以持续后来居上相去良多3.文化认同作为小到一个群体、大到一个民族向心力的有机“粘合剂”’是凝聚这个群体和民族伟大精神力量的——。
文化认同如果缺失,社会语境便趋于焦虑’人们的价值取向便会——,因为文化认同相对于政治认同和社会认同,具有更深远的——。
依次填入划横线部分最恰当的一项是:A.基础丧失意义B.根本丢失价值C.根基迷失内涵D.基础失落涵义4.“徒法不足以自行”。
在目前公车管理还不甚规范的大环境下,单一的公车尾号限行政策值得——。
真要实行的话,要——其负面作用。
至少’要——拿出措施防止公车因此而增加-依次填入划横线部分最恰当的一项是:A.商议提防临阵磨枪B.商榷谨防未雨绸缪C.商讨警惕居安思危D.商量防备有备无患《行政职业能力测验》题本第1 页(共28页)5.中国古代货币,是世界上起源最早的货币之一。
2014年412联考行测真题解析——资料分析华图教育2014年上半年全国春季联考行测部分已经结束,华图公务员考试研究中心对行测各部分做出精确解析,希望对广大考生有所帮助。
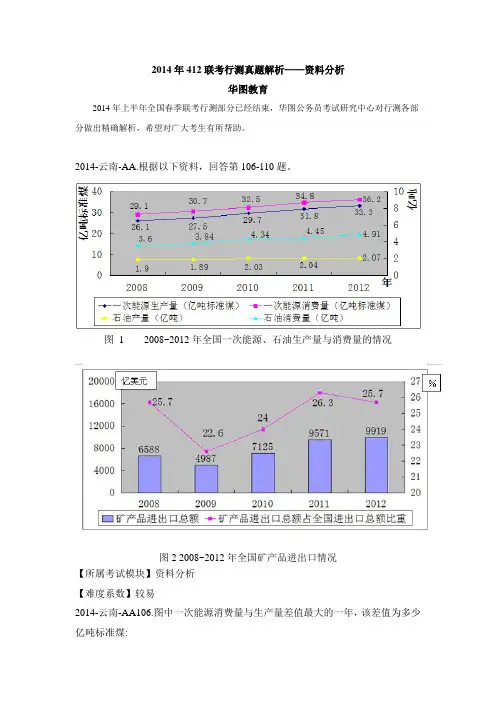
2014-云南-AA.根据以下资料,回答第106-110题。
图 1 2008~2012年全国一次能源、石油生产量与消费量的情况图2 2008~2012年全国矿产品进出口情况【所属考试模块】资料分析【难度系数】较易2014-云南-AA106.图中一次能源消费量与生产量差值最大的一年,该差值为多少亿吨标准煤:A.2.9B.3.0C.3.1D.3.2【答案】D【题型】【考点】简单计算【难度系数】易【作者】邱贻涛【华图教育】差值最大的一年为2009年,30.7-27.5=3.2 选D---------------------------------------------------------------2014-云南-AA107.2009-2012年间一次能源生产量增速最快的一年是?A.2009年B.2010年C.2011年D.2012年【答案】B【题型】【考点】增长率比较【难度系数】中等【作者】邱贻涛【华图教育】2009年的增长率为:(27.5-26.1)/26.1;2010年为:(29.7-27.5)/27.5;2011年为:(31.8-29.7)/29.7;2012年为:(33.3-31.8)/31.8;显然,2010年最大【技巧】分数的比较---------------------------------------------------------------2014-云南-AA108.2008-2012年间,全国石油消费量超过全国石油产量2倍的年份有几个?A.2B.3D.5【答案】C【题型】【考点】简单计算【难度系数】易【作者】邱贻涛【华图教育】石油消费量超过产量两倍的年份有2009,2010,2011,2012,共4年,选C---------------------------------------------------------------2014-云南-AA109.2009-2012年间全国商品进出口总额最高年份,矿产品进出口总额比上年:A.上升了348亿美元B.下降了1601亿美元C.上升了2138亿美元D.上升了2446亿美元【答案】A【题型】【考点】比重【难度系数】中等【作者】邱贻涛【华图教育】2009-2012年间全国商品进出口总额最高年份为2012年,矿产品进出口比上年增加9919-9571=348(亿美元),选A---------------------------------------------------------------2014-云南-AA110.关于2009-2012年全国矿产品贸易和能源生产、消费,能够从上述资料中推出的是:A.石油产量年均增速超过一次能源生产量B.矿产品进出口总额占全国商品进出口总额比重逐年递增C.矿产品进出口总额最低的年份,一次能源消费同比增量也最低D.平均每年一次能源生产量超过30亿吨标准煤【题型】【考点】综合分析【难度系数】易【作者】邱贻涛【华图教育】A选项,石油产量年均增速为:1.90×(1+r1)4=2.07 ,一次能源生产量年均增速为:26.1×(1+r2)4=33.3,显然,r1<r2,A项错;B选项,矿产品进出口总额占全国商品进出口总额比重2012年下降,B项错;C选项,矿产品进出口总额最低的年份为2009年,而一次能源消费同比增速最低的为2012年,C项错;D选项,平均每年一次能源生产量为(27.5+29.7+31.8+33.3)/4=30.575,所以选D【技巧】三难一易。


1951年普通高等学校招生全国统一考试数学第一部分:1.设有方程组x+y=8,2x-y=7,求x ,y.解略:⎩⎨⎧==35y x2.若一三角形的重心与外接圆圆心重合,则此三角形为何种三角形? 证:设△ABC 的重心与外接圆的圆心均为O (图1)∵OA=OC ,E 为AC 的中点,∴BE ⊥AC ;同理,CD ⊥AB ,AF ⊥BC 在Rt △ABE 与Rt △ACD 中,∠A 为公共角,BE=CD=R+21R=23R (R 为外接圆半径),所以△ABE ≌△ACD ,AB=AC ,同理可得AB=BC 由此可知△ABC 为等边三角形3.当太阳的仰角是600时,若旗杆影长为1丈,则旗杆长为若干丈? 解略:3丈0)()()(:)()(,)(,,:?,,,,.4=-+-+-=++-=-=-==-=-=-=++-=-=-t a c t c b t b a z y x t a c tz c b y t b a x t ac zc b y b a x z y x c b a a c zc b y b a x 由此可得则有设解则各不相等而若5.试题10道,选答8道,则选法有几种?解略:45810=c 6.若一点P 的极坐标是(r,θ),则它的直角坐标如何? 解:x=r θcos ,y=r θsin7.若方程x 2+2x+k=0的两根相等,则k=? 解:由Δ=b 2-4ac=0,得k=18.列举两种证明两个三角形相似的方法OABCEFD答:略9.当(x+1)(x-2)<0时,x 的值的范围如何? 解略:-1<x <210.若一直线通过原点且垂直于直线ax+by+c=0,求直线的方程解略:bx-ay=011.(x +x1)6展开式中的常数项如何? 解:由通项公式可求得是T 4=2012.02cos =θ的通解是什么? 解:).(4为整数k k π±π=θ13.系数是实数的一元三次方程,最少有几个根是实数,最多有几个根是实数?答:最少是一个,最多是三个14.解:原式=1003)5(4)2(4550554)5(55430)2(=⋅-⋅--⋅⋅-⋅⋅-⋅⋅-+⋅⋅+⋅⋅- 15.x 2-4y 2=1的渐近线的方程如何? 解略:02=±y x?345505542=--16.三平行平面与一直线交于A ,B ,C 三点,又与另一直线交于A ',B ',C '三点,已知AB=3,BC=7及A 'B '=9求A 'C '解:如图易证:3011=''∴''''==C A C A B A AC AB AC AB 17.有同底同高的圆柱及圆锥,已知圆柱的体积为18立方尺,求圆锥的体积略:6立方尺18.已知lg2=0.3010,求lg5. 略:lg5=1-lg2=0.699019.二抛物线y 2=12x 与2x 2=3y 的公共弦的长度是多少?解略:解方程组得两公共点为(0,0)及(3,6)故其公共弦长为:5320.国旗上的正五角星的每一个顶角是多少度? 解:由图可知:∠AFG=∠C+∠E=2∠C, ∠AGF=∠B+∠D=2∠B,∴∠A+∠AFG+∠AGF=∠A+2∠C+2∠B=5∠A ∴5∠A=1800,∴∠A=360 第二部分:A A ' αB B ' βB 1γ C C 'C 1FGAC EBD1.P ,Q ,R 顺次为△ABC 中BC ,CA ,AB 三边的中点,求证圆ABC 在A 点的切线与圆PQR 在P 点的切线平行证:如图:由AD 是大圆的切线, 可得: ∠1=∠2由RQ ∥BC ,可得:∠2=∠3, 由QP ∥AB ,可得:∠3=∠4由PE 是小圆的切线, 可得: ∠4=∠5由RP ∥AC ,可得:∠5=∠6综上可得:∠1=∠6,故AD ∥PE2.设△ABC 的三边BC=4pq,CA=3p 2+q 2,AB=3p 2+2pq-q 2,求∠B ,并证∠B 为∠A 及∠C 的等差中项解:由余弦定理可得:.C A B A,-B 60)180(60B 214)23(2)3()4()23(2cos 222222222222的等差中项与是∠∠∠∴∠∠=∠-︒=∠-∠-∠-︒=∠-∠︒=∠∴=⋅-+--+-+=⋅-+=A B B A B C pqq pq p q p pq q pq p BC AB CA BC AB B 3.(1)求证,若方程x 3+ax 2+bx+c=0的三根可排成等比数列, 则a 3c=b 3.证:设α,β,γ是方程x 3+ax 2+bx+c=0的三根,由根与系数关系可知:α+β+γ=-aαβ+βγ+γα=b αβγ=-c564321E QPRA BC又因α,β,γ排成等比数列,于是β2=αγ33333233a )()()(bc c a b ==αβγ-=β-=⎥⎦⎤⎢⎣⎡γ+β+αβγ+β+α-=⎥⎦⎤⎢⎣⎡γ+β+αβ+βγ+α-=⎥⎦⎤⎢⎣⎡γ+β+α-γα+βγ+αβ=⎪⎭⎫⎝⎛此即 (2)已知方程x 3+7x 2-21x-27=0的三根可以排成等比数列,求三根解:由⑴可知β3=-c ,∴β3=27,∴β=3代入α+β+γ=-7可得α+γ=-10,又由α,β,γ成等比数列,∴β2=αγ, 即αγ=9,故可得方程组:⎩⎨⎧--=γ--=α=αγ-=γ+α.91,19,910或或可得解之 于是,所求之三根为-9,3,-1或-1,3,-94.过抛物线顶点任做互相垂直的两弦,交此抛物线于两点,求证此两点联线的中点的轨迹仍为一抛物线证:设抛物线方程为y 2=2px ……………①过抛物线顶点O 任作互相垂直的二弦OA 和 OB ,设OA 的斜率为k ,则直线OB 的斜率为 -k 1,于是直线OA 的方程为: y =kx ………………………②直线OB 的方程为:x k y 1-=③ 设点A (x 1 ,y 1),点B(x 2 ,y 2)由①,②可得: .2,2121k p y k p x ==由①,③可得:YA·P (x,y)O XBx 2=2pk 2, y 2=-2pk设P (x ,y )为AB 的中点,由上可得: ④ ⑤ 由⑤可得: ⑥ 由④可知:px 2222k p kp +=,代入⑥,2p -px y 22222222222=-=-⎪⎪⎭⎫ ⎝⎛+=即p px p k p k p y 所以,点P 的轨迹为一抛物线1952年普通高等学校招生全国统一考试数学第一部分:1.因式分解x 4 – y 4 =?解:x 4 – y 4 =(x 2+y 2)(x+y)(x-y)2.若lg2x=21lgx ,问x=? 解:2x=x 21,x ≠0,∴202=X3.若方程x 3+bx 2+cx+d=0的三根为1,-1,21,则c=?解:由根与系数的关系可知:c=1·(-1)+(-1)·21+21·1=1pk kpy y y pk kp x x x -=+=+=+=222122212222222k p p kp y +-=4.若x x 求,0472=-+解:两边平方,得:x 2 +7=16,∴3±=x5.解:原式=-246.两个圆的半径都是4寸,并且一个圆过另一个圆的圆心,则此两圆的公共弦长是多少寸?解:设两圆O 1及O 2之公共弦为AB 连结O 1O 2交AB 于点C ,则AB垂直平分O 1O 2∴O 1C=21O 1O 2=2(寸)).(342),(3224222121寸寸==∴=-=-=AC AB C O AO AC连结AO 1,则△ACO 1为直角三角形, 7.三角形ABC 的面积是60平方寸,M 是AB 的中点,N 是AC 的中点,△AMN 的面积是多少? 解:∵MN ∥BC ,∴41ABC AMN 22==∆∆ANAM 的面积的面积, △AMN 的面积=41△ABC 的面积=15(平方寸)8.正十边形的一个内角是多少度? 解:由公式,)2(180nn -︒此处n=10于是一个内角为:︒144AO 1 O 2CB?123054321=9.祖冲之的圆周率π=? 答:22/7,355/13310.球的面积等于大圆面积的多少倍? 解:球的面积4πR 2为大圆面积πR 2的4倍11.直圆锥之底半径为3尺,斜高为5尺,则其体积为多少立方尺? 解:圆锥高h=4(尺),故此直圆锥的体积:V 锥 =31πR 2h=12π(立方尺) 12.正多面体有几种?其名称是什么?答:共有五种,其名称为:正四面体,正六面体,正八面体,正十二面体和正二十面体13.已知 sin θ=31,求cos2θ=? 解:cos2θ=1-2sin 2θ=97 14.方程tg2x=1的通解x=? 解:).(82为整数k k x π+π=15.太阳的仰角为300时,塔影长为5丈,求塔高是多少? 解:塔高=5×tg300=335(寸) 16.△ABC 的b 边为3寸,c 边为4寸,A 角为300,问△ABC 的面积为多少平方寸?解:).(330sin 4321sin 21平方寸的面积=︒⋅⋅⋅==∆A bc ABC17.已知一直线经过(2,3),其斜率为-1,则此直线方程如何? 解:即x+y –5=018.若原点在一圆上,而此圆的圆心为(3,4)则此圆的方程如何?解:圆的半径.54322=+=R所以,圆的方程为:(x-3)2+(y-4)2=25,也即:x 2+y 2-6x-8y=019.原点至3x+4y+1=0的距离是什么? 解:.51431040322=++⋅+⋅=d 20.抛物线y 2-8x+6y+17=0的顶点坐标是什么? 解:原方程可变形为:(y+3)2=8(x-1), 故顶点坐标为(1,-3)第二部分:1.解方程x 4+5x 3-7x 2-8x-12=0解:左式=(x 4+5x 3-6x 2)-(x 2+8x+12)=(x+6)[x 2(x-1)-(x+2)] =(x+6)(x 3-x 2-x-2) =(x+6)[(x 3-2x 2)+(x 2-x-2)] =(x+6)(x-2)(x 2+x+1)=0 可得原方程的四根为:.231,231,2,64321ix i x x x --=+-==-= 2.△ABC 中,∠A 外角的平分线与此三角形外接圆相交于P ,求证:BP=CP证:如图,∠CBP=∠CAP=∠PAD 又∠1=∠2由∠CAD=∠ACB+∠CBA=∠ACB+∠CBP+∠2=∠ACB+∠1+∠CBP =∠BCP+∠CBP∴∠BCP=∠CBP ,∴BP=CP 3.设三角形的边长为a =4,b=5,c=6,其对角依次为A ,B ,C 求A B C C sin ,sin ,sin ,cos .问A ,B ,C 三角为锐角或钝角? 解:应用余弦定理,可得: .812cos 222=-+=ab c b a C由此可知C 为锐角;另外,由已知条件,三边边长适合关系式a <b <c ,从而可知∠A <∠B <∠C 由于C 为锐角,故A ,B 亦为锐角.741c asinC sinA .7165sin sin ,.783)81(-1sinC cos -1sinC 22=======c C b B C 可得应用正弦定理可得由 4.一椭圆通过(2,3)及(-1,4)两点,中心为原点,长短轴重合于坐标轴,试求其长轴,短轴及焦点解:由于椭圆过(2,3)及(-1,4)两点,所以将此两点代入标准方程可得:C1P2D A B.75522,35522,355,755,1161194222222==∴==⎪⎩⎪⎨⎧=+=+a b b a b ab a 短轴长轴解之 .2155221220,22222==-=∴-=a b c a b c 又 ).21552,0(),21552,0(21F F -故焦点坐标为1954年普通高等学校招生全国统一考试数学1.甲、化简.])()()[(317212131223b ab b a --- 解:原式=.)()(32310231272321223a b a b b a b a ==--乙、解c b a x lg lg 2lg 31lg 61++= 解略:x=a 2b 12c 6.丙、用二项式定理计算(3.02)4,使误差小于千分之一.,,,001.0)1002()1002(34)1002(36100234310023)02.3(:43223444千分之一其误差必小于计算可到第三项为止所以可知第四项之值已小于解+⋅⋅+⋅⋅+⋅⋅+=⎪⎭⎫ ⎝⎛+=.182.830216.016.281)02.3(4=++=丁、试证直角三角形弦上的半圆的面积,等于勾上半圆的面积与股上半圆的面积的总和证:由c 2 =a 2+b 2∴弦上半圆的面积= 22222221221421221⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+=⎪⎭⎫ ⎝⎛b a b a c ππππ=勾上半圆的面积+股上半圆的面积戊、已知球的半径等于r ,试求内接正方形的体积解:内接正方体的中心即该球的球心正方体过中心的对角线为该球的直径,故其长为2r 若设内接正方体的边长为a ,则有3a 2=4r 2,.398332.332333r r a r a =⎪⎭⎫⎝⎛==∴=内接正方体的体积己、已知a 是三角形的一边,β及γ是这边的两邻角,试求另一边b 的计算公式解:由正弦定理可知.)sin(sin )](180sin[sin ,sin )](180sin[γββγβββγβ+=--︒=∴=--︒a a b b a2.描绘y=3x 2-7x-1的图象,并按下列条件分别求x 的值所在的范围: 1)y >0, 2)y <0).1261(31)67(:2+=-y x 将原方程变形可得解 ).1261,67(,-抛物线顶点为于是)0,6617(,)0,6617(:+-N M x 轴的交点为与).,6617(),6617,(,0+∞+--∞>的值所在范围为时当x y ).6617,6617(,0+-<的值所在范围为时当x y YM O N X)1261,67(-3.假设两圆互相外切,求证用连心线做直径的圆,必与前两圆的外公切线相切证:设⊙O 1及⊙O 2为互相外切之二圆,其一外公切线为A 1A 2,切点为A 1及A 2令点O 为连心线O 1O 2的中点,过O 作OA ⊥A 1A 2∵OA=21(O 1A 1+O 2A 2)=21O 1O 2,∴以O 1O 2为直径,即以O 为圆心,OA 为半径的圆必与直线A 1A 2相切同理可证,此圆必切于⊙O 1及⊙O 2的另一条外公切线4.试由.,2sin 111通值求的x x tgxtgx+=-+ )(0sin 4,1,0sin cos ,0sin )sin (cos 20)sin cos 1)(sin (cos )sin (cos sin cos sin cos :22222为整数或者即或者所以解k k x x k x tgx x x x x x x x x x x x x x x x π=∴=π-π=∴-==+=⋅+=+-++=-+由检验可知,均为其通解5.有一直圆锥,另外有一与它同底同高的直圆柱,假设a 是圆锥的全面积,a '是圆柱的全面积,试求圆锥的高与母线的比值解:设直圆锥的高为h ,底面半径为R ,母线长为L ,则,)(2)(2)(h R L R h R R L R R a a ++=++='ππ .2)2(),()(2,).()(222222222ah L a h L a a L h L a h h L a h L R L R a h R a -'=-'-+-'=+--=+'=+∴代入可得由A 2AA 1O 1 O O 2,.21)2(,2等式两边平方可得两边同除以L h a a L h a a L -'=⎪⎭⎫⎝⎛-'-.)2(4)2()2(22])2(4[2)2()2(44)48(2)2(164:,,0)2(16)4)(48(4)4(.0)4(4)48(,441)44(2222223322222222222222a a a a a a a a a a a a a a a a a a a a a a a a a a a a a L h a a a a a a a a a a a a Lha a a L h a a L h a a a a L h a L h a a a L h a a a a '-+'-'-±'='-+'-'-±'='+'-'-±'=∴>'-='+''+'--'-=∆='+'+'-⎪⎭⎫⎝⎛'+'-⎪⎭⎫⎝⎛+⋅'-'=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-'+'-母线的比此二实根即圆锥的高与实根该一元二次方程有二个式的一元二次方程的判别这个关于1958年普通高等学校招生全国统一考试数学1.甲、求二项式5)21(x +展开式中3x 的系数解:设求的项为.802,32)2(333354551x x C T r x C x C T r r r r r r ==∴===+今乙、求证.sin 88sin 4cos 2cos cos xxx x x =⋅⋅ 证:x x x 4cos 4sin 28sin =xx x x xx x 4cos 2cos cos sin 84cos 2cos 2sin 4=⌒ ⌒⌒ ⌒ ⌒ ⌒ .sin 88sin 4cos 2cos cos xxx x x =⋅⋅∴ 丙、设AB ,AC 为一个圆的两弦,D 为AB 的中点,E 为AC 的中点,作直线DE 交AB 于M ,交AC 于N ,求证:AM=AN证:联结AD 与AE (如图) ∵∠AMN=∠DAM+∠MDA , ∠ANM=∠EAN+∠NEA , 又∵AD=DB ,∠DAB=∠AED ,AE=EC ,∠ADE=∠EAC , ∴∠AMN=∠ANM , AM=AN.丁、求证正四面体ABCD 中相对的两棱(即异面的两棱)互相垂直证:因ABCD 是正四面体, 各个面都是等边三角形, 过A 作AE ⊥BC ,联结DE , 则DE ⊥BC , ∴BC 垂直平面AED , 而AD 在此平面内, ∴BC ⊥AD同理可证AB ⊥DC ,AC ⊥DB戊、求解.cos 3sin x x = 解:,cos 3sin x x =AD EM NBCDCA EB).(3,3为整数k k x tgx π+π==∴ 2.解方程组⎪⎪⎩⎪⎪⎨⎧=++=-+++)2(9122)1(4121 y y x y x y x v y x u yx y x y x =-+=+=-+++12,1,8)12()1()2(:设式变形为由解则原方程变形为⎩⎨⎧=+=+)4(8)3(422 v u v u 解方程组,可得.2,2==v u 将v u ,的值代回所设,可得⎪⎩⎪⎨⎧-==⎩⎨⎧====-==∴=--=--⎪⎩⎪⎨⎧=-+=+⎪⎩⎪⎨⎧=-+=+.21,6;1,3.6,3),5(.21,1,01,112)5()6()6(412)5(41,21221221121212y x y x x x y y y y y y y x y x y x y x 由检验可知代入即得得两边平方都是原方程组的解3.设有二同心圆,半径为R ,r(R>r ),今由圆心O 作半径交大圆于A ,交小圆于A ',由A 作直线AD 垂直大圆的直径BC ,并交BC 于D;由A '作直线A 'E 垂直AD ,并交AD 于E ,已知∠OAD= α,求OE 的长解:在直角△OAD 中, OD=Rsin α,AD=Rcos α 在直角△A 'AE 中, AE=(R-r )cos α ∴DE=AD-AE=Rcos α-(R-r )cos α=rcos α. OE=.cos sin 222222α+α=+r R DE OD4.已知三角形ABC ,求作圆经过A 及AB 中点M ,并与BC 直线相切已知:M 为△ABC 的AB 的中点.求作:一个经过A 、M 两点且与BC 直线相切的圆.AA ' EB O D C分析:设⊙O 即为合于要求的圆(如图)因⊙O 经过A 、M 两点且与直线BC 相切于点P ,这样,BP 为⊙O 的切线,BA 为⊙O 的割线,所以,应有 BP 2=BM ·BA而BM ,BA 均为已知,因此,BP 的长度可以作出,由此可得点P ,于是过A 、M 、P 三点就可确定所求之圆作法:1)作线段A 'B 'M ', 使A 'B '=AB ,B 'M '=BM2)以A 'M '为直径作半圆3)过B '作A 'M '的垂线B 'P '交半圆于点P ' 4)在△ABC 的边BC 上截取BP=B 'P ' 5)经过A 、M 、P 三点作⊙O 即为所求证明:由作图可知B 'P '2= A 'B '·B 'M ',A 'B '=AB ,B 'M '=BM ,所以BP 2=BM ·BA ,即BP 为⊙O 的切线,BMA 为其割线,且⊙O 经过A 、M 、P 三点,故⊙O 适合所要求的条件5.已知直角三角形的斜边为2,斜边上的高为23,求证此直角三角形的两个锐角是下列三角方程的根CPOA BMP 'A 'B ' M '043sin 231sin 2=++-x x 证:设AD=k (如图) ∵AB=2,∴DB=2-k. 由CD 2=AD ·DB ,.2123,0432),2()23(22或==+--=∴k k k k k在直角△ACD 中, 当23==k AD 时,,332323===AD CD tgA ∴A=300,B=600.当21==k AD 时,,32123===AD CD tgA ∴A=600,B=300. 总之,两锐角一为300,一为600. 当x=300时,代入原方程中得;04321231)21(4330sin 23130sin 22=+⋅+-=+︒+-︒ 当x=600时,代入原方程中得.04323231)23(4360sin 23160sin 22=+⋅+-=+︒+-︒ 故这个直角三角形的两个锐角是原三角方程的根CA D B1959年普通高等学校招生全国统一考试数学1.甲、已知lg2=0.3010,lg7=0.8451,求lg35解:原式=2lg 10lg 7lg 2107lg 270lg-+=⨯= =0.8451+1-0.3010=1.5441.乙、求ii +-1)1(3的值.解:.21)1(21221331133132-=++-=+--=++--=+-+-=ii i i i i i i i i i 原式 丙、解不等式.3522<-x x 解:原式移项得,03522<--x x ∴原不等式的解为.321<<-x 丁、求︒165cos 的值解:)3045cos(15cos )15180cos(165cos ︒-︒-=︒-=︒-︒=︒.426)21222322()30sin 45sin 30cos 45(cos +-=⋅+⋅-=︒︒+︒︒-=戊、不在同一平面的三条直线c b a ,,互相平行,A 、B 为b 上两定点,求证另两顶点分别在c a 及上的四面体体积为定值证:因为A 、B 为直线b 上两定点,而直线b ∥直线c ,所以,不论点C 在直线c 的什么位置上,△ABC 的面积均为一定值(同底等高的三角形等积)又因直线a 平行于直线 c b ,,所以,直线a ∥平面α(已知c b a ,,不在同一平面内),因此,不论点D 在直线a 的什么位置上,从点D 到平面α的距离h 为一定值,故四面体ABCD 的体积=定值高底面积=⋅⋅=⨯⨯∆h S ABC 3131己、圆台上底面积为225cm π,下底直径为cm 20,母线为cm 10,求圆台的侧面积解:设此圆台上底半径为r ,下底半径为R ,由已知条件,252π=πr 所以r=5(cm).又下底半径R=10cm ,母线,10cm l =圆台侧面积=πl (R+r)=π·10·(10+5)=150π(cm 2). 2.已知△ABC 中,∠B=600,AC=4,面积为3,求AB 和BC. 解:设AB=c ,BC=a ,则有⎪⎩⎪⎨⎧︒-+==︒),(60cos 24)(360sin 21222余弦定理两边夹角求面积公式ac c a ac D ahA B bOα cC.37,37.32,12)(,72,28)(,,1642222=±=∴±=-∴=-=+∴=+⎩⎨⎧=-+=c a c a c a c a c a ac c a ac 由由解之即故所求AB ,BC 之长为⎩⎨⎧+=-=⎩⎨⎧-=+=.37,37;37,37BC AB BC AB 3.已知三个数成等差数列,第一第二两数的和的3倍等于第三个数的2倍,如果第二个数减去2,则成等比数列,求这三个数解:设所求之三数为d a a d a +-,,则根据题意有⎩⎨⎧==⎪⎩⎪⎨⎧==⎩⎨⎧=-=⎩⎨⎧+-=-+=+-.45;1,45:4454).)(()2(),(2])[(3221122d a d a d a d a d a d a a d a a d a 解得化简后得 故所求三数为.9,5,149,45,41或4.已知圆O 的两弦AB 和CD 延长相交于E ,过E 点引EF ∥CB 交AD 的延长线于F ,过F 点作圆O 的切线FG ,求证:EF=FG. 证:∵FG 为⊙O 的切线,而FDA 为⊙O 的割线,∴FG 2=FD ·FA …………① 又∵EF ∥CB ,∴∠1=∠2.而∠2=∠3, ∴∠1=∠3,∠EFD=∠AFE 为公共角 ∴△EFD ∽△AFE ,,FAEF EF FD =即EF 2=FD ·FA …………②由①,②可得EF 2=FG 2 ∴EF=FG.5.已知A 、B 、C 为直线l 上三点,且AB=BC=a ;P 为l 外一点,且∠APB=900,∠BPC=450,求(1)∠PBA 的正弦、余弦、正切; (2)PB 的长; (3)P 点到l 的距离.解:过P 点作PD ⊥AB 交AB 于点D (如图) (1)过点B 作BE ∥AP 交PC 于点E 则∠PBE=900,∠PEB=450,PB=BE. ∵△CPA ∽△CEB ∴,22==a aBE PA 因PB=BE , ∴.2,2=∠=PBA tg PBPA C G2 FO D1A 3 EBP450 EA a DB a C又∵,sec 122PBA PBA tg ∠=∠+∠PBA 为锐角, ∴,51sec 2=∠+=∠PBA tg PBA.552cos sin ,5551cos =∠⋅∠=∠==∠PBA PBA tg PBA PBA(2).55cos a PBA AB PB =∠⋅= (3),552sin ,55=∠=PBA a PB ∴.52sin a PBA PB PD =∠⋅= 综上,所求为(1)∠PBA 的正弦、余弦、正切分别是2,551,552 (2)PB 的长为;551a (3)P 点到l 的距离为.52a1957年普通高等学校招生全国统一考试数学1.甲、化简32221)27102(1.0)972(--++解:原式=.481110216910035)2764()101()925(32221=++=++--乙、求适合不等式22<+x x 的实数x 的范围解:原式为022<-+x x 解为:-2<x<1. 故x 的范围为-2<x<1. 丙、求证.210322+='︒ctg 证:.2145sin 45cos 12450322+=︒︒+=︒='︒ctgctg丁、在四面体ABCD 中,AC=BD ,P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点,求证:PQRS 为一个菱形证:由于点P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点,根据三角形两边中点连线的性质可得.////,21////BD SP RQ AC RS PQ ====而由题设,AC=BD , ∴PQ=QR=RS=SP , 故 PQRS 为一个菱形 戊、设b a ,为异面直线,EF 为ba ,的公垂线,α为过EF 的中点且与b a ,平行的平面,M 为a 上任一点,N 为b 上任一点求证线段MN 被平面α二等分 证:过直线b 作平面β//α(如图)过直线a 及公垂线EF 作一平面,在此平面内作MC ∥EF ,且与平面α,β分别交于B 、C 两点设EF 、MN 分别与平面α交于点A 、D∵点A 是EF 的中点,ASPDRC BQM E aB Aα DC bN F β又ME ∥BA ∥CF , ∴点B 是MC 的中点又∵DB ∥NC , ∴D 是MN 的中点另法:如图,连接EN ,AB,BD 由AB b BD a b a //,////,//⇒αα由A 是EF 的中点得,D 为MN 的中点此即线段MN 被平面α二等分 2.解方程组⎩⎨⎧⋅==-++)2(101010)1(1)2lg()12lg( yx xy y x 解:由(1)可得,10)2)(12(=-+y x)3(01242 =-+-y x xy由(2)可得)4( y x xy +=将(4)代入(3)可得,012422=-+-+y x y x,01232=-+-y x)5(3212 xy +=再将(5)代入(4)可得,32123212xx x x ++=+⋅ 化简,得,012722=-+x x.41457±-=∴x 将x 值代入(5).6145173212±=+=x y abαEFAMNBD此即⎪⎪⎩⎪⎪⎨⎧-=--=⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457;614517,414572211y x y x 因为,0122<+x 所以(1)式无意义(负数无对数),故原方程组的解仅为⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457y x 3.设△ABC 的内切圆半径为r ,求证BC 边上的高.2sin2cos 2cos 2A CB r AD ⋅⋅=证:在直角△ABC 中,2cos2sin 2sin B B c Bc AD ⋅⋅=⋅=另外,EB AE c +=)22(Bctg A ctgr += 2sin2sin )22sin()2sin 2cos 2sin 2cos (B A B A r B B A A r ⋅+⋅=+=AEc r bOB Ca D.2sin2cos2cos 22cos 2sin2sin 2sin2cos22sin 2sin2cosA CB r B B BA Cr AD B A C r ⋅⋅=⋅⋅⋅⋅=∴⋅⋅= 4.设△ABC 为锐角三角形,以BC 为直径作圆,并从A 作此圆的切线AD 与圆切于D 点,由在AB 边上取AE=AD ,并过E 作AB 的垂线与AC 边的延长线交于F ,求证: (1)AE:AB=AC:AF.(2)△ABC 的面积=△AEF 的面积.证(1):设AB 与⊙O 相交于点G ,联结EC ,CG ,BF.∵EF ⊥AB ,CG ⊥AB ,∴GC ∥EF ,AC:AF=AG:AE ………………① 又∵AD 是⊙O 的切线,∴AD 2=AG ·AB ,也即AG:AD=AD:AB但∵AD=AE ,∴AG:AE=AE:AB ……………② 由①、②可得AE:AB=AC:AF证(2):由(1)AE:AB=AC:AF ,则EC ∥BF ,△EBC 的面积=△EFC 的面积 ∴△ABC 的面积=△AEC 的面积+△EBC 的面积=△AEC 的面积+△EFC 的面积 =△AEF 的面积5.求证方程0)2()12(23=+-++-Q x Q x x 的一个根是1设这个方程的三个根是△ABC 的三个内角的正弦,sin ,sin ,sin C B A 求A 、B 、C 的度数以及Q 的值解:将x=1代入这个方程式, 则01)2(1)12(123=+⋅-+⋅+-Q Q , 故知1是原方程的一个根由于1是原方程的一个根,所以方程左边能被x-1整除AGE DB GOF用x-1除方程左边后得商式.022=--Q x x根据题设条件(即有一个根为1,不妨设1sin =C )及根与系数的关系可得⎪⎩⎪⎨⎧-=⋅=+=)3(sin sin )2(2sin sin )1(1sin Q B A B A C 由(1)可知C=900,于是A+B=900,B=900-A ,代入(2)得.212222sin sin )3(45459045,045,1)45cos(,1cos 45cos sin 45sin ,1cos 22sin 22,2cos sin ,2)90sin(sin -=⋅-=⋅-=︒=︒-︒=︒=∴=︒-∴=︒-=⋅︒+⋅︒=+∴=+=-︒+B A Q B A A A A A A A A A A A 式可得从即1957年普通高等学校招生全国统一考试数学1.甲、化简32221)27102(1.0)972(--++解:原式=.481110216910035)2764()101()925(32221=++=++--乙、求适合不等式22<+x x 的实数x 的范围解:原式为022<-+x x 解为:-2<x<1. 故x 的范围为-2<x<1. 丙、求证.210322+='︒ctg证:.2145sin 45cos 12450322+=︒︒+=︒='︒ctgctg 丁、在四面体ABCD 中,AC=BD ,P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点,求证:PQRS 为一个菱形证:由于点P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点,根据三角形两边中点连线的性质可得.////,21////BD SP RQ AC RS PQ ====而由题设,AC=BD , ∴PQ=QR=RS=SP , 故 PQRS 为一个菱形 戊、设b a ,为异面直线,EF 为ba ,的公垂线,α为过EF 的中点且与b a ,平行的平面,M 为a 上任一点,N 为b 上任一点求证线段MN 被平面α二等分 证:过直线b 作平面β//α(如图)过直线a 及公垂线EF 作一平面,在此平面内作MC ∥EF ,且与平面α,β分别交于B 、C 两点设EF 、MN 分别与平面α交于点ASPDRC BQM E aB Aα DC bN FβA 、D∵点A 是EF 的中点, 又ME ∥BA ∥CF , ∴点B 是MC 的中点又∵DB ∥NC , ∴D 是MN 的中点另法:如图,连接EN ,AB,BD 由AB b BD a b a //,////,//⇒αα由A 是EF 的中点得,D 为MN 的中点此即线段MN 被平面α二等分 2.解方程组⎩⎨⎧⋅==-++)2(101010)1(1)2lg()12lg( yx xy y x 解:由(1)可得,10)2)(12(=-+y x)3(01242 =-+-y x xy由(2)可得)4( y x xy +=将(4)代入(3)可得,012422=-+-+y x y x,01232=-+-y x)5(3212 xy +=再将(5)代入(4)可得,32123212xx x x ++=+⋅ 化简,得,012722=-+x x.41457±-=∴x abαEFAMNBD将x 值代入(5).6145173212±=+=x y 此即⎪⎪⎩⎪⎪⎨⎧-=--=⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457;614517,414572211y x y x 因为,0122<+x 所以(1)式无意义(负数无对数),故原方程组的解仅为⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457y x 3.设△ABC 的内切圆半径为r ,求证BC 边上的高.2sin2cos 2cos 2A CB r AD ⋅⋅=证:在直角△ABC 中,2cos2sin 2sin B B c Bc AD ⋅⋅=⋅=另外,EB AE c +=)22(Bctg A ctgr += 2sin2sin )22sin()2sin 2cos 2sin 2cos (B A B A r B B A A r ⋅+⋅=+=AEc r bOB Ca D.2sin2cos2cos 22cos 2sin2sin 2sin2cos22sin 2sin2cosA CB r B B BA Cr AD B A C r ⋅⋅=⋅⋅⋅⋅=∴⋅⋅= 4.设△ABC 为锐角三角形,以BC 为直径作圆,并从A 作此圆的切线AD 与圆切于D 点,由在AB 边上取AE=AD ,并过E 作AB 的垂线与AC 边的延长线交于F ,求证: (1)AE:AB=AC:AF.(2)△ABC 的面积=△AEF 的面积.证(1):设AB 与⊙O 相交于点G ,联结EC ,CG ,BF.∵EF ⊥AB ,CG ⊥AB ,∴GC ∥EF ,AC:AF=AG:AE ………………① 又∵AD 是⊙O 的切线,∴AD 2=AG ·AB ,也即AG:AD=AD:AB但∵AD=AE ,∴AG:AE=AE:AB ……………② 由①、②可得AE:AB=AC:AF证(2):由(1)AE:AB=AC:AF ,则EC ∥BF ,△EBC 的面积=△EFC 的面积 ∴△ABC 的面积=△AEC 的面积+△EBC 的面积=△AEC 的面积+△EFC 的面积 =△AEF 的面积5.求证方程0)2()12(23=+-++-Q x Q x x 的一个根是1设这个方程的三个根是△ABC 的三个内角的正弦,sin ,sin ,sin C B A 求A 、B 、C 的度数以及Q 的值解:将x=1代入这个方程式, 则01)2(1)12(123=+⋅-+⋅+-Q Q , 故知1是原方程的一个根由于1是原方程的一个根,所以方程左边能被x-1整除AGE DB GOF用x-1除方程左边后得商式.022=--Q x x根据题设条件(即有一个根为1,不妨设1sin =C )及根与系数的关系可得⎪⎩⎪⎨⎧-=⋅=+=)3(sin sin )2(2sin sin )1(1sin Q B A B A C 由(1)可知C=900,于是A+B=900,B=900-A ,代入(2)得.212222sin sin )3(45459045,045,1)45cos(,1cos 45cos sin 45sin ,1cos 22sin 22,2cos sin ,2)90sin(sin -=⋅-=⋅-=︒=︒-︒=︒=∴=︒-∴=︒-=⋅︒+⋅︒=+∴=+=-︒+B A Q B A A A A A A A A A A A 式可得从即1957年普通高等学校招生全国统一考试数学1.甲、化简32221)27102(1.0)972(--++解:原式=.481110216910035)2764()101()925(32221=++=++--乙、求适合不等式22<+x x 的实数x 的范围解:原式为022<-+x x 解为:-2<x<1. 故x 的范围为-2<x<1. 丙、求证.210322+='︒ctg证:.2145sin 45cos 12450322+=︒︒+=︒='︒ctgctg 丁、在四面体ABCD 中,AC=BD ,P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点,求证:PQRS 为一个菱形证:由于点P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点,根据三角形两边中点连线的性质可得.////,21////BD SP RQ AC RS PQ ====而由题设,AC=BD , ∴PQ=QR=RS=SP , 故 PQRS 为一个菱形 戊、设b a ,为异面直线,EF 为ba ,的公垂线,α为过EF 的中点且与b a ,平行的平面,M 为a 上任一点,N 为b 上任一点求证线段MN 被平面α二等分 证:过直线b 作平面β//α(如图)过直线a 及公垂线EF 作一平面,在此平面内作MC ∥EF ,且与平面α,β分别交于B 、C 两点设EF 、MN 分别与平面α交于点ASPDRC BQM E aB Aα DC bN FβA 、D∵点A 是EF 的中点, 又ME ∥BA ∥CF , ∴点B 是MC 的中点又∵DB ∥NC , ∴D 是MN 的中点另法:如图,连接EN ,AB,BD 由AB b BD a b a //,////,//⇒αα由A 是EF 的中点得,D 为MN 的中点此即线段MN 被平面α二等分 2.解方程组⎩⎨⎧⋅==-++)2(101010)1(1)2lg()12lg( yx xy y x 解:由(1)可得,10)2)(12(=-+y x)3(01242 =-+-y x xy由(2)可得)4( y x xy +=将(4)代入(3)可得,012422=-+-+y x y x,01232=-+-y x)5(3212 xy +=再将(5)代入(4)可得,32123212xx x x ++=+⋅ 化简,得,012722=-+x x.41457±-=∴x abαEFAMNBD将x 值代入(5).6145173212±=+=x y 此即⎪⎪⎩⎪⎪⎨⎧-=--=⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457;614517,414572211y x y x 因为,0122<+x 所以(1)式无意义(负数无对数),故原方程组的解仅为⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457y x 3.设△ABC 的内切圆半径为r ,求证BC 边上的高.2sin2cos 2cos 2A CB r AD ⋅⋅=证:在直角△ABC 中,2cos2sin 2sin B B c Bc AD ⋅⋅=⋅=另外,EB AE c +=)22(Bctg A ctgr += 2sin2sin )22sin()2sin 2cos 2sin 2cos (B A B A r B B A A r ⋅+⋅=+=AEc r bOB Ca D.2sin2cos2cos 22cos 2sin2sin 2sin2cos22sin 2sin2cosA CB r B B BA Cr AD B A C r ⋅⋅=⋅⋅⋅⋅=∴⋅⋅= 4.设△ABC 为锐角三角形,以BC 为直径作圆,并从A 作此圆的切线AD 与圆切于D 点,由在AB 边上取AE=AD ,并过E 作AB 的垂线与AC 边的延长线交于F ,求证: (1)AE:AB=AC:AF.(2)△ABC 的面积=△AEF 的面积.证(1):设AB 与⊙O 相交于点G ,联结EC ,CG ,BF.∵EF ⊥AB ,CG ⊥AB ,∴GC ∥EF ,AC:AF=AG:AE ………………① 又∵AD 是⊙O 的切线,∴AD 2=AG ·AB ,也即AG:AD=AD:AB但∵AD=AE ,∴AG:AE=AE:AB ……………② 由①、②可得AE:AB=AC:AF证(2):由(1)AE:AB=AC:AF ,则EC ∥BF ,△EBC 的面积=△EFC 的面积 ∴△ABC 的面积=△AEC 的面积+△EBC 的面积=△AEC 的面积+△EFC 的面积 =△AEF 的面积5.求证方程0)2()12(23=+-++-Q x Q x x 的一个根是1设这个方程的三个根是△ABC 的三个内角的正弦,sin ,sin ,sin C B A 求A 、B 、C 的度数以及Q 的值解:将x=1代入这个方程式, 则01)2(1)12(123=+⋅-+⋅+-Q Q , 故知1是原方程的一个根由于1是原方程的一个根,所以方程左边能被x-1整除AGE DB GOF用x-1除方程左边后得商式.022=--Q x x根据题设条件(即有一个根为1,不妨设1sin =C )及根与系数的关系可得⎪⎩⎪⎨⎧-=⋅=+=)3(sin sin )2(2sin sin )1(1sin Q B A B A C 由(1)可知C=900,于是A+B=900,B=900-A ,代入(2)得.212222sin sin )3(45459045,045,1)45cos(,1cos 45cos sin 45sin ,1cos 22sin 22,2cos sin ,2)90sin(sin -=⋅-=⋅-=︒=︒-︒=︒=∴=︒-∴=︒-=⋅︒+⋅︒=+∴=+=-︒+B A Q B A A A A A A A A A A A 式可得从即1957年普通高等学校招生全国统一考试数学1.甲、化简32221)27102(1.0)972(--++解:原式=.481110216910035)2764()101()925(32221=++=++--乙、求适合不等式22<+x x 的实数x 的范围解:原式为022<-+x x 解为:-2<x<1. 故x 的范围为-2<x<1. 丙、求证.210322+='︒ctg 证:.2145sin 45cos 12450322+=︒︒+=︒='︒ctgctg丁、在四面体ABCD 中,AC=BD ,P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点,求证:PQRS 为一个菱形证:由于点P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点,根据三角形两边中点连线的性质可得.////,21////BD SP RQ AC RS PQ ====而由题设,AC=BD , ∴PQ=QR=RS=SP , 故 PQRS 为一个菱形 戊、设b a ,为异面直线,EF 为ba ,的公垂线,α为过EF 的中点且与b a ,平行的平面,M 为a 上任一点,N 为b 上任一点求证线段MN 被平面α二等分 证:过直线b 作平面β//α(如图)过直线a 及公垂线EF 作一平面,在此平面内作MC ∥EF ,且与平面α,β分别交于B 、C 两点设EF 、MN 分别与平面α交于点A 、D∵点A 是EF 的中点,ASPDRC BQM E aB Aα DC bN F β又ME ∥BA ∥CF , ∴点B 是MC 的中点又∵DB ∥NC , ∴D 是MN 的中点另法:如图,连接EN ,AB,BD 由AB b BD a b a //,////,//⇒αα由A 是EF 的中点得,D 为MN 的中点此即线段MN 被平面α二等分 2.解方程组⎩⎨⎧⋅==-++)2(101010)1(1)2lg()12lg( yx xy y x 解:由(1)可得,10)2)(12(=-+y x)3(01242 =-+-y x xy由(2)可得)4( y x xy +=将(4)代入(3)可得,012422=-+-+y x y x,01232=-+-y x)5(3212 xy +=再将(5)代入(4)可得,32123212xx x x ++=+⋅ 化简,得,012722=-+x x.41457±-=∴x 将x 值代入(5).6145173212±=+=x y abαEFAMNBD此即⎪⎪⎩⎪⎪⎨⎧-=--=⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457;614517,414572211y x y x 因为,0122<+x 所以(1)式无意义(负数无对数),故原方程组的解仅为⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457y x 3.设△ABC 的内切圆半径为r ,求证BC 边上的高.2sin2cos 2cos 2A CB r AD ⋅⋅=证:在直角△ABC 中,2cos2sin 2sin B B c Bc AD ⋅⋅=⋅=另外,EB AE c +=)22(Bctg A ctgr += 2sin2sin )22sin()2sin 2cos 2sin 2cos (B A B A r B B A A r ⋅+⋅=+=AEc r bOB Ca D.2sin2cos2cos 22cos 2sin2sin 2sin2cos22sin 2sin2cosA CB r B B BA Cr AD B A C r ⋅⋅=⋅⋅⋅⋅=∴⋅⋅= 4.设△ABC 为锐角三角形,以BC 为直径作圆,并从A 作此圆的切线AD 与圆切于D 点,由在AB 边上取AE=AD ,并过E 作AB 的垂线与AC 边的延长线交于F ,求证: (1)AE:AB=AC:AF.(2)△ABC 的面积=△AEF 的面积.证(1):设AB 与⊙O 相交于点G ,联结EC ,CG ,BF.∵EF ⊥AB ,CG ⊥AB ,∴GC ∥EF ,AC:AF=AG:AE ………………① 又∵AD 是⊙O 的切线,∴AD 2=AG ·AB ,也即AG:AD=AD:AB但∵AD=AE ,∴AG:AE=AE:AB ……………② 由①、②可得AE:AB=AC:AF证(2):由(1)AE:AB=AC:AF ,则EC ∥BF ,△EBC 的面积=△EFC 的面积 ∴△ABC 的面积=△AEC 的面积+△EBC 的面积=△AEC 的面积+△EFC 的面积 =△AEF 的面积5.求证方程0)2()12(23=+-++-Q x Q x x 的一个根是1设这个方程的三个根是△ABC 的三个内角的正弦,sin ,sin ,sin C B A 求A 、B 、C 的度数以及Q 的值解:将x=1代入这个方程式, 则01)2(1)12(123=+⋅-+⋅+-Q Q , 故知1是原方程的一个根由于1是原方程的一个根,所以方程左边能被x-1整除AGE DB GOF用x-1除方程左边后得商式.022=--Q x x根据题设条件(即有一个根为1,不妨设1sin =C )及根与系数的关系可得⎪⎩⎪⎨⎧-=⋅=+=)3(sin sin )2(2sin sin )1(1sin Q B A B A C 由(1)可知C=900,于是A+B=900,B=900-A ,代入(2)得.212222sin sin )3(45459045,045,1)45cos(,1cos 45cos sin 45sin ,1cos 22sin 22,2cos sin ,2)90sin(sin -=⋅-=⋅-=︒=︒-︒=︒=∴=︒-∴=︒-=⋅︒+⋅︒=+∴=+=-︒+B A Q B A A A A A A A A A A A 式可得从即1957年普通高等学校招生全国统一考试数学1.甲、化简32221)27102(1.0)972(--++解:原式=.481110216910035)2764()101()925(32221=++=++--乙、求适合不等式22<+x x 的实数x 的范围解:原式为022<-+x x 解为:-2<x<1. 故x 的范围为-2<x<1. 丙、求证.210322+='︒ctg证:.2145sin 45cos 12450322+=︒︒+=︒='︒ctgctg 丁、在四面体ABCD 中,AC=BD ,P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点,求证:PQRS 为一个菱形证:由于点P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点,根据三角形两边中点连线的性质可得.////,21////BD SP RQ AC RS PQ ====而由题设,AC=BD , ∴PQ=QR=RS=SP , 故 PQRS 为一个菱形 戊、设b a ,为异面直线,EF 为ba ,的公垂线,α为过EF 的中点且与b a ,平行的平面,M 为a 上任一点,N 为b 上任一点求证线段MN 被平面α二等分 证:过直线b 作平面β//α(如图)过直线a 及公垂线EF 作一平面,在此平面内作MC ∥EF ,且与平面α,β分别交于B 、C 两点设EF 、MN 分别与平面α交于点ASPDRC BQM E aB Aα DC bN FβA 、D∵点A 是EF 的中点, 又ME ∥BA ∥CF , ∴点B 是MC 的中点又∵DB ∥NC , ∴D 是MN 的中点另法:如图,连接EN ,AB,BD 由AB b BD a b a //,////,//⇒αα由A 是EF 的中点得,D 为MN 的中点此即线段MN 被平面α二等分 2.解方程组⎩⎨⎧⋅==-++)2(101010)1(1)2lg()12lg( yx xy y x 解:由(1)可得,10)2)(12(=-+y x)3(01242 =-+-y x xy由(2)可得)4( y x xy +=将(4)代入(3)可得,012422=-+-+y x y x,01232=-+-y x)5(3212 xy +=再将(5)代入(4)可得,32123212xx x x ++=+⋅ 化简,得,012722=-+x x.41457±-=∴x abαEFAMNBD。

科信教育公考研究院2014年412多省联考辽宁真题解析【命题意图】第一时间拿到这篇不到六千字的材料,逻辑看似很杂乱,就像打太极一样,看似玄乎,但是仔细琢磨,我们便会很清楚的发现门道,这是一则典型的事实性的逻辑材料。
今年多省联考,让很多培训机构都会想不到,命题人原来是个跟的上时代的潮人。
但是,也凸显出了命题思路缺乏创新性,仔细研究真题的同学可能会发现,材料主题是不是似曾相识呢?就想电影里的夏尔洛一样,不被关心,但是又被无限制的夸大他的痛苦呢?材料主题围绕国外文化受到全球的瞩目,电视文化起到了传递本国文化和讲述本国历史的作用。
然而,反观中国传统文化虽然历史悠久,博大精深,但是近些年不断的受到国外文化冲击,同时,部分国人崇洋媚外的思想也给中国传统文化带来了毁灭性的影响。
加之,近些年中国传统文化走出国门却屡屡遭到西方列强的轻视,这其实凸显出了中国文化软实力的“虚胖”。
我想,这也是命题人屡屡以“文化”为主题去命制题目的原因。
2012年山东政法干警考了中国文化的传播与输出;2013年国考地市和副省级也考了中国文化的传播,2014年河北同样考了保护中国传统非物质文化遗产,2014年辽宁再考文化,其实按照我自己的理解是:命题人需要呼吁国人,尤其是青年人,对于传输和发扬中国传统文化我们这一代义不容辞,更从侧面来呼吁,我们政府需要注重文化内功的修炼,把提升文化软实力真正“做实”。
一、“给定资料1”介绍了美剧、韩剧的成功事例,请根据“给定资料1”,概括我们从中能借鉴到哪些经验。
(15分)要求:全面、准确、简明,不超过100字。
【解析思路】:这是一道很典型的概括经验题目,从题干我们可以很明显的看出我们的要点范围就在给定资料1里,而且是概括国外成功的经验。
所以这道题目难度不大,只需要把材料要点稍微加工,规范书写即可。
【参考答案】当前,国外在弘扬文化价值和打造主流电视产品经验值得借鉴,具体如下:一、打造精品文化产品,提升内功和文化传输能力;第二;打造电视精品节目,以观众为主导,创新电视题材、播出方式和影视制作,接受市场批评。

常识判断:(共20题)1.为提高社会管理科学化水平,全国各地积极出台加强和创新社会管理的措施,下列措施中不属于创新社会管理的是( B )A.组织社区志愿者开展邻里互动活动B.提高临床一线医护人员的待遇水平C.能过微博向群众提供政务服务资讯D.设奖鼓励市民投诉举报食品安全问题2.2011年12月中央经济工作会议提出“牢牢把握发展实体经济这一坚实基础”。
下列产业中属于实体经济的是( B )①房地产业②仓储服务业③旅游产业④收藏业⑤电信产业A.③⑤B.②③⑤C.①②③⑤D.①②③④⑤3.我国作为非成员国参加的政府间国际组织是( C )A.上合组织B.金砖国家C.东盟10国D.G204.2011年我国改革开放和社会主义现代化建设取得新的重大成就,其中包括( C )A.人均GDP超过3000美元B.外汇储备首次超过日本居世界第一C.城镇化率超过50%D.粮食总产量首次超过10万亿斤5.下列选项中三国典故与哲学论断对应错误的是( B )A.士别三日,当刮目相看――用发展的眼光看问题B.望梅止渴――理性认识依赖于感性认识C.张飞醉酒失徐州,借酒破张郃―― 矛盾是对立统一的D.草船借箭――人可以认识并利用规律6.下列影视剧情景设计符合历史常识的是( D )A.越王勾践兵败后给吴王差夫当奴仆,以红薯充饥,每晚则睡在柴垛上B.燕子丹与荆轲分坐八仙桌两侧,秉烛夜谈,谋划赴咸阳刺杀秦王计划C.魏征劝谏李世民时,说道:陛下当先天下之忧而忧,后天下之乐而乐D.毛泽东与李宗仁幽默地说:德邻先生,你这次归国,是误上了贼船啊7.中国古典戏剧作品塑造了王昭君、李香君、杜丽娘和崔莺莺等经典女性形象,下列作品与上述人物对应关系正确的是( C )A.《西厢记》――《汉宫秋》――《桃花扇》――《牡丹亭》B.《汉宫秋》――《牡丹亭》――《桃花扇》――《西厢记》C.《汉宫秋》――《桃花扇》――《牡丹亭》――《西厢记》D.《西厢记》――《桃花扇》――《汉宫秋》――《牡丹亭》8.中美关系是全国最重要的双边关系之一,中美建交前后曾发生过一下事件:①邓小平访美②中美发布上海联合公报③ 尼克松总统访华④福特总统访华按时间先后顺序排列正确的是( D )A.②③①④B.②③④①C.③②①④D.③②④①9.要了解一件艺术品、一个艺术家,必须正确地设想他们所处的时代精神和风俗概况,要解读玛格丽特马切尔的《飘》,我们应了解的重大历史事件是( A )A.美国南北战争B.美西战争C.美国独立运动D.美国西进运动10.《诗经.卫风.氓》中有“抱布贸丝”的说法,意指进行商品交易。
2014年多省联考行测真题及答案解析第一部分常识判断(共20题)根据题目要求,在四个选项中选出一个最恰当的答案。
请开始答题:1.关于中国地理,下列说法错误的是:A.九寨沟国家地质公园以雅丹地貌闻名B.藏羚羊主要生活在可可西里国家级自然保护区C.张家界国家森林公园处于武陵山脉的腹地D.三江并流风景名胜区已被列入《世界遗产名录》2.下列说法错误的是:A.蓝藻对地球表面从无氧变成有氧的大气环境起了巨大作用B.植物光合作用主要在细胞的线粒体中进行C.呼吸作用分为有氧呼吸和无氧呼吸两种类型D.种子植物是地球表面绿色的主体3.关于政治思想,下列表述错误的是:A.孟德斯鸠提出三权分立学说B.伏尔泰最早提出社会契约论的思想C.柏拉图主张建立哲学王统治的国家D.让·布丹提出君主主权学说4.下列关于火山的表述错误的是:A.喷出的物质有气态、液态和固态三种B.可分为死火山、活火山和休眠火山C.王大连池的形成与火山喷发有关D.页岩是最常见的岩浆岩5.下列哪组物品均属可燃固体?A.香蕉水、酒精B.面粉、油漆C.沥青、松香D.甲烷、乙炔6.关于海水及其运动,下列说法错误的是:A.海水的冰点湿度比淡水低B.北海道光渔场位于寒流与暖流的交汇处C.波罗的海是异界上盐度最高的海域D.波浪、潮汐和洋流是海水运动的主要形式7.下列关于石灰的说法错误的是:A.生石灰通常可以作为食品干燥剂B.澄清石灰水放置在空气中易变浑浊C.汉白玉与石灰石的主要成分相同D.“烈火焚烧若等闲”指熟石灰的高温煅烧8.下列关于铅的说法错误的是:A.铅笔芯的主要成分是铅B.香烟中是含铅的C.铅在人体内日积月累,不会分解D.汽油中添加铅元素可以起到防爆的作用9.下列塑料制品中,能够作为食物容器放入微波炉中加热的是:A.聚氧乙烯(PVC)B.聚乙烯(PE)C.聚丙烯(PP)D.聚苯乙烯(PS)10.下列哪组不属于夺命“急症”?A.肺栓塞、哮喘B.冠心病、毒品过量C.脑出血、急性坏死性胰腺炎D.阑尾炎、腹膜炎11.关于天体及其运行,下列表述错误的是:A.天球是为了确定天体位置和运动而假想的圆球B.在火星和木星轨道之间存在一个小行星带C.黄道面是指月球绕地球运行的轨道面D.星座是指在天球上投影位置相近的恒星群落12.下列犯罪嫌疑人、被告人中,哪个人不适用取保候审?A.有证据证明甲犯故意杀人罪,有可能被判十年以上有期徒刑B.乙在逮捕后侦查羁押期限届满仍需继续查证C.丙涉嫌侮辱罪被起诉D.丁被逮捕后发现其怀孕3个月13.关于矿产资源及其主要分布国,下列对应错误的是:A.硝石加拿大B.磷矿摩洛哥C.铜矿智利秘鲁D.金矿南非14.关于农作物,下列说法正确的是:A.中国是最早栽培大豆的国家B.玉米是通过丝绸之路传入中国的C.花生是世界上最主要的油料作物D.印度是世界上最大的稻米出口国15.关于下列各组人物说法错误的是:A.苏格拉底、柏拉图和亚里士多德被称为“古希腊三贤”B.颜回、曾子都属孔子七十二门徒C.荀子及其弟子韩非子是法家学派的代表人物D.康有为、梁启超都是“公车上书”的发起人16.下列体育人物与其擅长领域对应错误的是:A.罗尼·奥沙利文:斯诺克台球B.泰格·伍兹:高尔示C.罗杰·费德勒:网球D.拉菲尔·纳达尔:棒球17.根据民事诉讼法的规定,下列说法错误的是:A.人民法院调解好的离婚案件,可以不制作调解书B.修改后的民事诉讼法增加了“公益诉讼”的内容C.修改后的民事诉讼法规定,当事人所在社区可推荐公民作为诉讼代理人D.人民法院可以根据实际情况,决定采取传真的方式送达判决书18.下列事件与相关人物对应错误的是:A.三藩之乱:吴三桂、康熙B.七国之乱:吴王刘濞、汉景帝C.八王之乱:苻坚、谢玄D.安史之乱:郭子仪、史思明19.关于我国[公务员]制度,下列叙述正确的是:A.正在接受纪律审查的[公务员]不得辞去公职B.我国[公务员]培训基地是党校C.[公务员]对降职不服,可以向人民法院提出申诉D.[公务员]考核的基本内容包括德、能、勤、绩、才20.下列思想流派与产生时代对应错误的是:A.儒学——汉代B.玄学——魏晋C.理学——宋代D.心学——明代第二部分 [言语]理解与表达(共40题,参考时限40分钟)本部分包括表达与理解两方面的内容。
1.在数千年历史发展过程中,陕西⼈创造了独具特⾊的“陕西精神”,下列不属于“陕西精神”的是( )。
A.爱国守信 B.弃农兴商 C.宽厚包容 D.勤劳质朴 【答案】B 【华图解析】陕西省委宣传部向社会征集新时期陕西精神表述语,经过梳理、分析和研究,形成了“爱国守信、勤劳质朴、宽厚包容、尚德重礼、务实进取”20字,并写进2012年5⽉召开的省第⼗⼆次党代会报告中。
这是陕西省深⼊贯彻落实党的⼗七届六中全会精神的重要成果,是陕西省⼈民推动⽂化繁荣发展⾃觉和⾃信的集中体现,所以B项错误。
这道题选择B。
2. 关于四⼤⽂明古国及其数学成就,下列对应错误的是( )。
A.古埃及:“0”的发现 B.古印度:阿拉伯数字 C.古巴⽐伦:六⼗进位制 D.古中国:勾股定理 【答案】A 【华图解析】“0”这个数字由古印度⼈在约公元5世纪时发明,A项错误。
六⼗进位制起源于古巴⽐伦,C项正确。
这道题选择A。
3. 关于中国地理,下列说法错误的是( )。
A.九寨沟国家地质公园以雅丹地貌闻名 B.藏羚⽺主要⽣活在可可西⾥国家⾃然保护区 C.张家界国家森林公园处于武陵⼭脉的腹地 D.三江并流风景名胜区已被列⼊《世界遗产名录》 【答案】A 【华图解析】雅丹地貌是⼀种典型的风蚀地貌,在极⼲旱地区的⼀些⼲涸的湖底,常因⼲涸裂开,风沿着这些裂隙吹蚀,裂隙愈来愈⼤,使原来平坦的地⾯发育成许多不规则的背鲫形垄脊和宽浅沟槽,这种⽀离破碎的地⾯称为雅丹地貌。
有些地貌外观如同古城堡,俗称魔⿁城。
中国的雅丹地貌⾯积约2万多平⽅公⾥,主要分布于青海柴达⽊盆地西北部,疏勒河中下游和新疆罗布泊周围,九寨沟属于⾼⼭峡⾕类型,A项错误。
4.下列说法错误的是( )。
A.蓝藻对地球表⾯从⽆氧变成有氧的⼤⽓环境起了巨⼤作⽤ B.植物光合作⽤主要在细胞的线粒体中进⾏ C.呼吸作⽤分为有氧呼吸和⽆氧呼吸两种类型 D.种⼦植物是地球表⾯绿⾊的主体 【答案】B 【华图解析】绿⾊植物通过叶绿体,利⽤光能,把⼆氧化碳和⽔转化成贮存着能量的有机物(主要是淀粉),并且释放氧⽓的过程就是绿⾊植物的光合作⽤,B项错误。
2012年421公务员联考《行测》卷(解析)1、A项错误,2008年中国的人均GDP已经达到3266.8美元,登上了3000美元的新台阶;B项错误,2006年2月底,我国已超过日本成为全球外汇储备最多的国家;C项正确,2012年中国政府工作报告第一部分“2011年工作回顾”中提到,“城镇化率超过50%,这是中国社会结构的一个历史性变化”;D项错误,2012年中国政府工作报告第一部分“2011年工作回顾”中提到,“粮食产量57121万吨,再创历史新高”,57121万吨等于1.14242万亿斤,并未达到“10万亿斤”。
故正确答案为C。
2、本题考查历史地理常识。
A项错误,燕国的纬度最高;B项正确,楚国的纬度最低;C、D项错误,秦国的经度最小。
故正确答案为B。
3、本题考查文学常识。
A项正确,出自王之涣《凉州词》,戍边的军士听到《杨柳枝》引发对故乡的思念,诗人劝慰大家“羌笛何须怨杨柳,春风不度玉门关”;B项正确,《渭城曲》是王维的一首极负盛名的送别之作;C项正确,《雨霖铃》为柳永离开汴京南下时与恋人惜别之作;D项错误,出自欧阳修的《蝶恋花》,描写闺中少妇的伤春之情。
本题为选非题,故正确答案为D。
4、本题考查文化常识。
王昭君是马致远《汉宫秋》中的人物,李香君是孔尚任《桃花扇》中的人物,杜丽娘是汤显祖《牡丹亭》中的女主人公,而崔莺莺是王实甫《西厢记》中的人物。
故正确答案为C。
5、本题考查历史常识。
A项错误,荆轲刺秦发生于战国时期,当时没有发明桌子,桌子的名称在五代时才诞生。
B项正确,李宗仁原为国民党代总统,后因和谈未果出走美国,1965年回到北京。
李宗仁字德邻,称呼他人的字表示对他的尊重。
C项错误,发生在唐太宗时期,而“先天下之忧而忧”出自北宋范仲淹《岳阳楼记》,在唐代之后。
D项错误,勾践是春秋末期人物,而红薯在明朝万历十年才从吕宋(今菲律宾)引进中国。
故正确答案为B。
6、本题考查哲学常识。
A项对应正确,“士别三日”出自《三国志》,意思是指人离开后不久。
2014-福建-1.下列各组任务说法错误的是:( )。
A.苏格拉底,柏拉图和亚里士多德被称为“古希腊三贤”B.颜回、曾子都属孔子七十二门徒C.荀子及其弟子韩非子是法学家派的代表人物D.康有为,梁启超都是“公车上书”的发起人1.【答案】C。
荀子及其弟子韩非子是法家学派的代表人物中公解析:荀子对儒家思想有所发展,提倡“性恶论”,其学说常被后人拿来跟孟子的“性善说”比较,荀子对重新整理儒家典籍也有相当显著的贡献,属于儒家代表人物。
故本题答案选C。
2014-福建-2.下列思想流派于产生时代对应错误的是:( )。
A.儒学——汉代B.玄学——魏晋C.理学——宋代D.心学——明代2.【答案】A3.儒家学说,亦称儒学,起源于东周春秋时期,为“道家”、“墨家”“法家”“阴阳家”等诸子百家之一,汉朝汉武帝时期起,成为中国社会的正统思想。
故本题答案选A。
2014-福建-3.关于政治思想,下列表述错误的是:( )。
A.孟德斯鸠提出三权分立学说B.伏尔泰最早提出社会契约论的思想C.柏拉图主张建立哲学王统治的国家D.让·布丹提出君主主权学说3.【答案】B。
伏尔泰最早提出社会契约论的思想中公解析:卢梭最早提出社会契约论的思想,并提出“天赋****说”。
故本题答案选B2014-福建-4.关于我国公务与制度,下列叙述正确的是:( )。
A.正在接受纪律审查的公务员不得辞去公职B.我国公务员培训基地是党校C.公务员对降职不服,可以向人民法院提出申诉D.公务员考核的基本内容包括德、能、勤、绩、廉4.【答案】A。
正在接受纪律审查的公务员不得辞去公职中公解析:《公务员法》第81条规定,公务员有下列情形之一的,不得辞去公职:(一)未满国家规定的最低服务年限的;(二)在涉及国家秘密等特殊职位任职或者离开上述职位不满国家规定的脱密期限的;(三)重要公务尚未处理完毕,且须由本人继续处理的;(四)正在接受审计、纪律审查,或者涉嫌犯罪,司法程序尚未终结的;(五)法律、行政法规规定的其他不得辞去公职的情形。
历年真题汇编试卷(一)参考答案及解析第Ⅰ卷(单项选择题,共60分)1.【答案】D。
解析:该题考察地质过程以及地貌对聚落形成的影响。
由于距今2300万年前的岩层被侵蚀,可以判断河流形成于后,排除A;根据地质过程推断,①地应该为先沉积后侵蚀,排除B;②处地层由下向上明显分为三层,不可能是连续的,排除C;根据河流流向和凹岸侵蚀、凸岸沉积特点,D项正确。
2.【答案】C。
解析:聚落主要分布在河流阶地上,应该是外力侵蚀发生后,排除A、B;河滩地区易发生洪涝灾害,不适宜聚落的发展,排除D。
根据自然带分布规律,欧洲北纬50°中部应该为落叶阔叶林,故选C。
3.【答案】C。
解析:太阳直射点一般在每年6月22日左右到达北回归线,接着往赤道移动。
此图中A城市在7月1日这天的正午太阳高度角为90°(直射),由此可知,A城市在北回归线以南,且7月1日这天为A城市该年度第二次经历太阳直射,第一次直射时间应在6月22日之前。
粗略估计,下一次太阳直射A城市的时间应在下一年的6月22日之前八、九天左右。
由此,选C。
4.【答案】B。
解析:由图中比例尺可知,A城市和B城市之间的经度相差大于12°小于17°(地球赤道经度1°对应的弧长约为111km,45°纬线上的1°对应的弧长约为111×cos45°km)。
1°的弧长对应的时间为4分钟,因此A城市和B城市之间的时差大于48分钟小于68分钟,排除C、D选项;由比例尺可知,A城市和B城市之间的纬度差约为10°,由此可知B城市的正午太阳高度角约为80°,又因正午太阳高度角为一天中太阳高度最大值,所以此时B城市的太阳高度必然不可能大于80°,答案为B。
5.【答案】B。
解析:根据“还有竹纤维制成的毛巾、内衣内裤”可知,竹纤维是竹毛巾的制作材料,二者有生产协作关系。
6.【答案】D。
2012年421联考行测真题及答案解析2012年上半年全国17个省份公务员考试将联合举行,时间为2012年4月21日。
具体省份如下:山西省辽宁省黑龙江省福建省湖北省湖南省广西壮族自治区海南省四川省重庆市云南省西藏自治区陕西省甘肃省青海省宁夏回族自治区新疆生产建设兵团。
第一部分常识判断1.2011年我国改革开放和社会主义现代化建设取得新的重大成就,其中包括A. 人均GDP超过3000美元B. 外汇储备首次超过日本居世界第一C. 城镇化率超过50%D. 粮食总产量首次超过10万亿斤2.关于我国战国七雄地理位臵描述准确的是( )。
A. 齐国的纬度最高B. 楚国的纬度最低C. 燕国的经度最小D. 秦国的经度最大3.杨柳是我国古代诗词里面较为常见的意象,往往蕴涵离别之情,下列名句中不是表达送别意象的是( )。
A. 芜笛何须怨杨柳,春风不度玉门关B. 渭城朝雨浥轻尘,客舍青青柳色新C. 今宵酒醒何处,杨柳岸、晓风残月D. 庭院深深深几许?杨柳堆烟、幕帘无重数4.中国古典戏剧作品塑造了王昭君、李香君、杜丽娘和崔莺莺等经典女性形象,下列作品与上述人物对应关系正确的是( )。
A. 《西厢记》——《汉宫秋》——《桃花扇》——《牡丹亭》B. 《西厢记》——《桃花扇》——《汉宫秋》——《牡丹亭》C. 《汉宫秋》——《柳花扇》——《牡丹亭》——《西厢记》D. 《汉宫秋》——《牡丹亭》——《桃花扇》——《西厢记》5.下列影视剧情景设计符合历史常识的是( )。
A. 燕子丹与荆轲分坐八仙桌两侧,秉烛夜谈,谋划赴咸阳刺杀秦王计划B. 毛泽东与李宗仁幽默地说:德邻先生,你这次归国,是误上了贼船啊C. 魏征劝谏李世民时,说道:陛下当先天下之忧而忧,后天下之乐而乐D. 越王勾践兵败后给吴王差夫当奴仆,以红薯充饥,每晚则睡在柴垛上6.下列选项中三国典故与哲学论断对应错误的是( )。
A. 士别三日,当刮目相看——用发展的眼光看问题B.草船借箭——人可以认识并利用规律C. 张飞醉酒失徐州,借酒破张郃——矛盾是对立统一的D. 望梅止渴——理性认识依赖于感性认识7.中美关系是全国最重要的双边关系之一,中美建交前后曾发生过以下事件:①邓小平谈美②中美发布上海联合公报③尼克松总统访华④福特总统访华按时间先后顺序排列正确的是( )。
历年真题汇编试卷(一)参考答案及解析1.【答案】B。
解析:首先,该公司免费提供的产品和服务不是公共物品,而属于商品,具有使用价值和价值,A、C、D错误;题干中公司提供的产品和服务不是通过费用的方式进行交换,而是通过隐性交换方式来实现其价值,即价值通过其他形式实现,B正确。
2.【答案】C。
解析:在投资总量中,三种经济成分都占相应的比例,体现C;A、B观点正确,但题干没有反映;社会主义经济是公有制经济,非公有制经济是社会主义市场经济的重要组成部分,D观点错误。
3.【答案】A。
解析:③不属于企业所能控制的范围;④与题干无关。
4.【答案】D。
解析:首先要读懂材料的中心。
菜贱伤农,是菜价低,销售不畅。
解决这个问题,一个是稳定蔬菜的价格,另外是解决蔬菜的销售问题。
①不选,因为农业劳动生产率的提高带来的是蔬菜价格的下降;②正确,这样能让农民了解市场的需求,科学合理地种植,能解决销路问题;③不选,减少流通环节和提高产品附加值都无法让农民真正获益;④正确,这是政府在运用宏观调控手段,对农民的权益进行保护。
本题选D。
5.【答案】C。
解析:科学发展观的核心是以人为本,天津的做法都是使人生活得更好,①入选;科学发展观的基本要求是全面协调可持续,全面,是讲总体布局全面推进经济、政治、文化、社会等发展,材料并未涉及此,故排除②;天津的做法是坚持人与自然和谐、实现可持续发展,故③④入选。
6.【答案】A。
解析:本题考查政府扶持新能源产业的原因,①应该是我国需要能源,否则政府不会大力扶持;②符合科学发展观的要求;③不符合我国当前能源实际状况;④不构成我国政府大力扶持的原因。
7.【答案】B。
解析:A说法不符合题意,该材料并没有讲文化的竞争;B说法符合题意,中外文化的交流促进了文化的发展;C说法错误,民族文化的融合不能说是文化发展的关键;D说法与题目无关。
本题答案选B。
8.【答案】C。
9.【答案】B。
解析:本题主要考查文化与经济政治的关系,“运用3D技术制作电影”是文化现象,“创造27亿元的全球票房”、“带动了3D相关产业的发展”是强调文化对经济的重大影响,文化生产力的重要性。
②④与题干主旨不一致。
答案选B。
10.【答案】D。
解析:题干意思是说,天不因为人们厌恶冬天就不要冬天,地也不会因为人们厌恶路途遥远而失去广阔,反映了自然界的变化有其客观规律,不以人的意志为转移,D符合题意;A、B观点正确,与题意不符;意识是人脑特有的生理机能,C观点错误。
11.【答案】A。
解析:本题以“超级病菌”为时事背景材料,人们对抗生素的滥用,导致了超级病菌的出现,这体现了量变与质变的关系;同时也说明,在客观规律面前,人们必须遵守,①②符合题意,③不符合题意,④说法错误,本题答案选A。
12.【答案】D。
13.【答案】B。
解析:本题考查矛盾对立统一的观点。
“太极图”是中国传统文化的精髓,它体现了矛盾既对立又统一的观点。
就是矛盾双方在一定条件下既相互依存,又相互转化。
②说法错误,事物没有绝对的同一。
排除②,本题答案就出来了,选B。
14.【答案】C。
解析:本题考查矛盾特殊性原理和具体问题具体分析的方法论。
①说法与题目无关;②说法正确,体现了具体问题具体分析的重要性;③说法错误,因为具体的历史的统一是主观与客观的统一,矛盾的普遍性和特殊性都是客观的,二者不能说具体历史的统一;④说法正确,符合题意。
本题选C。
15.【答案】D。
解析:本题考查矛盾与事物发展的关系。
16.【答案】ABCD。
解析:本题考查马克思主义哲学的辩证唯物论知识,物质决定意识,意识对于物质具有能动的反作用,本题强调意识的能动作用。
17.【答案】ACD。
解析:本题题干说明我们在实现思想理论创新过程中,必须要坚持以解放思想为先导,农村家庭联产承包责任制的确立就是解放思想、实事求是的产物。
解放思想,不是打破一切理论的约束,而是打破一切僵化的、教条的理论的约束,是对于理论的批判继承的过程。
在实践的过程中还需要科学理论的指导,并且要——91求我们要关注民生,关注基层群众需求,就是关注基层群众生活实践的需要,尊重人民群众的诉求。
因此,本题正确答案是ACD。
18.【答案】AC。
解析:本题考查科学技术的作用,先进的生产工具是人们先进的科学技术的物化,它运用于生产过程就会加快生产发展的速度,提高生产的效率。
科技革命推动生产方式的变革,进而推动社会制度的变革。
在本题中,手推磨、蒸汽磨是先进的生产工具,是科学技术的物化,由于它们的广泛应用,推动了生产方式的变革,分别产生了封建主义的社会和工业资本家的社会,所以,AC正确;B选项明显错误,科学技术不是历史变革中的唯一决定性力量。
科学技术是间接的生产力,不是自主性力量,自主性力量只能是运用科技的劳动者,D 选项错误。
因此,本题正确答案为AC。
19.【答案】ABCD。
解析:首先要将题干所讲述的事实即《城市生活无着的流浪乞讨人员救助管理办法》的正式发布一事,圈定在“上层建筑的变化”范畴之内,以此为前提再逐一分析题中所给定的4个备选答案:这一《管理办法》的正式发布,正好反映了上层建筑中“政治文明的进步”,当然也是“对人民群众根本利益的维护”和“对人权的尊重和保护”,从根本上说是“上层建筑不断变革完善的要求”。
20.【答案】ABCD。
解析:本题考查知识点是:学习和践行社会主义核心价值体系的重要意义。
平时应多注意一些党的文件中关于社会主义核心价值体系的权威表述。
21.【答案要点】(1)我国是人民民主专政的社会主义国家,人民是国家的主人,依法享有选举权和被选举权,享有言论、出版、集会、结社、游行、示威的自由,享有监督权等政治权利,它们是人民当家作主地位的体现。
(2)在我国人民不仅享有政治权利和自由,而且在经济、文化等方面也享有广泛的权利和自由,它们也是人民当家作主地位的体现。
(3)人民当家作主地位是由人民的基本权利和义务构成,并通过权利和义务的统一体现出来。
权利和义务是相辅相成,不可分离的。
只有权利与义务的统一才能充分体现人民当家作主的地位。
(4)所以题中观点具有片面性。
22.【答案要点】(1)经济增长是指产量或生产规模的扩大;经济发展是指在经济增长的基础上发生的结构性体制性的变化,强调在优化结构、提高效益、降低消耗、保护环境的基础上实现的持续长久发展,二者的内涵是不同的。
(2)单纯追求经济的增长,往往会带来一系列社会问题,甚至出现“没有发展的增长”,导致资源短缺,环境污染,生态破坏,难以实现持续发展。
(3)用“转变经济发展方式”代替了过去的“转变经济增长方式”的表述,体现了党在领导人民建设全面小康社会的过程中发展观理论的又一突破。
这也是在科学发展观的指导下,全面建设小康社会的客观要求。
(4)此观点是错误的。
23.【答案要点】转变经营战略,通过自主创新、提高员工素质等提升企业竞争力;加快产业结构升级,从劳动密集型生产方式向技术密集型生产方式转变;政府出台优惠措施,鼓励企业加大研发投入;实现从粗放型增长向集约型增长发展方式的转变。
24.【答案要点】(1)图表1表明近年来江苏省地区生产总值(GDP)不断增长,财政收入随之逐年增多;图表2表明江苏省财政支出逐年增多,对教育、社会保障等民生领域的投入逐年增加。
图表1、2表明经济发展是财政收入和财政支出增长的基础。
(2)江苏省政府以改善民生为重点,加大对民生领域的投入,加强社会建设,是贯彻落实“以人为本”的科学发展观的要求;发挥了财政在促进社会公平、改善人民生活中的物质保障作用;对于实现全面建设小康社会的奋斗目标具有重要意义。
25.【答案要点】广东省政府编制和推行发展规划、指导意见,注重于财政投放改善民生、地区差异缩小、公共服务均等化和收入分配公平。
这符合:(1)社会公平需要合理的收入分配。
政府对收入分配要进行调节。
(2)市场经济需要发挥财政的调控职能。
财政可以弥补市场失灵导致的收入差距拉大。
(3)社会主义的本质要求和共同富裕——92的目标。
(4)全面小康社会建设中形成区域协调互动发展机制、合理有序的收入分配格局的要求。
(5)科学发展观以人为本、推动区域协调发展、缩小区域差距的要求。
26.【答案要点】(1)拓展思想品德课的教材资源。
(2)创造思想品德课的实践资源。
(3)联接思想品德课的信息资源。
(4)广辟思想品德课的人力资源。
27.【答案要点】(1)表格显示,东部地区农民工工资高于中西部地区,但增幅小于中西部地区。
图表明,东部地区吸纳了全国外出农民工的绝大部分,但2009年的比例下滑。
相对于2008年,2009年农民工在东部、长三角、珠三角就业的比例下降,在中西部地区的比例上升,省内就业比例上升,省外就业比例下降。
(2)劳动者是生产过程的主体,在生产力发展中起主导作用,企业招不到工人,生产要素与劳动力无法结合,不能创造财富,必然影响企业和地区经济的发展,小张的观点有道理。
企业提高工资一定程度上可缓解“用工荒”,但企业不转变发展方式,就不可能持续提高工人工资,何况,企业要招到工人,还应为工人提供劳动安全、社会保险等。
从根本上讲,解决“用工荒”的出路在于企业转变发展方式。
小王的观点不全面。
在我国,市场在资源配置中起基础性作用,但市场有局限性,要更好更快地解决“用工荒”,还需要政府的宏观调控。
小周的观点是片面的。
28.【答案要点】(1)学习课程改革理论,转变教育教学观念;(2)注意学科知识与生活主题相结合;(3)坚持正确的价值导向,采取灵活的教学策略;(4)强化实践环节,丰富教学内容;(5)促使学生的学习方式由传统的被动接受式向“自主、探究、合作”式转变,倡导研究性学习方式;(6)建立民主、平等、和谐的师生关系,促使师生共同成长;(7)运用现代教学手段,提高学生学习效率;(8)重视与其他学习阶段课程的衔接和其他德育途径的联系,提高学生思想道德素质。
——93。