下载文档原格式
应用多元统计分析R实验上机讲义应用多元统计分析 (4)Applied Multivariate Statistical Analysis (4)第一章绪论 (4)第二章矩阵 (4)2.1矩阵的建立 (4)2.2矩阵的下标(index)与子集(元素)的提取 (6)2.3 矩阵四则运算 (7)2.3.1 矩阵的加减运算 (7)2.3.2 矩阵的相乘 (8)2.3.3 矩阵的求逆 (8)2.4矩阵的其他一些代数运算 (8)2.4.1 求转置矩阵 (8)2.4.2 提取对角元素 (8)2.4.3矩阵的合并与拉直 (8)2.4.4方阵的行列式 (9)2.4.5 矩阵的特征根和特征向量 (9)2.4.6 其它函数 (9)2.5 矩阵的统计运算 (11)2.5.1 求均值 (11)2.5.2 标准化 (11)2.5.3 减去中位数 (11)第三章多元正态分布及参数的估计 (12)3.1 绘制二元正态密度函数及其相应等高线图 (12)3.2 多元正态分布的参数估计 (14)3.2.1 多元正态总体的相关量 (14)3.2.2 极大似然估计 (14)第四章多元正态总体参数的假设检验 (15)4.1 几个重要统计量的分布 (15)4.2 单总体均值向量的检验及置信域 (16)4.2.1均值向量的检验 (16)4.2.2样本协方差阵的特征值和特征向量 (17)4.3多总体均值向量的检验 (17)4.3.1 两正态总体均值向量的检验 (17)4.3.2 多个正态总体均值向量的检验-多元方差分析 (19)4.4协方差阵的检验 (20)4.4.2 多总体协方差阵的检验 (20)4.5独立性检验 (20)4.6正态性检验 (21)第五章判别分析 (22)5.1距离判别 (22)5.1.1 马氏距离 (22)5.1.2 两总体的距离判别 (22)5.1.3 多个总体的距离判别 (26)5.2贝叶斯判别法及广义平方距离判别法 (26)5.2.1 先验概率(先知知识) (26)5.2.2 广义平方距离 (26)5.2.3 后验概率（条件概率） (27)5.2.4 贝叶斯判别准则 (27)5.3费希尔（Fisher）判别 (29)第六章聚类分析 (30)6.2距离和相似系数 (30)6.2.1距离 (31)6.2.2数据中心化与标准化变换 (31)6.2.3相似系数 (31)6.3 系统聚类法 (31)6.4类个数的确定 (34)6.5动态聚类法 (36)6.7变量聚类方法 (36)第七章主成分分析 (37)7.2 样本的主成分 (38)7.3 主成分分析的应用 (39)第八章因子分析 (42)8.3 参数估计方法 (42)8.4 方差最大的正交旋转 (45)8.5 因子得分 (45)第九章对应分析方法 (46)第十章典型相关分析 (48)应用多元统计分析Applied Multivariate Statistical Analysis第一章绪论在实际问题中，很多随机现象涉及到的变量不是一个，而是经常是多个变量，并且这些变量间又存在一定的联系。
多元统计分析基于R课程设计引言多元统计分析是现代统计学的重要组成部分，具有广泛的应用背景。
在数据科学领域，R语言是一种非常受欢迎的统计计算工具，能够方便地进行多元统计分析和可视化。
本课程设计旨在通过R语言进行多元统计分析的基础学习，提高学生对多元统计分析方法和应用的理解。
课程内容第一章：多元统计分析基础本章主要介绍多元统计分析的基本概念、理论与应用背景，包括多元正态分布、协方差矩阵、多元线性回归、主成分分析等内容。
通过使用R语言的数据分析工具和可视化包，学生将学习多元统计分析的基本方法、数据处理和可视化等方面的技能。
第二章：多元方差分析该章节主要介绍多元方差分析的理论和方法，包括单因素设计和多因素设计的多元方差分析。
本章还将介绍如何使用R语言进行多元方差分析，包括如何构建模型、计算方差分析表、进行置信区间分析和产生可视化图形等方面的技能。
第三章：判别分析本章将介绍判别分析的基本原理、方法和应用。
特别是线性判别分析和二次判别分析的主要方法和算法。
还将介绍R语言中的相关包，包括MASS和caret等，以进行判别分析的学习。
第四章：聚类分析本章将介绍聚类分析的基本理论和方法、层次聚类和分类聚类的原理和方法。
包括k均值算法、K中心点算法和高斯混合模型等的算法和应用。
还将介绍R语言中的相关包，包括stats和cluster等，以进行聚类分析的学习。
课程安排本课程设计分为7个星期，每周授课3个小时左右。
每个星期的课程安排如下：第一周•介绍课程内容和教学目标•多元统计分析基础概念：多元正态分布、协方差矩阵、多元线性回归、主成分分析等。
第二周•多元方差分析介绍•单因素设计的多元方差分析第三周•多因素设计的多元方差分析•使用R语言进行多元方差分析第四周•判别分析概述和应用•线性判别分析和二次判别分析第五周•介绍聚类分析•基于类簇的分析方法：K均值算法、K中心点算法第六周•分层聚类分析和分类聚类分析•高斯混合模型第七周•课程总结和讨论•提高阅读和写作技能的方法课程评估课程评估主要包括三个方面：作业、期末项目和参与度。
统计学专业《多元统计分析》课程实验指导书主撰人：李燕辉主审人：潘文荣刖言《多元统计分析》是统计学专业的一门重要的专业主干课。
它主要用于研究多维随机变量之间相互关系及内在统计规律，是认识和探索社会经济现象数量方面关系的重要方法和工具，在实际工作中具有广泛的应用前景。
由于其理论涉及的数学知识多而深,是本科生中最难学的一门课。
传统的教学方法主要是从理论上讲授，由于计算复杂、工作量大、分析过程长、计算工具和硬件条件等原因，讲授过程中举例比较困难，脱离实践，教学效果不理想。
由于统计专业学习多元统计分析，主要是掌握每个方法的基本原理，能够运用多元统计分析方法分析社会经济现象，该课程的教学更应强调方法的应用、学生实际操作能力和解决实际问题能力的培养。
为此，我们对该课程的教学进行多方面改革，以培养学生应用能力为主线，将多媒体技术、统计分析软件、案例教学、实践教学等有机结合起来，达到提高课堂教学效率和教学质量的目的，使学生真正掌握多元统计分析方法，培养了学生动手能力、数据分析能力、使用统计分析软件能力以及对实际经济问题的综合统计分析能力。
在我们的教学实践中，将《多元统计分析》总课时分解为课堂教学和实验教学两个部分。
该实验指导书就是为《多元统计分析》实验课设计的。
目录第一部份绪论（2）第二部份基本实验指导（3）实验一均值检验、多元方差分析（3）实验二聚类分析、判别分析（3）实验三因子分析、主成分分析（4）实验四联合分析（5）实验五对应分析（6）实验六多元数据综合分析（7）第一部份绪论本指导书是根据《多元统计分析》课程实验教学大纲编写的，适用于统计学专业。
一、本课程实验的作用与任务本课程为统计学专业必修的技术课程。
通过实验教学，使学生能够更好地了解多元统计分析的基本概念和基本原理，对一些常用的多元统计思想和统计方法有更深的认识，提高学生处理常见的多元统计问题的实际操作能力。
要求学生密切关注社会经济中的热点问题，独立进行思考，查找自己感兴趣的研究资料，自己动手设计多元变量，以提高学生解决实际问题的能力。
多元统计方法的R语言实现一、主成分分析主成分分析是一种降维技术，用于从原始数据中提取出最重要的特征，以减少变量的数量。
R语言中有多个包可以进行主成分分析的实现，比如FactoMineR、psych等。
以下是使用FactoMineR包进行主成分分析的示例代码：```R# 安装并加载FactoMineR包install.packages("FactoMineR")library(FactoMineR)#读取数据data <- read.csv("data.csv")#主成分分析result <- PCA(data)#结果展示summary(result) # 查看主成分分析的结果plot(result) # 绘制主成分分析的结果```二、聚类分析聚类分析是一种将相似的对象分组为簇的分析方法。
R语言中有多个包可以进行聚类分析的实现，比如cluster、kmeans等。
以下是使用cluster包进行聚类分析的示例代码：```R# 安装并加载cluster包install.packages("cluster")library(cluster)#读取数据data <- read.csv("data.csv")#聚类分析result <- kmeans(data, 3) # 将数据分为3个簇#结果展示summary(result) # 查看聚类分析的结果plot(result, data) # 绘制聚类分析的结果```三、判别分析判别分析是一种用于确定变量与分类之间关系的分析方法。
R语言中有多个包可以进行判别分析的实现，比如MASS、caret等。
以下是使用MASS包进行判别分析的示例代码：```R#安装并加载MASS包install.packages("MASS")library(MASS)#读取数据data <- read.csv("data.csv")#判别分析result <- lda(class ~ ., data) # 将class变量与其他变量进行判别分析#结果展示summary(result) # 查看判别分析的结果plot(result) # 绘制判别分析的结果```四、因子分析因子分析是一种用于确定变量的共同因素的分析方法。
一、实验背景随着社会经济的发展和科学技术的进步，数据量日益庞大，如何从大量数据中提取有价值的信息，成为统计学研究的热点问题。
多元统计分析作为统计学的一个重要分支，通过对多个变量之间的关系进行分析，为决策者提供有力的数据支持。
本实验旨在通过实际操作，让学生熟练掌握多元统计分析方法，提高数据分析能力。
二、实验目的1. 掌握多元统计分析的基本概念和方法；2. 学会运用多元统计分析方法解决实际问题；3. 提高数据分析能力，为后续课程打下坚实基础。
三、实验内容本次实验以某城市居民消费数据为例，运用多元统计分析方法对其进行分析。
四、实验步骤1. 数据导入首先，将实验数据导入统计软件（如SPSS、R等）。
本实验采用SPSS软件，数据集包含以下变量：（1）收入（y）：居民年收入；（2）教育程度（x1）：居民最高学历；（3）年龄（x2）：居民年龄；（4）家庭人口（x3）：家庭人口数量；（5）住房面积（x4）：家庭住房面积。
2. 描述性统计分析对数据集进行描述性统计分析，包括各变量的均值、标准差、最大值、最小值等。
3. 相关性分析运用皮尔逊相关系数、斯皮尔曼等级相关系数等方法，分析变量之间的相关关系。
4. 主成分分析运用主成分分析方法，提取主要成分，降低数据维度。
5. 聚类分析运用K-means聚类分析方法，将居民划分为不同的消费群体。
6. 随机森林回归分析运用随机森林回归分析方法，预测居民收入。
五、实验结果与分析1. 描述性统计分析根据描述性统计分析结果，可知居民年收入、教育程度、年龄、家庭人口、住房面积的平均值、标准差、最大值、最小值等。
2. 相关性分析通过相关性分析，发现收入与教育程度、年龄、家庭人口、住房面积之间存在显著的正相关关系。
3. 主成分分析根据主成分分析结果，提取出两个主成分，累计方差贡献率为84.95%，可以解释大部分的变量信息。
4. 聚类分析通过K-means聚类分析，将居民划分为3个消费群体。
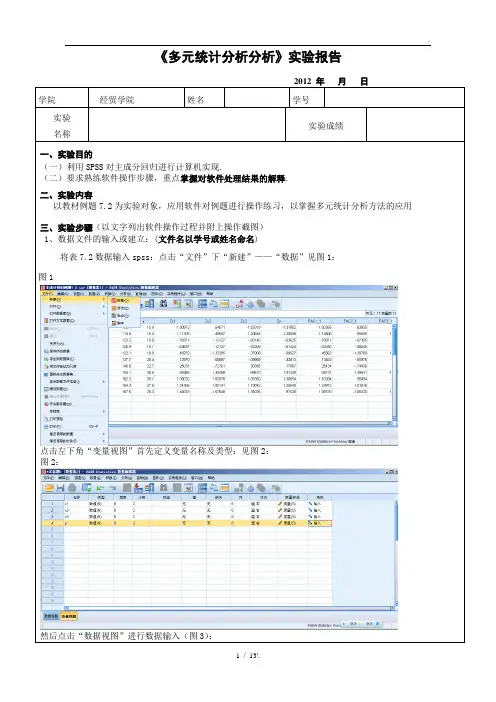
《多元统计分析分析》实验报告2012 年月日学院经贸学院姓名学号实验实验成绩名称一、实验目的（一）利用SPSS对主成分回归进行计算机实现.（二）要求熟练软件操作步骤，重点掌握对软件处理结果的解释.二、实验内容以教材例题7.2为实验对象，应用软件对例题进行操作练习，以掌握多元统计分析方法的应用三、实验步骤（以文字列出软件操作过程并附上操作截图）1、数据文件的输入或建立：(文件名以学号或姓名命名)将表7.2数据输入spss：点击“文件”下“新建”——“数据”见图1：图1点击左下角“变量视图”首先定义变量名称及类型：见图2：图2：然后点击“数据视图”进行数据输入（图3）：图3完成数据输入2、具体操作分析过程：（1）首先做因变量Y与自变量X1-X3的普通线性回归：在变量视图下点击“分析”菜单，选择“回归”-“线性”（图4）：图4将因变量Y调入“因变量”栏，将x1-x3调入“自变量”栏（图5）：然后选择相关要输出的结果：①点击右上角“统计量（s）”：“回归系数”下选择“估计”；“残差”下选择“D.W”；在右上角选择输出“模型拟合度”、“部分相关和偏相关”“共线性诊断”（后两项是做多重共线性检验）。
选完后点击“继续”（见图6）②如果需要对因变量与残差进行图形分析则需要在“绘制”下选择相关项目（图7），一般不需要则继续③如果需要将相关结果如因变量预测值、残差等保存则点击“保存”（图8），选择要保存的项目④如果是逐步回归法或者设置不带常数项的回归模型则点击“选项”（图9）其他选项按软件默认。
最后点击“确定”，运行线性回归，输出相关结果（见表1-3）图5 图6图7图8图9回归分析输出结果：的协差阵也就是相关阵进行分解做因子分析或主成分分析），如果不需要对变量做标准化处理就选“协方差矩阵”；“输出”中的两项都选，要求输出没有旋转的因子解（主成分分析必选项）和碎石图（用图形决定提取的主成分或因子的个数）；“抽取“下，默认的是基于特征值（大于1表示提取的因子或主成分至少代表1个单位标准差的变量信息，因为标准化后的变量方差为1，因子或者主成分作为提取的综合变量应该至少代表1个变量的信息），也可以自选提取的因子个数（即第二项），本例中做主成分回归，选择提取全部可能的3个主成分，所以自选个数填3。
统计分析中利用R语言进行多元回归分析统计分析是一种数据分析方法，它通过收集、整理和分析数据，推断出数据之间的关系，并对未来趋势作出预测，以支撑决策。
多元回归分析是其中的一种方法，它通过多个自变量对一个因变量的影响进行分析。
在实践中，R语言成为了一种非常流行的工具，帮助研究人员进行多元回归分析。
本文将介绍如何使用R语言进行多元回归分析。
一、R语言介绍R语言是一种自由软件，被广泛应用于统计学、数据挖掘和机器学习等领域。
R语言具有开放源代码、跨平台、多维数据结构和强大的统计分析功能等特点。
二、多元回归分析介绍在多元回归分析中，研究人员通常需要了解多个因素对一个变量的影响。
例如，许多研究都会使用多元回归分析来了解教育、经济和人口统计学因素对收入的影响。
在多元回归分析中，有一个因变量和多个自变量。
因变量是需要预测或理解的变量，而自变量是用来解释因变量的变量。
通过分析不同自变量与因变量之间的关系，可以更好地理解它们之间的相互作用。
多元回归分析常用的公式为：Y = b0 + b1X1 + b2X2 + b3X3 + … + bnXn其中，Y为因变量，X1、X2、X3、…、Xn为自变量，b0、b1、b2、b3、…、bn为回归系数。
三、使用R语言进行多元回归分析R语言提供了多种函数用于执行回归分析。
其中，通常使用的是 lm 函数。
lm函数是 R 语言中最基本的回归函数之一，它用于创建一个线性回归模型。
下面我们以一个案例来介绍如何使用 R 语言进行多元回归分析。
在这个案例中，我们使用的数据集是 mtcars。
该数据集包含了32辆不同的车型，其中每个车型有11个变量，其中 mpg 是其燃油效率，其他变量包括马力、排量、车重、加速度等等。
首先，我们需要加载数据集，代码如下：```library(datasets)data(mtcars)head(mtcars)```然后，我们选择自变量和因变量。
在这个案例中，我们选择mpg 作为因变量，选择所有其他变量作为自变量。
