一次函数的图像和性质

中国教育培训行业十大领军品牌成都戴氏精品堂学校 1 函数性质和图像一次函数性质：1.y 的变化值与对应的x 的变化值成正比例，比值为k.K 为常数. 即：y=kx+b （k ，b 为常数，k ≠0）， 当x 增加m ，k （x+m)+b=y+km,km/m=k 。

2.当x=0时，b 为函数在y 轴上的点,坐标为(0，b)。

3.、当b=0时(即 y=kx)，一次函数图像变为正比例函数，正比例函数是特殊的一次函数。

4.在两个一次函数表达式中：（1）当两一次函数表达式中的k 相同，b 也相同时，两个一次函数图像重合；(2) 当两一次函数表达式中的k 相同，b 不相同时，两一次函数图像平行；（3）当两一次函数表达式中的k 不相同，b 不相同时，两一次函数图像相交；（4）当两一次函数表达式中的k 不相同，b 相同时，两一次函数图像交于y 轴上的同一点（0，b ）。

(5)若两个变量x,y 间的关系式可以表示成y=kx+b(k,b 为常数，k 不等于0）则称y 是x 的一次函数图像性质：1．作法与图形：通过如下3个步骤：（1）列表.（2）描点；[一般取两个点,根据“两点确定一条直线”的道理，也可叫“两点法”。

A:一般的y=kx+b(k ≠0）的图象过（0，b ）和（-b/k ，0）两点画直线即可。

B:正比例函数y=kx(k ≠0）的图象是过坐标原点的一条直线，一般取（0,0）和（1，k ）两点。

（3）连线，可以作出一次函数的图象——一条直线。

因此，作一次函数的图象只需知道2点，并连成直线即可。

（通常找函数图象与x 轴和y 轴的交点分别是-k 分之b 与0，0与b ）.2．性质：（1）在一次函数上的任意一点P （x ，y ），都满足等式：y=kx+b(k ≠0)。

（2）一次函数与y 轴交点的坐标总是（0，b)，与x 轴总是交于（-b/k ，0）正比例函数的图像都是过原点。

3. 函数不是数，它是指某一变化过程中两个变量之间的关系。

一次函数的图象和性质【知识要点】1.一次函数的概念：函数y=kx ＋b （k ，b 为常数，k ≠0）叫做x 的一次函数。

学习这个定义应明确下面几点：函数y=kx ＋b （k ≠0）中b 可以为任意常数，当b=0时，一次函数y=kx ＋b 就成y=kx （k 为常数，且（k ≠0）），这时y 叫做x 的正比例函数，也可以说y 与x 成正比例，常数k 叫做因变量y 与自变量x 的比例系数．因此正比例函数是一次函数的特例，但一次函数不一定是正比例函数。

2.一次函数的图像：一次函数y ＝kx ＋b （k ≠0）的图像是一条与坐标轴斜交的直线。

因此，只需求出直线y ＝kx ＋b 上的两点，就可得到它。

一般，作正比例函数y ＝kx 的图像常取点（0，0）和（1，k ）；作一次函数)0(≠+=b b kx y 的图像常取（b ,0）和（0,k b-）两点，这两点是直线与坐标轴的交点。

3.一次函数的性质：（1）参数k 、b 的意义和对一次函数y ＝kx ＋b 的图像与性质的影响。

当k>0时，图像一定过一、三象限，y 随x 的增大而增大，这时函数的图像从左到右呈上升趋势；当k<0时，图像一定过二、四象限，y 随x 的增大而减小，这时函数的图像从左到右呈下降趋势；（因此，k 的符号与直线的方向、函数的增减性是相互决定的。

）（2）b 是一次函数y ＝kx ＋b 中，当x ＝0时所对应的函数值，因此直线y ＝kx ＋b 与y 轴交于点（0，b ），b 是直线y ＝kx ＋b 与y 轴上的交点的纵坐标，所以，b 的符号和直线与y 轴交点位置是相互对应的。

（3）k 、b 的符号对直线位置的影响：【小试牛刀】 1、一个正比例函数y kx=的图象经过点A （-2，4），写出这个正比例函数的表达式 ．2、一辆汽车和一辆摩托车分别从A ,B 两地去同一城市,它们离A 地的路程随时间变化的图象如图所示.则下列结论错误．．的是（ ） A.摩托车比汽车晚到1 h B. A , B 。

一次函数的定义和性质一次函数是指形如y=ax+b的函数，其中a和b为常数，且a不等于零。

它也被称为线性函数，因为它的图像是一条直线。

一次函数是数学中的基础概念之一，具有一些重要的性质和应用。

一. 定义一次函数是指以x为自变量，以y为因变量的函数，其表达式为y=ax+b，其中a和b为实数，且a不等于零。

其中，a称为一次项的系数，b称为常数项。

当x取不同的值时，y的取值也相应地发生变化，这种对应关系可以通过一条直线来表示。

二. 图像特征1. 直线特征：一次函数的图像总是一条直线，因此它具有线性特征；2. 斜率特征：一次函数的斜率表示为常数a，描述了图像在x轴正方向上的倾斜程度。

斜率为正时，表示图像向上倾斜；斜率为负时，表示图像向下倾斜；3. 截距特征：一次函数的截距表示为常数b，描述了图像与y轴的交点位置。

截距为正时，表示图像与y轴正半轴交于正值点；截距为负时，表示图像与y轴负半轴交于负值点。

三. 性质1. 单调性：一次函数的单调性由斜率的正负决定。

当a大于零时，函数单调递增；当a小于零时，函数单调递减；2. 定义域和值域：一次函数的定义域为所有实数；值域为所有实数，即函数的取值范围没有限制；3. 零点：一次函数的零点即为函数的根，表示当x取某个值时，函数的值等于零。

对于一次函数，当且仅当x=-b/a时，函数的值为零；4. 最值：一次函数没有最大值和最小值，因为它的图像是一条直线；5. 平移：通过给定一次函数的表达式，可以进行平移操作来得到新的函数。

平移操作可以在x轴和y轴上分别进行，通过改变常数a和b的值，可以使图像在平面上发生移动。

四. 应用一次函数在现实生活中有着广泛的应用，例如：1. 财务收入：一些经济指标和统计数据的变化趋势可以通过一次函数来表示，如年度收入的增长率；2. 运动模型：一次函数可以表示一些常见的运动模型，如匀速运动的位移和速度关系；3. 经济学模型：在经济学中，一次函数可以用来表示供求关系、成本和收益关系等；4. 工程预测：一次函数可以用来进行工程测量、预测物理量的变化趋势等。

课题 一次函数的图像与性质1、一次函数的图像的画法（1）画函数图像的三步：列表－描点－连线. （2）一次函数的图象是一条直线。

一次函数y=kx+b （k 、b 是常数，且k ≠0）的图象是一条直线。

一次函数y=kx+b 也称为直线y=kx+b ，这时，我们把一次函数的解析式y=kx+b 称为这一直线的表达式。

（3）因为一次函数y=kx+b （k 、b 是常数，且k ≠0）的图象是一条直线，根据“两点确定一条直线”的基本性质，画一次函数的图象时只需描出图象上的两个点，再作过这两点的直线即可。

2、一次函数的图像的性质（1）一次函数与x 轴交点的纵坐标为0，与y 轴交点的横坐标为0.（2）一次函数111(y k x b k =+、110b k ≠为常数，）与222(y k x b k =+、220b k ≠为常数，）的图像平行时，则12k k =。

反之，当12k k =时，两直线平行，且当12k k =，12b b =时，两直线重合。

（3）当一次函数111(y k x b k =+、110b k ≠为常数，）与222(y k x b k =+、220b k ≠为常数，）的图像的截距相同且不平行时，则12b b =，12k k ≠。

（4）一次函数y=kx+b （k 、b 是常数，且k ≠0）当k>0时函数值随着x 的增大而增大、减小而减小，即该函数为增函数；当k<0时函数值随着x 的增大而减小、减小而增大。

即该函数为减函数。

3、一次函数图像的平移一次函数y=kx+b （k 、b 是常数，且k ≠0）的图象向上平移h 个单位后的函数解析式为y=kx+b+h;向下平移h 个单位后的函数解析式为y=kx+b-h 。

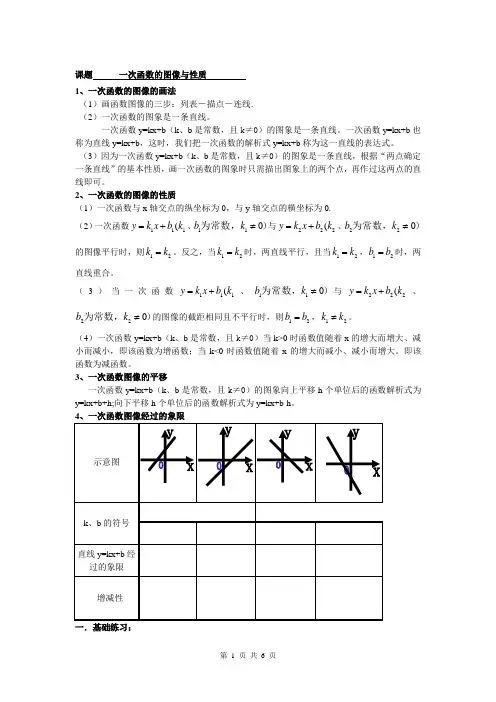
4、一次函数图像经过的象限示意图k 、b 的符号直线y=kx+b 经过的象限增减性一．基础练习：1.一次函数y=3x-6的图像是，它与x轴的交点坐标是，它与y轴的交点坐标是2.将直线y=x向下平移4个单位，得到直线3.将直线y=-3x-5向上平移4个单位，得到直线4.若直线y=3x-5与直线y=kx-4相互平行，则k=5.若直线y=-2x-5与直线y=6x+b相交于y轴上同一点，则b=6. 请你在不同的平面直角坐标系中画出下列函数的图像（1）y=2x+6 （2）1722 y x=+（3）4833y x=--（4）1344y x=--7,做一做：画出函数y=-2x+2 的图像，结合图象回答下列问题：（ 1 ）这个函数中，随着x 的增大，y 将增大还是减小？（ 2 ）当x 取何值时，y=0 ？当y 取何值时，x=0 ？（ 3 ）当x 取何值时，y>0 ？（ 4 ）函数的图像不经过哪个象限？8、完成下列各题：（1）下列函数中，y的值随着x的增大而减小的是（）A.y=2x-7B.y=0.5x+2C.y=(2-1)x+3D.y=-0.3x+1（2）函数y=4x-3中，y的值随着x值的增大而____（3）函数y=(2m-1)x+2的函数值随x的增大而减小，则m的值为______ （4）一次函数y=2x+4的图像上有两点A(3,a)，B(4,b)，请判断a与b的大小（5）y=x+5与y=2x-5的增减性（y 随着x 的增加而增加，还是随着x 的增加而减小）是否一样？（6）y=-2x+5与y=-2x-5的增减性是否一样？（7）A(a,6)和B(b,-2)在函数y=2x-5的图像上，请你判断a ，b 的大小关系 9、已知一次函数2(2)28y k x k =--+，分别根据下列条件求k 的值或k 的取值范围： （1）它的图像经过原点（2）它的图像经过点（0,－2）（3）它的图像与y 轴的交点在x 轴上方 （4）y 随着x 的增大而减小（5）这条直线经过一、二、三象限10、要使一次函数y=-3x+4的函数值大于4，求自变量x 的取值范围。

一次函数的图像与性质函数图象性质经过象限变化规律y=kx+b（k、b为常数，且k≠0）k＞0b＞0b=0b＜0 k＜0b＞0b=0b＜0☆一次函数y=kx+b（k≠0）中k、b的意义：k(称为斜率)表示直线y=kx+b（k≠0）的倾斜程度；b（称为截距）表示直线y=kx+b（k≠0）与y轴交点的，也表示直线在y 轴上的。

☆同一平面内，不重合的两直线 y=k1x+b1（k1≠0）与 y=k2x+b2（k2≠0）的位置关系：当时，两直线平行。

当时，两直线垂直。

当时，两直线相交。

当时，两直线交于y轴上同一点。

☆特殊直线方程：X轴 : 直线 Y轴 : 直线与X轴平行的直线与Y轴平行的直线一、三象限角平分线二、四象限角平分线1、对于函数y＝5x+6，y的值随x值的减小而___________。

2、对于函数1223y x =-, y 的值随x 值的________而增大。

3、一次函数 y=(6-3m)x ＋(2n －4)不经过第三象限，则m 、n 的范围是__________。

4、直线y=(6-3m)x ＋(2n －4)不经过第三象限，则m 、n 的范围是_________。

5、已知直线y=kx+b 经过第一、二、四象限，那么直线y=-bx+k 经过第_______象限。

6、无论m 为何值，直线y=x+2m 与直线y=-x+4的交点不可能在第______象限。

7、已知一次函数（1）当m 取何值时，y 随x 的增大而减小？ （2）当m 取何值时，函数的图象过原点？练习：理解解析式和图象的关系，掌握一次函数图象的有关性质. 一、选择题1.函数y =kx 的图象经过点P （3，－1），则k 的值为（ ）A.3B.－3C.31D.－31 2.下列函数中，图象经过原点的为（ ） A.y =5x +1 B.y =－5x －1 C.y =－5xD.y =51-x 3.若一次函数y =kx +b 中，y 随x 的增大而减小，则（ ） A.k ＜0,b ＜0 B.k ＜0,b ＞0 C.k ＜0,b ≠0 D.k ＜0,b 为任意数4.当x =5时一次函数y =2x +k 和y =3kx －4的值相同，那么k 和y 的值分别为（ ） A.1,11 B.－1,9 C.5,11 D.3,35.若直线y =kx +b 经过A （1，0），B （0，1），则（ ） A.k =－1,b =－1 B.k =1,b =1 C.k =1,b =－1 D.k =－1,b =1 二、填空题6.把一个函数的自变量x 与对应的因变量y 的值分别作为点的______和______,在直角坐标系中描出它的对应点，所有这些点组成的图形叫做该函数的______.7.作函数图象的一般步骤为______，______，______；一次函数的图象是一条______. 8.直线y =3－9x 与x 轴的交点坐标为______，与y 轴的交点坐标为______.9.一次函数y =5kx －5k －3,当k =______时，图象过原点；当k ______时，y 随x 的增大而增大.10.在一次函数y =2x －5中，当x 由3增大到4时，y 的值由______；当x 由－3增大到－2时，y 的值______.。

一次函数的图像和性质一次函数是一个代数函数，也称为线性函数或直线函数。

它是最简单的一种函数形式，在数学和物理等领域中都有广泛的应用。

一次函数的一般形式为y = ax + b，其中a和b是常数，且a≠0。

一次函数的图像是一个直线，在平面直角坐标系中表示为一根斜率为a的直线，并且通过点(0,b)。

斜率a表示函数的变化率，即y随x的变化速度。

当a>0时，表明随着x增大，y也增大；当a<0时，表明随着x增大，y减小；当a=0时，函数是一个常数函数。

一次函数图像的性质包括斜率、截距、与坐标轴的交点等。

1.斜率：一次函数的斜率表示函数图像在x轴方向每单位变化时，y轴方向的变化量。

斜率的计算可以通过选择两个不同的x值，计算对应的y值的差异，然后除以对应x值的差异。

即斜率a=Δy/Δx。

斜率为正的函数图像向上倾斜，斜率为负的函数图像向下倾斜，斜率为零的函数图像是水平的。

2. 截距：一次函数的截距表示函数图像与y轴的交点，它的值可以从函数的形式y=ax+b中得到。

当x=0时，y=b，因此截距为b。

3. 与坐标轴的交点：一次函数的图像与x轴的交点为y=0时的x值，可以通过令y=0，解方程ax+b=0，得到x=-b/a。

图像与y轴的交点已经在上述截距部分提到，为(0, b)。

4.平行：两个斜率相等的一次函数图像是平行的，它们可能在坐标轴上的交点不同，但是平行于同一直线。

5. 垂直平分线：对于一次函数y = ax + b，它的垂直平分线为x =-a/2、如果两个函数的图像关于该直线对称，那么它们是互为反函数。

6. 对称轴：对于一次函数y = ax + b，它的对称轴为x = -b/(2a)。

如果交换a和b的位置，可以得到该函数关于y轴对称函数。

如果交换x和y的位置，可以得到原函数的倒数。

7.等差数列：一次函数的图像可以表示等差数列，其中公差为斜率a。

数列的第一个项为截距b。

8.增长率：一次函数的增长率等于斜率a的绝对值。

15一次函数的图像与性质1.图像特点：一次函数的图像是一条直线，它经过原点(0,0)。

直线的斜率k可以表示函数的性质，决定了直线的倾斜程度和方向。

当k大于0时，直线向右上方倾斜；当k小于0时，直线向右下方倾斜；当k等于0时，直线平行于x轴。

2.变化趋势：一次函数的变化趋势与自变量x的变化直接相关。

当x变大时，若k大于0，则y也会增大；若k小于0，则y会减小。

反之，当x变小时，则y的变化情况也相应地相反。

由此可见，一次函数的图像呈现出一个直线，且变化趋势具有确定性。

3.斜率性质：斜率k是一次函数的重要性质，它表示了函数图像的倾斜程度和方向。

一次函数的斜率有以下几个关键性质：-当k大于0时，函数图像是向上倾斜的，即从左下向右上。

斜率越大，直线越陡峭。

-当k小于0时，函数图像是向下倾斜的，即从左上向右下。

斜率越小，直线越平缓。

-当k等于0时，函数图像是平行于x轴的水平直线。

4.截距性质：一次函数还有一个重要的性质是截距。

截距表示了一条直线与y轴的交点，记作（0，b）。

对于一次函数y=kx来说，截距b等于函数在x=0处的取值，即b=k*0=0。

因此，一次函数经过原点（0，0），并且与y轴没有交点。

5.定比关系：一次函数的数值关系具有一种特殊的定比关系。

对于一次函数y=kx来说，当x增大或减小时，y的值与x的比值始终保持不变，即y/x=k。

这称为一次函数的定比关系，可以用来解决一些实际问题，如单位换算、速度、密度等概念的计算。

6.定义域和值域：一次函数的定义域为所有实数集R，即函数在实数范围内都有定义。

值域则取决于斜率k的正负。

当k大于0时，一次函数的值域是(0，+∞)；当k小于0时，值域是(-∞，0)。

由于一次函数的图像是直线，所以图像在纵轴方向上没有上下界限。

7.相关性质：一次函数的图像与直线的性质有密切关联，因为一次函数的图像就是一根直线。

因此，一次函数也具有直线的一些基本性质，如：-一次函数的斜率等于直线的斜率。