自动控制原理第三章课后习题-答案(最新)要点

第3章 控制系统的时域分析【基本要求】1. 掌握时域响应的基本概念，正确理解系统时域响应的五种主要性能指标；2. 掌握一阶系统的数学模型和典型时域响应的特点，并能熟练计算其性能指标和结构参数；3. 掌握二阶系统的数学模型和典型时域响应的特点，并能熟练计算其欠阻尼情况下的性能指标和结构参数；4. 掌握稳定性的定义以及线性定常系统稳定的充要条件，熟练应用劳斯判据判定系统稳定性；5. 正确理解稳态误差的定义，并掌握系统稳态误差、扰动稳态误差的计算方法。

微分方程和传递函数是控制系统的常用数学模型，在确定了控制系统的数学模型后，就可以对已知的控制系统进行性能分析，从而得出改进系统性能的方法。

对于线性定常系统，常用的分析方法有时域分析法、根轨迹分析法和频域分析法。

本章研究时域分析方法，包括简单系统的动态性能和稳态性能分析、稳定性分析、稳态误差分析以及高阶系统运动特性的近似分析等。

根轨迹分析法和频域分析法将分别在本书的第四章和第五章进行学习。

这里先引入时域分析法的基本概念。

所谓控制系统时域分析方法，就是给控制系统施加一个特定的输入信号，通过分析控制系统的输出响应对系统的性能进行分析。

由于系统的输出变量一般是时间t 的函数，故称这种响应为时域响应，这种分析方法被称为时域分析法。

当然，不同的方法有不同的特点和适用范围，但比较而言，时域分析法是一种直接在时间域中对系统进行分析的方法，具有直观、准确的优点，并且可以提供系统时间响应的全部信息。

3.1 系统的时域响应及其性能指标为了对控制系统的性能进行评价，需要首先研究系统在典型输入信号作用下的时域响应过程及其性能指标。

下面先介绍常用的典型输入信号。

3.1.1 典型输入信号由于系统的动态响应既取决于系统本身的结构和参数，又与其输入信号的形式和大小有关，而控制系统的实际输入信号往往是未知的。

为了便于对系统进行分析和设计，同时也为了便于对各种控制系统的性能进行评价和比较，需要假定一些基本的输入函数形式，称之为典型输入信号。

自动控制原理（上）习 题3-1 设系统的结构如图3-51所示，试分析参数b 对单位阶跃响应过渡过程的影响。

考察一阶系统未知参数对系统动态响应的影响。

解 由系统的方框图可得系统闭环响应传递函数为/(1)()()111K Ts Ks Kbs T Kb s Ts +Φ==++++ 根据输入信号写出输出函数表达式：111()()()()()11/()K Y s s R s K s T Kb s s s T bK =Φ⋅=⋅=-++++对上式进行拉式反变换有1()(1)t T bKy t K e-+=-当0b >时，系统响应速度变慢；当/0T K b -<<时，系统响应速度变快。

3-2 设用11Ts +描述温度计特性。

现用温度计测量盛在容器内的水温，发现1min 可指示96%的实际水温值。

如果容器水温以0.1/min C ︒的速度呈线性变化，试计算温度计的稳态指示误差。

考察一阶系统的稳态性能分析(I 型系统的，斜坡响应稳态误差)解 由开环传递函数推导出闭环传递函数，进一步得到时间响应函数为：()1t T r y t T e -⎛⎫=- ⎪⎝⎭其中r T 为假设的实际水温，由题意得到：600.961Te-=-推出18.64T =，此时求输入为()0.1r t t =⋅时的稳态误差。

由一阶系统时间响应分析可知，单位斜坡响应的稳态误差为T ，所以稳态指示误差为：lim ()0.1 1.864t e t T →∞==3-3 已知一阶系统的传递函数()10/(0.21)G s s =+今欲采用图3-52所示负反馈的办法将过渡过程时间s t 减小为原来的1/10，并保证总的放大倍数不变，试选择H K 和0K 的值。

解 一阶系统的调节时间s t 与时间常数成正比，则根据要求可知总的传递函数为10()(0.2/101)s s Φ=+由图可知系统的闭环传递函数为000(10()()1()0.211010110()0.21110H HHHK G s K Y s R s K G s s K K K s s K ==++++==Φ++）比较系数有101011011010HHK K K ⎧=⎪+⎨⎪+=⎩ 解得00.9,10H K K ==3-4 已知二阶系统的单位阶跃响应为1.5()1012sin(1.6+53.1t y t e t -=-）试求系统的超调量%σ，峰值时间p t ，上升时间r t 和调节时间s t 。

⾃动控制原理---丁红主编---第三章习题答案习题3-1.选择题：（1）已知单位负反馈闭环系统是稳定的，其开环传递函数为：)1(2)s )(2+++=s s s s G （，系统对单位斜坡的稳态误差是： 3-2 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。

解Φ()()./(.)s L k t s ==+001251253-3 ⼀阶系统结构图如图3-45所⽰。

要求系统闭环增益2=ΦK ，调节时间4.0≤s t s ，试确定参数21,K K 的值。

图题3-3图解由结构图写出闭环系统传递函数111)(212211211+=+=+=ΦK K sK K K s K sK K s K s 令闭环增益212==ΦK K ，得：5.02=K 令调节时间4.03321≤==K K T t s ，得：151≥K 。

3-4 设⼆阶控制系统的单位阶跃响应曲线如图所⽰。

如果该系统为单位反馈控制系统，试确定其开环传递函数。

图题3-4图解：由图知，开环传递函数为3-5 设⾓速度指⽰随动统结构图如图3-40所⽰。

若要求系统单位阶跃响应⽆超调，且调节时间尽可能短，问开环增益K 应取何值，调节时间s t 是多少图3-40 题3-5图解：依题意应取 1=ξ，这时可设闭环极点为02,11T -=λ。

写出系统闭环传递函数Ks s Ks 101010)(2++=Φ闭环特征多项式20022021211010)(++= +=++=T s T s T s K s s s D ⽐较系数有==K T T 101102200 联⽴求解得 ??==5.223-6 图所⽰为某控制系统结构图，是选择参数K 1和K 2，使系统的ωn =6，ξ=1.3-7 已知系统的特征⽅程，试判别系统的稳定性，并确定在右半s 平⾯根的个数及纯虚根。

（1）01011422)(2 345=+++++=s s s s s s D （2）0483224123)(2345=+++++=s s s s s s D （3）022)(45=--+=s s s s D（4）0502548242)(2345=--+++=s s s s s s D解（1）1011422)(2345+++++=s s s s s s D =0Routh ： S 5 1 2 11 S 4 2 4 10 S 3 ε 6 S 2 εε124- 10 S 6 S 0 10第⼀列元素变号两次，有2个正根。

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t 25.1e 0125.0)t (k -=，试求系统闭环传递函数)s (Φ。

解 [])25.1s /(0125.0)t (k L )s (+==Φ3-2 一阶系统结构如图所示。

要求单位阶跃输入时调节时间4.0t s ≤s （误差带为5%），稳态输出为2，试确定参数21k ,k 的值。

解 由结构图写出闭环系统传递函数 1k k s k 1k k s k sk k 1s k )s (212211211+=+=+=Φ 闭环增益2k 1k 2==Φ， 得：5.0k 2= 令调节时间4.0k k 3T 3t 21s ≤==，得：15k 1≥。

3-3 给定典型二阶系统的设计指标：超调量0<%32.4%≤σ，调节时间 s 5.0t s <，峰值时间s 1t p <，试确定系统极点配置的区域，以获得预期的响应特性。

解 依题 %32.4%≤σ， )45(707.0︒≤≥⇒βξ；5.05.3t ns <ωξ=， 7n >ωξ⇒； n p t ωξπ21-=1<， 14.312>-⇒n ωξ综合以上条件可画出满足要求的特征根区域如图所示。

3-4 电子心脏起博器心律控制系统结构如图所示，其中模仿心脏的传递函数相当于一纯积分环节。

解 依题，系统传递函数为2n n 22n 2s 2s 05.0K s 05.01s 05.0K)s (ω+ξω+ω=++=Φ ⎪⎪⎩⎪⎪⎨⎧ω⨯=ξ=ωn n 205.0105.0K 令 5.0=ξ可解出 ⎩⎨⎧=ω=2020K n将 s 1t =代入二阶系统阶跃响应公式 ()β+ωξ-ξ--=ξω-t 1sin 1e 1)t (h n 22tn 可得 min 00145.60s 000024.1)1(h 次次==5.0=ξ时，系统超调量 %3.16%=σ，最大心速为min 78.69163.1163.01t (h p 次次）==+=3-5 机器人控制系统结构如图所示, 试确定参数21k ,k 值，使系统阶跃响应的峰值时间5.0t p =s ，超调量%2%=σ。

3-1 设系统的微分方程式如下：（1） )(2)(2.0t r t c =&（2） )()()(24.0)(04.0t r t c t c t c =++&&&试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。

已知全部初始条件为零。

解：（1） 因为)(2)(2.0s R s sC = 闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应：s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c（2）)()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C 闭环传递函数124.004.01)()()(2++==s s s R s C s φ 单位脉冲响应：124.004.01)(2++=s s s C t e t g t 4sin 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s Ct e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ，用其测量容器内的水温，1min 才能显示出该温度的98%的数值。

若加热容器使水温按10ºC/min 的速度匀速上升，问温度计的稳态指示误差有多大？解法一 依题意，温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知：o o T c 98)4(=，因此有 min 14=T ，得出 min 25.0=T 。

视温度计为单位反馈系统，则开环传递函数为Tss s s G 1)(1)()(=Φ-Φ=⎩⎨⎧==11v TK 用静态误差系数法，当t t r ⋅=10)( 时，C T Ke ss ︒===5.21010。

第三章3-4 已知二阶系统的单位阶跃响应为1.20()1012.5sin(1.653.1)th t e t-=-+试求系统的超调量σ％、峰值时间ｔp和调节时间ｔs。

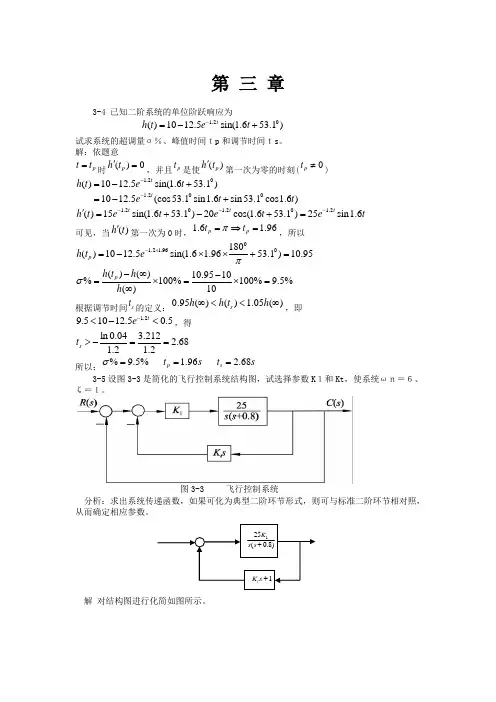
解：依题意pt t=时()0ph t'=，并且pt是使()ph t'第一次为零的时刻(pt≠)1.20()1012.5sin(1.653.1)th t e t-=-+1.2001012.5(cos53.1sin1.6sin53.1cos1.6)te t t-=-+1.20 1.20 1.2()15sin(1.653.1)20cos(1.653.1)25sin1.6t t th t e t e t e t---'=+-+=可见，当()h t'第一次为0时，1.6 1.96p pt tπ=⇒=，所以1.21.960180()1012.5sin(1.6 1.9653.1)10.95ph t eπ-⨯=-⨯⨯+=()()10.9510%100%100%9.5%()10ph t hhσ-∞-=⨯=⨯=∞根据调节时间st的定义：0.95()() 1.05()sh h t h∞<<∞，即1.29.51012.50.5te-<-<，得ln0.04 3.2122.681.2 1.2st>-==所以：%9.5% 1.96 2.68p st s t sσ===3-5设图3-3是简化的飞行控制系统结构图，试选择参数K１和Kt，使系统ωｎ＝６、ζ＝１。

图3-3 飞行控制系统分析：求出系统传递函数，如果可化为典型二阶环节形式，则可与标准二阶环节相对照，从而确定相应参数。

解对结构图进行化简如图所示。

故系统的传递函数为1121112525(0.8)()25(1)(0.825)251(0.8)t t K K s s s K K s s K K s K s s +Φ==++++++和标准二阶系统对照后可以求出：21120.81.44,0.312525nn t K K K ωζω-====3-7已知系统特征方程如下，试求系统在s 右半平面的根数及虚根值。

3-1设温度计需要在一分钟内指示出响应值的98%，并且假设温度计为一阶系统，求时间常数T 。

如果将温度计放在澡盆内，澡盆的温度以10C/min 的速度线性变化。

求温度计的误差。

解：c(t)=c(∞)98%t=4T=1 min r(t)=10te(t)=r(t)-c(t)c(t)=10(t-T+e )-t/T =10(T-e )-t/T =10T =2.5T=0.253-2电路系统如图所示，其中F C k R k R μ5.2,200,20110=Ω=Ω=。

设系统初始状态为零，试求：系统的单位阶跃响应8)()(1=t u t u c c 以及时的1t 值；解:R 1Cs+1R 1/R 0G (s )= u c (t)=K(1–e t T -)KTs +1=T=R 1C=0.5 K=R 1/R 0=10=10(1–e -2t )8=10(1–e -2t)0.8=1–e-2te -2t =0.2 t=0.8g(t)=e -t/T T Kt 1=0.8=4u c (t)=K(t-T+T e -t/T )=4R(s)=1s 2R(s)=1R(s)=1s 3T 2=K(s s+1/T+T s 2-1s 3-T 2)=1.2Ts 1s 3K +1U c (s)= -0.5t+0.25-0.25e -2t )12t 2u c (t)=10(3-3已知单位反馈系统的开环传递函数为)5(4)(+=s s s G 试求该系统的单位阶跃响应。

解:C(s)=s 2+5s+4R(s)4s(s+1)(s+4)C(s)=4R(s)=s1s+41+1/3s =4/3s +1-c(t)=1+ 4e 13-4t -t 3-e3-4已知单位负反馈系统的开环传递函数为 )1(1)(+=s s s G 试求该系统的上升时间r t 。

、峰值时间p t 、超调量%σ和调整时间s t 。

1s(s+1)G(s)=t p =d ωπ 3.140.866= =3.63t s = ζ3ωn=6t s = ζ4ωn =8解:C(s)=s 2+s+1R(s)12= 1ωn 2ωn ζ=1ζ=0.5=1ωn =0.866d ω= ωn 2 ζ1-=60o -1ζ=tg β21-ζt r =d ωπβ-= 3.14-3.14/30.866=2.42σ%=100%e -ζζπ1-2=16%e -1.83-6已知系统的单位阶跃响应为t te et c 10602.12.01)(---+= ，试求：（1）系统的闭环传递函数；（2）系统的阻尼比ζ和无阻尼自然震荡频率n ω；解:s+60+C(s)=0.21s 1.2s +10-s(s+60)(s+10)=600=s 2+70s+600C(s)R(s)600R(s)=s 12=600ωn2ωn ζ=70ζ=1.43=24.5ωn3-7设二阶控制系统的单位阶跃响应曲线如图所示，如果该系统为单位负反馈系统，试确定其开环传递函数。

自动控制理论第三章作业答案题3-4解：系统的闭环传递函数为由二阶系统的标准形式可以得到因此，上升时间 2.418r dd t s ππβωω--===峰值时间 3.6276p d t s πω=== 调整时间：35% 642% 8s n s n t s t s ωζωζ∆=≈=∆=≈=超调量：100%16.3%p M e =⨯=题3-5解：题3-7解：题3-8 （1）2100()(824)G s s s s =++ 解：闭环传递函数为2()100()(824)100C s R s s s s =+++ 特征方程为328241000s s s +++=列出劳斯表：第一列都是正数，所以系统稳定（2）10(1)()(1)(5)s G s s s s +=-+ 解：闭环传递函数()10(1)()(1)(5)10(1)C s s R s s s s s +=-+++ 特征方程为3255100s s s +++=列出劳斯表：第一列都是正数，所以系统稳定（3）10()(1)(23)G s s s s =-+ 解：闭环传递函数()10()(1)(23)10C s R s s s s =-++ 特征方程为3223100s s s +-+=列出劳斯表：劳斯表第一列的数符号变了2次，因此在s 平面的右半部分有两个特征根，系统不稳定。

题3-9（1）320.10s s s K +++=解：列出劳斯表要使系统稳定，则有（2）432413360s s s s K ++++=解：列出劳斯表：要使系统稳定，则有题3-10解：系统的闭环传递函数为：特征方程为2(2)(4)(625)=0s s s s K +++++系统产生等幅振荡，则特征根在虚轴上令s j ω=，有43212691982000j j K ωωωω--+++=题3-12解：闭环传递函数为特征方程为列出劳斯表：要使系统稳定，有。

3-1（1） )(2)(2.0t r t c= （2） )()()(24.0)(04.0t r t c t c t c=++ 试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。

已知全部初始条件为零。

解：（1） 因为)(2)(2.0s R s sC =闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应：s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c（2）)()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C 闭环传递函数124.004.01)()()(2++==s s s R s C s φ 单位脉冲响应：124.004.01)(2++=s s s C t e t g t 4sin 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s Ct e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ，用其测量容器内的水温，1min 才能显示出该温度的98%的数值。

若加热容器使水温按10ºC/min 的速度匀速上升，问温度计的稳态指示误差有多大？解法一 依题意，温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知：o o T c 98)4(=，因此有 min 14=T ，得出 min 25.0=T 。

视温度计为单位反馈系统，则开环传递函数为Ts s s s G 1)(1)()(=Φ-Φ= ⎩⎨⎧==11v T K用静态误差系数法，当t t r ⋅=10)( 时，C T Ke ss ︒===5.21010。

解法二 依题意，系统误差定义为 )()()(t c t r t e -=，应有 1111)()(1)()()(+=+-=-==ΦTs TsTs s R s C s R s E s e C T s Ts Ts ss R s s e s e s ss ︒==⋅+=Φ=→→5.210101lim )()(lim 23-3 已知二阶系统的单位阶跃响应为)1.536.1sin(5.1210)(2.1o tt et c +-=-试求系统的超调量σ％、峰值时间ｔp 和调节时间ｔs 。