第二章复变函数的积分

复变函数题库第一章 复变函数 1. 复数21ii +的指数表示为 主辐角为 三角式为 , z=i ，则Arg z= , 复数z 3/5+4i/5=，则z 为( ), 复数1-的三角式为 , Arg(z+2i)=（）2. 复数的指数式 ，复数11ii -+的三角式 ，复数1i e +的三角式 ，z y ix =+的辐角为3. Im(32)i -= ，Re(32)i += ，arg(22)i += ，复数z 16/25+8i/25=的主辐角为4. 内点指 ，外点指 ，边界点指 ，闭区域指 ,柯西-黎曼方程是复变函数可导的 条件5. 推导直角坐标系和极坐标系下的柯西-黎曼第二章 复变函数的积分1. 极坐标系中的柯西-黎曼方程为2. 调和函数的表达式为3. 复连通区域柯西定理的数学表达形式为4. 单连通区域柯西定理的数学表达形式为5. 柯西公式为6.()nl z dz α-=⎰Ñ ,若z 和α为复数，则1l dz z α=-⎰Ñ7. ()()n f z =8. 已知一个解析函数)(z f 的实部是y x sin e u =,求该解析函数9. 已知一个解析函数)(z f 的实部是22u x y xy =-+，(0)0f =,求该解析函数 10. 已知一个解析函数)(z f 的实部是32u 3x xy =-，(0)0f =,求该解析函数 11. 已知一个解析函数)(z f 的虚部是22v yx y=+,求该解析函数 12. 已知一个解析函数)(z f 的实部是u (cos sin )x e x y y y =-，(0)0f =,求该解析函数。

第三章 幂级数展开1. 幂级数11()kk z i k ∞=-∑的收敛圆半径为 ，幂级数1!()k k z k k ∞=∑的收敛圆半径为 ,幂级数1!kk z k k ∞=⎛⎫⎪⎝⎭∑的收敛圆半径为 , 幂级数0k k k e t ∞=∑(其中t为复变数)的收敛圆半径为2. 32382(4)z z z +=-是的 阶极点，z i=是221()(1)f z z =+的 阶极点，00zz e =是的 ，若某函数的展开式为0100000!()()kk k f z z z -=-=-∑，则0z 为该函数的 ，若某函数的展开式为00()!()k f z k z z ∞=-∑，则0z 为该函数的 。

第二章 复变函数的积分在微积分学中，微分法与积分法是研究函数性质的重要方法。

同样，在复变函数中，积分法也跟微分法一样是研究复变函数性质十分重要的方法和解决实际问题的有力工具。

§2.1 复变函数积分的概念一、复变函数的积分设C 为平面上给定的一条光滑(或按段光滑)曲线。

若选定C 的两个可能方向中的一个作为正方向，那么就把C 理解为带有方向的曲线，称为有向曲线。

设曲线C 的两个端点为A 与B ，如果从A 到B 的方向作为C 的正方向，那么从B 到A 的方向就是C 的负方向，并把它记作-C 。

在今后的讨论中，常把两个端点中的一个作为起点，另一个作为终点。

除特殊声明外，正方向总是指从起点到终点的方向。

关于简单闭曲线的正方向是指当曲线上的点P 顺此方向沿该曲线前进时，临近P 点的曲线内部始终位于P 点的左方。

与之相反的方向就是曲线的负方向。

若光滑或逐段光滑的曲线C 的参数方程为)()()(t iy t x t z z +==，)(βα≤≤t （2.1） t 为实参数，则规定t 增加的方向为正方向，即由)(αz a =到)(βz b =的方向为正方向。

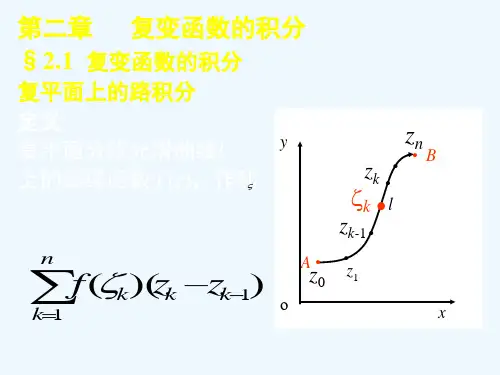
定义2.1 设函数)(z f w =定义在区域D 内，C 为区域D 内起点为A 终点为B 的一条光滑有向曲线，把曲线C 任意分成n 个弧段，设分点为：B z z z z z A n n ==-,...,,,1210 在每个小弧段上任取一点k ζ（图3.1），作和∑=∆=nk k k n z f S 1)(ζ其中1--=∆k k k z z z ，记=∆k s 的长度，}Δ{max 1k nk s δ≤≤=。

当n 无限增加，且δ趋于零时，如果不论对C 的分法及k ζ的取法如何，当n S 有唯一极限，那么称这个极限值为函数)(z f 沿曲线C 的积分，记作∑⎰=→=nk k kδCz ζf dz z f 1Δ)(lim )( （2.2）图2.1C 称为积分路径，⎰Cdz z f )(表示沿C 的正方向的积分，⎰-C dz z f )(表示沿C的负方向的积分。

第一章 复变函数1.1 复数与复数运算【1】下列式子在复数平面上各具有怎样的意义？ 5，arg ,Re ,z a z b αβ<<<<（,,a αβ和b 为实常数）解：射线ϕα=与ϕβ=，直线x a =与x b =所围成的梯形。

7，111z z -≤+解：11111z z z z -≤⇒-≤++，令z x iy =+，则11z z -≤+即()()2222110x y x y x -+≤++⇒≥。

即复数平面的右半平面0x ≥。

【2】将下列复数用代数式，三角式和指数式几种形式表示出来。

3，1+解：代数式即：1z =+；2ρ=，且z 的辐角主值arg 3z π=，因此三角式：2cos2sin33z i ππ=+；指数式：232i k i z e eππϕρ⎛⎫+ ⎪⎝⎭==，k ∈ 。

7，1i 1i-+解：21i (1i)2i i 1i(1i)(1i)2---===-++-，因此，其代数式：i z =-，三角式：33cos sin22z i ππ=+；指数式：322i k i z e eππϕρ⎛⎫+ ⎪⎝⎭==，k ∈ 。

【3】计算下列数值。

（a ，b 和ϕ为实常数）2，解：将被开方的i 用指数式表示：22ei k i ππ⎛⎫+ ⎪⎝⎭=，k ∈ 。

那么2322eexp 63i k k i ππππ⎛⎫+ ⎪⎝⎭⎡⎤⎛⎫==+ ⎪⎢⎥⎝⎭⎣⎦，k ∈ 。

7，cos cos 2cos 3cos n ϕϕϕϕ++++ 解：因为，cos R e (1)ik k e k n ϕϕ=≤≤，因此()[]2323cos cos 2cos 3cos R e R e R e R e (1)R e R e 1cos cos(1)sin sin(1)R e 1cos sin 222sin sin cos 222R e 2sin sin 2i i i in i in i i i in i n e eeee e eeeee n i n i n n n i ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ++++=++++⎡⎤-=++++=⎢⎥-⎣⎦⎧⎫-++-+⎪⎪=⎨⎬--⎪⎪⎩⎭++⎛⎫- ⎪⎝⎭= 222(1)2sin 2R e sin cos 2221(1)sin sin sin sin cos 22222R e sin sin2sin222n i i n i n e i e n n n n e ϕϕϕϕϕϕϕϕϕϕϕϕϕϕ++⎡⎤⎢⎥⎢⎥=⎛⎫⎢⎥- ⎪⎢⎥⎝⎭⎣⎦⎛⎫++- ⎪⎝⎭===1.2 复变函数【2】计算下列数值。

数学物理方法总结第一章 复变函数复数的代数式:z=x+iy复数的三角式和指数式:(cos sin )z ρϕϕ=+和i z e ϕρ=欧拉公式:{1sin ()21cos ()2iz iz iz izz e e iz e e --=-=+柯西-黎曼方程(或称为柯西-黎曼条件):{u u x yv v x y∂∂=∂∂∂∂=-∂∂ (其中f(z)=u+iv)函数f(z)=u+iv 在点0z 及其领域上处处可导,则称f(z)在0z 点解析.在区域B 上每一点都解析,则称f(z)是在区域B 上的解析函数.解析函数的性质:1.若函数f(z)=u+iv 在区域B 上解析,则12(,),(,)u x y C v x y C ==(12,C C 为常数)是B 上的两组正交曲线族.2.若函数在区域B 上解析,则u,v 均为B 上的调和函数,即22220u vx y ∂∂+=∂∂ 例题: 已知某解析函数f(z)的实部22(,)u x y x y =-,求虚部和这个解析函数.解答: 由于22ux∂∂=2;22v y ∂∂=-2;则22220u v x y ∂∂+=∂∂曲线积分法u x ∂∂=2x;u y ∂∂=-2y.根据C-R 条件有:v x∂∂=2y;v y ∂∂=2x.于是 22dv ydx xdy =+;(,0)(,)(0,0)(,0)(,)(,)(,0)(22)(22)(22)22x x y x x y x y x v ydx xdy C ydx xdy ydx xdy Cxdy C xy C=++=++++=+=+⎰⎰⎰⎰凑全微分显式法由上式可知dv=2ydx+2xdy贝易得dv=d(2xy)则显然v=2xy+C不定积分法上面已有—=2y;丝=2xdx dy则第一式对y积分,x视为参数，有v=J2xy+(p(x)=2xy+(p(x)......................dv...上式对x求导有一=2y+^\x),而由C-R条件可知(p\x)=0,dx从而(p(x)=C.故v=2xy+C.f(z)=x2-y2+i(2x y+C)=z2+iC第二章复变函数的积分单连通区域柯西定理如果函数f(z)在闭单连通区域B上解析，则沿B上任意一分段光滑闭合闭合曲线1(也可以是B的边界)，有血/⑵也=0.复连通区域柯西定理如果f(z)是闭复连通区域上的单值解析函数，则山任)也+£由/(z)也=0.式中1为区域外边界线，诸l为区域内边界线，积分均沿边界线的正方向进行.即血力＞)也=力血/(z)d z.柯西公式f(a)=t^-也""dz2m z-an次求导后的柯西公式f(〃)(z)=£山声舄化2mi中(。

第二章 复变函数的积分在微积分学中，微分法、积分法是研究函数性质的重要方法。

在复变函数中，微分法、积分法是研究复变函数性质的重要方法和解决实际问题的有力工具。

§2.1 复变函数的积分—复平面上的线积分一、复变函数积分的定义例：计算2421iiz dz++∫1.沿抛物线2y x =2.沿连接点124i i ++到的直线段3.1224i i i +++沿到然后再到的折线 解:1．抛物线参数方程为22,()(12)x t y t d z d t it i t d t==≤≤=+=+2其中1t 2则z =x +i y =t +i t242222222443241111()(12)[()4][22()]iiz dz t it i t dt t t t dt i t t t t dt++=++=−−++−∫∫∫∫三、解析函数的定积分公式在单通区域内，解析函数的积分值只与端点有关而与路径无关，可定义一个以终点z 为自变量的单值函数：()()zz F z f d ξξ=∫定理：设f (z )是单通区域D 内的解析函数， 是D的内点，则 是D 内的解析函数，且 F’(z )=f (z )F (z )是f (z )的原函数：F’(z )=f (z )定理证明略。

0z ξξd f z F zz ∫=0)()(由于()F z 是()f z 的一个原函数，所以()F z C +构成原函数族，则有：()()zz f d F z C ξξ=+∫上式中令 ，则有 从而0()()()zz f d F z F z ξξ=−∫——形式上与牛顿——莱布尼兹公式相似0z z =0)(0=+c z F )(0z F c −=⇒。