波动之练习题及参考答案

大学物理波动练习题1、下列哪一种波属于机械波？A.电磁波B.声波C.地震波D.核辐射波2、在机械波的传播过程中，介质中的质点发生的是（）A.随波逐流的相对运动B.周期性变化的相对运动C.振幅变化的相对运动D.垂直于波传播方向的相对运动3、下列哪一种说法正确地描述了波动现象的特征？A.波动现象是独立存在的，与振动源无关B.波动现象与振动源无关，只与传播介质有关C.波动现象是振动源和传播介质共同作用的结果D.波动现象只与传播介质有关，与振动源无关4、在波动现象中，下列说法正确的是（）A.各质点的起振方向都与振源的起振方向相同B.各质点的振动周期都与振源的振动周期相同C.各质点的振动方向都与振源的振动方向相同D.各质点的振动步调都与振源的振动步调相同二、解答题5.什么是机械波的传播速度？它与介质有关吗？如果有关，是怎样的关系？6.在机械波的形成过程中，介质中的各质点是如何随波迁移的？为什么？1、在以下物理量中，哪个是矢量？A.路程B.速率C.速度D.时间答案：C.速度解释：矢量是具有大小和方向的物理量，而速度是既有大小又有方向的物理量，因此是矢量。

而路程、速率和时间都只有大小，没有方向，因此是标量。

2、下列哪个选项可以表示物体的惯性？A.速度B.质量C.加速度D.动量答案：B.质量解释：惯性是物体抵抗运动状态被改变的性质，是物体的固有属性。

质量是惯性的唯一量度，因此质量可以表示物体的惯性。

速度、加速度和动量都与物体的运动状态有关，但它们都不能直接表示物体的惯性。

3、在以下哪个条件下，物体的运动状态会发生改变？A.受到力的作用B.受到重力C.受到支持力D.受到摩擦力答案：A.受到力的作用解释：物体的运动状态会发生改变，即物体的速度会发生改变，这只有当物体受到力的作用时才会发生。

力是改变物体运动状态的原因。

重力、支持力和摩擦力都是具体的力，但它们并不能独自改变物体的运动状态。

二、填空题4、在物理学中，我们将物体相对于其他物体位置的变化称为______。

⼤学物理练习册习题及答案6--波动学基础习题及参考答案第五章波动学基础参考答案思考题5-1把⼀根⼗分长的绳⼦拉成⽔平，⽤⼿握其⼀端，维持拉⼒恒定，使绳端在垂直于绳⼦的⽅向上作简谐振动，则（A ）振动频率越⾼，波长越长；（B ）振动频率越低，波长越长；（C ）振动频率越⾼，波速越⼤；（D ）振动频率越低，波速越⼤。

5-2在下⾯⼏种说法中，正确的说法是（A ）波源不动时，波源的振动周期与波动的周期在数值上是不同的；（B ）波源振动的速度与波速相同；（C ）在波传播⽅向上的任⼆质点振动位相总是⽐波源的位相滞后；（D ）在波传播⽅向上的任⼀质点的振动位相总是⽐波源的位相超前 5-3⼀平⾯简谐波沿ox 正⽅向传播，波动⽅程为010cos 2242t x y ππ??=-+ ?. (SI)该波在t =0.5s 时刻的波形图是（）5-4图⽰为⼀沿x 轴正向传播的平⾯简谐波在t =0时刻的波形，若振动以余弦函数表⽰，且此题各点振动初相取-π到π之间的值，则（）（A ）1点的初位相为φ1=0(m)(A )(m)(m)(B )(C )(D )思考题5-3图思考题5-4图（B ）0点的初位相为φ0=-π/2 （C ）2点的初位相为φ2=0 （D ）3点的初位相为φ3=05-5⼀平⾯简谐波沿x 轴负⽅向传播。

已知x=b 处质点的振动⽅程为[]0cos y A t ωφ=+，波速为u ，则振动⽅程为（）(A)()0cos y A t b x ωφ??=+++??(B)(){}0cos y A t b x ωφ??=-++??(C)(){}0cos y A t x b ωφ??=+-+?? (D)(){}0cos y A t b x u ωφ??=+-+?? 5-6⼀平⾯简谐波，波速u =5m?s -1，t =3s 时刻的波形曲线如图所⽰，则0x =处的振动⽅程为（）（A ）211210cos 22y t ππ-??=?- (SI) （B ）()2210cos y t ππ-=?+ (SI) （C ）211210cos 22y t ππ-??=?+ (SI) （D ）23210cos 2y t ππ-?=-(SI) 5-7⼀平⾯简谐波沿x 轴正⽅向传播，t =0的波形曲线如图所⽰，则P 处质点的振动在t =0时刻的旋转⽮量图是（）5-8当⼀平⾯简谐机械波在弹性媒质中传播时，下述各结论⼀哪个是正确的？（A ）媒质质元的振动动能增⼤时，其弹性势能减少，总机械能守恒；（B ）媒质质元的振动动能和弹性势能都作周期变化，但两者的位相不相同；（C ）媒质质元的振动动能和弹性势能的位相在任⼀时刻都相同，但两者的数值不相等；（D ）媒质质元在其平衡位置处弹性势能最⼤。

高中波动练习题及答案高中物理波动练题及答案选择题1. 真空中，波速恒定不变，下列哪种波型的频率最高？A. 声波B. 电磁波C. 水波D. 弹性波答案：B2. 下列哪种波是纵波？A. 水波B. 声波C. 电磁波D. 横波答案：B3. 一束光线从空气射入玻璃中，表述正确的是：A. 速度降低，波长变短，频率不变B. 速度降低，波长不变，频率不变C. 速度较缓，波长变长，频率不变D. 速度较缓，波长不变，频率不变答案：B4. 下面哪些特性属于光的波动性？A. 光的直线传播B. 光的反射C. 光的干涉D. 光的光电效应答案：C填空题1. 声音的频率越高，波长越(shorter)______。

2. 球面内必有一点使其到三个等势面的距离相差（$\lambda$ /2)__________。

3. 一束光在真空中的速度是( 3 $\times$ 10^8) _______。

4. 单色光干涉中，当相差为(n $\times$ λ)时，会出现(n-1)条明环，中央仍然为(n-1)条条纹。

但是在双色光干涉中，当相差为(n $\times$ λ)时，会出现明暗相间的(n-1)条条纹，无明环。

这是因为双色光的光色不同，波长不同，所以相差相等时，得到的光程差并不相等。

计算题1. 一束平行光射入光密介质，以折射角30°折射，则光的速度是光速的(inverse tangent)__________倍。

解：根据折射定律$\frac{sin i}{sin r}=\frac{v_1}{v_2}$可求出速度与入射角度的正切成反比。

$tan 30° = \frac{1}{\sqrt{3}}$ ，所以光的速度是光速的$\frac{1}{\sqrt{3}}$倍。

2. 一个长80cm，重8.0g的弹性细线用于悬挂一个质量为180g的砝码，当砝码沿竖直方向振动时，依次通过平衡位置时，其振动的周期是2.8s，求细线的劲度系数k（g=9.8m/s^2）。

六、练习题（一）选择题1、频率是200Hz 的波，它在骨头中的波长是（骨头中的波速3400m/s ）：A 17mB 170mC 0.17mD 1.7m2、频率为30KHz 的机械波属于A 次声波B 声波C 物质波D 超声波3、对于频率为1000Hz ，人的听觉范围声强级A 0dB 到120dB B 0dB 到12dBC 10dB 到12dBD 12dB 到12db4、机械波在通过不同介质时，不会发生变化的物理量是A 波速B 强度C 波长D 频率5、频率为10Hz 的机械波属于A 次声波B 声波C 超声波D 物质波6、波源振动方程0.04cos(2.5)s t m π=，以100m/s 的速度在介质中传播，波动方程为 A 0.04cos 2.5()100x s t m π=-； B 0.04cos 2.5()100x s t m π=+； C 0.04cos(2.5)s t m π=； D 0.04cos(2.5100)s t m π=⨯。

7、波源振动方程0.04cos(2.5)s t m π=，以100m/s 的速度在介质中传播，距波源20m 处质点的振动方程为A 0.04cos 2.5(20)s t m π=-；B 0.04cos 2.5(0.2)s t m π=-；C 0.04cos 2.5(20)s t m π=+；D 0.04cos 2.5(0.2)s t m π=+。

8、波源振动方程0.04cos(2.5)S t m π=，以100m/s 的速度在介质中传播，在波源起振后1.0S 距波源20m 处质点的振动速度A V=0.04m/sB V ≠0C V=2m/sD V=09、设有波动方程0.02cos 2(1000.25)S t x m π=-，则波长A 4.0m λ=；B 0.25m λ=；C 0.5m λπ=；D 0.50m λ=。

10、设有波动方程0.02cos 2(1000.25)S t x m π=-，频率为A 200Hz ν=；B 100Hz ν=；C 50Hz ν=；D 0.50Hz ν=。

物理波动试题波动是物理学中重要的一个分支，它涉及到波的传播、干涉、衍射等现象。

本试题将涵盖波动的基本概念、公式和应用，旨在考察学生对波动知识的理解和应用能力。

1.简答题（每题10分）（1）什么是波动？简要说明波动的特点及分类。

波动是指能量或信息沿着空间传播的现象。

特点：波动是在介质中传播的，介质不随波传播而移动；波动是由某种原因（振动源）激发产生的；波动可以传播能量和动量；波动可以壁相互作用产生干涉、衍射等现象。

分类：机械波和电磁波。

（2）什么是机械波？它们传播的基本特点是什么？机械波是指需要介质来传播的波动现象。

机械波传播的基本特点是：需要介质来传播，介质的微小部分进行振动，振动的能量沿波的传播方向传递。

（3）什么是波长和频率？它们之间的关系是怎样的？波长是指一次完整振动所对应的距离，用符号λ表示。

频率是指在单位时间内波动上通过某一点的次数，用符号f表示。

它们之间的关系可以由式子v = fλ表示，其中v代表波速。

波速等于波长乘以频率。

（4）什么是相位差？简要说明相位差对波动干涉的影响。

相位差是指两个波源相对于某一点的等效相位差。

它是由波源到该点距离的变化与波长之比所决定。

相位差对波动干涉的影响是：当相位差为整数倍的倍数时，波峰和波峰或波谷和波谷同时到达干涉点，形成增强干涉；当相位差为奇数倍的半数时，波峰和波谷同时到达干涉点，形成减弱干涉。

2.计算题（每题20分）（1）一根被两端固定的弦子上，泛起了两个频率相同且弦长相同的基本振动波。

若两波的相位差为π/4，求出相邻两个波腹之间的距离。

解析：相邻两个波腹之间的距离等于半个波长，即λ/2。

根据相位差为π/4，可以得出相位差对应的距离变化为λ/8。

所以，λ/2 = λ/8，化简可得λ = 4d，其中d为波腹之间的距离。

所以相邻两个波腹之间的距离为4d。

（2）一个平面波以速度v在某介质中传播，当波长λ减小一倍，频率f变为2f，则速度v变为多少？解析：根据波速公式v = fλ，代入新的波长和频率，得到新的波速v' = 2v。

（500nm)
31、如图正入射光线间距相等，那么光线1和光线３在屏上相遇 的位相差为多少？Ｐ点应为亮点还是暗点？
答案：２，暗点
P １ ２
３ ４ ５
2
32、如果缝被分成６个半波带，则Ｐ点为第几级暗纹？若缝缩小 一半，则Ｐ点为第几级明条纹？
答案：３，第一级
33、 如图所示，将折射率 n=1.58 的薄云母片盖在双缝实验中 的一条狭缝上（S1),这时屏幕上的零级明纹往上移到原来第七 级明纹的位置上，如果入射光波波长为５５０nm,试求此云母 片的厚度d。
[A]
7、在双缝干涉实验中，屏E上的P点处是明条纹。若将缝S2盖
住，并在S1S2的连线的垂直平分面处放一高折射率介质反射面
M，如图所示，则此时
（A）P点处仍为明条纹
[B]
（B） P点处为暗条纹
（C）不能确定P点处为暗条纹还是明条纹
（D）无干涉条纹
S1
P
S S2
E
8、某元素的特征光谱中包含有波长分别为1=450nm,2=750nm
i0
arctg n2 n1
,时，反射
光成为线偏振光，其光矢量的振动方向垂直入射面。
23、如图，透镜可以上下移动，从上向下观察到中心是一个 暗斑，此时透镜顶点距离平板的距离最少是多少？
答案：
2nek
k
2
emin 4n
＝500nm
n1=1.58 n=1.60
n=1.54
24、在迈克尔逊干干涉仪中可 平面镜移动一微小距离过程中， 观察到条纹移动1468条，所用单色光波长为546.1nm,由此可 此，反射镜平移的距离为多少？给出四位有效数字）
光学练习题
1、在双缝实验中，若保持双缝S1和S2的中心之间的距离d不变,而把两条 缝的宽度a略微加宽，则（A）单缝衍射的中央主极大变宽，其中所包含 的干涉条纹数目变少； （B）单缝衍射的中央主极大变宽，其中所包含的干涉条纹数目变多； （C）单缝衍射的中央主极大变宽，其中所包含的干涉条纹数目不变； （D）单缝衍射的中央主极大变窄，其中所包含的干涉条纹数目变少； （E）单缝衍射的中央主极大变窄，其中所包含的干涉条纹数目变多；

(A) x 0 .12 cos （ t 4、机械波的表达式为 y 0.05cos 6πt 0. 06πx m ，则 （ （Ａ） 波长为100 ｍ （Ｂ） 波速为10 ｍ·ｓ-1 ） ）
（Ｃ） 周期为1/3 ｓ （Ｄ） 波沿x 轴正方向传播 5、 两分振动方程分别为 x1=3cos (50πt+π/4) ㎝ 和 x2=4cos (50πt+3π/4)㎝， 则它们的合振动的振幅为 （ (A) 1 ㎝ （B）3 ㎝ （C）5 ㎝ （D）7 ㎝ 6、一平面简谐波，波速为 =5 cm/s，设t= 3 s时刻的波形 如图所示，则x=0处的质点的振动方程为 （ － (A) y=2×10 2cos (πt/2－π/2) (m) － (B) y=2×10 2cos (πt + π) (m) －2 (C) y=2×10 cos(πt/2+π/2) (m) －2 (D) y=2×10 cos (πt－3π/2) (m) ）
y
u
A X －A
17．一平面简谐波，沿 X 轴负方向传播，波长λ=8 m。已知 x=2 m 处质点的振动方程为 y 4 cos(10t
5 x ) ; 8 12 2 （C） y 4 cos(10 t x ); 4 3
（A）
) ， 则该波的波动方程为（ 6
（B）
20．在驻波中，两个相邻波节间各质点的振动（
1、一个弹簧振子和一个单摆，在地面上的固有振动周期分别为 T1 和 T2，将它们拿到月球上去，相应 的周期分别为 1 和 2 ，则它们之间的关系为 1 T1 且 2 T2 。 。
2、一弹簧振子的周期为T，现将弹簧截去一半，下面仍挂原来的物体，则其振动的周期变为 3、一平面简谐波的波动方程为 y 0.08cos 4 πt 2 πx

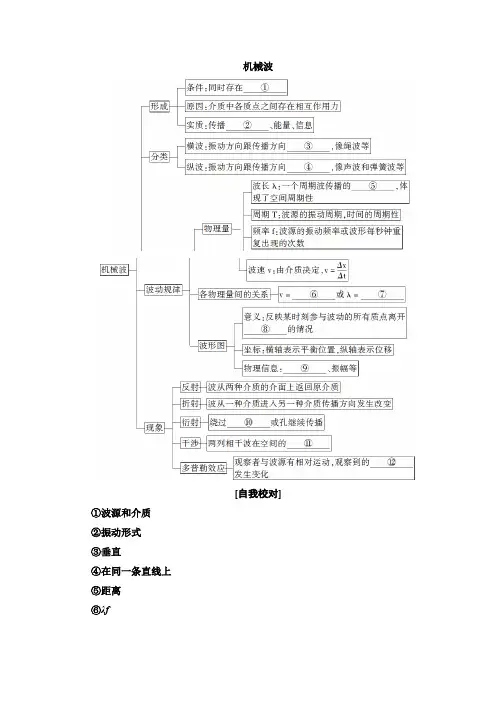
机械波[自我校对]①波源和介质②振动形式③垂直④在同一条直线上⑤距离⑥λf⑦v f⑧平衡位置⑨波长⑩障碍物⑪叠加⑫频率波的图象表示某一时刻各个质点相对平衡位置的位移情况，从波的图象上可直接读出振幅和波长．随着时间的推移，波的图象将沿波速方向匀速移动．振动图象表示单个质点振动的位移随时间的变化规律，由振动图象上可直接读出振幅、周期和任意时刻的振动方向，随着时间的推移，振动图象继续延伸，原有图象保持不变．2．由波的图象画振动图象给出波的图象，已知波的传播方向时，可粗略画出任一点的振动图象(周期T 未知)．如果能再给出波速便可准确画出任一质点的振动图象．3．由振动图象画波的图象这类问题一般见到的情况是：给出振动图象和波的传播方向，便可画出任一时刻的波形图；或是给出两个质点的振动图象，加上两质点平衡位置的间距和波源方位，便可画出多种情况下的波形图．【例1】图(a)为一列简谐横波在t＝0.10 s时刻的波形图，P是平衡位置在x ＝1.0 m处的质点，Q是平衡位置在x＝4.0 m处的质点；图(b)为质点Q的振动图象．下列说法正确的是()(a)(b)A．在t＝0.10 s时，质点Q向y轴正方向运动B．在t＝0.25 s时，质点P的加速度方向与y轴正方向相同C．从t＝0.10 s到t＝0.25 s，该波沿x轴负方向传播了6 mD．从t＝0.10 s到t＝0.25 s，质点P通过的路程为30 cmE．质点Q简谐运动的表达式为y＝0.10sin 10πt(国际单位制)解析：由y-t图象可知，t＝0.10 s时质点Q沿y轴负方向运动，选项A错误；由y-t图象可知，波的振动周期T＝0.2 s，由y-x图象可知λ＝8 m，故波速v＝λT＝40 m/s，根据振动与波动的关系知波沿x轴负方向传播，则波在0.10 s到0.25 s内传播的距离Δx＝vΔt＝6 m，选项C正确；其波形图如图所示，此时质点P的位移沿y轴负方向，而回复力、加速度方向沿y轴正方向，选项B正确；Δt＝0.15 s＝34T，质点P在其中的12T内路程为20 cm，在剩下的14T内包含了质点P通过最大位移的位置，故其路程小于10 cm，因此在Δt＝0.15 s内质点P通过的路程小于30 cm，选项D错误；由y-t图象可知质点Q做简谐运动的表达式为y＝0.10sin 2π0.2t(m)＝0.10sin10πt(m)，选项E正确．答案：BCE双向性是指波沿x轴正、负两方向传播时，若正、负两方向传播的时间之和等于周期的整数倍，则正、负两方向传播的那一时刻波形相同．2.由于波的时间周期性而导致多解波的时间周期性是指每经过一个周期T，同一质点振动状态相同，波的形状也相同；每经过半个周期，质点振动状态相反，波的形状也相反．因此在波的传播过程中，经过整数倍周期时，波形图线相同．3．由于波的空间周期性而导致多解波的空间周期性是指每经过一个波长λ，波的形状相同，质点振动状态也相同；每经过半个波长，波的形状相反，质点振动状态也相反．因此在波的传播方向上相距为波长整数倍距离的质点振动情况相同．4．两质点间关系不确定形成多解在波的传播方向上，如果两个质点间的距离不确定或者两者相位之间关系不确定，就会形成多解．若不能联想到所有可能的情况，就会出现漏解．【例2】一列横波的波形如图所示，实线表示t1＝0时刻的波形图，虚线表示t2＝0.05 s时刻的波形图，则：(1)若2T＞t2－t1＞T，波速可能为多大？(T为周期)(2)若T＜t2－t1，并且波速为360 m/s，则波向哪个方向传播？解析：(1)由图象可知：若波向右传播，则在Δt＝0.05 s内波传播的距离为Δx＝10 m.则波速v1＝ΔxΔt＝100.05m/s＝200 m/s.若波向左传播，则在Δt＝0.05 s内波传播的距离为Δx＝14 m.则波速v2＝ΔxΔt＝140.05m/s＝280 m/s.(2)由图象可知：波长λ＝8 m.在Δt＝0.05 s内波传播的距离为Δx＝vΔt＝360×0.05 m＝18 m.则Δx＝188λ＝2λ＋14λ，所以波向右传播．答案：(1)见解析(2)向右此题是由波的传播方向导致的多解，所以应该先假设一个传播方向，再由已知条件求解．【例3】一列简谐横波沿水平方向向右传播，M，N为介质中相距Δx的两质点，M在左，N在右．t时刻，M，N均通过平衡位置，且M，N之间只有一个波峰，经过Δt时间N质点恰处于波峰位置，求这列波的波速．解析：由题意可知t时刻的波形可能有四种情况，如图所示．对(a)图，N质点正经过平衡位置向上振动，则Δt可能为T4，5T4，9T4……即Δt＝(n＋14)T(n＝0，1，2，…)，则v0＝λT＝2ΔxT，所以v a＝（n＋14）λΔt＝（4n＋1）Δx2Δt(n＝0，1，2，…)．同理，对于(b)，(c)，(d)分别有：v b＝（4n＋3）Δx4Δt(n＝0，1，2，…)，v c＝（4n＋1）Δx4Δt(n＝0，1，2，…)，v d＝（4n＋3）Δx6Δt(n＝0，1，2，…)．答案：见解析在波的传播方向上，如果两个质点间的距离不确定或者相位之间的关系不确定，就会形成多解，应通过认真分析，确定出所有可能的情况．1.某同学漂浮在海面上，虽然水面波正平稳地以1.8 m/s的速率向着海滩传播，但他并不向海滩靠近．该同学发现从第1个波峰到第10个波峰通过身下的时间间隔为15 s．下列说法正确的是()A．水面波是一种机械波B．该水面波的频率为6 HzC．该水面波的波长为3 mD．水面波没有将该同学推向岸边，是因为波传播时能量不会传递出去E．水面波没有将该同学推向岸边，是因为波传播时振动的质点并不随波迁移解析：水面波是一种机械波，说法A正确．根据题意得周期T＝159s＝53s，频率f＝1T＝0.6 Hz，说法B错误．波长λ＝vf＝1.80.6m＝3 m，说法C正确．波传播过程中，传播的是振动形式，能量可以传递出去，但质点并不随波迁移，说法D 错误，说法E正确．答案：ACE2．一列沿x轴正方向传播的简谐横波在t＝0时刻的波形如图所示，质点P 的x坐标为3 m．已知任意振动质点连续2次经过平衡位置的时间间隔为0.4 s．下列说法正确的是()A．波速为4 m/sB．波的频率为1.25 HzC．x坐标为15 m的质点在t＝0.6 s时恰好位于波谷D．x坐标为22 m的质点在t＝0.2 s时恰好位于波峰E．当质点P位于波峰时，x坐标为17 m的质点恰好位于波谷解析：任意振动质点连续2次经过平衡位置的时间间隔0.4 s，可知振动周期T＝0.8 s，频率f＝1T＝1.25 Hz，B正确．从题图中可以看出波长λ＝4 m，根据v＝λf得v＝5 m/s，A错误．由于波在传播过程中具有空间周期性，x坐标为15 m处的质点运动规律与x＝3 m处相同，从t＝0时刻经过0.6 s，即经历34周期，质点应位于平衡位置，C错误．用同样的方法可判断出D、E正确．答案：BDE3．由波源S形成的简谐横波在均匀介质中向左、右传播．波源振动的频率为20 Hz，波速为16 m/s.已知介质中P、Q两质点位于波源S的两侧，且P、Q和S 的平衡位置在一条直线上，P、Q的平衡位置到S的平衡位置之间的距离分别为15.8 m、14.6 m．P、Q开始振动后，下列判断正确的是()A．P、Q两质点运动的方向始终相同B．P、Q两质点运动的方向始终相反C．当S恰好通过平衡位置时，P、Q两点也正好通过平衡位置D．当S恰好通过平衡位置向上运动时，P在波峰E．当S恰好通过平衡位置向下运动时，Q在波峰解析：简谐横波的波长λ＝vf＝1620m＝0.8 m．P、Q两质点距离波源S的距离PS＝15.8 m＝19λ＋34λ，SQ＝14.6 m＝18λ＋14λ.因此P、Q两质点运动的方向始终相反，说法A错误，说法B正确．当S恰好通过平衡位置向上运动时，P在波峰的位置，Q在波谷的位置．当S恰好通过平衡位置向下运动时，P在波谷的位置，Q在波峰的位置．说法C错误，说法D、E正确．答案：BDE4．一列简谐横波在介质中沿x轴正向传播，波长不小于10 cm.O和A是介质中平衡位置分别位于x＝0和x＝5 cm处的两个质点．t＝0时开始观测，此时质点O的位移为y＝4 cm，质点A处于波峰位置；t＝13s时，质点O第一次回到平衡位置，t＝1 s时，质点A第一次回到平衡位置．求：(1)简谐波的周期、波速和波长；(2)质点O的位移随时间变化的关系式．解析：(1)设振动周期为T.由于质点A在0到1 s内由最大位移处第一次回到平衡位置，经历的是14个周期，由此可知T＝4 s ①由于质点O与A的距离5 cm小于半个波长，且波沿x轴正向传播，O在t＝13s时回到平衡位置，而A在t＝1 s时回到平衡位置，时间相差23s．两质点平衡位置的距离除以传播时间，可得波的速度v＝7.5 cm/s ②利用波长、波速和周期的关系得，简谐波的波长λ＝30 cm. ③(2)设质点O的位移随时间变化的关系为y ＝A cos ⎝ ⎛⎭⎪⎫2πt T ＋φ0 ④ 将①式及题给条件代入上式得⎩⎪⎨⎪⎧4＝A cos φ00＝A cos （π6＋φ0） ⑤ 解得φ0＝π3，A ＝8 cm ⑥ 质点O 的位移随时间变化的关系式为y ＝0.08cos ⎝ ⎛⎭⎪⎫πt 2＋π3(国际单位制) ⑦或y ＝0.08sin ⎝ ⎛⎭⎪⎫πt 2＋5π6(国际单位制)． 答案：(1)4 s 7.5 cm/s 30 cm(2)y ＝0.08cos ⎝ ⎛⎭⎪⎫πt 2＋π3(国际单位制) 或y ＝0.08sin ⎝ ⎛⎭⎪⎫πt 2＋5π6(国际单位制) 5．甲、乙两列简谐横波在同一介质中分别沿x 轴正向和负向传播，波速均为v ＝25 cm/s.两列波在t ＝0时的波形曲线如图所示．求：(1)t ＝0时，介质中偏离平衡位置位移为16 cm 的所有质点的x 坐标；(2)从t ＝0开始，介质中最早出现偏离平衡位置位移为－16 cm 的质点的时间． 解析：(1)t ＝0时，在x ＝50 cm 处两列波的波峰相遇，该处质点偏离平衡位置的位移为16 cm.两列波的波峰相遇处的质点偏离平衡位置的位移均为16 cm.从图线可以看出，甲、乙两列波的波长分别为λ1＝50 cm.λ2＝60 cm甲、乙两列波波峰的x 坐标分别为x 1＝50＋k 1λ1，k 1＝0，±1，±2，…x 2＝50＋k 2λ2，k 2＝0，±1，±2，…由以上三式得，介质中偏离平衡位置位移为16 cm 的所有质点的x 坐标为 x ＝(50＋300n )cm n ＝0，±1，±2，….(2)只有两列波的波谷相遇处的质点的位移为－16 cm.t ＝0时，两列波波谷间的x 坐标之差为Δx ′＝⎣⎢⎡⎦⎥⎤50＋（2m 2＋1）λ22－⎣⎢⎡⎦⎥⎤50＋（2m 1＋1）λ12 式中，m 1和m 2均为整数．解得Δx ′＝10(6m 2－5m 1)＋5由于m 1、m 2均为整数，相向传播的波谷间的距离最小为Δx ′0＝5 cm从t ＝0开始，介质中最早出现偏离平衡位置位移为－16 cm 的质点的时间为t ＝Δx ′02v代入数值得t ＝0.1 s.答案：(1)(50＋300n )cm n ＝0，±1，±2，… (2)0.1 s。

选D
8
洛埃境 半波损失
E/ S1 M o E
S2
装置：S: 线光源(或点光源) M: 平玻璃片作反射镜
S发出的光一部分直接投射到屏上，一部分经 M反射后到屏 上，在重叠区干涉。 干涉的两部分光可以看作是一个实光源S1和一个虚光源 S2 9 发出的。
干涉图样 • 入射角很大，接近90o 。反射系数近于1，故反射很强。 • 两光的振幅几乎相等，可看成等幅干涉。 • 干涉条纹只出现在镜面上半部。 相位 如把屏紧靠镜端o，在o点因有s2o=s1o, 似乎o点应是亮点， 但实验给出o点却是暗点。 (原因：反射光有 “半波损失”，即反射光和直接射来的 光在屏上 o 处实际是反相的。) 发生半波损失的条件： 1、由光疏媒质入射，光密媒质反射； 2、正入射或掠入射。
试写出其波动方程。
1
1 一列平面简谐波以波速 u 沿 x 轴正方向传播，波长为。 已知在x0＝处的质元振动表达式为 y A cos( t ) 2 试写出波动方程。 解： y A cos (t d x ) A cost 2 d 2 x u u 2 2 将 d x0 2 代入，有
10
在空气中用波长为 的单色光进行双缝干涉 实验时，观察到干涉条 纹相邻明条纹的间距为 1.3mm，当把实验装置放 在水中时（水的折射率 为1.33)，则相邻明条纹 的间距变为————————
—
P
S1 S r1 r2 O
x
dS
B
2
D
解：如图：在空气中，光程差：
k x r2 r1 d sin dtg .d D 2k 1 2
d x y A cos2 (t ) 0 u u

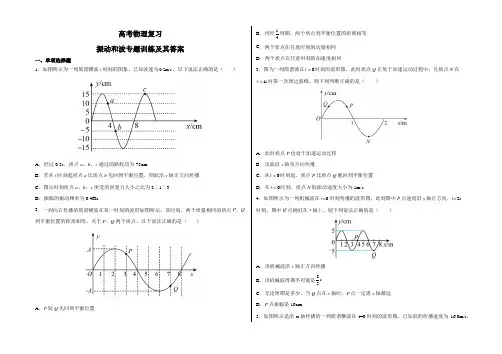
高考物理复习振动和波专题训练及其答案一、单项选择题1．如图所示为一列简谐横波t时刻的图象，已知波速为0.2m/s，以下说法正确的是（）A．经过0.5s，质点a、b、c通过的路程均为75cmB．若从t时刻起质点a比质点b先回到平衡位置，则波沿x轴正方向传播C．图示时刻质点a、b、c所受的回复力大小之比为2∶1∶3D．振源的振动频率为0.4Hz2．一列向右传播的简谐横波在某一时刻的波形如图所示，该时刻，两个质量相同的质点P、Q 到平衡位置的距离相等。

关于P、Q两个质点，以下说法正确的是（）A．P较Q先回到平衡位置B．再经14周期，两个质点到平衡位置的距离相等C．两个质点在任意时刻的动量相同D．两个质点在任意时刻的加速度相同3．图为一列简谐波在0=t时刻的波形图，此时质点Q正处于加速运动过程中，且质点N在1st=时第一次到达波峰。

则下列判断正确的是（）A．此时质点P也处于加速运动过程B．该波沿x轴负方向传播C．从0=t时刻起，质点P比质点Q晚回到平衡位置D．在0=t时刻，质点N的振动速度大小为1m/s4．如图所示为一列机械波在t=0时刻传播的波形图，此刻图中P点速度沿y轴正方向，t=2s 时刻，图中Q点刚好在x轴上。

则下列说法正确的是（）A．该机械波沿x轴正方向传播B．该机械波周期不可能是8s3C．无论周期是多少，当Q点在x轴时，P点一定离x轴最远D．P点振幅是10cm5．如图所示是沿x轴传播的一列简谐横波在t=0时刻的波形图，已知波的传播速度为16.0m/s，从此时起，图中的P质点比Q质点先经过平衡位置．那么下列说法中正确的是（）A．这列波一定沿x轴正向传播B．这列波的频率是3.2HzC．t=0.25s时Q质点的速度和加速度都沿y轴负向D．t=0.25s时P质点的速度和加速度都沿y轴负向6．如图（a）所示为波源的振动图象（在t=0时刻之前波源就已经开始振动了），图（b）为xy 平面内沿x轴传播的简谐横波在t=0时刻的波形图象，t=0时刻P点向y轴负方向运动，关于图（b）上x=0.4m处的Q点的说法正确的是（）.A．t=0时，速度最大，其大小为0.1m/s，方向沿y轴正方向B．t=0到t=5s内，通过的路程为20cmC．t=2s时，运动到x=0.2m处D．t=3s时，加速度最大，且方向向下7．一列简谐横波在某时刻的波形图如图所示，已知图中质点b的起振时刻比质点a延迟了0.5s，b和c之间的距离是5m，以下说法正确的是（）A．此列波的波长为2.5mB．此列波的频率为2HzC．此列波的波速为2.5m/sD．此列波的传播方向为沿x轴正方向传播8．P、Q、M是某弹性绳上的三个质点，沿绳建立x坐标轴。

1.机械波的波长,频率,周期和波速四个量中,当波从一 种介质进入另一种介质时,哪些量是不变的?
设在一种介质中,波长,频率,周期和波速分别为λ,f,T,u.
进入另一种介质时,
频率不变,周期不变T 波速变为u1,波长变为λ1= u1T.
2.判断下面几种说法,哪些是正确的,那些错的?
(1)机械振动一定能产生机械波; 机械振动在弹性介质中传播形成的波,叫机械波 (2)质点振动的速度是和波的传播速度相等的; 错
vs 30m / s
10、A、B是简谐波波线上的两点，已知，B点的相位落
后于A点π/3，A，B两点相距0.5m，波的频率为100Hz，
则该波的波长λ=
m，波速u=
m/s。
λ=3m，2π*0.5/λ=π/3
u=300m/s
11、已知波源的振动周期为410-2s，波的传播速度为 300m/s，波沿x轴正方向传播，则位于x1=10m和x2=16m 的两质点振动相位差为: π 。ΔØ=2π*（16-10）/λ， 求出波长代入
靠近，听到的频率比1500Hz肯定大 等于340/（340-22）×1500
9.汽车过车站时，车站上的观察者测得声音的频率 由1200Hz变到1000Hz。设空气中声速为330m/s， 则汽车的速度为【 】
（A）90m/s； （B）66m/s； （C）55m/s； （D）30m/s
听到的频率变小，汽车在过站，肯定远离 等于330/（330+x）×1200=1000，解出x
它所形成的波以 30 m/s 的速度沿一直线传播，则该波的方
程为
y=0.04cos240π（t-x/30）
。
6. 一弦上的驻波方程为 y 0.03cos1.6x cos550t m，

1 一列平面简谐波以波速 u 沿 x 轴正方向传播，波长为。 已知在x0＝处的质元振动表达式为 y A cos( t ) 2 试写出波动方程。
2 设有一平面简谐波频率为，振幅为A以波速u沿x轴正向传播， 已知波线上距原点为d的B点的振动方程为
yB A cos(2t 0 )
答：全部对。
15
一束单色光垂直入射在光栅上，衍射光谱中共出现5条明纹，若已知此光栅缝宽 与不透明部分宽度相等，那么在中央明纹一侧的两条明纹分别是第 级和第 级谱线。
解：∵a=b,故有缺级。
由 a sin k / ,
(a b) sin k
k 2 / k
时缺级
a b
0
D
k＝(n – 1)e/λ = 6.96 ≈7
零级明纹移到原第 7 级明纹处 …
13
例12－7 在双缝装置中，用一折射率为n的薄云母片覆盖其中 一条缝，这时屏幕上的第7条明纹恰好移到屏幕中央零级明纹缝 隙处，如果入射光的波长为，则这云母片的厚度为 （A）n-1, (B)7 C)7n, (D)（n-1/7） 解：因为
a
故
k 2k /
K/=1,则k＝2，即第二级缺级 故应为第一级和第三级谱线。
16
已知天空中两颗星相对于一望远镜的角距离为4.84×10-6rad，它们都发出波长 为5500Å的光，试问望远镜的口径至少要多大，才能分辨出这两颗星?
解：
1.22

D
5.500107 D 1.22 1.22 0.139m 6 4.8410
，试问： （1）油滴外围（最薄处）区域对应于亮区还是暗 区，为什么？ （2）如果总共可以观察到5条明纹，且中心为明 纹，问中心点油膜厚为多少？

振动、波动练习题一．选择题1．一质点在X 轴上作简谐振动，振幅A=4cm。

周期T=2s。

其平衡位置取作坐标原点。

若t=0 时刻质点第一次通过x= -2cm 处，且向X 轴负方向运动，则质点第二次通过x= -2cm 处的时刻为（）。

A 1sB 2sC 4sD 2s332．一圆频率为ω的简谐波沿X 轴的正方向传播，t=0 时刻的波形如图所示，则t=0 的波形t=0 时刻，X 轴上各点的振动速度υ与X轴上坐标的关系图应（）3．图示一简谐波在 t=0 时刻的波形图，波速υ =200m/s ，则图中O 点的振动加速度的表达式为（）2A a 0.4 2 cos( t ) 2 23B a 0.4 2 cos( t )22C a 0.4 2cos(2 t ) 4．频率为 100Hz ，传播速度为 300m/s 的平面简谐波，波线上两 点振动的相位差为 3 ，则这两点相距（ ）A 2mB 2.19mC 0.5mD 28.6m5．一平面简谐波在弹性媒质中传播，媒质质元从平衡位置运动到最大位置处的过程中， （ ）。

A 它的动能转换成势能B它的势能转换成动C 它从相邻的一段质元获得能量其能量逐渐增大Da20.4 2 cos(2 t2)υ (m/s)Bυ (m/s)DX(m)D 它把自己的能量传给相邻的一段质元，其能量逐渐减小6．在下面几种说法中，正确的说法是：（）。

A 波源不动时，波源的振动周期与波动的周期在数值上是不同的B 波源振动的速度与波速相同C 在波传播方向上的任一质点振动位相总是比波源的位相滞后D 在波传播方向上的任一质点振动位相总是比波源的位相超前7．一质点作简谐振动，周期为T，当它由平衡位置向X 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为（）。

A TBTCTDT4 12 6 88．在波长为λ的驻波中两个相邻波节之间的距离为（）。

A λB 3 λ/4C λ/2D λ /49．在同一媒质中两列相干的平面简谐波的强度之比I1I 4是，则两列波的振幅之比是：（）A A1 4 BA1 2 CA1 16 DA11A2 A2 A2 A2 410．有二个弹簧振子系统，都在作振幅相同的简谐振动，二个轻质弹簧的劲度系数K 相同，但振子的质量不同。

NO.2 机械波一 选择题1.如图所示，一平面简谐波沿x 轴正向传播，已知P 点的振动方程为)cos(0φω+=t A y ，则波的表达式为(A) }]/)([cos{0φω+--=u l x t A y ． (B) })]/([cos{0φω+-=u x t A y ． (C) )/(cos u x t A y -=ω．(D) }]/)([cos{0φω+-+=u l x t A y ．【 A 】 2.一沿x 轴负方向传播的平面简谐波在t = 2 s 时的波形曲线如图所示，则原点O 的振动方程为(A) )21(cos 50.0ππ+=t y ， (SI)． (B) )2121(cos 50.0ππ-=t y ， (SI)．(C) )2121(cos 50.0ππ+=t y ， (SI)．(D) )2141(cos 50.0ππ+=t y ， (SI)．【 C 】 3. 振动方向相同的两平面简谐波的波源S 1、S 2，其振动方程分别为：t A x ωcos 11=、t A x ωsin 22=，则与两波源等距离的P 点的振幅为： (A) A 1+A 2 (B) | A 1-A 2| (C)2221A A +(D) 振幅随时间变化。

【 C 】二 填空题1．如图所示为一平面简谐波在t=2s 时刻的波形图，该简谐波的波动方程是m u x t uA y ]23)2(2cos[πλπ+--=；P 处质点的振动方程是 m t uA y ]2)2(2cos[πλπ+-= 。

（该波的振幅A 、波速u 、波长λ为已知量）y (m) u2. 一平面简谐波在某时刻的波形如图所示，则λ= 30m 。

3. 如图所示，P 点距波源S 1和S 2的距离分别为λλλ，和3/103为两列波在介质中的波长，若P 点的合振幅总是极大值，则两波源应满足的条件是2122(0,1,2)3k k πϕϕπ-=±+= 。

4. 一平面简谐波沿x 轴正向传播，波动方程]2)(cos[1πω+-=u x t A y 。

人教版选择性必修1《4.3 光的干涉》练习题(1)一、单选题（本大题共7小题，共28.0分）1.抽制细丝时可用激光监控其粗细，如图所示，激光束越过细丝时产生的条纹和它通过遮光板上的一条同样宽度的窄缝规律相同，则()①这是利用光的干涉现象②这是利用光的衍射现象③如果屏上条纹变宽，表明抽制的丝变粗了④如果屏上条纹变宽，表明抽制的丝变细了．A. ①③B. ②④C. ①④D. ②③2.关于光的干涉和衍射现象，下列说法正确的是()A. 光的干涉现象遵循波的叠加原理，衍射现象不遵循波的叠加原理B. 光的干涉条纹是彩色的，衍射条纹是黑白相间的C. 光的干涉现象说明光具有波动性，光的衍射现象不能说明这一点D. 光的干涉和衍射现象都是光波叠加的结果3.为了减少光学元件的反射损失，可在光学元件表面镀上一层增透膜，利用薄膜的干涉相消来减少反射光．如果照相机镜头所镀膜对绿光的折射率为n，厚度为d，它使绿光在垂直入射时反射光完全抵消，那么绿光在真空中的波长λ0为()A. d4B. nd4C. 4dD. 4nd4.理论联系实际是物理学科特点之一．以下给出的几组表述中，实际应用与相应的物理理论相符合的是()①干涉法检查平面的平整度应用了光双缝干涉原理②伦琴射线管应用了光电效应原理③光纤通信应用了光的折射原理④光谱分析应用了原子光谱理论⑤立体电影应用了光的偏振理论．A. ①②B. ②③C. ③④D. ④⑤5.关于下列光学现象，说法正确的是()A. 水中蓝光的传播速度比红光快B. 光从空气射入玻璃时可能发生全反射C. 摄影机镜头镀膜增透是利用了光的衍射特性D. 分别用蓝光和红光在同一装置上做双缝干涉实验，用红光时得到的条纹间距更宽6.图为双缝干涉的实验示意图，光源发出的红光照射到双缝上，在光屏上出现明暗相间的条纹。

在其他条件都不变的情况下：A. 若遮住一条缝，光屏上还会出现明暗相间的条纹B. 若改用蓝光照射双缝，光屏上的条纹间距会变大C. 若增加入射光的强度，光屏上的条纹间距会变大D. 若将光屏远离双缝一小段距离，光屏上有可能不会出现明暗相间的条纹了7.用a、b、c、d表示四种不同颜色的单色点光源，若：①将a、b、c放在水中相同深度处，有人在水面上方同等条件下观测发现，b在水下的像最深，c照亮水面的面积比a的大;②分别用b、c和d发出的单色光在相同条件下做双缝干涉实验，b光的亮条纹间距最大;③a、c和d发出的光在同种玻璃中传播，d光的传播速度最大;则推断a、b、c、d的折射率正确的是()A. n b<n d<n c<n aB. n b<n a<n d<n cC. n a=n b=n c=n dD. n b=n a<n d=n c二、多选题（本大题共5小题，共20.0分）8. 下列有关说法中正确的是()A. 在“探究单摆的周期与摆长的关系”实验中，为减小偶然误差，应测出单摆做n次全振动的求出单摆的周期时间t，利用tnB. 变化的磁场一定会产生变化的电场C. X射线是比紫外线频率低的电磁波D. 只有障碍物的尺寸比波长小或相差不多的时候才会发生明显的衍射现象E. 在光的双缝干涉实验中，若仅将入射光由绿色光变为红色光，则条纹间距变宽9. 图中给出了“用双缝干涉测量光的波长”实验示意图，双缝S1和S2间距为0.80mm，双缝到屏的距离为0.80m，波长为500nm的单色平行光垂直入射到双缝S1和S2上，在屏上形成干涉条纹，中心轴线OO′上方第1条亮纹中心位置在P1处，第3条亮纹中心位置在P2处，现有1号、2号虫子分别从S1和S2出发以相同速度沿垂直屏方向飞行，1号虫子到达屏后，沿屏直线爬行到P1，2号虫子到达屏后，沿屏直线爬行到P2，假设两条虫子爬行速率均为10−3m/s，正确的是()A. 1号虫子运动路程比2号短B. 两只虫子运动的时间差为0.2sC. 两只虫子运动的时间差为1.0sD. 已知条件不够，两只虫子运动时间差无法计算10. 下列说法正确的是()A. 用透明的标准样板和单色光检查平面的平整度是利用了光的偏振B. 由黄光和蓝光组成的一细光束从水中射向空气，在不断增大入射角时水面上首先消失的是蓝光C. 电子束通过双缝实验装置后可以形成干涉图样D. 机械波和电磁波都能在真空中传播E. 机械波和电磁波都能发生衍射和干涉现象11. 下列说法中正确的是()A. 波从一种介质进入另一种介质时，频率保持不变B. 机械波的频率越高，在介质中的传播速度越大C. 两列波发生稳定的干涉现象，则两列波的频率必然相同D. 光的偏振现象说明光波是横波12. 下列说法正确的是()A. 光在真空中传播的速度与光的频率有关B. 雨后路面上的油膜形成的彩色条纹是由光的干涉形成的C. 杨氏双缝干涉实验中，若仅将入射光从红光改为紫光，则相邻亮条纹间距一定变大D. 光的偏振现象说明光是横波E. 麦克斯韦预言了电磁波的存在，赫兹用实验证实了电磁波的存在三、计算题（本大题共1小题，共10.0分）13. 半径为R、折射率n=√2的透明四分之一圆柱体的横截面如图所示，一束足够宽的平行单色光以入射角i从OA面射入圆柱体，其中一部分入射.不考虑光能通过圆柱体从曲面射出，射出点的纵坐标的最大值y m=√3R2光线在透明圆柱体内经一次或多次反射后再射出圆柱体的复杂情形，已知sin(α−β)=sinαcosβ−cosαsinβ.求入射角i的正弦值．(结果可用根式表示)【答案与解析】1.答案：B解析：解：当障碍物的尺寸与波的波长相当，或小于波的波长，会发生明显的衍射，该装置的原理是运用光的衍射现象，如果屏上条纹变宽，则金属丝变细；上述现象符合光的衍射产生的条件，故②正确；由衍射产生的条件可知：丝越细衍射现象越明显，故④也正确，故选：B。

振动、波动练习题一．选择题1．一质点在X 轴上作简谐振动，振幅A=4cm 。

周期T=2s 。

其平衡位置取作坐标原点。

若t=0时刻质点第一次通过x= -2cm 处，且向X 轴负方向运动，则质点第二次通过x= -2cm 处的时刻为（ ）。

A 1sB 32s C 34s D 2s2．一圆频率为ω的简谐波沿X 轴的正方向传播，t=0时刻的波形如图所示，则t=0时刻，X 轴上各点的振动速度υ与X 轴上坐标的关系图应（ ）。

3．图示一简谐波在t=0时刻的波形图，波速υ=200m/s ，则图中O 点的振动加速度的表达式为（ ）。

)22cos(4.0)2cos(4.0)23cos(4.0)2cos(4.02222ππππππππππππ+-=--=-=-=t a D t a C t a B t a A4．频率为100Hz点振动的相位差为3π，则这两点相距（ ）。

A 2mB 2.19mC 0.5mD 28.6m5．一平面简谐波在弹性媒质中传播，媒质质元从平衡位置运动到最大位置处的过程中，（ ）。

A 它的动能转换成势能B 它的势能转换成动能C 它从相邻的一段质元获得能量其能量逐渐增大D 它把自己的能量传给相邻的一段质元，其能量逐渐减小6．在下面几种说法中，正确的说法是：（ ）。

A 波源不动时，波源的振动周期与波动的周期在数值上是不同的B 波源振动的速度与波速相同C 在波传播方向上的任一质点振动位相总是比波源的位相滞后D 在波传播方向上的任一质点振动位相总是比波源的位相超前7．一质点作简谐振动，周期为T ，当它由平衡位置向X 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为（ ）。

A 4T B 12T C 6T D 8T8．在波长为λ的驻波中两个相邻波节之间的距离为（ ）。

A λ B 3λ/4 C λ/2 D λ/49．在同一媒质中两列相干的平面简谐波的强度之比421=I I 是，则两列波的振幅之比是：（ ） A=21A A 4 B =21A A 2 C =21A A 16 D =21A A 4110．有二个弹簧振子系统，都在作振幅相同的简谐振动，二个轻质弹簧的劲度系数K 相同，但振子的质量不同。

物理学《波动》考试题及答案10-1 图（a ）表示t ＝0 时的简谐波的波形图，波沿x 轴正方向传播，图（b ）为一质点的振动曲线．则图（a ）中所表示的x ＝0 处振动的初相位与图（b ）所表示的振动的初相位分别为（ ）题10-1 图（Ａ） 均为零 （Ｂ） 均为2π （Ｃ） 均为2π- （Ｄ） 2π 与2π- （Ｅ） 2π-与2π 分析与解 本题给了两个很相似的曲线图，但本质却完全不同．求解本题要弄清振动图和波形图不同的物理意义．图（a ）描述的是连续介质中沿波线上许许多多质点振动在t 时刻的位移状态．其中原点处质点位移为零，其运动方向由图中波形状态和波的传播方向可以知道是沿y 轴负向，利用旋转矢量法可以方便的求出该质点振动的初相位为π/2．而图（b ）是一个质点的振动曲线图，该质点在t ＝0 时位移为0，t ＞0 时，由曲线形状可知，质点向y 轴正向运动，故由旋转矢量法可判知初相位为－π/2，答案为（D ）． 10-2 机械波的表达式为()()m π06.0π6cos 05.0x t y +=，则（ ）（Ａ） 波长为100 ｍ （Ｂ） 波速为10 ｍ·ｓ-1（Ｃ） 周期为1/3 ｓ （Ｄ） 波沿x 轴正方向传播分析与解 波动方程的一般表式为⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=ϕωu x t A y cos ，其中A 为振幅，φ为初相，u 为波速．x /u 前的“-”表示波沿x 轴正向传播，“+”表示波沿x 轴负向传播．因此将原式写为()()()m 100/π6cos 05.0x t y +=和一般式比较可知（Ｂ）、（Ｄ） 均不对．而由ω＝2π/T ＝6πｓ-1 可知T ＝（1/3）ｓ．则λ＝uT ＝33.3 m ，因此（Ａ）也不对．只有（Ｃ）正确．10-3 一平面简谐波，沿x 轴负方向传播，角频率为ω，波速为u ．设4T t =时刻的波形如图（a ）所示，则该波的表达式为（ ） ()()()()⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=πωπωπωπωu x t A y u x t A y u x t A y u x t A y cos B 2cos C 2cos B cos A题10-3 图分析与解 因为波沿x 轴负向传播，由上题分析知（Ａ）、（B ）表式不正确．找出（C ）、（D ）哪个是正确答案，可以有很多方法．这里给出两个常用方法．方法一：直接将t ＝T /4，x ＝0 代入方程，那么对（C ）有y 0 ＝A 、对（D ）有y 0 ＝0，可见（D ）的结果与图一致．方法二：用旋转矢量法求出波动方程的初相位．由图（a ）可以知道t ＝T /4 时原点处质点的位移为0，且向y 轴正向运动，则此时刻的旋转矢量图如图（b ）所示．要求初相位，只要将该时刻的旋转矢量反转（顺时针转）Δφ＝ω·Δt ＝ω·T /4 ＝π/2，如图（b ）所示，即得φ0 ＝π．同样得（D ）是正确答案．题10-4 图10-4 如图所示，两列波长为λ的相干波在点P 相遇．波在点S 1 振动的初相是φ1 ，点S 1 到点P 的距离是r 1 ．波在点S 2的初相是φ2 ，点S 2 到点P 的距离是r 2 ，以k 代表零或正、负整数，则点P 是干涉极大的条件为（ ）()()()()()()πλπϕϕπλπϕϕπϕϕπk r r k r r k k r r 22A 22A 2A A 211212121212=-+-=-+-=-=-// 分析与解 P 是干涉极大的条件为两分振动的相位差π2Δk =，而两列波传到P点时的两分振动相位差为()λr r /π2Δ1212---=，故选项（D ）正确．10-5 在驻波中，两个相邻波节间各质点的振动（ ）（A ） 振幅相同，相位相同 （B ） 振幅不同，相位相同（C ） 振幅相同，相位不同 （D ） 振幅不同，相位不同分析与解 驻波方程为t λx A y v π2cos π2cos 2=，因此根据其特点，两波节间各点运动同相位，但振幅不同．因此正确答案为（B ）．10-6 频率为υ＝1.25 ×104 Hz 的平面简谐纵波沿细长的金属棒传播，棒的弹性模量为E ＝1.90 ×1011 N·m -2 ，棒的密度ρ ＝7.6 ×103 Kg·m -3 ．求该纵波的波长．分析 因机械波传播速度与介质性质有关，固体中纵波传播速度ρ/E u =．而波的特征量波长λ与波速u 、频率υ之间有λ＝u /υ．所以，频率一定的振动在不同介质中传播时，其波长不同．由上述关系可求得波长．解 由分析可知金属棒中传播的纵波速度ρ/E u =，因此，该纵波的波长为m 40.0//2===v v ρE u λ10-7 一横波在沿绳子传播时的波动方程为()()m 52cos 200x y ππ-=..．（1） 求波的振幅、波速、频率及波长；（2） 求绳上质点振动时的最大速度；（3） 分别画出t ＝1s 和t ＝2 s 时的波形，并指出波峰和波谷．画出x ＝1.0 ｍ处质点的振动曲线并讨论其与波形图的不同．分析 （1） 已知波动方程（又称波函数）求波动的特征量（波速u 、频率υ、振幅A 及波长λ等），通常采用比较法．将已知的波动方程按波动方程的一般形式⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=0cos ϕωu x t A y 书写，然后通过比较确定各特征量（式中u x 前“-”、“+”的选取分别对应波沿x 轴正向和负向传播）．比较法思路清晰、求解简便，是一种常用的解题方法．（2） 讨论波动问题，要理解振动物理量与波动物理量之间的内在联系与区别．例如区分质点的振动速度与波速的不同，振动速度是质点的运动速度，即v ＝d y /d t ；而波速是波线上质点运动状态的传播速度（也称相位的传播速度、波形的传播速度或能量的传播速度），其大小由介质的性质决定．介质不变，波速保持恒定．（3） 将不同时刻的t 值代入已知波动方程，便可以得到不同时刻的波形方程y ＝y （x ），从而作出波形图．而将确定的x 值代入波动方程，便可以得到该位置处质点的运动方程y ＝y （t ），从而作出振动图．解 （1） 将已知波动方程表示为()[]()m 5.2/π5.2cos 20.0x t y -=与一般表达式()[]0cos ϕω+-=u x t A y /比较，可得0s m 52m 20001=⋅==-ϕ,.,.u A则 m 0.2/,Hz 25.1π2/====v u λωv（2） 绳上质点的振动速度 ()[]()1s m 5.2/π5.2sin π5.0d /d -⋅--==x t t y v则 1max s m 57.1-⋅=v （3） t ＝1ｓ 和t ＝2ｓ 时的波形方程分别为()()()()m ππ5cos 20.0m ππ5.2cos 20.021x y x y -=-=波形图如图（a ）所示．x ＝1.0m 处质点的运动方程为 ()()m π5.2cos 20.0t y -=振动图线如图（b ）所示．波形图与振动图虽在图形上相似，但却有着本质的区别．前者表示某确定时刻波线上所有质点的位移情况，而后者则表示某确定位置的一个质点，其位移随时间变化的情况．题10-7 图10-8 波源作简谐运动，其运动方程为()m t πcos240100.43-⨯=y ，它所形成的波形以30ｍ·ｓ-1 的速度沿一直线传播．（1） 求波的周期及波长；（2） 写出波动方程．分析 已知波源运动方程求波动物理量及波动方程，可先将运动方程与其一般形式()ϕω+=t cos A y 进行比较，求出振幅A 、角频率ω及初相φ0 ，而这三个物理量与波动方程的一般形式()[]0cos ϕω+-=u x t A y /中相应的三个物理量是相同的．再利用题中已知的波速u 及公式ω＝2πν ＝2π／T 和λ＝u T 即可求解．解 （1） 由已知的运动方程可知，质点振动的角频率1s π240-=ω．根据分析中所述，波的周期就是振动的周期，故有 s 1033.8/π23-⨯==ωT波长为λ＝uT ＝0.25 ｍ（２） 将已知的波源运动方程与简谐运动方程的一般形式比较后可得A ＝4.0 ×10-3m ，1s π240-=ω，φ0 ＝0故以波源为原点，沿x 轴正向传播的波的波动方程为()[]()()m π8π240cos 100.4/cos 30x t u x t ωA y -⨯=+-=- 10-9 已知一波动方程为()()m 2-π10sin 05.0x t y =．（1） 求波长、频率、波速和周期；（2） 说明x ＝0 时方程的意义，并作图表示．题10-9 图分析 采用比较法．将题给的波动方程改写成波动方程的余弦函数形式，比较可得角频率ω、波速u ，从而求出波长、频率等．当x 确定时波动方程即为质点的运动方程y ＝y （t ）．解 （1） 将题给的波动方程改写为()[]()m 2/ππx /5t π10cos 05.0--=y 与()[]0cos ϕω+-=u x t A y /比较后可得波速u ＝15.7 ｍ·ｓ-1 ， 角频率ω＝10πｓ-1 ，故有m 14.3,s 2.0/1,Hz 0.5π2/======uT l v T ωv（2） 由分析知x ＝0 时，方程()()m 2/ππ10cos 05.0-=t y 表示位于坐标原点的质点的运动方程（如图）．10-10 波源作简谐运动，周期为0.02ｓ，若该振动以100m·ｓ-1 的速度沿直线传播，设t ＝0时，波源处的质点经平衡位置向正方向运动，求：（1） 距波源15.0ｍ 和5.0 m 两处质点的运动方程和初相；（2） 距波源为16.0 m 和17.0m 的两质点间的相位差．分析 （1） 根据题意先设法写出波动方程，然后代入确定点处的坐标，即得到质点的运动方程．并可求得振动的初相．（2） 波的传播也可以看成是相位的传播．由波长λ的物理含意，可知波线上任两点间的相位差为Δφ＝2πΔx ／λ．解 （1） 由题给条件1s m 100s 020-⋅==u T ,.，可得 m 2;s m π100/π21==⋅==-uT λT ω当t ＝0 时，波源质点经平衡位置向正方向运动，因而由旋转矢量法可得该质点的初相为φ0 ＝－π／2（或3π／2）．若以波源为坐标原点，则波动方程为()[]2/π100π100cos --=x/t A y距波源为x 1 ＝15.0 m 和x 2 ＝5.0 m 处质点的运动方程分别为()()π5.5t π100cos π15.5t π100cos 21-=-=A y A y它们的初相分别为φ10 ＝－15.5π和φ10 ＝－5.5π（若波源初相取φ0＝3π/2，则初相φ10 ＝－13.5π，φ10 ＝－3.5π．）（2） 距波源16.0m 和17.0 m 两点间的相位差()π/π2Δ1212=-=-=λx x10-11 有一平面简谐波在空间传播．已知在波线上某点B 的运动规律为()ϕ+=ωt A y cos ，就图（a ）（b ）（c ）给出的三种坐标取法，分别列出波动方程．并 用这三个方程来描述与B 相距为b 的P 点的运动规律．分析 （1） 波动方程的一般表式为()[]0cos ϕω+=u x t A y / ，式中振幅A 、角频率ω和波速u 从B 点运动方程和所给图均已知．因此只要求出原点的初相φ0 ．而对（a ）、（b ）情况，B 点即为原点，所以φ0＝φ，对情况（c ），原点比B 点超前相位Δφ＝ω1 ／u ，则φ0 ＝φ＋ω1／u ．（2） 写出三种情况下波动方程后只要将P 点相应的坐标代入即可写出P 点的运动规律．解 （1） 根据分析和图示波的传播方向，有（a ） 情况下：()[]ϕω+-=u x t A y /cos（b ） 情况下：()[]ϕω++=u x t A y /cos（c ） 情况下：()⎥⎦⎤⎢⎣⎡++-=u l u x t A y ωϕω/cos题10-11图（2） 将P 点的x 坐标值分别代入上述相应的波动方程可得三种情况下均有：()[]ϕω+-=u b t A y /cos P讨论 由于三种情况下，在沿波传播方向上，P 点均落在B 点后距离为b 处，即P 点的振动均比B 点的振动落后时间b /u ，落后相位ωb /u ，因而P 点的运动方程均为()[]ϕω+-=u b t A y /cos P ．10-12 图示为平面简谐波在t ＝0 时的波形图，设此简谐波的频率为250Hz ，且此时图中质点P 的运动方向向上．求：（1） 该波的波动方程；（2） 在距原点O 为7.5 m 处质点的运动方程与t ＝0 时该点的振动速度．分析 （1） 从波形曲线图获取波的特征量，从而写出波动方程是建立波动方程的又一途径．具体步骤为：1. 从波形图得出波长λ、振幅A 和波速u ＝λυ；2. 根据点P 的运动趋势来判断波的传播方向，从而可确定原点处质点的运动趋向，并利用旋转矢量法确定其初相φ0 ．（2） 在波动方程确定后，即可得到波线上距原点O 为x 处的运动方程y ＝y （t ），及该质点的振动速度υ＝d y /d t ．解 （1） 从图中得知，波的振幅A ＝0.10 m ，波长λ＝20.0m ，则波速u ＝λυ＝5.0 ×103 ｍ·ｓ-1 ．根据t ＝0 时点P 向上运动，可知波沿Ox 轴负向传播，并判定此时位于原点处的质点将沿Oy 轴负方向运动．利用旋转矢量法可得其初相φ0 ＝π/3．故波动方程为()[]()[]()m 3/π5000/π500cos 10.0/cos 0++=++=x t u x t ωA y（2） 距原点O 为x ＝7.5ｍ 处质点的运动方程为 ()()m 12π13π5000.10cos y /t +=t ＝0 时该点的振动速度为 ()-10s m 40.6/12πsin13π50/d d ⋅=-===t t y v题10-12 图10-13 如图所示为一平面简谐波在t ＝0 时刻的波形图，求（1）该波的波动方程；（2） P 处质点的运动方程．题10-13 图分析 （1） 根据波形图可得到波的波长λ、振幅A 和波速u ，因此只要求初相φ，即可写出波动方程．而由图可知t ＝0 时，x ＝0 处质点在平衡位置处，且由波的传播方向可以判断出该质点向y 轴正向运动，利用旋转矢量法可知φ＝－π/2．（2） 波动方程确定后，将P 处质点的坐标x 代入波动方程即可求出其运动方程y P ＝y P （t ）．解 （1） 由图可知振幅A ＝0.04 ｍ， 波长λ＝0.40 ｍ， 波速u ＝0.08ｍ·ｓ-1 ，则ω＝2π/T ＝2πu /λ＝（2π/5）ｓ-1 ，根据分析已知φ＝－π/2，因此波动方程为()m 208.05π20.04cos y ⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-=πx t（2） 距原点O 为x ＝0.20ｍ 处的P 点运动方程为 ()m 2520.04cos y ⎥⎦⎤⎢⎣⎡+=ππ10-14 一平面简谐波，波长为12 m ，沿O x 轴负向传播．图（a ）所示为x ＝1.0 m 处质点的振动曲线，求此波的波动方程．题10-14图分析 该题可利用振动曲线来获取波动的特征量，从而建立波动方程．求解的关键是如何根据图（a ） 写出它所对应的运动方程．较简便的方法是旋转矢量法．解 由图（a ）可知质点振动的振幅A ＝0.40 ｍ，t ＝0 时位于x ＝1.0 m 处的质点在A /2 处并向Oy 轴正向移动．据此作出相应的旋转矢量图（b ），从图中可知3/π0-='．又由图（a ）可知，t ＝5 s 时，质点第一次回到平衡位置，由图（b ）可看出ωt ＝5π／6，因而得角频率ω＝（π/6） s -1 ．由上述特征量可写出x ＝1.0 m 处质点的运动方程为()m 3π6π0.04cos y ⎥⎦⎤⎢⎣⎡-=t 将波速1s m 0.1π2//-⋅===ωλT λu 及x ＝1.0 m 代入波动方程的一般形式()[]0cos ϕω++=u x t A y /中，并与上述x ＝1.0 m 处的运动方程作比较，可得φ0 ＝－π／2，则波动方程为()()m 2π10/6π0.04cos y ⎥⎦⎤⎢⎣⎡-+=x t10-15 图中（Ⅰ）是t ＝0 时的波形图，（Ⅱ）是t ＝0.1 s 时的波形图，已知T ＞0.1 s ，写出波动方程的表达式．题10-15 图分析 已知波动方程的形式为()[]02cos ϕλπ+-=//x T t A y从如图所示的t ＝0 时的波形曲线Ⅰ，可知波的振幅A 和波长λ，利用旋转矢量法可确定原点处质点的初相φ0 ．因此，确定波的周期就成为了解题的关键．从题给条件来看，周期T 只能从两个不同时刻的波形曲线之间的联系来得到．为此，可以从下面两个不同的角度来分析．（1） 由曲线（Ⅰ）可知，在t ＝0 时，原点处的质点处在平衡位置且向Oy 轴负向运动，而曲线（Ⅱ）则表明，经过0.1s 后，该质点已运动到Oy 轴上的-A 处．因此，可列方程kT +T /4 ＝0.1s ，在一般情形下，k ＝0，1，2，…这就是说，质点在0.1s 内，可以经历k 个周期振动后再回到-A 处，故有T ＝0.1／(k ＋0.25） s ．（2） 从波形的移动来分析．因波沿Ox 轴正方向传播，波形曲线（Ⅱ）可视为曲线（Ⅰ）向右平移了Δx ＝u Δt ＝λΔt ／T ．由图可知，Δx ＝kλ＋λ/4，故有kλ＋λ/4 ＝λΔt ／T ，同样也得T ＝0.1/(k ＋0.25)s ．应当注意，k 的取值由题给条件T ＞0.1 s 所决定．解 从图中可知波长λ＝2.0 m ，振幅A ＝0.10 m ．由波形曲线（Ⅰ）得知在t ＝0 时，原点处质点位于平衡位置且向Oy 轴负向运动，利用旋转矢量法可得φ0 ＝π/2．根据上面的分析，周期为()()(),...,,./.210250s 10=+=k k T由题意知T ＞0.1 s ，故上式成立的条件为k ＝0，可得T ＝0.4 s ．这样，波动方程可写成 ()[]()m 5002402cos 100ππ.././.++=x t y 10-16 平面简谐波的波动方程为()()m 24cos 080πx πt y -=.．求：（1） t ＝2.1 s 时波源及距波源0.10m 两处的相位；（2） 离波源0.80 m 及0.30 m 两处的相位差．解 （1） 将t ＝2.1 s 和x ＝0 代入题给波动方程，可得波源处的相位π4.81=将t ＝2.1 s 和x ′＝0.10 m 代入题给波动方程，得0.10 m 处的相位为π2.82=（2） 从波动方程可知波长λ＝1.0 m ．这样，x 1 ＝0.80 m 与x 2 ＝0.30 m 两点间的相位差π/Δπ2Δ=⋅=λx π10-17 为了保持波源的振动不变，需要消耗4.0 W 的功率．若波源发出的是球面波（设介质不吸收波的能量）．求距离波源5.0 m 和10.0 m 处的能流密度．分析 波的传播伴随着能量的传播．由于波源在单位时间内提供的能量恒定，且介质不吸收能量，故对于球面波而言，单位时间内通过任意半径的球面的能量（即平均能流）相同，都等于波源消耗的功率P ．而在同一个球面上各处的能流密度相同，因此，可求出不同位置的能流密度I ＝P /S ．解 由分析可知，半径r 处的能流密度为2π4/r P I =当r 1 ＝5.0 m 、r 2 ＝10.0m 时，分别有22211m W 1027.1π4/--⋅⨯==r P I22222m W 1027.1π4/--⋅⨯==r P I10-18 有一波在介质中传播，其波速u ＝1.0 ×103m·s -1 ，振幅A ＝1.0 ×10-4 m ，频率ν ＝1.0 ×103Hz ．若介质的密度为ρ ＝8.0×102 kg·m -3 ，求：（1） 该波的能流密度；（2） 1 min 内垂直通过4.0 ×10-4m 2 的总能量．解 （1） 由能流密度I 的表达式得 2522222m W 10581221-⋅⨯===.v uA uA I ρπωρ （2） 在时间间隔Δt ＝60 s 内垂直通过面积S 的能量为J 107933⨯=∆⋅=∆⋅=.t IS t P W 10-19 如图所示，两振动方向相同的平面简谐波波源分别位于A 、B 两点．设它们相位相同，且频率均为υ＝30Hz ，波速u ＝0.50 m·s -1 ．求在P 点处两列波的相位差．分析 在均匀介质中，两列波相遇时的相位差Δφ一般由两部分组成，即它们的初相差φA -φB 和由它们的波程差而引起的相位差2πΔr /λ．本题因φA ＝φB ，故它们的相位差只取决于波程差．解 在图中的直角三角形ABP 中cm 5130sin o .==AP BP两列波在点P 处的波程差为Δr ＝AP －BP ，则相位差为π8.1/π2/π2Δ===u r Δλr Δv题10-19图10-20 如图所示，两相干波源分别在P 、Q 两点处，它们发出频率为ν、波长为λ，初相相同的两列相干波．设PQ ＝3λ/2，R 为PQ 连线上的一点．求：（1） 自P 、Q 发出的两列波在R 处的相位差；（2） 两波在R 处干涉时的合振幅．题10-20 图分析 因两波源的初相相同，两列波在点R 处的相位差Δφ仍与上题一样，由它们的波程差决定．因R 处质点同时受两列相干波的作用，其振动为这两个同频率、同振动方向的简谐运动的合成，合振幅ϕ∆++=cos 2212221A A A A A ．解 （1） 两列波在R 处的相位差为πλr 3/Δπ2Δ==（2） 由于π3Δ=，则合振幅为21212221cos32A A A A A A A -=++=π10-21 两相干波波源位于同一介质中的A 、B 两点，如图（a ）所示．其振幅相等、频率皆为100 Hz ，B 比A 的相位超前π．若A 、B 相距30.0m ，波速为u ＝400 m·s -1 ，试求AB 连线上因干涉而静止的各点的位置．题10-21 图分析 两列相干波相遇时的相位差λr Δπ2Δ12--=．因此，两列振幅相同的相干波因干涉而静止的点的位置，可根据相消条件()π12Δ+=k 获得．解 以A 、B 两点的中点O 为原点，取坐标如图（b ）所示．两波的波长均为λ＝u /υ＝4.0 m ．在A 、B 连线上可分三个部分进行讨论．1. 位于点A 左侧部分()π14π2ΔA B A B -=---=r r因该范围内两列波相位差恒为2π的整数倍，故干涉后质点振动处处加强，没有静止的点．2. 位于点B 右侧部分()π16π2ΔA B A B =---=r r显然该范围内质点振动也都是加强，无干涉静止的点．3. 在A 、B 两点的连线间，设任意一点P 距原点为x ．因x r -=15B ，x r +=15A ，则两列波在点P 的相位差为()()π1/π2ΔA B A B +=---=x λr r根据分析中所述，干涉静止的点应满足方程()()π152π1+=+k x x得 ()2,...1,0,k m 2±±==k x因x ≤15 m ，故k ≤7．即在A 、B 之间的连线上共有15 个静止点．10-22 图（a ）是干涉型消声器结构的原理图，利用这一结构可以消除噪声．当发动机排气噪声声波经管道到达点A 时，分成两路而在点B 相遇，声波因干涉而相消．如果要消除频率为300 Hz 的发动机排气噪声，则图中弯管与直管的长度差Δr ＝r 2 －r 1 至少应为多少？ （设声波速度为340 m·s -1 ）题10-22 图分析 一列声波被分成两束后再相遇，将形成波的干涉现象．由干涉相消条件，可确定所需的波程差，即两管的长度差Δr ．解 由分析可知，声波从点A 分开到点B 相遇，两列波的波程差Δr ＝r 2 - r 1 ，故它们的相位差为()λr λr r /Δπ2/π2Δ12=-=由相消静止条件Δφ＝（2k ＋1）π，（k ＝0，±1，±2，…）得 Δr ＝（2k ＋1）λ／2根据题中要求令k ＝0 得Δr 至少应为m 57022.//===∆v u r λ讨论 在实际应用中，由于噪声是由多种频率的声波混合而成，因而常将具有不同Δr 的消声单元串接起来以增加消除噪声的能力．图（b ）为安装在摩托车排气系统中的干涉消声器的结构原理图．10-23 如图所示，x ＝0 处有一运动方程为t A y ωcos =的平面波波源，产生的波沿x 轴正、负方向传播．MN 为波密介质的反射面，距波源3λ／4．求：（1） 波源所发射的波沿波源O 左右传播的波动方程；（2） 在MN 处反射波的波动方程；（3） 在O ～MN 区域内形成的驻波方程，以及波节和波腹的位置；（4） x ＞0区域内合成波的波动方程．题10-23 图分析 知道波源O 点的运动方程t A y ωcos =，可以写出波沿x 轴负向和正向传播的方程分别为()u x t A y /+=ωcos 1和()u x t A y /-=ωcos 2．因此可以写出y 1 在MN 反射面上P 点的运动方程．设反射波为y 3 ，它和y 1 应是同振动方向、同振幅、同频率的波，但是由于半波损失，它在P 点引起的振动和y 1 在P 点引起的振动反相．利用y 1 在P 点的运动方程可求y 3 在P 点的运动方程，从而写出反射波y 3 ．在O ～MN 区域由y 1 和Y 3 两列同频率、同振动方向、同振幅沿相反方向传播的波合成形成驻波．在x ＞0区域是同传播方向的y 2 和y 3 合成新的行波．解 （1） 由分析已知：沿左方向和右方向传播的波动方程分别为()u x t A y /+=ωcos 1和()u x t A y /-=ωcos 2（2） y 1 在反射面MN 处引起质点P 振动的运动方程⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=2π3π2cos 43π2π2cos P 1t T A λλt TA y 因半波损失反射波y 3 在此处引起的振动为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+-=2ππ2cos ππ23π2cos P 3t TA t T A y 设反射波的波动方程为()/π2/π2cos 3+-=λx T t A y ，则反射波在x ＝－3λ/4处引起的振动为 ⎪⎭⎫ ⎝⎛++=π23π2cos P 3t T A y 与上式比较得π2-=，故反射波的波动方程为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--=x λt TA x λt T A y π2π2cos π2π2π2cos 3（3） 在O ～MN 区域由y 1 和y 3 合成的驻波y 4 为()⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+=+=t T x λA x λt T A x λt T A y y x t y π2cos π2cos 2π2π2cos π2π2cos ,314 波节的位置：4/2/,2/ππ/π2λλk x k λx +=+=，取k ＝－1， －2，即x ＝－λ/4， －3λ/4 处为波节．波腹的位置：2/,π/π2λk x k λx ==，取k ＝0，－1，即x ＝0，－λ/2 处为波腹．（4） 在x ＞0 区域，由y 2 和y 3 合成的波y 5 为()⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+=x λt TA x λt T A x λt T A y y x t y π2π2cos 2π2π2cos π2π2cos ,325 这表明：x ＞0 区域内的合成波是振幅为2A 的平面简谐波．10-24 一弦上的驻波方程式为()()()m π550cos π6.1cos 100.32t x y -⨯=（1） 若将此驻波看成是由传播方向相反，振幅及波速均相同的两列相干波叠加而成的，求它们的振幅及波速；（2） 求相邻波节之间的距离；（3） 求t ＝3.0 ×10-3 s 时位于x ＝0.625 m 处质点的振动速度．分析 （1） 采用比较法．将本题所给的驻波方程，与驻波方程的一般形式相比较即可求得振幅、波速等．（2） 由波节位置的表达式可得相邻波节的距离．（3） 质点的振动速度可按速度定义v ＝d y /d t 求得．解 （1） 将已知驻波方程 ()()()m π550cos π6.1cos 100.32t x y -⨯=与驻波方程的一般形式()()t λx A y v π2cos /π2cos 2=作比较，可得两列波的振幅A ＝1.5 ×10-2 m ，波长λ＝1.25 m ，频率υ＝275 Hz ，则波速u ＝λυ＝343.8m·s -1 ．（2） 相邻波节间的距离为()[]()m625024124112k 1k .///==+-++=-=∆+λλλk k x x x （3） 在t ＝3.0 ×10-3 s 时，位于x ＝0.625 m 处质点的振动速度为 ()()1s m 2.46π550cos π6.1cos π5.16d /d -⋅-=-==t x t y v*10 －25 在下述两种情况下，求长度为0.15 m 的风琴管的基频和前四个谐频．（1） 管子两端开口；（2） 管子的一端封闭，一端开口．设声速为340m·s -1 ．分析 当风琴管的某个端口封闭时，那么风琴管内形成的驻波在该端口就是波节．而当风琴管的端口开口时，就形成波腹．根据限定区域内驻波形成条件（如图所示），当管子两端为波腹时，其管长与波长有关系式L ＝kλk /2 成立，k 为正整数．而当管子一端为波节、另一端为波腹时，管长与波长有关系式L ＝（2k －1）λk /4 成立．可见取不同的k 值，得到不同的λk ，管内就出现不同频率υk 的波．对应k ＝1 称为基频，k ＝2，3，4，…称为各次谐频．题10-25 图解 （1） 根据分析由L ＝kλk /2 和νk ＝u /λk 可得υk ＝ku /2L （k ＝1，2，3，…）因此，基频：υ 1 ＝1133 Hz二次谐频：υ2 ＝2267 Hz三次谐频：υ3 ＝3400 Hz四次谐频：υ4 ＝4533 Hz五次谐频：υ5 ＝5667 Hz（2） 同样根据分析由L ＝（2k －1）λk /4 和νk ＝u /λk 可得υk ＝（2k －1）u /4L （k ＝1，2，3，…）因此，基频：υ1 ＝567 Hz二次谐频：υ2 ＝1700 Hz三次谐频：υ3 ＝2833 Hz四次谐频：υ4 ＝3967 Hz五次谐频：υ5 ＝5100 Hz10-26 一平面简谐波的频率为500 Hz ，在空气（ρ ＝1.3 kg·m -3 ）中以u ＝340 m·s -1 的速度传播，到达人耳时，振幅约为A ＝1.0 ×10 -6 m ．试求波在耳中的平均能量密度和声强．解 波在耳中的平均能量密度2622222m J 10426221--⋅⨯===.v A A ρπωρω 声强就是声波的能流密度，即23m W 10182--⋅⨯==.ωu I这个声强略大于繁忙街道上的噪声，使人耳已感到不适应．一般正常谈话的声强约1.0×10-6W·m -2 左右．10-27 面积为1.0 m 2 的窗户开向街道，街中噪声在窗口的声强级为80dB．问有多少“声功率”传入窗内？分析 首先要理解声强、声强级、声功率的物理意义，并了解它们之间的相互关系．声强是声波的能流密度I ，而声强级L 是描述介质中不同声波强弱的物理量．它们之间的关系为L ＝lg （I /I 0 ），其中I 0 ＝1.0 ×10-12 W·m -2为规定声强．L 的单位是贝尔（B ），但常用的单位是分贝（dB ），且1 B ＝10 dB ．声功率是单位时间内声波通过某面积传递的能量，由于窗户上各处的I 相同，故有P ＝IS ．解 根据分析，由L ＝lg （I ／I 0 ）可得声强为I ＝10L I 0则传入窗户的声功率为P ＝IS ＝10L I 0 S ＝1.0 ×10-4 W10-28 若在同一介质中传播的，频率分别为1200 Hz 和400 Hz 的两声波有相同的振幅．求：（1） 它们的强度之比；（2） 两声波的声强级差．解 （1） 因声强222/ωρuA I =，则两声波声强之比9222121==ωω//I I （2） 因声强级L ＝lg （I ／I 0 ），则两声波声强级差为()()()dB 549B 9540lg lg lg 210201..///===-=∆I I I I I I L10-29 一警车以25 m·s -1 的速度在静止的空气中行驶，假设车上警笛的频率为800 Hz ．求：（1） 静止站在路边的人听到警车驶近和离去时的警笛声波频率；（2） 如果警车追赶一辆速度为15m·s -1 的客车，则客车上人听到的警笛声波的频率是多少？ （设空气中的声速u ＝330m·s -1 ）分析 由于声源与观察者之间的相对运动而产生声多普勒效应，由多普勒频率公式可解得结果．在处理这类问题时，不仅要分清观察者相对介质（空气）是静止还是运动，同时也要分清声源的运动状态．解 （1） 根据多普勒频率公式，当声源（警车）以速度v s ＝25 m·s -1 运动时，静止于路边的观察者所接收到的频率为sv u u v v =' 警车驶近观察者时，式中v s 前取“－”号，故有Hz 6.8651=-='sv u u v v 警车驶离观察者时，式中v s 前取“＋”号，故有Hz 7.7432=+='sv u u v v （2） 声源（警车）与客车上的观察者作同向运动时，观察者收到的频率为Hz 7.7432=+='sv u u v v 10-30 一次军事演习中，有两艘潜艇在水中相向而行，甲的速度为50.0 km·h -1 ，乙的速度为km·h -1 ，如图所示．甲潜艇发出一个1.0×103 Hz 的声音信号，设声波在水中的传播速度为5.47×103 km·h -1 ，试求（1） 乙潜艇接收到的信号频率；（2） 甲潜艇接收到的从乙潜艇反射回来的信号频率．分析 （1） 甲潜艇是声源，发出信号频率为υ，乙潜艇是观察者，两者相向运动，利用多普勒频率公式，即可求得乙潜艇接收到的信号频率υ′．（2） 要求甲潜艇接收到的乙潜艇的信号频率，可将乙潜艇看成是声源，它发出的信号频率是υ′，将甲潜艇看成是观察者，两者相向运动，同样利用多普勒频率公式，可求出甲潜艇接收到的信号频率υ″．题10-30 图解 由题已知v 1 ＝50.0 km·h -1 ， v 2 ＝70.0 km·h -1 ， u ＝5.47 ×103 km·h -1 ，v ＝1000 Hz ，由分析可知：（1） Hz 102212=-+='v v v v u u （2） Hz 104521='-+=''v v v v u u *10-31 一广播电台的辐射功率是10 kW ，假定辐射场均匀分布在以电台为中心的半球面上．（1） 求距离电台为r ＝10 kW 处的坡印廷矢量的平均值；（2） 若在上述距离处的电磁波可看作平面波，求该处的电场强度和磁场强度的振幅．分析 坡印廷矢量是电磁波的能流密度矢量，它是随时间作周期性变化的．求其平均值，也就是指在一周期内的平均值．在忽略电磁波传播过程中的能量损耗时，按题意，波源的辐射功率就应等于单位时间通过半球面（面积A ＝2πr 2 ）的电磁波能量，即P ＝S ·A ，而平均能流密度值S ＝EH ．另外，由电磁波的性质可知，E 与H 垂直，相位相同，且有关系式H E 00με=．因此，平面电磁波的坡印廷矢量大小的平均值可表示为2m 00m m 2121H H E S εμ==，由此可求电场强度振幅m E 和磁场强度振幅m H ． 解 （1） 因为辐射场分布在半球面上，则坡印廷矢量的平均值为252m W 1059.1π2/--⋅⨯==r P S（2） 根据分析，2m 00m m 212H H E EH S εμ===/ ，则磁场强度和电场强度的振幅分别为 ()142100m m A 109122--⋅⨯==.//εμS H1m m m V 10902-⋅==./H S E*10-32 真空中有一平面电磁波的电场表达式如下：0x =E ()[]()0,m V /10π2cos 60.018y =⋅-⨯=-z E c x t E ．求：（1） 波长，频率；（2） 该电磁波的传播方向；（3） 磁场强度的大小和方向；（4） 坡印廷矢量．分析 根据电磁波的特性，电场强度E 和磁场强度H 均垂直于波的传播方向．而E 和H 又互相垂直且同相位，E ×H 的方向为波速u 的方向．在数值上有关系00με//=H E 成立．因此由题中给出的电场表达式可以求磁场表达式，而坡印廷矢量可由公式S ＝E ×H 求出．解 （1） 由电场表达式可知，角频率ω＝2π×108 s -1 ，波速u 等于光速c ，则电磁波的波长和频率分别为Hz 10π2m ;3/π28=====ω/ωc cT λv（2） 由电场表达式看出，电磁波沿x 轴正方向传播，E 矢量是在Oxy 平面内 偏振的．（3） 磁场强度表达式：00y x ==H H ,()[]()183y 00m A /10π2cos 106.1/--⋅-⨯⨯==c x t E μεH zH 矢量在Oxz 平面内偏振．（4） ()[]()2824m W i /10π2cos 106.9H E S --⋅-⨯⨯=⨯=c x t。