下载文档原格式
大学物理习题答案第一章质点运动学1-1 D 。
1-2 23 m/s 1-3 解：)/(16)/(0.80.4/16/0.8)(5.02.0,0.0/0.4222s m j j a i a a s m j i j v i v v sm a s m dt dyv t v y x y t v x x t a s m V y x y x y y x x x X=+=+=+====∴=∴==∴===∴=即又因方程当1-4 解：由加速度420232,3102)310()46()/(46)46(22220000-==+=∴++=⇒+==+=⇒+==⎰⎰⎰⎰⎰⎰x y ty t x j t i t r dt j t i t dt v r d s m j t i t v dt j i dt a v d tt rr ttv轨迹方程为1-5 解：(1)取如图所示的坐标，物品下落时在水平和竖直方向的运动方程分别为m gyvx m y s m v gt y vt x 4522100,/10021,2==∴==== (2) 视线和水平线的夹角为5.12==xyarctgθ （3）在任意时刻 物品的速度与水平轴夹角为vgt arctgv v arctgxy ==α 取自然坐标，物品在抛出2S 时，重力加速度的切向分量与法向分量分别为22/62.9)cos(cos /88.1)sin(sin s m v gtarctg g g a s m vgtarctgg g a n t ======αα第二章 牛顿定律2-1 140 N/S ；24 M/S 。
2-2 解：取沿斜面为坐标轴OX ，原点O 位于斜面顶点，则由牛顿第二定律有ma mg mg =-ααcos sin （1）又物体在斜面上作匀变速直线运动，故有)2()cos (sin cos 2)cos (sin 2121cos 22αμαααμαα-=∴-==g lt t g at l为使下滑的时间最短，可令dt/da=0 , 由式（2）有)(99.0)cos (sin cos 249120)sin (cos cos )cos (sin sin min s g lt tg o =-==-==++--αμαααμααμαααμαα则可得2-3 解：因加速度a=dv/dt ,在直线运动中，根据牛顿定律有 120t+40=mdv/dt 根据初始条件， 积分得)(0.20.20.60.5)0.60.40.6(0.5,0/)/(0.60.40.6)0.40.12(3220020m t t t x dt t t dx x t dt dx v s m t t v dtt dv txx tvv +++=∴++====++=⇒+=⎰⎰⎰⎰2-4解：以地面飞机滑行方向为坐标正方向，由牛顿定律及初始条件，有)(4676)2()/(0.302/3002002000m t mt v x x s dt t mv dx s m v t mv v dt mt dv tdt mdv ma F txx tvv =-=-=∴-==⇒-=⇒-=-===⎰⎰⎰⎰ααααα2-5解：（1）)(11.6)1ln()1(00s mgkv k m t kvmg dvmdtdtdv mkv mg vt≈+=⇒+-==--⎰⎰（2）)(183)1ln()1(000m kv mg kv mg k m y kvmg mvdv dy dydvmvkv mg dyvdv dt dy dy dv dt dv v y=⎥⎦⎤⎢⎣⎡-+-=∴+-==--⇒==⎰⎰代入第三章 动量守恒定律和能量守恒定律3-1 [B]3-2 解： 取图示坐标，绳索拉力对物体所作的功为⎰⎰=⋅=ddx F x d F W θcos)(69.1212J dx xd Fx x x =+-=⎰3-3 解：3732034320003432422237279180cos 993lkc dx x kc dxF x d F W x kc t kc kv F ct dtdxv ct x ttt ⎰⎰⎰-=-==⋅======∴=第四章刚体的转动4-1 [A]4-2 6.54 rad/s 2; 4.8 s .4-3 解1：s n n MJJ Mt J M t8.10)(200=-=-=⇒=-=πωωαωωα由 解2：根据角动量定理s n n MJJ Mt J Mdt t8.10)(2)(00=-=-=-=⎰πωωωω4-4 [C] 4-5 解：αα2121r m J r F T ==张力为下落的距离为时mm m gt m at s B s t m m gm a r a F F a m F g m F P T T T T 45.2221,0.122,,21222212'2'2'2=+===+=∴===-=-α()N g m m m m a g m F T 2.3922121=+=-=4-6 解：根据角动量守恒定律()1212212'222211'2121.29362,2,12,)(-=+=+==⎪⎭⎫⎝⎛==+=s lm m v m J J J lv l m J l m J J J J ωωωωω4-7 解：小孩与转台作为一转动系统，系统的角动量守恒。
大学物理学上册习题解答HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】大学物理学习题答案习题一答案习题一1.1 简要回答下列问题：(1)位移和路程有何区别在什么情况下二者的量值相等在什么情况下二者的量值不相等(2) 平均速度和平均速率有何区别在什么情况下二者的量值相等(3) 瞬时速度和平均速度的关系和区别是什么瞬时速率和平均速率的关系和区别又是什么(4)质点的位矢方向不变，它是否一定做直线运动质点做直线运动，其位矢的方向是否一定保持不变(5) (6)r ∆和r ∆有区别吗？v ∆和v ∆有区别吗？0dv dt =和0d v dt=各代表什么运动？ (7)设质点的运动方程为：()x x t =，()y y t =，在计算质点的速度和加速度时，有人先求出r =dr v dt= 及 22d r a dt =而求得结果；又有人先计算速度和加速度的分量，再合成求得结果，即v = 及 a = 你认为两种方法哪一种正确两者区别何在(7) 如果一质点的加速度与时间的关系是线性的，那么，该质点的速度和位矢与时间的关系是否也是线性的？(8)“物体做曲线运动时，速度方向一定在运动轨道的切线方向，法向分速度恒为零，因此其法向加速度也一定为零.”这种说法正确吗？(9)(9) 任意平面曲线运动的加速度的方向总指向曲线凹进那一侧，为什么？(10) 质点沿圆周运动，且速率随时间均匀增大，n a 、t a 、a 三者的大小是否随时间改变？(11) 一个人在以恒定速度运动的火车上竖直向上抛出一石子，此石子能否落回他的手中如果石子抛出后，火车以恒定加速度前进，结果又如何1.2 一质点沿x 轴运动，坐标与时间的变化关系为224t t x -=，式中t x ,分别以m 、s 为单位，试计算：(1)在最初s 2内的位移、平均速度和s 2末的瞬时速度；(2)s 1末到s 3末的平均加速度；(3)s 3末的瞬时加速度。
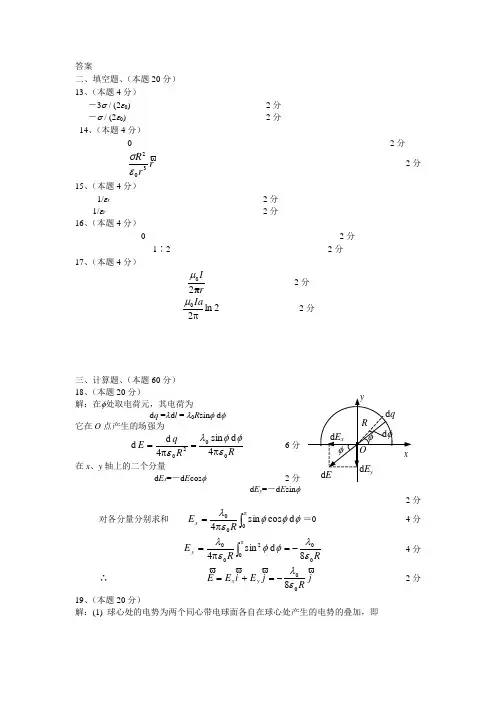
答案二、填空题、（本题20分） 13、（本题4分）－3σ / (2ε0) 2分 －σ / (2ε0) 2分 14、（本题4分）0 2分r r R 302εσ 2分15、（本题4分）1/εr 2分 1/εr 2分 16、（本题4分）0 2分 1∶2 2分17、（本题4分）rIπ20μ 2分2ln 20πIaμ 2分三、计算题、（本题60分） 18、（本题20分）解：在φ处取电荷元，其电荷为d q =λd l = λ0R sin φ d φ它在O 点产生的场强为R RqE 00204d sin 4d d εφφλεπ=π= 6分 在x 、y 轴上的二个分量 d E x =－d E cos φ 2分d E y =－d E sin φ2分对各分量分别求和 ⎰ππ=000d c o s s i n 4φφφελR E x ＝04分RR E y 0002008d sin 4ελφφελ-=π=⎰π 4分 ∴ j Rj E i E E y x008ελ-=+= 2分19、（本题20分）解：(1) 球心处的电势为两个同心带电球面各自在球心处产生的电势的叠加，即⎪⎪⎭⎫ ⎝⎛+π=22110041r q r q U ε⎪⎪⎭⎫ ⎝⎛π-ππ=22212104441r r r r σσε()210r r +=εσ7分2100r r U +=εσ＝8.85×10-9 C / m 2 4分 (2) 设外球面上放电后电荷面密度为σ'，则应有()21001r r U σσε'+='= 0 4分 即σσ21r r -=' 2分 外球面上应变成带负电，共应放掉电荷 ()⎪⎪⎭⎫ ⎝⎛+π='-π='212222144r r r r q σσσ ()20021244r U r r r εσπ=+π=＝6.67×10-9 C 3分20（本题20分） 解：其中3/4圆环在D 处的场 )8/(301a I B μ= 5分 AB 段在D 处的磁感强度 )221()]4/([02⋅π=b I B μ 5分 BC 段在D 处的磁感强度 )221()]4/([03⋅π=b I B μ 5分 1B 、2B 、3B方向相同，可知D 处总的B 为)223(40ba I B +ππ=μ 5分。
1。
一质点在平面上作一般曲线运动，其瞬时速度为，瞬时速率为v，某一时间内的平均速度为,平均速率为，它们之(A) (B）(C）（D）参考答案：D2.一质点在平面上运动，已知质点位置矢量的表示式为(其中a、b为常量)，则该质点作(A) 匀速直线运动． (B) 变速直线运动．（C）抛物线运动． (D）一般曲线运动．参考答案：B3。
如图所示,湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动．设该人以匀速率收绳,绳不伸（A）匀加速运动．（B）匀减速运动． (C）变加速运动．（D) 变减速运动．参考答案：C4.一飞机相对空气的速度大小为200 km/h, 风速为56 km/h，方向从西向东．地面雷达站测得飞机速度大小为192 k(A) 南偏西16。
3°．(B）北偏东16。
3°（C) 向正南或向正北．(D) 西偏北16.3°．(E) 东偏南16参考答案：C5。
一光滑的内表面半径为10 cm的半球形碗,以匀角速度绕其对称OC旋转．已知放在碗内表面上的一个小球P相对于碗静此可推知碗旋转的角速度约为（A） 10 rad/s．（B) 13 rad/s．（C) 17 rad/s (D） 18 rad/s．参考答案：B6。
站在电梯中的人，看到用细绳连接的质量不同的两物体,跨过电梯内一个挂在天花板上的无摩擦的定滑轮而处于“平衡静作加速度运动,加速度是：(A) 大小为g,方向向上．（B）大小为g，方向向下． (C) 大小为，方向向上． (D) 大小为,方向向下．参考答案：B（A） mv．（B)？ mv．（C） ?mv． (D) mv．参考答案:C9.一质量为60 kg的人起初站在一条质量为300 kg,且正以2 m/s的速率向湖岸驶近的小木船上，湖水是静止的，其阻力速率v沿船的前进方向向河岸跳去,该人起跳后，船速减为原来的一半,v应为(A) 2 m/s．(B） 3 m/s．(C) 5 m/s．参考答案：D10.在水平冰面上以一定速度向东行驶的炮车,向东南（斜向上)方向发射一炮弹，对于炮车和炮弹这一系统，在此过程中（忽力)（A) 总动量守恒．（B）总动量在炮身前进的方向上的分量守恒，其它方向动量不守恒．（C) 总动量在水平面上任意方向的分量守恒，竖直方向分量不守恒．（D) 总动量在任何方向的分量均不守恒参考答案：C11。
大学物理作业答案一、选择题第1题,答案D ，第2题,答案C ， 第3题,答案A C ，第4题,答案C ，第5题,答案B ， 第6题,答案C ，第7题,答案A D ，第8题,答案A ，第9题,答案D ，第10题,答案ADEH 第11题,答案C ，第12题,答案C ，第13题,答案BDF ，第14题,答案C ，第15题,答案A ， 第16题,答案ACE ，第17题,答案AC ，第18题,答案A ，第19题,答案A ，第20题,答案D ， 第21题,答案B ， 二、计第算题100. 质量为M 的木块静止在光滑的水平面上．质量为m 、速率为v 的子弹沿水平方向打入木块并陷在其中，试计算相对于地面木块对子弹所作的功W 1及子弹对木块所作的功W 2． 解：设子弹打入木块后二者共同运动的速率为V ，水平方向动量守恒，有 V M m m )(+=v , )/(M m m V +=v木块对子弹作的功 2212121v m mV W -=22)(2)2(v m M m M Mm ++-=101. 如图所示，质量为m 2的物体与轻弹簧相连，弹簧另一端与一质量可忽略的挡板连接，静止在光滑的桌面上．弹簧劲度系数为k ．今有一质量为m 1速度为0v 的物体向弹簧运动并与挡板正碰，求弹簧最大的被压缩量．km 2m 1v解：弹簧被压缩量最大距离时，m 1、m 2相对速度为零．这时动量守恒 vv )(2101m m m +=机械能守恒 222120121)(2121kx m m m ++=v v 由上二式可解得弹簧的最大被压缩量为)(21210m m k m m x +=v102. 一质量为m 的子弹，水平射入悬挂着的静止砂袋中，如图所示．砂袋质量为M ，悬线长为l ．为使砂袋能在竖直平面内完成整个圆周运动，子弹至少应以多大的速度射入？mMlO解:子弹对木块作的功 2221mV W =222)(2v m M Mm +=解：动量守恒越过最高点条件机械能守恒解上三式，可得103. 如图所示，一内半径为a、外半径为b的金属球壳，带有电荷Q，在球壳空腔内距离球心r 处有一点电荷q．设无限远处为电势零点，试求：(1) 球壳内外表面上的电荷．(2) 球心O点处，由球壳内表面上电荷产生的电势．(3) 球心O点处的总电势．解：(1) 由静电感应，金属球壳的内表面上有感生电荷-q，外表面上带电荷q+Q．(2)(3104. 图示为一半径为a的、带有正电荷Q的导体球．球外有一内半径为b、外半径为c的不带电的同心导体球壳．设无限远处为电势零点，试求内球和球壳的电势.．ROaQbc解：105. 载有电流I的平面闭合回路由半径为R1及R2(R1> R2)的两个同心半圆弧和两个直导线段组成．已知两个直导线段在半圆弧中心O点产生的磁感强度均为零．若闭合回路在O点产生的总的磁感强度B大于半径为R2的半圆弧在O点产生的磁感强度B2，(1) 画出载流回路的形状；(2) 求出O点的总磁感强度B．解：(1) 可知．故闭合回路形状如图所示.qQabOr(2) ，106. 空中电流分布如图，两个半圆共面，且具有公共圆心，试求O 点处的磁感强度．I II OR 2R解：设半径分别为R 和2R 的两个载流半圆环在O 点产生的磁感强度的大小分别 为B1和B2．O 点总磁感强度为 (方向指向纸内)107. 一无限长的直导线载有如图所示的电流，长度为b 的金属杆CD 与导线共面且垂直，相对位置如图．CD 杆以速度v 平行直线电流运动，求CD 杆中的感应电动势，并判断C 、D两端哪端电势较高？a bI CDv解：建立坐标(略)：，方向⊙感应电动势方向为C→D，D 端电势较高108有电流的I 长直导线附近，放一导体半圆环MeN 与长直导线共面，且端点MN 的连线与长直导线垂直．半圆环的半径为b ，环心O 与导线相距a ．设半圆环以速度 v 平行导线平移，求半圆环内感应电动势的大小和方向以及MN 两端的电压U M U N ．b MNeaI Ov解：动生电动势为计算简单，可引入一条辅助线MN ，构成闭合回路MeNM, 闭合回路总电动势负号表示的方向与x 轴相反．方向N→M109已知一平面简谐波的表达式为 )37.0125cos(25.0x t y -= (SI) (1) 分别求x 1 = 10 m ，x 2 = 25 m 两点处质点的振动方程； (2) 求x 1，x 2两点间的振动相位差； (3) 求x 1点在t = 4 s 时的振动位移． 解：(1) x1 = 10 m 的振动方程为(SI)x2 = 25 m 的振动方程为(SI)(2) x2与x1两点间相位差 Df = f2 - f1 = -5.55 rad (3) x1点在t = 4 s 时的振动位移 y = 0.25cos(125×4－3.7) m= 0.249 m 110 一质点按如下规律沿x 轴作简谐振动：)328cos(1.0π+π=t x (SI)．求此振动的周期、振幅、初相、速度最大值和加速度最大值． 解: 周期 s ， 振幅 A = 0.1 m ， 初相 f = 2p/3，vmax = w A = 0.8p m/s ( = 2.5 m/s )， amax = w 2A = 6.4p2 m/s2 ( =63 m/s2 )．111 图示一平面简谐波在t = 0 时刻的波形图，求(1) 该波的波动表达式；x (m) O-0.040.20 u = 0.08 m/sy (m)P0.400.60(2) P 处质点的振动方程. 解：(1) O 处质点，t = 0 时，所以又(0.40/ 0.08) s= 5 s故波动表达式为(SI)(2) P 处质点的振动方程为(SI)112 如图，一平面波在介质中以波速u = 20 m/s 沿x 轴负方向传播，已知A 点的振动方程为 t y π⨯=-4cos 1032 (SI)．(1) 以A 点为坐标原点写出波的表达式； ABxu (2) 以距A 点5 m 处的B 点为坐标原点，写出波的表达式． 解：(1) 坐标为x 点的振动相位为波的表达式为 (SI)(2) 以B 点为坐标原点，则坐标为x 点的振动相位为(SI)波的表达式为(SI) 113 有一平面电磁波其电场强度为 x E t z ˆe 100)102102(i 62⨯π-⨯π-= （SI ）其中x ˆ是x 方向的单位矢量．（以下计算中，答案中要写明单位） (1) 判断电场的振动方向和波传播的方向． (2) 确定该波的圆频率和波长． (3) 确定该波的波速．(4) 若此波的磁场强度为 yH t z ˆe 25)102102(i 62⨯π-⨯π-π= (SI)(1) 电场强度振动的方向与平行，波传播方向为(2) 圆频率w = 2p×106 Hz = 6.28×106 Hz波长l = 2p / k = 2p / 2p×10-2 = 100 m(3) 波速 u = l / T = w l / 2p = 108 m /s(4) 坡印亭矢量，S0 = 79.6 J？m-2？s-1 平均功率79.6 W （A表示面积）。
第1章常用半导体器件A. B. D.参考答案：CA. B. C. D.参考答案：BA. B. D.参考答案：Cui=10sin tVA. B. C. D.参考答案：CA. B. D.参考答案：D稳定电压与相应电流稳压管端电压变化量UZ与相应电流变化量IZA. B. C. D.参考答案：BA. B. D.参考答案：BA. B. D.参考答案：AA. B. D. 参考答案：BA. B. C. D. 参考答案：C是指A. B. D. 参考答案：BA. B.C.A. B. C. D.A. B. D.参考答案：BA. B. C. D.参考答案：B约A. B. D. 参考答案：CA. B. C. D. 参考答案：AA. B. D. 参考答案：BA. B. D. 参考答案：C.A. B. D. 参考答案：AA.6VB.0VC.0.6VD.5.3VA. B. C. D. 参考答案：AA. B. D.参考答案：CA. B. C. D.参考答案：A确定电压放大倍数A. B. D.参考答案：C管子的值太小电路电源电压太高偏置电阻太小偏置电阻太大A. B. C. D. 参考答案：CA. B. D. 参考答案：CA. B. C. D. 参考答案：AA. B. D.参考答案：AA. B. D.参考答案：BA. B. D.参考答案：B第二级的基极电流随之而改变(..)第二级的静态电流不改变但要改变A. B. C. D.参考答案：BA. B. C. D. 参考答案：CA. B. D. 参考答案：AA. B. C. D. 参考答案：AA. B. D. 参考答案：BA. B. C. D.参考答案：DA. B. D.参考答案：BA. B. C. D.参考答案：AA. B. D.参考答案：CA. B. C. D.参考答案：D.时的输出电压A. B. D.参考答案：DA. B. D. 参考答案：CA. B. D. 参考答案：AA. B. D. 参考答案：AA. B. D. 参考答案：BA. B. C. D. 参考答案：CA. B. D. 参考答案：BA. B. D. 参考答案：CA. B. D. 参考答案：BA. B. D. 参考答案：CB.A. B. D.参考答案：C若将源极旁路电容去掉A. B. C. D.参考答案：B约几十微法大于 C.小得多A. B. D.参考答案：C等于A. C.A. B. D. 参考答案：AA. B. D. 参考答案：BA. B. C. D. 参考答案：AA. B. D. 参考答案：AA. B. D. 参考答案：CA. B. D. 参考答案：AA. B. C. D. 参考答案：BA. B. D. 参考答案：CA. B. C. D.参考答案：C.A. B. C.A. B. D.参考答案：D一个正弦波振荡器的开环电压放大倍数为.A. B. C.A. B. C. D.参考答案：C反馈电压反馈电压反馈电压A. B. D.参考答案：C一个正弦波振荡器的反馈系数.开环电压放大倍数必须等于A. B. C.A. B. C. D.参考答案：C答题： A. B. C. D.A. B. D.参考答案：BA. B. C. D.参考答案：CA. B. D.参考答案：AA. B. C. D.参考答案：B..消耗的功率为A. D.A. B. D.参考答案：BA. B. C. D.A. B. D. 参考答案：CA. B. C. D. 参考答案：CA. B. D.参考答案：A.弦信号A. B. D.参考答案：AA. B. D.参考答案：CA. B. C. D.参考答案：CA. B. D.参考答案：CA. B. C. D.参考答案：A≤0.2sin出A.12sin V C.A. B. D.参考答案：CA. B. C. D.A. B. C. D.参考答案：B静态时电容两端的电压等于A. B. C. D.A. B. C. D.参考答案：BA. B. D.参考答案：B设变压器副边电压有效值为.输出电流平均值为。
大学物理习题答案HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】B 班级 学号 姓名第1章 质点运动学1-2 已知质点的运动方程为r i 3j 6k e e t t -=++。
(1)求：自t =0至t =1质点的位移。
(2)求质点的轨迹方程。
解：(1) ()k j i r 630++= ()k j i r 6e 3e 1-1++=质点的位移为()j i r ⎪⎭⎫⎝⎛-+-=3e31e ∆(2) 由运动方程有t x e =，t y -=e 3， 6=z 消t 得轨迹方程为 1=xy 且6=z1-3运动质点在某瞬时位于矢径()y x,r 的端点处，其速度的大小为( D )(A)dt dr (B)dt d r(C)dt d r (D)22⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛dt dy dt dx1-5某质点的运动方程为k j i r 251510t t ++-=，求：t =0，1时质点的速度和加速度。
解：由速度和加速度的定义得k j r v t dt d 1015+==， k va 10==dtd 所以 t =0，1时质点的速度和加速度为 015==t jv 11015=+=t kj v 1010,ka ==t1-8 一质点在平面上运动，已知质点的运动方程为j i r 2235t t +=，则该质点所作运动为[ B ](A) 匀速直线运动 (B) 匀变速直线运动(C) 抛体运动 (D) 一般的曲线运动*1-6一质点沿Ox 轴运动，坐标与时间之间的关系为t t x 233-=(SI)。
则质点在4s 末的瞬时速度为 142m ·s -1 ，瞬时加速度为 72m ·s -2 ；1s 末到4s 末的位移为 183m ，平均速度为 61m ·s -1 ，平均加速度为 45m ·s -2。
解题提示：瞬时速度计算dt dxv =，瞬时加速度计算22dtx d a =；位移为()()14x x x -=∆，平均速度为()()1414--=x x v ，平均加速度为 ()()1414--=v v a 1-11 已知质点沿Ox 轴作直线运动，其瞬时加速度的变化规律为t a x 3=2s m -⋅。
大学物理（一）练习册 参考解答3. 质点作曲线运动，r 表示位置矢量，v表示速度，a 表示加速度，S 表示路程，a t 表示切向加速度，下列表达式中，(1) a t d /d v ， (2) v t r d /d ， (3) v t S d /d ， (4) t a t d /d v．(A) 只有(1)、(4)是对的． (B) 只有(2)、(4)是对的． (C) 只有(2)是对的． (D) 只有(3)是对的． 答案： (D) 参考解答：质点作曲线运动，应该考虑速度v，加速度a 的矢量性。
注意正确书写矢量公式，例如：.d d ,d d v vtr a t速度和速率是两个不同概念。
前者为矢量，后者为标量；瞬时速度的大小和瞬时速率相同：v t S d /d . 所以只有(3)是对的。
大学物理（一）练习册 参考解答第1章 质点运动学一、选择题1(D)，2(D)，3(B)，4(D)，5(B)，6(D)，7(D)，8(E)，9(B)，10(B)， 二、填空题 (1).1221n (n = 0,1,… ), t A sin 2 (2). 8 m ，10 m. (3). 23 m/s. (4). 16Rt 2(5). 4t 3-3t 2 (rad/s)，12t 2-6t (m/s 2). (6).331ct ，2ct ，c 2t 4/R . (7). 2.24 m/s 2，104o(8).)5cos 5sin (50j t i tm/s ，0，圆. (9). K m x /0max v(10). 02121v v kt三、计算题1. 有一质点沿x 轴作直线运动，t 时刻的坐标为x = 4.5 t 2 – 2 t 3 (SI) ．试求：(1) 第2秒内的平均速度； (2) 第2秒末的瞬时速度； (3) 第2秒内的路程．解：(1) 5.0/ t x v m/s(2) v = d x /d t = 9t - 6t 2, v (2) =-6 m/s. (3) S = |x (1.5)-x (1)| + |x (2)-x (1.5)| = 2.25 m.2. 一质点沿半径为R 的圆周运动．质点所经过的弧长与时间的关系为221ct bt S其中b 、c 是大于零的常量，求从0 t 开始到切向加速度与法向加速度大小相等时所经历的时间．解： ct b t S d /d v c t a t d /d v R ct b a n /2根据题意： a t = a n 即 R ct b c /2解得 cb c R t3. 一质点沿x 轴运动，其加速度为a 4t (SI)，已知t 0时，质点位于x 10 m 处，初速度v 0．试求其位置和时间的关系式．解： a d v /d t 4 t ， d v 4 t d tvv 0d 4d tt t v = 2t 2v d x /d t 2 t 2t t x txx d 2d 020x 2 t 3 /3+x 0 (SI)4. 一物体悬挂在弹簧上作竖直振动，其加速度为 a ky ，式中k 为常量，y 是以平衡位置为原点所测得的坐标. 假定振动的物体在坐标y 0处的速度为v 0，试求速度v 与坐标y 的函数关系式．解： yt y y t a d d d d d d d d v v v v又 a ky ∴ -k y v d v / d yC ky y ky 222121 , d d v v v已知 y y 0 ， v v 0 则 20202121ky C v)(220202y y k v v5. 一飞机驾驶员想往正北方向航行，而风以60 km/h 的速度由东向西刮来，如果飞机的航速（在静止空气中的速率）为 180 km/h ，试问驾驶员应取什么航向？飞机相对于地面的速率为多少？试用矢量图说明．解：设下标A 指飞机，F 指空气，E 指地面，由题可知：v FE =60 km/h 正西方向 v AF =180 km/h 方向未知v AE 大小未知， 正北方向由相对速度关系有： FE AF AE v v vAE v 、 AF v 、EE v 构成直角三角形，可得 km/h 17022 v v v FE AF AE 4.19/tg 1 AE FE v v（飞机应取向北偏东19.4 的航向）．四 研讨题1. 在下列各图中质点M 作曲线运动，指出哪些运动是不可能的？参考解答： (1)、(3)、(4)是不可能的． (1) 曲线运动有法向加速度，加速度不可能为零； (3) 曲线运动法向加速度要指向曲率圆心；(4) 曲线运动法向加速度不可能为零.2. 设质点的运动方程为)(t x x ，)(t y y 在计算质点的速度和加速度时：第一种方法是，先求出22y x r ，然后根据 t d d rv 及 22d d tr a 而求得结果；第二种方法是，先计算速度和加速度的分量，再合成求得结果，即22)d d ()d d (t y t x v 和 222222)d d ()d d (ty t x a .你认为两种方法中哪种方法正确？参考解答：第二种方法是正确的。
