使用Maple键盘命令将曲线拟合
- 格式:doc
- 大小:127.50 KB
- 文档页数:2

Part 7:数据处理西希安工程模拟软件(上海)有限公司,20087.0 介绍本节内容:数据处理,学习如何输入和输出数据,以及使用Maple的统计、可视化、和数据分 析工具。
7.1 输入和输出数据使用交互式工具或命令输入和输出数据。
使用Maple,您可以输入许多格式的数据,以及输出 数据到文件中。
输入数据操作步骤 使用输入数据助手 输入数据文件,支持的格式包括 Excel, MATLAB, 图片,声音,矩 阵,分隔符文件。
例子:从【工具 -> 分析助手】菜 单,选择 输入数据... 读入数据文件 ExcelData.xls(这个 文件位于Maple安装目录下 data/portal 子文件夹)。
选择Excel格式。
依次点击【下一步】,【下一步 】,【下一步】。
您可以添加一个 名称指向该数据,最后点击【完成 】。
输入的数据是数组格式。
现在,使用图形生成器绘制数据对 结果21应的图形。
鼠标右键点击输入的数据,从弹出 的关联菜单中选择【 Plots>Plot Builder】。
点击【 Plot】。
012使用 ExcelTools 程序包 您也可以使用 ExcelTools 程序包中 的命令输入和输出Excel格式的数 据。
例子: 输入Excel文件 ExcelData.xls. 如果文件没有位于当前的文件夹 下,您需要输入数据文件的完整路 径。
在这里,数据文件位于Maple安装 目录下面的 data/portal 子文件夹 中。
命令 kernelopts(datadir) 返回 数据文件夹的路径,然后用 cat 命 令将两个字符串串联组成数据文件 的完整路径。
60 返回和检查第一行数据。
返回数组中元素的个数。
"C:\Program Files\Maple 13\data/portal/ExcelData.xls" (2.1.1)(2.1.2)(2.1.3) (2.1.4)(2.1.4)使用 plots[pointplot] 画出数据的图 形。

Matlab中的曲线拟合方法引言在科学与工程领域,数据拟合是一个重要的技术,可用于分析实验数据、预测未知的对应关系,并量化观察到的现象。
其中,曲线拟合是一种常见的数据拟合方法,而Matlab作为一种功能强大的科学计算软件,提供了多种曲线拟合工具和函数,方便用户进行数据分析和模型建立。
本文将对Matlab中的曲线拟合方法进行详细介绍和讨论。
一、线性拟合线性拟合是最简单且常见的曲线拟合方法,其基本思想是通过一条直线拟合数据点,找到最佳拟合直线的参数。
在Matlab中,可以使用polyfit函数实现线性拟合。
该函数接受两个输入参数,第一个参数为数据点的x坐标,第二个参数为数据点的y坐标。
返回结果为一个一次多项式拟合模型的参数。
例如,我们有一组实验测量数据如下:x = [1, 2, 3, 4, 5];y = [3, 5, 7, 9, 11];通过polyfit函数进行线性拟合:coeff = polyfit(x, y, 1);其中,1表示要拟合的多项式的次数,这里我们选择了一次多项式(直线)。
coeff即为拟合得到的直线的参数,可以通过polyval函数将参数代入直线方程,得到对应x的y值。
y_fit = polyval(coeff, x);接下来,我们可以使用plot函数将原始数据点和拟合曲线都绘制在同一张图上:figure;plot(x, y, 'o', 'MarkerSize', 10); % 绘制原始数据点hold on;plot(x, y_fit); % 绘制拟合曲线xlabel('x');ylabel('y');legend('原始数据点', '拟合曲线');通过观察图像,我们可以初步判断拟合的效果如何。
如果数据点较为分散,直线拟合效果可能较差。
在此情况下,可以考虑使用更高次的多项式进行拟合。
二、多项式拟合多项式拟合是一种常见的曲线拟合方法,其基本思想是通过一个一定次数的多项式函数来拟合数据点。
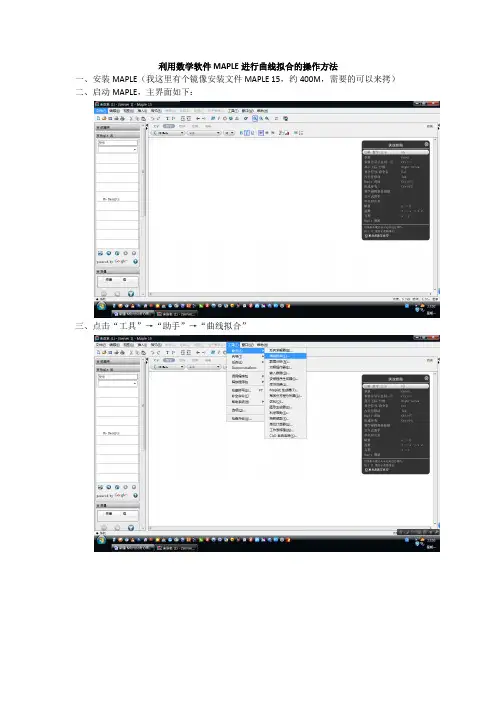
利用数学软件MAPLE进行曲线拟合的操作方法
一、安装MAPLE(我这里有个镜像安装文件MAPLE 15,约400M,需要的可以来拷)
二、启动MAPLE,主界面如下:
三、点击“工具”→“助手”→“曲线拟合”
弹出如下界面,填入数值,第一列是X的值,第二列是Y的值,
然后点击按钮“Fit”,弹出如下界面:
四、点击上图中红色部分按钮“Plot”,即可生成曲线,如下图所示:
图中,
区域2:调节曲线的圆滑度,数值8最圆滑最贴近;
区域3:可以选择进行几次多项式的拟合,如二次、三次、四次等等,注意表达式的书写方式,如三次表达式为a*x^3 + b*x^2 + c*x + d,四次表达式为a*x^4 + b*x^3 + c*x^2 + d*x +e,以此类推;
区域4:显示所指定次数多项式最终拟合曲线的函数表达式。
(此式便可以用来计算刘星老师所布置的不同温度下的吉布斯自由能)。
默认显示最贴近的拟合函数。
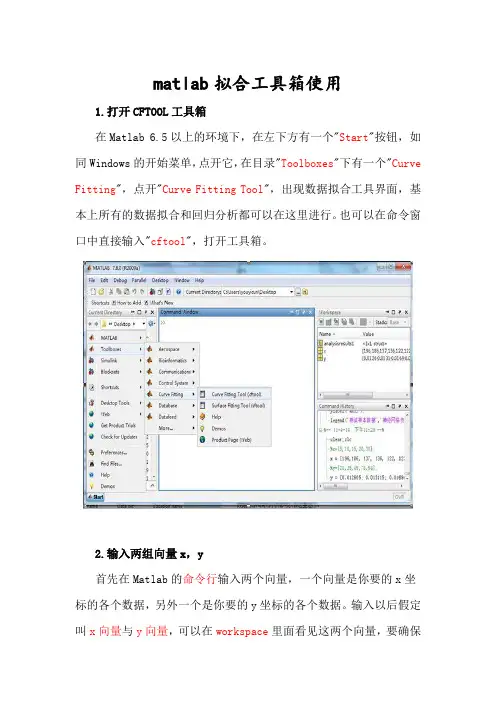
matlab拟合工具箱使用1.打开CFTOOL工具箱在Matlab 6.5以上的环境下,在左下方有一个"Start"按钮,如同Windows的开始菜单,点开它,在目录"Toolboxes"下有一个"Curve Fitting",点开"Curve Fitting Tool",出现数据拟合工具界面,基本上所有的数据拟合和回归分析都可以在这里进行。
也可以在命令窗口中直接输入"cftool",打开工具箱。
2.输入两组向量x,y首先在Matlab的命令行输入两个向量,一个向量是你要的x坐标的各个数据,另外一个是你要的y坐标的各个数据。
输入以后假定叫x向量与y向量,可以在workspace里面看见这两个向量,要确保这两个向量的元素数一致,如果不一致的话是不能在工具箱里面进行拟合的。
例如在命令行里输入下列数据:x = [196,186, 137, 136, 122, 122, 71, 71, 70, 33];y = [0.012605; 0.013115; 0.016866; 0.014741; 0.022353;0.019278; 0.041803; 0.038026; 0.038128; 0.088196];3.选取数据打开曲线拟合共工具界面,点击最左边的"Data..."按钮,出现一个Data对话框,在Data Sets页面里,在X Data选项中选取x向量,Y Data选项中选取y向量,如果两个向量的元素数相同,那么Create data set按钮就激活了,此时点击它,生成一个数据组,显示在下方Data Sets列表框中。
关闭Data对话框。
此时Curve Fitting Tool窗口中显示出这一数据组的散点分布图。
4.拟合曲线(幂函数power)。
点击Fitting...按钮,出现Fitting对话框,Fitting对话框分为两部分,上面为Fit Editor,下面为Table of Fits,有时候窗口界面比较小,Fit Editor部分会被收起来,只要把Table of Fits 上方的横条往下拉就可以看见Fit Editor。

matlab曲线拟合函数的具体步骤编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(matlab曲线拟合函数的具体步骤)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为matlab曲线拟合函数的具体步骤的全部内容。
matlab曲线拟合函数的具体步骤是什么1、在命令行输入数据:2、启动曲线拟合工具箱》cftool3、进入曲线拟合工具箱界面“Curve Fitting tool"(1)点击“Data”按钮,弹出“Data”窗口;(2)利用X data和Y data的下拉菜单读入数据x,y,可修改数据集名“Data set name”,然后点击“Create data set”按钮,退出“Data”窗口,返回工具箱界面,这时会自动画出数据集的曲线图;(3)点击“Fitting”按钮,弹出“Fitting"窗口;(4)点击“New fit”按钮,可修改拟合项目名称“Fit name”,通过“Data set"下拉菜单选择数据集,然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:Custom Equations:用户自定义的函数类型Exponential:指数逼近,有2种类型, a*exp(b*x)、 a*exp(b*x) + c*exp(d*x)Fourier:傅立叶逼近,有7种类型,基础型是 a0 + a1*cos(x*w) + b1*sin(x*w)Gaussian:高斯逼近,有8种类型,基础型是 a1*exp(—((x—b1)/c1)^2) Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape—preservingPolynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~Power:幂逼近,有2种类型,a*x^b 、a*x^b + cRational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4—5th degree ~;此外,分子还包括constant型Smoothing Spline:平滑逼近(翻译的不大恰当,不好意思)Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是 a1*sin(b1*x+ c1)Weibull:只有一种,a*b*x^(b-1)*exp(—a*x^b)选择好所需的拟合曲线类型及其子类型,并进行相关设置:——如果是非自定义的类型,根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数;——如果选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口。

matlab curve fitting tool拟合方式-回复本文将详细介绍MATLAB的曲线拟合工具(curve fitting tool)以及其使用方式。
我们将按照一步一步的方式,逐个回答以下问题:1. 什么是MATLAB的曲线拟合工具?MATLAB的曲线拟合工具是一个强大的数学分析工具,可以帮助用户找到给定数据集最佳拟合曲线的参数。
该工具可以适用于各种类型的曲线拟合问题,包括多项式、指数、对数、幂函数等。
用户可以使用该工具来分析数据,并根据需要进行曲线拟合和预测。
2. 如何打开curve fitting tool?要打开MATLAB的曲线拟合工具,可以通过在MATLAB命令窗口中输入"curve fitting"命令或者直接在主菜单中选择"APPS"->"Curve Fitting"。
这将打开一个新窗口,显示曲线拟合工具的界面。
3. 如何导入数据进行曲线拟合?要导入数据进行曲线拟合,可以选择"File"菜单中的"Import Data"选项。
这将打开一个对话框,允许您选择要导入的数据文件(例如,CSV、TXT 等)。
MATLAB将自动将这些数据加载到曲线拟合工具中。
4. 如何选择拟合的曲线类型?在曲线拟合工具界面的"Fit"选项卡中,有一个"Type"下拉菜单,用于选择拟合的曲线类型。
您可以从多项式、指数、对数、幂函数等类型中选择,并根据需要指定曲线的阶数。
5. 如何调整拟合算法和参数?在曲线拟合工具界面的"Fit Options"选项卡中,您可以调整拟合算法和参数。
例如,您可以选择最小二乘法或非线性最小二乘法等拟合算法。
您还可以设置拟合的约束条件和起始点,并选择是否启用权重等。
6. 如何进行曲线拟合和显示结果?在曲线拟合工具界面的"Fit"选项卡中,点击"Fit"按钮即可进行曲线拟合。

Part 7:数据操作西希安工程模拟软件(上海)有限公司,20087.0 介 绍本节内容:数据处理,学习如何输入和输出数据,以及使用Maple的统计,可视化,和数据分析工具.7.1 输入和输出数据使用交互式工具或命令输入和输出数据.使用Maple,您可以输入许多格式的数据,以及输出数据到文件 中.输入数据操作步骤 使用输入数据助手 输入数据文件,支持的格式包括 Excel, MATLAB, 图片,声音,矩阵,分隔符文 件. 例子:从 工具 -> 分析助手 菜单,选择 输入数据... 读入数据文件 ExcelData.xls(这个文件位 于Maple安装目录下 data/portal 子文件 夹). 选择Excel格式. 点击下一步,然后确认. 数据以数组格式输入. 使用图形生成器画出数据的图形. 鼠标右键点击输入的数据,从弹出的关 联菜单中选择 Plots>Plot Builder. 点击 Plot. 结果21012使 用 ExcelTools 程序包中的命令 您也可以使用 ExcelTools 程序包中的命 令输入和输出Excel格式的数据. 例子: 输入Excel文件 ExcelData.xls. 如果文件没有位于当前的文件夹下,您 需要输入数据文件的完整路径. 在这里,数据文件位于Maple安装目录下 面的 data/portal 子文件夹中.命令 kernelopts(datadir) 返回数据文件夹的路 径,然后用 cat 命令将两个字符串串联组 成数据文件的完整路径."C:\Program Files\Maple 13\data/portal/ExcelData.xls"(2.1.1)(2.1.2)返回和检查第一行数据. 返回数组中元素的个数.(2.1.3) 60 (2.1.4)使用 plots[pointplot] 画出数据的图形.(2.1.4)21012使 用readdata命 令 readdata 命令从文本文件中读入数值数 据. 调用格式是 readdata("fileID", n), 这里 n 是数据的列数. readdata 的输出是一个列表,因此可以使 用列表选择命令查看中 Data1 的项. 然后对数据绘图."C:\Program Files\Maple 13\data/portal/DataP2.dat"(2.1.5)3938(2.1.6) (2.1.7) (2.1.8)(2.1.8)60 50 40 30 20 10 0ImportMatrix 命令读入数据文件的方式 类似于 readdata 命令,但是 ImportMatrix 的输出是一个矩阵,而不是一个列表.(2.1.9)60 50 40 30 20 10 0输出数据操作步骤 结果输出一个Excel文 件 使用 ExcelTools 输出文件.默认情况 下,文件被输出到当前文件夹. 使用可以 currentdir() 显示当前文件路 径.作为实验,输入文件的前面10行到Maple 中.(2.2.1)输出一个文本文件 writedata 命令将数据写入到一个文本文 件. 调用格式:writedata(fileID,data,format) 这里,fileID是输出的数据文件名称,data 是数据自身,format 是数据写入的格式. 格式的可选参数可以是 integer,float,或 string. 例子: 创建一个列表,使用 seq 命令填入数据 项. 写入数据到文件中. 作为实验,输入一个数据文件到Maple 中.(2.2.2)(2.2.3)7.2 随机分布操作步骤 使用 rand 命令生成一个数据数. 最简单的调用格式生成一个随机的12位正 结果(3.1)整数. rand(a..b) 调用格式返回一个程序,可以生 成介于 a 和 b 之间的数. 为了确保代码每次运行时生成不同的程 序,使用 randmonize 命令重新置入随机数 生成器的种子. 例子: 生成一个介于 -10 到 10 之间的随机数. RandomTools 程序包提供了许多工具和算 法用于生成随机数和随机对象,rand 命令 是一个面向这个程序包的简单方式.395718860534(3.1)9(3.2) (3.3)6(3.4)Maple 内置的 Statistics 程序包提供了大量 的连续和离散分布,可用于生成随机数. 在使用这些分布前,首先需要加载 Statistics 程序包. 例子: 使用平均值为5,标准差为1的正态分布, 生成100个随机数._R(3.5)创建样本数据的线图. 鼠标右击生成的数据.从关联菜单中选择 Statistics>Visualization>Histogram. 预览图形后,点击 Quit 返回柱状图到文件 中.histogram(3.6)034567您也可以使用分布生成一个随机数生成 器. 这里,X1 是一个程序,以 n 为参数,n 是 生成随机数的个数.(3.7)每次使用 X1,它会生成新的随机数.(3.8)(3.9) (3.10)例子: 使用 X1(10) 生成10个随机数,然后使用 LineChart命令创建数据的线图.(3.11)(3.11)765 1 2 3 4 5 6 7 8 9 10Data7.3 统计,回归,和曲线拟合基础工具操作步骤 使用Maple,您可以非常容易使用统计工具,曲线 拟合,回归分析. 您可以直接通过右键菜单使用许多有用的命令. 统计操作 对于一维数组,矢量,或列表,亡灵鼠标右击数 据时,右键菜单将包含统计操作菜单.在 Statistics 下有子目录 Data Manipulation, Quantities, Summary and Tabulation, 和 Visualization 提供了许 多统计操作命令. 例子: 定义如下的列表.鼠标右击输出,选择 Statistics > Quantities > Mean. 结果(4.1.1)mean2.498510331也可从右键菜单中进入曲线拟合助手. 例子: 在这个例子中,我们首先列出数据对. 鼠标右击数据,从右键菜单中选择 Curve Fitting. 选择 Curve Fitting>Interactive Curve Fitting.弹出 定义变量名对话框,点击确认.打开曲线拟合助 手,交互式使用Maple的曲线拟合命令.curve fitting assistant(4.1.2)您可以选择曲线的类型,并预览结果. 函数显示在图形的下方. 选择Splines曲线,然后选择对应的Plot按钮. 您可以选择是否返回插值函数或图形.在窗口左 下侧的下拉菜单,将选项从 Interpolant 改为 Plot. 然后点击完成.11 9 7 5 3 0 1 2 x 3 4 5使用命令进入曲线拟合助手. 例子: 使用前面段落中的数据集合. 1. 输入命令"CurveFitting[Interactive](DataSet)", 打开曲线拟合助手. 2.3.2 1噪音信号信号102 4Noisy SignalFitted Modelx10。

数学软件Maple使⽤教程数学实验数学软件Maple使⽤教程序⾔⼀.什么是数学实验?我们都熟悉物理实验和化学实验,就是利⽤仪器设备,通过实验来了解物理现象、化学物质等的特性。
同样,数学实验也是要通过实验来了解数学问题的特性并解决对应的数学问题。
过去,因为实验设备和实验⼿段的问题,⽆法解决数学上的实验问题,所以,⼀直没有听说过数学实验这个词。
随着计算机的飞速发展,计算速度越来越快,软件功能也越来越强,许多数学问题都可以由计算机代替完成,也为我们⽤实验解决数学问题提供了可能。
数学实验就是以计算机为仪器,以软件为载体,通过实验解决实际中的数学问题。
⼆.常⽤的数学软件⽬前较流⾏的数学软件主要有四种:1.MathACD其优点是许多数学符号键盘化,通过键盘可以直接输⼊数学符号,在教学⽅⾯使⽤起来⾮常⽅便。
缺点是⽬前仅能作数值运算,符号运算功能较弱,输出界⾯不好。
2.Matlab优点是⼤型矩阵运算功能⾮常强,构造个⼈适⽤函数⽅便很⽅便,因此,⾮常适合⼤型⼯程技术中使⽤。
缺点是输出界⾯稍差,符号运算功能也显得弱⼀些。
不过,在这个公司购买了Maple公司的内核以后,符号运算功能已经得到了⼤⼤的加强。
再⼀个缺点就是这个软件太⼤,按现在流⾏的版本5.2,⾃⾝有400多兆,占硬盘空间近1个G,⼀般稍早些的计算机都安装部下。
我们这次没⽤它主要就是这个原因。
3.Mathematica其优点是结构严谨,输出界⾯好,计算功能强,是专业科学技术⼈员所喜爱的数学软件。
缺点是软件本⾝较⼤,⽬前流⾏的3.0版本有200兆;另⼀个缺点就是命令太长,每⼀个命令都要输⼊英⽂全名,因此,需要英语⽔平较⾼。
4.Maple优点是输出界⾯很好,与我们平常书写⼏乎⼀致;还有⼀个最⼤的优点就是它的符号运算功能特别强,这对于既要作数值运算,⼜要作符号运算时就显得⾮常⽅便了。
除此之外,其软件只有30兆,安装也很⽅便(直接拷贝就可以⽤)。
所以,我们把它放到学校⽹上直接调⽤。

Maple教程Maple是一款强大的数学软件,它被广泛用于科学研究、工程设计、教育等领域。
本教程将为你介绍Maple的基本使用方法和一些常用功能,帮助你快速上手和利用Maple解决数学问题。
一、Maple的安装与启动1. 安装MapleMaple的安装非常简单,你只需要从官方网站下载Maple 的安装程序,然后按照提示进行安装即可。
2. 启动Maple安装完成后,你可以在桌面或开始菜单中找到Maple的启动图标,双击它即可启动Maple。
二、Maple的基本功能1. Maple的界面Maple的界面非常直观和友好,主要包括以下几个部分:•菜单栏:包含了各种功能和工具的菜单选项;•工具栏:提供了常用功能的快捷操作按钮;•输入框:可以输入和编辑Maple代码;•输出区:显示Maple执行代码的结果。
2. Maple的基本操作在Maple中,你可以通过输入和执行代码来完成各种数学运算和数据处理。
下面是一些常用的基本操作方法:•输入代码:在输入框中输入Maple代码,然后按下回车键执行;•注释代码:使用#符号可以在代码中添加注释,注释的内容将被忽略;•查看帮助:通过菜单栏的帮助选项或使用?键,可以查看Maple的帮助文档和函数说明。
3. Maple的数学计算Maple支持各种数学计算,包括基本运算、符号计算、数值计算等。
下面是一些常用的数学计算方法:•基本运算:Maple可以进行各种基本运算,如加减乘除、幂运算、取余等;•符号计算:Maple可以处理符号表达式,进行符号计算、方程求解、微分积分等;•数值计算:Maple可以进行数值计算,如数值积分、方程数值求解、函数拟合等。
三、Maple的扩展功能除了基本功能外,Maple还提供了许多强大的扩展功能,帮助用户进行更复杂的数学运算和数据处理。
1. 绘图功能Maple具有强大的绘图功能,可以绘制各种类型的图形,如曲线图、散点图、三维图等。
你可以使用Maple提供的绘图函数来创建自定义的图形,并对图形进行样式设置。

文章标题:深度剖析MATLAB绘图中的曲线拟合技术1. 引言在MATLAB中,绘图是一项常见的任务,而曲线拟合则是其中一个重要的技术。
本文将深入剖析MATLAB中的曲线拟合技术,探讨其原理、应用和优缺点。
2. 曲线拟合的基本概念曲线拟合是一种数学方法,旨在找到最符合一组数据点的曲线或函数。
在MATLAB中,可以使用多种方法进行曲线拟合,如最小二乘法、多项式拟合和样条插值等。
曲线拟合可以帮助我们分析数据的趋势和规律,从而更好地理解数据背后的规律和关系。
3. MATLAB中的曲线拟合方法在MATLAB中,可以使用fit函数或polyfit函数来进行曲线拟合。
fit函数可以拟合各种类型的曲线,包括线性、指数、幂函数等,而polyfit函数则主要用于多项式拟合。
MATLAB还提供了一些其他的拟合函数,如lsqcurvefit、nlinfit等,可以根据需要选择合适的方法进行曲线拟合。
4. 深度探讨MATLAB中的曲线拟合技术4.1 曲线拟合的原理曲线拟合的基本原理是通过最小化拟合曲线与实际数据之间的误差,找到最优的拟合曲线。
在MATLAB中,可以通过调整拟合函数的参数、添加约束条件等方式来改善拟合效果。
4.2 曲线拟合的应用曲线拟合在MATLAB中有着广泛的应用,包括数据分析、趋势预测、信号处理等领域。
通过曲线拟合,可以更好地理解数据的规律,预测未来的趋势,并对数据进行合理的处理和分析。
4.3 曲线拟合的优缺点曲线拟合的优点在于能够对数据进行较好的拟合和分析,可以帮助我们直观地理解数据的规律和特点。
但是,曲线拟合也存在着局限性,比如对异常值敏感,需要谨慎选择拟合方法和参数,以及需要充分理解数据的特点和背景。
5. 个人观点和理解通过对MATLAB中曲线拟合技术的深度剖析,我深刻认识到曲线拟合在数据分析中的重要性和应用价值。
在实际应用中,需要充分理解曲线拟合的原理和方法,灵活选择合适的拟合函数和参数,以提高数据分析的准确性和可靠性。

曲线拟合方法在MATLAB中的应用本篇文章主要介绍了曲线拟合方法在MATLAB中的应用,包括曲线拟合的基本原理、MATLAB中的曲线拟合工具箱、曲线拟合的步骤以及应用实例。
通过本篇文章的学习,读者可以掌握曲线拟合方法在MATLAB中的应用,为解决实际问题提供有力支持。
曲线拟合方法在MATLAB中的应用曲线拟合是数学中常见的一种数据处理方法,通过拟合曲线可以更好地描述数据之间的关系。
在科学研究和工程实践中,曲线拟合方法的应用非常广泛。
MATLAB作为一种常用的数学软件,提供了强大的曲线拟合工具箱,使得曲线拟合变得更加方便和简单。
一、曲线拟合的基本原理曲线拟合是指通过寻找一条曲线,使得这条曲线尽可能地贴近原始数据点。
在数学上,曲线拟合可以表示为一个方程组,即要求解一个多元非线性方程组。
通过最小二乘法等方法,可以求得最优解,即拟合曲线。
二、MATLAB中的曲线拟合工具箱MATLAB中的曲线拟合工具箱提供了多种拟合方法,包括线性回归、非线性回归、多项式拟合等。
用户可以根据需要选择不同的拟合方法,并进行参数调整和优化。
通过工具箱提供的可视化工具,可以直观地观察拟合结果,并进行相应的调整。
三、曲线拟合的步骤1. 准备数据:将原始数据导入MATLAB中,并进行必要的预处理,如去除异常值、标准化等。
2. 选择拟合方法:根据数据的特点和需求选择合适的拟合方法,如线性回归、非线性回归、多项式拟合等。
3. 拟合曲线:使用所选的拟合方法进行曲线拟合,得到拟合曲线和参数。
4. 可视化结果:使用MATLAB中的可视化工具,将原始数据和拟合曲线可视化展示出来。
5. 结果分析:根据可视化结果和拟合参数进行分析,得出结论。
四、应用实例1. 股票价格预测:通过收集股票历史价格数据,使用曲线拟合方法预测未来价格趋势。
2. 气象数据分析:通过收集气象数据,使用曲线拟合方法分析气温、湿度等因素之间的关系。
3. 生物医学研究:通过曲线拟合方法分析基因序列与蛋白质结构之间的关系。
Maple⼆维曲线图命令介绍
Maple⼆维曲线图命令介绍
Maple作图的功能很强⼤且界⾯简单直观,能够对图形进⾏修改。
并且Maple作图可以作出平⾯图也可以作出⽴体图,下⾯介绍⼀些常见的Maple⼆维曲线图的命令。
参数⽅程曲线:
plot([x(t),y(t),t=t1..t2],x=a..b,y=c..d,选项);
动画曲线:
动画曲线不是基本作图命令,必需先调⼊图形包,才能运⾏。
Aninate(f(x,t),x=a..b,t=t1..t2,选项);其中t为参数
当点击动画图后,会显⽰动画按钮,由按钮控制动画。
极坐标:
注:如果函数由f:=proc(x)定义,作图由plot(f)或plot(f,a..b)或plot(f(x),x=a..b)
多边形及填⾊:polygon([顶点坐标],颜⾊)要调⽤图形⼯具包
曲边梯形⾯积:y=sin(x),y=0,x=π/2所围图形⾯积。
隐函数图:implicitplot(⽅程,范围,选项);
注:⼆元⽅程为平⾯曲线,没有等号默认为等于0。
以上内容向⼤家介绍了常见的Maple⼆维曲线图的命令及调⽤格式,Maple不仅可以绘制⼆维图形,三维也可以。
maple的用法Maple是一款强大的数学软件,用于符号演算、数值计算、可视化和编程。
它是由加拿大滑铁卢大学开发的,自1980年发布以来一直是学术和工业中最广泛使用的数学软件之一。
Maple 在计算带有基于数学的问题方面有着广泛的用途,包括专业的科学计算、数学教育、科研开发等等。
本文将解释Maple的用法和功能。
1.符号演算Maple是一种强大的符号数学软件。
它可以用来计算各种基本数学问题,如代数、微积分、线性代数等。
您可以使用Maple进行代数计算,包括解方程、化简式子、展开式子和约分式子。
Maple具有强大的微积分功能,例如求导,积分,极限和级数计算。
它还可以用于线性代数,例如矩阵和向量计算,和解线性方程组。
2.数值计算Maple具有许多数值计算功能,可以用于对数值问题进行模拟。
Maple可以用于数值解决方案,包括求根、求极值、数值积分、微分方程等。
它还可以用于数据分析,例如拟合数据,统计分析,和数据可视化等。
3.可视化Maple具有强大的可视化功能。
它可以用来可视化基本数学问题,如曲面、曲线和方程。
Maple还可以生成2D和3D图像,包括函数图形、散点图形和轮廓图形等。
Maple 还具有可编程图形的功能,使用户可以从数据计算中生成定制的绘图。
4.编程Maple有自己的编程语言,Maple语言。
Maple的编程主要运用于算法的开发和优化,和自定义的函数和程序。
Maple 的程序也被广泛应用,用于大规模的数值计算,分析和模拟等等。
5. Maple的优势Maple具有强大的符号演算能力,支持复杂数学问题的求解,大大减轻了数学工作的负担。
它还拥有大量的数值计算工具,可以用于模拟和验证数学模型。
Maple 具有可视化功能,让用户可以直观的了解数学问题。
Maple还有一个丰富的社区,用户可以在社区中获得支持和帮助。
综合而言,Maple是一个多功能的数学软件,可用于解决符号和数值问题,以及数据分析和可视化等。
Maple中基本函数指令Maple用法Maple 函数用法一、基本命令重新开始:restart 命名:名字:= 引用前值:% 字符连接:|| 保护命名:protect 解除保护命名:unprotrct 变量类型:whattype 检验命名:assigned 别名:alias 宏:macro 帮助:?函数名 map 把命令作用到每一个元素,seq 生成序列,add 生成和,mul 生成积二、基本运算1. 近似计算:evalf(表达式,小数位数),用 Digits 命令提前设定小数位数2. 取整运算:round 四舍五入,trunc 向 0 取整, ceil 向-∝取整,floor 向∝取整3. 范围限定:assume(限定变量范围)frac 小数部分4. 绝对值(模):abs(表达式),复数求其模5. 同余:mod(数 1,数 2),或者:数 1 mod 数 26. 平方根:sqrt(表达式),平方根最接近整数:isqrt(表达式)7. 阶乘:factorial(数),双阶乘:doublefactorial(数)8. 分解质因数:ifactor(数),分解质因数成组 ifactors(数)9. 商与余数:商iquo(除数,被除数),余数irem(除数,被除数)10.最大公约数:igcd(数1,数2),最小公倍数:ilcm(数1,数 2)11.形如 as+bt=(a,b)分解:igcdex(a,b,’s’,’t’)12.数组最大最小值:max(数1,数2,…),min(数1,数2,…)13.实部、虚部与幅角:实部Re(复数),虚部Im(复数),幅角 argument14.共轭复数:conjugate(复数)15.形如 a+bi 整理:evalc(表达式)16.并集:集合 1 union 集合 2,交集:intersect,差集:minus17.元素个数:nops(集合),用 op 可把集合转化成表达式三、多项式1. 降幂排列:sort(多项式),字典排序 plex(第三个参数)2. 次数:degree(多项式),系数:coeff(多项式,项),首项系数:lcoeff 尾项系数:tcoeff,所有系数:coeffs(多项式,变量,‘power‘)3. 合并同类项:collect(多项式,合并参数)4. 商式:quo(除式,被除式,变量),余式:rem,整除检验:divide5. 最大公因式:gcd(多项式 1,多项式 2),最小公倍式 lcm6. 因式分解:factor(多项式),可用第二个参数限定数域缺省代表有理数域7. 分母有理化:rationalize(多项式),有理分式化简:normal 或者 factor8. 化简表达式:simplify,带假设化简:simplify(表达式,assume=范围)附加关系化简:simplify(表达式,{条件})代换:subs(条件,表达式)9. 展开与合并:展开 expand(表达式),合并 combine(表达式)10.等价转换:convert(函数,转化成的函数)四、解方程1. 方程(组):solve({方程(组)},{未知量(缺省对所有变量求解})2. 数值解:fsolve(方程,变量范围(可缺省),数域(可缺省))3. 三角方程:添加_EnvAllSolutions:=ture 以求得所有解4. 多项式方程解的区间:realroot(多项式)5. 不等式(组):solve({不等式(组)},{变量})6. 整数解:isolve(方程,变量)7. 模 m 的解:msolve(方程,模 m)8. 递推关系的通项:rsolve({递推关系,初值},{通项})9. 函数方程:solve(函数方程,函数)10.系数匹配:match(式子 1=式子 2,变量,’s’)11.Grobner 基原理:先调用 with(grobner),此命令将方程的解等价化简 Gsolve ({式子 1,式子 2,…},[变量 1,变量 2,…]12.微分方程:dsolve({方程,初值(可缺)},函数,’explicit’(可缺))13.微分方程组:dsolve({方程 1、2,…,初值},{函数 1,函数2,…})14.拉普拉斯变换法:dsolve({微分方程},函数,method=laplace)15.微分方程级数解:dsolve({微分方程},函数,type=series)16.微分方程数值解:dsolve({微分方程},函数,type=numeric)17.微分方程图形解:DEplot 图形表示微分方程,dfielplot 箭头表示向量场,phaseportrait 向量场及积分曲线,DEplot3d 三维空间图形表示微分方程18.偏微分方程:pdsolve(偏微分方程,求解函数)19.分离变量解偏微分方程:pdsolve(方程,函数,HINT=’*’,’build’)20.偏微分方程图形解:PDEplot(方程,函数,ini 边界s,s 范围)五、数据处理1. 统计软件包:先调用程序包with(stats) ,有7 个子包:anova 方差分析, describe 描述数据分析,fit 拟合回归分析,transform 数据形式变换, random 分布产生随机数,statevalf 分布的数值计算,statplots 统计绘图2. 基本命令:平均值mean,方差variance,标准差standarddeviation,中位数median,众数mode,数据求和sumdata,协方差 covariance,相对标准差(标准差/平均值)coefficientofvariation,计数(非缺失)count,计缺失数countmissing,范围range,几何平均值geometricmean,线性相关数 linearcorrelation3. 统计图形:直方图 histogram,散点图 scatter2d、quantile2(先从小到大排序再作图),箱式图 boxplot4. 统计分布函数值:正态分布随机分布命令 normald[期望,方差] 先调用程序包 with (statevalf)用法 statevalf(分布函数,求解函数)连续分布:cdf 累积密度函数,icdf 逆累积密度函数,pdf 概率密度函数离散分布:dcdf 离散累积概率函数,idcdf 逆离散累积函数,pf 概率函数5. 插值插值:整体插值命令f:=interp(数据1,数据2,变量)分段插值命令 f:=spline(数据 1,数据 2,变量,次数)6. 回归回归:leastsquare[[x,y],y=多项式,{多项式系数}]([数据1,数据 2])f:=fit(数据 1,数据 2,拟合函数,变量)六、微积分1. 函数定义:函数名:=->表达式,复合函数:f(g(x):=f@g )2. 表达式转换成函数:unapply(表达式,函数变量)3. 极值:极大值maximize(函数,变量,范围,location=true (极值点))极小值minimize(函数,变量,范围,location=true (极值点))条件极值:extreme(函数,约束条件,{变量},’s’(极值点))4. 极限:limit(函数,x=趋值,方向(省缺,left,right,complex))5. 连续性:判断iscont(函数,x=范围)第三个参数closed 表示闭区间求解 discont (函数,变量)6. 微分:显函数 diff(函数,变量)对 x 多次求导用 x$n 微分算子 D 隐函数implicitdiff(函数,依赖关系 y(x),对象 y,变量 x)7. 切线作图:showtangent(函数,x=点,view=[x 范围,y 范围])8. 不定积分:int(函数,积分变量),定积分:int(函数,x=下限..上限)9. 复函数积分:先求奇点solve(denom(函数)),再用留数规则求解 2*Pi*I(residue(f,z=奇点 1)+ residue(f,z=奇点 2)+…)10.定积分矩形:下矩形:作图 leftbox(f,x=范围,块数)面积leftsum (f,x=范围,块数)。
maple画图命令1 二维图形制作Maple所提供的二维绘图指令plot可以绘制二维的函数图、参数图、极坐标图、等高线图、不等式图,等等. 这些绘图指令有些已经内嵌在其核心程序里, Maple启动时即被装入,直接调用函数命令即可,有些则需要使用with(plots)调用plots函数库才能完成.1.1 基本二维绘图指令plot (f(x), x=xmin .. xmax);plot (f(x), x=xmin .. xmax, y=ymin .. ymax);plot ([f1(x), f2(x), …], x=xmin .. xmax);plot (f(x), x=xmin .. xmax, option);其中,xmin..xmax为x的变化范围,ymin..ymax为y(即f(x))的变化范围. option选项参数主要有:axes:设定坐标轴的显示方式, 一般有FRAME(坐标轴在图形的左边与下面)、BOXED(坐标轴围绕图形)、NORMAL(一般方式显示)或NONE(无)color:设定图形所要涂的颜色(可选用也可自设)coords:指定绘图时所用的坐标系(笛卡尔坐标系(cartesian,默认)、极坐标系(polar)、双极坐标系(bipolar)、logarthmic(对数坐标系)等discont:设定函数在不是否用线段连接起来(discont=true则不连接, 默认是discont=false) labels:设定坐标轴的名称(labels=[x, y], x与y分别为x与y坐标轴的名称)linestyle:设定所绘线条的线型(linestyle=n, n为1是实线, 2为点, 3为虚线, 4为虚线与点交错)numpoints:设定产生一个函数图形所需的最少样点scaling:设置x与y轴的比例(unconstrained非约束,constrained约束,比例为1:1)style:设定图形的显示样式(LINE(线形)、POINT(点)、PATCH(显示多边形与边线)、PA TCHNOGRID(只显示色彩而无边界) symbol:设定点的格式(主要有BOX(方块)、CROSS(十字)、CIRCLE(圆形)、POINT(点)、DIAMOND(菱形)等几项)thickness:设定线条的粗细(0、1、2、3几种参数, 数值越大线条越粗)tickmarks:设定坐标轴刻度的数目(设定tickmarks=[m, n], 则x 轴刻度为m, y轴为n)title:定义图形的标题(要用" "把标题引起来)view:设定屏幕上图形显示的最大坐标和最小坐标,缺省是整个曲线下面通过一些实例学习:> plot(sin(1/x),x=-0.1..0.1,title="y=sin(1/x)",axes=normal);> plot(1/(2*sin(x)),x=-10..10,y=-30..30);试比较下述三图的效果:> plot(tan(x),x=-2*Pi..2*Pi);> plot(tan(x),x=-2*Pi..2*Pi, y=-5..5);> plot(tan(x),x=-2*Pi..2*Pi, y=-5..5,discont=true);(此处命令discont=true的作用是去除垂直渐近线)> plot(sin(cos(6*x))/x, x=0..15*Pi, y=-0.6..0.5, axes=NONE);> plot(Zeta(x),x=-3..3,y=-3..3,discont=true);除了绘制基本的函数图之外, plot还可绘制自定义函数的图形, 也可以同时绘制多个函数图. > f:=x->sin(x)+cos(x)^2;plot(f(x),x=0..16);> plot([sin(x),sin(x^2),sin(x^3/10)],x=-2*Pi..2*Pi);利用seq指令产生一个由函数所组成的序列, 并将此函数的序列赋给变量, 然后将函数序列绘于同一张图上.> f:=x->sin(x)+cos(x);fs:=seq(f(x)^(n-1)+f(x)^n,n=1..4):plot([fs],x=0..20);> f:=x->x*ln(x^2):g:=x->ln(x):plot({f,g},0..2,-1.5..1.5);也可以直接把seq指令放在plot里来绘出一系列的函数图.> plot([seq(f(x)^(2/n),n=1..3)],x=0..10);1.2 二维参数绘图更多情况下,我们无法把隐函数化成显函数的形式, 因而plot指令无法在二维的平面里直接绘图. 但是, 在某些情况下, 我们可以把平面上的曲线f(x, y)化成x=x(t), y=y(t)的形式, 其中t为参数(parameter). 据此即可绘图, 其命令格式如下:plot ([x(t), y(t), t=tmin .. tmax]);plot ([x(t), y(t), t=tmin .. tmax], xmin .. xmax, y=ymin .. ymax);plot ([x(t), y(t), t=tmin .. tmax], scaling=CONSTRAINED);plot ([[x1(t), y1(t), t1=t1min .. t1max], [x2(t), y2(t), t2=t2min .. t2max],…]);> plot([t*exp(t),t,t=-4..1],x=-0.5..1.5,y=-4..1);> plot([sin(t),cos(t),t=0..2*Pi]);> plot([sin(t),cos(t),t=0..2*Pi],scaling=CONSTRAINED);上述两上语句都是绘制圆的命令, 但由于后者指定的x、y坐标的比例为1:1, 所以才得到了一个真正的圆, 而前者由于比例不同, 则像个椭圆. 下面则是内摆线的图形:> x:=(a,b)->(a-b)*cos(t)+b*cos((a-b)*t/b);> y:=(a,b)->(a-b)*sin(t)-b*sin((a-b)*t/b);当a=1, b=0.58时,(x(a,b), y(a,b))图形绘制命令为:> plot ([x(1,0.58), y(1,0.58), t=0..60*Pi], scaling=CONSTRAINED);再作a, b取其它值时的情形:> plot([x(2,1.2),y(2,1.2),t=0..6*Pi],scaling=CONSTRAINED);> plot([x(2,8),y(2,8),t=0..16*Pi],scaling=CONSTRAINED);> plot([x(2,12),y(2,12),t=0..16*Pi],scaling=CONSTRAINED);下面再看同时绘制多个图形的情形.> plot([[cos(3*t),sin(2*t),t=0..2*Pi],[sin(t),cos(3*t),t=0..2*Pi]]);1.3 数据点绘图如果所绘的图形是间断性的数据, 而不是一个连续的函数, 那么我们可以把数据点绘在x-y 坐标系中, 这就是所谓的数据点绘图. 其命令格式如下:plot([[x1, y1], [x2, y2], …], style=point);plot([[x1, y1], [x2, y2], …] );> data1:=seq([2*n,n^3+1],n=1..10):plot([data1],style=point);> data2:=seq([n,1+(-1)^n/n],n=1..15):plot([data2],style=point,view=[0..20,0..2]);> data3:=seq([t*cos(t/3),t*sin(t/3)],t=1..30):plot([data3],style=point);1.4 其它坐标系作图由于所研究的问题的特殊性,常常需要选用不同的坐标系, 在Maple中除笛卡尔坐标系(cartesian, 也称平面直角坐标系, 默认)外,还提供了polar(极坐标系)、elliptic(椭圆坐标系)、bipolar(双极坐标系)、maxwell(麦克斯韦坐标系)、logarithmic(双数坐标系)等14种二维坐标系,其中最常用的是极坐标系。
怎样使用Maple将曲线拟合
在使用Maple将函数的图象绘制出来后,为了解决一系列的数学问题,会需要将图象进行拟合以进行更深入的分析。
那么怎样使用Maple来拟合曲线呢?
更多Maple基本操作的使用方法介绍请访问Maple中文版网站。
操作步骤:
首先绘制函数图象。
本教程中的图象是噪音信号图象,具体处理过程请参考教程:怎样用Maple键盘命令解决数学问题。
将曲线进行拟合时要使用Statistics 函数包中的Fit命令拟合噪声数据的函数模型。
步骤一:用noiseData中的两列数据创建两个列表Xdata和Ydata。
步骤二:使用Statistics 函数包中的Fit命令拟合噪声数据的函数模型。
调用格式是Fit(f,X,Y,v),这里f是函数模型,X 和Y分别是x和y的坐标数据,v是函数的自变量名。
步骤三:绘制f和noisyData 的图形。
提示:我们经常对一个数据结构中的各个元素完成某种操作。
这里,我们使用了i=1..nops(noisyData)。
nops是获取元素数目的命令。
使用(实验)数据拟合数学模型,模型函数是f=c*x*sin(a*x)+b ,如果是多元数据拟合,数据需要写成列的形式,然后提取列,例如:
拟合数学模型:
Statistics和CurveFitting 函数包提供大量的命令用于对数据点拟合,例如线性、指数、多项式、最小二乘、样条等。
以上内容向大家介绍了使用Maple将曲线进行拟合的键盘命令。
Maple函数包有很多种,能够解决各种不同的数学问题,Maple基本操作需要大家逐步熟悉才能全部都了解清楚,如果需要了解更多Maple入门操作,可以参考Maple中文版网站教程:教你在Maple中输入不同类型的数学式。