通信原理答案第7章
- 格式：doc
- 大小：858.00 KB
- 文档页数：22
下载文档原格式
合集下载
现代通信原理指导书第七章信源编码习题详解
第七章 信源编码7-1已知某地天气预报状态分为六种：晴天、多云、阴天、小雨、中雨、大雨。
① 若六种状态等概出现，求每种消息的平均信息量及等长二进制编码的码长N 。
② 若六种状态出现的概率为：晴天—；多云—；阴天—；小雨—；中雨—；大雨—。
试计算消息的平均信息量，若按Huffman 码进行最佳编码，试求各状态编码及平均码长N 。
解: ①每种状态出现的概率为6,...,1,61==i P i因此消息的平均信息量为∑=-===6122/58.26log 1log i ii bit P P I 消息 等长二进制编码的码长N ＝[][]316log 1log 22=+=+L 。
②各种状态出现的概率如题所给，则消息的平均信息量为6212222221log 0.6log 0.60.22log 0.220.1log 0.10.06log 0.060.013log 0.0130.007log 0.0071.63/i i iI P P bit -== = ------ ≈ ∑消息Huffman 编码树如下图所示：由此可以得到各状态编码为：晴—0，多云—10，阴天—110，小雨—1110，中雨—11110， 大雨—11111。
平均码长为：6110.620.2230.140.0650.01350.0071.68i ii N n P == =⨯+⨯+⨯+⨯+⨯+⨯ =∑—7-2某一离散无记忆信源（DMS ）由8个字母(1,2,,8)i X i =⋅⋅⋅组成，设每个字母出现的概率分别为：，，，，，，，。
试求：① Huffman 编码时产生的8个不等长码字； ② 平均二进制编码长度N ； ③ 信源的熵，并与N 比较。
解：①采用冒泡法画出Huffman 编码树如下图所示可以得到按概率从大到小8个不等长码字依次为：0100,0101,1110,1111,011,100,00,1087654321========X X X X X X X X②平均二进制编码长度为8120.2520.2030.1530.1240.140.0840.0540.052.83i ii N n P == =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯ =∑ ③信源的熵∑=≈-=81279.2log)(i i i P P x H 。
通信原理课后答案第七章
7．5 设一个5位巴克码序列的前后都是+1码元，试画出其自相关函数曲线。
解：
7．6 设用一个7位巴克码作为群同步码，接收误码率为410−。
试分别求出容许错码数为0和1时的漏同步概率。
解：
0m =471(1)1(110) 6.9979e-004n e P P −=−−=−−=1m = 111(1)(1)n n e n P P C P P −=−−−−
474461(110)710(110) 2.0993e-007−−−=−−−××−=
7.8 设一个二进制通信系统传输信息的速率为100，信息码元的先验概率相等，要求假同步每年至多发生一次。
试问群同步码组的长度最小应设计为多少？若信道误码率为10，试问此系统的漏同步概率等于多少？
/b s 5−
解：设码组长度为n
① 每年收到的码元长度有 100365243600N =××× ， 连续n 位的码组有 个， 1N n −+即此 中至多只有1钟和同步码组相同， 1N n −+对于n 位码组来说共有 2个组合。
n 所以，21
n N n ≥−+27n ⇒=
② 5271(110) 2.6996e-004e P −=−−=。
现代通信原理7第七章增量调制
14
以下是M的编码波形示意
实线正弦信号为输入的消息信号。 虚线折线部分是预测值（积分器输出），实线 阶梯波是另一种积分器输出形式。
15
M调制的波形图
16
在信号变化比较缓慢的区域内，编码后得 到的序列会是“1”和“0”交替变化的，这种现 象称为颗粒噪声。
17
M斜率过载问题: 当输入信号的斜率比采样周期决定的固有斜率
2、将所检出的脉冲送入平滑电路（积分器， 时常数为5-20ms)，产生一缓慢变化电压，这个电 压与语音信号的平均斜率成正比。
3、将这个电压对输入脉冲串进行调幅，当连码 多导致平滑电路输出电平高（输入信号斜率大），调 幅器输出信号大，扩张了量化电平。
29
30
数字压扩增量调制对信噪比的改进情况如图所示
∆M的主要优越性: (1) 低比特率时，量化信噪比高于PCM。 (2) 抗误码性能好,能在误码率较高的信道里工作 (3) ∆M的编码、译码比PCM 简单。
包括: 改进型增量调制 差分脉冲编码调制
4
7.1简单增量调制的原理
M可以看成是DPCM的一种特例。它只用 一位编码，不是表示采样值的大小，而是表示 采样时刻波形的变化趋势。
2
单元学习提纲
（1）简单增量调制原理，本地译码信号、 重建信号、量化噪声、斜率过载；
（2）简单增量调制量化信噪比与抽样频 率、输入信号频率的关系；
（3）数字压扩自适应增量调制改善增量 调制动态范围的原理；
（4）增量总和调制的特点； （5）简单增量调制的抗误码性能优于脉 冲编码调制。
3
第七章 增量调制
32
7.3 增量总和调制
高频丰富的信号,如果用简单增量调制,高 频端的信噪比要下降.
采用-调制方式来解决.
以下是M的编码波形示意
实线正弦信号为输入的消息信号。 虚线折线部分是预测值（积分器输出），实线 阶梯波是另一种积分器输出形式。
15
M调制的波形图
16
在信号变化比较缓慢的区域内，编码后得 到的序列会是“1”和“0”交替变化的，这种现 象称为颗粒噪声。
17
M斜率过载问题: 当输入信号的斜率比采样周期决定的固有斜率
2、将所检出的脉冲送入平滑电路（积分器， 时常数为5-20ms)，产生一缓慢变化电压，这个电 压与语音信号的平均斜率成正比。
3、将这个电压对输入脉冲串进行调幅，当连码 多导致平滑电路输出电平高（输入信号斜率大），调 幅器输出信号大，扩张了量化电平。
29
30
数字压扩增量调制对信噪比的改进情况如图所示
∆M的主要优越性: (1) 低比特率时，量化信噪比高于PCM。 (2) 抗误码性能好,能在误码率较高的信道里工作 (3) ∆M的编码、译码比PCM 简单。
包括: 改进型增量调制 差分脉冲编码调制
4
7.1简单增量调制的原理
M可以看成是DPCM的一种特例。它只用 一位编码，不是表示采样值的大小，而是表示 采样时刻波形的变化趋势。
2
单元学习提纲
（1）简单增量调制原理，本地译码信号、 重建信号、量化噪声、斜率过载；
（2）简单增量调制量化信噪比与抽样频 率、输入信号频率的关系；
（3）数字压扩自适应增量调制改善增量 调制动态范围的原理；
（4）增量总和调制的特点； （5）简单增量调制的抗误码性能优于脉 冲编码调制。
3
第七章 增量调制
32
7.3 增量总和调制
高频丰富的信号,如果用简单增量调制,高 频端的信噪比要下降.
采用-调制方式来解决.
通信原理答案第7章
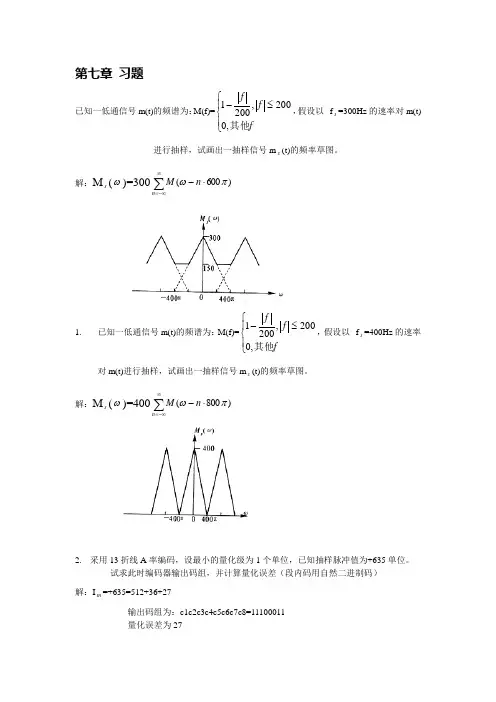
第七章 习题已知一低通信号m(t)的频谱为：M(f)=⎪⎩⎪⎨⎧≤-f f f其他,0200,2001，假设以f s =300Hz 的速率对m(t)进行抽样，试画出一抽样信号m s (t)的频率草图。
解：M s (ω)=300∑∞-∞=⋅-n n M )600(πω1.已知一低通信号m(t)的频谱为：M(f)=⎪⎩⎪⎨⎧≤-f f f其他,0200,2001，假设以f s =400Hz 的速率对m(t)进行抽样，试画出一抽样信号m s (t)的频率草图。
解：M s (ω)=400∑∞-∞=⋅-n n M )800(πω2. 采用13折线A 率编码，设最小的量化级为1个单位，已知抽样脉冲值为+635单位。
试求此时编码器输出码组，并计算量化误差（段内码用自然二进制码） 解：I m =+635=512+36+27输出码组为：c1c2c3c4c5c6c7c8=11100011 量化误差为273. 采用13折线A 率编码，设最小的量化级为1个单位，已知抽样脉冲值为-95单位。
试求此时编码器输出码组，并计算量化误差（段内码用折叠二进制码） 解：-95= -（64+74⨯+3） c5c6c7c8=0000输出码组为：c1c2c3c4c5c6c7c8=00110000 量化误差为74. 采用13折线A 率编码器电路，设接收端收到的码组为“01010011”，最小量化单位为1个单位，并已知段内码为折叠二进码。
试问译码器输出为多少单位。
解：I 0= -(256+4.5⨯16)=-3285. 采用13折线A 率编码器电路，设接收端收到的码组为“01010011”，最小量化单位为1个单位，并已知段内码为自然二进码。
试问译码器输出为多少单位 解：I 0= -(256+3.5⨯16)=-3126. 单路话音信号的最高频率为4KHz ，抽样速率为8kHz ，将所得的脉冲由PAM 方式或PCM方式传输。
设传输信号的波形为矩形脉冲，其宽度为τ，且占空比为1。
通信原理第7章(樊昌信第七版)
整理知识 梳理关系 剖析难点 强化重点
归纳结论 引导主线 解惑疑点 点击考点
曹丽娜
樊昌信
编著
国防工业出版社
谢谢！
3 QPSK 解调
原理：分解为两路2PSK信号的相干解调。
x 带通 输入 滤波器 低通 x1 (t ) 滤波器 位定时 低通 滤波器 抽样 判决 抽样 判决
a
并/串 变换 输出
y (t ) cos c t
sin c t
x 载波 恢复
x2 (t )
b
存在问题：存在900的相位模糊（0, 90, 180, 270） 解决方案：采用四相相对相位调制，即QDPSK。
QPSK 特点：
01
Q 11
相位跳变：0°,± 90°,± 180° 跳变周期 2Tb 带宽 B=Rb
0
I
误码性能与BPSK相同
00
10
最大相位跳变：180°
发生在0011或0110交替时，
即双比特ab同时跳变时，信号点沿对角线移动。
21
QPSK 缺点：
最大相位跳变180°，使限带的QPSK信号包络起
744多进制差分相移键控mdpsk1基本原理?qdpsk与qpsk的关系如同2dpsk与2psk关系?4dpsk也称qdpsk?qdpsk的矢量图与qpsk的矢量图相似只是参考相位是前一码元的载波相位n??双比特码元ab载波相位naba方式b方式0?111110?10?10?1111109018027022531545135参考相位a?矢量图aba前一码元载波相位t?波形t参考相位atc?cos?也有法正交调相法和相位选择法?仅需在qpsk调制器基础上增添差分编码码变换2qdpsk调制tc?sin2??差分编码将绝对码ab
《通信原理》课后习题答案及每章总结(樊昌信,国防工业出版社,第五版)第七章
《通信原理》习题参考答案第七章7-7. 设输入抽样器的信号为门函数)(t G τ，宽度ms 20=τ，若忽略其频谱第10个零点以外的频率分量，试求最小抽样速率。
解：ff f Sa f G t G πτπτπτττsin )()()(==⇔ 在第十个零点处有：10=τf 即最高频率为：Hz f m 500102010103=⨯==-τ根据抽样定理可知：最小抽样频率要大于m f 2，即最小抽样频率为1000KHz7-8. 设信号t A t m ωcos 9)(+=，其中A ≤10V 。
若m(t)被均匀量化为40个电平，试确定所需的二进制码组的位数N 和量化间隔υ∆。
解： 402≥N ，所以N ＝6时满足条件信号m(t)的最大电压为V max ＝19V ，最小电压为V min ＝-1V即信号m(t)的电压差ΔV ＝20V∴V V 5.0402040==∆=∆υ7-10. 采用13折线A 律编码电路，设最小量化间隔为1个单位，已知抽样脉冲值为+653单位： （1） 试求此时编码器输出码组，并计算量化误差； （2） 写出对应于该7位码（不包括极性码）的均匀量化11位码。
（采用自然二进制码。
） 解：（1）极性码为正，即C 7＝1即段落码C 6C 5C 4＝110抽样脉冲值在段内的位置为：653－512＝123个量化单位 由于段内采用均匀量化，第7段内量化间隔为：32251210244=- 而32×3≤123≤32×4，所以可以确定抽样脉冲值在段内的位置在第3段，即C 3C 2C 1C 0＝0011所以编码器输出码组为：C 7C 6C 5C 4C 3C 2C 1C 0＝11100011 量化误差：11)232332512(635=+⨯+- （2）635对应的量化值为：624232332512=+⨯+ 对应的11位自然二进制码元为：010********7-11. 采用13折线A 律编码电路，设接收端收到的码组为“01010011”、最小量化间隔为1个量化单位，并已知段内码改用折叠二进制码：（1）试问译码器输出为多少量化单位；（2）写出对应于该7位码（不包括极性码）的均匀量化11位自然二进码。
通信原理第7章
1 0 0
以概率P 发送“”时 1 以概率1 P 发送“0”时
1
载波
t
2ASK
t
4
第7章数字带通传输系统
2ASK信号的一般表达式 e2ASK (t ) st cosc t
其中
s(t ) an g (t nTs )
n
Ts － 码元持续时间； g(t) － 持续时间为Ts的基带脉冲波形，通常假设是高
10
第7章数字带通传输系统
P2 ASK 1 2 2 f s P (1 P ) G ( f f c ) G ( f f c ) 4
1 2 2 f s (1 P ) 2 G (0) ( f f c ) ( f f c ) 4
G( f ) TS Sa( f TS )
13
第7章数字带通传输系统
7.1.2 二进制频移键控（2FSK）
基本原理
表达式：在2FSK中，载波的频率随二进制基带信号在f1
和f2两个频率点间变化。故其表达式为
A cos(1t n ), e2FSK (t ) A cos( 2 t n ), 发送“”时 1 发送“ ”时 0
概率为 P 1, an 1, 概率为 1 P
即发送二进制符号“0‖时（an取+1），e2PSK(t)取0相位；发送
二进制符号“1‖时（ an取 -1）， e2PSK(t)取相位。这种以载
波的不同相位直接去表示相应二进制数字信号的调制方式， 称为二进制绝对相移方式。
26
第7章数字带通传输系统
键控法
开关电路
cos ct
e2 ASK (t )
以概率P 发送“”时 1 以概率1 P 发送“0”时
1
载波
t
2ASK
t
4
第7章数字带通传输系统
2ASK信号的一般表达式 e2ASK (t ) st cosc t
其中
s(t ) an g (t nTs )
n
Ts － 码元持续时间； g(t) － 持续时间为Ts的基带脉冲波形，通常假设是高
10
第7章数字带通传输系统
P2 ASK 1 2 2 f s P (1 P ) G ( f f c ) G ( f f c ) 4
1 2 2 f s (1 P ) 2 G (0) ( f f c ) ( f f c ) 4
G( f ) TS Sa( f TS )
13
第7章数字带通传输系统
7.1.2 二进制频移键控（2FSK）
基本原理
表达式：在2FSK中，载波的频率随二进制基带信号在f1
和f2两个频率点间变化。故其表达式为
A cos(1t n ), e2FSK (t ) A cos( 2 t n ), 发送“”时 1 发送“ ”时 0
概率为 P 1, an 1, 概率为 1 P
即发送二进制符号“0‖时（an取+1），e2PSK(t)取0相位；发送
二进制符号“1‖时（ an取 -1）， e2PSK(t)取相位。这种以载
波的不同相位直接去表示相应二进制数字信号的调制方式， 称为二进制绝对相移方式。
26
第7章数字带通传输系统
键控法
开关电路
cos ct
e2 ASK (t )
通信原理第7章教案和习题
双极性归零码（半占空，RZ）
与双极性不归零码相似，所不同的也只是脉冲的宽度
小于码元间隔。
特点：带宽比双极性不归零码的带宽要宽；直流分
2018年10月
西南交通大学电气工程学院
13
7.2 数字基带信号的码型和波形
总 结： 单极性：脉冲幅度为+A或0。 双极性：脉冲幅度为+A或-A。
1 0 A
0 A 0 -A
接收端：收到相对码bn后，可由bn恢复绝对码an。 根据式(7-3-1)可得
an bn bn1
2018年10月 西南交通大学电气工程学院 18
7.2 数字基带信号的码型和波形
极性交替码（AMI码）
它用无脉冲表示“0”，而“1”则交替地用正、负 极性的脉冲(可以为归零，也可以为不归零)表示。
2018年10月 西南交通大学电气工程学院 5
7.1 数字基带系统的构成
取样判决和码元再生
取样判决器的功能是在规定的时刻(由位定时脉冲控 制)对接收滤波器输出的信号进行取样，然后根据预 选确定的判决规则对取样值进行判决，确定发端发 的是“1”码还是“0”码。由于信号的失真及噪声 的影响，判决器会发生错判，如发端发送的是“1” 码，而判决器判决出“0”码，这种现象称为误码。
差分码的示意图。
2018年10月
西南交通大学电气工程学院
17
7.2 数字基带信号的码型和波形
波形特点： 观察图7.3.5中差分码相邻码元的变化情况及它与信息 码之间的关系，显然差分码相邻码元有变化表示信息 “1”，相邻两码元不发生变化表示信息“0”。
由于信息携带于差分码的相对变化上，所以差分码也 称为相对码，与此对应，原数字信息就称为绝对码。
2018年10月 西南交通大学电气工程学院 7
与双极性不归零码相似，所不同的也只是脉冲的宽度
小于码元间隔。
特点：带宽比双极性不归零码的带宽要宽；直流分
2018年10月
西南交通大学电气工程学院
13
7.2 数字基带信号的码型和波形
总 结： 单极性：脉冲幅度为+A或0。 双极性：脉冲幅度为+A或-A。
1 0 A
0 A 0 -A
接收端：收到相对码bn后，可由bn恢复绝对码an。 根据式(7-3-1)可得
an bn bn1
2018年10月 西南交通大学电气工程学院 18
7.2 数字基带信号的码型和波形
极性交替码（AMI码）
它用无脉冲表示“0”，而“1”则交替地用正、负 极性的脉冲(可以为归零，也可以为不归零)表示。
2018年10月 西南交通大学电气工程学院 5
7.1 数字基带系统的构成
取样判决和码元再生
取样判决器的功能是在规定的时刻(由位定时脉冲控 制)对接收滤波器输出的信号进行取样，然后根据预 选确定的判决规则对取样值进行判决，确定发端发 的是“1”码还是“0”码。由于信号的失真及噪声 的影响，判决器会发生错判，如发端发送的是“1” 码，而判决器判决出“0”码，这种现象称为误码。
差分码的示意图。
2018年10月
西南交通大学电气工程学院
17
7.2 数字基带信号的码型和波形
波形特点： 观察图7.3.5中差分码相邻码元的变化情况及它与信息 码之间的关系，显然差分码相邻码元有变化表示信息 “1”，相邻两码元不发生变化表示信息“0”。
由于信息携带于差分码的相对变化上，所以差分码也 称为相对码，与此对应，原数字信息就称为绝对码。
2018年10月 西南交通大学电气工程学院 7
樊昌信《通信原理》(第7版)配套题库【章节题库7-9章】【圣才出品】
4．2DPSK 信号采用相干解调—码反变换方法解调，若码反变换器输入端的误码率为 Pe,则码反变换器输出的误码率为______。
【答案】2Pe（1－Pe） 【解析】码反变换器的功能是将相对码变为绝对码。只有当码反变换器的两个相邻输入 码元中，有一个且仅有一个码元出错时，其输出码元才会出错。设码反变换器输入信号的误 码率是 Pe，则两个码元中前面码元出错且后面码元不错的概率是 Pe（1－Pe），后面码元出 错而前面码元不错的概率也是 Pe（1－Pe）。所以，输出码元发生错码的误码率为 2Pe（1－ Pe）。
7．先将矩形基带信号采用滚降系数为 0.5 的滚降滤波器滤波，然后采用 8PSK 调制方
式实现无码间干扰传输。若传输速率为 30kb／s，需要占用的信道带宽为______。
【答案】15kHz
【解析】对滚降系数α＝0.5，8PSK 无码间干扰传输，传输速率为 30kb／s 的信号，
其需要占用的信道带宽为 B = (1+a )Rb = (1+ 0.5)30 = 15kHz 。
2ASK
在相干解调下的误码率为
Pe
=
1 2
骣
erfc
琪 琪
桫
r 4
；
( ) 2PSK
在相干解调下的误码率为
Pe
=
1 2
erfc
r；
2FSK
在相干解调下误码率为
Pe
=
1 2
骣
erfc
琪 琪
桫
r 2
；
故采用相干解调方式时，抗加性高斯白噪声性能从优到劣的排列顺序是：2PSK、
2DPSK、2FSK、2ASK。
2．相同传码率条件下，下面四种方式中，（ ）的频带利用率最低。
【答案】2Pe（1－Pe） 【解析】码反变换器的功能是将相对码变为绝对码。只有当码反变换器的两个相邻输入 码元中，有一个且仅有一个码元出错时，其输出码元才会出错。设码反变换器输入信号的误 码率是 Pe，则两个码元中前面码元出错且后面码元不错的概率是 Pe（1－Pe），后面码元出 错而前面码元不错的概率也是 Pe（1－Pe）。所以，输出码元发生错码的误码率为 2Pe（1－ Pe）。
7．先将矩形基带信号采用滚降系数为 0.5 的滚降滤波器滤波，然后采用 8PSK 调制方
式实现无码间干扰传输。若传输速率为 30kb／s，需要占用的信道带宽为______。
【答案】15kHz
【解析】对滚降系数α＝0.5，8PSK 无码间干扰传输，传输速率为 30kb／s 的信号，
其需要占用的信道带宽为 B = (1+a )Rb = (1+ 0.5)30 = 15kHz 。
2ASK
在相干解调下的误码率为
Pe
=
1 2
骣
erfc
琪 琪
桫
r 4
；
( ) 2PSK
在相干解调下的误码率为
Pe
=
1 2
erfc
r；
2FSK
在相干解调下误码率为
Pe
=
1 2
骣
erfc
琪 琪
桫
r 2
；
故采用相干解调方式时，抗加性高斯白噪声性能从优到劣的排列顺序是：2PSK、
2DPSK、2FSK、2ASK。
2．相同传码率条件下，下面四种方式中，（ ）的频带利用率最低。
(完整版)通信原理——第七章
获得振幅键控、频移键控和相移键控三种基本的数字调制方式。
1
0
1
1
0
1
1
0
1
t
t
t
(a) 振幅键控 （ASK）
(b) 频移键控
(FSK) 正弦载波的三种键控波形
(c) 相移键控
(PSK)
绝对相移键控PSK 相对相移键控DPSK
7.1 二进制数字调制原理
7.1.1 二进制振幅键控（2ASK）
1
0
0
1
s(t)
课件
第7章
数字带通传输
通信原理（第7版） 樊昌信 曹丽娜 编著
本章内容:
第7章 数字调制
7.1 二进制数字调制原理 2ASK 2FSK 2PSK/2DPSK
7.2 二进制数字调制系统的抗噪声性能
7.3 二进制数字调制系统的性能比较
7.4 多进制数字调制原理（了解）
7.5 多进制数字调制系统的抗噪声性能（×）
➢ 数字调制：用数字信号控制载波某个参数的过程 ➢ 用数字基带信号对载波进行调制，产生各种已调数字信号 。 ➢ 数字带通传输系统（或 数字频带传输系统）：包括调制和解调过程的数
字传输系统 ➢ 调制的作用：
将信号频谱搬移至最佳频段 多路复用，高效利用信道 提高传输质量
数字调制方式：用数字基带信号改变 正弦型载波 的 幅度、频率 或 相
1. 2ASK基本原理
Ts
t
振幅键控是利用载波的幅度变化来
载波
t
传递数字信息，而其频率和初始相
位保持不变。
2ASK
t
2ASK信号的一般表达式可以写为
e2ASK (t) s(t) cosct 单极性
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第七章习题已知一低通信号m(t)的频谱为：M(f)=⎪⎩⎪⎨⎧≤-fff其他,0200,2001，假设以fs=300Hz的速率对m(t)进行抽样，试画出一抽样信号ms(t)的频率草图。
解：M s(ω)=300∑∞-∞=⋅-nnM)600(πω1.已知一低通信号m(t)的频谱为：M(f)=⎪⎩⎪⎨⎧≤-fff其他,0200,2001，假设以fs=400Hz的速率对m(t)进行抽样，试画出一抽样信号ms(t)的频率草图。
解：M s(ω)=400∑∞-∞=⋅-nnM)800(πω2.采用13折线A率编码，设最小的量化级为1个单位，已知抽样脉冲值为+635单位。
试求此时编码器输出码组，并计算量化误差（段内码用自然二进制码）解：Im=+635=512+36+27输出码组为：c1c2c3c4c5c6c7c8=11100011量化误差为273. 采用13折线A 率编码，设最小的量化级为1个单位，已知抽样脉冲值为-95单位。
试求此时编码器输出码组，并计算量化误差（段内码用折叠二进制码） 解：-95= -（64+74⨯+3） c5c6c7c8=0000输出码组为：c1c2c3c4c5c6c7c8=00110000 量化误差为74. 采用13折线A 率编码器电路，设接收端收到的码组为“01010011”，最小量化单位为1个单位，并已知段内码为折叠二进码。
试问译码器输出为多少单位。
解：I 0= -(256+4.5⨯16)=-3285. 采用13折线A 率编码器电路，设接收端收到的码组为“01010011”，最小量化单位为1个单位，并已知段内码为自然二进码。
试问译码器输出为多少单位 解：I 0= -(256+3.5⨯16)=-3126. 单路话音信号的最高频率为4KHz ，抽样速率为8kHz ，将所得的脉冲由PAM 方式或PCM方式传输。
设传输信号的波形为矩形脉冲，其宽度为τ，且占空比为1。
（1） 计算PAM 系统的最小带宽。
（2） 在PCM 系统中，抽样后信号按8级量化，求PCM 系统的最小带宽。
解：（1）s f s 41025.11-⨯==τ，系统最小带宽为：kHz f PAM 421==τ（2）采用8级量化，kHz f f PAM PCM 128log 2==7. 单路话音信号的最高频率为4KHz ，抽样速率为8kHz ，将所得的脉冲由PAM 方式或PCM方式传输。
设传输信号的波形为矩形脉冲，其宽度为τ，且占空比为1。
（1） 计算PAM 系统的最小带宽。
（2） 在PCM 系统中，抽样后信号按128级量化，求PCM 系统的最小带宽。
解：（1）s f s 41025.11-⨯==τ，系统最小带宽为：kHz f PAM 421==τ（2）采用8级量化，kHz f f PAM PCM 28128log 2==8. 已知信号m(t)的最高频率为f m ,如果用图(a)所示的q(t)对m(t)进行自然抽样，确定以抽样信号机其频谱表达式，并画出其示意图。
m(t)的频谱M(ω)的形状如图(b)所示。
解：)(*)(21)(ωωπωGMMs=)4()4(2)4()4(*)(2mmnmmmnmfnMfnGffnnfGMfπωππωδπω⨯-=⨯-⋅=∑∑∞-∞=∞-∞=9.已知信号m(t)的最高频率为fm,如果用图(a)所示的q(t)对m(t)进行自然抽样，确定以抽样信号机其频谱表达式，并画出其示意图。
m(t)的频谱M(ω)的形状如图(b)所示。
解：ωωωττωjnT jnT e Sa eG G --=⋅=)2()(20'0)(*)(21)('0ωωπωG M M s ⋅==)('0ωG10. 采用PCM24路复用系统，每路的抽样频率fs=8kHz ，各个抽样值用8bit 表示。
每帧共有24个时隙，并加1bit 作为帧同步信号。
求每路时隙宽度与总群路的数码率。
解：帧长us us f T s s 125108113=⎪⎭⎫ ⎝⎛⨯==时隙宽度 us us T s 2.52412524=⎪⎭⎫ ⎝⎛==τ 数码率 s Mb s kb f cp /544.1/1544)1824(8==+⨯⨯=11. 6路独立信源的频带分别为W,W,2W,2W,3W,3W ，如果采用时分复用制进行传输，每路信源采用8位对数PCM 编码。
设计该系统的帧结构和总时隙数，求每个时隙占有时隙宽度Ts 以及脉冲宽度。
解：对信源频带为W 的信号，抽样频率为2W ；对信源频带为2W 的信号，抽样频率为4W ； 对信源频带为3W 的信号，抽样频率为6W ； 帧长为 Ts=1/2W 时隙宽度 WT s 24112==τ 脉冲宽度 b T =W19218=τ12. 在简单ΔM 中，已知输入为f=1kHz 的正弦信号，fs=32kHz 低通滤波器的下截止频率Hz f Hz f H L 3400,160==。
计算在临界过载条件下，误码率比。
三种情况下的最大信噪32110,10,10---=b P解：在临界过载条件下，信噪比公式HL sb B s f f f P f f f SNR 22232max6183ππ+⋅=,其中Hz Hz f f f L H B 3240)1603400(=-=-= 将数据代入，当dBSNR P dBSNR P dBSNR P b b b 534.22206.179,10897.1488.30,102231.53289.3,10max 3max 2max 1=========---13. 32位电平线性PCM 系统，误码率比。
三种情况下的最大信噪32110,10,10---=b P解：线性PCM 系统的信噪比32,)1(4122=-+=L P L L SNB b在这里 将数据代入，当dBSNR P dB SNR P dBSNR P b b b 034.23,10879.13,10973.3,10321======---14. PCM 系统与ΔM 系统，如果输出信噪比都满足30dB 的要求，且kHz f kHz f k m 1,4==比较PCM 系统与ΔM 系统所需的带宽。
解：输出信噪比都满足30dB ，即S/N=1000kHz f f B N S PCM m PCM mB f PCMq m202lg /23B 31000lg 2lg 2100022======⎪⎪⎭⎫ ⎝⎛所以即系统：kHzf kHz f f f f N SM s M s m k s Mq2.23464002121B 4.46100004.023=⨯===⇒==⎪⎪⎭⎫⎝⎛∆∆∆所以系统：15. 如果，系统的码位数误码率为5N ,,1,4,04.0/1====PCM P kHz f kHz f f f e k m m 并使ΔM 系统的传输带宽与PCM 相同，试比较两系统的输出信噪比。
解：mm s s m M PCM m m f Nf f f N f B B kHzf f f f 1025.0,16.004.0,04.0/11=======∆所以即又已知，即已知eeP N S PCM P N S M 41076.915.21064.1143+⨯=⎪⎭⎫⎝⎛+⨯=⎪⎭⎫⎝⎛∆--系统：系统：16. 已知ΔM 调制系统接收端输入码组是c(n)=11101010000000101111，共二十位码元，。
绘出解调器输出波形)(x ,150,16t mV kHz f r s ==δ解：17. 已知ΔM 调制系统中，低通滤波器的截止频率为300-3400Hz,求在不过载条件下，该系统输出的最大信噪比SNR ，假定。
kHz kHz kHz f s 64,32,10= 解：dBSNR kHz f dB SNR kHz f dB SNR kHz f f f f f f f Hz f Hz f s s s Bs B s B 44.2497.277:64409.157476.34:32255.006.1:10038.083SNR 30031003003400max max max 23232max=========≈⋅===-=当当当所以取π18. 已知输入语音信号中含最高音频分量,321V ,4.3kHz f kHz f s H ==。
如果幅度为则增量调制量化器的量阶Δ=？ 解：为了不产生过载失真，要求sT dtt dm ∆≤m ax)(V f f f f A f A sHsH s 668.022,max ==∆∆=⋅∆=ππω所以即19. 已知输入信号x(t)=at ，抽样频率δ2/1=∆=，量化间隔s s T f ，求临界斜率过载时δ=？解：临界过载时：斜率ss T T a δ2=∆=所以 s aT =δ/220. 求A 律PCM 的最大量化间隔 Δmax 与最小量化间隔 Δmin 的比值。
解：'min 'max 2,128∆=∆∆=∆因为所以，64m inm ax=∆∆21. 计算L=32电平线性PCM 系统在信道误码率63210,10,10---=e P 情况下该系统的信噪比。
解：e eP P L L SSNR 125.0)1(41222≈-+==σ信噪比 105.2,102⨯==-SNR P e 当 23105.2,10⨯==-SNR P e 当 56105.2,10⨯==-SNR P e 当22. 若 输入A 律 PCM 编 码 器 的正 弦信 号为 x(t)=sin(1600πt) ,抽 样 序 列 为x(n)=sin(0.2πn),n=0,1,2...。
求n=0,1,2,3时，PCM 编码器的输出码组序列y(n)。
解：n=0：sin(2π⨯0) 所以y(0)=100000011111111)1(,8.20282048)]2.0sin(1600sin[,1==⨯⨯=y n 所以ππ01111010)2(,3.16922048)]22.0sin(1600sin[,2=-=⨯⨯⨯=y n 所以ππ01111010)3(,3.16922048)]32.0sin(1600sin[,3=-=⨯⨯⨯=y n 所以ππ23. 若 输入A 律 PCM 编 码 器 的正 弦信 号为 x(t)=sin(1600πt) ,抽 样 序 列 为x(n)=sin(0.2πn),n=0,1,2...。
求n=0,1,2,3时，PCM 编码器的输出码组序列y(n)。
解：第1子带0-800Hz 属于低通信号，所以它的抽样频率为 Hz Hz f f m s 1600)8002(21=⨯==第2子带是带通信号，B=800Hz ，并且每个子带的最高频率都是带宽的整数倍所以他们的抽样频率相等，都是带宽的2倍，即 Hz Hz B f f f s s s 1600)8002(2432=⨯====24. 12路载波电话信号占有频率范围为60-108Hz ，求出其最低抽样频率?min =s f 解：信号带宽B=(108-60)Hz=48HzkHzHz n k B f k kB nB f s H 108)811(482)/1(24/1,2n 4841482108min =+⨯=+===+=++⨯==所以，最低抽样频率。