下载文档原格式
初二数学杯赛试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 3.14B. √2C. 0.1010010001…（每两个1之间0的个数依次增加1）D. 1/7答案：B2. 如果一个三角形的两个内角分别是40°和60°，那么第三个内角是多少度？A. 80°B. 100°C. 120°D. 140°答案：C3. 一个数的相反数是-8，那么这个数是多少？A. 8B. -8C. 16D. -16答案：A4. 下列哪个选项是方程2x + 3 = 7的解？A. x = 1B. x = 2C. x = -2D. x = -1答案：B5. 一个数的平方是36，那么这个数是多少？A. 6B. -6C. ±6D. 36答案：C6. 一个数的绝对值是5，那么这个数可能是？A. -5B. 5C. -5或5D. 以上都不是答案：C7. 一个数的立方是-27，那么这个数是多少？A. -3B. 3C. -3或3D. 27答案：A8. 一个数的倒数是1/4，那么这个数是多少？A. 4B. 1/4C. 1/2D. 2答案：A9. 一个数的平方根是4，那么这个数是多少？A. 16B. -16C. 4D. ±4答案：D10. 一个数的立方根是2，那么这个数是多少？A. 8B. -8C. 2D. ±8答案：A二、填空题（每题4分，共20分）1. 一个数的平方是25，这个数是______。
答案：±52. 一个数的立方是-125，这个数是______。
答案：-53. 一个数的绝对值是3，这个数是______。
答案：-3或34. 一个数的倒数是2，这个数是______。
答案：1/25. 一个数的平方根是3，这个数是______。
答案：9三、解答题（每题10分，共50分）1. 解方程：x^2 - 5x + 6 = 0。
答案：x = 2 或 x = 32. 已知一个三角形的两边长分别为3cm和4cm，求第三边的取值范围。
学杯赛试题及答案1. 单项选择题A. 选项一B. 选项二C. 选项三D. 选项四答案：B2. 多项选择题A. 选项一B. 选项二C. 选项三D. 选项四E. 选项五答案：A、C、E3. 填空题请在空格处填入正确的词语。
句子：春天到了，花园里开满了____。
答案：鲜花4. 判断题A. 地球是太阳系中最大的行星。
答案：错误5. 简答题问题：请简述牛顿三大定律。
答案：牛顿的三大定律包括：第一定律（惯性定律），第二定律（加速度定律），第三定律（作用与反作用定律）。
6. 计算题问题：如果一个物体的重量是10千克，求它在月球上的重量，已知月球的重力加速度约为地球的1/6。
答案：物体在月球上的重量为10千克 * (1/6) = 1.67千克。
7. 论述题问题：请论述互联网对现代社会的影响。
答案：互联网极大地促进了信息的流通和交流，改变了人们的工作、学习和生活方式，同时也带来了网络安全等挑战。
8. 翻译题问题：请将以下句子翻译成英文。
句子：随着科技的发展，人工智能在各个领域都发挥着越来越重要的作用。
答案：With the development of technology, artificial intelligence plays an increasingly important role in various fields.9. 案例分析题问题：分析以下案例，说明其对企业运营的影响。
案例：某公司由于供应链中断导致产品无法按时交付。
答案：供应链中断可能导致企业信誉受损、客户流失以及经济损失。
10. 实验题问题：设计一个简单的电路，实现开关控制LED灯的亮灭。
答案：需要一个电池、一个开关、一个LED灯和一个电阻。
将电池正极连接到开关一端，开关另一端连接到LED灯的长脚，LED灯短脚通过电阻连接到电池负极。
以上即为学杯赛试题及答案的排版及格式。
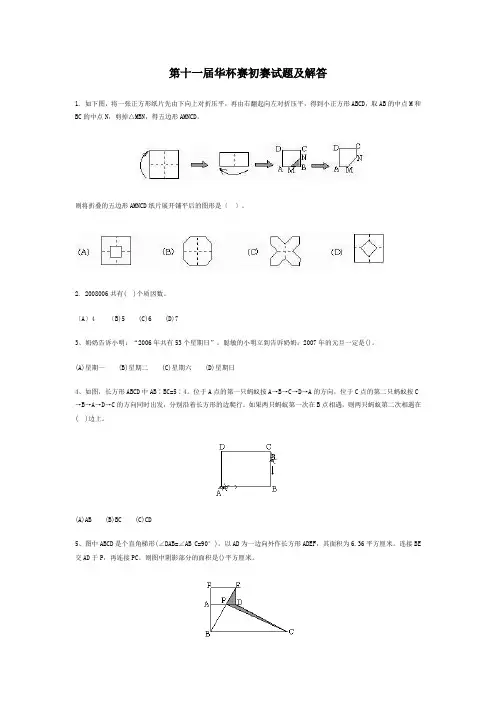
第十一届华杯赛初赛试题及解答1. 如下图，将一张正方形纸片先由下向上对折压平，再由右翻起向左对折压平，得到小正方形ABCD，取AB的中点M和BC的中点N，剪掉△MBN，得五边形AMNCD。
则将折叠的五边形AMNCD纸片展开铺平后的图形是〔〕。
2. 2008006共有( )个质因数。
〔A〕4 〔B)5 (C)6 (D)73、奶奶告诉小明：“2006年共有53个星期日”。
聪敏的小明立到告诉奶奶：2007年的元旦一定是()。
(A)星期一(B)星期二(C)星期六(D)星期日4、如图，长方形ABCD中AB∶BC=5∶4。
位于A点的第一只蚂蚁按A→B→C→D→A的方向，位于C点的第二只蚂蚁按C →B→A→D→C的方向同时出发，分别沿着长方形的边爬行。
如果两只蚂蚁第一次在B点相遇，则两只蚂蚁第二次相遇在( )边上。
(A)AB (B)BC (C)CD5、图中ABCD是个直角梯形(∠DAB=∠AB C=90°)，以AD为一边向外作长方形ADEF，其面积为6.36平方厘米。
连接BE 交AD于P，再连接PC。
则图中阴影部分的面积是()平方厘米。
(A)6.36 (B)3.18 (C)2.12 〔D〕1.596、五位同学扮成奥运会吉祥物福娃贝贝、晶晶、欢欢、迎迎和妮妮，排成一排表演节目。
如果贝贝和妮妮不相邻，共有( )种不同的排法。
(A)48 (B)72 (C)96 (D)120二、A组填空题7、在算式中，汉字“第、十、一、届、华、杯、赛”代表1，2，3，4，5，6，7，8，9中的7个数字，不同的汉字代表不同的数字，恰使得加法算式成立。
则“第、十、一、届、华、杯、赛”所代表的7个数字的和等于____。
8、全班50个学生，每人恰有三角板或直尺中的一种，28人有直尺，有三角板的人中，男生是14人，假设已知全班共有女生31人，那么有直尺的女生有____人。
9、下列图是一个直圆柱形状的玻璃杯，一个长为12厘米的直棒状细吸管(不考虑吸管粗细)放在玻璃杯内。
1. 小泉做一道除数是一位数的除法时，误把除数9看成6，结果算出的商是7，余数是3。
你知道正确的结果是（2012世奥（中国区）选拔赛三年级 A 卷）2. 杨阳是班里有名的小马虎，这次在做（200×9- □）÷ 25+13 时，又没看到题里的括号，算的结果是1788，正确的结果应该是（2012 世奥数浙江赛区四年级）。
3. 袋子里有若干个球，每次拿出其中的一半又一个球，这样共操作了4 次，袋中还有5 个球。
袋中原有__ 个球（2012年第十届走美杯三年级）。
4. 盒子里有若干个球。
小明每次拿出盒中的一半再放回一个球。
这样共操作了7 次，袋中还有3 个球。
袋中原有个球（2010 年走美杯三年级）。
5. 抽屉里有若干个玻璃球, 小军每次操作都取出抽屉中球数的一半再放回一个球。
如此操作了2012次后, 抽屉里还剩有2 个球。
那么原来抽屉里有个球（第十七届华杯赛小中组复赛）。
6. 黑板上写有一个数，男同学从黑板前走过时，把他乘以 3 再减去14，擦去原数，换上答案，女同学从黑板前走过时，把他乘以 2 再减去7，擦去原数，换上答案。
全班25 名男同学和15 名女同学都走过后，老师把最后的数乘以5，减去5，结果是30。
那么，黑板上最初的数字是（湖北第七届创新杯）。
7. 豆豆和苗苗各有一盒玻璃球，共108粒，豆豆给了苗苗10 粒，豆豆剩下的玻璃比苗苗还多8 粒。
原来苗苗有粒玻璃球（2010年第八届走美杯三年级）。
8. 甲、乙、丙三人的平均年龄为42 岁，若将甲的岁数增加7 岁，乙的岁数扩大 2 倍，丙的岁数缩小 2 倍，则三人岁数相等。
丙的年龄为______ 岁（第四届迎春杯）。
9. 甲、乙、丙、丁四人一共做了370 个零件，如果把甲做的个数加上10 个，乙做的个数减去20 个，丙做的个数乘以2，丁做的个数除以2，四人做的零件数就正好相等。
那么乙实际做了_____ 个零件（第二届迎春杯）。
10. 甲、乙、丙三所小学的学生人数的总和为1999。
历年华杯赛试题及答案小学华杯赛，全称“全国青少年数学华罗庚金杯赛”，是中国最具影响力的青少年数学竞赛之一，旨在激发青少年对数学的兴趣，培养他们的数学思维能力。
以下是一些历年华杯赛小学组的试题及答案，供参考。
试题一：小明有3个红球和2个蓝球，他随机从袋子里摸出一个球，然后放回。
接着，他又随机摸出一个球。
请问小明两次都摸到红球的概率是多少？答案：小明第一次摸到红球的概率是3/5，放回后，第二次摸到红球的概率仍然是3/5。
因此，两次都摸到红球的概率是(3/5) * (3/5) = 9/25。
试题二：有一个数字序列：1, 1, 2, 3, 5, 8, 13, 21, ... 这个序列的特点是每一项都是前两项的和。
请问这个序列的第10项是多少？答案：这是一个斐波那契数列。
根据题目给出的数列，第10项是第9项（21）和第8项（13）的和，即21 + 13 = 34。
试题三：一个班级有40名学生，其中20名男生和20名女生。
如果随机选择一名学生，那么选择到男生的概率是多少？答案：班级中有20名男生，总共40名学生，所以选择到男生的概率是20/40 = 1/2。
试题四：一个圆形的直径是14厘米，求这个圆的面积。
答案：圆的面积公式是A = πr²，其中r是圆的半径。
直径是14厘米，所以半径是14/2 = 7厘米。
代入公式得到面积A = π * 7² = 49π ≈ 153.94平方厘米。
试题五：小华有5个苹果，他决定将这些苹果平均分给3个朋友。
如果每个朋友分得的苹果数必须是整数，小华应该如何分配？答案：小华可以将5个苹果分成1, 2, 2的组合，这样每个朋友得到的苹果数都是整数。
试题六：一个长方体的长、宽、高分别是8厘米、6厘米和5厘米。
求这个长方体的体积。
答案：长方体的体积公式是V = 长 * 宽 * 高。
代入数值得到V = 8 * 6 * 5 = 240立方厘米。
试题七：如果一个数的平方等于这个数本身，那么这个数是什么？答案：这个数是0或1，因为0² = 0，1² = 1。
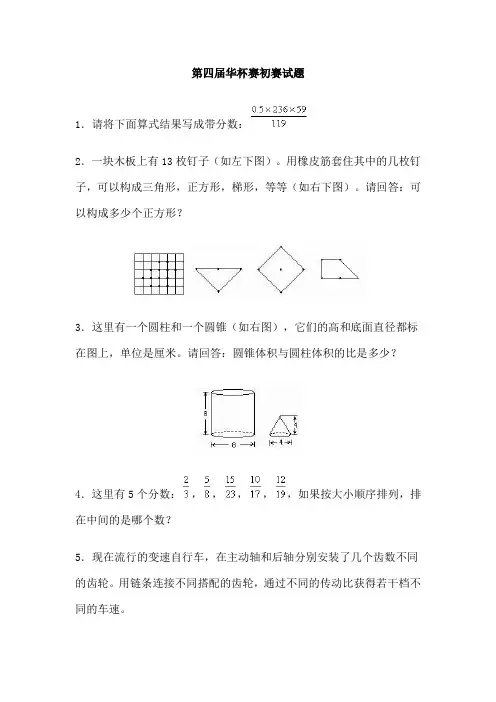
第四届华杯赛初赛试题1．请将下面算式结果写成带分数：2．一块木板上有13枚钉子（如左下图）。
用橡皮筋套住其中的几枚钉子，可以构成三角形，正方形，梯形，等等（如右下图）。
请回答：可以构成多少个正方形？3．这里有一个圆柱和一个圆锥（如右图），它们的高和底面直径都标在图上，单位是厘米。
请回答：圆锥体积与圆柱体积的比是多少？4．这里有5个分数：，，，，，如果按大小顺序排列，排在中间的是哪个数？5．现在流行的变速自行车，在主动轴和后轴分别安装了几个齿数不同的齿轮。
用链条连接不同搭配的齿轮，通过不同的传动比获得若干档不同的车速。
“希望牌”变速自行车主动轴上有三个齿轮，齿数分别是48，36，24；后轴上有四个齿轮，齿数分别是36，24，16，12。
问：“这种变速车一共有几档不同的车速？6．右图中的大正方形ABCD的面积是 1，其它点都是它所在的边的中点。
请问：阴影三角形的面积是多少？7．在右边的算式中，被加数的数字和是和数的数字和的三倍。
问：被加数至少是多少？8．筐中有60个苹果，将它们全部都取出来，分成偶数堆，使得每堆的个数相同。
问：有多少种分法？9．小明玩套圈游戏，套中小鸡一次得9分，套中小猴得5分，套中小狗得2分。
小明共套了10次，每次都套中了，每个小玩具都至少被套中一次。
小明套10次共得了61分。
问：小鸡至少被套中多少次？10．车库中停放若干辆双轮摩托车和四轮小卧车，车的辆数与车的轮子数之比是2∶5。
问：摩托车的辆数与小卧车的辆数之比是多少？11．有一个时钟，它每小时慢25秒，今年3月21日中午十二点它的指示正确。
请问：这个时钟下一次指示正确的时间是几月几日几点钟？12．某人由甲地去乙地。
如果他从甲地先骑摩托车行12小时，再换骑自行车9小时，恰好到达乙地。
如果他从甲地先骑自行车行21小时，再换骑摩托车行8小时，也恰好到达乙地。
问：全程骑摩托车需要几小时到达乙地？13．右图的二个圆只有一个公共点A，大圆直径48厘米，小圆直径30厘米。
杯赛考试题及答案****一、选择题（共20分，每题2分）1. 以下哪个选项是正确的数学公式？A. \( a^2 + b^2 = c^2 \)（勾股定理）B. \( a^2 - b^2 = c^2 \)C. \( a^2 + 2ab + b^2 = c^2 \)D. \( a^2 - 2ab + b^2 = c^2 \)答案：A2. 哪个国家是联合国安全理事会的五个常任理事国之一？A. 德国B. 巴西C. 中国D. 印度答案：C3. 以下哪个元素的化学符号是“Fe”？A. 铜B. 铁C. 锌D. 铅答案：B4. 光年是什么单位？A. 长度单位B. 时间单位C. 质量单位D. 速度单位答案：A5. 以下哪个国家不是G20成员国？A. 阿根廷B. 巴西C. 墨西哥D. 挪威答案：D6. 以下哪个是计算机编程语言？A. PythonB. JavaC. C++D. All of the above答案：D7. 以下哪个是人体最大的器官？A. 心脏B. 肝脏C. 皮肤D. 肺答案：C8. 以下哪个是国际象棋中的基本规则？A. 兵只能向前移动B. 象可以过河C. 马可以走直线D. 后可以跳过其他棋子答案：A9. 以下哪个是著名的物理学家？A. 爱因斯坦B. 牛顿C. 霍金D. All of the above答案：D10. 以下哪个是太阳系中的行星？A. 地球B. 月球C. 冥王星D. 彗星答案：A二、填空题（共20分，每题2分）11. 圆的面积公式是 \( \pi r^2 \)，其中 \( r \) 代表圆的________。
答案：半径12. 人体需要的主要营养素包括蛋白质、脂肪、碳水化合物、维生素和________。
答案：矿物质13. 国际单位制中，电流的单位是________。
答案：安培14. 元素周期表中，最轻的元素是________。
答案：氢15. 计算机存储的基本单位是________。
答案：字节16. 光在真空中的传播速度是________米/秒。
第一届华杯赛决赛一试试题1. 计算：2．975×935×972×〔〕,要使这个连乘积的最后四个数字都是“0〞，在括号内最小应填什么数？3．把＋、－、×、÷分别填在适当的圆圈中，并在长方形中填上适当的整数，可以使下面的两个等式都成立，这时，长方形中的数是几？9○13○7=100 14○2○5=□4．一条1米长的纸条，在间隔一端0.618米的地方有一个红点，把纸条对折起来，在对准红点的地方涂上一个黄点然后翻开纸条从红点的地方把纸条剪断，再把有黄点的一段对折起来，在对准黄点的地方剪一刀，使纸条断成三段，问四段纸条中最短的一段长度是多少米？5．从一个正方形木板锯下宽为米的一个木条以后，剩下的面积是平方米，问锯下的木条面积是多少平方米？6．一个数是5个2，3个3，2个5，1个7的连乘积。
这个数当然有许多约数是两位数，这些两位的约数中，最大的是几？7．修改31743的某一个数字，可以得到823的倍数，问修改后的这个数是几？8．蓄水池有甲、丙两条进水管，和乙、丁两条排水管，要灌满一池水，单开甲管需3小时，单开丙管需要5小时，要排光一池水，单开乙管需要4小时，单开丁管需要6小时，如今池内有池水，假如按甲、乙、丙、丁的顺序，循环各开水管，每天每管开一小时，问多少时间后水清苦始溢出水池？9．一小和二小有同样多的同学参加金杯赛，学校用汽车把学生送往考场，一小用的汽车，每车坐15人，二小用的汽车，每车坐13人，结果二小比一小要多派一辆汽车，后来每校各增加一个人参加竞赛，这样两校需要的汽车就一样多了，最后又决定每校再各增加一个人参加竞赛，二小又要比一小多派一辆汽车，问最后两校共有多少人参加竞赛？10．如以下图，四个小三角形的顶点处有六个圆圈。
假如在这些圆圈中分别填上六个质数，它们的和是20，而且每个小三角形三个顶点上的数之和相等。
问这六个质数的积是多少？11．假设干个同样的盒子排成一排，小明把五十多个同样的棋子分装在盒中，其中只有一个盒子没有装棋子，然后他外出了，小光从每个有棋子的盒子里各拿一个棋子放在空盒内，再把盒子重新排了一下，小明回来仔细查看了一番，没有发现有人动过这些盒子和棋子，问共有多少个盒子？12．如右图，把1.2，3.7, 6.5, 2.9, 4.6，分别填在五个○内，再在每个□中填上和它相连的三个○中的数的平均值，再把三个□中的数的平均值填在△中，找出一个填法，使△中的数尽可能小，那么△中填的数是多少？13．如以下图，甲、乙、丙是三个站，乙站到甲、丙两站的间隔相等。
湖州市初三数学竞赛试题（12月14日 上午9：00—11：00）题 号 一 二 三总分 1－8 9－14 15 16 17 18 得 分 评卷人 复查人答题时注意；1．用圆珠笔或钢笔作答． 2．解答书写时不要超过装订线．3．可以用计算器一、选取题（共8小题，每小题5分，满分40分)．1．已知|a+b|+|a-b|-2b=0，在数轴上给出了如图所示关于a ，b 四种位置关系，则也许成立有( )A ．1种B ．2种C ．3种D ．4种2．已知a 是方程3310x x +-=一种实数根，则直线1y ax a =+-不通过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3. 2612111012111010(2)x x a x a x a x x a --=++++…+a ，则12108642a a a a a a +++++=（ ）（A ）64 （B ）32 （C ） －32 （D ）－644. 如图，四边形ABCD 是菱形，∠A=60°，AB=2，扇形BEF 半径为2，圆心角为60°，则图中阴影某些面积是（ ）3-π2332-πA. B. C. D.5. A、B、C三个足球队举办单循环赛，下表给出了某些比赛信息：则A、B两队比赛时，A队与B队进球数之比为（）A.2∶0B.3∶0C.2∶1D.3∶16．定义新运算：a⊕b=⎪⎩⎪⎨⎧≠>-≤-)0()(1bbababaa且，则函数y=3⊕x图象大体是( )7．.如图，∠XOY＝90°，OW平分∠XOY，P A⊥OY，PB⊥OX，PC⊥OW．若OC＝2－1，则OA＋OB＋OC＝（）A．３B．２C．１D．218．咱们用()f x代替函数中变量y，如：3y x=+可以记作()3f x x=+，“当x=1，y=4”球队比赛场次胜负平进球数失球数A 2 2场 1B 2 1场 2 4C 2 3 7BCOyxPW第７题图A332-π3-π第4题可以记作“(1)4f =”．既有函数1()2f x x =，22()f x x=，3()6(1)(2)f x x x =---，记k I =100(1)99k k f f ⎛⎫-+ ⎪⎝⎭1001019999k k f f ⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭197(2)99k k f f ⎛⎫+- ⎪⎝⎭，其中k =1，2，3，则下列结论对的是（ ）A ．123I I I <<B ．213I I I <<C ．231I I I <<D ．321I I I << 二、填空题（共6小题，每小题5分，满分30分）9．有一组数满足, ,2 ,0 ,2 ,0,2,14635241321 =-=-=-=-==a a a a a a a a a a按此规律进行下去，则=++++100321a a a a ___________.10.如图，菱形ABCD 边长为a ，点O 是对角线A C 上一点， 且OA ＝a ，O B ＝OC ＝OD ＝1，则a 值等于__________．11．直线k x y +=21与x 、y 轴交点分别为A 、B ，如果S △AOB ≤1， 那么k 取值范畴是 。
小学杯赛试题及答案一、选择题（每题2分，共20分）1. 以下哪个选项是正确的？A. 地球是平的B. 地球是圆的C. 地球是方的D. 地球是三角形的答案：B2. 太阳系中，哪个行星离太阳最近？A. 火星B. 金星C. 土星D. 水星答案：D3. 以下哪个动物是哺乳动物？A. 鱼B. 鸟C. 蛇D. 猫答案：D4. 以下哪个选项是正确的？A. 2 + 3 = 5B. 2 + 3 = 6C. 2 + 3 = 4D. 2 + 3 = 7答案：A5. 以下哪个国家位于亚洲？A. 巴西B. 阿根廷C. 印度D. 法国答案：C6. 以下哪个选项是正确的？A. 一年有13个月B. 一年有12个月C. 一年有11个月D. 一年有10个月答案：B7. 以下哪个选项是正确的？A. 1小时有60分钟B. 1小时有100分钟C. 1小时有120分钟D. 1小时有150分钟答案：A8. 以下哪个选项是正确的？A. 0除以任何数都等于0B. 0除以任何数都等于1C. 0除以任何数都等于2D. 0除以任何数都等于3 答案：A9. 以下哪个选项是正确的？A. 地球的自转周期是一天B. 地球的自转周期是一年C. 地球的自转周期是一月D. 地球的自转周期是一周答案：A10. 以下哪个选项是正确的？A. 1千克等于1000克B. 1千克等于100克C. 1千克等于10克D. 1千克等于1克答案：A二、填空题（每题2分，共20分）1. 一个正方形的对角线长度是5厘米，那么它的边长是______厘米。
答案：约2.24厘米2. 一年中，有______个季节。
答案：43. 我们通常所说的“四大发明”是指______、______、______和______。
答案：造纸术、印刷术、火药、指南针4. 英文字母表中，字母“E”是第______个字母。
答案：55. 一个三角形的三个内角之和是______度。
答案：1806. 地球的赤道周长大约是______千米。
(中环杯初赛诊断试题第1题)200592005920059999999999999×+个“”个“”个“”的得数的末尾有( )个零。
(第九届中环杯四年级第1题)计算：345345×788＋690×105606＝( )(第九届中环杯四年级第5题)201×202×203×……×300的结果除以10，所得到的商再除以10……重复这样的操作，在第_____次除以10时，首次出现余数。
计算54÷64×51÷(27÷128×17)(第四届小机灵邀请赛)将6放在一个两位数的右侧，形成的三位数比原来的两位数多294，求原来的两位数八个正整数由小到大排列，从第三个数开始，每个数都是它前面两个数之和，如果第五个数是21，求第八个数是多少？2000×1999－1999×1998＋1998×1997－1997×1996＋…＋4×3－3×2＋2×1(第六届“中环杯”小学生思维能力训练活动五年级复赛第一大题填空题第1题)7999.99＋799.99＋79.99＋7.99＋8.99＋89.99＋899.99＋8999.9＋8999.99＝( )(第七届“中环杯”小学生思维能力训练活动五年级初赛第一大题填空题第3题)12＋22＋32＋42＋52＋…20052＋20062的和的末位数是( )。
测试题1.(第五届中环杯复赛)2222×17+3333×4＋6666×92. (2008年第八届“春蕾杯”小学数学邀请赛决赛)199772×199911－199771×199912 ＝3.247×285＋247×386＋671×253＝4.甲乙两数的平均数是30，乙丙两数的平均数是44，甲丙两数的平均数是34。
甲乙丙的三个数的平均数是多少？5.31000＋61000＋91000的末位数字是几？6．200×199－199×198＋198×197－197×196＋……＋2×1＝( )答案1.答案：原式＝1111×(2×17)＋1111×(3×4)＋1111×(6×9)＝1111×(34＋12＋54)＝1111×100＝1111002.答案：乘法分配律的逆用。
原式＝199772×199911－199771×(199911＋1)＝199911－199771＝1403.答案：247×285＋247×386＋671×253＝247×671＋671×253＝671×(247＋253)＝671×500＝3355004.答案：a＋b＝60 b＋c＝88 a＋c＝68 b＝40 a＝20 c＝48 (a＋b＋c)÷3＝35.答案：我们发现一个数的n次方的末位都是四个为一个周期，那么我们要求31000＋61000＋91000的末位数字是几，只要先用1000÷4，我们发现余0，所以我们算34＋64＋94的末位数字是几就可以了。
34的末位为1，64的末位为6，94的末位为1。
所以结果是1＋6＋1＝8。
6．答案：200×199－199×198＋198×197－197×196＋……＋2×1＝( )原式＝199×(200－198)＋197×(198－196)＋……＋3×(4－2)＋2×1＝199×2＋197×2＋……＋3×2＋1×2＝2×(199＋197＋……＋3＋1)＝2×(199＋1)×100÷2＝20000(第七届“中环杯”小学生思维能力训练活动五年级初赛第一大题填空题第9题)一只魔袋里装有30种不同颜色的魔球各30只，现在请你闭上眼睛到袋中去摸球，每次限摸3只。
要使摸出的球至少有三种颜色是不少于3只的，那么至少要摸( )次。
一只魔袋里装有4种不同颜色的筷子各10双，现在请你闭上眼睛从袋中拿筷子，每次限拿一根。
要使摸出的筷子至少能配成五双，那么至少要摸( )次。
(第六届“中环杯”四年级初赛)果园里有桃树、梨树、苹果树共552棵。
桃树的棵数比梨树棵数的2倍多12棵；苹果树的棵数比梨树棵数少20棵。
那么苹果树有( )棵，梨树有( )棵，桃树有( )棵。
在一次数学测试中，四(2)班的全班同学平均88分，男生平均92分，女生平均82分，则男生人数是女生人数的多少倍？(第六届“中环杯”小学生思维能力训练活动五年级复赛第一大题填空题第8题)(中环杯初赛诊断试题第10题)2005年小明家养了一只大母羊，第二年春天它生了2只小公羊和3只小母羊。
每只小母羊从出生的第三年起也生了2只小公羊和2只小母羊。
那么到2010年，小明家共有( )只羊。
(中环杯模拟题)玲玲用25元买了5支圆珠笔和4支铅笔，对于余下的钱，如果买1支圆珠笔就少1元，如果买1支铅笔就正好。
那么每支铅笔、圆珠笔各多少钱？一个月最多有5个星期日，在一年的12个月中，有5个星期日的月份最多有_______个。
用1到7可以组成_____个没有重复数字，且能被11整除的七位数。
(第五届“华杯赛”决赛)将自然数的平方按从小到大依次排列成一串有序数列：1491625364964……，问第612个位置的数字是几？测试题1.口袋里有70只球，其中20只是红球，20只是绿球，20只是黄球，其余的是白球和黑球。
任意从中取出( )只球，可确保取出的球中至少有10只同色的球。
2. 小军比小亮早出生几天，但是他俩的生日都在6月份，而且都生于星期四。
如果两人的生日日期的和是34，那么小军的生日是6月( )日。
3.六位同学的数学考试的平均成绩是92分，他们的成绩是互不相同的整数，最高的是98分，最低的81分，那么按高到低的顺序，居第四名的同学至少得多少分？4.一只布袋里有50只大小形状完全一样的球，其中红色的球10只，绿色的球10只，黄色的球10只，蓝色的球10只，其余的是白色的和黑色的球。
如果要确保取出同样颜色的球7只，至少要取( )只球。
5.(2008 年第八届“春蕾杯”小学数学邀请赛决赛)小丁买甲、乙两种练习本共30本，付出54元，找回0.5元。
甲种练习本每本1.5元。
乙种练习本每本2元。
问甲种练习本买了( )本。
6．1222×1223×1224×1225×……×2006×2007×2008的积的末尾有( )个零。
答案1.答案：这是一道抽屉问题，根据最不巧原则，将袋中其余的10只(黑球和白球)都取出，红、绿、黄球各取出9只，那么，再多取1只(无论是何颜色)，都能满足问题的要求，确保至少有10只同色的球。
10＋9×3＋1＝38(只)2.答案：他俩的生日都在6月份，而且都生于星期四，故两人生日日期的差是7的倍数。
又因两人生日日期之和已知，此题属和差问题，可用(和一差)÷2的算式求出小军的生目。
尝试(34—7) ÷2＝13．5，显然不对，则(34—72) ÷2＝10是本题的解。
3.答案：根据平均分得到总分为92×6＝552(分)552－98－97－96－81＝180 (分)180÷2＋1＝91(分)4．答案：我们从最“坏”的情况分析，设已经取出红色、绿色、黄色、蓝色的球各6只。
根据最不利原则，我们假设，白球和黑球均不到7只，那么，我们就可以取出所有的白球和黑球。
这时，我们就已经取出了共6×4＝34只，这时只要再多取出一只，便可一确保取出同样颜色的球7只。
所以，至少要取出35只。
5．答案：若全部买甲练习本，需要1.5×30＝45元，所以乙练习本买了(53.5－45)÷(2－1.5)＝17(本)，甲种练习本30－17＝13(本)。
6．答案：从1222至2008共有2008－1222＋1＝787个数。
在这些因数中，若有一个“2”和一个“5”，末尾就有一个0。
而在这787个因数中，因数2的个数远远多于因数5的个数，所以只需判断因数5的个数即可。
判断因数中含有因数5的个数，我们可以用以下方法求得。
2008÷5＝401......3，40l÷5＝80......1，80÷5＝16＋，16÷5＝3 (1)1——2008中含因数5：401＋80＋16＋3＝500(个)122l÷5＝244......1，244÷5＝48......4，48÷5＝9......3，9÷5＝l (4)l~1221中含因数5：244＋48＋9＋1＝302(个)所以1222－2008共含有因数5：500－302＝198(个)，得积的末尾有198个零。
(第九届中环杯四年级决赛解答题第三题)如图，阴影部分的每个小长方形的长相等，宽也相等，求空白部分的面积(单位：厘米)(第六届中环杯四年级决赛解答题第四题)长方形ABCD 被分成六个正方形，其中最小的正方形面积是1平方厘米，求长方形ABCD 的面积。
(第九届中环杯四年级决赛第九题)有一批砖，每块砖的长和宽都是自然数，而且长比宽长12厘米。
如果把这批砖横着铺(见图1)，可以铺897厘米；如果横竖相同铺(见图2)，可以铺657厘米长。
如果“两横一竖铺”(见图3)，那么可以铺( )厘米长。
如下图是一个园林的规划图，其中，正方形的34是草地；圆的67是竹林；竹林比草地多占地450平方米。
问：水池占地多少平方米？小池塘中有6片荷叶，如图所示，一只青蛙在荷叶A 上，想要跳到荷叶F 上，可以通过B 、C 、D 、E 任意一片或两片跳到荷叶F 上，也可以直接跳到荷叶F 上，但跳过的荷叶不能再跳。
它一共有( )种不同的跳法。
(第十届中环杯四年级初赛解答题第三题)平面上有一个圆，能把平面分成2部分；2个圆最多能把平面分成4部分。
现在有7个圆，最多能把平面分成( )部分。
71名选手参加大胃王比赛，比赛的内容是吃汉堡，最后吃得最多的选手吃了18个汉堡，吃得最少的选手吃了9个汉堡。
问至少有( )名选手吃的汉堡的数量是相同的。
(第十届中环杯四年级初赛)甲、乙两人分别从A、B两地同时出发，相向而行。
如果两人都按照原定速度行进，3小时可以相遇。
