带状态观测器的控制系统综合设计与仿真
- 格式:doc
- 大小:504.00 KB
- 文档页数:18


控制系统建模及仿真综合设计总结
控制系统建模及仿真是现代控制理论和工程实践中非常重要的环节。
通过对系统进行建模和仿真,可以实现对系统行为和性能的分析、优化和预测。
以下是控制系统建模及仿真综合设计的总结:
1. 确定系统的目标和需求:系统的目标和需求是建模和仿真的基础,需要明确系统的控制目标、工作条件、输入输出特性等。
2. 收集系统的信息:收集系统的相关信息,包括系统结构、工作原理、参数等。
可以通过文献调研、实验测试等方式获取。
3. 进行系统建模:根据系统的特性和要求,选择合适的建模方法。
常见的建模方法包括状态空间法、传递函数法、仿真模型法等。
根据建模方法,建立系统的数学模型。
4. 进行系统仿真:利用仿真软件,将系统的数学模型转化为计算机可执行的模型,并设计仿真实验。
根据实验设置系统的输入信号,进行仿真计算并得到系统的输出响应。
5. 分析和优化系统性能:对仿真结果进行分析,评估系统的控制性能。
可以利用仿真结果,进行参数调节、控制算法优化等操作,以提升系统的性能。
6. 验证仿真结果:将仿真结果与实际系统的实验结果进行比较,验证仿真模型的准确性和可靠性。
若有差异,可以对仿真模型进行修正和优化。
7. 编写综合设计报告:根据仿真结果和优化方案,编写综合设计报告,包括系统的建模过程、仿真实验的设置、仿真结果的分析和优化方案的描述等。


一种测控综合模拟训练系统的设计与实现一、引言随着科技的不断发展,测控技术在各个领域的应用越来越广泛。
为了提高测控技术人员的实战能力,设计与实现一种测控综合模拟训练系统是十分必要的。
本文将介绍这个系统的设计与实现,并探讨其在测控技术培训中的应用。
二、系统设计1. 系统功能测控综合模拟训练系统旨在提供一个模拟实际测控场景的环境,让学员能够进行真实的操作和实践。
其主要功能包括:- 提供多种测控设备的模拟操作界面,如传感器、执行器等;- 模拟不同测控场景,如温度测量、压力控制等;- 提供数据采集、处理和分析功能;- 实时监控和调试测控设备;- 提供故障模拟和排除功能。
2. 系统架构测控综合模拟训练系统由硬件和软件两部分组成。
硬件方面,系统需要搭建一个真实的测控实验平台,包括传感器、执行器、数据采集卡等设备。
软件方面,系统需要开发一个友好的用户界面,提供各种功能的实现。
3. 系统模块测控综合模拟训练系统主要包含以下几个模块:- 数据采集模块:负责采集传感器的数据,并传输给计算机进行处理。
- 数据处理模块:对采集到的数据进行处理和分析,生成相应的报表和图像。
- 控制模块:实现对执行器的控制,根据测量结果进行相应的动作。
- 人机交互模块:提供友好的用户界面,让用户能够方便地操作系统。
- 故障模拟模块:模拟各种设备故障,并提供相应的排除方法。
三、系统实现1. 硬件搭建需要选择适当的传感器、执行器和数据采集卡等设备,并将其连接到计算机上。
然后,根据实际需求搭建一个测控实验平台,包括安装传感器和执行器等。
2. 软件开发软件开发是测控综合模拟训练系统的核心部分。
在开发过程中,需要根据系统需求设计界面,实现各个模块的功能。
具体步骤包括:- 设计系统界面:根据用户需求,设计一个直观、易用的界面,包括菜单、按钮、输入框等。
- 开发数据采集模块:编写程序实现对传感器数据的采集,并将数据传输给计算机。
- 开发数据处理模块:编写程序对采集到的数据进行处理和分析,生成相应的报表和图像。
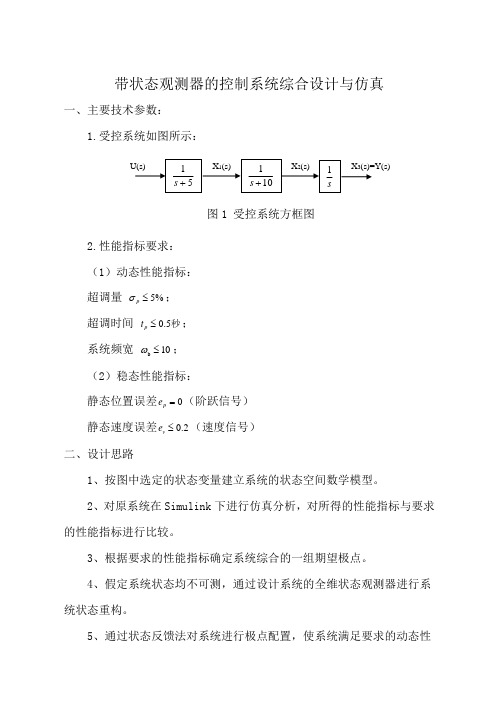
带状态观测器的控制系统综合设计与仿真一、主要技术参数:1.受控系统如图所示:图1 受控系统方框图2.性能指标要求: (1)动态性能指标: 超调量 5%p σ≤; 超调时间 0.5p t ≤秒; 系统频宽 10b ≤ω; (2)稳态性能指标:静态位置误差0=p e (阶跃信号) 静态速度误差2.0≤v e (速度信号) 二、设计思路1、按图中选定的状态变量建立系统的状态空间数学模型。
2、对原系统在Simulink 下进行仿真分析,对所得的性能指标与要求的性能指标进行比较。
3、根据要求的性能指标确定系统综合的一组期望极点。
4、假定系统状态均不可测,通过设计系统的全维状态观测器进行系统状态重构。
5、通过状态反馈法对系统进行极点配置,使系统满足要求的动态性能指标。
6、合理增加比例增益,使系统满足要求的稳态性能指标。
7、在Simulink 下对综合后的系统进行仿真分析,验证是否达到要求的性能指标的要求。
三、实验设计步骤I 、按照极点配置法确定系统综合的方案1、按图1中选定的状态变量建立系统的状态空间数学模型 ① 列写每一个环节的传递函数 由图1有:11223()()5()()10()()U s x s s x s x s s x s x s s ⎧=⎪+⎪⎪=⎨+⎪⎪=⎪⎩②叉乘拉式反变换得一阶微分方程组 由上方程可得12132(5)()()(10)()()()()s x s U s s x s x s sx s x s +=⎧⎪+=⎨⎪=⎩即1121232()5()()()()10()()()sx s x s U s sx s x s x s sx s x s =-+⎧⎪=-⎨⎪=⎩ 拉式反变换为1121232510x x U x x x x x ⎧=-+⎪⎪=-⎨⎪⎪=⎩输出由图1可知为3y x =③用向量矩阵形式表示1122335001110000100x x x x u x x ⎡⎤⎢⎥-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦[]001y x =2、对原系统在Simulink 下进行仿真分析,对所得的性能指标与要求的性能指标进行比较原受控系统仿真图如下:图2 原受控系统仿真图原受控系统的阶跃响应如下图:图3 原受控系统的阶跃响应曲线很显然,原系统是不稳定的。

带状态观测器的控制系统综合设计与仿真一、主要技术参数:1.受控系统如图所示:图1 受控系统方框图2.性能指标要求: (1)动态性能指标: 超调量 5%p σ≤; 超调时间 0.5p t ≤秒; 系统频宽 10b ≤ω; (2)稳态性能指标:静态位置误差0=p e (阶跃信号) 静态速度误差2.0≤v e (速度信号) 二、设计思路1、按图中选定的状态变量建立系统的状态空间数学模型。
2、对原系统在Simulink 下进行仿真分析,对所得的性能指标与要求的性能指标进行比较。
3、根据要求的性能指标确定系统综合的一组期望极点。
4、假定系统状态均不可测,通过设计系统的全维状态观测器进行系统状态重构。
5、通过状态反馈法对系统进行极点配置,使系统满足要求的动态性能指标。
6、合理增加比例增益,使系统满足要求的稳态性能指标。
7、在Simulink 下对综合后的系统进行仿真分析,验证是否达到要求的性能指标的要求。
三、实验设计步骤I 、按照极点配置法确定系统综合的方案1、按图1中选定的状态变量建立系统的状态空间数学模型 ① 列写每一个环节的传递函数 由图1有:112235()()510()()10()()U s x s s x s x s s x s x s s ⎧=⎪+⎪⎪=⎨+⎪⎪=⎪⎩②叉乘拉式反变换得一阶微分方程组 由上方程可得12132(5)()5()(10)()10()()()s x s U s s x s x s sx s x s +=⎧⎪+=⎨⎪=⎩即1121232()5()5()()10()10()()()sx s x s U s sx s x s x s sx s x s =-+⎧⎪=-⎨⎪=⎩ 拉式反变换为1121232551010x x U x x x x x ⎧=-+⎪⎪=-⎨⎪⎪=⎩ggg 输出由图1可知为3y x =③用向量矩阵形式表示11223350051010000100x x x x u x x ⎡⎤⎢⎥-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦g g g []001y x =2、对原系统在Simulink 下进行仿真分析,对所得的性能指标与要求的性能指标进行比较原受控系统仿真图如下:图2 原受控系统仿真图原受控系统的阶跃响应如下图:图3 原受控系统的阶跃响应曲线很显然,原系统是不稳定的。
现代控制实验状态反馈器和状态观测器的设计现代控制实验中,状态反馈器和状态观测器是设计系统的重要组成部分。
状态反馈器通过测量系统的状态变量,并利用反馈回路将状态变量与控制输入进行耦合,以优化系统的性能指标。
状态观测器则根据系统的输出信息,估计系统的状态变量,以便实时监测系统状态。
本文将分别介绍状态反馈器和状态观测器的设计原理和方法。
一、状态反馈器的设计:状态反馈器的设计目标是通过调整反馈增益矩阵,使得系统的状态变量在给定的性能要求下,达到所需的一组期望值。
其设计步骤如下:1.系统建模:通过对被控对象进行数学建模,得到描述系统动态行为的状态空间表达式。
通常表示为:ẋ=Ax+Buy=Cx+Du其中,x为系统状态向量,u为控制输入向量,y为系统输出向量,A、B、C、D为系统的状态矩阵。
2.控制器设计:根据系统的动态性能要求,选择一个适当的闭环极点位置,并计算出一个合适的增益矩阵。
常用的设计方法有极点配置法、最优控制法等。
3.状态反馈器设计:根据控制器设计得到的增益矩阵,利用反馈回路将状态变量与控制输入进行耦合。
状态反馈器的输出为:u=-Kx其中,K为状态反馈增益矩阵。
4.性能评估与调整:通过仿真或实验,评估系统的性能表现,并根据需要对状态反馈器的增益矩阵进行调整。
二、状态观测器的设计:状态观测器的设计目标是根据系统的输出信息,通过一个状态估计器,实时估计系统的状态变量。
其设计步骤如下:1.系统建模:同样地,对被控对象进行数学建模,得到描述系统动态行为的状态空间表达式。
2.观测器设计:根据系统的动态性能要求,选择一个合适的观测器极点位置,以及一个合适的观测器增益矩阵。
常用的设计方法有极点配置法、最优观测器法等。
3.状态估计:根据观测器设计得到的增益矩阵,通过观测器估计系统的状态变量。
状态观测器的输出为:x^=L(y-Cx^)其中,L为观测器增益矩阵,x^为状态估计向量。
4.性能评估与调整:通过仿真或实验,评估系统的状态估计精度,并根据需要对观测器的增益矩阵进行调整。
实验六利用MATLAB设计状态观测器*******学号1121*****实验目的:1、学习观测器设计算法;2、通过编程、上机调试,掌握基于观测器的输出反馈控制系统设计方法。
实验原理:1、全阶观测器模型:()()x Ax Bu L y Cx A LC x Bu Ly =++-=-++由极点配置和观测器设计问题的对偶关系,也可以应用MATLAB 中极点配置的函数来确定所需要的观测器增益矩阵。
例如,对于单输入单输出系统,观测器的增益矩阵可以由函数L=(acker(A ’,C ’,V))’得到。
其中的V 是由期望的观测器极点所构成的向量。
类似的,也可以用L=(place(A ’,C ’,V))’来确定一般系统的观测器矩阵,但这里要求V 不包含相同的极点。
2、降阶观测器模型:ˆˆˆw AwBy Fu =++ b x w Ly =+基于降阶观测器的输出反馈控制器是:ˆˆˆˆ()[()]()b a bb a b w A FK w B F K K L y u K w K K L y=-+-+=--+对于降阶观测器的设计,使用MATLAB 软件中的函数L=(acker(Abb ’,Aab ’,V))’或L=(place(Abb ’,Aab ’,V))’可以得到观测器的增益矩阵L 。
其中的V 是由降阶观测器的期望极点所组成的向量。
实验要求1.在运行以上例程序的基础上,考虑图6.3所示的调节器系统,试针对被控对象设计基于全阶观测器和降阶观测器的输出反馈控制器。
设极点配置部分希望的闭环极点是1,2223j λ=-±,希望的观测器极点是(a ) 对于全阶观测器,18μ=-和 28μ=-; (b ) 对于降阶观测器,8μ=-。
比较系统对下列指定初始条件的响应:(a ) 对于全阶观测器: 1212(0)1,(0)0,(0)1,(0)0x x e e ====(b ) 对于降阶观测器:121(0)1,(0)0,(0)1x x e ===进一步比较两个系统的带宽。
带状态观测器的控制系统综合设计与仿真一、主要技术参数:1.受控系统如图所示:图1 受控系统方框图2.性能指标要求: (1)动态性能指标: 超调量 5%p σ≤; 超调时间 0.5p t ≤秒; 系统频宽 10b ≤ω; (2)稳态性能指标:静态位置误差0=p e (阶跃信号) 静态速度误差2.0≤v e (速度信号) 二、设计思路1、按图中选定的状态变量建立系统的状态空间数学模型。
2、对原系统在Simulink 下进行仿真分析,对所得的性能指标与要求的性能指标进行比较。
3、根据要求的性能指标确定系统综合的一组期望极点。
4、假定系统状态均不可测,通过设计系统的全维状态观测器进行系统状态重构。
5、通过状态反馈法对系统进行极点配置,使系统满足要求的动态性能指标。
6、合理增加比例增益,使系统满足要求的稳态性能指标。
7、在Simulink 下对综合后的系统进行仿真分析,验证是否达到要求的性能指标的要求。
三、实验设计步骤I 、按照极点配置法确定系统综合的方案1、按图1中选定的状态变量建立系统的状态空间数学模型 ① 列写每一个环节的传递函数 由图1有:112235()()510()()10()()U s x s s x s x s s x s x s s ⎧=⎪+⎪⎪=⎨+⎪⎪=⎪⎩②叉乘拉式反变换得一阶微分方程组 由上方程可得12132(5)()5()(10)()10()()()s x s U s s x s x s sx s x s +=⎧⎪+=⎨⎪=⎩即1121232()5()5()()10()10()()()sx s x s U s sx s x s x s sx s x s =-+⎧⎪=-⎨⎪=⎩ 拉式反变换为1121232551010x x U x x x x x ⎧=-+⎪⎪=-⎨⎪⎪=⎩ggg 输出由图1可知为3y x =③用向量矩阵形式表示11223350051010000100x x x x u x x ⎡⎤⎢⎥-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦g g g []001y x =2、对原系统在Simulink 下进行仿真分析,对所得的性能指标与要求的性能指标进行比较原受控系统仿真图如下:图2 原受控系统仿真图原受控系统的阶跃响应如下图:图3 原受控系统的阶跃响应曲线很显然,原系统是不稳定的。
3、根据要求的性能指标确定系统综合的一组期望极点由于原系统为三阶系统,系统有3个极点,选其中一对为主导极点1s和s,另一个为远极点,并且认为系统的性能主要是由主导极点决定的,远2极点对系统的影响很小。
根据二阶系统的关系式,先定出主导极点。
p t =ep n b ωωσ==式中,ξ和n ω为此二阶系统的阻尼比和自振频率。
可以导出:①由p 5%=e σ≤2.996≥,从而有0.69ξ≥,于是选0.707ξ==。
②由0.5p t s ≤0.51nπω=≤ 90.50.707n πω≥≈⨯③由10b ω≤和已选的ξ=得10n ω≤,与②的结果比较,取10n ω=。
这样,便定出了主导极点1,2n s j ξωω=-±远极点应选择使它和原点的距离远大于15s 的点,现取317s s =,因此确定的希望极点为1237.077.077.077.0750s j s j s =-+⎧⎪=--⎨⎪=-⎩ 4、确定状态反馈矩阵K由步骤1所得状态空间方程知,受控系统的特征多项式为32500()det()101001(5)(10)1550s f s sI A s ss s s s s s+=-=-+-=++=++12315,50,0a a a ∴===而由希望的极点构成的特征多项式为*32()(7.077.07)(7.077.07)(50)64.148075000f s s j s j s s s s =+++-+=+++***12364.14,807,5000a a a ∴=== 于是状态反馈矩阵K ∧为[]***332211500075749.14K a a a a a a ∧⎡⎤=---⎣⎦=根据系统的能控性判据判断系统的能控性[]2c c Q b Ab A b rank Q n⎡⎤=⎣⎦=则5251250507500050c Q -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦[]3c rank Q n ==由上式知,原系统是完全能控的。
若做变换X P X ∧=,那么就可建立起给定的(A,B,C )和能控规范型(,,)A B C ∧∧∧之间的关系式1A P AP ∧-=,1B P B ∧-=,C C P ∧=。
32500det()101001(5)(10)1550s sI A s s s s s s s s+-=-+-=++=++12315,50,0a a a ∴===21211001011252551007505001510500050151050505005000P A b Ab b a a a ⎡⎤⎢⎥⎡⎤∴=⎣⎦⎢⎥⎢⎥⎣⎦-⎡⎤⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦1*1000.0200.0200.20.20P PP-∴=⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦[]1ˆ9.8 5.3100K KP-== 极点配置的Matlab 程序如下:A=[-5 0 0;10 -10 0;0 1 0];b=[5;0;0];c=[0 0 1];pc=[-7.07+7.07i,-7.07-7.07i,-50]; K=acker(A,b,pc) 运行结果为: K =9.8280 5.3114 99.96985、确定放大系数K由4知,对应的闭环传递函数为32()64.148075000Ks s s s Φ=+++所以由要求的跟踪阶跃信号的误差0p e =,有[][]03232001()0lim 1()lim 64.148075000lim 1()lim 64.14807500050005000p t s s s s e y t s s s s s s Ks s s s K →∞→→→Φ⎡⎤==-=-⎢⎥⎣⎦+++-=-Φ=+++-=所以5000K =对上面的初步结果,再用对跟踪速度信号的误差要求来验证,即[][]2200323223201()lim ()lim 1lim 1()164.1480764.14807500064.14807lim 64.1480750008070.16140.25000v t s s s s e t y t s s s s s s s s s s s s s s s s s →∞→→→Φ⎡⎤=-=-⎢⎥⎣⎦=-Φ++=+++++=+++==≤显然满足0.2v e ≤的要求,故5000K =。
对此系统进行仿真:图4 受控系统的闭环系统仿真图仿真结果如下:图5 闭环系统的阶跃响应曲线局部放大图:图6 闭环系统阶跃响应曲线局部放大图num=5000;den=[1 64.14 807 5000];sys=tf(num,den);step(sys)[y,t]=step(sys);ymax=max(y);mp=(ymax-1)*100tp=spline(y,t,ymax)mp = 4.2219tp = 0.4686由仿真图经matlanb 计算得: 4.2219%5%p σ=≤0.46860.5p t s s =≤,均满足要求。
II 、观测器的设计假定系统状态均不可测,通过设计系统的全维状态观测器进行系统状态重构1、确定原系统的能观性根据给定的受控系统,求能观测性矩阵及能观测性的秩2o C Q CA CA ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦[]o rank Q n =则[]0010********o rank Q rank n ⎡⎤⎢⎥===⎢⎥⎢⎥-⎣⎦又因之前以求得系统是完全能控的,所以系统既完全能控、又完全能观测。
因此,系统的极点可以任意配置。
2、 计算观测器的反馈矩阵G 该设计中系统的极点为1237.077.077.077.0750s j s j s =-+⎧⎪=--⎨⎪=-⎩取观测器极点,使观测器的极点实部是原系统极点实部的2-3倍。
因此,选择1,2321,150s s =-=-由所取极点,可得期望的闭环系统的特征多项式为*232()(150)(21)192674166150f s s s s s s ∴=++=+++1***23192,6741,66150a a a ===设状态观测器矩阵L 为;123l L l l ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦则闭环系统的特征多项式为:1322332321350(s)1010(l 15)s (15l l 50)s 50l +5l +10l 01+s l f SI A LC s l s s l +=-+=-+=++++++-比较f(s)和f(s*)的系数得33232115192155067415051066150l l l l l l +=⎧⎪++=⎨⎪++=⎩ 解得1233712,4036,177l l l ===所以状态观测器L 为37124036177L ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦则[]5003712()1010040360010101775037121010403601177A Lc -⎡⎤⎡⎤⎢⎥⎢⎥-=--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦因此观测器状态方程为ˆˆ()x 50371253712ˆ1010403604036011770177xA Lc bu Ly x u y =-++--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=--++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦& []ˆˆˆ001ycx x == 3、 画出带观测器的状态反馈系统的闭环图 带观测器状态反馈的闭环系统方框图如图7所示。
图7 带观测器的状态反馈系统由上面计算得出的带观测器状态反馈的闭环系统方框图如下图8 带观测器状态反馈的闭环系统方框图4、在simulink 环境下对控制系统进行仿真分析图九带观测器状态反馈的闭环系统阶跃响应曲线局部放大图如下;图10 带观测器状态反馈的闭环系统阶跃响应曲线注:由于观测性能很好,曲线经无限放大后为两条曲线。
由图可知,系统满足各性能指标。
四、参考书目1、《自动控制原理》主编:李素玲胡建出版社:西安电子科技大学出版社2、《现代控制理论》主编:王金城出版社:化学工业出版社3、《现代控制理论》主编:于长官出版社:哈尔滨工业大学出版社4、《控制系统的MATLAB仿真与设计》主编:王海英袁丽英吴勃出版社:高等教育出版社5、《MATLAB 7辅助控制系统设计与仿真》主编:飞思科技产品研发中心出版社:电子工业出版社6、《控制系统设计与仿真》主编:赵文峰出版社:西安电子科技大学出版社五、设计总结与心得体会不知不觉两周的课程设计马上就结束了,这两周虽然忙碌但也学了不少知识。