名义利率和有效利率的计算.doc
- 格式：doc
- 大小：54.00 KB
- 文档页数：3
下载文档原格式
合集下载
一建 经济 1Z101013 名义利率与有效利率的计算
1Z101013 名义利率与有效利率的计算在复利计算中，利率周期通常以年为单位，它可以与计息周期相同，也可以后同。
当计息周期小于一年时，就出现了名义利率和有效利率的概念。
名义利率的计算有效利率的计算计息周期有效利率计息周期小于（或等于）资金收付周期时的等值计算【考点分析】名义利率和有效利率的含义和大小比较；计息期有效利率的计算；资金收付周期有效利率的计算年有效利率的计算；计息周期小于资金收付周期时的等值计算。
【历年真题】(2006年)某施工企业向银行借款100万元，年利率8%，半年复利计息一次，第三年末还本付息，则到期时企业需偿还银行( )万元。
A.124.00B.125.97C.126.53D.158.69 【答案】C【解析】掌握利用终值和现值以及名义利率与有效利率的换算方法。
本题计息周期是半年，资金收付周期是3年，要求计算的是一次支付的终值。
计算方法有以下两种。
（1）%42%8===m r i53.126%)41(100)1(6=+=+=n i P F （万元）（2）()%16.81%)41(112=-+=-+=meff i i53.126%)16.81(100)1(3=+=+=n i P F （万元）(2007年)已知年利率 12%，每月复利计息一次，则季度的实际利率为( )。
A ．1.003%B ．3.00%C ．3.03%D ．4.00% 【答案】C【解析】已知名义利率r 为12%，计息周期为月，则季度实际利率的计算为：%112%12===m r i()%03.31%)11(113=-+=-+=meff i i(2007年)每半年末存款 2000 元，年利率 4%，每季复利计息一次，2 年末存款本息和为( )万元。
A ．8160.00B ．8243.22C ．8244.45D ．8492.93 【答案】C【解析】已知A 为2000元，r 为4%，计息周期为季度，要求计算2年末的终值F 。
名义利率与有效利率的计算
14250725名义利率与有效利率的计算公式当计息周期小于一年时就出现了名义利率和有效利率
一级建造师
ቤተ መጻሕፍቲ ባይዱ
1Z100000
建设工程经济
QQ：14250725
名义利率与有效利率的计算公式 当计息周期小于一年时，就出现了名义利率和有效利率。 一、名义利率 r：是指计算周期利率 i 乘以一年内的计息周期数 m 所得的年利率。即：r=i×m。 二、有效利率 ieff：指资金在计息中所发生的实际利率，包括计息周期有效利率和年有效利率。 即：年实际利率（即年有效利率 ）：ieff=I/P=(1+r/m)m-1。 三、名义利率与有效利率比较表： 序号 1 2 3 4 5 10% 年名义利率（r） 计息期 年 半年 季度 月 日 年计息次数（m） 1 2 4 12 365 计息期利率（i=r/m） 10%/1 10%/2 10%/4 10%/12 10%/365 10% 5% 2.5% 0.833% 年有效利率 ieff （1+10%/1）1-1 （1+10%/2） -1 （1+10%/4）4-1 （1+10%/12）12-1
2
10% 10.25% 10.38% 10.46%
0.0274% （1+10%/365）365-1 10.51%
注：1、每年计息周期越多，ieff 与 r 相差越大；
一级建造师
ቤተ መጻሕፍቲ ባይዱ
1Z100000
建设工程经济
QQ：14250725
名义利率与有效利率的计算公式 当计息周期小于一年时，就出现了名义利率和有效利率。 一、名义利率 r：是指计算周期利率 i 乘以一年内的计息周期数 m 所得的年利率。即：r=i×m。 二、有效利率 ieff：指资金在计息中所发生的实际利率，包括计息周期有效利率和年有效利率。 即：年实际利率（即年有效利率 ）：ieff=I/P=(1+r/m)m-1。 三、名义利率与有效利率比较表： 序号 1 2 3 4 5 10% 年名义利率（r） 计息期 年 半年 季度 月 日 年计息次数（m） 1 2 4 12 365 计息期利率（i=r/m） 10%/1 10%/2 10%/4 10%/12 10%/365 10% 5% 2.5% 0.833% 年有效利率 ieff （1+10%/1）1-1 （1+10%/2） -1 （1+10%/4）4-1 （1+10%/12）12-1
2
10% 10.25% 10.38% 10.46%
0.0274% （1+10%/365）365-1 10.51%
注：1、每年计息周期越多，ieff 与 r 相差越大；
AFP计算器计算名义年利率与有效年利率的转换
AFP计算器计算名义年利率与有效年利率的转换
AFP考试中，有效利率和名义利率的转换计算很常见，传统算法里，您需要记住转换公式，进行多步计算，利用金考易金融计算器的利率转换功能，您只需输入已知利率，便可轻松计算出对应的名义年利率或有效年利率，简单、方便、准确。
名义年利率：一般由银行给出
有效年利率：不同复利期间现金流的年华收益率
APR：名义年利率、m：1 年中复利期间数量、EAR：有效年利率
名义年利率与有效年利率的转换计算实例
【例】已知名义年利率为8%，按季计息，求有效年利率。
答案：8.24%
普通算法：
金考易金融计算器计算：
金考易金融计算器已更新至2.4 七大功能终生免费使用下载地址：/app/index.htm。
实际利率的两种测算方法比较
实际利率的两种测算方法比较实际利率是指考虑通货膨胀因素后的实际获得利率。
在计算实际利率时，存在两种常见的测算方法：名义利率调整法和利息率调整法。
下面将对这两种方法进行比较。
名义利率调整法是指通过调整名义利率来计算实际利率。
名义利率是指投资或借贷的利率，未考虑通货膨胀因素。
该方法利用通货膨胀率来调整名义利率，得到实际利率。
具体计算公式如下：实际利率=(1+名称利率)/(1+通货膨胀率)-1利息率调整法是指通过调整投资或借贷金额中的利息金额来计算实际利率。
该方法利用通货膨胀率来调整利息金额，得到实际利率。
具体计算公式如下：实际利率=(名义利率-通货膨胀率)/(1+通货膨胀率)这两种方法计算实际利率的核心思想是一致的，即在名义利率的基础上考虑通货膨胀因素。
它们的区别主要体现在计算公式和应用场景上。
名义利率调整法相对更为简单，适用于短期内的利率调整。
由于名义利率是原始利率，常常是固定的，只需通过通货膨胀率调整得到实际利率。
该方法的优点是易于理解和计算，可直接得到实际利率。
然而，它并未考虑到不同时期间的实际通货膨胀情况，可能存在一定的误差。
利息率调整法则更为精确，适用于较长期的资金借贷或投资。
由于利息金额随着时间的推移而变化，可以通过调整利息金额来计算实际利率。
该方法的优点是能够更精确地反映出不同时期的实际通货膨胀情况，并且可以用于比较不同投资或借贷项目的实际获利率。
然而，它的计算较为繁琐，需要考虑到具体的时间和利息变化。
总体来说，这两种方法都有其适用的场景和优缺点。
对于短期、临时性的利率调整，可以使用名义利率调整法，它简单、直接；而对于长期、重要性的利率调整，可以使用利息率调整法，它更为精确、有利于比较不同时期间的实际利率。
需要根据具体情况选择合适的方法来计算实际利率。
为了更准确地计算实际利率，还需要注意以下几点：首先，通货膨胀率的选择应该是合理且合适的，可以使用官方发布的通货膨胀数据或者相关经济指标。
计息有效利率计算公式
计息有效利率计算公式在金融领域，有效利率是指在考虑复利的情况下，计算出的实际利率。
有效利率计算公式是金融学中非常重要的一个概念，它帮助人们更准确地评估投资和贷款的收益率。
本文将介绍有效利率的概念和计算公式，并探讨其在金融实践中的应用。
首先，让我们来了解一下什么是有效利率。
在日常生活中，我们经常会听到年利率、月利率、日利率等概念。
然而，这些利率并不考虑复利的影响。
而在实际情况下，利息是按照复利计算的，也就是说每次计息的时候，都会将上一期的利息加入本金进行下一次的计算。
因此，有效利率就是考虑了复利的影响，计算出的实际利率。
计息有效利率的计算公式如下：\[ (1 + i)^n = (1 + r) \]其中，i为名义利率，n为计息期数，r为有效利率。
在这个公式中，名义利率是指未考虑复利的利率，计息期数是指利息计算的时间段，而有效利率则是我们要求解的目标。
通过这个公式，我们可以通过已知的名义利率和计息期数来计算出有效利率。
现在，让我们通过一个例子来说明如何使用这个公式进行计算。
假设有一笔贷款，名义利率为5%，计息期数为12个月。
我们来计算一下这笔贷款的有效利率。
首先，我们将已知的数据代入公式中：\[ (1 + 0.05)^{12} = (1 + r) \]接下来，我们计算出括号内的结果：\[ (1.05)^{12} = 1.795856 \]然后，我们将结果代入公式中：\[ 1.795856 = (1 + r) \]最后，我们解方程得出有效利率r的值：\[ r = 0.795856 \]因此，这笔贷款的有效利率为7.95856%。
通过这个例子，我们可以看到计息有效利率计算公式的应用。
这个公式能够帮助我们更准确地评估投资和贷款的收益率，从而做出更明智的金融决策。
在金融实践中，有效利率的计算公式被广泛应用于各种金融产品的定价和风险管理中。
比如在债券市场上，投资者可以通过计算债券的有效利率来评估其收益率和风险水平。
名义利率和有效利率的计算
（3）对需要比较的项目或方案应取相同的计算期。
lZl0l021 财务评价指标体系
注：凡是带“动态”、“内部”、“现值”的指标都是动态的；
凡是带“借款”“负债”“偿债”“利息”的指标都是偿债指标。
【2009考题】31．在工程建设中．对不同的新技术、新工艺和新材料应用方案进行经济分析可采用的静态分析方法有( )。
A．净年值法、净现值法、年折算费用法
B．年折算费用法、综合总费用法、净年值法
C．增量投资分析法、净年值法、综合总费用法
D．增量投资分析法、年折算费用法、综合总费用法
多智网校试题解析：D。
影响基准收益率的因素
lZl0l023 影响基准收益率的因素
一、基准收益率的概念（掌握）
也称基准折现率。是投资者以动态的观点所确定的、可接受的、应当获得的最低标准的收益水平。
三、财务评价的程序（了解）
收集数据→编制财务报表→财务评价。具体步骤如下：
1、首先进行融资前的盈利能力分析（论证方案设计的合理性，用于初步投资决策以及方案比选。即考察项目是否可行，是否值得去融资）。
2、再进行融资后分析（通过盈利能力分析和偿债能力分析比选融资方案）。
四、财务评价方案（理解）
（一）独立型方案
如项目完全由企业自有资金投资时，可参考行业的平均收益水平；
假资金来源于自有资金和贷款时，最低收益率不应低于行业平均收益水平与贷款利率的加权平均值。
（2）投资风险。
通常以风险贴补率ｉ2来提高ｉc值。风险越大，贴补率越高。
就风险而言，资金密集>劳动密集；资产专用性强>资产通用性强的；以降低成本为目的<以扩大市场份额为目的；资金雄厚的<资金拮据者。
C．10.25％
D．10.O0%
lZl0l021 财务评价指标体系
注：凡是带“动态”、“内部”、“现值”的指标都是动态的；
凡是带“借款”“负债”“偿债”“利息”的指标都是偿债指标。
【2009考题】31．在工程建设中．对不同的新技术、新工艺和新材料应用方案进行经济分析可采用的静态分析方法有( )。
A．净年值法、净现值法、年折算费用法
B．年折算费用法、综合总费用法、净年值法
C．增量投资分析法、净年值法、综合总费用法
D．增量投资分析法、年折算费用法、综合总费用法
多智网校试题解析：D。
影响基准收益率的因素
lZl0l023 影响基准收益率的因素
一、基准收益率的概念（掌握）
也称基准折现率。是投资者以动态的观点所确定的、可接受的、应当获得的最低标准的收益水平。
三、财务评价的程序（了解）
收集数据→编制财务报表→财务评价。具体步骤如下：
1、首先进行融资前的盈利能力分析（论证方案设计的合理性，用于初步投资决策以及方案比选。即考察项目是否可行，是否值得去融资）。
2、再进行融资后分析（通过盈利能力分析和偿债能力分析比选融资方案）。
四、财务评价方案（理解）
（一）独立型方案
如项目完全由企业自有资金投资时，可参考行业的平均收益水平；
假资金来源于自有资金和贷款时，最低收益率不应低于行业平均收益水平与贷款利率的加权平均值。
（2）投资风险。
通常以风险贴补率ｉ2来提高ｉc值。风险越大，贴补率越高。
就风险而言，资金密集>劳动密集；资产专用性强>资产通用性强的；以降低成本为目的<以扩大市场份额为目的；资金雄厚的<资金拮据者。
C．10.25％
D．10.O0%
利率定价方式转换公式
利率定价方式转换公式一、引言在金融领域，利率是非常重要的概念之一，它直接影响到各种金融产品的定价和投资收益。
利率定价方式转换公式则是计算不同利率之间的转换关系的数学公式。
本文将介绍利率定价方式转换公式的概念和应用。
二、利率定价方式转换公式的定义利率定价方式转换公式是指根据不同利率计算相应利率的数学关系表达式。
它可以帮助人们在不同利率之间进行换算和转换，从而更好地理解和比较不同利率所带来的影响。
三、利率定价方式转换公式的应用1. 从名义利率到实际利率的转换：名义利率是指未经考虑通胀因素的利率，而实际利率则是考虑了通胀因素后的利率。
两者之间的转换可以使用以下公式：实际利率 = （1 + 名义利率）/（1 + 通货膨胀率） - 12. 从年利率到月利率的转换：年利率和月利率之间的转换可以使用以下公式：月利率 = （1 + 年利率）^(1/12) - 13. 从复利到单利的转换：复利是指将利息加入本金后再计算利息的方式，而单利则是只计算本金的利息。
复利和单利之间的转换可以使用以下公式：单利 = 复利 / （1 + 利率 * 时间）四、利率定价方式转换公式的实例为了更好地理解利率定价方式转换公式的应用，以下举例说明：1. 假设某银行的年利率为5%，求该银行的月利率。
根据以上提到的转换公式，可以得到：月利率 = （1 + 5%）^(1/12) - 1计算可得，该银行的月利率约为0.4167%。
2. 假设某债券的名义利率为6%，通货膨胀率为2%，求该债券的实际利率。
根据以上提到的转换公式，可以得到：实际利率 = （1 + 6%）/（1 + 2%） - 1计算可得，该债券的实际利率为3.9216%。
3. 假设某投资的复利为1000元，利率为10%，时间为2年，求该投资的单利收益。
根据以上提到的转换公式，可以得到：单利 = 1000 / （1 + 10% * 2）计算可得，该投资的单利收益为500元。
五、结论利率定价方式转换公式是金融领域中重要的工具之一，它可以帮助人们在不同利率之间进行换算和转换。
名义利率与有效利率
由表可见，当计息期数m=1时，名义利率等于实际利率。
当m>1时，实际利率大于名义利率，且m越大，即一年中计算复利的 有限次数越多，则年实际利率相对与名义利率就越高。
2023/12/27
东南大学交通学院 冒刘燕
6
年名义利率为12％，不同计息期的实际利率
计算复利的方式 按年
按半年 按季 按月 按日
一年中的计息期数 1 2 4 12
2023/12/27
东南大学交通学院 冒刘燕
21
计息期间的存款放在期末，计息期间的提款放在 期初，计息期分界点处的支付保持不变。
现金流量如图所示：年利率为12%,每季度计息1次， 求年末终值F是多少？
100
100
0 1 2 3 4 5 6 7 8 9 10 11 12月
300
300
100
2023/12/27
东南大学交通学院 冒刘燕
25
名义利率( r )与实际利率( i )关系 i = r/m
年有效利率( I ) I= (1+r/m)m-1
连续计息 F= Per , I’ = er-1
2023/12/27
东南大学交通学院 冒刘燕
26
年每半年等额年末存款200元，问与其等值的第0年的现 值是多少？ 解：计息期为半年的有效利率i=r/m＝12％÷2＝6％,
计息期数n=m×年数＝2×3＝6次 则P=A ×（P/A, i, n）＝200 ×（P/A, 6％, 6）
＝200×4.9173＝983.46元
2023/12/27
东南大学交通学院 冒刘燕
300
+100
＝112.36元
本章小结
现金流量图
资金的时间价值
名义利率和有效利率
运用利息公式要注意的问题
方案的初始投资P，假设发生在寿命期初； 寿命期内各项收入或支出，均假设发生在各期 的期末； 本期的期末即是下一期的期初 寿命期末发生的本利和F，记在第n期期末； 等额支付系列A，发生在每一期的期末。 当问题包括P，A时，P 在第一期期初，A在 第一期期末 当问题包括F，A时，F和A同时在最后一期期 末发生。
年平均利润＝6000／5＝1200， 年平均折旧＝8000／5=1600， 投资收益率＝（1200+1600）/8000=35％。
简单收益率
指标评价
优点 • 计算简便直观 • 有利于对企业经理人员的评价 缺点 • 没有考虑货币的时间价值 • 它不能反映项目计算期不同时间的获益
净现值
概念
净现值
判别标准
若NPV > 0,该投资方案的原始投资能够回收，能够 支付资本成本费用，能够获得大于资本成本的盈利 的水平，因而应该接受该投资方案； 若NPV = 0，则原始投资能够被回收，能够支付资 本成本费用，这样该投资方案处于盈亏平衡点位置； 如果NPV < 0，则原始投资可能无法回收，可能支 付不起资本成本费用，因此该投资方案应被拒绝
计息期短于支付期
例7：年利率12%，每季度计息一次，每年年末 支付500元，连续支付6年，求其第0年的现值 为多少？
解：其现金流量如图
i=12%
方法一，计息期向支付期靠拢，求出支付期的有效 利率。 4 年有效利率 i 1 0.12 1 12.55%
4
P 500 P
按给定的折现率（或基准折现率）将投资方案在 NP V F (1 i) 寿命期内各年净现金流量折现到期初的现值代数 和就是净现值。若以NPV符号表示净现值，则
方案的初始投资P，假设发生在寿命期初； 寿命期内各项收入或支出，均假设发生在各期 的期末； 本期的期末即是下一期的期初 寿命期末发生的本利和F，记在第n期期末； 等额支付系列A，发生在每一期的期末。 当问题包括P，A时，P 在第一期期初，A在 第一期期末 当问题包括F，A时，F和A同时在最后一期期 末发生。
年平均利润＝6000／5＝1200， 年平均折旧＝8000／5=1600， 投资收益率＝（1200+1600）/8000=35％。
简单收益率
指标评价
优点 • 计算简便直观 • 有利于对企业经理人员的评价 缺点 • 没有考虑货币的时间价值 • 它不能反映项目计算期不同时间的获益
净现值
概念
净现值
判别标准
若NPV > 0,该投资方案的原始投资能够回收，能够 支付资本成本费用，能够获得大于资本成本的盈利 的水平，因而应该接受该投资方案； 若NPV = 0，则原始投资能够被回收，能够支付资 本成本费用，这样该投资方案处于盈亏平衡点位置； 如果NPV < 0，则原始投资可能无法回收，可能支 付不起资本成本费用，因此该投资方案应被拒绝
计息期短于支付期
例7：年利率12%，每季度计息一次，每年年末 支付500元，连续支付6年，求其第0年的现值 为多少？
解：其现金流量如图
i=12%
方法一，计息期向支付期靠拢，求出支付期的有效 利率。 4 年有效利率 i 1 0.12 1 12.55%
4
P 500 P
按给定的折现率（或基准折现率）将投资方案在 NP V F (1 i) 寿命期内各年净现金流量折现到期初的现值代数 和就是净现值。若以NPV符号表示净现值，则
名义利率与有效利率的计算
2
10% 10.25% 10.38% 10.46%
0.0274% （1+10%/365）365-1 10.51%
注：1、每年计息周期越多，ieff 与 r 相差越大；
一级建造师1Z100000建源自工程经济QQ：14250725
名义利率与有效利率的计算公式 当计息周期小于一年时，就出现了名义利率和有效利率。 一、名义利率 r：是指计算周期利率 i 乘以一年内的计息周期数 m 所得的年利率。即：r=i×m。 二、有效利率 ieff：指资金在计息中所发生的实际利率，包括计息周期有效利率和年有效利率。 即：年实际利率（即年有效利率 ）：ieff=I/P=(1+r/m)m-1。 三、名义利率与有效利率比较表： 序号 1 2 3 4 5 10% 年名义利率（r） 计息期 年 半年 季度 月 日 年计息次数（m） 1 2 4 12 365 计息期利率（i=r/m） 10%/1 10%/2 10%/4 10%/12 10%/365 10% 5% 2.5% 0.833% 年有效利率 ieff （1+10%/1）1-1 （1+10%/2） -1 （1+10%/4）4-1 （1+10%/12）12-1
10% 10.25% 10.38% 10.46%
0.0274% （1+10%/365）365-1 10.51%
注：1、每年计息周期越多，ieff 与 r 相差越大；
一级建造师1Z100000建源自工程经济QQ：14250725
名义利率与有效利率的计算公式 当计息周期小于一年时，就出现了名义利率和有效利率。 一、名义利率 r：是指计算周期利率 i 乘以一年内的计息周期数 m 所得的年利率。即：r=i×m。 二、有效利率 ieff：指资金在计息中所发生的实际利率，包括计息周期有效利率和年有效利率。 即：年实际利率（即年有效利率 ）：ieff=I/P=(1+r/m)m-1。 三、名义利率与有效利率比较表： 序号 1 2 3 4 5 10% 年名义利率（r） 计息期 年 半年 季度 月 日 年计息次数（m） 1 2 4 12 365 计息期利率（i=r/m） 10%/1 10%/2 10%/4 10%/12 10%/365 10% 5% 2.5% 0.833% 年有效利率 ieff （1+10%/1）1-1 （1+10%/2） -1 （1+10%/4）4-1 （1+10%/12）12-1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
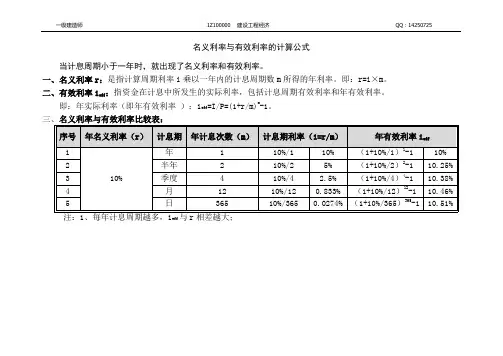
命题考点三名义利率和有效利率的计算
【教材解读】
一、名义利率的计算
所谓名义利率r是指计息周期利率i乘以一年内的计息周期数m所得的年利率，即：r=i×m
通常所说的年利率都是名义利率。
二、有效利率的计算
有效利率是指资金在计息中所发生的实际利率，包括计息周期有效利率和年有效利率两种情况。
(1)计息周期有效利率，即计息周期利率i的计算：
(2)年有效利率，即年实际利率。
若用计息周期利率来计算年有效利率，并将年内的利息再生因素考虑进去，这时所得的
年利率称为年有效利率(又称年实际利率)。
三、名义利率与实际利率的换算
名义利率与实际利率的换算见表1-2。
【命题考点】
名义利率；计息周期有效利率；年有效利率；名义利率与实际利率的换算。
【分析预测】
(1)基本上每年会单独考核一道有关名义利率与实际利率换算的题目，而且在其他的计算题中也会涉及名义利率与实际利率换算的问题。
(2)考生要根据表中的换算公式总结出规律来记忆，基本换算公式中的两个m的含义不同，考生一定要区分。
【考题回顾】
【2010年度考试真题】
年利率8%，按季度复利计息，则半年期实际利率为()。
A．4.00%
B．4.04%
C．4.07%
D．4.12%
【答案】B本题考核的是名义利率和实际利率的换算。
提示：r/m中的m等于一年计息的次数(本题中，一年有四个季度，就计息四次)，公式中的指数m等于所求实际利率的周期与计息周期的比值。
【2009年度考试真题】
已知年名义利率为10%，每季度计息1次，复利计息，则年有效利率为()。
A．10.47%
B．10.38%
C．10.25%
D．10.00%
【答案】B本题考核的是年有效利率的计算。
【2007年度考试真题】
已知年利率12%，每月复利计息一次，则季实际利率为()。
A．1.003%
B．3.00%
C．3.03%
D．4.00%
【答案】C本题考核的是季实际利率的计算。
有效利率=r/m=12%/12=1%，则季有效利率=(1+12%/12)3-1=3.03%。
【2006年度考试真题】
年名义利率为i，一年内计息周期数为m，则年有效利率为()。
【答案】B本题考核的是年有效利率的计算公式。
年有效利率的计算公式为F=(1+i/m)m-1。
【典型习题】
1.若名义利率一定，年有效利率与一年中计息周期数m的关系为()。
A．计息周期增加，年有效利率不变
B．计息周期增加，年有效利率减小
C．计息周期增加，年有效利率增加
D．计息周期减小，年有效利率增加
2.某笔贷款的利息按年利率为10%，每季度复利计息，其贷款的年有效利率为()。
A．10.38%
B．10.46%
C．10.00%
D．10.25%
3.年名义利率8%，按季计算，则利息期有效利率和年有效利率分别是()。
A．2.O0%，8.00%
B．2.00%，8.24%
C．2.06%，8.00%
D．2.06%，8.24%
4.现在存款2000元，年利率10%，半年复利一次，则第6年年末存款金额为()。
A．1254.23
B．2543.12
C．2865.14
D．3591.71
【答案】1.C2.A3.B4.D。