八年级数学知识点：确定圆的条件

初中数学圆的定义重要知识点总结初中数学圆的定义重要知识点总结
这一章节为大家带来的圆的定义包括了基础的圆的圆的定义和圆的集合定义。

圆的定义
在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆。

固定的.端点O叫做圆心。

(确定圆的位置)
线段OA叫做半径。

(确定圆的大小)
记法：以点O为圆心的圆，记作“⊙O”，读作“圆O”
注意：⑴圆指的是“圆周”而不是“圆面”。

是“铁环”，不是“烙饼”。

⑵半径指的是线段，为了方便也把半径的长称为半径。

圆的确定
⑴一个圆心一个半径
⑵圆心、圆上一个一个的已知点
⑶直径
圆的集合定义
⑴角平分线上的点到角两边的距离相等。

到角两边距离相等的点在角的平分线上。

所以：角平分线可以看做是到角的两边距离相等的点的集合。

⑵线段的垂直平分线上的点到线段的两个端点的距离相等。

到线段的两个端点的距离相等的点在线段的垂直平分线上。

线段的垂直平分线可以看做是和线段两个端点距离相等的点的集合。

*把一个图形看成是满足某种条件的点的集合，必须符合：
a. 图形上的每一点都满足某个条件，
b. 满足某个条件的每一个点，都在这个图形上。

⑶圆上各点到定点(圆心O)的距离都等于定长(半径r)，到定点的距离等于定长的点都在同一个圆上。

(圆心为O，半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形)
圆的集合定义：圆是到定点的距离等于定长的点的集合。

相信参加过竞赛测试的同学们都遇见关于圆的集合定义试题。

圆的基本概念和性质要点一、圆的定义及性质1.圆的定义(1)动态：如图，在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A 随之旋转所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径. 以点O为圆心的圆，记作“⊙O”，读作“圆O”．要点诠释：①圆心确定圆的位置，半径确定圆的大小；确定一个圆应先确定圆心，再确定半径，二者缺一不可；②圆是一条封闭曲线.(2)静态：圆心为O，半径为r的圆是平面内到定点O的距离等于定长r的点的集合.要点诠释：①定点为圆心，定长为半径；②圆指的是圆周，而不是圆面；③强调“在一个平面内”是非常必要的，事实上，在空间中，到定点的距离等于定长的点的集合是球面，一个闭合的曲面.2.圆的性质①旋转不变性：圆是旋转对称图形，绕圆心旋转任一角度都和原来图形重合；圆是中心对称图形，对称中心是圆心；②圆是轴对称图形：任何一条直径所在直线都是它的对称轴.或者说，经过圆心的任何一条直线都是圆的对称轴.要点诠释：①圆有无数条对称轴；②因为直径是弦，弦又是线段，而对称轴是直线，所以不能说“圆的对称轴是直径”，而应该说“圆的对称轴是直径所在的直线”.3.两圆的性质两个圆组成的图形是一个轴对称图形，对称轴是两圆连心线（经过两圆圆心的直线叫做两圆连心线）.要点二、与圆有关的概念1.弦：连结圆上任意两点的线段叫做弦.直径：经过圆心的弦叫做直径.弦心距：圆心到弦的距离叫做弦心距.要点诠释：直径是圆中通过圆心的特殊弦，也是圆中最长的弦，即直径是弦，但弦不一定是直径.2. 弧弧：圆上任意两点间的部分叫做圆弧，简称弧.以A、B为端点的弧记作，读作“圆弧AB”或“弧AB”.半圆：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆；优弧：大于半圆的弧叫做优弧；劣弧：小于半圆的弧叫做劣弧.要点诠释：①半圆是弧，而弧不一定是半圆；②无特殊说明时，弧指的是劣弧.3.同心圆与等圆圆心相同，半径不等的两个圆叫做同心圆.圆心不同，半径相等的两个圆叫做等圆.同圆或等圆的半径相等.4.等弧:在同圆或等圆中，能够完全重合的弧叫做等弧.要点诠释：①等弧成立的前提条件是在同圆或等圆中，不能忽视；②圆中两平行弦所夹的弧相等.垂径定理知识点一、垂径定理1.垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧.2.推论：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧.要点诠释：(1)垂径定理是由两个条件推出两个结论，即⎩⎨⎧⇒⎭⎬⎫平分弦所对的弧平分弦垂直于弦直径(2)这里的直径也可以是半径，也可以是过圆心的直线或线段. 知识点二、垂径定理的拓展根据圆的对称性及垂径定理还有如下结论：（1）平分弦（该弦不是直径）的直径垂直于弦，并且平分弦所对的两条弧； （2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧. 要点诠释：在垂径定理及其推论中：过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧，在这五个条件中，知道任意两个，就能推出其他三个结论.（注意：“过圆心、平分弦”作为题设时，平分的弦不能是直径）弧、弦、圆心角、圆周角要点一、弧、弦、圆心角的关系1.圆心角定义:如图所示，∠AOB的顶点在圆心，像这样顶点在圆心的角叫做圆心角．2.定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．3.推论：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦也相等．在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧也相等．要点诠释：(1)一个角要是圆心角，必须具备顶点在圆心这一特征；(2)注意定理中不能忽视“同圆或等圆”这一前提.要点二、圆周角1.圆周角定义：像图中∠AEB、∠ADB、∠ACB这样的角，它们的顶点在圆上，并且两边都与圆相交的角叫做圆周角．2.圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．3.圆周角定理的推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．要点诠释：(1)圆周角必须满足两个条件：①顶点在圆上；②角的两边都和圆相交.(2)圆周角定理成立的前提条件是在同圆或等圆中.4.圆内接四边形：（1）定义: 圆内接四边形：顶点都在圆上的四边形，叫圆内接四边形．（2）性质：圆内接四边形对角互补，外角等于内对角（即它的一个外角等于它相邻内角的对角）．5.弦、弧、圆心角、弦心距的关系：在同圆或等圆中，弦，弧，圆心角，弦心距等几何量之间是相互关联的，即它们中间只要有一组量相等，(例如圆心角相等)，那么其它各组量也分别相等(即相对应的弦、弦心距以及弦所对的弧也分别相等)。

专题30 圆的基本性质【知识要点】知识点一圆的基础概念圆的概念：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫圆．这个固定的端点O叫做圆心，线段OA叫做半径．以O点为圆心的圆记作⊙O，读作圆O．特点：圆是在一个平面内，所有到一个定点的距离等于定长的点组成的图形．确定圆的条件：⑴圆心；⑵半径，⑶其中圆心确定圆的位置，半径长确定圆的大小．补充知识：1）圆心相同且半径相等的圆叫做同圆；2）圆心相同，半径不相等的两个圆叫做同心圆；3）半径相等的圆叫做等圆．弦的概念：连结圆上任意两点的线段叫做弦。

经过圆心的弦叫做直径，并且直径是同一圆中最长的弦．⏜，读作弧AB．在同圆或弧的概念：圆上任意两点间的部分叫做圆弧，简称弧．以A、B为端点的弧记作AB等圆中，能够重合的弧叫做等弧．圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．在一个圆中大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧．弦心距概念：从圆心到弦的距离叫做弦心距．弦心距、半径、弦长的关系：（考点）知识点二垂径定理垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；常见辅助线做法（考点）：1）过圆心，作垂线，连半径，造RT△，用勾股，求长度；2）有弧中点，连中点和圆心，得垂直平分．知识点一圆的基础概念圆的概念：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫圆．这个固定的端点O叫做圆心，线段OA叫做半径．以O点为圆心的圆记作⊙O，读作圆O．特点：圆是在一个平面内，所有到一个定点的距离等于定长的点组成的图形．确定圆的条件：⑷圆心；⑸半径，⑹其中圆心确定圆的位置，半径长确定圆的大小．补充知识：1）圆心相同且半径相等的圆叫做同圆；2）圆心相同，半径不相等的两个圆叫做同心圆；3）半径相等的圆叫做等圆．弦的概念：连结圆上任意两点的线段叫做弦。

初中数学圆的知识点〔通用4篇〕篇1：初中数学圆知识点 1.圆的定义(1)在一个平面内，线段OA绕它的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆。

固定的端点O 叫做圆心，线段OA叫做半径，如右图所示。

(2)圆可以看作是平面内到定点的间隔等于定长的点的集合，定点为圆心，定长为圆的半径。

说明：圆的位置由圆心确定，圆的大小由半径确定，半径相等的两个圆为等圆。

2.圆的有关概念(1)弦：连结圆上任意两点的线段。

(如右图中的CD)。

(2)直径：经过圆心的弦(如右图中的AB)。

直径等于半径的2倍。

(3)弧：圆上任意两点间的局部叫做圆弧。

(如右图中的CD、CAD)其中大于半圆的弧叫做优弧，如CAD，小于半圆的弧叫做劣弧。

(4)圆心角：如右图中∠COD就是圆心角。

3.圆心角、弧、弦、弦心距之间的关系。

(1)定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦的弦心距相等。

(2)推论：在同圆或等圆中，假如两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等。

4.过三点的圆。

(1)定理：不在同一条直线上的三点确定一个圆。

(2)三角形的外接圆圆心(外心)是三边垂直平分线的交点。

5.垂径定理。

垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

推论：(1)①平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧;②弦的垂直平分线经过圆心，并且平分弦所对的两条弧;③平分弦所对的一条弦的直径，垂直平分弦，并且平分弦所对的另一条弧。

(2)圆的两条平行弦所夹的弧相等。

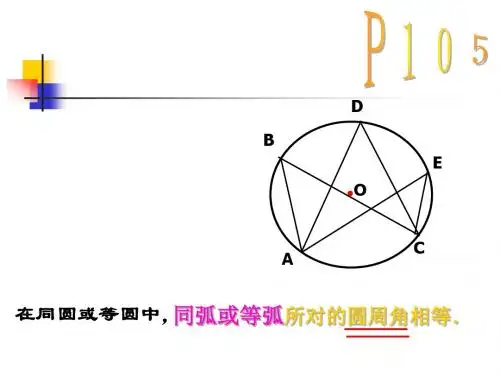
6.与圆相关的角(1)与圆相关的角的定义①圆心角：顶点在圆心的角叫做圆心角②圆周角：顶点在圆上且两边都和圆相交的角叫做圆周角。

③弦切角：顶点在圆上，一边和圆相交，另一连轴和圆相切的角叫做弦切角。

(2)与圆相关的角的性质AB①圆心角的度数等于它所对的弦的度数;②一条弧所对的圆周角等于它所对的圆心角的一半; ③同弧或等弧所对的圆周角相等; ④半圆(或直径)所对的圆周角相等; ⑤弦切角等于它所夹的弧所对的圆周角;⑥两个弦切角所夹的弧相等，那么这两个弦切角也相等;⑦圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角。

2021年八年级数学《暑假作业�新课程无忧衔接》（苏科版）考点13确定圆的条件【知识点梳理】确定圆的条件1.经过一个已知点能作无数个圆2.经过两个已知点A、B能作无数个圆，这些圆的圆心在线段AB的垂直平分线上；3.不在同一直线上的三个点确定一个圆.4.经过三角形各个顶点的圆叫做三角形的外接圆，外接圆的圆心叫做三角形的外心，这个三角形叫做圆的内接三角形.【新课程预习练·无忧衔接】一、单选题1．小明不慎把家里的圆形镜子打碎了（如图），其中四块碎片如图所示，为了配到与原来大小一样的圆形镜子，小明带到商店去的碎片应该是（）A．①B．①C．①D．①【答案】A【分析】要确定圆的大小需知道其半径．根据三角形外接圆的圆心的确定方法知第①块可确定半径的大小．【详解】解：第①块出现一段完整的弧，可在这段弧上任做两条弦，作出这两条弦的垂直平分线，两条垂直平分线的交点就是圆心，进而可得到半径的长．故选：A．【点睛】考查了确定圆的条件，解题的关键是熟练掌握：圆上任意两弦的垂直平分线的交点即为该圆的圆心．2．已知O的半径为6cm，点P在O上，则OP的长为（）A．4cm B．5cm C．6cm D．8cm【答案】C【分析】根据点在圆上，点到圆心的距离等于圆的半径求解．【详解】①①O的半径为6cm，点P在①O上，①OP=6cm．故选：C．【点睛】考查了点与圆的位置关系：设①O的半径为r，点P到圆心的距离OP=d，则有：点P在圆外①d＞r；点P在圆上①d=r；点P在圆内①d＜r．3．O的直径为10cm，圆心O到点A的距离为6cm，则点A与O的位置关系是（）A．点A在O外B．点A在O上C．点A在O内D．无法确定【答案】A，点在圆上，d＜r，点在【分析】由点与圆心的距离d与圆的半径r的关系：d＞r，点在圆外，d r圆内，可得答案．【详解】解：O的直径为10cm，∴O的半径为5cm，圆心O到点A的距离为6cm，而6＞5，∴点A在O外，故选：.A=，【点睛】考查的是点与圆的位置关系，掌握点与圆心的距离d与圆的半径r的关系：d＞r，点在圆外，d r 点在圆上，d＜r，点在圆内，是解题的关键．4．在ABC中，①C=90°，AB=5，BC=4，以A为圆心，以3为半径画圆，则点C与①A的位置关系是（）A．在①A外B．在①A上C．在①A内D．不能确定【答案】B【分析】根据勾股定理求出AC的值，根据点与圆的位关系特点，判断即可．【详解】解：由勾股定理得：3,AC===①AC=半径=3，①点C与①A的位置关系是：点C在①A上，故选：B．【点睛】考查了点与圆的位置关系定理和勾股定理等知识点的应用，点与圆（圆的半径是r，点到圆心的距离是d）的位置关系有3种：d=r时，点在圆上；d＜r点在圆内；d＞r点在圆外5．下列四个命题：①等边三角形是中心对称图形；①在同圆或等圆中，相等的弦所对的圆周角相等；①三角形有且只有一个外接圆；①平分弦的直径垂直于弦；①过三点有且只有一个圆．其中真命题的个数有（）A．1个B．2个C．3个D．4个【答案】A【分析】根据中心对称图形的定义、圆周角的性质、三角形的外接圆、垂径定理、圆的确定依次判断即可.【详解】①等边三角形是中心对称图形不是中心对称图形，故错误；①在圆中一条弦所对的圆周角有两个，则在同圆或等圆中，相等的弦所对的圆周角不一定相等，故错误；①三角形有且只有一个外接圆，故正确；①平分弦（不是直径）的直径垂直于弦，故错误；①过不在同一直线上的三点有且只有一个圆，故错误；故是真命题的是①，故选：A.【点睛】考查真命题：正确的命题是真命题，正确掌握中心对称图形的定义、圆周角的性质、三角形的外接圆、垂径定理、圆的确定是解此题的关键.6．如图，在等边①ABC中，AB＝12，点D在AB边上，AD＝4，E为AC中点，P为①ABC内一点，且①BPD ＝90°，则线段PE的最小值为（）A．2B．2C．4D．8【答案】C【分析】以BD为直径作①O，连接OE交①O于点P，则OE的长度最小，即EP最小，根据勾股定理即可求出答案．【详解】解：以BD为直径作①O，连接OE交①O于点P，则OE的长度最小，即EP最小，过点E作EF①AB于点F，在Rt①AEF中，①A＝60°，AE＝6，①AF＝3，EF＝在Rt①OEF中，EF＝OF＝5，①OE＝①PE＝4，即线段PE的最小值为4，故选：C．【点睛】考查了圆的性质，等边三角形的性质，勾股定理，根据题意判断出EP最小的情况是解题关键．7．已知①ABC的外接圆①O，那么点O是①ABC的（）A．三条中线交点B．三条高的交点C．三条边的垂直平分线的交点D．三条角平分线交点【答案】C【分析】根据三角形外接圆圆心的确定方法，结合垂直平分线的性质，即可求得.【详解】已知①O是①ABC的外接圆，那么点O一定是①ABC的三边的垂直平分线的交点，故选：C．【点睛】考查三角形外接圆圆心的确定，属基础题.8．下列说法正确的是（）A．经过三个点一定可以作一个圆B．圆中优弧所对的弦一定比劣弧所对的弦长C．圆上任意两点都能将圆分成一条劣弧和一条优弧D．任意一个三角形有且只有一个外接圆【答案】D【分析】根据优弧，劣弧的定义，“不在同一条直线上的三点，确定一个圆”，三角形的外接圆的定义，逐一判断选项，即可得到答案．【详解】①经过不在同一条直线上的三点，一定可以作一个圆，①A错误，①在同一个圆中，优弧所对的弦一定比劣弧所对的弦长，不同圆中，无法比较，①B错误，①当圆上两点的连线是直径时，两条弧都是半圆，①C错误，①任意一个三角形有且只有一个外接圆，①D正确．故选D．【点睛】考查圆的相关概念，掌握优弧，劣弧的定义，“不在同一条直线上的三点，确定一个圆”，三角形的外接圆的定义9．小明不慎把家里的圆形玻璃打碎了，带如图的玻璃碎片到商店配到与原来大小一样的圆形玻璃，以下是工作人员排乱的操作步骤：①连接AB和BC；①在玻璃碎片上任意找不在同一直线上的三点A、B、C；①以点O为圆心，OA为半径作O；①分别作出AB和BC的垂直平分线，并且相交于点O；正确的操作步骤是（）A．①①①①B．①①①①C．①①①①D．①①①①【答案】B【分析】根据题意可知所求的圆形玻璃是①ABC的外接圆，从而可以解答本题．【详解】由题意可得，所求的圆形玻璃是①ABC的外接圆，①这块玻璃镜的圆心是①ABC三边垂直平分线的交点，①正确的操作步骤是①①①①故选：B．【点睛】考查垂径定理的应用．10．下列语句中，正确的是A．同一平面上三点确定一个圆B．菱形的四个顶点在同一个圆上C．三角形的外心是三角形三边垂直平分线的交点D．三角形的外心到三角形三边的距离相等【答案】C【分析】根据确定圆的条件，三角形的外心的定义，以及圆内接四边形的对角互补的性质对各选项分析判断后利用排除法．【详解】A选项：同一平面上三点必须不在同一直线上才可以确定一个圆，故选项A错误；B选项：菱形的对角相等，但不一定互补，所以四个顶点不一定在同一个圆上，故选项B错误；C选项：三角形的外心是三角形三边中垂线的交点，是外心定义，故选项C正确；D选项：三角形的外心到三角形三个定点的距离相等，到三边的距离不一定相等，故选项D错误；故选C.【点睛】考查了三角形的外接圆与外心，圆内接四边形的性质，确定圆的条件，掌握三角形的外接圆与外心，圆内接四边形的性质，确定圆的条件是解题的关键.11．如图①，若BC是Rt①ABC和Rt①DBC的公共斜边，则A、B、C、D在以BC为直径的圆上，则叫它们“四点共圆”．如图①，①ABC的三条高AD、BE、CF相交于点H，则图①中“四点共圆”的组数为（）A．2B．3C．4D．6【答案】D【分析】根据两个直角三角形公共斜边时，四个顶点共圆，结合图形求解可得．【详解】解：如图，以AH为斜边的两个直角三角形，四个顶点共圆（A、F、H、E），以BH为斜边的两个直角三角形，四个顶点共圆（B、F、H、D），以CH为斜边的两个直角三角形，四个顶点共圆（C、D、H、E），以AB为斜边的两个直角三角形，四个顶点共圆（A、E、D、B），以BC为斜边的两个直角三角形，四个顶点共圆（B、F、E、C），以AC为斜边的两个直角三角形，四个顶点共圆（A、F、D、C），共6组．故选D．【点睛】考查四点共圆的判断方法．解题的关键是明确有公共斜边的两个直角三角形的四个顶点共圆．12．下列四个命题中，正确的个数有（）①圆的对称轴是直径所在的直线；①经过三点可以确定一个圆；①弦长相等，则弦所对的弦心距也相等；①平分弦的直径垂直于弦；①三角形的外心到三角形各顶点的距离都相等.A．1个B．2个C．3个D．4个【答案】B【分析】根据对称轴的概念、过三点的圆、弧、弦、圆心角的关系定理、三角形的外心的概念、垂径定理判断即可．【详解】解：圆的对称轴是直径所在的直线，①正确；经过不在同一直线上的三点可以确定一个圆，①错误；在同圆或等圆中弦长相等，则弦所对的弦心距也相等，①错误；平分弦（不是直径）的直径垂直于弦，①错误；三角形的外心到三角形各顶点的距离都相等，①正确；故选B．【点睛】考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．二、填空题13．如图，一圆弧过方格的格点A、B、C，在方格中建立平面直角坐标系，使点A的坐标为（﹣3，2），则该圆弧所在圆心坐标是_____【答案】（﹣2，﹣1）【分析】根据外心的定义作图即可．【详解】如图：分别作AC与AB的垂直平分线，相交于点O，则点O即是该圆弧所在圆的圆心．①点A的坐标为（﹣3，2），①点O的坐标为（﹣2，﹣1）．【点睛】考查了三角形外心，熟练掌握外心的定义，准确求作线段的垂直平分线是解题的关键．14．如图，点A，B，C均在6×6的正方形网格格点上，过A，B，C三点的外接圆除经过A，B，C三点外还能经过的格点数为________．【答案】5个【分析】连接AB、BC，然后分别作AC、AB的垂直平分线，进而可作①ABC的外接圆，然后根据图形可求解．【详解】如解图，连接AB、BC，先作AC，AB边的垂直平分线，两条垂直平分线的交点即为圆心O，再以OA 为半径作圆．格点与圆相交的有8个点．除A，B，C三点外，还有5个点．故答案为5个．【点睛】考查圆的作图，熟练掌握圆的尺规作图是解题的关键．15．如图，在平面直角坐标系x O y中，点A的坐标为（0，7），点B的坐标为（0，3），点C的坐标为（3，0），那么①ABC的外接圆的圆心坐标为____．【答案】(5，5)【分析】分别作出三角形任意两边的垂直平分线得到圆心的位置，进而得出答案．【详解】①B(0，3)，C(3，0)，①在网格中，BC可以看作边长为3的正方形的对角线，根据网格特征及正方形对角线互相垂直平分，分别作出AB、BC的垂直平分线，交于点E，则点E即为外接圆的圆心，如图所示，①A(0，7)，B(0，3)，①点E纵坐标为5，①由图可得，E(5，5)．故答案为：(5，5)．【点睛】考查了坐标与图形，三角形的外接圆与外心，熟练掌握定义及性质是解题的关键．16．如图1是一扇旋转门，它由一个圆柱形空间的三片旋转翼组成，三片旋转翼将圆柱形空间等分为三个扇形空间，AB与CD处为出入口，在旋转过程中，当某一片旋转翼的一端与点B重合时，另两片中的一片旋转翼的一端与点D重合；继续旋转，当某一片旋转翼的一端与点A重合时，另两片中的一片旋转翼的一端则与点C重合。