优化设计的数学模型
- 格式：pdf
- 大小：493.98 KB
- 文档页数：7
下载文档原格式
合集下载
优化设计的数学模型由设计变量目标函数和约束条件三部分组成
西 南
问题的方法叫图解法。
科 技
２、图解法的步骤
大 学
1）确定设计空间；
网 络
2）作出约束可行域；
教
育 系
3）画出目标函数的一簇等值线；
列 课
4）最后判断确定易优点。
程
5.1.6 优化问题的图解法
由图解法可解，
例5.2是一个二维
线性优化问题。
其可行域见图5.6，
目标函数的等值
西 南 科
线见图5.3，将这 两个图叠加在一
教 育
一种约束条件。是对设计变量所加的间接变量。
系 列
例如：零件的强度条件，刚度条件，稳定性条
课 程
件均属于性能约束。
5.1.5 约束条件与可行域
3、可行域
每一个不等式或等式约束都将设计空间分为两
个部分，满足所有约束的部分形成一个交集，该交 集称为此约束问题的可行域，记作φ。
西 南
可行域可看作满足所有约束条件的设计点的集
课 程
∴ x=1 为所求解。
5.1.2 数学模型的一般形式
实例可以看出，优化设计的数学模型由设计
变量、目标函数和约束条件三部分组成，可写成
以下统一形式：
设计变量
求变量
x1,x2, …..,xn
目标函数
西 南
使极小化函数 f(x1,x2, …..,xn)
科 技
满足约束条件
不等式约束条件
大
学 网
gu(x1,x2,…..,xn)≤0 (u=1,2,…m) 等式约束条件
西 南
g2 ( X ) x12 x2 1 0
科 技
g3( X ) x1 0
大
学
第一章 优化设计数学模型
参数最优化问题的关键是要建立设计参数与优化目标、约束 条件之间的数值关系。这实质上就是要建立一个优化数学模型。 那么，这种优化数学模型如何建立呢?下面就来讨论这个问题。
一、引 例 二、优化设计的数学模型 三、建立优化设计数学模型的几个实例 四、优化设计数学模型的评价
我们先用一个实例来分析优化设计的数学模型
任何一个机械设计方案一般都是由若干个设计参数所决定的。 在这些设计参数中，一部分是按具体要求事先给定的，它们在 优化设计过程中始终保持不变，故称为预定参数。例如我们在 零件和结构件设计时，经常是先选定材料，因而弹性模量和许 用应力就是预定参数。另一部分参数在优化设计过程中是可以 变化的，如构件截面尺寸大小等，这类设计参数就称为设计变 量。 以设计变量为坐标轴所构成的空间称设计空间。一般情况下， 设计变量的个数就是设计空间的维数。如设计变量为2个，则设 计空间就是二维的(即构成一个平面)。如有n个设计变量，则构 成n维设计空间(n维向量空间)。设计变量通常用下列向量表示： X＝(x1，x2，…，xn)T 该向量X即表示n维设计空间中的一个点。
从管柱优化设计这一具体例子可以看到，优化设计就 是寻求件的情况下使目标函数值最小(或者最大)。
通过管柱优化设计的例子，我们对什么是优化设计有了进一步 的直观认识。下面我们将进一步用数学形式来描述优化设计， 以便更深入地掌握优化设计的本质。首先我们来讨论一下在优 化设计中经常碰到的几个基本概念。 1．设计变量与设计空间 2．约束条件及可行区与非可行区 3．目标函数 4．优化设计的数学模型
一维迭代 无约束最优化方法
牛顿法；梯度法；共轭方向法；变尺度方法； 坐标轮换法；鲍威尔法
约束最优化问题变换技术
约束优化问题 无约束问题 线性规划（单纯形法）
优化设计的数学模型
优化设计的应用
生产计划优化
生产计划优化
通过数学模型，对生产计划进行优化，以最小化成本、最大化利润为目标，制定最优的生产计划 。
生产调度优化
利用数学模型对生产调度进行优化，以提高生产效率、减少生产成本、缩短生产周期。
资源分配优化
通过数学模型对资源进行合理分配，以最大化资源利用率、最小化资源浪费为目标，实现资源的 最优配置。
总结词
生产计划优化是利用数学模型对生产过程中的资源、时间和成本进行合理配置， 以提高生产效率和降低成本。
详细描述
生产计划优化案例包括对生产流程、生产计划、生产调度等方面的优化。通过 建立数学模型，对生产计划进行优化，可以减少生产过程中的浪费，提高生产 效率，降低生产成本。
物流优化案例
总结词
物流优化是利用数学模型对物流运输过程中的路线、时间和 成本进行合理规划，以提高物流效率和降低物流成本。
线性规划
线性规划是数学优化技术中的一 种，它通过找到一组变量的最优 组合，使得一个线性目标函数达
到最大或最小值。
线性规划问题通常表示为在一组 线性不等式约束下最大化或最小
化一个线性目标函数。
线性规划问题可以通过使用单纯 形法、对偶理论等算法进行求解。
非线性规划
非线性规划是数学优化技术中的一种， 它通过找到一组变量的最优组合，使 得一个非线性目标函数达到最大或最 小值。
04
优化算法的进展
遗传算法
1
遗传算法是一种模拟生物进化过程的优化算法， 通过选择、交叉和变异等操作，寻找问题的最优 解。
2
遗传算法适用于解决大规模、多变量和非线性优 化问题，尤其在组合优化、机器学习、数据挖掘 等领域有广泛应用。
3
优化设计数学模型
优化设计数学模型数学模型是对实际问题进行抽象和描述，以便能够进行解析和求解的一种工具。
一个优化设计的数学模型应该具备几个重要的特点，包括问题的明确定义，适当选择自变量和因变量，建立合适的约束条件，选择合适的目标函数，并采用适当的解析方法求解。
下面是一个关于优化设计数学模型的优化方法和步骤的详细介绍。
首先，一个优化设计数学模型的第一步就是对问题进行明确和准确的定义。
这包括了理解问题的背景、目的和限制条件，并将问题转化为数学形式。
问题定义的准确性和完整性对后续的模型建立和求解都非常重要。
其次，模型的自变量和因变量的选择非常关键。
自变量是我们可以进行调整和控制的变量，而因变量是我们希望最小化或最大化的目标。
根据问题的具体情况，选择适当的自变量和因变量是非常重要的。
然后，建立约束条件是模型设计的又一个重要步骤。
约束条件可以是关于自变量和因变量之间的限制条件，也可以是关于问题特定的限制条件。
约束条件的准确性和合理性对于模型的求解有很大的影响。
接下来，选择适当的目标函数是优化设计数学模型的关键。
目标函数是我们希望最小化或最大化的量，通常与问题的目的和要求密切相关。
目标函数的选择应考虑问题的实际需求，并与约束条件相匹配。
最后，选择适当的解析方法求解数学模型是一个重要的步骤。
解析方法可以是数学优化方法，如线性规划、非线性规划或动态规划，也可以是数值优化方法，如遗传算法或模拟退火算法。
根据问题的复杂性和求解的需求，选择合适的解析方法非常重要。
在进行数学模型的优化设计时，还需要对模型进行验证和优化。
模型验证是通过与实际数据和结果进行比较，以验证模型的准确性和可靠性。
对模型进行优化是通过调整和改进模型的相关参数和约束条件，以提高模型的性能和效果。
总结起来，优化设计数学模型的优化方法和步骤包括问题的明确定义，适当选择自变量和因变量，建立合适的约束条件，选择合适的目标函数，并采用适当的解析方法求解。
通过模型的验证和优化，可以提高模型的准确性和可靠性，从而为实际问题的优化设计提供有效的数学支持。
第一章 优化设计的数学模型
2012-3-24
11
1-1 优化设计实例
上述生产计划问题可归结为： 上述生产计划问题可归结为： 生产计划问题可归结为 求变量 使函数 满足条件
x1 , x 2 f ( x1 , x2 ) = 60 x1 + 120 x2
最大化
g1 ( x1 , x 2 ) = 9 x1 + 4 x 2 ≤ 360 g 2 ( x1 , x2 ) = 3 x1 + 10 x2 ≤ 300
为此，自古以来， 为此，自古以来，慎重的工程设计人员常常提供几种候 选设计方案，再从中择其“最优” 选设计方案，再从中择其“最优”者。
2012-3-24
2
常规设计与优化设计的区别
常规设计的特点
由于设计时间和经费的限制， 由于设计时间和经费的限制 ， 使所设计的候选方案的数目受 到很大限制。因此用常规的设计方法进行工程设计， 到很大限制 。 因此用常规的设计方法进行工程设计 ， 特别是当影 响设计的因素很多时， 只能得到有限候选方案中的最好方案、 响设计的因素很多时 ， 只能得到有限候选方案中的最好方案 、 不 可能得到一切可能方案的“最优设计方案” 可能得到一切可能方案的“最优设计方案”。
g 3 ( x1 , x 2 ) = 4 x1 + 5 x 2 ≤ 200
g 4 ( x1 , x2 ) = x1 ≥ 0
g 5 ( x1 , x 2 ) = x 2 ≥ 0
这就是该问题的数学模型。 这就是该问题的数学模型。
2012-3-24
12
1-1 优化设计实例
其中： 其中： f ( x1 , x2 )
x1 , x2
f ( x1 , x2 ) =
π
4
2 ( x12 − x2 )
优化设计的数学模型
—— —— —— —— —— —— ——
机械优化设计数学模型的一般形式： 机械优化设计数学模型的一般形式： 数学模型的一般形式 设 X =[x1,x2 ,…,xn]T ,x min. f(x) = f(x1, x2 ,…,xn ) ,x X∈Rn 不等式约束） （不等式约束） 1,2,…,m s.t. gu(x) ≤ 0 u = 1,2, ,m 等式约束） 1,2,…, hv(x) = 0 v = 1,2, , p< n （等式约束
* X 是极小点。 2) = (1,1,−
x1 =， 1
* 。
， x2 = 1
代入原函数，得函数的极小 x = −2
3
f (X ) = 0
例2-3 MATLAB 2-3 MATLAB实现，用M文件求函数的极值点： M
%例2-3 求函数的极值 syms x1 x2 x3 %定义函数f中的符号变量 f=2*x1^2+5*x2^2+x3^2+2*x2*x3+2*x1*x3-6*x2+3; %函数f的表达式 disp( '函数f的表达式：' ) pretty(simplify(f)); %按数学形式显示函数f latex(f); %符号表达式按LaTeX格式输 出 %计算函数的1阶偏导数
解：在MATLAB命令窗口输入主函数
syms t f=t^4-t^2-2*t+5; [x1,x2]=minJT(f,0,0.1)
第3章 一维搜索方法与MATLAB实现
各阶主子式的值为
a11 = 4 > 0
a11 a12
a12 4 0 = = 40 > 0 a22 0 10
a11 a12 a21 a22 a31 a32
3-优化设计的数学模型
D
d
为了简化目标函数，可以省略空心轴截
面面积的表达式中的常数，用一个与空
心轴截面面积等价的定量指标来建立目
标函数
min
f ( X ) x12
x
2 2
确定约束条件
g1(X ) x2 0
内径为正值
g2 ( X ) x1 x2 0
外径大于内径
g
3
(
X)Biblioteka 16 Mx1 x14 x24
0
g4
0.7E
x1 x2 2x1
1.5
16 Mx1
x14
x
4 2
0
扭转强度条件 扭皱稳定条件
这是一个有四个约束条件的二维非线性规划问题。
优化设计建模小结
优化设计的数学模型是优化设计问题的 数学表达形式，它反映了优化设计问题 中各个主要因素之间的内在联系。因此， 工程技术人员运用掌握专业技术理论和 数学知识，正确地从实际工程优化设计 问题中抽象出数学模型，是进行工程优 化设计的关键，也是优化设计必须解决 的首要问题。
根据材料力学，扭转轴的最大工作剪切应力
max
16 MD (D4 d
4
)
扭转轴的扭皱稳定临界剪应力
b
0.7E
Dd 2D
1.5
式中，E为材料弹性模量 ，d 与 D是轴的内径与外径。
确定设计变量和目标函数
将与空心轴截面面积直接相关的外径 D 和内径 d 为作为设计变量，即
X
x1
x2
教材习题1 提示
简支梁危险截面的弯曲应力和抗弯截面模量 的表达式分别为
Pl
22
W
W bh2 6
简支梁支承中点的最大挠度和惯性矩的表达
优化设计的数学模型
(1) 约束又可按其数学表达形式分成等式约束 不等 等式约束和不等 等式约束 式约束两种类型。 式约束 。 (2) 根据约束的性质可以把它们区分成： 性能约束——针对性能要求而提出的限制条件称 性能约束 作性能约束 例如 性能约束。例如 性能约束 例如，选择某些结构必须满足受力的强 度、刚度或稳定性等要求； 边界约束——只是对设计变量的取值范围加以限 边界约束 制的约束称作边界约束 例如 边界约束。例如 边界约束 例如，允许机床主轴选择的 尺寸范围，对轴段长度的限定范围就属于边界约束。
满足上述要求的计算过程或计算方法就是所谓的 数值迭代方法。 数值迭代过程 或 数值迭代方法
数值迭代的基本思想 基本思想是：从某一个选定的初始点 基本思想 X (0) 出发，按照某种最优化方法所规定的原则，确定适 当的方向和步长，获得第一个新的修改设计点 X (1) ， 计算此点的目标函数值 F ( X (1) ) 使满足：
二、设计点与设计空间
设计点: 设计点 X(k)（x1(k), x2 (k), …,x n(k)）： 是设计向量X(k)的端点，代表设计空间中的一 个点，也代表第 k 个设计方案。可能是可行方案、 也可能不是可行方案。 设计空间 Rn ： 以x1, x2 , …,xn 为坐标轴，构成 n 维欧氏实空 间Rn。它包含了所有可能的设计点，即所有设计方 即所有设计方 案。 欧氏空间 欧氏空间: 空间
§3-1设计变量 设计变量
一、设计变量
设计变量： 变化的， 设计变量：在优化设计过程中是变化的，需要优选的 量。 设计参数： 设计参数：在优化设计过程中保持不变或预先确定 数值。 可以是几何参数 几何参数：例，尺寸、形状、位置 几何参数 运动学参数： 运动学参数 例，位移、速度、加速度 动力学参数： 动力学参数 例，力、力矩、应力 其它物理量 例，质量、转动惯量、频率、挠度 物理量： 物理量 非物理量： 例，效率、寿命、成本 非物理量 设计向量： 设计向量：用 X =[x1, x2 , …,x n]T 表示， 是定义在 n 维欧氏空间中的一个向量。
满足上述要求的计算过程或计算方法就是所谓的 数值迭代方法。 数值迭代过程 或 数值迭代方法
数值迭代的基本思想 基本思想是：从某一个选定的初始点 基本思想 X (0) 出发，按照某种最优化方法所规定的原则，确定适 当的方向和步长，获得第一个新的修改设计点 X (1) ， 计算此点的目标函数值 F ( X (1) ) 使满足：
二、设计点与设计空间
设计点: 设计点 X(k)（x1(k), x2 (k), …,x n(k)）： 是设计向量X(k)的端点，代表设计空间中的一 个点，也代表第 k 个设计方案。可能是可行方案、 也可能不是可行方案。 设计空间 Rn ： 以x1, x2 , …,xn 为坐标轴，构成 n 维欧氏实空 间Rn。它包含了所有可能的设计点，即所有设计方 即所有设计方 案。 欧氏空间 欧氏空间: 空间
§3-1设计变量 设计变量
一、设计变量
设计变量： 变化的， 设计变量：在优化设计过程中是变化的，需要优选的 量。 设计参数： 设计参数：在优化设计过程中保持不变或预先确定 数值。 可以是几何参数 几何参数：例，尺寸、形状、位置 几何参数 运动学参数： 运动学参数 例，位移、速度、加速度 动力学参数： 动力学参数 例，力、力矩、应力 其它物理量 例，质量、转动惯量、频率、挠度 物理量： 物理量 非物理量： 例，效率、寿命、成本 非物理量 设计向量： 设计向量：用 X =[x1, x2 , …,x n]T 表示， 是定义在 n 维欧氏空间中的一个向量。
优化设计的数学模型由设计变量目标函数和约束条件三部分组成
络 教
hv(x1,x2,…..,xn)=0 (v=1,2,…p)
育
系
列
课
程
实例 2
某工厂生产甲、乙两种产品。生产每种产品所
需的材料、工时、电力和可获得的利润，以及能够
提供的材料、工时和电力见下表。试确定两种产品
西 每天的产量，以使每天可能获得的利润最大。
南
科 技
产品 材料 /kg 工时/h 电力/(kw.h) 利润/元
求变量 x1, x2 使函数 f (x1, x2 ) 60x1 120x极2大化
西 南
满足条件 g1(x1, x2 ) 9x1 4x2 360
科
技 大
g2 (x1, x2 ) 3x1 10x2 300
学 网 络
g3 (x1, x2 ) 4x1 5x2 200
教 育
西
1）目标函数的等值面，其数学表达式为f
南 科
(x)=c。
技 大
在这种线或面上所有点的函数值均相等，
学 网
因此，这种线或面就称为函数的等值线或等值
科 技
２）离散变量：只能在给定数列或集合中取
大 学
值的变量。
网 络
注：少数的机械优化问题的设计变量是离
教 育 系
散变量，对于离散变量的优化问题，可先将其 视为连续变量，用常规的优化方法最优解。
列
课
程
5.1.3 设计变量与设计空间
•3 设计空间
们形若成n的个向设量计X变=[量x1x,x1,2x,…2,…xnx]nT相的互n。
学 网
因此，目标函数的最小值及其对应的设计变量的
络 教
取值称为设计问题的最优解。
育 系
优化问题的数学模型及基本要素
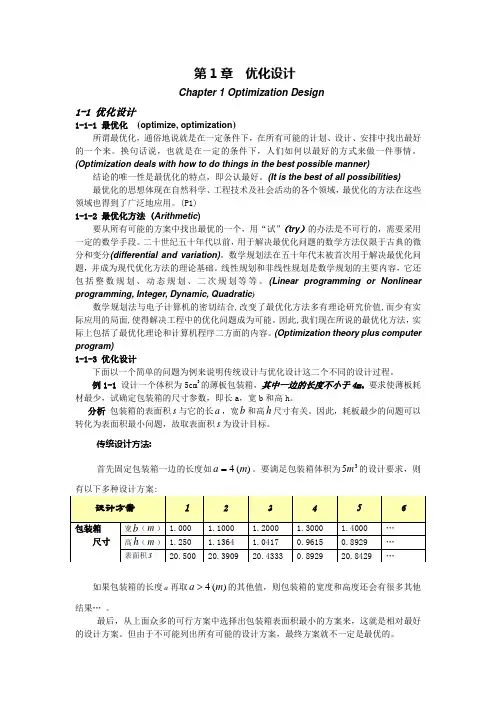
第1章 优化设计Chapter 1 Optimization Design1-1 优化设计1-1-1 最优化 (optimize, optimization )所谓最优化，通俗地说就是在一定条件下，在所有可能的计划、设计、安排中找出最好的一个来。
换句话说，也就是在一定的条件下，人们如何以最好的方式来做一件事情。
(Optimization deals with how to do things in the best possible manner)结论的唯一性是最优化的特点，即公认最好。
(It is the best of all possibilities) 最优化的思想体现在自然科学、工程技术及社会活动的各个领域，最优化的方法在这些领域也得到了广泛地应用。
(P1)1-1-2 最优化方法 (Arithmetic )要从所有可能的方案中找出最优的一个，用“试”（try ）的办法是不可行的，需要采用一定的数学手段。
二十世纪五十年代以前，用于解决最优化问题的数学方法仅限于古典的微分和变分(differential and variation)。
数学规划法在五十年代末被首次用于解决最优化问题，并成为现代优化方法的理论基础。
线性规划和非线性规划是数学规划的主要内容，它还包括整数规划、动态规划、二次规划等等。
(Linear programming or Nonlinear programming, Integer, Dynamic, Quadratic )数学规划法与电子计算机的密切结合,改变了最优化方法多有理论研究价值,而少有实际应用的局面,使得解决工程中的优化问题成为可能。
因此,我们现在所说的最优化方法，实际上包括了最优化理论和计算机程序二方面的内容。
(Optimization theory plus computer program)1-1-3 优化设计下面以一个简单的问题为例来说明传统设计与优化设计这二个不同的设计过程。
03有关优化设计数学模型
1)当原数据出自理论计算公式时，可直接按原 计算公式来编制程序。
2)当原数据虽没有理论公式，但有一定的函数 关系并以一些离散点的函数值形式给出时，可 用质值或曲线拟合的方法编制一个子程序。必 要时为提高精度或简化函数表达式，可逐段进 行拟合。
3) 当原数据给出的是一组无一定函数关系的具 体数字时，可把表中的数据以数组形式来标识存 储。如齿轮的标准模数系列，是一维数表，可用 一维数组来标识存储。数组括号中的标量就是相 应模数的代码，如J＝3时，标识M＝2．5MM。 在优化设计时，只要给定标识符的标量值，即可
2)有效性。对同一问题在同一精度同一初始 条件下，求解优化问题所用计算时间的多少。
3)简便性。指人们所需要准备的工作量大小、 包括学习使用程序，编制针对具体优化问题的 辅助子程序，程序中所需调用参数的多少，调 试操作复杂程度，输入、输出控制方式等等。
实际使用中，除了个别简单问题和学习需要外， 一般应尽量选用现有优化程序。因为使用通用 优化程序，对不同类型的具体优化问题仅仅只 要按规定格式编写目标函数相约束条件子程序。
计算结果的分析与处理
由于机械设计问题的复杂性，或建模中可能 的失误，对优化计算得到的结果要进行仔细的分 析，有时还需要进行适当的处理，以保证设计的 合理性。
对设计变量进行过尺度变换或离散型变量作 为连续型变量来计算的，则需对其计算结果相应 进行反变换和圆整为离散值的处理。
目标函数的最优值．是对计算结果进行分析的 重要依据，将它与原始方案的目标函数值作比较， 可看出优化设计的效果。若给几个不同的初始点进 行计．从其结果可以大致判断出全局最优解。
有关优化设计数学模型 及其求解中的几个问题
建立正确的数学模型，是解决最优化设 计问题的关键。总的说来对数学模型的基本要 求为：
2)当原数据虽没有理论公式，但有一定的函数 关系并以一些离散点的函数值形式给出时，可 用质值或曲线拟合的方法编制一个子程序。必 要时为提高精度或简化函数表达式，可逐段进 行拟合。
3) 当原数据给出的是一组无一定函数关系的具 体数字时，可把表中的数据以数组形式来标识存 储。如齿轮的标准模数系列，是一维数表，可用 一维数组来标识存储。数组括号中的标量就是相 应模数的代码，如J＝3时，标识M＝2．5MM。 在优化设计时，只要给定标识符的标量值，即可
2)有效性。对同一问题在同一精度同一初始 条件下，求解优化问题所用计算时间的多少。
3)简便性。指人们所需要准备的工作量大小、 包括学习使用程序，编制针对具体优化问题的 辅助子程序，程序中所需调用参数的多少，调 试操作复杂程度，输入、输出控制方式等等。
实际使用中，除了个别简单问题和学习需要外， 一般应尽量选用现有优化程序。因为使用通用 优化程序，对不同类型的具体优化问题仅仅只 要按规定格式编写目标函数相约束条件子程序。
计算结果的分析与处理
由于机械设计问题的复杂性，或建模中可能 的失误，对优化计算得到的结果要进行仔细的分 析，有时还需要进行适当的处理，以保证设计的 合理性。
对设计变量进行过尺度变换或离散型变量作 为连续型变量来计算的，则需对其计算结果相应 进行反变换和圆整为离散值的处理。
目标函数的最优值．是对计算结果进行分析的 重要依据，将它与原始方案的目标函数值作比较， 可看出优化设计的效果。若给几个不同的初始点进 行计．从其结果可以大致判断出全局最优解。
有关优化设计数学模型 及其求解中的几个问题
建立正确的数学模型，是解决最优化设 计问题的关键。总的说来对数学模型的基本要 求为：
优化设计数学模型的建立
优化设计数学模型的建立是一个复杂的过程，需要综合考虑问题的各个要素，将实际的问题抽象化，并转化为数学语言。
以下是一个基本的步骤和要点：
1. 明确问题：首先，需要明确优化设计的目标。
这可能涉及到最小化成本、最大化效益、优化性能等。
同时，也要明确约束条件，例如资源限制、时间限制、技术限制等。
2. 建立数学模型：将问题抽象化，用数学符号和公式来表示问题。
这通常涉及到变量（决策变量）、函数（目标函数）和约束条件。
例如，在最小化成本的问题中，可以将成本作为目标函数，各种影响成本的因素作为决策变量，而技术、资源等限制作为约束条件。
3. 选择合适的数学工具：根据问题的性质，选择合适的数学方法和算法。
例如，线性规划、非线性规划、整数规划、动态规划等。
这些方法和算法可以帮助解决各种复杂的优化问题。
4. 参数化和数据收集：根据建立的模型，需要收集相关的数据和参数。
这些数据和参数应该能够支持模型的建立和验证。
5. 模型验证：在模型建立后，需要进行验证以确保其准确性和有效性。
这可以通过对比历史数据、进行模拟实验或与其他模型进行比较来完成。
6. 模型实施与优化：一旦模型通过验证，就可以开始实施优化方案。
在实施过程中，可能需要对模型进行持续的优化和调整，以适应不断变化的情况和新的数据。
通过以上步骤，可以建立一个有效的优化设计数学模型，为决策提供科学依据，提高设计的效率和效果。
优化设计
五、例题
一维搜索的最优化方法
在确定了搜索区间以后，一维优化 的任务是采用某种方法将此区间逐步缩 小，在满足收敛精度或迭代精度的情况 下，使其达到包含极小点的一个很小的 邻域，以取得一个近似的最优点。 一维优化的方法有如下几种： 1、格点法 2、黄金分割法 3、二次插值法
格点法
一）基本思路
先将搜索区间[a,b]分成若干等分，计算出n个等分点 的目标函数值. 再通过比较,找出其中的最小点f(xm)， 则该点的两个邻近点围成缩短了的新区间[x m-1 , xm+1] 。
优化设计的数学模型
一、设计变量 一个设计方案可以用一组基本参数的数值 来表示，需要在优化设计过程中不断进行修改、 调整，一直处于变化的状态的基本参数称为设 计变量。 设计变量的全体实际上是一组变量，可以 用列向量表示
x [ 1 x2 xn ]
T
其中任一个特定的向量都可以称为一个 “设计”。由n个设计变量为坐标所组成的实 空间称作设计空间。记作 n R
一维搜索方法概述
一维搜索法就是一元函数极小化的数值迭代算 法，其求解过程称为一维搜索。 一维搜索法是非线性优化方法的基本算法， 多元函数的迭代算法都可以归结为在一系列逐 步产生的下降方向上的一维搜索。例如：下图 所示的二维优化的例子。 注意：二维优化问题的一维搜索方向s(k) 是由具体的优化方法决定的，迭代公式 x(k+1)=x(k)+(k)s(k) 因此，二维优化问题min f(x1, x2)就可以表示 为一维优化问题min f( )
=f(x(2))
x1 x2 x3
x
x1 x2 x3
前进计算
f
f1≥f2 是
x(3)=x(2)+h、 f3=f(x(3))
一维搜索的最优化方法
在确定了搜索区间以后，一维优化 的任务是采用某种方法将此区间逐步缩 小，在满足收敛精度或迭代精度的情况 下，使其达到包含极小点的一个很小的 邻域，以取得一个近似的最优点。 一维优化的方法有如下几种： 1、格点法 2、黄金分割法 3、二次插值法
格点法
一）基本思路
先将搜索区间[a,b]分成若干等分，计算出n个等分点 的目标函数值. 再通过比较,找出其中的最小点f(xm)， 则该点的两个邻近点围成缩短了的新区间[x m-1 , xm+1] 。
优化设计的数学模型
一、设计变量 一个设计方案可以用一组基本参数的数值 来表示，需要在优化设计过程中不断进行修改、 调整，一直处于变化的状态的基本参数称为设 计变量。 设计变量的全体实际上是一组变量，可以 用列向量表示
x [ 1 x2 xn ]
T
其中任一个特定的向量都可以称为一个 “设计”。由n个设计变量为坐标所组成的实 空间称作设计空间。记作 n R
一维搜索方法概述
一维搜索法就是一元函数极小化的数值迭代算 法，其求解过程称为一维搜索。 一维搜索法是非线性优化方法的基本算法， 多元函数的迭代算法都可以归结为在一系列逐 步产生的下降方向上的一维搜索。例如：下图 所示的二维优化的例子。 注意：二维优化问题的一维搜索方向s(k) 是由具体的优化方法决定的，迭代公式 x(k+1)=x(k)+(k)s(k) 因此，二维优化问题min f(x1, x2)就可以表示 为一维优化问题min f( )
=f(x(2))
x1 x2 x3
x
x1 x2 x3
前进计算
f
f1≥f2 是
x(3)=x(2)+h、 f3=f(x(3))
第2章优化设计的数学模型
第2章优化设计的数学模型第2章优化设计的数学模型优化设计的数学模型是对优化设计⼯程问题的数学描述，它包含设计变量、⽬标函数和设计约束三个基本要素。
2.1设计变量2.1.1基本参数1、定义：在设计过程中进⾏选择变化并最终确定的各项独⽴参数称为设计变量。
2、说明：在设计选择过程中，这些设计变量是变量，但它们⼀旦被确定后，设计对象也就完全确定了。
最优化设计是研究怎样合理地优选这些设计变量的⼀种现代设计⽅法。
在设计过程中，凡根据设计要求事先给定的，不是设计变量⽽是设计常量。
2.1.2设计⽅案的表现形式1、设计空间：由n 个设计变量为坐标所组成的时空间称作设计空间。
2、设计变量的表⽰法（1）坐标表⽰法：⼀维问题→⼀个设计变量→数轴上的⼀个点⼆维问题→两个设计变量→平⾯直⾓坐标系上的向量三维问题→三个设计变量→空间直⾓坐标系的向量n 维问题→n 个设计变量→n 维超越空间的向量⼀个“设计”⽅案，可⽤设计空间中的⼀点表⽰，此点可看成是设计变量向量的端点（始点取在坐标原点），称作设计点。
也即：在设计空间中的⼀个点，对应于⼀组设计变量的值，代表⼀个设计⽅案。
设计空间包含了该项设计所有可能的设计⽅案。
（2）向量表⽰法：⼆维问题→⼆维向量T x x X ],[21=三维问题→三维向量T x x x X ],,[321= n 维问题→n 维向量T n x x x X ],,,[21 = 2.1.3．设计变量的选取1、维数：设计变量的数⽬称为最优化问题的维数。
如有n个设计变量则称为n维问题。
2、常选⽤的设计变量（1）结构的总体布置尺⼨，如中⼼距。
（2）元件的⼏何尺⼨：长度，截⾯尺⼨，某些点的坐标值。
（3）材料的⼒学和物理特性：重量、惯性矩、⼒或⼒矩等。
通常选择的设计变量都是构件的⼏个尺⼨，因为这不仅可使问题相对简单些，⽽且由于很多实际结构的⼏个关系和材料特性已决定的缘故。
决定结构布置情况的设计变量的选取要复杂些。
较困难的是选取表⽰材料特性的变量，因为通常所⽤材料的特性是离散值，选择这些变量时出现了设计变量不连续变化的这⼀特殊问题。
优化设计的数学模型及基本要素
第2章 优化设计的数学模型及基本要素Chapter 2 Mathematical Modeling for Optimization2-1 数学模型的建立 (mathematical modeling)建立数学模型，就是把实际问题按照一定的格式转换成数学表达式的过程。
数学模型建立的合适、正确与否，直接影响到优化设计的最终结果。
建立数学模型，通常是根据设计要求，应用相关基础和专业知识，建立若干个相应的数学表达式。
如机械结构的优化设计，主要是根据力学、机械设计基础等专业基础知识及机械设备等专业知识来建立数学模型的。
当然，要建立能够反映客观实际的、比较准确的数学模型并非容易之事。
数学模型建的过于复杂，涉及的因素太多，数学求解时可能会遇到困难；而建的太简单，又不接近实际情况，解出来也无多大意义。
因此，建立数学模型的原则：抓主要矛盾，尽量使问题合理简化。
Principle ：The problem is simplified as much as possible.由于设计对象千变万化，即使对同一个问题，由于看问题的角度不同，数学模型建的可能也不一样。
建立数学模型不可能遵循一个不变的规则，本课也不准备把大量的时间花在数学模型的建立上。
仅想以几个例子来演示一下数学模型的建立过程，使学生从中得到一些启发。
Exp. 2-1例2-1 用宽度为cm 24，长度cm 100的薄铁皮做成cm 100长的梯形槽，确定折边的尺寸x 和折角θ（如图 2-1所示），使槽的容积最大。
解: 由于槽的长度就是板的长度，槽的梯形截面积最大就意味着其容积最大。
因此，该问题就由，求体积最大变成求截面积最大。
槽的梯形截面积为： 图 2-1⨯=21S 高 ⨯（上底边+下底边） 其中，上底边=x 224-；下底边=θcos 2224x x +-；高=θsin x 定义：该优化设计问题的目标函数是槽的梯形截面积S ，设计变量为θ,x 。
问题可以简单地归结为：选择适当的设计变量θ,x ，在一定的限制条件下，使目标函数S 达到最大，限制条件为: 120,20<<<<x πθExp. 2-2例2-2 如图 2-2所示是一根简化了的机床主轴。
第八章 优化设计的数学建模
第八章 优化设计的数学建模
由于数学模型本身存在一定的近似性， 追求理论上的严格最优解， 并无太大的实际意义。 因此，解决实际工程问题时，没有必要过分追求 精确的模型及其最优解
第一节 数学建模方法
在优化设计中，建立一个正确的数学模型，需 要具备专业基础理论、数学分析工具以及优化 设计理论和计算机求解等方面的知识。 1.提出要解决的具体问题； 2.找出要解决问题的主要参数； 3.找出要解决问题的次要参数，并分析次要参 数对主要参数的影响程度，或者是否有主要参 数决定次要参数的经验公式，行业推荐标准等；
第八章 优化设计的数学建模
本章知识要点及学习要求
1. 掌握建立数学模型的方法 2. 了解优化设计在求解实际问题时面临的困难 3. 基本掌握提高优化设计效率的方法和技巧
第八章 优化设计的数学建模
优化设计的数学模型仅仅是对实际问题进行简素， 优化设计所得到的最优解显然不应该是实际问题的 “最优解答”。 但这是一个良好的基础，在此基础上，设计人员根 据全面的判断，还可以进行一些必要的修改。
①数学模型的类型：如有约束或无约束，是连续 变量还是含有离散变量，函数是非线性的还是全 为线性的等； ②数学模型的规模：即设计变量维数和约束条件 数的多少； ③模型中函数的性质：如是否连续、一阶导数和 二阶导数是否存在等；
第三节 提高优化设计效率的技巧和方法
8.3.4 初始点的选取和优化设计方法的选择
第三节 提高优化设计效率的技巧和方法 8.3.2 约束条件的筛选 1.去除无效约束 在数学模型中，不一定所有约束条件 去除无效约束 都对优化结果有影响，此时，应设法去除这些无效约 束。 2.利用变换消除约束 当约束是设计变量的简单显式函 利用变换消除约束 数时，有时对变量作一次替换，其约束条件就能自动 得到满足。 3.准则设计的严约束 准则设计是工程结构中常用的一 准则设计的严约束 种方法，对于一个优化设计模型，若能准确区分严约 束和松约束，就可以从若干约束条件中舍弃那些无效 约束，从而将原优化问题转化为求严约束非线性方程 组在松约束条件限制下的解。
机械优化设计的数学模型建立
min Z = 0.0164x1 + 0.0463x2 + 0.1250x3 st. x + x + x =100 . 1 2 3 0.380x1 + 0.001x2 + 0.002x3 ≤ 0.012×100 0.380x1 + 0.001x2 + 0.002x3 ≥ 0.008×100 0.09x + 0.50x ≥ 0.22×100 2 3 0.02x2 + 0.08x3 ≤ 0.05×100 x ≥ 0 x2 ≥ 0 x3 ≥ 0 1
已知： 传动功率P 大小齿轮的材料， 已知：传动比i, 转速n, 传动功率P，大小齿轮的材料，设计该 齿轮副，使其重量最轻。 齿轮副，使其重量最轻。
直齿圆柱齿轮副的优化设计 分析： 分析：
圆柱齿轮的体积(v)与重量(w)的表达； (v)与重量(w)的表达 （1）圆柱齿轮的体积(v)与重量(w)的表达； 设计参数确定：模数m 齿宽b 齿数z1 z1； （2）设计参数确定：模数m，齿宽b，齿数z1； 设计约束条件： （3）设计约束条件： 大齿轮满足弯曲强度要求； 大齿轮满足弯曲强度要求； 小齿轮满足弯曲强度要求； 小齿轮满足弯曲强度要求； 齿轮副满足接触疲劳强度要求； 齿轮副满足接触疲劳强度要求； 齿宽系数要求； 齿宽系数要求； 最小齿数要求。 最小齿数要求。
数学模型： 数学模型：
设计参数： 设计参数：
m, z1 , b
ρ
4
设计目标： 设计目标： min W =
π b[(mz1 ) 2 + (miz1 )2 ]
约束条件： 约束条件： σ F 1 − [σ ]F 1 ≤ 0
σ F 2 − [σ ]F 2 ≤ 0 σ H − [σ ]H 1 ≤ 0
机械优化设计的数学模型
机械优化设计的数学模型是用于描述和求解机械系统设计问题的数学表达式或方程组。
这些模型旨在找到最优的设计参数或设计方案，以满足给定的设计目标和约束条件。
以下是机械优化设计中常用的数学模型：目标函数（Objective Function）：目标函数是描述设计目标的数学表达式。
它可以是最小化或最大化某个性能指标，如成本、重量、能量消耗、刚度、强度等。
目标函数的形式取决于具体的设计问题和优化目标。
约束条件（Constraints）：约束条件是限制设计参数或设计方案的数学条件。
约束条件可以包括等式约束和不等式约束，用于确保设计满足特定的要求和限制。
例如，材料强度约束、尺寸限制、运动学和动力学要求等。
设计变量（Design Variables）：设计变量是需要优化的参数或变量。
它们可以是连续的、离散的或混合的。
设计变量包括几何参数（如长度、宽度、高度）、材料属性（如弹性模量、密度）、工艺参数等。
约束函数（Constraint Functions）：约束函数是描述约束条件的数学表达式。
它们用于限制设计变量的取值范围，确保设计满足特定的约束要求。
约束函数可以是等式约束或不等式约束。
优化算法（Optimization Algorithm）：优化算法是用于求解优化问题的数学方法和算法。
常用的优化算法包括梯度下降法、遗传算法、粒子群优化算法、模拟退火算法等。
这些算法基于目标函数和约束条件，搜索最优的设计变量组合。
机械优化设计的数学模型可以采用不同的数学方法和工具进行建模和求解，以获得最优的设计方案。
在实际应用中，根据具体的设计问题和要求，需要选择合适的数学模型和优化算法来进行机械系统的优化设计。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
我们所说的基因遗传算法（简称 GA），系现如今最通用的优化算法之一。 在 现在能够检索的期刊文献内，通过基因遗传算法实施优化分析的论文，优化算法 研究相关的论文里占据了极大比例。GA 系 1975 年由美国学者 Holland 率先提出 的。基因遗传算法模拟生物进化过程，摒弃传统的搜索手段，针对目标空间，其 运用人工进化手段对其实施随机化的搜索。对于问题域内的可能解，GA 将其视 为群体的染色体或者某个个体，并将每一个个体编为符号串模式，进而模拟遗传 选择和自然淘汰的生物进化过程，使群体反复接受以遗传学为基础的操作，评价 每个个体依据的预定目标是适应度函数，根据进化法则——适者生存和优胜 劣汰，群体不断获得优化，并且搜索模式采用全局并行的模式，进而从优化群体 内搜索出最优的个体，从而将可以满足要求的最优解搜索出来。 3.2.3 优化设计手段的选取
（1）确定目标函数
确定评价设计方案优劣的指标是优化设计的重要决策，它直接影响到优化设 计结果的实际价值。
在确定评价指标时，应该对设计问题的任务、设计问题的特点、设计进程的 不同阶段可能达到的标准等进行分析，找到设计问题的主要目标，并以此为依据 确定目标函数。当设计问题中存在几个并重的目标要追求时，应该设立多个目标 函数，该类问题称为多目标优化问题。它比单目标优化更为复杂。 （2）建立目标函数应注意的问题
设计变量从数学意义上讲代表的是一个 维空间 ，每个分量 ������分别代表 n 维 空间的一维。而 X 的任一取值 X’的一个点。而从设计的角度来看，X 是所有可行 设计方案的综合，它构成一个 n 维的设计空间。凡 X 内的任意一点 X’个可行设计 方案。 （2）设计变量的选取
设计变量的选取一般应遵循以下原则： 1）应选取与目标函数有直接或间接联系的，对目标函数有较大影响的变量 作为设计变量。 2）设计变量应该是相互独立的。如果选取不独立的变量作为设计变量，实 际上是令其独立，而丢掉了它们之间的相互关系，优化结果将不符合实际。 3）应尽量选取有实际意义的无因次量作为设计变量。 4）在足以描述设计问题的前提下，应充分分析各设计变量的主次，减少设 计变量的数目，使优化设计问题简化。 （3）设计变量的处理
约束条件是设计变量之间和设计本身应该遵循限制条件。优化设计是根据数 学模型进行相关优化分析的，所以在优化过程当中应该进行分类，可将优化设计 方法分成显限制和隐限制两种，显限制是对优化设计当中设计变量的直接限制， 隐限制是对设计变量之间的间接限制，优化设计的过程就是通过限制因素找出优 秀的设计变量，使目标函数在设计过程当中达到优化值。
因此，在实际的优化设计计算中，使用的是设计变量 ���̅̅������̅���={������������1, ������������2 ⋯ ������������������}������
设计弹簧时，除选择材料及规定热处理要求外，主要是根据最大工作载荷、 最大变形以及结构要求等来确定弹簧的钢丝直径 d、中径 D、工作圈数 n、节距 t 或螺旋升角 α 和高度 H 等。通常取弹簧的钢丝直径 d，弹簧的中径 D，工 作圈数 n 和螺旋升角α为最优化设计的设计变量。 3.1.2 目标函数
弹簧约束条件一般有强度约束、刚度约束、振动稳定性约束及弹簧尺寸约束 等。约束条件可根据弹簧功能的要求和结构限制列出： 1.剪切强度约束条件
8������������ ������������������������ = ������ ������ ������3 式中：������������������������ 为弹簧丝截面上的最大切应力； k 为弹簧的曲度系数。 2.弹簧的疲劳强度约束条件 为了使设计的弹簧满足一定的疲劳强度，这里要求设计的弹簧疲劳安全系 必须大于要求的最小疲劳安全系数，即S ≥ ������������������������ = 1.2。 3.弹簧的共振约束条件 为了防止在工作中产生共振现象，要求设计的弹簧自振频率������ 应该远离工作 频率������������。 4.弹簧的刚度约束条件 弹簧刚度计算就是要求出满足变形量要求的弹簧圈数。弹簧刚度的满足条件
第三章 优化设计的数学模型 3.1 数学模型的变量形式 3.1.1 设计变量
在优化设计过程当中，存在设计变量，设计变量在优化过程当中必须考虑各 项参数和指标，各项指标的确立有利于设计方案的完成。很多的存在形式都是由 一个个变量组成，设计优化形式也不例外，变量的数值影响着工作当中优化的难 度系数。换言之，就是在具体机械优化设计当中，设计变量的数值变大，分析量 加大，机械优化设计难度也就加大，同时效益性也显著提升，因此在设计变量的 选择时应该注意相应的效益性和复杂性。
从理论上讲，在无约束优化设计问题中，设计变量的变化是连续的，变化区 间可以从负无穷到正无穷。但是在工程实际中，设计变量的变化区间是有限制的。 在由设计变量构成的正交轴系中，以各个设计变量的变化区间所界定的空间称为 探索空间，或称为变量空间。
在同一设计问题中，同时参与优选的各设计变量的数值在量级上可能相差十 分悬殊。例如弹性模量和蒙皮厚度。显然，这样的设计变量在寻优过程中如果都 使用真实值，计算误差对数量级小的变量影响会很大，从而造成失真。为了避免 这种情况的发生，通常将设计变量进行变换，即将设计变量的真实值转换为变量 区间的相对值，使各个设计变量的变化范围均在区间内。这种处理称为设计变量 的标准化。设变量������������的变化区间为[������, ������] ，则在优化设计问题中，可以用������������来取 代������������，而������������的变化区间为 [0,1]。
当然，计算机也就归为了数值优化措施工具中最关键的那一类。于此期间内，出
现了许多的优化算法，在这样些优化算法中，正常情况下用常用和效果好的优化
算法包括：可行方向法及罚函数法、随机方向法、简约梯度法、复合形法、 约
束变尺度法等。
20 世纪 80 年代末，如模拟退火，进化规划、混沌、人工神经网络、遗传算 法及禁忌搜索等一些优化方法层出不穷，上述算法经模拟自然现象及规律而获得
对于优化设计，方案是用一组参数来表达的。这些参数中，有些是给定的， 称为已知量。另一些是要在设计中确定的，也就是说要设计的，称为设计变量。 设计变量是能够用来描述结构方案特征的独立变量。 （1）设计变量的表达方式
设计变量通常用������1������2������3⋯������������表示，它们构成一个 n 维的列向量 X，即： X = {������1������2������3⋯������������}������
������
相邻两弹簧丝的间隙，通常取 δ ≥0.1d ， λ为极限行程， 所以有： 1.1d + λ −
n
πD tan α ≤ 0
8.弹簧安装空间的约束
3.2 优化设计方法 3.2.1 优化设计手段的论述
������������������������ − (������ + ������) ≤ 0
机械优化领域的设计灵魂即是优化设计方法，伴随计算机技术及数学科学迅
速段。20 世 纪的 50 年代初，最优化问题的两种最主要的数学方法是，古典的变分法与微分
法。此两种手段具计算精准及概念清晰的主要特征，可是，不足之处是仅限于解
决一些小型或是特殊问题， 于处理大型的实际问题之时，因过大的计算量，无
满足所有约束条件的设计方案是可行设计方案，优化设计的任务就是要对各 个设计方案进行比较，从而找出那个最佳的设计方案。而对设计方案进行优劣比 较的标准就是目标函数，或称为评价指标、评价函数。目标函数是反映机械优化 设计过程当中每一个自变量之间的相互联系，目标函数是机械优化设计当中的一 项重要组成部分，可以直接评定一个优化方案的可行性。变量的多少影响着整个 优化过程的难度系数，我们可以将其区分为单一目标函数和多目标函数优化，我 们在优化设计过程当中常见的是多目标函数。目标函数越多，设计的综合效果越 好，可以带来更高的优化设计效益。多函数目标在处理过程当中很可能遇到目标 函数之间相互矛盾，给优化设计带来一定程度的难度。这就要求设计者设计的同 时注意处理各个函数之间的关系。
所谓无约束化优化设计，也就是无约束函数的优化设计。其设计法包含坐标 轮换法、牛顿法、梯度法、单纯形法、共扼方向法、变尺度法等。在寻找最优活 动中，有无采取到目标函数的性态，系区分于无约束优化设计内的直接、间接法 的标准。此法的优势有稳定性佳以及计算效率高等特征。 2 有约束优化设计法
关于机械优化，大多情况下是指有约束优化问题，根据其解决约束条件时， 使用手段的不同，将其划分成直接法与间接法。(1)直接法，最常用的有约束坐标 轮换法、复合形法及网络法等。它的内涵系构建一迭代过程， 令每一次的迭代 点皆置于可行域内，且一步步的减少目标的函数值，直至找出最优解。(2)间接法， 最为常见的是增广拉式乘子法和罚函数法。它是将约束优化问题转化为无约束优 化问题，然后通过无约束优化手段进行求解。或者是将具有非线性的约束优化问 题转换成为线性的规划问题实施处理。 3 基因遗传算法
5° ≤ α ≤ 9° 6.弹簧的旋绕比的约束
旋绕比 C 是衡量弹簧曲率的重要参数，过大会使弹簧过软产生颤动；过小
又会使弹簧丝卷困难， 4 ≤ C ≤ 14。 即 ： D − 14d ≤ 0 . 4d − D ≤ 0。
7.弹簧行程约束
弹簧应满足极限行程的要求，即p ≥ d + ������ + ������,p = πD tan ������。δ为极限行程时，
1）必须选取设计中最为重要的设计目标作为目标函数。否则，设计将会偏 离目标。
2）目标函数必须是所有设计变量的函数。因为不包含在目标函数内的设计 变量的取值将是任意的，无法评定其优劣。
3）目标函数必须具有一定的灵敏度。既是说，当某一个设计变量变化时， 目标函数应该有较为明显的变化。否则，将难以完成寻优。 （3）多目标问题
优化设计中作为目标函数的项目较多，如要求弹簧在满足工作能力条件下， 质量最轻或外廓尺寸最小；或在一定空间的限制下能储存的能量最大或要求动态 性能最好等。目标函数可根据弹簧的工作特点和对它的专门要求来建立。对于气 门弹簧，本文将弹簧体积（即重量）最小作为最优化设计的目标。 3.1.3 约束条件
（1）确定目标函数
确定评价设计方案优劣的指标是优化设计的重要决策，它直接影响到优化设 计结果的实际价值。
在确定评价指标时，应该对设计问题的任务、设计问题的特点、设计进程的 不同阶段可能达到的标准等进行分析，找到设计问题的主要目标，并以此为依据 确定目标函数。当设计问题中存在几个并重的目标要追求时，应该设立多个目标 函数，该类问题称为多目标优化问题。它比单目标优化更为复杂。 （2）建立目标函数应注意的问题
设计变量从数学意义上讲代表的是一个 维空间 ，每个分量 ������分别代表 n 维 空间的一维。而 X 的任一取值 X’的一个点。而从设计的角度来看，X 是所有可行 设计方案的综合，它构成一个 n 维的设计空间。凡 X 内的任意一点 X’个可行设计 方案。 （2）设计变量的选取
设计变量的选取一般应遵循以下原则： 1）应选取与目标函数有直接或间接联系的，对目标函数有较大影响的变量 作为设计变量。 2）设计变量应该是相互独立的。如果选取不独立的变量作为设计变量，实 际上是令其独立，而丢掉了它们之间的相互关系，优化结果将不符合实际。 3）应尽量选取有实际意义的无因次量作为设计变量。 4）在足以描述设计问题的前提下，应充分分析各设计变量的主次，减少设 计变量的数目，使优化设计问题简化。 （3）设计变量的处理
约束条件是设计变量之间和设计本身应该遵循限制条件。优化设计是根据数 学模型进行相关优化分析的，所以在优化过程当中应该进行分类，可将优化设计 方法分成显限制和隐限制两种，显限制是对优化设计当中设计变量的直接限制， 隐限制是对设计变量之间的间接限制，优化设计的过程就是通过限制因素找出优 秀的设计变量，使目标函数在设计过程当中达到优化值。
因此，在实际的优化设计计算中，使用的是设计变量 ���̅̅������̅���={������������1, ������������2 ⋯ ������������������}������
设计弹簧时，除选择材料及规定热处理要求外，主要是根据最大工作载荷、 最大变形以及结构要求等来确定弹簧的钢丝直径 d、中径 D、工作圈数 n、节距 t 或螺旋升角 α 和高度 H 等。通常取弹簧的钢丝直径 d，弹簧的中径 D，工 作圈数 n 和螺旋升角α为最优化设计的设计变量。 3.1.2 目标函数
弹簧约束条件一般有强度约束、刚度约束、振动稳定性约束及弹簧尺寸约束 等。约束条件可根据弹簧功能的要求和结构限制列出： 1.剪切强度约束条件
8������������ ������������������������ = ������ ������ ������3 式中：������������������������ 为弹簧丝截面上的最大切应力； k 为弹簧的曲度系数。 2.弹簧的疲劳强度约束条件 为了使设计的弹簧满足一定的疲劳强度，这里要求设计的弹簧疲劳安全系 必须大于要求的最小疲劳安全系数，即S ≥ ������������������������ = 1.2。 3.弹簧的共振约束条件 为了防止在工作中产生共振现象，要求设计的弹簧自振频率������ 应该远离工作 频率������������。 4.弹簧的刚度约束条件 弹簧刚度计算就是要求出满足变形量要求的弹簧圈数。弹簧刚度的满足条件
第三章 优化设计的数学模型 3.1 数学模型的变量形式 3.1.1 设计变量
在优化设计过程当中，存在设计变量，设计变量在优化过程当中必须考虑各 项参数和指标，各项指标的确立有利于设计方案的完成。很多的存在形式都是由 一个个变量组成，设计优化形式也不例外，变量的数值影响着工作当中优化的难 度系数。换言之，就是在具体机械优化设计当中，设计变量的数值变大，分析量 加大，机械优化设计难度也就加大，同时效益性也显著提升，因此在设计变量的 选择时应该注意相应的效益性和复杂性。
从理论上讲，在无约束优化设计问题中，设计变量的变化是连续的，变化区 间可以从负无穷到正无穷。但是在工程实际中，设计变量的变化区间是有限制的。 在由设计变量构成的正交轴系中，以各个设计变量的变化区间所界定的空间称为 探索空间，或称为变量空间。
在同一设计问题中，同时参与优选的各设计变量的数值在量级上可能相差十 分悬殊。例如弹性模量和蒙皮厚度。显然，这样的设计变量在寻优过程中如果都 使用真实值，计算误差对数量级小的变量影响会很大，从而造成失真。为了避免 这种情况的发生，通常将设计变量进行变换，即将设计变量的真实值转换为变量 区间的相对值，使各个设计变量的变化范围均在区间内。这种处理称为设计变量 的标准化。设变量������������的变化区间为[������, ������] ，则在优化设计问题中，可以用������������来取 代������������，而������������的变化区间为 [0,1]。
当然，计算机也就归为了数值优化措施工具中最关键的那一类。于此期间内，出
现了许多的优化算法，在这样些优化算法中，正常情况下用常用和效果好的优化
算法包括：可行方向法及罚函数法、随机方向法、简约梯度法、复合形法、 约
束变尺度法等。
20 世纪 80 年代末，如模拟退火，进化规划、混沌、人工神经网络、遗传算 法及禁忌搜索等一些优化方法层出不穷，上述算法经模拟自然现象及规律而获得
对于优化设计，方案是用一组参数来表达的。这些参数中，有些是给定的， 称为已知量。另一些是要在设计中确定的，也就是说要设计的，称为设计变量。 设计变量是能够用来描述结构方案特征的独立变量。 （1）设计变量的表达方式
设计变量通常用������1������2������3⋯������������表示，它们构成一个 n 维的列向量 X，即： X = {������1������2������3⋯������������}������
������
相邻两弹簧丝的间隙，通常取 δ ≥0.1d ， λ为极限行程， 所以有： 1.1d + λ −
n
πD tan α ≤ 0
8.弹簧安装空间的约束
3.2 优化设计方法 3.2.1 优化设计手段的论述
������������������������ − (������ + ������) ≤ 0
机械优化领域的设计灵魂即是优化设计方法，伴随计算机技术及数学科学迅
速段。20 世 纪的 50 年代初，最优化问题的两种最主要的数学方法是，古典的变分法与微分
法。此两种手段具计算精准及概念清晰的主要特征，可是，不足之处是仅限于解
决一些小型或是特殊问题， 于处理大型的实际问题之时，因过大的计算量，无
满足所有约束条件的设计方案是可行设计方案，优化设计的任务就是要对各 个设计方案进行比较，从而找出那个最佳的设计方案。而对设计方案进行优劣比 较的标准就是目标函数，或称为评价指标、评价函数。目标函数是反映机械优化 设计过程当中每一个自变量之间的相互联系，目标函数是机械优化设计当中的一 项重要组成部分，可以直接评定一个优化方案的可行性。变量的多少影响着整个 优化过程的难度系数，我们可以将其区分为单一目标函数和多目标函数优化，我 们在优化设计过程当中常见的是多目标函数。目标函数越多，设计的综合效果越 好，可以带来更高的优化设计效益。多函数目标在处理过程当中很可能遇到目标 函数之间相互矛盾，给优化设计带来一定程度的难度。这就要求设计者设计的同 时注意处理各个函数之间的关系。
所谓无约束化优化设计，也就是无约束函数的优化设计。其设计法包含坐标 轮换法、牛顿法、梯度法、单纯形法、共扼方向法、变尺度法等。在寻找最优活 动中，有无采取到目标函数的性态，系区分于无约束优化设计内的直接、间接法 的标准。此法的优势有稳定性佳以及计算效率高等特征。 2 有约束优化设计法
关于机械优化，大多情况下是指有约束优化问题，根据其解决约束条件时， 使用手段的不同，将其划分成直接法与间接法。(1)直接法，最常用的有约束坐标 轮换法、复合形法及网络法等。它的内涵系构建一迭代过程， 令每一次的迭代 点皆置于可行域内，且一步步的减少目标的函数值，直至找出最优解。(2)间接法， 最为常见的是增广拉式乘子法和罚函数法。它是将约束优化问题转化为无约束优 化问题，然后通过无约束优化手段进行求解。或者是将具有非线性的约束优化问 题转换成为线性的规划问题实施处理。 3 基因遗传算法
5° ≤ α ≤ 9° 6.弹簧的旋绕比的约束
旋绕比 C 是衡量弹簧曲率的重要参数，过大会使弹簧过软产生颤动；过小
又会使弹簧丝卷困难， 4 ≤ C ≤ 14。 即 ： D − 14d ≤ 0 . 4d − D ≤ 0。
7.弹簧行程约束
弹簧应满足极限行程的要求，即p ≥ d + ������ + ������,p = πD tan ������。δ为极限行程时，
1）必须选取设计中最为重要的设计目标作为目标函数。否则，设计将会偏 离目标。
2）目标函数必须是所有设计变量的函数。因为不包含在目标函数内的设计 变量的取值将是任意的，无法评定其优劣。
3）目标函数必须具有一定的灵敏度。既是说，当某一个设计变量变化时， 目标函数应该有较为明显的变化。否则，将难以完成寻优。 （3）多目标问题
优化设计中作为目标函数的项目较多，如要求弹簧在满足工作能力条件下， 质量最轻或外廓尺寸最小；或在一定空间的限制下能储存的能量最大或要求动态 性能最好等。目标函数可根据弹簧的工作特点和对它的专门要求来建立。对于气 门弹簧，本文将弹簧体积（即重量）最小作为最优化设计的目标。 3.1.3 约束条件