大学物理《力学1·质点运动学》复习题及答案

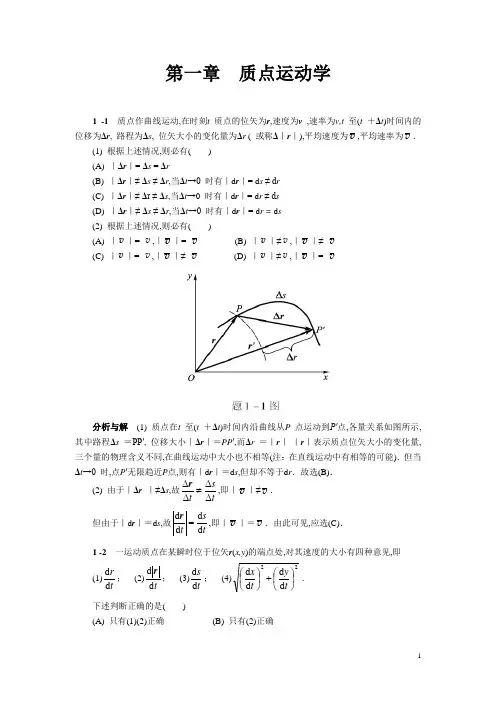
第一章 质点运动学1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v,t 至(t ＋Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ｜r ｜),平均速度为v ,平均速率为v ．(1) 根据上述情况,则必有( ) (A) ｜Δr ｜= Δs = Δr(B) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d s ≠ d r (C) ｜Δr ｜≠ Δr ≠ Δs ,当Δt →0 时有｜d r ｜= d r ≠ d s (D) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d r = d s (2) 根据上述情况,则必有( )(A) ｜v ｜= v ,｜v ｜= v (B) ｜v ｜≠v ,｜v ｜≠ v (C) ｜v ｜= v ,｜v ｜≠ v (D) ｜v ｜≠v ,｜v ｜= v分析与解 (1) 质点在t 至(t ＋Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs ＝PP′, 位移大小｜Δr ｜＝PP ′,而Δr ＝｜r ｜-｜r ｜表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注：在直线运动中有相等的可能)．但当Δt →0 时,点P ′无限趋近P 点,则有｜d r ｜＝d s ,但却不等于d r ．故选(B)．(2) 由于｜Δr ｜≠Δs ,故ts t ΔΔΔΔ≠r ,即｜v ｜≠v ． 但由于｜d r ｜＝d s ,故tst d d d d =r ,即｜v ｜＝v ．由此可见,应选(C)． 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t r d d ； (2)t d d r ； (3)t s d d ； (4)22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x ．下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解trd d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率．通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量；td d r表示速度矢量；在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解．故选(D)．1 -3 质点作曲线运动,r 表示位置矢量, v 表示速度,a 表示加速度,s 表示路程, a ｔ表示切向加速度．对下列表达式,即(1)d v /d t ＝a ；(2)d r /d t ＝v ；(3)d s /d t ＝v ；(4)d v /d t ｜＝a ｔ． 下述判断正确的是( )(A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的 (C) 只有(2)是对的 (D) 只有(3)是对的分析与解 td d v表示切向加速度a ｔ,它表示速度大小随时间的变化率,是加速度矢量沿速度方向的一个分量,起改变速度大小的作用；trd d 在极坐标系中表示径向速率v r (如题1 -2 所述)；ts d d 在自然坐标系中表示质点的速率v ；而t d d v 表示加速度的大小而不是切向加速度aｔ．因此只有(3) 式表达是正确的．故选(D)． 1 -4 一个质点在做圆周运动时,则有( ) (A) 切向加速度一定改变,法向加速度也改变 (B) 切向加速度可能不变,法向加速度一定改变 (C) 切向加速度可能不变,法向加速度不变 (D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a ｔ起改变速度大小的作用,而法向分量a n 起改变速度方向的作用．质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的．至于a ｔ是否改变,则要视质点的速率情况而定．质点作匀速率圆周运动时, a ｔ恒为零；质点作匀变速率圆周运动时, a ｔ为一不为零的恒量,当a ｔ改变时,质点则作一般的变速率圆周运动．由此可见,应选(B)．*1 -5 如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动．设该人以匀速率v 0 收绳,绳不伸长且湖水静止,小船的速率为v ,则小船作( )(A) 匀加速运动,θcos 0v v =(B) 匀减速运动,θcos 0v v = (C) 变加速运动,θcos 0v v =(D) 变减速运动,θcos 0v v = (E) 匀速直线运动,0v v =分析与解 本题关键是先求得小船速度表达式,进而判断运动性质．为此建立如图所示坐标系,设定滑轮距水面高度为h,t 时刻定滑轮距小船的绳长为l ,则小船的运动方程为22h l x -=,其中绳长l 随时间t 而变化．小船速度22d d d d h l t llt x -==v ,式中t l d d 表示绳长l 随时间的变化率,其大小即为v 0,代入整理后为θlh l cos /0220v v v =-=,方向沿x 轴负向．由速度表达式,可判断小船作变加速运动．故选(C)．讨论 有人会将绳子速率v 0按x 、y 两个方向分解,则小船速度θcos 0v v =,这样做对吗？1 -6 已知质点沿x 轴作直线运动,其运动方程为32262t t x -+=,式中x 的单位为m,t 的单位为 s ．求：(1) 质点在运动开始后4.0 s 内的位移的大小； (2) 质点在该时间内所通过的路程；(3) t ＝4 s 时质点的速度和加速度．分析 位移和路程是两个完全不同的概念．只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等．质点在t 时间内的位移Δx 的大小可直接由运动方程得到：0Δx x x t -=,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了．为此,需根据0d d =tx来确定其运动方向改变的时刻t p ,求出0～t p 和t p ～t 内的位移大小Δx 1 、Δx 2 ,则t 时间内的路程21x x s ∆+∆=,如图所示,至于t ＝4.0 s 时质点速度和加速度可用tx d d 和22d d t x两式计算．解 (1) 质点在4.0 s 内位移的大小m 32Δ04-=-=x x x(2) 由 0d d =tx 得知质点的换向时刻为s 2=p t (t ＝0不合题意)则m 0.8Δ021=-=x x xm 40Δ242-=-=x x x所以,质点在4.0 s 时间间隔内的路程为m 48ΔΔ21=+=x x s(3) t ＝4.0 s 时1s0.4s m 48d d -=⋅-==t t xv2s0.422m.s 36d d -=-==t t x a1 -7 一质点沿x 轴方向作直线运动,其速度与时间的关系如图(a)所示．设t ＝0 时,x ＝0．试根据已知的v -t 图,画出a -t 图以及x -t 图．分析 根据加速度的定义可知,在直线运动中v -t 曲线的斜率为加速度的大小(图中AB 、CD 段斜率为定值,即匀变速直线运动；而线段BC 的斜率为0,加速度为零,即匀速直线运动)．加速度为恒量,在a -t 图上是平行于t 轴的直线,由v -t 图中求出各段的斜率,即可作出a -t 图线．又由速度的定义可知,x -t 曲线的斜率为速度的大小．因此,匀速直线运动所对应的x -t 图应是一直线,而匀变速直线运动所对应的x –t 图为t 的二次曲线．根据各段时间内的运动方程x ＝x (t ),求出不同时刻t 的位置x ,采用描数据点的方法,可作出x -t 图．解 将曲线分为AB 、BC 、CD 三个过程,它们对应的加速度值分别为2s m 20-⋅=--=AB AB AB t t a v v (匀加速直线运动)0=BC a (匀速直线运动)2s m 10-⋅-=--=CD CD CD t t a v v (匀减速直线运动)根据上述结果即可作出质点的a -t 图［图(B)］．在匀变速直线运动中,有2021t t x x ++=v由此,可计算在0～2ｓ和4～6ｓ时间间隔内各时刻的位置分别为用描数据点的作图方法,由表中数据可作0～2ｓ和4～6ｓ时间内的x -t 图．在2～4ｓ时间内, 质点是作1s m 20-⋅=v 的匀速直线运动, 其x -t 图是斜率k ＝20的一段直线［图(c)］．1 -8 已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为ｓ．求： (1) 质点的运动轨迹；(2) t ＝0 及t ＝2ｓ时,质点的位矢；(3) 由t ＝0 到t ＝2ｓ内质点的位移Δr 和径向增量Δr ；*(4) 2ｓ 内质点所走过的路程s ．分析 质点的轨迹方程为y ＝f (x ),可由运动方程的两个分量式x (t )和y (t )中消去t 即可得到．对于r 、Δr 、Δr 、Δs 来说,物理含义不同,可根据其定义计算．其中对s 的求解用到积分方法,先在轨迹上任取一段微元d s ,则22)d ()d (d y x s +=,最后用⎰=s s d 积分求ｓ． 解 (1) 由x (t )和y (t )中消去t 后得质点轨迹方程为2412x y -=这是一个抛物线方程,轨迹如图(a)所示．(2) 将t ＝0ｓ和t ＝2ｓ分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t ＝0ｓ和t ＝2ｓ时质点所在位置． (3) 由位移表达式,得j i j i r r r 24)()(Δ020212-=-+-=-=y y x x其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r*(4) 如图(B)所示,所求Δs 即为图中PQ 段长度,先在其间任意处取AB 微元d s ,则22)d ()d (d y x s +=,由轨道方程可得x x y d 21d -=,代入d s ,则2ｓ内路程为m 91.5d 4d 402=+==⎰⎰x x s s QP1 -9 质点的运动方程为23010t t x +-= 22015t t y -=式中x ,y 的单位为m,t 的单位为ｓ．试求：(1) 初速度的大小和方向；(2) 加速度的大小和方向．分析 由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成算出速度和加速度的大小和方向．解 (1) 速度的分量式为t t xx 6010d d +-==v t ty y 4015d d -==v当t ＝0 时, v o x ＝-10 m·ｓ-1 , v o y ＝15 m·ｓ-1 ,则初速度大小为120200s m 0.18-⋅=+=y x v v v设v o 与x 轴的夹角为α,则23tan 00-==xy αv vα＝123°41′(2) 加速度的分量式为2s m 60d d -⋅==ta xx v , 2s m 40d d -⋅-==t a y y v则加速度的大小为222s m 1.72-⋅=+=y x a a a设a 与x 轴的夹角为β,则32tan -==x ya a β β＝-33°41′(或326°19′)1 -10 一升降机以加速度1.22 m·ｓ-2上升,当上升速度为2.44 m·ｓ-1时,有一螺丝自升降机的天花板上松脱,天花板与升降机的底面相距2.74 m ．计算：(1)螺丝从天花板落到底面所需要的时间；(2)螺丝相对升降机外固定柱子的下降距离．分析 在升降机与螺丝之间有相对运动的情况下,一种处理方法是取地面为参考系,分别讨论升降机竖直向上的匀加速度运动和初速不为零的螺丝的自由落体运动,列出这两种运动在同一坐标系中的运动方程y 1 ＝y 1(t )和y 2 ＝y 2(t ),并考虑它们相遇,即位矢相同这一条件,问题即可解；另一种方法是取升降机(或螺丝)为参考系,这时,螺丝(或升降机)相对它作匀加速运动,但是,此加速度应该是相对加速度．升降机厢的高度就是螺丝(或升降机)运动的路程．解1 (1) 以地面为参考系,取如图所示的坐标系,升降机与螺丝的运动方程分别为20121at t y +=v20221gt t h y -+=v当螺丝落至底面时,有y 1 ＝y 2 ,即20202121gt t h at t -+=+v vs 705.02=+=ag ht (2) 螺丝相对升降机外固定柱子下降的距离为m 716.021202=+-=-=gt t y h d v解2 (1)以升降机为参考系,此时,螺丝相对它的加速度大小a ′＝g ＋a ,螺丝落至底面时,有2)(210t a g h +-=s 705.02=+=ag ht (2) 由于升降机在t 时间内上升的高度为2021at t h +='v则 m 716.0='-=h h d1 -11 一质点P 沿半径R ＝3.0 m 的圆周作匀速率运动,运动一周所需时间为20.0ｓ,设t ＝0 时,质点位于O 点．按(a )图中所示Oxy 坐标系,求(1) 质点P 在任意时刻的位矢；(2)5ｓ时的速度和加速度．分析 该题属于运动学的第一类问题,即已知运动方程r ＝r (t )求质点运动的一切信息(如位置矢量、位移、速度、加速度)．在确定运动方程时,若取以点(0,3)为原点的O′x′y′坐标系,并采用参数方程x′＝x′(t )和y′＝y′(t )来表示圆周运动是比较方便的．然后,运用坐标变换x ＝x 0 ＋x ′和y ＝y 0 ＋y ′,将所得参数方程转换至Oxy 坐标系中,即得Oxy 坐标系中质点P 在任意时刻的位矢．采用对运动方程求导的方法可得速度和加速度．解 (1) 如图(B)所示,在O′x′y′坐标系中,因t Tθπ2=,则质点P 的参数方程为t TR x π2sin=',t TR y π2cos-=' 坐标变换后,在O x y 坐标系中有t TR x x π2sin='=, R t TR y y y +-=+'=π2cos0 则质点P 的位矢方程为j i r ⎪⎭⎫ ⎝⎛+-+=R t T R t T R π2cos π2sinj i )]π1.0(cos 1[3)π1.0(sin 3t t -+=(2) 5ｓ时的速度和加速度分别为j j i r )s m π3.0(π2sin π2π2cos π2d d 1-⋅=+==t TT R t T T R t v i j i r a )s m π03.0(π2cos )π2(π2sin )π2(d d 222222-⋅-=+-==t TT R t T T R t 1 -12 地面上垂直竖立一高20.0 m 的旗杆,已知正午时分太阳在旗杆的正上方,求在下午2∶00 时,杆顶在地面上的影子的速度的大小．在何时刻杆影伸展至20.0 m ？分析 为求杆顶在地面上影子速度的大小,必须建立影长与时间的函数关系,即影子端点的位矢方程．根据几何关系,影长可通过太阳光线对地转动的角速度求得．由于运动的相对性,太阳光线对地转动的角速度也就是地球自转的角速度．这样,影子端点的位矢方程和速度均可求得．解 设太阳光线对地转动的角速度为ω,从正午时分开始计时,则杆的影长为s ＝h tg ωt ,下午2∶00 时,杆顶在地面上影子的速度大小为132s m 1094.1cos d d --⋅⨯===tωωh t s v 当杆长等于影长时,即s ＝h ,则s 606034πarctan 1⨯⨯===ωh s ωt 即为下午3∶00 时．1 -13 质点沿直线运动,加速度a ＝4 -t2 ,式中a 的单位为m·ｓ-2 ,t 的单位为ｓ．如果当t ＝3ｓ时,x ＝9 m,v ＝2 m·ｓ-1 ,求质点的运动方程．分析 本题属于运动学第二类问题,即已知加速度求速度和运动方程,必须在给定条件下用积分方法解决．由t a d d v =和tx d d =v 可得t a d d =v 和t x d d v =．如a ＝a (t )或v ＝v (t ),则可两边直接积分．如果a 或v 不是时间t 的显函数,则应经过诸如分离变量或变量代换等数学操作后再做积分．解 由分析知,应有⎰⎰=tt a 0d d 0vv v得 03314v v +-=t t (1)由⎰⎰=txx t x 0d d 0v得 00421212x t t t x ++-=v (2) 将t ＝3ｓ时,x ＝9 m,v ＝2 m·ｓ-1代入(1) (2)得v 0＝-1 m·ｓ-1,x 0＝0.75 m ．于是可得质点运动方程为75.0121242+-=t t x 1 -14 一石子从空中由静止下落,由于空气阻力,石子并非作自由落体运动,现测得其加速度a ＝A -B v ,式中A 、B 为正恒量,求石子下落的速度和运动方程．分析 本题亦属于运动学第二类问题,与上题不同之处在于加速度是速度v 的函数,因此,需将式d v ＝a (v )d t 分离变量为t a d )(d =v v 后再两边积分． 解 选取石子下落方向为y 轴正向,下落起点为坐标原点．(1) 由题意知 v v B A ta -==d d (1) 用分离变量法把式(1)改写为 t B A d d =-vv (2) 将式(2)两边积分并考虑初始条件,有⎰⎰=-t t B A 0d d d 0v v v v v 得石子速度 )1(Bt e B A --=v 由此可知当,t →∞时,B A →v 为一常量,通常称为极限速度或收尾速度． (2) 再由)1(d d Bt e BA t y --==v 并考虑初始条件有 t e BA y t Bt y d )1(d 00⎰⎰--= 得石子运动方程)1(2-+=-Bt e B A t B A y 1 -15 一质点具有恒定加速度a ＝6i ＋4j ,式中a 的单位为m·ｓ-2 ．在t ＝0时,其速度为零,位置矢量r 0 ＝10 m i ．求：(1) 在任意时刻的速度和位置矢量；(2) 质点在Oxy 平面上的轨迹方程,并画出轨迹的示意图．分析 与上两题不同处在于质点作平面曲线运动,根据叠加原理,求解时需根据加速度的两个分量a x 和a y 分别积分,从而得到运动方程r 的两个分量式x (t )和y (t )．由于本题中质点加速度为恒矢量,故两次积分后所得运动方程为固定形式,即20021t a t x x x x ++=v 和20021t a t y y y y ++=v ,两个分运动均为匀变速直线运动．读者不妨自己验证一下． 解 由加速度定义式,根据初始条件t 0 ＝0时v 0 ＝0,积分可得⎰⎰⎰+==t t t t 000)d 46(d d j i a v v j i t t 46+=v 又由td d r =v 及初始条件t ＝0 时,r 0＝(10 m)i ,积分可得 ⎰⎰⎰+==tt r r t t t t 00)d 46(d d 0j i r v j i r 222)310(t t ++=由上述结果可得质点运动方程的分量式,即x ＝10＋3t 2y ＝2t 2消去参数t ,可得运动的轨迹方程3y ＝2x -20 m 这是一个直线方程．直线斜率32tan d d ===αx y k ,α＝33°41′．轨迹如图所示． 1 -16 一质点在半径为R 的圆周上以恒定的速率运动,质点由位置A 运动到位置B,OA 和OB 所对的圆心角为Δθ．(1) 试证位置A 和B 之间的平均加速度为)Δ(/)Δcos 1(22θR θa v -=；(2) 当Δθ分别等于90°、30°、10°和1°时,平均加速度各为多少？ 并对结果加以讨论．分析 瞬时加速度和平均加速度的物理含义不同,它们分别表示为td d v =a 和tΔΔv =a ．在匀速率圆周运动中,它们的大小分别为R a n 2v =,t a ΔΔv = ,式中｜Δv ｜可由图(B)中的几何关系得到,而Δt 可由转过的角度Δθ 求出．由计算结果能清楚地看到两者之间的关系,即瞬时加速度是平均加速度在Δt →0 时的极限值．解 (1) 由图(b)可看到Δv ＝v 2 -v 1 ,故θΔcos 2Δ212221v v v v -+=v)Δcos 1(2θ-=v而vv θR s t ΔΔΔ==所以 θR θt a Δ)cos Δ1(2ΔΔ2v -==v(2) 将Δθ＝90°,30°,10°,1°分别代入上式,得R a 219003.0v ≈,Ra 229886.0v ≈ R a 239987.0v ≈,Ra 24000.1v ≈ 以上结果表明,当Δθ→0 时,匀速率圆周运动的平均加速度趋近于一极限值,该值即为法向加速度R2v ． 1 -17 质点在Oxy 平面内运动,其运动方程为r ＝2.0t i ＋(19.0 -2.0t 2 )j ,式中r 的单位为m,t 的单位为s ．求：(1)质点的轨迹方程；(2) 在t 1＝1.0s 到t 2 ＝2.0s 时间内的平均速度；(3) t 1 ＝1.0ｓ时的速度及切向和法向加速度；(4) t ＝1.0s 时质点所在处轨道的曲率半径ρ．分析 根据运动方程可直接写出其分量式x ＝x (t )和y ＝y (t ),从中消去参数t ,即得质点的轨迹方程．平均速度是反映质点在一段时间内位置的变化率,即t ΔΔr =v ,它与时间间隔Δt 的大小有关,当Δt →0 时,平均速度的极限即瞬时速度td d r =v ．切向和法向加速度是指在自然坐标下的分矢量a ｔ 和a n ,前者只反映质点在切线方向速度大小的变化率,即t t te a d d v =,后者只反映质点速度方向的变化,它可由总加速度a 和a ｔ 得到．在求得t 1 时刻质点的速度和法向加速度的大小后,可由公式ρa n 2v =求ρ． 解 (1) 由参数方程x ＝2.0t , y ＝19.0-2.0t 2消去t 得质点的轨迹方程：y ＝19.0 -0.50x 2(2) 在t 1 ＝1.00ｓ 到t 2 ＝2.0ｓ时间内的平均速度j i r r 0.60.2ΔΔ1212-=--==t t t r v (3) 质点在任意时刻的速度和加速度分别为j i j i j i t ty t x t y x 0.40.2d d d d )(-=+=+=v v v j j i a 222220.4d d d d )(-⋅-=+=s m ty t x t 则t 1 ＝1.00ｓ时的速度v (t )｜t ＝1ｓ＝2.0i -4.0j切向和法向加速度分别为t t y x t t t tt e e e a 222s 1s m 58.3)(d d d d -=⋅=+==v v v n n t n a a e e a 222s m 79.1-⋅=-=(4) t ＝1.0ｓ质点的速度大小为122s m 47.4-⋅=+=y x v v v则m 17.112==na ρv 1 -18 飞机以100 m·ｓ-1 的速度沿水平直线飞行,在离地面高为100 m 时,驾驶员要把物品空投到前方某一地面目标处,问：(1) 此时目标在飞机正下方位置的前面多远？ (2) 投放物品时,驾驶员看目标的视线和水平线成何角度？(3) 物品投出2.0ｓ后,它的法向加速度和切向加速度各为多少？分析 物品空投后作平抛运动．忽略空气阻力的条件下,由运动独立性原理知,物品在空中沿水平方向作匀速直线运动,在竖直方向作自由落体运动．到达地面目标时,两方向上运动时间是相同的．因此,分别列出其运动方程,运用时间相等的条件,即可求解．此外,平抛物体在运动过程中只存在竖直向下的重力加速度．为求特定时刻t 时物体的切向加速度和法向加速度,只需求出该时刻它们与重力加速度之间的夹角α或β．由图可知,在特定时刻t ,物体的切向加速度和水平线之间的夹角α,可由此时刻的两速度分量v x 、v y 求出,这样,也就可将重力加速度g 的切向和法向分量求得．解 (1) 取如图所示的坐标,物品下落时在水平和竖直方向的运动方程分别为x ＝vt , y ＝1/2 gt 2飞机水平飞行速度v ＝100 m·s -1 ,飞机离地面的高度y ＝100 m,由上述两式可得目标在飞机正下方前的距离m 4522==gy x v(2) 视线和水平线的夹角为 o 5.12arctan ==xy θ(3) 在任意时刻物品的速度与水平轴的夹角为 v v v gt αx yarctan arctan == 取自然坐标,物品在抛出2s 时,重力加速度的切向分量与法向分量分别为2s m 88.1arctan sin sin -⋅=⎪⎭⎫ ⎝⎛==v gt g αg a t 2s m 62.9arctan cos cos -⋅=⎪⎭⎫ ⎝⎛==v gt g αg a n 1 -19 如图(a)所示,一小型迫击炮架设在一斜坡的底端O 处,已知斜坡倾角为α,炮身与斜坡的夹角为β,炮弹的出口速度为v 0,忽略空气阻力．求：(1)炮弹落地点P 与点O 的距离OP ；(2) 欲使炮弹能垂直击中坡面．证明α和β必须满足αβtan 21tan =并与v 0 无关． 分析 这是一个斜上抛运动,看似简单,但针对题目所问,如不能灵活运用叠加原理,建立一个恰当的坐标系,将运动分解的话,求解起来并不容易．现建立如图(a)所示坐标系,则炮弹在x 和y 两个方向的分运动均为匀减速直线运动,其初速度分别为v 0cos β和v 0sin β,其加速度分别为g sin α和gcos α．在此坐标系中炮弹落地时,应有y ＝0,则x ＝OP ．如欲使炮弹垂直击中坡面,则应满足v x ＝0,直接列出有关运动方程和速度方程,即可求解．由于本题中加速度g 为恒矢量．故第一问也可由运动方程的矢量式计算,即20g 21t t +=v r ,做出炮弹落地时的矢量图［如图(B)所示］,由图中所示几何关系也可求得OP (即图中的r 矢量)．(1)解1 由分析知,炮弹在图(a)所示坐标系中两个分运动方程为αgt βt x sin 21cos 20-=v (1) αgt βt y cos 21sin 20-=v (2) 令y ＝0 求得时间t 后再代入式(1)得)cos(cos sin 2)sin sin cos (cos cos sin 2220220βααg ββαβααg βx OP +=-==v v 解2 做出炮弹的运动矢量图,如图(b)所示,并利用正弦定理,有βgt αt βαsin 212πsin 2πsin 20=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛--v r 从中消去t 后也可得到同样结果．(2) 由分析知,如炮弹垂直击中坡面应满足y ＝0 和v x ＝0,则0sin cos 0=-=αgt βx v v (3)由(2)(3)两式消去t 后得αβsin 21tan = 由此可知．只要角α和β满足上式,炮弹就能垂直击中坡面,而与v 0 的大小无关．讨论 如将炮弹的运动按水平和竖直两个方向分解,求解本题将会比较困难,有兴趣读者不妨自己体验一下．1 -20 一直立的雨伞,张开后其边缘圆周的半径为R ,离地面的高度为h ,(1) 当伞绕伞柄以匀角速ω旋转时,求证水滴沿边缘飞出后落在地面上半径为g ωh R r /212+=的圆周上；(2) 读者能否由此定性构想一种草坪上或农田灌溉用的旋转式洒水器的方案？分析 选定伞边缘O 处的雨滴为研究对象,当伞以角速度ω旋转时,雨滴将以速度v 沿切线方向飞出,并作平抛运动．建立如图(a)所示坐标系,列出雨滴的运动方程并考虑图中所示几何关系,即可求证．由此可以想像如果让水从一个旋转的有很多小孔的喷头中飞出,从不同小孔中飞出的水滴将会落在半径不同的圆周上,为保证均匀喷洒对喷头上小孔的分布还要给予精心的考虑．解 (1) 如图(a)所示坐标系中,雨滴落地的运动方程为t ωR t x ==v (1)h gt y ==221 (2) 由式(1)(2)可得 g h ωR x 2222= 由图(a)所示几何关系得雨滴落地处圆周的半径为22221ωgh R R x r +=+= (2) 常用草坪喷水器采用如图(b)所示的球面喷头(θ0 ＝45°)其上有大量小孔．喷头旋转时,水滴以初速度v 0 从各个小孔中喷出,并作斜上抛运动,通常喷头表面基本上与草坪处在同一水平面上．则以φ角喷射的水柱射程为gR 2sin 0v = 为使喷头周围的草坪能被均匀喷洒,喷头上的小孔数不但很多,而且还不能均匀分布,这是喷头设计中的一个关键问题．1 -21 一足球运动员在正对球门前25.0 m 处以20.0 m·ｓ-1 的初速率罚任意球,已知球门高为3.44 m ．若要在垂直于球门的竖直平面内将足球直接踢进球门,问他应在与地面成什么角度的范围内踢出足球？ (足球可视为质点)分析 被踢出后的足球,在空中作斜抛运动,其轨迹方程可由质点在竖直平面内的运动方程得到．由于水平距离x 已知,球门高度又限定了在y 方向的范围,故只需将x 、y 值代入即可求出．解 取图示坐标系Oxy ,由运动方程θt x cos v =, 221sin gt θt y -=v 消去t 得轨迹方程222)tan 1(2tan x θg θx y +-=v以x ＝25.0 m,v ＝20.0 m·ｓ-1 及3.44 m≥y ≥0 代入后,可解得71．11°≥θ1 ≥69．92°27．92°≥θ2 ≥18．89°如何理解上述角度的范围？在初速一定的条件下,球击中球门底线或球门上缘都将对应有两个不同的投射倾角(如图所示)．如果以θ＞71．11°或θ ＜18.89°踢出足球,都将因射程不足而不能直接射入球门；由于球门高度的限制,θ 角也并非能取71.11°与18.89°之间的任何值．当倾角取值为27.92°＜θ ＜69．92°时,踢出的足球将越过门缘而离去,这时球也不能射入球门．因此可取的角度范围只能是解中的结果．1 -22 一质点沿半径为R 的圆周按规律2021bt t s -=v 运动,v 0 、b 都是常量．(1) 求t 时刻质点的总加速度；(2) t 为何值时总加速度在数值上等于b ？(3) 当加速度达到b 时,质点已沿圆周运行了多少圈？分析 在自然坐标中,s 表示圆周上从某一点开始的曲线坐标．由给定的运动方程s ＝s (t ),对时间t 求一阶、二阶导数,即是沿曲线运动的速度v 和加速度的切向分量a ｔ,而加速度的法向分量为a n ＝v 2 /R ．这样,总加速度为a ＝a ｔe ｔ＋a n e n ．至于质点在t 时间内通过的路程,即为曲线坐标的改变量Δs ＝s t -s 0．因圆周长为2πR,质点所转过的圈数自然可求得．解 (1) 质点作圆周运动的速率为bt ts -==0d d v v 其加速度的切向分量和法向分量分别为b t s a t -==22d d , Rbt R a n 202)(-==v v 故加速度的大小为R )(402222bt b a a a a t tn -+=+=v 其方向与切线之间的夹角为⎥⎦⎤⎢⎣⎡--==Rb bt a a θt n 20)(arctan arctan v (2) 要使｜a ｜＝b ,由b bt b R R=-+4022)(1v 可得 bt 0v = (3) 从t ＝0 开始到t ＝v 0 /b 时,质点经过的路程为b s s s t 2200v =-=因此质点运行的圈数为bRR s n π4π220v == 1 -23 一半径为0.50 m 的飞轮在启动时的短时间内,其角速度与时间的平方成正比．在t ＝2.0ｓ 时测得轮缘一点的速度值为4.0 m·ｓ-1．求：(1) 该轮在t′＝0.5ｓ的角速度,轮缘一点的切向加速度和总加速度；(2)该点在2.0ｓ内所转过的角度．分析 首先应该确定角速度的函数关系ω＝kt 2．依据角量与线量的关系由特定时刻的速度值可得相应的角速度,从而求出式中的比例系数k ,ω＝ω(t )确定后,注意到运动的角量描述与线量描述的相应关系,由运动学中两类问题求解的方法(微分法和积分法),即可得到特定时刻的角加速度、切向加速度和角位移．解 因ωR ＝v ,由题意ω∝t 2 得比例系数322s rad 2-⋅===Rtt ωk v 所以 22)(t t ωω== 则t ′＝0.5ｓ 时的角速度、角加速度和切向加速度分别为12s rad 5.02-⋅='=t ω2s rad 0.24d d -⋅='==t tωα 2s m 0.1-⋅==R αa t总加速度n t t n R ωR αe e a a a 2+=+= ()()2222s m 01.1-⋅=+=R ωR αa在2.0ｓ内该点所转过的角度 rad 33.532d 2d 203202200====-⎰⎰t t t t ωθθ 1 -24 一质点在半径为0.10 m 的圆周上运动,其角位置为342t θ+=,式中θ 的单位为rad,t 的单位为ｓ．(1) 求在t ＝2.0ｓ时质点的法向加速度和切向加速度．(2) 当切向加速度的大小恰等于总加速度大小的一半时,θ 值为多少？(3) t 为多少时,法向加速度和切向加速度的值相等？分析 掌握角量与线量、角位移方程与位矢方程的对应关系,应用运动学求解的方法即可得到．解 (1) 由于342t θ+=,则角速度212d d t tθω==．在t ＝2 ｓ 时,法向加速度和切向加速度的数值分别为 22s 2s m 30.2-=⋅==ωr a t n2s 2s m 80.4d d -=⋅==t ωr a t t(2) 当22212/t n t a a a a +==时,有223n t a a =,即 ()()422212243t r rt = 得 3213=t此时刻的角位置为 rad 15.3423=+=t θ(3) 要使t n a a =,则有()()422212243t r rt = t ＝0.55ｓ1 -25 一无风的下雨天,一列火车以v 1＝20.0 m·ｓ-1 的速度匀速前进,在车内的旅客看见玻璃窗外的雨滴和垂线成75°角下降．求雨滴下落的速度v2 ．(设下降的雨滴作匀速运动)分析 这是一个相对运动的问题．设雨滴为研究对象,地面为静止参考系Ｓ,火车为动参考系Ｓ′．v 1 为Ｓ′相对Ｓ 的速度,v 2 为雨滴相对Ｓ的速度,利用相对运动速度的关系即可解．解 以地面为参考系,火车相对地面运动的速度为v 1 ,雨滴相对地面竖直下落的速度为v 2 ,旅客看到雨滴下落的速度v 2′为相对速度,它们之间的关系为1'22v v v += (如图所示),于是可得 1o 12s m 36.575tan -⋅==v v 1 -26 如图(a)所示,一汽车在雨中沿直线行驶,其速率为v 1 ,下落雨滴的速度方向偏于竖直方向之前θ 角,速率为v 2′,若车后有一长方形物体,问车速v 1为多大时,此物体正好不会被雨水淋湿？分析 这也是一个相对运动的问题．可视雨点为研究对象,地面为静参考系Ｓ,汽车为动参考系Ｓ′．如图(a)所示,要使物体不被淋湿,在车上观察雨点下落的方向(即雨点相对于汽车的运动速度v 2′的方向)应满足hl αarctan≥．再由相对速度的矢量关系122v v v -=',即可求出所需车速v 1．解 由122v v v -='［图(b)］,有θθαcos sin arctan221v v v -= 而要使hlαarctan ≥,则 hl θθ≥-cos sin 221v v v ⎪⎭⎫ ⎝⎛+≥θh θl sin cos 21v v 1 -27 一人能在静水中以1.10 m·ｓ-1 的速度划船前进．今欲横渡一宽为1.00 ×103 m 、水流速度为0.55 m·ｓ-1 的大河．(1) 他若要从出发点横渡该河而到达正对岸的一点,那么应如何确定划行方向？ 到达正对岸需多少时间？ (2)如果希望用最短的时间过河,应如何确定划行方向？ 船到达对岸的位置在什么地方？分析 船到达对岸所需时间是由船相对于岸的速度v 决定的．由于水流速度u 的存在, v 与船在静水中划行的速度v ′之间有v ＝u ＋v ′(如图所示)．若要使船到达正对岸,则必须使v 沿正对岸方向；在划速一定的条件下,若要用最短时间过河,则必须使v 有极大值．。

大学物理力学一、二章作业答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第一章 质点运动学一、选择题1、一质点在xoy 平面内运动，其运动方程为2,ct b y at x +==，式中a 、b 、c 均为常数。

当运动质点的运动方向与x 轴成450角时，它的速率为[ B ]。

A ．a ；B ．a 2；C ．2c ；D ．224c a +。

2、设木块沿光滑斜面从下端开始往上滑动，然后下滑，则表示木块速度与时间关系的曲线是图1-1中的[ D ]。

3、一质点的运动方程是j t R i t R rωωsin cos +=，R 、ω为正常数。

从t ＝ωπ/到t =ωπ/2时间内该质点的路程是[ B ]。

A ．2R ；B ．R π；C ． 0；D ．ωπR 。

4、质量为0.25kg 的质点，受i t F =(N)的力作用，t =0时该质点以v=2j m/s 的速度通过坐标原点，该质点任意时刻的位置矢量是[ B ]。

A ．22t i +2j m ； B ．j t i t2323+m ；C ．j t i t343243+； D ．条件不足，无法确定。

二、填空题1、一质点沿x 轴运动，其运动方程为225t t x -+=（x 以米为单位，t 以秒为单位）。

质点的初速度为 2m/s ，第4秒末的速度为 -6m/s ，第4秒末的加速度为 -2m/s 2 。

2、一质点以π（m/s ）的匀速率作半径为5m 的圆周运动。

该质点在5s 内的平均速度的大小为 2m/s ，平均加速度的大小为 22m /5s π 。

3、一质点沿半径为0.1m 的圆周运动，其运动方程为22t +=θ（式中的θ以弧度计，t 以秒计），质点在第一秒末的速度为 0.2m/s ，切向加速度为 0.2m/s 2 。

4、一质点沿半径1m 的圆周运动，运动方程为θ=2+3t 3，其中θ以弧度计，t 以秒计。

T =2s 时质点的切向加速度为 36m/s 2 ；当加速度的方向和半径成45º角时角位移是 38rad 。

第1章 质点运动学1 下面各种判断中, 错误的是A. 质点作直线运动时, 加速度的方向和运动方向总是一致的B.质点作匀速率圆周运动时, 加速度的方向总是指向圆心C . 质点作斜抛运动时, 加速度的方向恒定D . 质点作曲线运动时, 加速度的方向总是指向曲线凹的一边[ ]答案：A难易程度：中答案解析：无题型：单选题2. 质点作圆周运动时，下列说表述中正确的是（ ）A. 速度方向一定指向切向，加速度方向一定指向圆心B. 速度方向一定指向切向，加速度方向也一般指向切向C. 由于法向分速度为零，所以法向加速度也一定为零D. 切向加速度仅由速率的变化引起答案：D难易程度：中答案解析：无题型：单选题3 有两个各自作匀变速运动的物体, 在相同的时间间隔内所发生的位移大小应有A. 加速度大的位移大B. 路程长的位移大C.平均速率大的位移大D. 平均速度大的位移大[ ]答案：D难易程度：中答案解析：无题型：单选题4 质点作曲线运动, r 表示位置矢量的大小, s 表示路程, a 表示加速度大小, 则下列各式中正确的是 A. a t =d d v B. v =t r d d C. v =t s d d D. a t=d d v [ ] 答案：C难易程度：中答案解析：无题型：单选题5. 关于加速度的物理意义, 下列说法正确的是A. 加速度是描述物体运动快慢的物理量B. 加速度是描述物体位移变化率的物理量C. 加速度是描述物体速度变化的物理量D. 加速度是描述物体速度变化率的物理量 [ ]答案：D难易程度：中答案解析：无题型：单选题5 作匀变速圆周运动的物体A.法向加速度大小不变B. 切向加速度大小不变C. 总加速度大小不变D. 以上说法都不对[ ]答案：B难易程度：中答案解析：无题型：单选题7 作圆周运动的物体A. 加速度的方向必指向圆心B.切向加速度必定等于零C. 法向加速度必定等于零D.总加速度必定不总等于零[ ]答案：D难易程度：中答案解析：无题型：单选题8 一质点在平面上运动, 已知质点位置矢量的表示式为j t b i t a r22+=(其中a 、b 为常量) , 则该质点作A. 匀速直线运动B. 变速直线运动C. 抛物曲线运动D.一般曲线运动[ ]答案：B难易程度：中答案解析：无题型：单选题9 一质点在xOy 平面内运动, 其运动方程为Rt t R x ωω+=sin , R t R y +=ωcos ,式中R 、ω均为常数．当y 达到最大值时该质点的速度为A ．0,0==y x v v B. 0,2==y x R v v ωC . ωR y x −==v v ,0 D. ωωR R y x −==v v ,2[ ]答案：B难易程度：难答案解析：无题型：单选题10某物体的运动规律为t k t2d d v v −=, 式中k 为常数．当t = 0时，初速度为0v ．则速度v 与时间t 的函数关系是 A. 0221v v +=t k B. 0221v v +−=t k C. 02121v v +=t k D. 02121v v +−=t k [ ] 答案：C难易程度：难答案解析：无题型：单选题11 某质点作直线运动的运动学方程为x ＝3t -5t 3 + 6 (SI)，则该质点作A. 匀加速直线运动，加速度沿x 轴正方向．B. 匀加速直线运动，加速度沿x 轴负方向．C. 变加速直线运动，加速度沿x 轴正方向．D. 变加速直线运动，加速度沿x 轴负方向． ( )答案：D难易程度：中答案解析：无题型：单选题12 物体不能出现下述哪种情况?A.运动中, 瞬时速率和平均速率恒相等B. 运动中, 加速度不变, 速度时刻变化C. 曲线运动中, 加速度越来越大, 曲率半径总不变D. 曲线运动中, 加速度不变, 速率也不变[ ]答案：D难易程度：中答案解析：无题型：单选题13.下列说法中，哪一个是正确的？A. 一质点在某时刻的瞬时速度是2 m/s ，说明它在此后1 s 内一定要经过2 m 的路程．B. 斜向上抛的物体，在最高点处的速度最小，加速度最大．C. 物体作曲线运动时，有可能在某时刻的法向加速度为零．D.物体加速度越大，则速度越大． ［ ］答案：C难易程度：中答案解析：无题型：单选题第2章牛顿运动定律一、选择题1．牛顿第一定律告诉我们A 物体受力后才能运动B 物体不受力也能保持本身的运动状态C 物体的运动状态不变, 则一定不受力D 物体的运动方向必定和受力方向一致[ ]答案：B难易程度：中答案解析：无题型：单选题2. 下列说法中正确的是A. 运动的物体有惯性, 静止的物体没有惯性B. 物体不受外力作用时, 必定静止C. 物体作圆周运动时, 合外力不可能是恒量D. 牛顿运动定律只适用于低速、微观物体[ ] 答案：C难易程度：中答案解析：无题型：单选题3. 下列诸说法中, 正确的是A.物体的运动速度等于零时, 合外力一定等于零B. 物体的速度愈大, 则所受合外力也愈大C.物体所受合外力的方向必定与物体运动速度方向一致D.以上三种说法都不对[ ]答案：D难易程度：中答案解析：无题型：单选题4. 一个物体受到几个力的作用, 则A. 运动状态一定改变B. 运动速率一定改变C.必定产生加速度D. 必定对另一些物体产生力的作用[ ]答案：D难易程度：中答案解析：无题型：单选题5. 对一运动质点施加以恒力, 质点的运动会发生什么变化?A.质点沿着力的方向运动B.质点仍表现出惯性C.质点的速率变得越来越大D. 质点的速度将不会发生变化[ ]答案：B难易程度：中答案解析：无题型：单选题6. 一物体作匀速率曲线运动, 则A. 其所受合外力一定总为零B.其加速度一定总为零C.其法向加速度一定总为零D.其切向加速度一定总为零[ ]答案：D难易程度：中答案解析：无题型：单选题7. 一炮弹由于特殊原因在飞行中突然炸成两块, 其中一块作自由下落, 则另一块着地点A. 比原来更远B. 比原来更近C. 仍和原来一样D.条件不足不能判定[ ]答案：A难易程度：中答案解析：无题型：单选题8用水平力F N把一个物体压着靠在粗糙的竖直墙面上保持静止．当F N逐渐增大时,物体所受的静摩擦力F f的大小( )A.不为零,但保持不变B．随F N成正比地增大C ． 开始随F N 增大,达到某一最大值后,就保持不变D ． 无法确定答案：A难易程度：中答案解析：无题型：单选题 9. 一物体沿固定圆弧形光滑轨道由静止下滑,在下滑过程中,则( )A. 它的加速度方向永远指向圆心,其速率保持不变B.它受到的轨道的作用力的大小不断增加C. 它受到的合外力大小变化,方向永远指向圆心D.它受到的合外力大小不变,其速率不断增加答案：B难易程度：中答案解析：无题型：单选题第4章 振动与波动一、选择题1. 已知四个质点在x 轴上运动, 某时刻质点位移x 与其所受合外力F 的关系分别由下列四式表示(式中a 、b 为正常数)．其中不能使质点作简谐振动的力是[ ]A. abx F =B. abx F −=C. b ax F +−=D. a bx F /−=答案：A难易程度：中答案解析：无题型：单选题2. 在下列所述的各种物体运动中, 可视为简谐振动的是[ ]A. 将木块投入水中, 完全浸没并潜入一定深度, 然后释放B. 将弹簧振子置于光滑斜面上, 让其振动C. 从光滑的半圆弧槽的边缘释放一个小滑块D. 拍皮球时球的运动答案：B难易程度：中答案解析：无题型：单选题3. 在简谐振动的运动方程中，振动相位)(ϕω+t 的物理意义是[ ]A.表征了简谐振子t 时刻所在的位置B. 表征了简谐振子t 时刻的振动状态C. 给出了简谐振子t 时刻加速度的方向D. 给出了简谐振子t 时刻所受回复力的方向答案：B难易程度：中答案解析：无题型：单选题4. 一质点作简谐振动, 振动方程为)cos(ϕω+=t A x ． 则在2T t =(T 为振动周期) 时, 质点的速度为[ ]A.ϕωsin A −B.ϕωsin AC. ϕωcos A −D.ϕωcos A答案：B难易程度：中答案解析：无题型：单选题5. 一质点以周期T 作简谐振动, 则质点由平衡位置正向运动到最大位移一半处的最短时间为[ ] A.6T B. 8T C. 12T D. T 127 答案：C难易程度：中答案解析：无题型：单选题6. 某物体按余弦函数规律作简谐振动, 它的初相位为2π3, 则该物体振动的初始状态为[ ]A. x 0 = 0 , v 0 > 0B. x 0 = 0 , v 0＜0C. x 0 = 0 , v 0 = 0D. x 0 = −A , v 0 = 0答案：A难易程度：中答案解析：无题型：单选题7. 一作简谐运动质点的振动方程为π)21π2cos(5+=t x , 它从计时开始, 在运动一个周期后[ ]A. 相位为零B. 速度为零C. 加速度为零D. 振动能量为零答案：C难易程度：中答案解析：无题型：单选题8. 当一质点作简谐振动时, 它的动能和势能随时间作周期变化．如果ν是质点振动的频率, 则其动能变化的频率为[ ]A.ν4B.ν2C. νD.2ν 答案：B难易程度：中答案解析：无题型：单选题9. 两个同方向、同频率、等振幅的谐振动合成, 如果其合成振动的振幅仍不变, 则此二分振动的相位差为[ ] A.2π B.3π2 C. 4π D. π 答案：B难易程度：中答案解析：无题型：单选题10. 谐振子作简谐振动时, 速度和加速度的方向[ ]A. 始终相同B. 始终相反C. 在某两个41周期内相同, 另外两个41周期内相反 D.在某两个21周期内相同, 另外两个21周期内相反 答案：C难易程度：中答案解析：无题型：单选题11. 关于振动和波, 下面几句叙述中正确的是[ ]A.有机械振动就一定有机械波B.机械波的频率与波源的振动频率相同C.机械波的波速与波源的振动速度相同D.机械波的波速与波源的振动速度总是不相等的答案：B难易程度：中答案解析：无题型：单选题12. 按照定义，振动状态在一个周期内传播的距离就是波长．下列计算波长的方法中错误的是[ ]A. 用波速除以波的频率B. 用振动状态传播过的距离除以这段距离内的波数C.测量相邻两个波峰的距离D.测量波线上相邻两个静止质点的距离答案：D难易程度：中答案解析：无题型：单选题13. 当x 为某一定值时, 波动方程)π(2cos λx T t A x −=所反映的物理意义是[ ] A. 表示出某时刻的波形B. 说明能量的传播C. 表示出x 处质点的振动规律D. 表示出各质点振动状态的分布答案：C难易程度：中答案解析：无题型：单选题14. 下列方程和文字所描述的运动中，哪一种运动是简谐振动? [ ]A.x A t =1cos ωB.x A t A t =+123cos cos ωωC.d d 2222x tx =−ω D.两个同方向、频率相近的谐振动的合成答案：A难易程度：中答案解析：无题型：单选题15. 下列函数f ( x , t )可以用来表示弹性介质的一维波动, 其中a 和b 是正常数．则下列函数中, 表示沿x 轴负方向传播的行波是[ ]A. )sin(),(bt ax A t x f +=B. )sin(),(bt ax A t x f −=C. )cos()cos(),(bt ax A t x f =D.)sin()sin(),(bt ax A t x f =答案：A难易程度：中答案解析：无题型：单选题16. 已知一波源位于x = 5 m 处, 其振动方程为: )cos(ϕω+=t A y (m)．当这波源产生的平面简谐波以波速u 沿x 轴正向传播时, 其波动方程为[ ] A.)(cos ux t A y −=ω B. ])(cos[ϕω+−=ux t A y C.])5(cos[ϕω++−=ux t A y D.])5(cos[ϕω+−−=u x t A y 答案：D难易程度：中答案解析：无题型：单选题17. 已知一平面余弦波的波动方程为)01.05.2π(cos 2x t y −=, 式中 x 、y 均以cm 计．则在同一波线上, 离x = 5 cm 最近、且与 x = 5 cm 处质元振动相位相反的点的坐标为[ ]A.7.5 cmB. 55 cmC.105 cmD. 205 cm答案：C难易程度：中 答案解析：无 题型：单选题18. 若一平面简谐波的波动方程为)cos(cx bt A y −=, 式中A 、b 、c 为正值恒量．则[ ] A. 波速为cB.周期为b 1 C. 波长为c π2D.角频率为bπ2答案：C难易程度：中 答案解析：无 题型：单选题19. 一平面简谐横波沿着Ox 轴传播．若在Ox 轴上的两点相距8λ（其中λ为波长）, 则在波的传播过程中, 这两点振动速度的[ ] A. 方向总是相同 B. 方向有时相同有时相反C.方向总是相反D. 大小总是不相等答案：B难易程度：中 答案解析：无 题型：单选题20. 一简谐波沿Ox 轴正方向传播，t ＝0时刻波形曲线如图所示，其周期为2 s ．则P 点处质点的振动速度v 与时间t 的关系曲线为 [ ]AωsD ωsω−ω−s图 波形图难易程度：中 答案解析：无 题型：单选题静电场2. 将某电荷Q 分成q 和(Q −q )两部分, 并使两部分离开一定距离, 则它们之间的库仑力为最大的条件是 [ ] (A) 2Q q = (B) 4Qq = (C) 8Qq =(D) 16Qq =答案：A难易程度：易 答案解析：无 题型：单选题5. 关于静电场, 下列说法中正确的是[ ] (A) 电场和检验电荷同时存在, 同时消失(B) 由qF E =知, 电场强度与检验电荷电荷量成反比(C) 电场的存在与否与检验电荷无关(D) 电场是检验电荷与源电荷共同产生的 答案：C难易程度：易 答案解析：无 题型：单选题8. 关于电场强度, 以下说法中正确的是[ ] (A) 电场中某点场强的方向, 就是将点电荷放在该点所受电场力的方向 (B) 在以点电荷为中心的球面上, 由该点电荷所产生的场强处处相同(C) 场强方向可由qFE =定出, 其中q 可正, 可负(D) 以上说法全不正确难易程度：易 答案解析：无 题型：单选题11. 在静电场中, 电场线为平行直线的区域内 [ ] (A) 电场相同, 电势不同(B) 电场不同, 电势相同(C) 电场不同, 电势不同(D) 电场相同, 电势相同 答案：A难易程度：易 答案解析：无 题型：单选题15、如图所示，一均匀带电球面, 面内电场强度处处为零, 则球面上的带电量为S d σ的电荷元在球面内产生的场强[ ] (A) 处处为零(B) 不一定为零(C) 一定不为零 (D) 是一常数答案：C难易程度：易 答案解析：无 题型：单选题18. 半径为R 的均匀带电球面, 若其面电荷密度为σ, 则在球面外距离球面R 处的电场强度大小为 [ ] (A)εσ(B)2εσ(C)04εσ(D)8εσ 答案：C难易程度：中 答案解析：无 题型：单选题24. 高斯定理0d ε∑⎰⎰=⋅isqS E, 说明静电场的性质是[ ] (A) 电场线是闭合曲线(B) 库仑力是保守力 (C) 静电场是有源场 (D) 静电场是保守场答案：C难易程度：易 答案解析：无 题型：单选题26. 电场中一高斯面S , 内有电荷q 1、q 2，S 面外有电荷q 3、q 4．关于高斯定理d ε∑⎰⎰=⋅isqS E , 正确的说法是[ ] (A) 积分号内E只是q 1、q 2共同激发的(B) 积分号内E是q 1、q 2、q 3、q 4共同激发的(C) 积分号内E只是q 3、q 4共同激发的(D) 以上说法都不对答案：B难易程度：中 答案解析：无 题型：单选题33. 将点电荷Q 从无限远处移到相距为2l 的点电荷＋和－q 的中点处, 则电势能的增加量为[ ] (A) 0(B)l q0π4ε(C) l Qq 0π4ε(D) lQq0π2ε答案：A难易程度：中 答案解析：无题型：单选题35. 下面关于某点电势正负的陈述中, 正确的是 [ ] (A) 电势的正负决定于试探电荷的正负(B) 电势的正负决定于移动试探电荷时外力对试探电荷做功的正负(C) 空间某点电势的正负是不确定的, 可正可负, 决定于电势零点的选取 (D) 电势的正负决定于带电体的正负答案：C难易程度：易 答案解析：无 题型：单选题37. 由定义式⎰∞⋅=RR l E Ud 可知[ ] (A) 对于有限带电体, 电势零点只能选在无穷远处(B) 若选无限远处为电势零点, 则电场中各点的电势均为正值 (C) 已知空间R 点的E , 就可用此式算出R 点的电势(D) 已知R →∞积分路径上的场强分布, 便可由此计算出R 点的电势答案：D难易程度：中 答案解析：无 题型：单选题 D41. 两个点电荷相距一定距离, 若这两个点电荷连线的中垂线上电势为零, 则这两个点电荷的带电情况为[ ] (A) 电荷量相等, 符号相同 (B) 电荷量相等, 符号不同(C) 电荷量不同, 符号相同 (D) 电荷量不等, 符号不同答案：B难易程度：易 答案解析：无 题型：单选题44. 如图5-1-45所示，等边三角形的三个顶点上分别放置着均为正的点电荷q 、2 q 、和3 q , 三角形的边长为a , 若将正电荷Q 从无穷远处移至三角形的中心点处, 所需做的功为[ ] (A) aQq0π44.3ε(B) aQq0π7.1ε (C) aQq0π6.2ε (D) aQq0π4.3ε 答案：C难易程度：难 答案解析：无 题型：单选题48. 关于电场强度和电势的关系, 下列说法中正确的是 [ ] (A) 电势不变的空间, 电场强度一定为零 (B) 电势不变的空间, 电场强度不为零 (C) 电势为零处, 电场强度一定为零 (D) 电场强度为零处, 电势一定为零 答案：A难易程度：易 答案解析：无 题型：单选题52. 带电－q 的粒子在带电＋q 的点电荷的静电力作用下在水平面内绕点电荷作半径为R 的匀速圆周运动. 如果带电粒子质量及点电荷的电量均增大一倍, 并使粒子的运动速率也增大一倍, 则粒子的运动半径将变为 [ ] (A) 4R(B)2R(C) 2R (D) 4R答案：A难易程度：中 答案解析：无 题型：单选题56. 边长为a 的正方体中心放置一电荷Q , 则通过任一个侧面S 的电通量⎰⎰⋅sS E d 为[ ] (A) 04εQ(B)6εQ(C)08 Q(D) 6Q答案：B难易程度：易 答案解析：无 题型：单选题第7章 恒定磁场一、选择题1. 磁场可以用下述哪一种说法来定义? (A) 只给电荷以作用力的物理量 (B) 只给运动电荷以作用力的物理量(C) 贮存有能量的空间(D) 能对运动电荷做功的物理量 答案：B难易程度：易 答案解析：无 题型：单选题2. 下列叙述中不能正确反映磁感应线性质的是 (A) 磁感应线是闭合曲线(B) 磁感应线上任一点的切线方向为运动电荷的受力方向 (C) 磁感应线与载流回路象环一样互相套连 (D) 磁感应线与电流的流向互相服从右手定则答案：B难易程度：中 答案解析：无 题型：单选题3. 一电荷放置在行驶的列车上, 相对于地面来说, 电荷产生电场和磁场的情况将是A) 只产生电场 (B) 只产生磁场 (C) 既产生电场, 又产生磁场(D) 既不产生电场, 又不产生磁场答案：C难易程度：中 答案解析：无 题型：单选题4. 通以稳恒电流的长直导线, 在其周围产生电场和磁场的情况将是 (A) 只产生电场 (B) 只产生磁场(C) 既产生电场, 又产生磁场(D) 既不产生电场, 又不产生磁场答案：C难易程度：中 答案解析：无 题型：单选题5. 磁场的高斯定理⎰⎰=⋅sS B 0d, 说明(A) 穿入闭合曲面的磁感应线的条数必然等于穿出的磁感应线的条数(B) 穿入闭合曲面的磁感应线的条数不等于穿出的磁感应线的条数 (C) 一根磁感应线可以终止在闭合曲面内 (D) 一根磁感应线不可能完全处于闭合曲面内答案：A难易程度：中 答案解析：无 题型：单选题 6. 下述情况中能用安培环路定律求磁感应强度的是 (A) 一段载流直导线 (B) 无限长直线电流(C) 一个环形电流(D) 任意形状的电流 答案：B难易程度：中 答案解析：无 题型：单选题7. 取一闭合积分回路L , 使三根载流导线穿过L 所围成的面，如图所示. 现改变三根导线之间的相互间隔, 但不越出积分回路, 则(A) 回路L 内的∑I 不变, L 上各点的B 不变(B) 回路L 内的∑I 不变, L 上各点的B 改变(C) 回路L 内的∑I 改变, L 上各点的B 不变(D) 回路L 内的∑I 改变, L 上各点的B 改变答案：B难易程度：中 答案解析：无 题型：单选题 8. 一无限长直圆柱体, 半径为R , 沿轴向均匀流有电流，如图所示．设圆柱体内(r ＜R )的磁感应强度大小为B 1, 圆柱体外( r ＞R )感应强度大小为B 2, 则有(A) B 1、B 2均与 r 成正比 (B) B 1、B 2均与 r 成反比(C) B 1与 r 成反比, B 2与 r 成正比2B •(D) B 1与r成正比, B 2与r成反比答案：D难易程度：中答案解析：无题型：单选题9. 运动电荷受洛伦兹力后, 其动能、动量的变化情况是(A) 动能守恒(B) 动量守恒(C) 动能、动量都守恒(D) 动能、动量都不守恒答案：A难易程度：中答案解析：无题型：单选题10. 如图所示，一个长直螺线管通有交流电, 把一个带负电的粒子沿螺线管的轴线射入管中, 粒子将在管中作(A) 圆周运动(B) 沿管轴来回运动(C) 螺旋线运动(D) 匀速直线运动答案：D难易程度：中答案解析：无题型：单选题11. 在均匀磁场中放置三个面积相等且通过相同电流的线圈: 一个是矩形, 一个是正方形, 另一个是三角形, 如图所示．下列叙述中正确的是(A) 正方形线圈受到的合磁力为零, 矩形线圈受到的合磁力最大(B) 三角形线圈受到的最大磁力矩为最小(C) 三线圈所受的合磁力和最大磁力矩均为零(D) 三线圈所受的最大磁力矩均相等答案：D难易程度：中答案解析：无B题型：单选题12. 两个电子同时由两电子枪射出, 它们的初速度与均匀磁场垂直, 速率分别为2v 和v , 经磁场偏转后(A) 第一个电子先回到出发点 (B) 第二个电子先回到出发点(C) 两个电子同时回到出发点 (D) 两个电子都不能回到出发点答案：C难易程度：中 答案解析：无 题型：单选题13. 电荷为(+q )的粒子以速度为v ＝0.01c 沿x 轴方向运动, 磁感应强度B的方向沿y轴．要使粒子不偏转需加一个什么样的电场? (A) E ＝B , 沿－y 方向 (B) E ＝B , 沿z 方向 (C) E ＝v B , 沿－z 方向 (D) E ＝v B , 沿z 方向答案：C难易程度：中 答案解析：无 题型：单选题14. 如图所示，在磁感应强度为B的均匀磁场中，有一圆形载流导线，a 、b 、c 是其上三个长度相等的电流元，则它们所受安培力大小的关系为(A) a F >b F >c F (B) a F <b F <c F (C) b F >c F >a F(D) a F >c F >b F 答案：C难易程度：中 答案解析：无 题型：单选题15. 若用条形磁铁竖直插入木质圆环, 则在环中是否产生感应电流和感应电动势的判断是(A) 产生感应电动势, 也产生感应电流 (B) 产生感应电动势, 不产生感应电流 (C) 不产生感应电动势, 也不产生感应电流(D) 不产生感应电动势, 产生感应电流 答案：B难易程度：中 答案解析：无 题型：单选题第八章 光学测验题1. 如右图所示，1S 、2S 是两个相干光源，他们到P 点的距离分别为 1r 和 2r 。

大学物理-质点运动学(答案)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第一章 力和运动（质点运动学）一. 选择题:［ B ］1、一质点沿x 轴作直线运动，其v t 曲线如图所示，如t =0时，质点位于坐标原点，则t =4.5 s 时，质点在x 轴上的位置为 (A) 5m ． (B) 2m ． (C) 0． (D) -2 m ．(E) -5 m.(1 2.5)22(21)122()x m =+⨯÷-+⨯÷=提示：［ C ］2、如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动．设该人以匀速率0v 收绳，绳不伸长、湖水静止，则小船的运动是 (A) 匀加速运动． (B) 匀减速运动．(C) 变加速运动． (D) 变减速运动． (E) 匀速直线运动． 提示：如图建坐标系，设船离岸边x 米，222l h x =+22dl dxl xdt dt= 22dx l dl x h dldt x dtx dt+==0dlv dt=- 220dx h x v i v i dt x+==-2203v h dv dv dxa i dt dx dt x==⋅=-［ D ］3、一运动质点在某瞬时位于矢径()y x r ,的端点处, 其速度大小为(A) t r d d (B) t r d d(C) t r d d (D) 22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x1 4.5432.52-112t (s)v (m/s)vxo提示：22, dxdy dx dy v i j v dt dt dt dt ⎛⎫⎛⎫⎛⎫=+∴=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭［ B ］4、质点沿半径为R 的圆周作匀速率运动，每T 秒转一圈．在2T 时间间隔中，其平均速度大小与平均速率大小分别为(A) 2πR /T , 2πR/T ． (B) 0 , 2πR /T (C) 0 , 0．提示：平均速度大小：0rv t ∆==∆ 平均速率：2s R v t T∆==∆π ［ B ］5、在相对地面静止的坐标系内，A 、B 二船都以2 m/s 速率匀速行驶，A 船沿x 轴正向，B 船沿y 轴正向．今在A 船上设置与静止坐标系方向相同的坐标系(x 、y 方向单位矢用i 、j表示)，那么在A 船上的坐标系中，B 船的速度（以m/s 为单位）为(A) 2i＋2j ．(B) -2i ＋2j ． (C) －2i －2j ． (D) 2i－2j ．提示：2(2)B A B A v v v j i →→→=+=+-地地［ D ］6、某人骑自行车以速率v 向西行驶，今有风以相同速率从北偏东30o 方向吹来，人感到风从哪个方向吹来？(A)北偏东30︒ (B)北偏西60︒ (C) 北偏东60︒ (D) 北偏西30︒提示：根据v 风对人=v 风对地+v 地对人，三者的关系如图所示：这是个等边三角形，∴人感到风从北偏西300方向吹来。

第一章质点运动学一选择题1．以下说法中，正确的选项是：（）A.一物体若拥有恒定的速率，则没有变化的速度；B.一物体拥有恒定的速度，但仍有变化的速率；C.一物体拥有恒定的加快度，则其速度不行能为零；D. 一物体拥有沿x 轴正方向的加快度而有沿x 轴负方向的速度。

解：答案是 D。

2.长度不变的杆 AB，其端点 A 以 v0匀速沿 y 轴向下滑动， B 点沿 x 轴挪动，则 B 点的速率为：（）A . v0 sinB .v0 cos C.v0 tan D.v0 / cos解：答案是 C。

简要提示：设 B 点的坐标为 x， A 点的坐标为 y，杆的长度为l，则x2y2l 2对上式两边关于时间求导：dx dy0，因dxv，dyv0，所以2 x 2 ydtdt dt dt2xv2yv0 = 0即v=v0 y/x =v0tan所以答案是 C。

3.如图示，路灯距地面高为 H，行人身高为 h，若人以匀速 v 背向路灯行走，灯y人头A H vv0hθvx影sB选择题 3图选择题 2图则人头影子挪动的速度u 为（）H h Hv h HA.vB.H H h H h 解：答案是 B 。

简要提示：设人头影子到灯杆的距离为 x ，则x s h ， x Hs ， x H H hdx H ds HvuH h dt Hdt h所以答案是 B 。

4. 某质点作直线运动的运动学方程为x ＝ 3t-5t 3 + 6 (SI)，则该质点作A. 匀加快直线运动，加快度沿 x 轴正方向．B. 匀加快直线运动，加快度沿 x 轴负方向．C. 变加快直线运动，加快度沿 x 轴正方向．D. 变加快直线运动，加快度沿x 轴负方向．()解： 答案是 D5. 一物体从某一确立高度以v 0 的初速度水平抛出，已知它落地时的速度为v t ，那么它的运动时间是： （）v t - v 0v t v 0v t2 22v v 0 v t A.B.C.gD.2 gg2 g解：答案是 C 。

大学物理练习题一一、选择题1. 一质点在平面上运动，已知质点位置矢量的表示式为j bti at r22（其中a 、b为常量），则该质点作（A ）匀速直线运动； （B ）变速直线运动；（C ）抛物线运动； （D ）一般曲线运动.[ B ]解：由2at x ，2bt y 可得x a by 。

即质点作直线运动。

j bt i at dtr d v 22 是变量，故为变速直线运动。

2. 一质点在平面上作一般曲线运动，其瞬时速度为v ，瞬时速率为v ，某一段时间内的平均速度为v,平均速率为v ，它们之间的关系必定有（A ）v v ，v v. （B ）v v ，v v . （C ）v v ，v v. （D ）v v ，v v .[ D ]解：定义式dt rd v，dt ds v ; t r v ，t s v ；因为 ds r d ||，s |r |（单向直线运动除外），所以 v v v v ,3. 质点作半径为R 的变速圆周运动时的加速度大小为 （v 表示任一时刻质点的速率）（A ）dt dv . (B)R v 2. (C) dt dv+R v 2. (D)21222R v dt dv .[ D ]4. 某物体的运动规律为2kv dt dv ，式中的k 为大于零的常数.当t=0时，初速为v 0，则速度v 与时间t 的函数关系是（A ）v=kt+v 0. （B ）v=-kt+v 0.（C ）011v kt v . （D ）011v kt v . 了 [ C ]解：由2kv dt dv 得 kdt v dv 2，tvv dt k v dv 020，ktv vv 01， kt v v 011，011v kt v5. 某人骑自行车以速率v 向正东方行驶，遇到由北向南刮的风（设风速大小也为v ），则他感到风是从 [ A ]（A ）东北方向吹来。

（B ）东南方向吹来。

（C ）西北方向吹来。

（D ）西南方向吹来。

解：人地风地地人风地风人＝v v v v v，人地风人风地v v v矢量关系图示如右.6. 一飞机相对空气的速度大小为200h km ，风速为56h km ，方向从西向东，地面雷达测得飞机速度大小为192h km ，方向是 （A ）南偏西16.30。

大学物理习题集上习题解答文档编制序号：[KKIDT-LLE0828-LLETD298-POI08])2(选择题(5)选择题单元一 质点运动学（一）一、选择题1. 下列两句话是否正确：(1) 质点作直线运动，位置矢量的方向一定不变；【 】(2) 质点作园周运动位置矢量大小一定不变。

【 】 2. 一物体在1秒内沿半径R=1m 的圆周上从A 点运动到B 点，如图所示，则物体的平均速度是： 【 A 】(A) 大小为2m/s ，方向由A 指向B ； (B) 大小为2m/s ，方向由B 指向A ； (C) 大小为s ，方向为A 点切线方向； (D) 大小为s ，方向为B 点切线方向。

3. 某质点的运动方程为x=3t-5t 3+6(SI)，则该质点作 【 D 】(A) 匀加速直线运动，加速度沿X 轴正方向； (B) 匀加速直线运动，加速度沿X 轴负方向;(C) 变加速直线运动，加速度沿X 轴正方向; (D)变加速直线运动，加速度沿X 轴负方向4. 一质点作直线运动，某时刻的瞬时速度v=2 m/s ，瞬时加速率a=2 m/s 2则一秒钟后质点的速度:【 D 】(A) 等于零 (B) 等于-2m/s (C) 等于2m/s (D) 不能确定。

5. 如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向边运动。

设该人以匀速度V 0收绳，绳不伸长、湖水静止，则小船的运动是 【 C 】(7)选择题(A)匀加速运动; (B) 匀减速运动; (C) 变加速运动; (D) 变减速运动; (E) 匀速直线运动。

6. 一质点沿x 轴作直线运动，其v-t 曲线如图所示，如t=0时，质点位于坐标原点，则t=时，质点在x 轴上的位置为 【 C 】(A) 0； (B) 5m ； (C) 2m ； (D) -2m ； (E) -5m *7. 某物体的运动规律为t kv dtdv2-=，式中的k 为大于零的常数。

当t=0时，初速为v 0，则速度v 与时间t 的函数关系是 【 C 】(A) 02v kt 21v += (B) 02v kt 21v +-= (C) 02v 1kt 21v1+= (D)2v 1kt 21v 1+-= 二、填空题1. )t t (r )t (r ∆+ 与为某质点在不同时刻的位置矢量，)t (v 和)t t (v ∆+为不同时刻的速度矢量，试在两个图中分别画出s ,r ,r ∆∆∆ 和v ,v ∆∆。

第一章 质点运动学1-1 一质点在平面上运动，已知质点位置矢量的表示式为j i r 22bt at += （其中b a ,为常量） 则该质点作（A ）匀速直线运动 （B ）变速直线运动（C ）抛物线运动 （D ）一般曲线运动 [B]解：由j i rv bt at t 22d d +==知 v 随t 变化，质点作变速运动。

又由x aby bt y at x =⎪⎭⎪⎬⎫==22 知质点轨迹为一直线。

故该质点作变速直线运动。

1-2 质点作曲线运动，r 表示位置矢量，s 表示路程，t a 表示切向加速度，下列表达式中，① a t v =d ② v t r =d ③ v t s =d d ④ t a t =d d v （A ）只有（1）、（4）是对的。

（B ）只有（2）、（4）是对的。

（C ）只有（2）是对的。

（D ）只有（3）是对的。

[D]解：由定义：t vt a d d d d ≠=v ； t r t s t v d d d d d d ≠==r ； t t v a d d d d v ≠=τ只有③正确。

1-3 在相对地面静止的坐标系内，A 、B 二船都以21s m -⋅的速率匀速行驶，A 船沿x 轴正向，B 船沿y 轴正向。

今在A 船上设置与静止坐标系方向相同的坐标系（x ，y 方向单位矢用j i ,表示），那么在A 船上的坐标系中，B 船的速度（以1s m -⋅为单位）为（A ）j i 22+ （B ）j i 22+-（C ）j i 22-- （D ）j i 22- [B]解：由i v 2=对地A ，j v 2=对地B 可得 A B A B 地对对地对v v v +=⎰对地对地A B v v -=i j 22-=j i 22+-= （1s m -⋅）1-4 一质点沿x 方向运动，其加速度随时间变化关系为)SI (23t a +=如果初始时质点的速度0v 为51s m -⋅，则当t 为3s 时，质点的速度1s m 23-⋅=v解：⎰+=tta v v 00d13s m 23d )23(5-⋅=++=⎰tt1-5 一质点的运动方程为SI)(62t t x -=，则在t 由0至4s 的时间间隔内，质点的位移大小为 8m ，在t 由0到4s 的时间间隔内质点走过的路程为 10m 。

第一章 质点运动学1-1 一质点在平面上运动，已知质点位置矢量的表示式为j i r 22bt at += （其中b a ,为常量） 则该质点作（A ）匀速直线运动 （B ）变速直线运动（C ）抛物线运动 （D ）一般曲线运动 [B]解：由j i rv bt at t 22d d +==知 v 随t 变化，质点作变速运动。

又由x aby bt y at x =⎪⎭⎪⎬⎫==22 知质点轨迹为一直线。

故该质点作变速直线运动。

1-2 质点作曲线运动，r 表示位置矢量，s 表示路程，t a 表示切向加速度，下列表达式中，① a t v =d ② v t r =d ③ v t s =d d ④ t a t =d d v （A ）只有（1）、（4）是对的。

（B ）只有（2）、（4）是对的。

（C ）只有（2）是对的。

（D ）只有（3）是对的。

[D]解：由定义：t vt a d d d d ≠=v ； t r t s t v d d d d d d ≠==r ； t t v a d d d d v ≠=τ只有③正确。

1-3 在相对地面静止的坐标系内，A 、B 二船都以21s m -⋅的速率匀速行驶，A 船沿x 轴正向，B 船沿y 轴正向。

今在A 船上设置与静止坐标系方向相同的坐标系（x ，y 方向单位矢用j i ,表示），那么在A 船上的坐标系中，B 船的速度（以1s m -⋅为单位）为（A ）j i 22+ （B ）j i 22+-（C ）j i 22-- （D ）j i 22- [B]解：由i v 2=对地A ，j v 2=对地B 可得 A B A B 地对对地对v v v +=⎰对地对地A B v v -=i j 22-=j i 22+-= （1s m -⋅）1-4 一质点沿x 方向运动，其加速度随时间变化关系为)SI (23t a +=如果初始时质点的速度0v 为51s m -⋅，则当t 为3s 时，质点的速度1s m 23-⋅=v解：⎰+=tta v v 00d13s m 23d )23(5-⋅=++=⎰tt1-5 一质点的运动方程为SI)(62t t x -=，则在t 由0至4s 的时间间隔内，质点的位移大小为 8m ，在t 由0到4s 的时间间隔内质点走过的路程为 10m 。

第一章质点运动学单元测验题一、选择题1.一质点沿x 轴运动，加速度与位置的关系为a (x )=2x +4x 2(SI 单位).已知质点在x =0处的速度为2m/s ，则质点在x =3m 处的速度为A.42m/s; B.26m/s ; C.94m/s ; D.34m/s .答案：C 解：根据题意：224dv a x x dt ==+，两边同乘dx 有：2(24)dv dx x x dx dt ⋅=+⋅由dx v dt=,上式化为:2(24)v dv x x dx ⋅=+对上式两边积分得到：223423v x x c =++由x =0，v =2m/s ，确定c =2.则当x =3m 时，解得：v =94m/s.2.一质点沿x 轴做直线运动，其速度v 随时间t 的变化关系如图所示.则下列哪个图可表示质点加速度a 随时间t 变化关系？2-•/s m a 2-•/s m a AB C答案：B 解：依据质点在一维运动时，速度-时间曲线的斜率对应加速度可知B 为加速度曲线.3.质点的运动学方程为33(21)t t =++r i j (SI 单位).则t =1s 时质点的速度为(SI单位)A.ji 6+3; B.j i 3+3; C.j i 6+6; D.j i 3+6.答案：A解：根据题意：33(21)t t =++r i j ，微分得：236d t dt ==+r v i j ，()136=+v i j 4.质点运动学方程为：kbt j t a i t a r +sin +cos =ωω，其中a 、b 、ω均为正的常数.问质点作什么运动？A.平面圆周运动；B.平面椭圆运动；C.螺旋运动；D.三维空间的直线运动.答案：C解：把质点的运动分解到三个方向上：cos sin x a t y a t z bt ωω===，，整理可知：222x y a z bt+==，则质点是以z 5.如图所示，在桌面的一边，—小球作斜抛运动，初速度v 0=4.7m/s.已知桌面宽a =2.0m.欲使小球能从桌面的另—边切过，小球的抛射角θ为A.30°;B.38°;C.50°;D.58°.答案：D 解：根据题意，小球沿x 和y 方向的运动方程为：t v x ⋅=θcos 0，201sin 2y v t gt θ=⋅-由x =2.0m 时，y =0，解得：o 58θ=.6.如图，有一半径为R 的定滑轮，沿轮周绕着一根绳子，悬在绳子一端的物体按s =(1/2)bt 2的规律向下运动.若绳子与轮周间没有相对滑动，轮周上一点A 在任一时刻t 的总加速度大为A.2t b a ;B.222/=R t b a ；C.b a =;D.R t b b a /+=22.答案：A 解：已知221bt s =，微分可得速度大小：t b dtds v ⋅==切向加速度大小：b dt dv a ==τ;法向加速度大小：Rt b R v a n 222==总加速度大小：a ==.7.当蒸汽船以15km/h 的速度向正北方向航行时，船上的人观察到船上的烟囱里冒出的烟飘向正东方向.过一会儿，船以24km/h 的速度向正东方向航行，船上的人则观察到烟飘向正西北方向.若在这两次航行期间风速不变，则风速的大小为A.9km/h; B.17.5km/h ; C.26.9km/h ; D.41km/h.答案：B解：地面为静系，船为动系，风为研究对象，则风对地的速度为绝对速度：风v v =船对地的速度为牵连速度：船牵连v v =风对船的速度为相对速度：风对船牵连v v =由绝对速度、牵连速度和相对速度的关系可得v v v =+船风对船，其矢量几何关系如图所示由此几何关系可得：1cos v v θ=船风，o 2145sin v v ctg v θ-=风船船联立解得：o 31θ=，5.17=v km /h .8.一个自由落体在它运动的最后一秒内所通过的路程等于全程的1/3.则物体通过全程所需的时间为A.3s ;B.6-3s ;C.6+3s ;D.6s答案：C解：设自由落体的全程下落时间和下落的高度分别为t 、S t 。

⼤学物理复习题及答案期末复习⼀、⼒学（⼀）填空题： 1、质点沿x 轴运动，运动⽅程23262x t t =+-，则其最初4s 内位移是 -32m i ，最初4s 内路程是 48m 。

2、质点的加速度(0),0a mx m t =->=时，00,x v v ==，则质点停下来的位置是x = 0m 。

3、半径为30cm 的飞轮，从静⽌开始以s 2匀⾓加速度转动。

当飞轮边缘上⼀点转过o 240时，切向加速度⼤⼩ m/s 2 ，法向加速度⼤⼩ m/s 2 。

4、⼀⼩车沿Ox 轴运动，其运动函数为233x t t =-，则2s t =时的速度为 -9m/s ，加速度为 -6m/s 2 ，2s t =内的位移为－6m 。

5、质点在1t 到2t 时间内,受到变⼒2At B F x +=的作⽤(A 、B 为常量)，则其所受冲量为 3321211()()3B t t A t t -+-。

6、⽤N 10=F 的拉⼒，将g k 1=m 的物体沿 30=α的粗糙斜⾯向上拉1m ，已知1.0=µ，则合外⼒所做的功A 为。

7、银河系中有⼀天体，由于引⼒凝聚，体积不断收缩。

设它经⼀万年后，体积收缩了1%，⽽质量保持不变，那时它绕⾃转轴的转动动能将增⼤； (填：增⼤、减⼩、不变)。

；8、 A 、B 两飞轮的轴杆在⼀条直线上，并可⽤摩擦啮合器C 使它们连结。

开始时B 轮静⽌，A 轮以⾓速度A ω转动，设啮合过程中两飞轮不再受其他⼒矩的作⽤，当两轮连结在⼀起后，其相同的⾓速度为ω。

若A 轮的转动惯量为A I ，则B 轮的转动惯量B I 为 A AA I I ωω- 。

9、斜⾯固定于卡车上，在卡车沿⽔平⽅向向左匀速⾏驶的过程中，斜⾯上物体m 与斜⾯⽆相对滑动。

则斜⾯对物体m 的静摩擦⼒的⽅向为。

沿斜⾯向上；10、⽜顿第⼆定律在⾃然坐标系中的分量表达式为n n F ma =；F ma ττ=11、质点的运动⽅程为22r ti t j =-，则在1s t =时的速度为 22v i j =-，加速度为2a j =-；12、⼀质点沿半径为的圆周运动，其⾓位移342t +=θ，则2s t =时的法向加速度为 s 2 ，切向加速度为 s 2 。

大学物理题库 第一章 质点运动学一、选择题：1、在平面上运动的质点，如果其运动方程为j bt i at r22+= (其中b a ,为常数)，则该质点作[ ]（A ） 匀速直线运动 （B ） 变速直线运动 （C ） 抛物线运动 （D ） 一般曲线运动2、质点以速度124-⋅+=s m t v 作直线运动，沿质点运动方向作ox 轴，并已知s t 3=时，质点位于m x 9=处，则该质点的运动方程为[ ](A) t x 2= (B) 2214t t x += (C) 123143-+=t t x (D) 123143++=t t x3、某雷达刚开机时发现一敌机的位置在j i96+处,经过3秒钟后，该敌机的位置在处,若i 、j分别表示直角坐标系中y x ,的单位矢量，则敌机的平均速度为[ ]（A ）j i 36+ （B ）j i 36-- （C ）j i -2 （D ）j i +-24、质点沿半径为R 的圆周作匀速率运动，每T 秒转一圈．在2T 时间间隔中，其平均速度大小与平均速率大小分别为(A) 2πR /T , 2πR/T ． (B) 0 , 2πR /T(C) 0 , 0． (D) 2πR /T , 0. ［ ］5、一质点在平面上作一般曲线运动，其瞬时速度为v，瞬时速率为v ，某一时间内的平均速度为v，平均速率为v ，它们之间的关系必定有：（A ）v v v,v == （B ）v v v,v =≠（C ）v v v,v ≠≠（D ）v v v,v ≠=[ ] 6、一运动质点的位置矢量为)y ,x (r，其速度大小为[ ](A)dt dr （B ）dt r d （C ）dt r d （D ）dtr d （E ）22)()(dt dydt dx +7、某物体的运动规律为t kv dtdv2-=,式中的k 为大于零的常数，当0=t 时，初速度为0v ，则速度v 与时间t 的函数关系是：[ ]（A ）0221v kt v += （B ） 0221v kt v +-=（C ） 021211v kt v += （D ） 021211v kt v +-=8、一质点作直线运动，某时刻的瞬时速度=v 2 m/s ，瞬时加速度2/2s m a -=，则一秒钟后质点的速度(A) 等于零． (B) 等于-2 m/s ．ji 612+(C) 等于2 m/s ． (D) 不能确定． ［ ］ 9、质点作曲线运动，r 表示位置矢量，v 表示速度，a表示加速度，S 表示路程，a 表示切向加速度，下列表达式中，(1) a t = d /d v ， (2) v =t r d /d ， (3) v =t S d /d ， (4) t a t =d /d v．(A) 只有(1)、(4)是对的． (B) 只有(2)、(4)是对的． (C) 只有(2)是对的．(D) 只有(3)是对的． ［ ］ 10、一质点在运动过程中，0=dtr d ,而=dtdv常数，这种运动属于[ ] （A ）初速为零的匀变速直线运动； （B ）速度为零而加速度不为零的运动； （C ）加速度不变的圆周运动； （D ）匀变速率圆周运动。

第一章 质点运动学一 选择题1． 下列说法中，正确的是：（ ）A. 一物体若具有恒定的速率，则没有变化的速度；B. 一物体具有恒定的速度，但仍有变化的速率；C. 一物体具有恒定的加速度，则其速度不可能为零；D. 一物体具有沿x 轴正方向的加速度而有沿x 轴负方向的速度。

解：答案是D 。

2. 长度不变的杆AB ，其端点A 以v 0匀速沿y 轴向下滑动，B 点沿x 轴移动，则B 点的速率为：（ ）A . v 0 sin θB . v 0 cos θC . v 0 tan θD . v 0 / cos θ 解：答案是C 。

简要提示：设B 点的坐标为x ，A 点的坐标为y ，杆的长度为l ，则222l y x =+ 对上式两边关于时间求导：0d d 2d d 2=+t y y t x x ，因v =tx d d ，0d d v -=t y ，所以 2x v -2y v 0 = 0 即 v =v 0 y /x =v 0tan θ所以答案是C 。

3. 如图示，路灯距地面高为H ，行人身高为h ，若人以匀速v 背向路灯行走，则人头影子移动的速度u 为（ ） A.v H h H - B. v h H H - C. v H h D. v hH 解：答案是B 。

v x选择题2图灯s选择题3图简要提示：设人头影子到灯杆的距离为x ，则H h x s x =-，s hH H x -=， v hH H t s h H H t x u -=-==d d d d 所以答案是B 。

4. 某质点作直线运动的运动学方程为x ＝3t -5t 3 + 6 (SI)，则该质点作A. 匀加速直线运动，加速度沿x 轴正方向．B. 匀加速直线运动，加速度沿x 轴负方向．C. 变加速直线运动，加速度沿x 轴正方向．D. 变加速直线运动，加速度沿x 轴负方向． ( )解：答案是D5. 一物体从某一确定高度以v 0的初速度水平抛出，已知它落地时的速度为v t ，那么它的运动时间是：（ ） A. g 0v v -t B. g 20v v -t C. g 202v v -t D. g2202v v -t 解：答案是C 。

第一章 质点运动学1–1 描写质点运动状态的物理量是 。

解：加速度是描写质点状态变化的物理量，速度是描写质点运动状态的物理量，故填“速度”。

1–2 任意时刻a t =0的运动是 运动；任意时刻a n =0的运动是 运动；任意时刻a =0的运动是 运动；任意时刻a t =0，a n =常量的运动是 运动。

解：匀速率；直线；匀速直线；匀速圆周。

1–3 一人骑摩托车跳越一条大沟，他能以与水平成30°角，其值为30m/s 的初速从一边起跳，刚好到达另一边，则可知此沟的宽度为 （)m/s 102=g 。

解：此沟的宽度为m 345m 1060sin 302sin 220=︒⨯==g R θv1–4 一质点在xoy 平面内运动，运动方程为t x 2=，229t y -=，位移的单位为m ，试写出s t 1=时质点的位置矢量__________；s t 2=时该质点的瞬时速度为__________，此时的瞬时加速度为__________。

解：将s t 1=代入t x 2=，229t y -=得2=x m ，7=y ms t 1=故时质点的位置矢量为j i r 72+=（m ）由质点的运动方程为t x 2=，229t y -=得质点在任意时刻的速度为m/s 2d d ==t x x v ，m/s 4d d t tx y -==v s t 2=时该质点的瞬时速度为j i 82-=v （m/s ）质点在任意时刻的加速度为0d d ==ta x x v ，2m/s 4d d -==t a y y v s t 2=时该质点的瞬时加速度为j 4-m/s 2。

1–5 一质点沿x 轴正向运动，其加速度与位置的关系为x a 23+=，若在x =0处，其速度m/s 50=v ，则质点运动到x =3m 处时所具有的速度为__________。

解：由x a 23+=得x xt x x t 23d d d d d d d d +===v v v v 故x x d )23(d +=v v积分得⎰⎰+=305d )23(d x x v v v则质点运动到x =3m 处时所具有的速度大小为 61=v m/s=7.81m/s ；1–6 一质点作半径R =1.0m 的圆周运动，其运动方程为t t 323+=θ，θ以rad 计，t 以s 计。

第一章 力学的基本概念(一)质点运动学序号 学号 姓名 专业、班级一 选择题[ A ]1. 一小球沿斜面向上运动，其运动方程为285t t s -+=(SI)，则小球运动到最高点的时刻是：(A) s 4=t ;(B) s 2=t ; (C) s 8=t ;(D) s 5=t 。

[ D ]2. 一运动质点在某瞬时位于矢径 r (x,y)的端点处，其速度大小为 (A)dtdr(B) dt d r (C)dt d r (D)22)()(dt dy dt dx +[ D ]3. 某质点的运动方程x=3t-53t +6 (SI),则该质点作： （A ） 匀加速直线运动，加速度沿x 轴正方向； （B ） 匀加速直线运动，加速度沿x 轴负方向； （C ） 变加速直线运动，加速度沿x 轴正方向； （D ） 变加速直线运动，加速度沿x 轴负方向。

[ C ]4. 某物体的运动规律为dtdv=-k 2v t,式中k 为常数，当t=0时，初速度为0v ,则速度v 与时间的函数关系为：（A ） v=21k 2t +0v ; （B ） v=-21k 2t +0v（C ） v 1=21k 2t +01v（D ） v1=-21k 2t +01v[ D ]5. 一质点从静止出发，沿半径为1m 的圆周运动，角位移θ=3+92t ,当切向加速度与合加速度的夹角为︒45时，角位移θ等于：(A) 9 rad, （B ）12 rad, (C)18 rad, (D)3.5 rad[ D ]6. 质点作曲线运动，r 表示位置矢量，s 表示路径，t a 表示切向加速度，下列表达式中： （1）dt dv =a; (2)dt dr =v; (3)dtds=v; (4)dt d v =t a ,则，（A ） 只有（1）、（4）是对的； （B ） 只有（2）、（4）是对的； （C ） 只有（2）是对的； （D ） 只有（3）是对的。

二 填空题1. 设质点在平面上的运动方程为r =Rcos t ωi +Rsin tωj ,R 、ω为常数，则质点运动的速度v =j t con R i t R ϖϖωωωω+-sin ，轨迹为 半径为R 的圆 。

《大学物理》试题库管理系统内容第一章 质点运动学1 题号：01001 第01章 题型：选择题 难易程度：容易 试题: 下列那一个物理量是被称为质点的运动方程（ ）．A.位置矢量B.位移C.速度D.加速度 答案: A2 题号：01002 第01章 题型：选择题 难易程度：适中试题: 某物体作单向直线运动，它通过两个连续相等位移后，平均速度的大小分别为1211s m 15,s m 10--⋅=⋅=v v ．则在全过程中该物体平均速度的大小为（ ）．A.1s m 12-⋅B.1s m 5.12-⋅C.1s m 75.11-⋅D.1s m 75.13-⋅ 答案: A3 题号：01003 第01章 题型：选择题 难易程度：适中试题: 在相对地面静止的坐标系内，A 、B 两船都以1s m 2-⋅的速率匀速行驶，A 船沿x 轴正向，B 船沿y 轴正向．今在A 船上设置与静止坐标系方向相同的坐标系（x ，y 方向的单位矢量用j i,表示），那么在A 船上看，B 船的速度（以1s m -⋅为单位）为（ ）．A.j i 22+-B.j i 22--C.j i 22+D.j i 22-答案: A4 题号：01004 第01章 题型：选择题 难易程度：较难试题: 某质点的运动方程为j Bt At i Bt At r θθsin )(cos )(22+++=，其中θ,,B A 均为常量，且,0,0>>B A 则质点的运动为（ ）．A.匀加速直线运动B.匀减速直线运动C.圆周运动D.一般的平面曲线运动 答案: A5 题号：01005 第01章 题型：选择题 难易程度：适中试题: 某质点的速度为j t i v82-=，已知0=t 时它过点（3，-7），则该质点的运动方程为（ ）．A.j t i t )74()32(2+-+B.j t i t 242-C.j8- D.不能确定答案: A6 题号：01006 第01章题型：选择题难易程度：较难试题: 在下列情况下，不可能出现的是（）．A.一质点向前的加速度减小了，其前进速度也随之减小B.一质点具有恒定的速率，但却有变化的速度C.一质点加速度恒定，而速度方向不断改变D.一质点具有零速度，同时具有不为零的加速度答案: A7 题号：01007 第01章题型：选择题难易程度：较难试题: 下列表述中正确的是（）．A.在曲线运动中质点的加速度必定不为零B.若质点的加速度为恒矢量，则质点的运动轨迹必为直线C.质点沿x轴运动，若加速度的大小为负值，则质点必作减速运动D.质点在作抛体运动的过程中，其法向加速度和切向加速度都在随时间不断变化，因此和加速度也在随时间不断变化答案: A8 题号：01008 第01章题型：选择题难易程度：适中试题: 两辆汽车甲、乙在平直公路上以相同的速率v沿相同的方向并排行驶．下列说法中错误的是（）．A.以相同速率迎面驶来的汽车丙为参考系，汽车甲、乙相对于汽车丙都是静止的B.以相同速率迎面驶来的汽车丙为参考系，汽车甲、乙都以v2的速率运动C.以汽车甲为参考系，汽车乙相对于甲是静止的D.以地面为参考系，汽车甲、乙均以速率v运动答案: A9 题号：01009 第01章题型：选择题难易程度：适中试题: 如图所示，质点作匀速率圆周运动，其半径为R ，从P 点出发，经过半个圆周而运动到了Q 点，则下列表达式中不正确的是（ ）．A.速度增量0=v∆ B.速率增量0=v ∆ C.位移大小R r 2=∆ D.路程R S π= 答案: A10 题号：01010 第01章 题型：选择题 难易程度：较难试题: 质点沿半径m 1=R 的轨道作圆运动，在某时刻的角速度为1s rad -⋅=1ω，角加速度为2s rad -⋅=1β，则质点在该时刻的速度和加速度的大小分别是（ ）．A.1s m -⋅1，2s m -⋅2 B.1s m -⋅1，2s m -⋅1 C.1s m -⋅2，2s m -⋅1 D.1s m -⋅2，2s m -⋅2答案: A11 题号：01011 第01章 题型：选择题 难易程度：难试题: 一质点沿x 轴作直线运动的运动方程为3224t t x -=，当质点再次返回到原点时，其速度和加速度分别为（ ）．A. 1s m -⋅-8，2s m -⋅-16B.1s m -⋅-8，2s 16m -⋅C. 1s m -⋅8，2s m -⋅16D.1s m -⋅8，2s 16m -⋅- 答案: A12 题号：01012 第01章 题型：选择题 难易程度：适中试题: 质点在xoy 平面内作曲线运动，则质点速率的表达式不正确的是（ ）．A.dt dr v =B.dt r d v =C.22⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=dt dy dt dx v D.dt ds v =答案: A13 题号：01013 第01章 题型：选择题 难易程度：适中Q试题: 以初速0v 将一物体斜向上抛，抛射角为θ，不计空气阻力，则物体在轨道最高点处的曲率半径为（ ）．A.g v θ220cosB.20v g C.g v θsin 0 D.不能确定答案: A14 题号：01014 第01章 题型：选择题 难易程度：适中试题: 根据瞬时速度v的定义，若在直角坐标系中，则下列那一个选项可表示速度的大小（ ）．A.k dt dz j dt dy i dt dx ++B.dtdz dt dy dt dx ++ C.222⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛dt dz dt dy dt dx D.dt dr答案: A15 题号：01015 第01章 题型：选择题 难易程度：适中试题: 根据瞬时加速度a的定义，若在直角坐标系中，则下列那一个选项可表示加速度的大小（ ）．A.k dt z d j dt y d i dt x d222222++ B.222222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛dt z d dt y d dt x d C. D.22dtr d 答案: A16 题号：01016 第01章 题型：选择题 难易程度：适中试题: 已知质点以速率()124-⋅+=s m t v 作直线运动，把质点运动的直线作为ox 轴，并已知s 3=t 时，质点位于m 3=x 处，则质点的运动学方程为（ ）．A.123143-+=t t x B.123143++=t t x C.3314t t x += D.331t x = 答案: A17 题号：01017 第01章 题型：选择题 难易程度：适中222222dt z d dt y d dt x d ++试题: 下图中能正确表示质点在曲线轨迹上P 点的运动为减速运动的是（ ）． 答案: A18 题号：01018 第01章 题型：选择题 难易程度：适中 试题: 质点在平面上作圆运动时，下列那一选项是正确的（ ）．A.0=dt dr ，0≠dt r dB.0=dt dr ，0=dtr dC.0≠dt dr ，0=dt r dD.0≠dt dr ，0≠dtr d答案: A19 题号：01019 第01章 题型：选择题 难易程度：较难 试题: 质点在平面上作匀速率曲线运动时，下列那一选项是正确的（ ）．A.0=dt dv ，0≠dt v dB.0≠dt dv ，0=dtv d C.0=dt dv ，0=dt v d D.0≠dt dv ，0≠dtv d答案: A20 题号：01020 第01章 题型：选择题 难易程度：难 试题: 质点在平面上作匀变速率曲线运动时，下列那一选项是正确的（ ）．A.0=dt da ，0≠dt a dB.0≠dt da ，0=dta d C.0=dt da ，0=dt a d D.0≠dt da ，0≠dta d答案: A21 题号：01021 第01章 题型：填空题 难易程度：适中A.B.C.D.试题: 物理学中把研究机械运动的规律及其应用的学科称之为力学，而研究物体位置随时间的变化或运动轨道问题但不涉及物体发生运动变化原因的学科称之为 ． 答案: 运动学22 题号：01022 第01章 题型：填空题 难易程度：适中试题: 位置矢量和位移是描述质点运动状态的物理量， 是描述质点运动状态变化的物理量． 答案: 加速度23 题号：01023 第01章 题型：填空题 难易程度：适中 试题: 由于运动具有相对性所以描述运动时我们首先必须选 ． 答案: 参照系24 题号：01024 第01章 题型：填空题 难易程度：适中 试题: 宇宙中的所有物体都处于永不停止的运动中，这说明运动具有 ． 答案: 绝对性25 题号：01025 第01章 题型：填空题 难易程度：适中试题: 若速度与加速度之间满足关系a v⊥，则速度的方向与加速度的方向 ． 答案: 相互垂直26 题号：01026 第01章 题型：填空题 难易程度：适中试题: 若速度与加速度之间满足关系a v//，则该质点一定作 ，但既有可能作加速度运动，也有可能作减速运动． 答案: 直线运动27 题号：01027 第01章 题型：填空题 难易程度：适中 试题: 若矢量B A -=，则矢量A 与B的大小相等，方向 ． 答案: 相反28 题号：01028 第01章 题型：填空题 难易程度：适中试题: 若质点在t 时刻的位置矢量为t r ，在t t ∆+时刻的位置矢量为t t r ∆+，则该质点在t ∆时间内的位移为 ．答案: t t t r r r-=+∆∆试题: 对于同一参考系而言，若在t 时刻质点A 的运动速度为A v、质点B 的运动速度为B v，则质点B 相对于A 的速度为 ． 答案: A B v v-30 题号：01030 第01章 题型：填空题 难易程度：容易试题: 在国际单位制中，若描述质点运动的位置矢量为()()j t i t r 3232+= ，则质点在t 时刻的加速度为 ．答案: ()[]j t i a184+=31 题号：01031 第01章 题型：填空题 难易程度：较难试题: 若质点作曲线运动时，切线加速度的大小0>τa ，则该质点作曲线运动的速率 ． 答案: 增大32 题号：01032 第01章 题型：填空题 难易程度：较难试题: 若质点作曲线运动时，切线加速度的大小0=τa ，则该质点一定作 ． 答案: 匀速率圆周运动33 题号：01033 第01章 题型：填空题 难易程度：较难 试题: 若运动质点的法线加速度的大小0=n a ，则该质点一定作 ． 答案: 直线运动34 题号：01034 第01章 题型：填空题 难易程度：适中试题: 若某时刻质点作曲线运动的法线加速度大小为n a ，速率为v ，则该时刻质点所在位置处曲线的曲率半径为 ．答案: na v 235 题号：01035 第01章 题型：填空题 难易程度：容易试题: 对于作圆运动的质点而言，若圆的半径为R ，质点的角加速度为β，则质点的切线加速度的大小为 ． 答案: βτR a =试题: 对于作圆运动的质点而言，若圆的半径为R ，质点在某时课的角加速度为β，速率为v ，则质点的加速度为 ．答案: τβR n Rv +2 37 题号：01037 第01章 题型：填空题 难易程度：适中 试题: 某质点沿半径为1m 的圆周运动，在国际单位制中其角运动方程为2t t ππθ+=，则质点的角加速度β为 ．答案: 2s rad -⋅π238 题号：01038 第01章 题型：填空题 难易程度：难试题: 某质点沿半径为1m 的圆周运动，在国际单位制中其角运动方程为2t πθ=，则质点的加速度a为 ． 答案: ()()τππ222+n t39 题号：01039 第01章 题型：填空题 难易程度：难 试题: 某质点从j r50-=位置开始运动，在国际单位制中其速度与时间的关系为,532j i t v += 则质点到达x 轴所需的时间为 ．答案: s 1=t40 题号：01040 第01章 题型：填空题 难易程度：难 试题: 某质点从j r50-=位置开始运动，在国际单位制中其速度与时间的关系为,532j i t v += 则此时质点在x 轴上的位置为 ．答案: m 3=x41 题号：01041 第01章 题型：计算题 难易程度：适中试题: 已知一质点的运动方程为2218,2t y t x -==，其中x 、 y 以m 计，t 以s 计．求：（1）质点的轨道方程并画出其轨道曲线；（2）质点的位置矢量；（3）质点的速度；（4）前2 s 内的平均速度；（5）质点的加速度．答案: （1）将质点的运动方程消去时间参数t ，得质点轨道方程为2182x y -=，质点的轨道曲线如图所示．（2）质点的位置矢量为j t i t r )218(22-+=．（3）质点的速度为j t i r v 42-==． （4）前2s 内的平均速度为2)0()2(--=r r v []{}j i j j i 4218)2218(22212-=-⨯-+⨯= （5）质点的加速度为j r a4-== 42 题号：01042 第01章 题型：计算题 难易程度：适中试题: 如图所示，A 、B 两物体由一长为l 的刚性细杆相连，A 、B 两物体可在光滑轨道上滑行．若物体A 以确定的速率v 向x 轴正向滑行，当6πα=时，物体B 的速度是多少？ 答案: 根据题意，得i v i dt dx v A == j dt dy v B =因为 222)()(l t y t x =+所以 022=+dt dy y dt dxx故 j v j dt dx y x j dt dy v B αtan -=-== 当6πα=时，j v j v v B 336tan -=-=π43 题号：01043 第01章 题型：计算题 难易程度：适中试题: 证明假定质点沿x 轴作匀加速直线运动，加速度a 不随时间变化，初位置为0x ，初速度为0v ，则)(2022x x a v v -=-． 答案: 因为dtdva =，所以adt dv =对其两边取定积分可得 ⎰⎰=tvv adt dv 0， at v v +=0 （1） 又因为at v dt dx+=0，所以 ()dt at v dx +=0，对其两边取定积分可得 ()⎰⎰+=t x x dt at v dx 000 ， 20021at t v x x ++= （2）联立（1）和（2）可得)(2022x x a v v -=-． 44 题号：01044 第01章 题型：计算题 难易程度：适中试题: 一质点沿x 轴正向运动，其加速度为kt a =，若采用国际单位制（SI ），则式中常数k 的单位（即量纲）是什么？当0=t 时，00,x x v v ==，试求质点的速度和质点的运动方程．答案: 因为kt a =，所以tak =．故32T L T T L dim dim dim --⋅=⋅==t a k ．又因为kt dt dv a ==，所以有ktdt dv =，作定积分有⎰⎰=t v v ktdt dv 00，2021kt v v +=而2021kt v dt dx v +==，所以dt kt v dx ⎪⎭⎫ ⎝⎛+=2021，再作定积分有⎰⎰⎪⎭⎫⎝⎛+=t x x dt kt v dx 020210，得 30061kt t v x x ++=．45 题号：01045 第01章 题型：计算题 难易程度：较难试题: 一人乘摩托车跳越一个大矿坑，他以与水平成22．5︒夹角的初速度1s m 65-⋅从西边起跳，准确地落在坑的东边．已知东边比西边低70m ，忽略空气阻力，且取2s m 10-⋅=g ，问：（1）矿坑有多宽，他飞越的时间有多（2）他在东边落地时的速度多大？速度与水平面的夹角多大？ 答案: 据题意建立坐标系如图所示．（1）若以摩托车和人作为一质点，则其运动方程为()()⎪⎩⎪⎨⎧-+==20000021sin cos gt t v y y t v x θθ运动速度为⎩⎨⎧-==gt v v v v yx 0000sin cos θθ当到达东边落地时0=y 有()021sin 2000=-+gt t v y θ，将m 700=y ，2s m 10-⋅=g ，10s m 65-⋅=v ，5.220=θ︒代入解之得他飞越矿坑的时间为s 0.7=t （另一根舍去），矿坑的宽度为m 420=x ．（2）在东边落地时s 0.7=t ，其速度为⎪⎩⎪⎨⎧⋅-=-=⋅==--100100s m 9.44sin sm 1.60cos gt v v v v yx θθ 于是落地点速度的量值为122s m 0.75-⋅=+=y x v v v此时落地点速度与水平面的夹角为37tan 1==-xy v v θ︒46 题号：01046 第01章 题型：计算题 难易程度：适中试题: 一质点沿半径为R 的圆周运动，其角位置与时间的函数关系式（即角量运动方程）为2t t ππθ+=，取SI 制，则质点的角速度、角加速度、切向加速度和法向加速度各是什么？答案: 因为2t t ππθ+=，所以质点的角速度t dtd ππθω2+==，质点的角加速度为πωβ2==dtd ，质点的切向加速度为R R a πβτ2==，质点的法向加速度为()R t R a n 222ππω+==．47 题号：01047 第01章 题型：计算题 难易程度：难试题: 已知某质点的运动方程为()()j t d c i t b a rωωsin cos +++=，取SI 制，其中a 、b 、c 、d 、ω均为常量．（1）试证明质点的运动轨迹为一椭圆；（2）试证明质点的加速度恒指向椭圆的中心；（3）试说明质点在通过图中给定点P 时，其速率是增大还是减小？答案: （1）由题意知⎩⎨⎧+=+=t d c y tb a x ωωsin cos ，所以消去时间参数得质点的运动轨迹为1)()(2222=-+-dc y b a x （椭圆） （2）质点的速度为()()j t d i t b r ωωωωcos sin +-=质点的加速度为()()j t d i t b r ωωωωsin cos 22-+-=()()[](){}j c i a j t d c i t b a+-+++-=ωωωsin cos 2()[]j c i a r+--=2ω可见，质点的加速度与矢量()j c i a r+-的方向相反，由图可知，加速度的方向恒指向椭圆的中心（a ，b ）（3）当0=t ω时，⎩⎨⎧=+=c y b a x 质点位于),(c b a +点；当2πω=t 时，⎩⎨⎧+==d c y a x ，质点位于),(d c a +点．由图可知，质点从),(c b a +点向着),(d c a +点运动，所以质点在作逆时针运动．在P 点处，由于切向加速度τa 与运动速度v的方向相反，所以质点通过P 点时的速率在减小．48 题号：01048 第01章 题型：计算题 难易程度：适中试题: 已知某质点在0=t 时刻位于)m (320j i r +=点处，且以初速00=v，加速度)s m (432-⋅+=j i a运动．试求：（1）质点在任意时刻的速度；（2）质点的运动方程． 答案: （1）由题意可知j i dtvd 43+=即()dt j i v d 43+=，对其两边取积分有()⎰⎰+=t v v dt j i v d 0430所以质点在任意时刻的速度为j t i t v43+=．（2）由j t i t v 43+=可得j t i t dtrd 43+=，即()dt j t i t r d 43+=，对其两边取积分有()⎰⎰+=t rr dt j t i t r d 0430 即022223r j t i t r ++= 所以代入j i r 320+=可得质点的运动方程为()j t i t r3222322++⎪⎭⎫ ⎝⎛+=．49 题号：01049 第01章 题型：计算题 难易程度：难试题: 已知某质点的运动方程为()()(m)4322j t i t r++=，试求：（1）s 1=t 时切向加速度和法向加速度的大小；（2）s 1=t 时的曲率半径．答案: （1）因为 ()()j t i t r4322++=所以质点在任意时刻的速度和加速度分别为j t i dt r d v 62+==；j dtvd a 6==故质点在任意时刻速度的大小即速率为()22291262t t v +=+= 于是质点在任意时刻切向加速度的大小为()2912t dt ddt dv a +==τ29118tt +=由此可知，质点在s 1=t 时切向加速度的大小为2s m 69.59118-⋅=+=τa 质点在s 1=t 时法向加速度的大小为()22222s m 91.169.56-⋅=-=-=τa a a n（2）因为质点在s 1=t 时速度的大小为12s m 1021912-⋅=⨯+=v所以s 1=t 时的曲率半径为m 2191.1402===n a v R50 题号：01050 第01章 题型：计算题 难易程度：适中试题: 一质点在平面上作曲线运动，1t 时刻位置矢量为j i r621+-=，2t 时刻的位置矢量为j i r422+=，求：（1）在12t t t -=∆时间内质点的位移矢量式；（2）该段时间内位移的大小和方向；（3）在坐标图上画出1r ，2r及r ∆．（题中r 以m 计，t 以s 计）答案: （1）在12t t t -=∆时间内质点的位移矢量式为m )24(12j i r r r-=-=∆（2）该段时间内位移的大小为m 52)2(422=-+=∆r该段时间内位移的方向与x 轴的夹角为16.2642tan -=⎪⎭⎫⎝⎛-=-α （3）坐标图上的表示如图．51 题号：01051 第01章 题型：计算题 难易程度：适中试题: 某质点作直线运动，其运动方程为241t t x -+=，其中x 以m 计，t 以s 计．求：（1）第三秒末质点的位置；（2）头三秒内的位移大小；（3）头三秒内经过的路程． 答案: （1）第三秒末质点的位置为m 43341)3(2=-⨯+=x（2）头三秒内的位移大小为m 3)0()3(=-x x （3）因为质点作反向运动时有0)(=t v ，所以令0=dtdx，即024=-t ，s 2=t ，因此头三秒内经过的路程为m 51554)0()2()2()3(=-+-=-+-x x x x52 题号：01052 第01章 题型：计算题 难易程度：较难试题: 已知某质点的运动方程为22,2t y t x -==，式中t 以s 计，x 和y 以m 计．（1）计算并图示质点的运动轨迹；（2）求出s 1=t 到s 2=t 这段时间内质点的平均速度；（3）计算s 1末和s 2末质点的速度；（4）计算s 1末和s 2末质点的加速度．答案: （1）由质点运动的参数方程22,2t y t x -==消去时间参数t 得质点的运动轨迹为)0(,422>-=x x y(运动轨迹如图所示．（2）根据题意可得质点的位置矢量为j t i t r )2()2(2-+=所以s 1=t 到s 2=t 这段时间内质点的平均速度为)s (m 3212)1()2(1-⋅-=--=∆∆=j i r r t r v（3）由位置矢量求导可得质点的速度为j t i r v )2(2-==所以s 1末和s 2末质点的速度分别为)s (m 22)1(1-⋅-=j i v 和)s (m 42)2(1-⋅-=j i v．（4）由速度求导可得质点的加速度为j v a 2-==所以s 1末和s 2末质点的加速度为)s (m 2)2()1(-2⋅-==j a a53 题号：01053 第01章 题型：计算题 难易程度：适中试题: 湖中有一小船，岸边有人用绳子跨过离河面高H 的滑轮拉船靠岸如图所示．设绳子的原长为0l ，人以匀速0v拉绳，试描述小船的运动．答案: 建立坐标系如图所示．按题意，初始时刻（0=t ），滑轮至小船的绳长为0l ，在此后某时刻t ，绳长减小到t v l 00-，此时刻船的位置为()2200H t v l x --=这就是小船的运动方程，将其对时间求导可得小船的速度为()()αcos 02200000v H t v l v t v l dtdxv -=----==将其对时间再求导可得小船的加速度为()[]322032200220x H v Ht v lH v dtdv a -=---==其中负号说明了小船沿x 轴的负向（即向岸靠拢的方向）作变加速直线运动，离岸越近（x 越小），加速度的绝对值越大．54 题号：01054 第01章 题型：计算题 难易程度：容易 试题: 大马哈鱼总是逆流而上，游到乌苏里江上游去产卵，游程中有时要跃上瀑布．这种鱼跃出水面的速度可达1h km 32-⋅．它最高可跃上多高的瀑布？和人的跳高记录相比如何？答案: 鱼跃出水面的速度为11s m 89.8h km 32--⋅=⋅=v ，若竖直跃出水面，则跃出m 03.422==gv h此高度和人的跳高记录相比较，差不多是人所跳高度的两倍．55 题号：01055 第01章 题型：计算题 难易程度：较难试题: 一人站在山坡上，山坡与水平面成α角，他扔出一个初速为0v 的小石子，0v 与水平面成θ角（向上）如题图所示．（1）若忽略空气阻力，试证小石子落到了山坡上距离抛出点为S 处，有αθαθ220cos cos )sin(2g v S +=．（2）由此证明对于给定的0v 和α值时S 在24απθ-=时有最大值.cos )1(sin 220max ααg v S +=答案: （1）建立如题图所示的坐标系，则小石子的运动方程为 ()()⎪⎩⎪⎨⎧-==20021sin cos gt t v y t v x θθ 当小石子落在山坡上时，有 ⎩⎨⎧-==ααsin cos S y S x 联立以上四个方程，求解可得小石子在空中飞行的时间（即从抛出到落在山坡上时所经历的时间）t 所满足的方程为0)cos tan (sin 202=+-t gv t θαθ 解之得)cos tan (sin 20θαθ+=gv t 0=t 是不可能的，因0=t 时小石子刚要抛出．所以小石子落在山坡上的距离为()αθαθαθα2200cos cos )sin(2cos cos cos g v t v xS +===（2）给定0v 和α值时，有)(θS S =，求S 的最大值，可令0=θd dS，即 0cos )2cos(2220=+ααθg v亦即 24απθ-=此时022<θd S d ，所以S 有最大值，且最大值为.cos )1(sin 220max ααg v S +=56 题号：01056 第01章 题型：计算题 难易程度：难试题: 一人扔石子的最大出手速度为10s m 25-⋅=v ．他能击中一个与他的手水平距离为m 50=L ，高为m 13=h 处的一目标吗？在这个距离上他能击中的最大高度是多少？答案: 设抛射角为θ, 则已知条件如图所示, 于是石子的运动方程为()()⎪⎩⎪⎨⎧-==20021sin cos gt t v y tv x θθ可得石子的轨迹方程为θθ2202cos 2tan v gxx y -=假若石子在给定距离上能够击中目标，可令L x =此时有 θθ2202cos 2tan v gL L y -=，即20222022tan tan 2v gL L v gL y -+-=θθ若以θtan 为函数，令0)(tan =θd dy，有gL v 20tan =θ，此时0)(tan 22<θd y d ，即在给定已知条件及给定距离上能够击中目标的最大高度为m 3.12max =y ，故在给定距离上他不能击中m 13=h 高度处的目标．x57 题号：01057 第01章 题型：计算题 难易程度：适中试题: 如果把两个物体A 和B 分别以初速度A v 0和B v 0抛出去．A v 0与水平面的夹角为α，B v 0与水平面的夹角为β，试证明在任意时刻物体B 相对于物体A 的速度为常矢量．答案: 两物体在忽略风力的影响之后，将在一竖直面内作上抛运动，如图所示．则两个物体的速度分别为()()()()⎪⎩⎪⎨⎧-+=-+=jgt v i v v j gt v i v v B B B AA Aββααsin cos sin cos 0000 所以在任意时刻物体B 相对于物体A 的速度为()()jv v iv v v v A B A B A Bαβαβsin sin cos cos 0000-+-=-是一与时间无关的常矢量．58 题号：01058 第01章 题型：计算题 难易程度：适中试题: 如果已测得上抛物体两次从两个方向经过两个给定点的时间，即可测出该处的重力加速度．若物体沿两个方向经过水平线A 的时间间隔为A t ∆，而沿两个方向经过水平线A 上方h 处的另一水平线B 的时间间隔为B t ∆，设在物体运动的范围内重力加速度为常量，试求该重力加速度的大小．答案: 设抛出物体的初速度为0v ，抛射角为θ，建立如图所示的坐标系，则()()⎪⎪⎩⎪⎪⎨⎧-=-=202021sin 21sin B B B A A A gt t v h gt t v h θθ 所以⎪⎪⎩⎪⎪⎨⎧=+-=+-02sin 202sin 20202g h t g v t g h t g v t B B BA A Aθθ 于是有⎪⎪⎩⎪⎪⎨⎧-=-+=∆-=-+=∆g h g v t t t t t g h g v t t t t t B B B B B B A A A A A A 8sin 44)(8sin 44)(222021221222021221θθ 此二式平方相减可得22228)(8BABAA B t t htt h h g ∆-∆=∆-∆-=． 注意此方法也是实验测量重力加速度的一种方法．59 题号：01059 第01章 题型：计算题 难易程度：容易试题: 一质点从静止出发沿半径为R =1m 的圆周运动，其角加速度随时间的变化规律是）（SI 6122t t -=β，试求质点的角速度和切向加速度的大小．答案: 因为t t 6122-=β，所以()dt t t d 6122-=ω，于是有()⎰⎰-=tdt t t d 020612ωω，故质点的角速度的大小为2334t t -=ω，切向加速度的大小为，t t R a 6122-==βτ．60 题号：01060 第01章 题型：计算题 难易程度：适中试题: 一质点作圆周运动的方程为242t t -=θ（θ以rad 计，计以s t ）．在0=t 时开始逆时针旋转，问：（1）s 5.0=t 时，质点以什么方向转动；（2）质点转动方向改变的瞬间，它的角位置θ等于多大？答案: （1）因质点作圆运动角速度方向改变瞬时，0==dtd θω，即082=-t ，s 25.0=t 所以s 5.0=t 时，质点将开始以顺时针方向转动．（2）质点转动方向改变的瞬间，它的角位置为rad 25.0)25.0(425.02)25.0(2=⨯-⨯=θ61 题号：01061 第01章 题型：计算题 难易程度：较难试题: 质点从静止出发沿半径R =3m 的圆周作匀变速运动，切向加速度2s m 3-⋅=τa ．问：（1）经过多少时间后质点的总加速度恰好与半径成o 45角？（2）在上述时间内，质点所经历的角位移和路程各为多少？答案: 因为3==dtdva τ，所以dt dv 3=，即⎰⎰=t v dt dv 003故质点作圆运动的瞬时速率为t v 3=．质点的法向加速度的大小为()222333t t R v a n ===其方向恒指向圆心．于是总加速度为()ττ 332+=+=n t a a a n ，其中n 为沿半径指向圆心的单位矢量，τ为切向单位矢量．（1）设总加速度a与半径的夹角为α，如图所示，则ταa a =sin ，n a a =αcos当045=α时有τa a n =，即332=t ，1=t （负根舍去），所以s 1=t 时，a与半径成045角．（2）因为t v dtds3==，所以⎰⎰=100)3(dt t ds s 故在这段时间内质点所经过的路程为m 5.1=s ，角位移为rad 5.035.1===R s θ∆．62 题号：01062 第01章 题型：计算题 难易程度：适中试题: 汽车在半径为m 400=R 的圆弧弯道上减速行驶．设某一时刻，汽车的速率为1s m 10-⋅=v ，切向加速度的大小为2s m 2.0-⋅=τa ．求汽车的法向加速度和总加速度的大小和方向．答案: 已知条件如图所示．汽车的法向加速度为222s m 25.040010-⋅===R v a n汽车的总加速度为()()22222s m 32020250-⋅=+=+=...a a a n τ所以)s (m )2.0(25.02-⋅-+=+=ττ n a a a n ，故加速度a与v 的夹角为041282.025.0tan tan 011'=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛=--ταa a nττ。