小学思维数学讲义：基本图形的面积计算-带详解

小学数学之面积计算
面积计算是小学数学中比较重要的一个概念，学生们在学习这个概念时，需要理解它的定义、特点和习题解答等方面。

本文将就面积计算在小
学数学中的概念、特点及计算习题进行详细介绍，以期能帮助学生能够更
加快速地掌握面积计算的知识。

一、面积计算的概念
面积计算是指用解释几何图形面积的方法来计算所需要的其中一种特
定面积值。

它的定义比较宽泛，但是它主要是用来求解几何图形中的面积。

在学习中，重点在于理解它是如何计算几何图形的面积，如何根据图形的
比例和形状来判断面积的大小。

二、面积计算的特点
1、面积计算是一种特定的数学概念，它同时涉及几何图形的形状和
特征，以及面积的计算，它特殊的地方在于，面积的计算是根据形状的不
同而不同的。

所以，当学生在计算面积时，不仅要理解面积的定义，还要
根据形状情况，结合图形来推断出相应的公式，以计算出所求的面积。

2、面积计算是根据图形的形状来定义的，它具有一定的通用性。

当
学生进行面积计算时，可以使用相同的公式来计算对应图形的面积，这样
可以极大地提高计算的速度和精确度。

三、面积计算的习题。

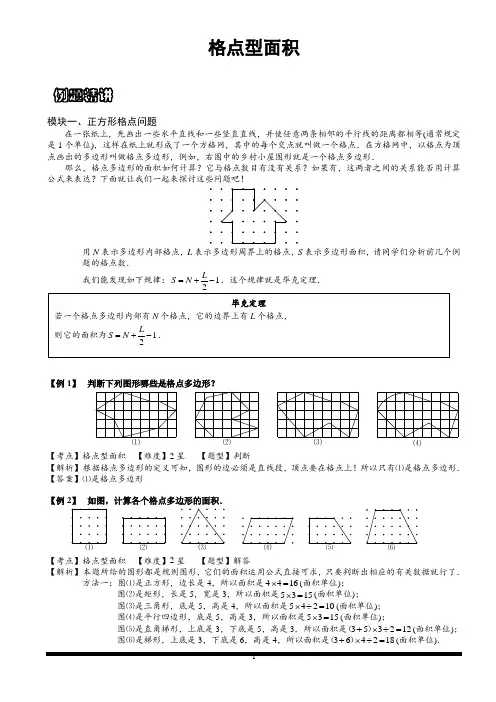
格点型面积模块一、正方形格点问题在一张纸上，先画出一些水平直线和一些竖直直线，并使任意两条相邻的平行线的距离都相等(通常规定是1个单位)，这样在纸上就形成了一个方格网，其中的每个交点就叫做一个格点．在方格网中，以格点为顶点画出的多边形叫做格点多边形，例如，右图中的乡村小屋图形就是一个格点多边形．那么，格点多边形的面积如何计算？它与格点数目有没有关系？如果有，这两者之间的关系能否用计算公式来表达？下面就让我们一起来探讨这些问题吧！用N表示多边形内部格点，L表示多边形周界上的格点，S表示多边形面积，请同学们分析前几个例题的格点数．我们能发现如下规律：12LS N=+-．这个规律就是毕克定理．【例1】判断下列图形哪些是格点多边形？⑴⑵⑶【考点】格点型面积【难度】2星【题型】判断【解析】根据格点多边形的定义可知，图形的边必须是直线段，顶点要在格点上！所以只有⑴是格点多边形．【答案】⑴是格点多边形【例2】如图，计算各个格点多边形的面积．【考点】格点型面积【难度】2星【题型】解答【解析】本题所给的图形都是规则图形，它们的面积运用公式直接可求，只要判断出相应的有关数据就行了．方法一：图⑴是正方形，边长是4，所以面积是4416⨯=(面积单位)；图⑵是矩形，长是5，宽是3，所以面积是5315⨯=(面积单位)；图⑶是三角形，底是5，高是4，所以面积是54210⨯÷=(面积单位)；图⑷是平行四边形，底是5，高是3，所以面积是5315⨯=(面积单位)；图⑸是直角梯形，上底是3，下底是5，高是3，所以面积是353212+⨯÷=（）(面积单位)；图⑹是梯形，上底是3，下底是6，高是4，所以面积是364218+⨯÷=（）(面积单位)．毕克定理若一个格点多边形内部有N个格点，它的边界上有L个格点，则它的面积为12LS N=+-．例题精讲如果两格点之间的距离是2，能利用刚计算的结果说出相应面积么？(教师总结：面积数值均扩大4倍．) 方法二：以上部分图形除了利用各自的面积公式直接求出外，我们还可以从推导它们的面积公式过程中得到启发，即用“割补法”或“扩展法”分别转化成长方形来求．这一种方法很重要，在下面的题目中我们还将使用这种方法！如图⑶，我们利用“扩展法”将其转化，如图所示，从图中易知三角形面积是长方形面积的一半．如图⑷，我们利用“割补法”将其阴影部分面积平移到右边，转化成一个长方形，从中易得平行四边形面积．同理，图⑸、⑹也可利用同样的思想．【答案】图⑴16；图⑵15；图⑶10；图⑷15；图⑸12；图⑹18．【例 3】 如图(a )，计算这个格点多边形的面积．【考点】格点型面积 【难度】2星 【题型】解答 【解析】 方法一(扩展法)．这是个三角形，虽然有三角形面积公式可用，但判断它的底和高却十分困难，只能另想别的办法：这个三角形是处在长是6、宽是4的矩形内，除此之外还有其他三个直角三角形，如下右图(b )，这三个直角三角形面积很容易求出，再用矩形面积减去这三个直角三角形面积，就是所要求的三角形面积．矩形面积是6424⨯=；直角三角形Ⅰ的面积是：6226⨯÷=；直角三角形Ⅱ的面积是：4224⨯÷=；直角三角形Ⅲ面积是4224⨯÷=；所求三角形的面积是2464410-++=（）(面积单位)．方法二(割补法)．将原三角形分割成两个我们方便计算面积的三角形，如(c )图．因此三角形的面积是：52252210⨯÷+⨯÷=(面积单位)．【答案】10【例 4】 右图是一个方格网，计算阴影部分的面积．【考点】格点型面积 【难度】2星 【题型】解答 【关键词】新加坡小学数学奥林匹克竞赛 【解析】 扩展法．把所求三角形扩展成正方形ABCD 中．这个正方形中有四个三角形：一个是要求的AEF V ；另外三个分别是：△ABE 、△FEC 、△DAF ，它们都有一条边是水平放置的，易求它们的面积分别为21.5cm ，22cm ，21.5cm ．所以，图中阴影部分的面积为：33 1.5224⨯-⨯+=（）(2cm )．【答案】4【例 5】 分别计算图中两个格点多边形的面积．【考点】格点型面积 【难度】3星 【题型】解答 【解析】 利用“扩展法”和“割补法”我们都可以简单的得到第一幅图的面积均为9面积单位．第二幅图的面积均为10面积单位．【点评】“一个格点多边形面积的大小很可能是由哪些因素决定呢？”“格点多边形内部的格点数和周界上的格点数与格点多边形的面积有没有什么内在联系呢？”下面我们就来探讨一下！在巩固中，我们发现两个图形面积相等．进一步还可以发现第一个图形边界上的格点数是8个；第二个图形边界上的格点数是10个，包含在图形内的格点数也相等，都是6个．【答案】第一幅图的面积均为9；第二幅图的面积均为10．【巩固】 求下列各个格点多边形的面积．（1） （2） （3） （4）【考点】格点型面积 【难度】3星 【题型】解答【解析】 ⑴ ∵12L =；10N =，∴1211011522L S N =+-=+-=(面积单位)；⑵ ∵10L =；16N =，∴1011612022L S N =+-=+-=(面积单位)；⑶ ∵6L =；12N =，∴611211422L S N =+-=+-=(面积单位)；⑷ ∵10L =；13N =，∴1011311722L S N =+-=+-=(面积单位)．用N 表示多边形内部格点，L 表示多边形周界上的格点，S 表示多边形面积，请同学们分析前几个例题的格点数．我们能发现如下规律：12LS N =+-．这个规律就是毕克定理．【答案】⑴15；⑵ 20；⑶14；⑷17【例 6】 “乡村小屋”的面积是多少？【考点】格点型面积 【难度】3星 【题型】解答【解析】 图形内部格点数9N =；图形边界上的格点数20L = ；根据毕克定理， 则1182LS N =+-=(单位面积)． 【答案】18【例 7】 右图是一个812⨯面积单位的图形．求矩形内的箭形ABCDEFGH 的面积．H GFED C BA【考点】格点型面积 【难度】3星 【题型】解答 【解析】 箭形ABCDEFGH 的面积810214842121232246=+÷-+⨯+÷-⨯=++=（）（）(面积单位)． 【答案】46【例 8】 比较图中的两个阴影部分①和②的面积，它们的大小关系______【考点】格点型面积【难度】3星【题型】填空【关键词】希望杯，五年级，二试，第9题，6分【解析】①的面积为：1112111313222⨯⨯+⨯⨯+⨯⨯=，②的面积也为3223⨯÷=。

小学数学点知识归纳面积的认识与计算小学数学点知识归纳：面积的认识与计算在小学数学中，面积是一个重要的概念，它涉及到我们日常生活中的很多问题，比如房屋的面积、地板的面积等等。

面积是物体表面的大小，通过认识与计算面积，我们可以更好地解决实际问题。

本文将对小学数学中与面积相关的知识进行归纳总结。

一、面积的认识1. 平面图形的面积：平面图形是我们最常见的图形，比如矩形、正方形、三角形等等。

这些平面图形的面积可以通过计算边长或底边高的乘积来求得，具体计算公式如下：- 矩形的面积 = 长 ×宽- 正方形的面积 = 边长 ×边长- 三角形的面积 = 底边 ×高 ÷ 22. 长方体与立方体的表面积：长方体和立方体是常见的立体图形，它们的表面积也是我们经常需要计算的。

对于一个长方体来说，它的表面积等于所有面的面积之和，即：- 长方体的表面积 = 2 × (长 ×宽 + 长 ×高 + 宽 ×高)而立方体的表面积则特殊一些，因为它的六个面都是相等的，所以可以通过计算一个面的面积再乘以6来求得。

二、面积的计算1. 分割法：对于一些复杂的图形，可以通过将其分割成若干简单的图形，然后计算每个简单图形的面积，最后将这些面积相加得到整个图形的面积。

2. 直接计算法：对于一些较为规则的图形，我们可以直接使用相应的公式来计算面积，比如矩形、正方形、三角形等。

这种方法更加简便快捷。

3. 近似计算法：当无法准确测量实际图形的边长或角度时，我们可以通过近似计算来求得一个接近实际面积的数值。

例如，通过大致测量一个房间的长和宽，然后使用矩形的面积计算公式来计算其面积。

三、面积计算的实际应用1. 房屋面积的计算：在购买房屋或者设计房屋时，了解房屋的面积是非常重要的。

通过计算各个房间的面积，我们可以评估出每个房间的大小和整个房屋的总面积，从而更好地选择合适的房屋。

2. 地板面积的计算：在选购地板时，了解地板的面积可以帮助我们选择合适的尺寸和数量。

小学数学基础知识点面积的认知与面积的计算在小学数学学习中，面积是一个非常重要的基础知识点。

它是描述一个平面图形所占的空间大小的概念。

正确认知和计算面积是培养学生数学思维和判断能力的关键环节。

本文将结合具体例子，介绍小学生对面积的认知和面积的计算方法。

一、面积的认知小学生对面积的认知是从直观的观察和感知开始的。

在生活中，我们经常接触到各种各样的图形，比如正方形、长方形、圆形等。

面积就是用来描述这些图形所占空间大小的概念。

以正方形为例，我们可以通过观察和感知来认知其面积。

让学生拿一张正方形的纸片，让他们感受纸片表面所占的空间大小，这样他们就能够理解什么是面积。

同样的，通过观察长方形、圆形等不同图形，我们可以帮助学生逐渐认知不同图形的面积概念。

二、面积的计算方法在认知了面积的概念之后，我们就可以引导学生学习计算面积的方法。

下面将介绍几种常见的计算面积的方法。

1. 长方形和正方形的面积计算对于长方形和正方形来说，计算它们的面积非常简单。

可以使用公式：面积 = 长 ×宽。

例如，如果一个长方形的长为5厘米，宽为3厘米，那么它的面积就是15平方厘米。

2. 圆形的面积计算计算圆形的面积需要使用π（pi）这个数值，它是一个无限不循环小数，约等于3.14159。

圆形的面积公式为：面积= π × 半径的平方。

例如，如果一个圆的半径为2厘米，那么它的面积就是4π平方厘米。

3. 其他图形的面积计算对于其他的图形，如三角形、梯形等，计算面积的方法会有所不同。

三角形的面积可以使用公式：面积 = 底边长 ×高的一半。

梯形的面积计算需要用到上底和下底的长度，以及高的长度。

具体的计算方法需要根据不同的图形来确定。

三、巩固和拓展面积知识在学习了面积的认知和计算方法之后，为了巩固和拓展学生的面积知识，可以进行一些练习和实践活动。

1. 练习题给学生提供一些面积计算的练习题，让他们运用所学知识进行计算。

可以设计一些情境题，让学生运用面积概念解决实际问题。

小学数学重点之面积的认识与计算在小学数学中，面积是一个重要的概念。

掌握面积的认识与计算方法对于学生来说至关重要。

本文将介绍小学数学中面积的认识与计算方法，帮助学生更好地理解和运用面积知识。

一、面积的认识面积是描述一个平面图形占据的大小的量度，常用单位有平方厘米、平方米等。

在小学数学中，我们会遇到一些常见的平面图形，如矩形、正方形、三角形等，我们可以通过计算其面积来得知它们的大小。

1. 矩形的面积计算矩形是最容易计算面积的图形。

矩形的面积等于底边长乘以高，即面积= 底边长×高。

例如，一张矩形纸片的长为5厘米，宽为3厘米，那么它的面积就是 5厘米 × 3厘米 = 15平方厘米。

2. 正方形的面积计算正方形是一种特殊的矩形，它的边长相等。

因此，正方形的面积可以直接用边长的平方表示，即面积 = 边长 ×边长。

例如，一块正方形的边长为4厘米，那么它的面积就是 4厘米 × 4厘米 = 16平方厘米。

3. 三角形的面积计算对于三角形，面积计算稍微复杂一些。

我们可以利用底边长和高来计算三角形的面积，即面积 = 底边长 ×高 ÷ 2。

例如，一个底边长为6厘米，高为3厘米的三角形，它的面积就是 6厘米 × 3厘米 ÷ 2 = 9平方厘米。

二、面积的计算方法除了直接计算图形的面积，我们还可以通过已知图形的其他属性来计算面积。

下面我将介绍两种常见的计算方法。

1. 分割法分割法是一种常用的计算面积的方法，尤其适用于复杂图形。

我们可以将复杂的图形分割成若干简单的图形，计算每个简单图形的面积，然后将它们相加得到整个图形的面积。

举个例子，如果需要计算一个不规则图形的面积，我们可以将它分割成几个矩形、三角形或者其他简单的形状，计算每个形状的面积，然后将它们相加。

这样我们就可以得到整个图形的面积。

2. 面积的变化在实际生活中，我们经常遇到图形面积的变化问题。

小學數學平面圖形計算公式：1 、正方形：周長＝邊長×4；面積=邊長×邊長2 、正方體：表面積=棱長×棱長×6；體積=棱長×棱長×棱長3 、長方形：周長=(長+寬)×2；面積=長×寬4 、長方體：表面積(長×寬+長×高+寬×高)×2；體積=長×寬×高5、 三角形：面積=底×高÷26 平行四邊形：面積=底×高7 梯形：面積=(上底+下底)×高÷ 2 模組一、基本公式的應用【例 1】 如圖，兩個正方形邊長分別是5釐米和4釐米，圖中陰影部分為重疊部分。

則兩個正方形的空白部分的面積相差多少平方釐米？ 【考點】基本圖形的面積計算 【難度】2星 【題型】解答【關鍵字】華杯賽，五年級，決賽，第9題，10分【解析】 5×5－4×4=9（平方釐米），兩個正方形的空白部分的面積相差9平方釐米。

【答案】9平方釐米【巩固】 如圖12，邊長為4cm 的正方形將邊長為3cm 的正方形遮住了一部分，則空白部分的面積的差等於 2cm 。

例題精講知識點撥4-2-1.基本圖形的面積計算【考點】基本圖形的面積計算【難度】2星【題型】填空【關鍵字】希望杯，4年級，初賽，19題【解析】空白部分的面積差等於兩個正方形的面積差，即⨯-⨯=44337（平方釐米）。

【答案】7平方釐米【例 2】在一個正方形水池的四周，環繞著一條寬2米的路(如圖)，這條路的面積是120平方米，那麼水池的面積是______ 平方米。

水池【考點】基本圖形的面積計算【難度】2星【題型】填空【關鍵字】希望杯，4年級，初賽，19題【解析】四個邊角的面積和為2×2×4=16，則水池的邊長為：104÷2÷4=13，所以水池的面積是：13×13=169平方米。

小学数学知识归纳面积的概念与计算面积是数学中的一个重要概念，在小学数学中，学生需要学习如何理解和计算面积。

本文将对小学数学中面积的概念及其计算方法进行归纳总结。

一、面积的概念面积是描述平面区域大小的一个量，通常用单位平方来表示。

在小学数学中，我们主要关注的是矩形和正方形的面积。

1. 矩形的面积矩形的面积计算公式为：面积 = 长 ×宽。

在矩形中，长和宽是两条相邻的边，可以用任意单位进行计量，但计算结果的单位是面积单位平方。

例如，一个矩形的长为5米，宽为3米，那么它的面积就是5米 ×3米 = 15平方米。

2. 正方形的面积正方形是一种特殊的矩形，它的四条边都相等。

正方形的面积计算公式为：面积 = 边长 ×边长。

例如，一个正方形的边长为4厘米，那么它的面积就是4厘米 × 4厘米 = 16平方厘米。

二、面积的计算我们可以利用已知的长度和宽度来计算矩形和正方形的面积，也可以通过分割图形并重新组合的方法来计算面积。

1. 利用已知长度和宽度计算当我们已经知道了矩形或正方形的长度和宽度时，只需将长度和宽度代入相应的面积公式即可计算出面积。

例如，一个矩形的长为7米，宽为4米，则它的面积为7米 × 4米= 28平方米。

2. 分割图形并重新组合对于不规则形状的图形，我们可以通过将其分割成多个矩形或正方形，计算各个矩形或正方形的面积后再相加，得到整个图形的面积。

例如，一个不规则形状的图形可以分割成一个矩形和一个三角形。

我们可以先计算矩形的面积，然后计算三角形的面积，最后将两个面积相加，得到整个图形的面积。

三、面积的单位转换在实际问题中，我们可能需要将面积的单位进行转换。

常见的面积单位有平方厘米、平方米和平方千米。

1. 单位换算1平方米 = 10000平方厘米，即1平方米等于10000平方厘米。

1平方千米= 1000000平方米，即1平方千米等于1000000平方米。

2. 单位转换计算当我们需要在不同的面积单位之间进行转换时，可以利用上述换算关系进行计算。

小学数学知识归纳正方形和长方形的面积计算正方形和长方形是小学数学中常见的几何形状，计算它们的面积是学习数学的基础内容之一。

本文将对正方形和长方形的面积计算进行详细归纳，帮助小学生更好地理解和掌握这部分知识。

一、正方形的面积计算正方形是一种四边长度相等的四边形，四个角都是直角。

计算正方形的面积，只需要知道正方形的边长即可。

设正方形的边长为a，则正方形的面积S等于边长的平方。

公式：S = a²例如，如果一个正方形的边长是3cm，那么它的面积可以通过公式计算：S = 3² = 9cm²。

因此，这个正方形的面积是9平方厘米。

二、长方形的面积计算长方形是一种具有两组相等的对边的四边形，两组对边分别平行且相互垂直。

计算长方形的面积，需要知道长方形的两个边长。

设长方形的长为a，宽为b，则长方形的面积S等于长和宽的乘积。

公式：S = a * b例如，如果一个长方形的长是5cm，宽是3cm，那么它的面积可以通过公式计算：S = 5 * 3 = 15cm²。

因此，这个长方形的面积是15平方厘米。

三、正方形和长方形面积计算的联系正方形和长方形在面积计算上有一些联系。

当长方形的长和宽相等时，即a=b，那么这个长方形就是一个正方形。

此时，正方形的面积计算公式可以变形成长方形的面积计算公式。

从正方形的面积公式可以推导出长方形的面积公式：由于正方形的边长a=b，所以正方形的面积公式可以写成：S = a² = a * a由此，可以得到长方形的面积公式：S = a * b可以看出，当长方形的长和宽相等时，长方形的面积公式和正方形的面积公式是相同的。

四、案例分析接下来，我们来通过几个案例进一步巩固对正方形和长方形面积计算的理解。

案例1：一个正方形的边长是7cm，求它的面积。

解析：根据正方形的面积计算公式，可以得知这个正方形的面积为7² = 49cm²。

因此，这个正方形的面积是49平方厘米。

小学数学重点认识简单的形面积形面积是小学数学中的重点内容之一。

通过学习形面积可以帮助孩子们认识和理解各种形状的大小。

本文将以简单的形状为例，介绍小学数学中重点认识的形面积知识。

一、正方形的面积计算正方形是一个边长相等的四边形，它的面积计算公式为：面积 = 边长 ×边长。

比如一个正方形的边长为3cm，那么它的面积为3cm × 3cm = 9cm²。

二、长方形的面积计算长方形是一个拥有两组相互垂直的边的四边形，它的面积计算公式为：面积 = 长 ×宽。

比如一个长方形的长为4cm，宽为6cm，那么它的面积就是4cm × 6cm = 24cm²。

三、三角形的面积计算三角形是一个拥有三条边的多边形，它的面积计算公式为：面积 = 底边长 ×高÷2。

比如一个三角形的底边长为5cm，高为4cm，那么它的面积就是5cm × 4cm ÷ 2 = 10cm²。

四、圆的面积计算圆是一个没有边的几何形状，它的面积计算公式为：面积= π × 半径²。

其中，π是一个数学常数，约等于3.14。

如果一个圆的半径为2cm，那么它的面积就是3.14 × 2cm × 2cm ≈ 12.56cm²。

五、总结通过以上的例子，我们可以看出不同形状的面积计算公式是不同的。

在小学数学中，我们需要记住这些公式，并能够准确地计算各种形状的面积。

例如，在解决有关形面积的问题时，我们需要先观察所给图形的形状是什么，然后根据所学的面积计算公式进行计算。

同时，还要注意单位的统一，确保计算结果的准确性。

通过学习形面积的知识，可以帮助孩子们培养准确观察、辨认形状的能力，掌握简单形面积的计算方法，为进一步学习几何学打下坚实的基础。

总之，形面积是小学数学中的重点之一，通过合理运用面积计算公式，孩子们可以在解决实际问题时更加灵活和准确。

小学数学重点认识简单的面积计算一、什么是面积计算数学中，面积是指平面上一个封闭图形所围成的区域的大小。

面积计算是数学中的重要内容之一，在小学数学中也是重点内容之一，是培养学生准确计算和逻辑思维能力的基础。

二、简单的面积计算方法1. 正方形与长方形的面积计算正方形的边长为a，那么它的面积为a的平方，即S=a²。

长方形的长为a，宽为b，那么它的面积为长乘宽，即S=a*b。

2. 三角形的面积计算三角形的面积计算公式为S=(底边长*高)/2。

其中，底边长即为三角形底部边的长度，高为从底边到不在底边上的对角线上的垂直距离。

3. 平行四边形的面积计算平行四边形的面积计算公式为S=底边长*高。

其中，底边长为平行四边形底部边的长度，高为从底边到不在底边上的平行边的垂直距离。

4. 梯形的面积计算梯形的面积计算公式为S=((上底+下底)*高)/2。

其中，上底和下底分别为梯形的上边和下边的长度，高为从上底到下底的垂直距离。

5. 圆的面积计算圆的面积计算公式为S=π*r²。

其中，r为圆的半径，π为一个常数，约等于3.14159。

三、面积计算的应用面积计算在现实生活中有着广泛的应用。

例如：1. 装修房间时需要计算墙壁的面积，以确定购买合适的涂料和壁纸数量。

2. 种植花草时需要计算花坛的面积，以确定购买适量的土壤和肥料。

3. 建造游泳池时需要计算池子的面积，以确定购买适量的瓷砖和水泵等设备。

四、面积计算的扩展除了上述简单图形的面积计算方法，还可以应用于更复杂的图形，例如圆环的面积计算、多边形的面积计算等。

这些计算需要使用更复杂的公式或将复杂图形分解为多个简单图形进行计算。

五、总结通过学习简单的面积计算方法，可以帮助小学生培养准确计算和逻辑思维能力，为将来更深入的数学学习奠定基础。

面积计算不仅在数学中有着重要的应用，也在日常生活中有着广泛的实际应用。

因此，掌握面积计算方法对于小学生来说具有重要意义。

小学数学认识简单的面积计算数学是一门具有普遍性的学科，在小学阶段，数学的学习内容之一就是面积的计算。

面积是描述平面图形大小的概念，它在我们生活中有着广泛的应用。

本文将介绍小学数学中关于面积计算的基本概念和方法。

一、正方形的面积计算正方形是最简单的平面图形之一，它的四条边长度相等，四个角都是直角。

正方形的面积计算公式是：面积 = 边长 ×边长。

例如，如果一个正方形的边长为5厘米，则它的面积为5厘米 × 5厘米 = 25平方厘米。

二、长方形的面积计算长方形和正方形一样，也是常见的平面图形，它的两条边长度分别称为长和宽，长方形的面积计算公式是：面积 = 长 ×宽。

例如，如果一个长方形的长为6厘米，宽为4厘米，则它的面积为6厘米 × 4厘米= 24平方厘米。

三、三角形的面积计算三角形由三条边和三个内角组成，它的面积计算公式是：面积 = 底边长度 ×高 ÷ 2。

其中，底边长度是三角形任意一条边的长度，高是从底边到顶点的垂直距离。

例如，如果一个三角形的底边长度为8厘米，高为5厘米，则它的面积为8厘米 × 5厘米 ÷ 2 = 20平方厘米。

四、平行四边形的面积计算平行四边形是一种特殊的四边形，它有两组平行的边。

平行四边形的面积计算公式是：面积 = 底边长度 ×高。

其中，底边长度是平行四边形的任意一条底边的长度，高是从底边到对边的垂直距离。

例如，如果一个平行四边形的底边长度为7厘米，高为6厘米，则它的面积为7厘米 × 6厘米 = 42平方厘米。

五、圆的面积计算圆是一个特殊的图形，它由一个圆心和一条半径组成。

圆的面积计算公式是：面积= π × 半径 ×半径，其中的π是一个固定的数值，约等于3.14。

例如，如果一个圆的半径为10厘米，则它的面积为3.14 × 10厘米 × 10厘米 = 314平方厘米。