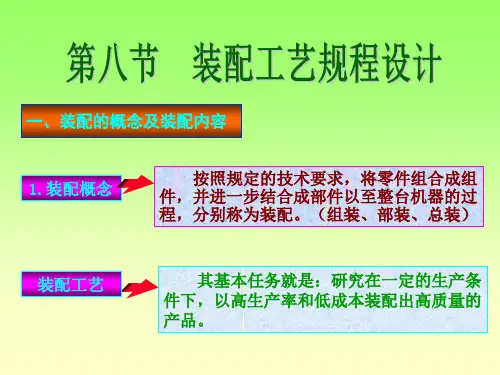
i2 ki2Ti 2
i 1
T aqvA T0 m (0.10 4)mm 0.05mm
与极值法计算得到的各组成环平均公差TavA=0.025mm相比, TavqA放大了100%,组成环的制造变得容易了。
(4) 确定A1、A2、A3、A4的制造公差。仍取A1为协调环。以 组成环平均平方公差为基础,参考各组成环尺寸大小和加工
公差为
T1=T0-(T2+T3+T4)=0.1-(0.018+0.015+0.018) mm=0.049mm 4) 确定各组成环零件的上、下偏差。将组成环A2、A3和A4的偏差按
“入体原则”标注:A2=A4=170-0.018mm,A3=70-0.015mm 5) 计算协调环A1的上、下偏差。
ES1=ES0+EI2+EI3+EI4 =[0.15+(-0.018)+(-0.015)+(-0.018)]mm=+0.099mm
EI1=ES1-T1=(0.099-0.049)mm=+0.05mm
所以A1=
410.099 0.050
mm
2.统计互换装配法
统计互换装配法又称不完全互换装配法。其实质是将组成环 的制造公差适当放大,使零件容易加工,这会使极少数产品 的装配精度超出规定要求,但这种事件是小概率事件,很少 发生,从总的经济效果分析,仍然是经济可行的。 例4-12 已知条件与例4-11相同,若各尺寸误差均服从正态分 布,分布中心与公差带中心重合,即k0=k1=k2=k3=k4=1, α1=α2=α3=α4=0。试以统计互换装配法解算各组成环的公差 和极限偏差。
T1=0.062mm。
(5) 确定组成环的上、下偏差。按“入体原则”取。由式(4-10),