☆两点受力简支梁

两端简支梁力学计算公式
1.弯矩计算公式：
弯矩是梁中最常见的力学特征之一，用来描述梁的弯曲性质。

在两端简支梁中，弯矩可以通过以下公式计算：
M=(wL^2)/8
其中，M表示弯矩，w表示分布载荷的单位长度，L表示梁的长度。

2.剪力计算公式：
剪力是横截面梁中的各个部分之间的内力，用来描述梁的抗剪能力。

在两端简支梁中，剪力可以通过以下公式计算：
V=(wL)/2
其中，V表示剪力，w表示分布载荷的单位长度，L表示梁的长度。

3.轴力计算公式：
轴力是梁中的纵向内力，用来描述梁的受力性质。

在两端简支梁中，轴力可以通过以下公式计算：
N=(wL)/2
其中，N表示轴力，w表示分布载荷的单位长度，L表示梁的长度。

4.梁的挠度计算公式：
梁的挠度是梁受到外力作用后发生的弯曲变形。

在两端简支梁中，梁的挠度可以通过以下公式计算：
δ=(5wL^4)/(384EI)
其中，δ表示梁的挠度，w表示分布载荷的单位长度，L表示梁的长度，E表示梁的弹性模量，I表示梁的截面惯性矩。

5.梁的应力计算公式：
在两端简支梁中，梁的应力可以通过以下公式计算：
σ=(My)/I
其中，σ表示梁的应力，M表示弯矩，y表示离梁轴心的距离，I表示梁的截面惯性矩。

以上公式只涵盖了两端简支梁力学计算中的一部分，实际应用中还需要考虑其他因素，例如温度变化、应变等。

此外，梁的材料性质和截面形状也会对计算结果产生影响，因此在具体应用中需要根据实际情况进行调整。

简支梁集中力弯矩计算公式
简支梁集中力弯矩计算公式是用来计算在简支梁上作用的集中力所产生的弯矩
值的公式。

弯矩是指物体在外力作用下发生弯曲时，单位截面上由于拉伸或压缩产生的力矩。

在简支梁上作用的集中力产生的弯矩计算公式为：
M = F * a
其中，M表示弯矩，F表示作用在简支梁上的集中力的数值，a表示集中力与
梁端点的距离。

这个公式适用于简支梁上的集中力作用点与梁端点之间的距离较小，即F作用在梁的近端或远端。

需要注意的是，在计算弯矩时，单位制要保持一致，例如力的单位为牛顿(N)，长度的单位为米(m)，则弯矩的单位为牛顿·米(N·m)。

通过使用简支梁集中力弯矩计算公式，我们可以快速准确地计算出集中力作用
在简支梁上产生的弯矩值，这对于工程设计和结构分析非常重要。

弯矩值的计算可以帮助我们评估梁的强度和稳定性，并确保结构的安全可靠性。

需要提醒的是，除了集中力产生的弯矩，还有均匀分布载荷、集中力矩等不同
情况下的弯矩计算公式。

在实际应用中，需要根据具体的情况选择正确的公式进行计算，并考虑到梁的几何形状和边界条件等因素，以得到更精确的结果。

总结而言，简支梁集中力弯矩计算公式为M = F * a，它是一种重要的工具，用于计算简支梁上作用的集中力所产生的弯矩值。

了解和应用这个公式可以帮助我们更好地理解和分析结构的力学性能。

建筑结构选型复习资料1、简述简支梁和多跨连接梁的受力和变形特点？简支梁的缺点是内力和挠度较大，常用于中小跨度的建筑物。

简支梁是静定结构，当两端支座有不均匀沉降时，不会引起附加内力。

因此，当建筑物的地基较差时采用简支梁结构较为有利。

简支梁也常被用来作为沉降缝之间的连接结构。

多跨连续梁为超静定结构，其优点是内力小，刚度大，抗震性能好，安全储备高，其缺点是对支座变形敏感，当支座产生不均匀沉降时，会引起附加内力。

2、桁架结构的受力计算采用了哪些基本假定?一、组成桁架结构的所有各杆都是直杆，所有各杆的中心线都在同一平面内，这一平面称为桁架的中心平面。

二、桁架的杆件和杆件的相连接的节点都是铰接节点。

三、所有外力都作用在桁架的中心平面内，并集中作用于节点上。

3、桁架斜腹杆的布置方向对腹杆受力的符号（拉或压）有何关系？斜腹杆的布置方向对腹杆受力符号（拉或压）有直接关系。

对于矩形桁架，斜腹杆外倾受拉，内倾受压，竖腹杆受力方向与斜腹杆相反。

对于三角形桁架，斜腹杆外倾受压，内倾受拉，而竖腹杆总是受拉。

4、屋架结构的布置有哪些具体要求？一、屋架的跨度：一般以3米为模数二、屋架的间距：宜等间距平行排列，与房屋纵向柱列的间距一致，屋架直接搁置在柱顶三、屋架的支座：当跨度较小时，一般把屋架直接搁置在墙、跺、柱或圈梁上。

当跨度较大时，则应该采取专门的构造措施，以满足屋架端部发生转动的要求。

5、钢筋混凝土刚架在构件转角处为避免受力过大，可采取什么措施？在构件转角处，由于弯矩过大，且应力集中，可采取加腋的形式，也可适当的用圆弧过渡。

为了减少材料用量，减轻结构自重，也可采用空腹刚架，其形式有两种：一种是把杆件做成空心截面，另一种是在杆件上留洞。

6、刚架结构的支撑系统起何作用？应怎样布置？为保证结构的整体稳定性，应在纵向柱之间布置连系梁及柱间支撑，同时在横梁的顶面设置上弦横向水平支撑。

柱间支撑和横梁上弦横向水平支撑宜设置在同一开间内。

简支梁跨中集中力作用下,跨中截面竖向位移计算公式我们要找出简支梁在跨中集中力作用下，跨中截面的竖向位移计算公式。

首先，我们需要了解简支梁的基本结构和受力特点。

简支梁是一种一端固定，另一端自由的梁。

当在简支梁的跨中施加一个集中力时，梁会发生弯曲，并产生竖向位移。

假设简支梁的长度为 L，集中力的大小为 F，梁的截面惯性矩为 I，梁的材料弹性模量为 E。

根据材料力学中的弯曲理论，我们可以得到以下公式来描述跨中截面的竖向位移：
Δ = FL^3/(48EI)
其中Δ 是跨中截面的竖向位移，F 是集中力，L 是梁的长度，E 是材料的弹性模量，I 是截面的惯性矩。

这个公式是基于材料力学中的弯曲理论推导出来的，它可以帮助我们计算简支梁在跨中集中力作用下的竖向位移。

计算结果为：Δ = FL3/(48EI)
所以，简支梁在跨中集中力作用下，跨中截面的竖向位移计算公式为：Δ = FL^3/(48EI)。

简支梁桥桥梁方案比选范文咱们今天来唠唠简支梁桥的桥梁方案比选这事儿。

就好比你要去一个地方，有好几条路可以走，但每条路都有它自己的优缺点，咱们得挑出最适合的那一个。

一、混凝土简支梁桥方案。

1. 结构特点。

混凝土简支梁桥呢，它的结构相对简单。

就像搭积木一样，梁是一块一块独立的，两端简单地搁在支座上。

这种结构让它在施工的时候比较容易理解，就像按照说明书组装东西一样，工人们比较容易上手。

它的整体性也不错，因为混凝土本身就有一定的黏聚力。

而且混凝土材料到处都能找到，取材方便，就像在自己家后院挖宝藏一样，不会因为材料供应不上而耽误工期。

2. 造价方面。

从造价来看，混凝土的成本相对比较低。

不过呢，要是对混凝土的强度等性能有特殊要求，可能需要在原材料或者添加剂上多花点钱，但总体来说还是比较经济实惠的。

就像你去超市买东西，虽然有贵的商品，但混凝土就像是那种性价比超高的基础款。

但是，它也有个小缺点，就是自身重量比较大。

这就好比一个大胖子，需要更强壮的基础来支撑它。

所以在基础建设上可能要投入更多的资金，不然这个“大胖子”站不稳。

3. 适用范围。

这种桥比较适合中小跨度的桥梁。

就像在小河或者小山谷上，它就像是一个朴实的小助手，稳稳地完成任务。

因为跨度大了的话，它的自重会成为一个大麻烦，就像让一个小马拉大车，很吃力的。

二、钢简支梁桥方案。

1. 结构特点。

钢简支梁桥就显得很“洋气”了。

它的结构很轻盈，就像一个灵活的舞者。

钢材的强度高，能够承受很大的力，所以在同样的跨度下，它可以比混凝土梁桥做得更纤细。

这就好比一个肌肉发达的运动员，虽然身材好但力量可不小。

而且钢结构的构件可以在工厂里预制，然后运到现场组装。

就像搭乐高积木一样，速度可快了，能够大大缩短施工工期。

这对于着急通车的地方来说，可是个大优点。

2. 造价方面。

不过呢，钢材的价格相对比较高，这就像是买奢侈品一样，初始投资比较大。

而且钢结构还需要定期进行防腐维护，这就像你买了一件昂贵的皮衣，得时不时保养一下，不然就容易坏。

简支梁受力组合变形-概述说明以及解释1.引言概述部分的内容可以如下所示：1.1 概述简支梁是一种常见的结构形式，由于其结构简单、使用方便，广泛应用于建筑、桥梁、机械等领域。

简支梁在受到外力作用时，会发生变形，这种变形对于梁的安全性和使用寿命至关重要。

因此，研究简支梁受力组合变形是提高梁的设计和使用性能的重要方面。

本文将深入探讨简支梁受力组合变形的原因、特点以及对梁结构的影响。

首先，我们将介绍简支梁的定义和特点，包括它的基本结构和建筑原理。

接着，我们将通过对简支梁的受力分析，揭示不同受力组合对梁的变形产生的原因。

随后，我们将对梁的变形进行详细的分析，包括弯曲变形、剪切变形和挠度等。

最后，我们将研究受力组合在简支梁上的影响，探讨其对梁的变形程度和安全性的影响。

通过本文的研究，我们将对简支梁受力组合变形的机理有更深入的了解，同时也能为简支梁的设计和使用提供有用的指导。

这对于提高梁的结构性能、延长梁的使用寿命具有重要意义。

此外，对于简支梁受力组合变形的应用前景，本文也将进行展望，探讨其在未来工程领域中的可能应用和发展方向。

总之，通过本文的研究和分析，我们将为读者提供一个全面的简支梁受力组合变形的概述，从而增进对该领域的理解和应用。

相信本文的内容将对相关领域的研究人员和工程师具有一定的参考价值。

1.2 文章结构文章结构部分的内容可以参考以下示例：2.文章结构本文将按照以下结构进行叙述和分析简支梁受力组合变形的相关内容：2.1 简支梁的定义和特点首先，我们将介绍简支梁的定义和特点。

简支梁是一种常见的结构形式，其特点是两端支座可以自由转动，同时梁自身在受力作用下会发生弯曲变形。

我们将详细探讨简支梁的定义、结构特征以及其在工程实践中的应用。

2.2 受力分析在本节中，我们将进行简支梁的受力分析。

通过分析简支梁在不同荷载作用下的受力情况，我们可以了解到梁的内力分布以及受力大小。

我们将介绍常见的荷载类型，并利用力学原理进行受力计算和分析。

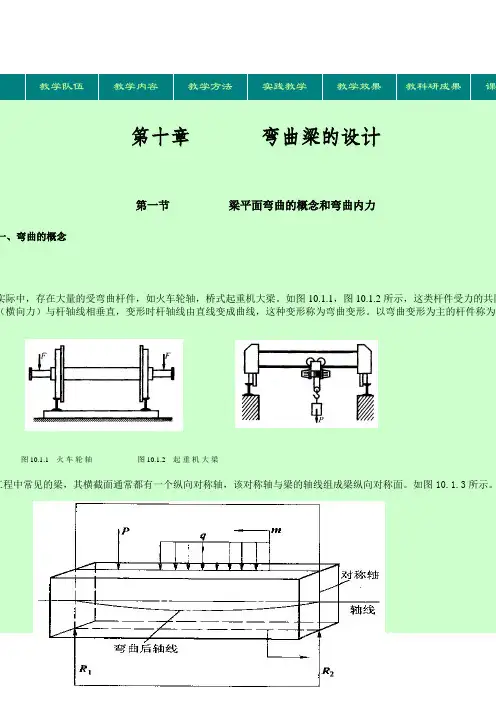
简支梁的剪力计算公式简支梁是一种常见的结构形式，在建筑、机械等领域广泛应用。

在设计这种结构时，需要计算其面对荷载时的剪力，即作用于梁的横向拉力。

本文将介绍简支梁的剪力计算公式，并解释其基本原理。

一、剪力的定义和计算方法剪力是指作用于物体横向的拉力，常用符号为V。

对于简支梁而言，其剪力大小为距离荷载作用点的梁端距离x处的荷载分量，即V=Qx。

其中，Q表示单位长度的荷载大小，x表示距离荷载作用点的梁端距离。

在实际计算中，为了方便起见，可以将梁截面按纵向划分为若干小段，然后通过受力平衡，计算出每一小段的剪力大小，最终将所有小段的剪力加和得到梁整体的剪力大小。

二、剪力计算公式对于简支梁而言，其剪力的计算公式为：V=Qx其中，Q表示单位长度的荷载大小，x表示距离荷载作用点的梁端距离。

具体说来，可以将梁截面按纵向划分为若干小段，然后对每一个小段进行受力平衡，得到该小段的剪力大小。

这里以一段长度为dx的小段为例，其剪力大小可以通过以下公式计算：dV=Qdx其中，Q表示单位长度的荷载大小，dx表示小段长度。

最后将所有小段的剪力加和，即可得到整体的剪力大小。

三、剪力计算的基本原理简支梁在受荷载作用时，会在横向方向上产生拉力，即剪力。

这种拉力不仅取决于荷载的大小和分布，还与梁的固定方式、材料等因素有关。

因此，在进行剪力计算时，需要考虑这些因素对剪力大小的影响。

具体说来，剪力计算的基本原理是受力平衡。

在进行受力平衡时，需要将梁截面按纵向划分为若干小段，然后对每一小段分别进行受力分析。

根据受力平衡原理，梁的每一小段所受的剪力大小应该等于两侧的力的合力，即：V1+V2=Qdx其中，V1和V2分别表示小段左右两侧的剪力大小。

通过这个公式，可以计算出每一小段的剪力大小，并得到整体的剪力大小。

四、总结简支梁的剪力计算是建筑、机械等领域中的一项基本任务。

在实际应用中，可以将梁截面按纵向划分为若干小段，然后通过对每一小段进行受力分析，计算出其剪力大小。

两个集中力简支梁最大弯矩好啦，今天咱们来聊聊一个看起来有点枯燥的东西——两个集中力简支梁的最大弯矩。

别急，听我慢慢说，你会发现其实并不复杂，还能从中找到些有趣的地方，嘻嘻。

首先啊，集中力简支梁是啥？其实它就像是把一根长木头，两端支撑好，中间加点重量。

你看过桥吧，那桥就是个典型的“简支梁”，两头靠支撑，中间可以走车或者行人，桥上的重量就算是“集中力”了。

想象下，你站在桥上，背包丢在桥中间，这个背包就是咱们所说的“集中力”——就是在某一个点上加的重物。

通常我们研究这种简支梁，是为了知道它在受力后会怎么样，最重要的一个问题就是，梁会在什么地方发生最大弯曲，啥？你没听错，就是“最大弯矩”。

简单来说，就是梁中间的“弯”最大，咱们想搞明白这个弯最大是怎么来的。

哎哟，咱们不能只停留在表面，得好好琢磨。

假设梁上加了两块“重物”，它们分别在梁的两个不同地方。

每块重物的作用就像是一个小小的“炸弹”，它们在各自的位置上往下砸，梁就开始弯了。

也就是说，梁会在这两个点的附近，弯得更厉害。

那么最大弯矩在哪儿呢？这是个好问题，不是说把这两个重物加在一块，就能直接得出答案。

实际上，这个最大弯矩通常出现在梁的中间，或者说最容易出现在两块重物之间的地方。

咱们就像是站在中间，感受一下四周的重压，梁的中间就成了“受压王”，弯得最厉害。

好啦，讲得这么深奥，咱们来点实际的。

举个例子，有一根简支梁，两头支撑着，两个重物分别放在梁的1/3和2/3的位置上，这时候最大弯矩在哪？嘿，别看问题简单，实际上它的位置和大小得靠公式算出来。

每个重物带来的“弯矩”就是它对梁造成的弯曲力。

公式可以算得很精准，结果显示梁的中间部分肯定会有最大弯矩。

咋算呢？说实话，这个公式稍微有点吓人，不过放心，我保证它不难理解。

简单来说，最大弯矩的大小取决于每块重物的质量以及它们离支点的距离。

你可以想象，越重或者越靠近支点的重物，越容易让梁弯得更厉害。

再细想想，梁受力后的表现像不像一个人？就像你背着两个大包包，站着不动，你的背一定会弯，背包越重、越靠近中间，弯得就越厉害。

简支梁均布荷载跨中弯矩简支梁是一种常见的结构形式，其在跨中受到荷载作用时会产生弯曲变形和弯矩。

本文将详细介绍简支梁跨中的弯矩计算方法以及相关的参考内容，着重介绍经典的梁计算理论和方法。

1. 弯矩计算方法简支梁均布荷载作用下的弯矩计算可以使用弯矩公式求解，其中最常用的是Euler-Bernoulli梁理论和一阶小变形梁理论。

这两种理论都可以求解出简支梁在跨中任意位置的弯矩。

Euler-Bernoulli梁理论适用于梁材料具有均匀强度且弯曲变形较小的情况。

该理论基于德国科学家欧拉和瑞士科学家伯努利的研究成果，假设梁在弯曲时纵杆轴线保持直线，切变形小到可以忽略不计。

依据该理论，简支梁跨中处的弯矩计算公式为M = (qL^2)/8，其中M为弯矩，q为均布荷载，L为跨中长度。

一阶小变形梁理论适用于梁材料具有非均匀强度且弯曲变形较大的情况。

该理论基于弹性力学的基本原理，假设梁材料在受力下产生弯曲，但纵杆轴线不再保持直线。

依据该理论，简支梁跨中处的弯矩计算公式可以通过解一阶微分方程求解得到。

2. 相关参考内容（1）“结构力学”（第三版）- 郭士广、高志远编著该书是国内一流的结构力学教材，详细介绍了梁的力学性能以及弯矩的计算方法。

该书内容系统全面，理论结合实际案例进行讲解，适合作为学习和参考资料。

（2）《钢结构设计原理与计算》- 郭心钠、黄宗义编著该书是国内经典的钢结构设计教材，其中包含了梁的弯矩计算方法和相关理论。

书中通过实例进行讲解，深入浅出地介绍了梁的力学性能和荷载计算方法。

（3）《混凝土结构设计规范》（GB 50010-2010）该规范是我国建筑领域最重要的规范之一，其中包含了混凝土结构设计的基本原理和计算方法。

规范详细介绍了简支梁的设计方法，包括弯矩计算等内容。

（4）《钢结构设计规范》（GB 50017-2017）该规范是我国建筑领域最重要的规范之一，其中包含了钢结构设计的基本原理和计算方法。

规范中介绍了钢结构梁的设计方法和弯矩计算等内容。

普及力学知识，从简支梁说起！想要跨越一段距离时，最简单的方法就是将粗棒状的物体横置于两个支点之间。

这种方法，我们的祖先在几万年前就已经知道了。

在他们的原始生活中被风挂到的树木偶然横跨在小河上，被当作原木桥使用。

横架于支点之间的棒状物称为梁，梁是现代建筑以及桥梁结构中应用最广泛的用于跨越的构件。

本文试图从梁的角度，找寻跨越结构的一些共性。

一．从力的传递角度看梁1）弯矩是力沿其法向传递过程中的副作用结构是通过组织材料将力从一个地方传递到另一个地方。

力是一个矢量，矢量就有方向。

所以力可以有两种传递的方式，一种是沿着力的矢量方向传递；另一种是沿着力的法线方向传递。

承担这两种传递方式的构件通常分别称为柱（受轴力）和梁（受剪力、弯矩）。

最常见的梁是悬臂梁和简支梁。

简支梁与悬臂梁对于一根悬臂梁来说，传递力的理想状态应该是这样的。

横向剪力的传递但实际的状态是这样子的。

纵向剪力及弯矩的产生梁的目的是要将力水平传递到支座，即只希望产生横向的剪力，但是有一个定理叫“剪力互等定理”（具体怎么证明请翻材料力学教材）。

横向剪力就是力传递过程的一种体现，当横向剪力到达支座时，梁的使命就完成了。

但这个过程中还产生了纵向剪力，纵向剪力进而产生了弯矩，而且纵向剪力是随着力传递的距离累积的。

可以说弯矩是梁搬运力时产生的一个副作用，我们一直在做的就是想办法克服这个副作用。

2）简支梁与悬臂梁的异同当荷载对称于简支梁中轴线分布时，将简支梁取半结构，其形式如下图所示。

这种将力往其法线方向一边传递的方式看似与悬臂梁不同，但只要是沿着其法线方向传递力，就会在梁内产生剪力和弯矩。

而简支梁可以看成这种传力方式的镜像组合。

简支梁同样需要承受横向剪力、纵向剪力和弯矩因此，当力作用于简支梁跨中，由简支梁将力向两边支座传递时，也需要承受横向剪力、纵向剪力和弯矩。

从力传递的角度来说，简支梁和悬臂梁的区别仅在于是将力传递到一边还是两边。

3）简支梁与悬臂梁的组合简支梁和悬臂梁可以组合出各种各样的梁，但其受力特性是一样的，都需要抵抗横向剪力、纵向剪力和弯矩。

简支梁的弯矩计算公式简支梁是一种常见的结构形式，其弯矩计算是结构工程中的重要内容之一。

弯矩是指在梁的截面上由于外力作用而引起的内力，它是梁在弯曲过程中的重要参数。

本文将介绍简支梁的弯矩计算公式及其相关内容。

简支梁的弯矩计算公式主要包括静力平衡方程和梁的几何关系。

在计算简支梁的弯矩时，需要先确定外力作用的位置和大小，然后根据梁的几何形状和边界条件，利用静力平衡方程求解梁的弯矩分布。

我们需要明确简支梁的几何形状和边界条件。

简支梁是指两个端点可以自由旋转的梁，即在两个端点处没有弯矩和剪力的作用。

在计算弯矩时，可以采用坐标系的方法，将梁的一端作为原点，建立坐标系。

我们需要确定外力作用的位置和大小。

外力可以是集中力、分布力或者集中力和分布力的组合。

在简支梁的弯矩计算中，一般将外力作用在梁的中点处，这样可以简化计算。

外力的大小可以通过静力平衡方程求解，即将外力的合力与弯矩的大小相等。

然后，我们可以利用静力平衡方程求解梁的弯矩分布。

静力平衡方程是指在平衡状态下，梁的受力和力矩之间满足平衡条件。

根据平衡条件，我们可以得到弯矩计算的基本方程。

在简支梁的弯矩计算中，常用的方法有力矩法和受力分析法。

力矩法是指在梁上取一小段，通过受力分析和力矩平衡方程求解该小段的弯矩。

受力分析法是指在梁上取一小段，通过受力分析和弯矩的性质求解该小段的弯矩。

这两种方法可以互相转化，根据具体情况选择适合的方法进行计算。

对于均布载荷作用下的简支梁，可以使用受力分析法求解弯矩。

假设均布载荷为q，梁的长度为L，则梁上任意一点的弯矩M可以表示为M=qLx/2，其中x为该点的横坐标。

对于集中力作用下的简支梁，可以使用力矩法求解弯矩。

假设集中力为F，作用点距离梁的左端点的距离为a，则梁上任意一点的弯矩M可以表示为M=Fa。

在实际工程中，简支梁的弯矩计算是结构设计和分析的基础。

通过弯矩计算，可以确定梁的截面尺寸和材料的选择，保证梁在使用过程中的安全性和稳定性。