四年级奥数专题--图形周长与面积word版本

第一讲图形周长和面积知识导航亲爱的同学们，我们已经学会长方形、正方形的周长与面积的计算，利用公式很容易算出它们的面积与周长。

但在遇到一些较复杂的有关长方形和正方形的周长和面积计算时，一些同学就会感到棘手。

这一讲我们将学习用平移、转化、分解、合并等技巧解决难题，使大家在解题中能顺利地找到突破口，化难为易，化繁为简。

精典例题例1：下图是由16个同样大小的正方形组成的，如果这个图形的面积是400平方厘米，那么它的周长是多少厘米?思路点拨每个正方形的面积为：400÷16=25(平方厘米)，所以每个正方形的边长是5厘米。

从上下方向来看有14条边是周长的一部分，从左右方向来看有20条边是周长的一部分，所以……模仿练习计算右面图形的周长(单位：厘米)。

例2：有9个小长方形，它们的长和宽分别相等，用这9个小长方形拼成的大长方形(如图)的面积是45平方厘米，求这个大长方形的周长。

思路点拨从图上可以知道，小长方形的长的4倍等于宽的5倍，所以长是宽的5÷4=1.25倍。

每个小长方形的面积为45÷9=5平方厘米，所以1.25×宽×宽=5，所以宽为2厘米，长为2.5厘米。

模仿练习下图的长方形被分割成5个正方形，已知原长方形的面积为120平方厘米，求原长方形的长与宽。

例3：一块正方形的苗圃（如右图实线所示），若将它的边长各增加30米，则面积增加9900平方米，问原来这块正方形苗圃的面积是多少平方米？思路点拨通过画图可以算出：小正方形的面积为：30×30=900平方米。

用增加的面积减去小正方形的面积就得到增加的两个长方形的面积之和，9900-900=9000平方米。

而增加的两个长方形的面积相等，于是其中一个长方形的面积为9000÷2=4500平方米。

模仿练习喜阳阳小学的操场长90米，宽45米。

改造后，长增加10米，宽增加5米。

现在操场面积比原来增加了多少平方分米？例4：如下图，用标号为1,2,3,4,5的五种大小不同的正方形拼成一个大长方形，大长方形的长和宽分别是18，14，则标号为5的正方形的面积是多少？（2006年“希望杯”第二试）思路点拨如果标号为5的正方形的边长是a ，那么1号比2号大a ，2号比3号大a ，所以1号比3号大2a ，又因为2号和3号的边长之和是14，1号和2号的边长之和是18，所以1号比3号大18-14=4。

上课日期： 上课时间： 教师姓名：知识点一：格点面积 一、正方形格点问题在一张纸上，先画出一些水平直线和一些竖直直线，并使任意两条相邻的平行线的距离都相等(通常规定是1个单位)，这样在纸上就形成了一个方格网，其中的每个交点就叫做一个格点．在方格网中，以格点为顶点画出的多边形叫做格点多边形，例如，右图中的乡村小屋图形就是一个格点多边形．那么，格点多边形的面积如何计算？它与格点数目有没有关系？如果有，这两者之间的关系能否用计算公式来表达？下面就让我们一起来探讨这些问题吧！用N 表示多边形内部格点，L 表示多边形周界上的格点，S 表示多边形面积，请同学们分析前几个例题的格点数．我们能发现如下规律：12LS N =+-．这个规律就是毕克定理．二、 三角形格点问题1、定义：所谓三角形格点多边形是指：每相邻三点成“∵”或“∴”，所形成的三角形都是等边三角形．规定它的面积为1，以这样的点为顶点画出的多边形为三角形格点多边形．2、公式：关于三角形格点多边形的面积同样有它的计算公式：如果用S 表示面积，N 表示图形内包含的格点数，L 表示图形周界上的格点数，那么有22S N L =⨯+-，就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2．知识点二：图形剪拼巧求面积知识框架毕克定理若一个格点多边形内部有N 个格点，它的边界上有L 个格点，则它的面积为12LS N =+-．本讲中很多类型的题目还要求同学们去动手尝试．通过本讲知识的学习，让同学们了解不同图形的分割、拼合、剪拼的方法，锻炼同学们的平面想象能力以及增强学生的动手操作能力．（1）把一个几何图形按某种要求分成几个图形，就叫做图形的分割．（2）反过来，按一定的要求也可以把几个图形拼成一个完美的图形，就叫做图形的拼合．（3）将一个或者多个图形先分割开，再拼成一种指定的图形，则叫做图形的剪拼．我们在图形的分割、拼合和剪拼的过程中，都要结合所提供的图形特点来思考．（1）如果把一个图形分割成若干个大小、形状相等的部分，那么就要想办法找图形的对称点，把图形先分少，再分多．（2）图形中，如果有数量方面的要求，可以先从数量入手，找出平分后每块上所含数量的多少，再结合数量来分割图形．（3）如果是要把几个图形拼合成一个大图形，要特别注意每条边的长度，把相等的边长拼合在一起，先拼少的，再拼多的．（4）如果是剪拼图形，要抓住“剪、拼前后图形的面积相等”这个关键，根据已知条件和图形的特点，通过分析推理和必要的计算，确定剪拼的方法．一、解题关键：分割其实就是运用特殊的三角形（等角直角三角形、等边三角形等）、正方形、等边图形的特殊性质进行分割而得，所以分割的关键是利用了特殊图形的关系解题。

第一讲图形周长和面积知识导航的同学，我已学会方形、正方形的周与面的算，利用公式很简单算出它的面与周。

但在遇到一些复的有关方形和正方形的周和面算，一些同学就会感觉棘手。

一我将学用平移、化、分解、合并等技巧解决，使大家在解中能利地找到打破口，化易，化繁。

精典例题例 1：以下列图是由16个同样大小的正方形组成的，若是这个图形的面积是400 平方厘米，那么它的周长是多少厘米?思路点拨每个正方形的面： 400÷ 16=25( 平方厘米 ) ，所以每个正方形的是 5 厘米。

从上下方向来看有 14 条是周的一局部，从左右方向来看有20条是周的一局部，所以⋯⋯模拟练习计算右侧图形的周长 ( 单位：厘米 ) 。

例 2：有9个小长方形，它们的长和宽分别相等，用这9 个小长方形拼成的大长方形( 如图 )的面积是 45 平方厘米，求这个大长方形的周长。

思路点拨从上可以知道，小方形的的 4 倍等于的 5 倍，所以是的 5÷ 4=1.25 倍。

每个小方形的面45÷ 9=5 平方厘米，所以 1.25 × ×=5，所以 2 厘米， 2.5 厘米。

模拟练习以下列图的长方形被切割成 5 个正方形，原长方形的面积为120平方厘米，求原长方形的长与宽。

例 3：一块正方形的苗圃〔如右图实线所示〕，假设将它的边长各增加 30 米，那么面积增加 9900 平方米，问原来这块正方形苗圃的面积是多少平方米？思路点拨通画可以算出：小正方形的面：30×30=900 平方米。

用增加的面减去小正方形的面就获取增加的两个方形的面之和，1 / 49900-900=9000 平方米。

而增加的两个长方形的面积相等，于是其中一个长方形的面积为 9000÷ 2=4500 平方米。

模拟练习喜阳阳小学的操场长 90 米，宽 45 米。

改造后，长增加 10 米，宽增加 5 米。

现在操场面积比原来增加了多少平方分米？例 4：以以下列图，用标号为1,2,3,4,5的五种大小不同样的正方形拼成一个大长方形，大长方形的长和宽分别是18，14，那么标号为 5 的正方形的面积是多少？〔 2006 年“希望杯〞第二试〕思路点拨若是标号为 5 的正方形的边21长是 a，那么 1号比 2 号大 a，2号比 3 号大 a，所以 1号比 3号大 2a，又因为 2 号和 3 号的边5长之和是 14，1 号和2 号的边长之和是 18，所34以1号比 3号大 18-14=4 。

图形的周长与面积的计算一、图形的周长计算1.1 定义：周长是指图形一周的长度。

1.2 计算方法：1.2.1 矩形：周长 = (长 + 宽) × 21.2.2 正方形：周长 = 边长 × 41.2.3 三角形：周长 = 边长1 + 边长2 + 边长31.2.4 圆：周长= 2 × π × 半径二、图形的面积计算2.1 定义：面积是指图形所占平面的大小。

2.2 计算方法：2.2.1 矩形：面积 = 长 × 宽2.2.2 正方形：面积 = 边长 × 边长2.2.3 三角形：面积 = 底 × 高 ÷ 22.2.4 圆：面积= π × 半径²2.2.5 梯形：面积 = (上底 + 下底) × 高 ÷ 2三、特殊图形的周长与面积计算3.1 圆柱：3.1.1 周长：底面周长= 2 × π × 半径3.1.2 面积：侧面积 = 底面周长 × 高；底面积= π × 半径²3.2 圆锥：3.2.1 周长：底面周长= 2 × π × 半径3.2.2 面积：侧面积 = 底面周长 × 斜高 ÷ 2；底面积= π × 半径²四、实际应用4.1 计算一块土地的面积，已知其长和宽。

4.2 计算一个游泳池的周长和面积。

4.3 计算一本书的封面面积。

五、知识点拓展5.1 平面图形的周长和面积之间的关系。

5.2 立体图形的表面积和体积的计算。

5.3 图形放大和缩小的原理。

6.1 计算一个边长为5厘米的正方形的周长和面积。

6.2 计算一个底边长为6厘米，高为4厘米的三角形的周长和面积。

6.3 计算一个半径为3厘米的圆的周长和面积。

6.4 计算一个上底长为8厘米，下底长为12厘米，高为5厘米的梯形的周长和面积。

第四讲巧求面积*知识点拨本讲主要通过求一些不规则图形的面积，体会一种转化思想，重点在于把不规则图形转化为规则图形的方法，包括平移、旋转、害U补、差不变原理，通过这些方法的学习，让学生体会求面积的技巧, 提高学生的观察能力、动手操作能力、综合运用能力.封令31%例题精讲【例1】你有什么好的方法计算所给图形的面积呢？（单位：厘米）【巩固】如图是学校操场一角，请计算它的面积（单位：米）【例2】求图中五边形的面积.【例3】（第三届”华杯赛口试试题”这是一个楼梯的截面图，高280厘米，每级台阶的宽和高都是20厘米.问，此楼梯截面的面积是多少？如图是一个楼梯的截面图， 每级台阶的宽和高都是 20厘米.这楼梯的截面积是多少平方厘米?有一块菜地长16米，宽8米，菜地中间留了宽 2米的路，把菜地平均分成四块，每一块地的 面积是多少？有10张长3厘米，宽2厘米的纸片，将它们按照下图的样子摆放在桌面上，那么这 片所盖住的桌面的面积是多少平方厘米？卜图（单位：厘米）是两个相同的直角梯形重叠在一起，求阴影部分的面积【巩固】两个相同的直角三角形如下图所示 （单位：厘米）重叠在一起，求阴影部分的面积【例7】（第六届"走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛初赛 ）右图中甲的面积比乙的面积大 平方厘米.右图中，矩形ABCD 的边AB 为4厘米，BC 为6厘米，三角形ABF 比三角形EDF 的面积大9 平方厘米，求ED 的长.【巩固】【例【例10张纸 【例26米【巩固】如图，平行四边形 ABCD 中，BC 10cm,直角三角形ECB 的边EC 8cm,已知阴影部分的 总面积比三角形EFG 的面积大10cm2,求平行四边形 ABCD 的面积.【例9】有一个长方形菜园，如果把宽改成 50米，长不变，那么它的面积减少680平方米，如果使宽为60米，长不变，那么它的面积比原来增加2720平方米，原来的长和宽各是多少米？【巩固】有一个长方形，如果宽减少 2米，或长减少3米，则面积均减少24平方米，求这个长方形的面积？【巩固】一个正方形，如果把它的相邻两边都增加 6厘米，就可以得到一个新正方形，新正方形的面积比原正方形大120平方厘米.求原正方形的面积？【巩固】 一个长方形，如果长减少 5厘米，宽减少2厘米，那么面积就减少的部分恰好成为一个正方形，求原来长方形的面积?【例11】 一块正方形的钢板，先截去一个宽5分米的长方形，又截去一个宽8分米的长方形（如图）,面积就比原来正方形减少 181平方分米.原正方形的边长是多少分米？【例10】 一块长方形铁板，长 15分米，宽12分米，如果长和宽各减少多少平方分米？2分米，面积比原来减少66平方厘米，这时剩下5 2【例12] 如图长方形被分成两部分，已知阴影面积比空白部分面积大 34平方厘米，求阴影部分的面积.18cm【例13】 一个边长为20厘米的正方形，依次连接四边中点得到第二个正方形，这样继续下去可得到第三个、第四个、第五个正方形.求第五个正方形的面积？【巩固】（2008年第七届“小机灵杯”数学竞赛决赛）如图是由5个大小不同的正方形叠放而成的，如果 最小的正方形（阴影部分）的周长是8,那么最大的正方形的边长是 .【例14】 有一个边长为16厘米的正方形，连接每边的中点构成第二个正方形,构成第三个正方形，第四个正方形.求图中阴影部分的面积？【例15] 如图，大正方形的边长为10厘米.连接大正方形的各边中点得小正方形， 将小正方形每边三等分，再将三等分点与大正方形的中心和一个顶点相连，那么图中阴影部分的面积总和 等于多少平方厘米？【巩固】一张长方形纸片，先把长剪去时面积又减少了 60平方厘米, 8厘米，这时面积减少了 72平方厘米，又把宽剪去 5厘米，这 原来这张长方形纸片的面积是多少平方厘米？10cm5再连第6髓的中点【例16】有一个正方形水池（图中阴影部分），在它的周围修一个宽是8米的草地，草地的面积为480平方米，求水池的边长？【巩固】一块长方形草坪（图中阴影部分）长是宽的2倍，它的四周围的总面积是34平方米的1米宽的小路.求草坪的面积是多少平方米？【巩固】（2008年北京”数学解题能力展示”读者评选活动复赛）如图所示，一个长方形广场的正中央有一个长方形的水池. 水池长8米、宽3米.水池周围用边长为1米的方砖一圈一圈地向外铺. 恰好铺了若干圈，共用了152块方砖，那么共铺了圈.水池【例17】一条白色的正方形手帕，它的边长是18厘米，手帕上横竖各有二道黑条，黑条宽都是2厘米，这条手帕白色部分的面积是多少？【例18】用同样大小的瓷砖铺一个正方形地面，两条对角线上铺黑色的，其它地方铺白色的，如图所示.如果铺满这块地面共用101块黑色瓷砖，那么白色瓷砖用了多少块？7个完全相同的长方形拼成了图中阴影部分，图中空白部分的面积是多少平方厘米?【例19】【巩固】如图所示，7个完全相同的长方形拼成了图中的阴影部分，图中空白部分的面积是多少平方 厘米？练习1.如右图所示，图中的ABEFGD 是由一个长方形 ABCD 及一个正方形CEFG 拼成的，线段的长 度如图所示（单位：厘米），求ABEFGD 的周长和面积.10练习2. 一块长方形纸片，在长边剪去 5cm,宽边剪去2cm 后（如图），得到的正方形面积比原长方形 面积少31cm 2.求原长方形纸片的面积.【例20】（第五届“祖冲之杯”数学邀请赛）如右图所示，在长方形 同的长方形（尺寸如图），图中阴影部分的面积是ABCD 中，放入六个形状大小相课后作业104C（希望杯培训题）如右图所示，在一个正方形上先截去宽 11分米的长方形，再截去宽 7分米的长方形，所得图形的面积比原正方形减少 301平方分米.原正方形的边长是 分米.7I I 11图中有6个正方形，较小的正方形都由较大的正方形的 4边中点连接而成.已知最大的正方形的边长为16厘米，那么最小的正方形的面积等于多少平方厘米？四个完全相同的长方形拼成右图，大正方形的面积是 100平方分米，小正方形的面积是 16平方分米，求每个长方形的面积是多少？长方形的短边是多少分米？16练习3. 练习4. 练习5.。

• 答案：面积 = 3.14 × (12.56 / (2 × 3.14))^2 = 12.56平方厘米 • 解析：根据圆的周长公式，周长 = 2πr，可以求出半径r的值，再根据圆的面积公式，面积 = πr^2，可以求出面积的值。
• 题目：一个平行四边形的周长是20厘米，其中一条边长是a厘米，则其他三条边的长度是多少？ 答案：其他三条边长度分别是：5 a厘米、5 - a厘米、a厘米 解析：根据平行四边形的周长公式，周长 = 2(a + b)，其中a和b为平行四边形相邻的两边，可以求出其他 三条边的长度。
• 题目：一个长方形的周长是20厘米，长是a厘米，则宽是多少厘米？ 答案：宽 = (20 - 2a) / 2 = 10 - a厘米 解析：根据长方形的周长 公式，周长 = 2(长 + 宽)，可以求出宽的表达式。
• 答案：宽 = (20 - 2a) / 2 = 10 - a厘米 • 解析：根据长方形的周长公式，周长 = 2(长 + 宽)，可以求出宽的表达式。
• 答案：其他三条边长度分别是：5 - a厘米、5 - a厘米、a厘米 • 解析：根据平行四边形的周长公式，周长 = 2(a + b)，其中a和b为平行四边形相邻的两边，可以求出其他三条边的长度。
感谢观看
汇报人：XX
确性
圆形面积的计算
圆的面积公式： A = πr²，其 中r是圆的半径
推导过程：通 过将圆分割成 若干个小的扇 形，然后重新 排列组合成近 似长方形，利 用长方形面积 公式推导得出
计算方法：根 据给定的半径 值，代入公式
中进行计算
注意事项：计 算时要注意单 位的统一，以 及π取值的小
数位数
其他常见图形面积的计算
提高题目练习

例 4：一块正方形的钢板，先截去宽 5 分米的长方形，又截去宽 8 分米的
长方形（如图），面积比原来的正方形减少 181 平方分米。原正方形的边长是多 少？
hing at a time and All things in their being are good for somethin
思路点拨
把阴影部分剪下来，并把剪下的两个小长方形拼起来（如图），再被上长、宽分别是 8 分米、5 分米的小长方形，这个拼合成的长方形的面积是 181+8×5=221 平方分米，长是原 来正方形的边长，宽是 8+5=13 分米。
杯 1 试）
2.一个长方形，如果它的长减少 3 米，或它的宽减少 2 米，那么它的面积
都减少 36 平方米，求这个长方形原来的面积和周长。
hing at a time and All things in their being are good for somethin
3.一个长方形木板，如果宽减少 6 分米，长减少 10 分米，那么它的面积减少 172 平
模仿练习
一个长方形，如果宽不变，长减少 3 米，那么它的面积减少 24 平方米；如 果长不变，宽增加 4 米，那么它的面积增加 60 平方米。这个长方形原来的面积 是多少平方米？
例 3：用若干个边长都是 2 厘米的平行四边形与三角形（如下图）
拼接成一个大的平行四边形，已知大平行四边形的周长是 244 厘米，那 么平行四边形和三角形各有多少个？
思路点拨
大的平行四边形上、下两边的长为（244-2×2）÷2=120 厘米，观察上边，每 6 厘 米有两个平行四边形的边，所以共有小平行四边形 120÷6×2=40 个……
模仿练习
用若干个边长都是 2 厘米的平行四边形与三角形（如右图）拼接成 一个大的平行四边形，已知大平行四边形的周长是 236 厘米，那么平行 四边形和三角形各有多少个？

（完整word版）四年级奥数图形⾯积专题第四讲：图形(⼀)爱学教育⽼师奥数2015·四年级·竞赛·秋三⾓形种类：⾯积公式：三⾓形的⾼：1、如图，?ABC⾯积是30平⽅分⽶，D是BC的中点，AE的长是ED的2倍。

那么?BED的⾯积是多少平⽅分⽶？2、如图，三⾓形ABC的⾯积是240平⽅厘⽶，D是BC的中点，AD的长是AE的3倍，EF的长BF的3倍，那么三⾓形AEF的⾯积是多少平⽅厘⽶？3、如图，三⾓形ABC中，D、E为两个三等分点，F是AB的中点，若三⾓形DEF的⾯积是12平⽅厘⽶，那么四边形AFEC的⾯积为多少平⽅厘⽶？4、如图，BD=3AD, CE=4AE,三⾓形ADE的⾯积是2平⽅厘⽶，求三⾓形ABC的⾯积？5、如图，在△ABC中，BD=2DC,AE=BE，已知△BDE的⾯积为6平⽅厘⽶，求四边形ACDE 的⾯积。

6、将三⾓形ABC的BA延长1倍到D，CB边延长2倍到E，AC边延长3倍到F。

若三⾓形ABC的⾯积是1平⽅厘⽶，求三⾓形DEF的⾯积？7、如图，三⾓形ABC是正三⾓形，D、E分别是AB、BC的中点，已知三⾓形BDE的⾯积是6平⽅厘⽶，求三⾓形ABC的⾯积。

8、已知三⾓形ABC的⾯积为180平⽅厘⽶，D、E把三⾓形分成两部分，BD=3AD，CE=2AE,求三⾓形ADE的⾯积。

9、如图，在平⾏四边形BCEF中，有⼀个直⾓△ABC,BC=8厘⽶，AC=7厘⽶，阴影部分⾯积⽐△ADH⼤12平⽅厘⽶，求AH的长度。

10、如图所⽰，已知⼀个四边形的两条边的长度和三个⾓，求这个四边形的⾯积是多少？11、如图，边长为20厘⽶和30厘⽶的两个正⽅形拼在⼀起，求阴影△ABC的⾯积。

●家庭作业●1、如图，在三⾓形ABC中，CD=2BD,CE=3AE，阴影部分的⾯积是20平⽅厘⽶，求三⾓形ABD与三⾓形EDC⾯积之和是多少平⽅厘⽶？2、如图，在三⾓形ABC中，D是BC的中点，E、F是AC的三等分点。

本组+1 对组+2
对组-1
本组+3
扭屁股1下
对组+2
如下图，里面正方形的周长是16厘米，并且外面长方形的各边分别平 行于正方形的四条边，那么外面长方形的周长是多少厘米？
如下图，正方形ABCD的边长是6厘米，过正方形内的任意两点画直线， 可把正方形分成9个小长方形。这9个小长方形的周长之和是多少厘米？
本组+3
对组-2
本组-1
个人+3
对组+5
对自己说加油
一个打谷场宽45米，长60米，扩建后长增加了15米，宽增加了8 米，这个打谷场的面积增加了多少平方米？
一个长方形操场，长80米，宽60米，扩建后长增加20米， 宽增加15米，这个操场的面积增加了多少？
本组-1
对自己说我是最棒 的
对组+2
对组-2
四个周长为17厘米的长方形拼成一个大长方形，如右图所示， 求大长方形的周长。
唱首歌吧
个人+5
对组-2
表扬表扬自己
对组+2
对组+5
下图中的阴影部分FGCB是正方形，线段FH长18厘米， AC长24厘米， 则长方形ADHE的周长是多少厘米？
有一条长24分米的铁丝，用它围成一个长方形，如果这个长方形的宽 是5分米，这个长方形的面积是多少平方分米？
一块正方形的苗圃（如右图实线所示），若将它的边 长各增加30米（如图虚线所示），则面积增加9900平 方米，问原来这块正方形苗圃的面积是多少平方米？
如图，有一大一小两个重叠的正方形，其正方形 边长分别为6厘米和3厘米，两块没有重合的阴影 部分面积相差多少平方厘米？
对组+5
本组+3

7÷6的平方=7/360（米）=1又17/18（厘米）
例题2：一个底面半径是10厘米的圆柱形瓶中，水深8厘米，要在瓶中放入长和宽都是8厘米、高是15厘米的一块铁块，把铁块竖放在水中，水面上升几厘米？
在瓶中放铁块要考虑铁块是全部沉入水中，还是部分沉入水中。如果铁块是全部沉入水中，排开水的体积是8×8×15=960（立方厘米）。而现在瓶中水深是8厘米，要淹没15厘米高的铁块，水面就要上升15—8=7（厘米），需要排开水的体积是（3.14×10×10—8×8）×7=1750（立方厘米），可知铁块是部分在水中。
专题简析： 在组合图形中，三角形的面积出现的机会很多，解题时我们还可以记住下面三点： 1，两个三角形等底、等高，其面积相等； 2，两个三角形底相等，高成倍数关系，面积也成倍数关系； 3，两个三角形高相等，底成倍数关系，面积也成倍数关系。
例题2 下图中，边长为10和15的两个正方体并放在一起，求三角形ABC（阴影部分）的面积。
分析：
1，因为三角形ABD与三角形ACD等底等高，所以面积相等。因此，三角形ABO的面积和三角形DOC的面积相等，也是6平方厘米。
2，因为三角形BOC的面积是三角形DOC面积的2倍，所以BO的长度是OD的2倍，即三角形ABO的面积也是三角形AOD的2倍。所以，三角形AOD的面积是6÷2=3平方厘米。
03
例题1 ： 下图是一个楼梯的侧面图，求此图 形的周长。
例题2 ：下图是由6个边长2厘米的正方形拼成的，这个图形的周长是多少厘米？
分析：这题我们可以用平移的方法将它转化 为一个长方形，如下图：
例题3 ： 两个大小相同的正方形拼成一个 长方形后，周长比原来两个正方形周长的和减 少了6厘米。原来一个正方形的周长是多少厘？
第三节 体积

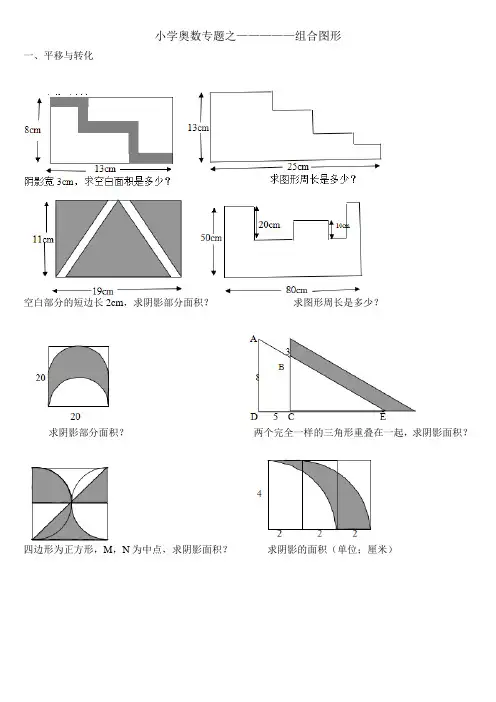
小学奥数专题之—————组合图形一、平移与转化空白部分的短边长2cm，求阴影部分面积？求图形周长是多少？求阴影部分面积？两个完全一样的三角形重叠在一起，求阴影面积？四边形为正方形，M，N为中点，求阴影面积？求阴影的面积（单位；厘米）求阴影面积（单位；厘米）小圆半径为1cm，花瓣图形的周长和面积是多少？正方形的边长为4cm，求阴影的面积？求梯形的面积？正方形的边长为4cm，求阴影面积？正方形的边长为4cm，求阴影周长和面积？正方形的边长为4cm，求阴影面积？正方形的边长为4cm，求阴影面积？正方形的边长为4cm，求阴影面积？三个圆的半径相等都是2cm，求阴影的面积？正方形的面积是16平方厘米求阴影面积？求阴影的面积？（单位；厘米）下图中圆的半径是4厘米，O是圆心，AB和正方形的边长为4cm，求阴影部分周长和面积？DC互相垂直，OE=1厘米，EF=2厘米，那么图中阴影部分的面积是多少平方厘米？求阴影部分面积？平行四边形面积是24 平方厘米，求阴影部分面积？求阴影部分面积？圆的半径是6厘米，求图中的阴影面积。

大小正方形的边长分别为5cm，4cm 长方形的面积与圆的面积相等，已知圆的半径为3cm，求阴影部分面积？求阴影部分面积？求阴影面积？（单位；厘米）三角形ABC和三角形都是等腰直角三角形，阴影部分是正方形。

三角形ABC与三角形DEC的面积比是多少？梯形的面积是54平方厘米，求图中阴影部分的面积？圆的直径是16cm，求阴影部分的面积？阴影部分为正方形，求大长方形的周长？图中两个正方形的边长都为4厘米，求阴影部分面积？求阴影部分面积？图中三角形为等腰直角三角形，求阴影部分面积？求阴影部分面积？ 求阴影部分面积？ 重叠类如下图，两个41圆扇形AOB 与A ′O ′B ′重叠放在一起，其中POQO ′的面积是5平方厘米的正方形，那么阴影部分的面积是多少？大圆半径为4cm ，小圆半径为2cm ，求大圆白色部分比小圆白色部分面积多多少平方厘米如图平行四边形的长边是6cm ，短边 有红黄绿三块大小相同的正方形纸片，放在一个底为正方形 是3cm ，长边上的高是2.6cm ，求阴 的盒子内，他们相互重叠，在露出部分的中红色面积是，黄色 影部分的面积？ 面积是17，绿色面积是7，求正方形盒子底的面积？ABCD 是边长为a 的正方形， 每个小圆的半径都是2cm ，求阴影部分面积？利用割补法求阴影的面积（单位；厘米）小圆半径为2 小圆半径为3加减法求下面阴影面积（单位：厘米）6旋转法求下列各图阴影部分面积（单位厘米）梯形上底为3厘米，下底是5厘米，高是4厘米，E是DC的中点，求阴影部分的面积是多少？一个等腰三角形的斜边长6厘米，求它的面积？一个正方形的对角线长5厘米，求这个正方形的面积?一个三角形的斜边长是10厘米，两直角边的差是3厘米，求这个直角三角形的面积？一个直角三角形的斜边长是15厘米，两直角边的差是4厘米，求这个直角三角形的面积？小正方形的边长是3厘米，大正方形的边长是5厘米，求阴影部分的面积是多少？四边形的对角线，将四边形分成四个小三角形，已知其中的三个三角形的面积分别是15平方米，75平方米，65平方米，求阴影部分的面积？一个长方形被两条直线分成四个长方形，其中三个的面积是20平方米，25平方米，30平方米，另一个长方形的面积是多少平方米？一个长方形被四条直线分成九个长方形，其中五个的面积分别是1,2,3,4,5平方厘米，求阴影部分的面积是多少平方厘米？图形内所标数据分别为各长方形的面积，那么大长方形的面积是多少？在梯形ABCD中，两条对角线相交于O，下底是上底的3倍，三角形AOD的面积是12平方厘米，那么梯形的面积是多少平方厘米？已知梯形中两个小三角形的面积分别为3平方厘米，9平方厘米，求梯形ABCD的面积？在梯形ABCD中，三角形CDE的面积为20,AE:CD=2:5，求梯形ABCD的面积？在梯形ABCD中，三角形ACE的面积为60，AB:CD=1:3,求梯形ABCD的面积？在正方形中方了三个同样大的小正方形，已知绿色部分的面积是20，蓝色部分的面积是14，红色部分的面积是10，求大正方形的面积？如图数据为各三角形部分的面积，求阴影部分的面积。

1、上节学习了几何计数问题，利用上节课学到的知识和技能解答下面题目：（1）数一数下图中，各有多少条线段？各有多少个三角形？（2）如下图数一数图中长方形的个数。

一、专题导入同学们都知道，长方形的周长=（长＋宽）×2，正方形的周长=边长×4。

长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。

如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长，还需同学们灵活应用已学知识，掌握转化的思考方法，把复杂的问题转化为标准的图形，以便计算它们的周长。

二、专题精讲【例1】有5张同样大小的纸如下图（a）重叠着，每张纸都是边长6厘米的正方形，重叠的部分为边长的一半，求重叠后图形的周长。

分析解答：根据题意，我们可以把每个正方形的边长的一半同时向左、右、上、下平移（如图b），转化成一个大正方形，这个大正方形的周长和原来5个小正方形重叠后的图形的周长相等。

因此，所求周长是18×4=72厘米。

【例2 】一块长方形木板，沿着它的长度不同的两条边各截去4厘米，截掉的面积为192平方厘米。

现在这块木板的周长是多少厘米？分析解答：思路导航把截掉的192平方厘米分成A、B、C三块（如图），其中AB的面积是192－4×4=176（平方厘米）。

把A和B移到一起拼成一个宽4厘米的长方形，而此长方形的长就是这块木板剩下部分的周长的一半。

176÷4=44（厘米），现在这块木板的周长是44×2=88（厘米）。

【例3 】已知下图中，甲是正方形，乙是长方形，整个图形的周长是多少？分析解答：从图中可以看出，整个图形的周长由六条线段围成，其中三条横着，三条竖着。

三条横着的线段和是（a＋b）×2，三条竖着的线段和是b×2。

所以，整个图形的周长是（a＋b）×2＋b×2，即2a＋4b。

【例4 】下图是边长为4厘米的正方形，求正方形中阴影部分的周长。

精心整理页脚内容第一讲图形周长和面积知识导航亲爱的同学们，我们已经学会长方形、正方形的周长与面积的计算，利用公式很容易算出它们的面积与周长。

但在遇到一些较复杂的有关长方形和正方形的周长和面积计算时，一些同学就会感到棘手。

这一讲我们将学习用平移、例例求这个大长思路点拨从图上可以知道，小长方形的长的4倍等于宽的5倍，所以长是宽的5÷4=1.25倍。

每个小长方形的面积为45÷9=5平方厘米，所以1.25×宽×宽=5，所以宽为2厘米，长为2.5厘米。

页脚内容模仿练习下图的长方形被分割成5个正方形，已知原长方形的面积为120平方厘米，求原长方形的长与宽。

例3：一块正方形的苗圃（如右图实线所示），若将它的边长各增加30米，则面积增加9900平方米，问原来这块正方形苗圃例少？31号和2号的边长之和是18，所以1号比3号大18-14=4。

模仿练习小孙同学用编号为1，2，3，4，5的大小不同的正方形拼出一个长方形，如右图所示，则中间阴影部分正方形的周长是多少厘米？（希望杯培训试题）页脚内容学以致用A 级1.求图1和图2两个图形的周长。

（单位：厘米）2.如下图是两个正方形，边长分别是8厘米和4厘米，那么阴影部分的面积是多少？3.如图是由5个相同的小长方形拼成的大长方形，大长方形的周长是44厘米，求大长方形的面积。

4.5.20 6.7.分米？8.9.图1110.有一大一小两块正方形试验田，他们的周长相差40米，面积相差220平方米，那么小正方形试验田的面积是多少平方米？图b。

解：
4分米=40厘米 15×（40÷2—15） =15×5 =75（平方厘米）
答：这个长方形的面积是75平方厘米。
(4a) 第十四章 周长与面积
【热身演练 】
1、 一位农民伯伯用３０米长的篱笆围成一块 长方形的菜地，其中一边利用了一面９米 长的墙壁（如图），求菜地的面积？
墙壁
×
×
×
菜
地
×
×
×
××××××××××××××××××××
答：有两种不同的拼法，周长分别是42厘米和30厘米， 面积都是54平方厘米。
仔细观察：六个小正方形拼成一个大长方形有两种 不同的方法，算出来的周长不相同分别是42厘米和30厘 米，但是算出来的面积却相同都是54平方厘米。
(4a) 第十四章 周长与面积
【热身演练 】
3、 将１０个边长为4厘米的小正方形拼成一个大长方 形，怎么拼？画下来。并求出拼成后大长方形的周 长、面积分别是多少？
金杯数学（4a）
第十四章 周长与面积
(4a) 第十四章 周长与天面积津科学技术出版社
桌子 有多大？
单车骑一圈 能走多远？
卧室 有多大？
绕操场跑一圈 是多少米？
(4a) 第十四章 周长与面积
同学们， 今天我们就一起来
学习周长和面积 的计算。
(4a) 第十四章 周长与面积
【知识领航】
围绕封闭图形一周的长度叫周长，计算周长用长度单位，常用的单位 有千米、米、分米、厘米和毫米。
(4a) 第十四章 周长与面积
【技巧感悟 】
列表如下：
长（厘米）
11
10
9
8
7
6
宽（厘米）ຫໍສະໝຸດ 1234

四年级第十六讲四边形的周长和面积例1 下图是一块实验地，已知条件如下左图所示，求这块地的周长是多少？解（80+30）╳2=220（米）例2 有一块菜地长37米、宽25米，地中间留了1米宽的路，路把菜地分成4块（下左图），求菜地的实有面积是多少？解（37-1）╳(25-1)=864(平方米)例3 求下左图阴影部分的周长（说明：4角是每边长10厘米的正方形）。

解法一（100-10╳2）+（60-10╳2）╳2+10╳8=320（厘米）解法二 [(100-10╳2) +（60-10╳2）+10╳4] ╳2 =320（厘米）例4 求图A阴影部分的面积(单位：厘米)。

分析一图B是把图A分成两个长方形，分别求出它们的面积再相加。

解法一 20╳4+4╳（20-4）=144（平方厘米）图B分析二图C把图A分割成两个长方形，分别求出它们的面积再相加。

解法二 4╳（20-4）+20╳4=144（平方厘米）图C分析三把图A分割成两个相等的梯形（图D），先求出一个梯形的面积，然后乘2。

解法三12╳[(20-4)+20] ╳4╳2=144（平方厘米）图D分析四把图A添补成一个正方形（图E），阴影部分的面积等于大、小正方形面积之差。

解法四20╳20-（20-4）╳（20-4）=144(平方厘米)分析五把图A看作两个长20厘米、宽4厘米的长方形部分面积重叠在一起（重叠部分为连长4厘米的正方形）。

两个长方形面积之和减去重叠部分的面积，就是阴影部分的面积。

解法五 20╳4 ╳2-4╳4=144(平方厘米)分析六把长（20-4）厘米、宽4厘米的长方形割下，拼在另一个长方形旁，两个长方形拼成了一个长（20+20-4）厘米、宽4厘米的长方形（图F）。

解法六（20+20-4）╳4=144(平方厘米)特别指导以上6种解法中，解法一和解法二最简便，是本例的最佳解法。

例5 两张边长6厘米的正方形，一部分叠在一起放在桌上（如图），问桌子审美被盖住的面积是多少？（单位：厘米）解两个正方形面积 6╳6╳2=72（平方厘米）被盖住面积是 72-3╳3=63（平方厘米）例6 图A是一座楼房的平面图（单位：米），那么这座楼房的周长是多少？解图A楼房平面图的周长就转化为图B的周长与2条10米长的线段和。

如图，在一个正方形的小花园周围，环绕着宽５米的水池，水池 面积为３００平方米，正方形花园的面积是多少平方米？ 分析：要想求出花园的面积，必须知道小 正方形的边长或大长方形的面积．因此解 题的关键就在于根据水池的面积求出小正 方形的边长或大正方形的面积．（或边长）
５
小花园
水池中四个小正方形的面积：５×５×４＝１００㎡ 水池中的四个长方形面积：３００－１００＝２００㎡ 一个长方形的面积：２００÷４＝５０㎡ 长方形的长即花园边长：５０÷５＝１０m 花园面积：１０×１０＝１００㎡
减少了两条边=6厘米
6÷2×4=12(厘米)
请你练一练 如图:用4个一样大的长方形和一个小正方形,拼成一个长是16厘米的大 正方形,每个长方形的周长是多少?
长
16 厘 米
长+宽=16厘米 长方形的周长=16×2=32(厘米)
宽
把一个正方形分成甲、乙两个部分,比较甲、乙两个部分周长的长 短，并求出乙的周长。（单位：分米）
也可以这样理解：长方形的长=3条宽 长方形的周长=8条宽
1条宽：24÷8=3厘米
正方形的边长：3×3=9厘米 正方形的周长：9×4=36（厘米）
请你试一试
把一个长10厘米，宽5厘米的长方形，分成两个大小一样的正方形， 每个正方形的周长是多少？
10厘米
5厘米
10÷2×4=20(厘米)
两个大小相同的正方形拼成一个长方形后,周长比原来的两个 正方形周长的和减少了6厘米.原来一个正方形的周长是多少 厘米?
甲的周长＜乙的周长 甲 乙的周长=5×4=20（分米）
5
乙
一个长方形的长是宽的4倍，如果宽延长9厘米，长不变，这样就成一个 正方形，原来长方形的周长是（ ）厘米。