数理经济学试题3

《数理经济学》参考习题说明：以下习题主要在于帮助读者进一步理解和掌握相关的最优化方法。

而对相关数学最优化定理推导的深入理解将非常有助于对该原理的掌握，因此相关定理的证明可以作为习题，鉴于篇幅，在习题中不再重复。

另一方面，对经济学分析如何应用最优化数学方法，建议读者进一步阅读参考文献中的相关微观经济学和宏观经济学的高级教程。

另，以下习题中相关定理和例题的编号为教材中的编号。

第一部分 非线性规划与应用1. 如序中所提到的，目标函数和约束函数均为线性函数时称为线性规划问题，线性是非线性的一个特例，考虑以下的线性规划问题，min : T c x..:0s t Ax ≤ 0x ≥其中nx R ∈，c 为维向量，为n A m n ×矩阵。

导出该线性规划问题的Kuhn-Tucker 最优性条件。

2. 当非线性规划问题中的目标函数为二次函数，约束函数为线性函数时，称为二次规划问题。

导出以下二次规划问题的Kuhn-Tucker 最优性条件。

1min : 2T Ta c x x Hx ++..:s t Ax b =0x ≥其中为常数，为维向量，为a c n H n n ×对称矩阵，为A m n ×矩阵。

3. 考虑以下非线性规划问题：12max : x x −221..:0s t x x −+≤110x −≤ 20x −≤画图分析该问题的最优解，并讨论在最有解点是否满足Kuhn-Tucker 条件或Fritz John 条件。

14. 求解以下非线性规划问题：221122min : 23x x x x x −+− 212..:42s t x x −+≤1234x x +≤6)2 10x ≥，20x ≥5. 分析点*(4,3)是否为满足以下非线性规划问题的二阶条件的最优解：x =()(2212max : 34x x −+− 2212..:25s t x x +≤127x x +≥ 10x ≥，20x ≥6. 考虑下述含参数的非线性规划问题：11min : x u x −− 2212..:1s t x x u +≤−2用()x u 表示最优解，表示最优值函数，利用定理2.1.2和定理2.2.1的公式计算()u Φ()x u ∇，在和的值。

数理金融练习题1. 简答题1.1 请简述数理金融的定义，并说明其在金融领域中的应用。

数理金融是数学、统计学和金融学的交叉学科，研究运用数学和统计方法解决金融问题的理论和方法。

它主要运用概率论、微积分、随机过程等数学工具来分析和建模金融市场的风险和回报，为金融决策制定提供科学依据。

在金融领域中，数理金融可用于风险管理、资产定价、投资组合优化等方面。

例如，通过运用数理金融方法，可以衡量金融资产的价格波动风险，为金融机构提供风险控制措施；同时，数理金融还可以帮助投资者在不同资产之间进行有效的配置，以最大化投资组合的预期收益。

1.2 请简要介绍一下随机过程在数理金融中的应用。

随机过程是数理金融中常用的一种数学模型，它刻画了一系列随机事件随时间的变化过程。

在数理金融中，随机过程可以用来描述金融市场中的价格走势、利率变动等不确定性因素。

常见的随机过程模型包括布朗运动、几何布朗运动、扩散过程等。

随机过程在数理金融中的应用广泛，例如，通过建立随机过程模型，可以预测股票价格的未来演变，为投资者提供决策参考。

此外，随机过程还可用于衡量金融产品的风险价值，对金融衍生品的定价进行分析，以及评估投资组合的风险收益特征等方面。

2. 计算题2.1 假设某股票的价格服从几何布朗运动模型，其价格演化满足如下随机微分方程：dS = u * S * dt + σ * S * dz其中，S为股票价格，t为时间，u为收益率，σ为波动率，dz为布朗运动的微分项。

请计算在给定参数下，该股票的价格在一年之后的期望值和方差。

解：根据几何布朗运动的性质，该股票的价格演化方程可以写成如下形式：dln(S) = (u - 0.5 * σ^2) * dt + σ * dz其中，ln(S)为股票价格的对数。

根据该方程，可以推导出ln(S)的解析解为：ln(S(t)) = ln(S(0)) + (u - 0.5 * σ^2) * t + σ * W(t)其中，W(t)为标准布朗运动。

数理金融习题答案数理金融是一门结合了数学和金融学的学科，它运用数学模型和统计方法来分析金融市场和金融产品。

在数理金融的学习过程中，习题是不可或缺的一部分。

通过解答习题，我们可以加深对数理金融理论的理解，并提高解决实际问题的能力。

下面，我将为大家提供一些数理金融习题的答案，希望能对大家的学习有所帮助。

第一题：假设某只股票的价格服从几何布朗运动，其漂移率为0.05，波动率为0.2。

如果当前股票价格为100元，且时间为1年，求1年后股票价格为120元的概率。

答案：根据几何布朗运动的性质，股票价格的对数服从正态分布。

设股票价格的对数为X，则有X ~ N((0.05-0.2^2/2)*1, 0.2^2*1)，即X ~ N(0.03, 0.04)。

将120元转化为对数形式，即ln(120)，然后代入正态分布的公式，可以计算出概率为P(X > ln(120))。

最后，利用统计软件或查表工具，可以得到答案。

第二题：假设某只期权的价格为5元，行权价为100元，无风险利率为0.05，期权到期时间为3个月，波动率为0.3。

求该期权的Delta值。

答案：Delta值表示期权价格对标的资产价格变动的敏感性。

对于欧式期权，Delta值可以通过期权定价模型计算得到。

常用的期权定价模型有布莱克-斯科尔斯模型和它的变种。

根据布莱克-斯科尔斯模型，Delta值可以通过期权定价公式中的一阶偏导数来计算。

对于看涨期权，Delta值为N(d1)，对于看跌期权，Delta值为N(d1)-1，其中N(x)表示标准正态分布函数，d1的计算公式为：d1 = (ln(S/X) + (r + σ^2/2)T) / (σ√T)其中，S为标的资产价格，X为行权价，r为无风险利率，σ为波动率，T为期权到期时间。

将题目中给定的参数代入公式，即可计算出该期权的Delta值。

第三题：假设某只债券的到期时间为5年，票面利率为5%，市场利率为4%，票面价值为100元。

Problem Set 4 光滑函数1.（3.2）计算 CES 函数()( )⁄的 Hessi 矩阵解：一阶导数为：( )⁄( )⁄二阶导数为：()( )( )( )( ) ( )( )( )( ) ( )( )( )( ) ( )()( )( )( )( ) ( )Hessi 矩阵为：()[]()( )()( )[] ()( )()( ) []()( )2.（3.3）计算二次函数()在点(0,0)附近的二次Taylor 展开式。

3.(3.5)证明以下结论成立：（1）CES函数()( )⁄是1次齐次的。

证明:令t>0，则有：(t )[(t )(t )(t )]⁄t( )⁄t ( )从而可知，CES函数()( )⁄是1次齐次的。

（2）证明：令t>0，则有：v(tp,tm)[m u() s.t. (tp)≤(tm)][m u() s.t. p ≤m]v(p,m)故v(p,m)在p和m中是0次齐次的。

（3）证明：令t>0，则有：Π(tp)[m (tp)T y s.t. ( )≥y]t[m (p)T y s.t. ( )≥y]tΠ(p)从而可知利润函数Π(p)是1次齐次的。

（4）证明：令t>0，则有(tw,y)[min(tw)T s.t. ( )≥y]t[min(w)T s.t. ( )≥y]t (w,y)可知成本函数(w,y)在投入价格w中是1次齐次的。

证明：由于生产函数是1次齐次的，有：(w,y)[min(w)T s.t. ()≥y][min(w)T s.t. (y)≥ ]y[min(w)Ty s.t. (y)≥ ]y[min(w)T z s.t. (z)≥ ]y (w,)其中，令zy证毕。

Problem Set 5 凹函数1. (3.7)必要性：由已知可得f()函数是凹函数，变量都在其定义域内。

对于α∀∈[0 1],有1212[(1)][((1))]g t t f x t t v αααα+-=++- 12[()(1)()]f x t v x t v αα=++-+ 12()(1)()f x t v f x t v αα≥++-+ 12()(1)()g t g t αα=+- 从而可知函数g （t ）是在定义域上是凹函数。

一、集合的证明：1. 证明： (1) 任意闭集类的交集是闭集；(2) 有限闭集类的并集是闭集。

证：（1）对于所有i I ∈，I 是一个指标集，i S 是闭集，即其补集C i S 是开集。

根据德·莫甘定律，有 CC i i i I i I S S ∈∈⎛⎞=⎜⎟⎝⎠∩∪，因为开集的并集是开集，即Ci i IS ∈∪是开集。

Ci i I S ∈⎛⎞∴⎜⎟⎝⎠∩是开集。

i i I S ∈∴∩是闭集，即任意闭集的交是闭集。

（2）同理，对于所有的 1,2,...i n =，i S 是闭集，即说明其补集C i S 是开集。

根据德·莫甘定律，有()11CnnC ii i i S S ===∪∩，因为任何有限个开集的交集是开集，即1nCi i S =∩是开集。

()1Cnii S =∴∪是开集。

1ni i S =∴∪是闭集，即有限个闭集的并集是闭集。

2. 设函数i f S T →：是一个连续函数，其中{}220,1,2,...,i S x i n ≡≤≤=x ，{}410T x x ≡≤≤。

证明：()0i i f x −=x 有解。

证明：在S 中任取两点1x ，2x ，对于[0,1]t ∀∈，令12(1)t t t =+−x x x ，即有12(1)t i i i x tx t x =+−。

依题意，有1220i x ≤≤，2220i x ≤≤。

则1220i t tx t ≤≤，22(1)(1)20(1)i t t x t −≤−≤−；122(1)20i i tx t x ∴≤+−≤，即220t i x ≤≤。

t ∴x 也在S 中。

∴S 是凸集。

又{}220,1,2,...,i S x i n ≡≤≤=x ∵，∴显然的，S 是紧集。

令12()((),(),,())n T F x f x f x f x = ，显然，F （x ）为连续函数，且4()82()20,1,2,,i i f x f x i n ≤≤⇒≤≤= ， 这表明()F x S ∈，即F 为S S →的连续映射。

注意：答案按题序写在专用答题纸上，写在本试卷或草稿纸上者一律不给分（因答题纸不够而另外由考场添加的答题纸除外）。

考试后要求试卷和答题纸同时上交.1. (12%)设S 与T 是凸集。

证明下面每个集合也是凸的：（1）、{}S s -s,x x ∈=≡-S（2）、{}T t ,S s t,-s x x ∈∈=≡-T S2. (12%)设f 和g 为nR D ⊆上的实值凹函数，,0,0>>g f 证明：它们的乘积)x ()x ()x (g f h =在D 上是拟凹的。

3. (12%)解答下列最优化问题：（1）、的局部极值点求222121212123126),(x x x x x x x x f ++++=及对应的函数值；（2）、函数33121212(,)3f x x x x x x =--是否存在极值，如果存在，求出极值，并判断是极大值还是极小值。

4. (12%)设函数T S f i →:是一个连续函数，其中},...,2,1,202{n i x X S i =≤≤=，}104{≤≤=x x T 。

证明：0)x (=-i i x f 有解。

5. (12%)考虑下面的问题：22121),(max x x x x f = a x x t s =+22212..已知3=a 时此问题的最优解为：)5.0,1,1())(),(),((21=a a x a x λ增加0.3个单位时，目标函数的最优值增加多少？6. (12%)求解最优化问题： ∏=∈+n i i R X i x 12max αm X P t s T ≤..厦门大学《数理经济学》课程试卷 经济 学院＿2009＿年级 研究生各专业其中.2,1,0,,=>i m p i i α7. (14%)求解下列微分方程系统，并分析系统的稳定性（1）X X ⎪⎪⎭⎫ ⎝⎛--=1243 （2）⎩⎨⎧--=+-=xy x yy x x 2 8. (14%)考虑微分方程y y dtdy ln 3--= （1）证明存在一点*y 使得**--y y ln 3=0，因此微分方程有均衡点*y ；（2）画出y y dtdy ln 3--=的相位图的略图； （3）讨论时间路径的定性性质（即均衡点的稳定性）；。

第三章作业参考答案 3.2 解： 由题意知，AT = f(x)/x 在 x*处达到极值，由极值的必要条件知， (AT)′|x=x* = [x*f′ (x*) − f(x*)]/(x*)2 = 0 从而 f ′(x*) = f(x*)/ x*，因此总函数在 x*处的点弹性为E=df ( x) dxf ( x) x * f ′( x*) = =1 x f ( x*)即此点弹性为单位弹性。

3.3 证明： 令 u = f(x)，v = g(x)，二者的乘积记为 y = uv = f(x)g(x)。

需证明，Eyx = Eux+Evx。

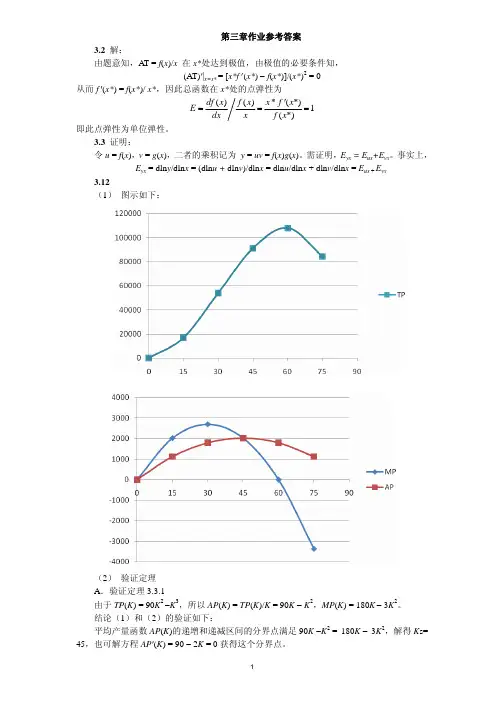
事实上， Eyx = dlny/dlnx = (dlnu + dlnv)/dlnx = dlnu/dlnx + dlnv/dlnx = Eux + Evx 3.12 （1） 图示如下：（2） 验证定理 A．验证定理 3.3.1 由于 TP(K) = 90K2 −K3，所以 AP(K) = TP(K)/K = 90K − K2，MP(K) = 180K − 3K2。

结论（1）和（2）的验证如下： 平均产量函数 AP(K)的递增和递减区间的分界点满足 90K −K2 = 180K − 3K2，解得 Ks= 45，也可解方程 AP′(K) = 90 − 2K = 0 获得这个分界点。

1经验证，在区间(0，45)上 AP′(K) > 0，在区间(45，+∞)上 AP′(K) < 0，因此 AP(K)在[0 ， 45]上递增，在[45 ， +∞)上递减；在区间(45，+∞)上 MP(K) > AP(K)，在区间[45 ， +∞) 上 MP(K) < AP(K)。

（3）的验证如下: 若 AP(K)在 KS 处获得极大值，由极值的必要条件，则 AP′(KS) = 0，即 90 − 2KS = 0，即 KS = 45，且有 AP(KS) = MP(KS) = 2025。

《数理金融分析—基础原理与方法》习题参考答案第一章（P52）题1-1 希德劳斯基模型的金融学含义是什么？解：参考方程（1.2.13）式后面的一个自然段。

题1-2 欧拉方程的经济学和金融学的含义是什么？解：参考方程（1.5.9）式和方程（1.5.10）式后面的一个自然段。

题1-3 如果你借款1000美元，并以年利率8%按每季度计息一次的复利形式支付利息，借期为一年。

那么一年后你欠了多少钱？解： 每季度计息一次的8%的年复合利率，等价于每个季度以2%的单利利率支付一次利息，而每个季度索要的利息，不仅要考虑原有的本金，而且还要加上累计到该时刻的利息。

因此，一个季度后你的欠款为： 1000(1+0.02)两个季度后你的欠款为： 21000(1+0.02)(1+0.02)1000(1+0.02)=三个季度后你的欠款为： 231000(1+0.02)(10.02)1000(1+0.02)+=四个季度后你的欠款为：341000(1+0.02)(10.02)1000(1+0.02)1082.40+==题1-4 许多信用卡公司均是按每月计息一次的18%的年复合利率索要利息的。

如果在一年的年初支付金额为P ，而在这一年中并没有发生支付，那么在这一年的年末欠款将是多少？ 解：这样的复合利率相当于每个月以月利率1812%1.5%=支付利息，而累计的利息将加到下一个月所欠的本金中。

因此，一年后你的欠款为： 12P(1+0.015)1.1956P =题1-5 如果一家银行所提供的利息是以名义利率5%连续地计算利息，那么每年的有效利率应该是多少？解：有效利率应为：0.050.05eff Pe P r e 10.05127P-==-≈ 即有效利率是每年5.127%。

题1-6 一家公司在未来的5年中需要一种特定型号的机器。

这家公司当前有一台这种机器，价值6000美元，未来3年内每年折旧2000美元，在第三年年末报废。

该机器开始使用后，第一年运转费用在该年年初值为9000美元，之后在此基础上每年增加2000美元。

1、已知生产函数为5.05.0K L Q =，证明 (a)该生产过程是规模报酬不变；(b)该生产过程受报酬递减规律的支配。

2、已知生产函数为2232.05.0K L KL Q --=，Q 表示产量，K 表示资本，L 表示劳动。

令上式的K=10，求(a)写出劳动的平均产量(L AP )函数和边际产量(L MP )函数。

(b)分别计算出总产量、平均产量和边际产量达到极大值时厂商雇佣的劳动。

(c)证明当L AP 达到极大时L AP =L MP =2。

3、以L 表示劳动力的投入，K 表示资本的投入。

试验证下面的函数关系是一阶齐次函数：(1)、里昂惕夫函数：⎭⎬⎫⎩⎨⎧=b K a L Y ,min ，)0,0(>>b a这里，{}y x ,min 的定义为：当y x <时，{};,min x y x =当y x ≥时，{}.,min y y x =(2) CES 函数[]ρρραα1)1(----+=KL A Y ()0,1,10,0≠-><<>ρραA (3)柯布-道格拉斯函数αα-=1K AL Y ， ().1,10><<A α4、消费),(21x x x =的消费者的效用函数为2212x x u =，求该消费者的补偿需求函数和最小支出函数。

5、已知6.04.010L K Q =，(a) 求资本和劳动的边际生产率K MP 和L MP (b) 当20,8==L K 时，求增加一单位的资本和劳动对产出的影响。

6、设某君消费偏好函数为3,2,6.04.0===y x P P y x U 。

求： (a)、当效用水平为9时x 与y 的均衡值(b)、当效用水平为9时所需支出的金额。

7、、消费产品21,x x 的消费者的效用为u ，最小支出函数为3/123/213/123)(p p u p E x =，其中，21,p p 为21,x x 的价格，试求：消费者的效用函数。

《数理经济学》练习一、解答下列最优化问题1、的局部极值点求222121212123126),(x x x x x x x x f ++++=及对应的函数值 2、1,8m ax 44=++y x y x 受约束于）（ 二、消费者的边际消费倾向是收入Y 的函数：212.08.0)(-+=YY f ，并且当他的收入Y=100时，他会将其全部收入用于消费，求他的消费函数应如何取值。

、、、含义讨论么根据其经济是一个总成本函数，那三、如果d c b a dQ cQ bQ a Q f +++=23)(四、证明：Cobb-Douglas 效用函数1212(,)αβ=u x x x x其中：0 >0 αβ>是连续的、严格单调的和严格拟凹的。

五、一个消费者面对价格分别为 p 1和p 2的商品1和商品2的效用函数)2(3)(2121ααx x x x U +=， 其中10<<α还是互补？关系是替代化？这表明它们之间的的需求将发生怎样的变价格增加的时候，商品当商品求其需求函数。

最大化的时候，，那么当他实现其效用算约束是如果该消费者面对的预什么？是不是齐次函数吗？为21)3()2(),()1(221121y x p x p x x U ≤+ 六、如果只存在两种商品，消费者所面对的预算约束是 ，他对于这两种商品的效用函数形式为：u(x 1,x 2)=max[ax 1,ax 2]+min[x 1, x 2] ，其中0<a<1 。

求其需求函数。

七、假设消费者的效用函数为1/1122()()u x x x ρρραα=+， 1、证明：当ρ→-∞时，这一效用函数与Leontief 效用函数{}1212(,)min ,u x x x x =所代表的偏好相同2、求其该效用函数对应的需求函数3、若效用函数是Leontief 效用函数{}1212(,)min ,u x x x x =形式的，求其对应的需求函数。

鲁东大学 2010 — 2011 学年第 一 学期级 校公选课 专业 科卷 课程名称 数理经济学课程号（ 1621080 ）考试形式（ 开卷笔试） 时间（120分钟）一、本题共1小题，满分20分。

1、设某消费者的效用函数为 U=min(aX 1，X 2)，a 为大于0的常数，X 1、X 2是两种商品，x 1的价格为P 1，X 2的价格为P 2，消费者的收入为M 。

① 画出该消费者的无差异曲线。

② 试给出该消费者对商品X 1的需求函数。

③ 试说明X 1的替代效应、收入效应和总效应。

④ 画出收入扩展曲线以及对商品X 1的恩格尔曲线。

.解：（1）由于11212(,)min{,}u x x ax x =消费者要保持其效用最大化，须始终保持ax 1=x 23—50所示。

消费者的无差异曲线其中x 1对x 2的边际替代率恒为a 。

（2）由（1）可知消费者要保持效用最大化，必须满足ax 1=x 2 ①且 p 1x 1+p 2x 2=M ②由①②联立得112Ix p ap =+（3）由于消费者始终会以21x x =a 的比例消费两物品，x 1物品的替代效应为0，这一点也可以从图3—51中看出。

比例消费替代效应又因为总效应=替代效应+收入效应 所以总效应与收入效应相同。

其中TE 指总效应，IE 指收入效应 总效应为∂=-∂+()x p p ap 121121∴总效应为-+()I p ap 212，收入效应为-+()Ip ap 212，替代效应为0。

（4）收入消费曲线指：价格p 1/p 2给定的前提下，由于收入变化，预算线与无差异曲线的共切点的轨迹。

其形状如图3—52所示。

恩格尔曲线是描述某种均衡购买与货币收入之间的关系。

因为112Ix p ap =+，x 1与I成正比例关系。

所以对应的恩格尔曲线为一从原点出发的射线（图3—53）。

恩格尔曲线A本二、本题共1小题，满分20分。

假定行业需求曲线为Q=250-P，每家厂商的边际成本为4。

2006~2008硕数理经济学试题总结一、集合的证明1.（06’）判断如下集合14~H H 是否为凸集，并加以说明。

(1) }|),{(21x e y R y x H =∈= (2) 欧氏空间中的超平面2{|,}n n H x p x p αα=∈⋅=∈∈\\\其中为常向量，为实常数。

(3) 欧氏空间n \上的以原点为中心、半径为r 的超球23{|}n H x x x r =∈⋅≤\。

(4) 41{|,,}nn i i i i i i i H a a A A i =1,,n λλ==∈∈⊂∑为凸集，2．（07’ ）证明下列集合是凸集： (1)(){}2,2S x y y x=≥(2){},)3:0,0S x y xy x y =≥>>（3. （08’） 对于 n i ,...2,1=，设 n i A ⊂R 是一个凸集。

证明下面集合是凸集： (1) i n i A 1=×，即集合的笛卡尔乘积 (2)11{|,}n ni i i i i i i i i A a a A ααα==≡∈∈∑∑R ，即集合的线性组合。

4. （08’）设120,0,0ααβ>>>均为实数，考虑由{}21122x x x ααβ+Ω≡∈+≤\给出的2+\中的点的子集。

(1) 证明Ω是凸集； (2) 证明Ω是有界的。

二、函数凹性证明1. （06’&07’）考察任何线性函数()f x ax b =+，对于,n a b ∈∈\\， (1) 表明：每个线性函数既凹又凸,尽管它们既非严格凹也非严格凸。

(2) 表明：每个线性函数既是拟凹的又是拟凸的,尽管它们并不是严格的。

2．（07’ ） 柯布-道格拉斯函数0,0,)(21>>=βαβα其中x x x f（1）如果证明它是凹函数,1≤+βα（2）如果1,αβ+>证明它不是凹函数，但是拟凹函数3. （07’ ）如果实值函数h 可写成(())g f X ,那么，该函数在n D ⊂ 上被称为位似函数。

数理金融考研题目及答案在数理金融领域，考研题目通常涉及概率论、数理统计、随机过程、微分方程等基础数学工具，以及金融市场的模型和理论。

以下是一些模拟的考研题目及答案：### 题目一：概率论与数理统计问题：设随机变量 \( X \) 和 \( Y \) 独立同分布，其概率密度函数为 \( f(x) = 2x \)，\( 0 \leq x \leq 1 \)。

求 \( X + Y \) 的分布函数 \( F_{X+Y}(z) \)。

答案：首先，我们知道 \( X \) 和 \( Y \) 的累积分布函数\( F_X(x) \) 和 \( F_Y(y) \) 可以通过概率密度函数 \( f(x) \) 积分得到：\[ F_X(x) = F_Y(y) = \int_0^x 2t \, dt = 2x^2, \quad 0 \leq x \leq 1 \]由于 \( X \) 和 \( Y \) 独立，\( X + Y \) 的分布函数可以通过\( X \) 和 \( Y \) 的累积分布函数的卷积得到：\[ F_{X+Y}(z) = P(X + Y \leq z) = \int_0^z P(Y \leq z - x)f(x) dx \]\[ = \int_0^z (1 - F_Y(z - x)) 2x \, dx \]\[ = \int_0^z (1 - 2(z - x)^2) 2x \, dx \]计算积分，得到 \( X + Y \) 的分布函数 \( F_{X+Y}(z) \)。

### 题目二：随机过程问题：考虑一个股票价格遵循几何布朗运动模型 \( dS_t = \mu S_t dt + \sigma S_t dW_t \)，其中 \( \mu \) 是期望收益率，\( \sigma \) 是波动率，\( W_t \) 是标准布朗运动。

求股票价格\( S_t \) 的期望值和方差。

答案：根据伊藤引理，我们可以推导出股票价格 \( S_t \) 的微分形式。

附录：练习题目 第一章练习及参考答案1. 假设1期有两个概率相等的状态a 和b 。

1期的两个可能状态的状态价格分别为a φ和b φ。

考虑一个参与者，他的禀赋为(011;;a b e e e )。

其效用函数是对数形式0110111(;;)log (log log )2a b a b U c c c c c c =++问：他的最优消费／组合选择是什么？解答：给定状态价格和他的禀赋，他的总财富是011a a b b w e e e φφ=++。

他的最优化问题是011011,,0110111maxlog (log log )2s.t.()0,,0a b a b c c c a a b b a b c c c w c c c c c c φφ++-++=≥ 其一阶条件为：00110111/1(1/)21(1/)20,0,,a a a b b b a a b b i i c c c c c c wc i a bλμλφμλφμφφμ=+=+=+++===给定效用函数的形式，当消费水平趋近于0时，边际效用趋近于无穷。

因此，参与者选择的最优消费在每一时期每一状态都严格为正，即所有状态价格严格为正。

在这种情况下，我们可以在一阶条件中去掉这些约束(以及对应的乘子)而直接求解最优。

因此，0(0,,)i i c i a b μ==。

对于c 我们立即得到如下解：1c λ=, 11112a a c λφ=, 21112b bc λφ=把c 的解代人预算约束，我们可以得到λ的解： 2λω=最后，我们有12c w =, 114a a w c φ=, 114b aw c φ= 可以看出，参与者把一半财富用作现在的消费，把另外一半财富作为未来的消费。

某一状态下的消费与对应的状态价格负相关。

状态价格高的状态下的消费更昂贵。

结果，参与者在这些状态下选择较低的消费。

2. 考虑一个经济，在1期有两个概率相等的状态a 和b 。

经济的参与者有1和2，他们具有的禀赋分别为：10:1000e --- ，2200:050e ---两个参与者都具有如下形式的对数效用函数：01()log (log log )2a b U c c c c =++在市场上存在一组完全的状态或有证券可以交易。