霍尔效应Hall Effect

霍尔和磁条面距离摘要：1.霍尔效应的定义和原理2.霍尔效应在磁场中的应用3.磁条面的概念及其与霍尔效应的关系4.霍尔和磁条面距离的测量方法5.霍尔和磁条面距离在实际应用中的重要性正文：1.霍尔效应的定义和原理霍尔效应（Hall Effect）是一种电磁效应，当一个导体在磁场中运动或者磁场发生变化时，会在导体的两端产生电势差。

这个现象最早由美国物理学家爱德华·霍尔（Edward Hall）在1879 年发现，因此得名霍尔效应。

霍尔效应的原理是电子在磁场中受到洛伦兹力作用，导致电子在导体内部形成横向电场，从而在导体两端产生电势差。

2.霍尔效应在磁场中的应用霍尔效应在磁场中的应用非常广泛，其中最典型的应用是霍尔传感器。

霍尔传感器是一种磁敏传感器，能够将磁场变化转换为电信号。

这种传感器在工业、航空航天、汽车电子等领域具有重要的应用价值。

此外，霍尔效应还在磁浮列车、磁性材料制造等领域发挥着重要作用。

3.磁条面的概念及其与霍尔效应的关系磁条面（Magnetic Stripe）是指磁性材料表面的一个特定区域，该区域具有较强的磁场。

磁条面通常用于磁卡、磁盘等磁性存储介质中。

在磁条面中，霍尔效应发挥着重要作用。

通过测量霍尔效应产生的电势差，可以读取磁条面上存储的信息。

4.霍尔和磁条面距离的测量方法测量霍尔和磁条面距离的方法主要有两种：接触式测量和非接触式测量。

接触式测量方法是将霍尔传感器与磁条面直接接触，通过测量霍尔效应产生的电势差来计算距离。

非接触式测量方法则是通过霍尔传感器产生一个磁场，然后测量磁场对磁条面的影响，从而间接计算距离。

5.霍尔和磁条面距离在实际应用中的重要性霍尔和磁条面距离在实际应用中具有重要意义。

在磁性存储介质中，准确的距离测量可以保证数据的正确读取和写入。

此外，在磁浮列车等高速运输系统中，精确测量霍尔和磁条面距离有助于提高系统的稳定性和安全性。

【實驗名稱】 霍爾效應（金屬） （Hall Effect, Metal ）【實驗目的】實驗金屬之霍爾效應，並由實驗結果求得金屬之電荷載子之型式及霍爾係數。

【相關觀念】霍爾效應（Hall effect ）、霍爾係數（Hall coefficient ）、磁阻抗（magnetoresistance ）、電洞（hole ）、能帶理論（Band theory ）、移動率（mobility ）。

【實驗背景與說明】通電導體置於磁場中，如圖一所示。

磁場沿著z-軸方向，電流順著x-軸方向，則在y-軸方向上之兩截面， 產生一電位差，即所謂的霍爾電壓（Hall voltage ）。

此霍爾效應於1879年由一位在Johns Hopkins University ，年僅24歲之研究生，E. H. Hall 首先觀察到的。

圖一 霍爾效應之實驗示意圖(一)假設導體為均向性的（isotropic ），且導體內之導電載子（charge carrier ） 只有一種型態。

載子之電荷為e ，其移動率（mobility ）為μ。

假設載子之平均漂移速度（drift velocity ）為v ，其受電磁場作用之力為 F e E v B=+⨯♎♓，則由移動率之定義得v E v B =±+⨯μ♎♓(1) 在式(1)中，如果導電載子是電子，則取 “－”號；如果為電洞（hole ），則取 “＋”號。

因為電流密度 J nev =（n 為載子密度），J ne E v B neE J B x x y z x y z =±+=±+μμ♎♓♎♓J ne E v B neEJ B yyxzyxz=±-=±-μμ♎♓♎♓J ne E z z =±μ(2)在穩定狀態下J J y z ==0，所以E z =0與E J B ne y x z=，再由霍爾係數(Hallcoefficient) 之定義R E J B H y x z =(3) 得R ne H =1(4)R H 值之正負決定載子之正負。

foc 霍尔计算角度【原创版】目录1.霍尔效应的定义与原理2.霍尔计算角度的方法3.霍尔计算角度的应用4.总结正文1.霍尔效应的定义与原理霍尔效应（Hall Effect）是一种磁敏半导体现象，当半导体材料在磁场中载流子受到洛伦兹力作用时，会在材料中产生电势差。

这种现象最早由美国物理学家爱德华·霍尔（Edward Hall）在 1879 年发现，并在随后的研究中被广泛应用于磁场检测、磁头读写和霍尔效应传感器等领域。

2.霍尔计算角度的方法霍尔计算角度的方法主要基于霍尔效应的原理，通过测量霍尔电势差和磁场强度来计算角度。

在霍尔效应中，电势差的大小与磁场强度和载流子浓度有关，可以通过下列公式计算：U_H = R_H * I_H = (1/ne) * (B * d * l)其中，U_H 为霍尔电势差，R_H 为霍尔系数，I_H 为霍尔电流，ne 为电子浓度，B 为磁场强度，d 为霍尔片的厚度，l 为霍尔片的长度。

通过解这个公式，我们可以得到磁场强度 B 与角度之间的关系：B = (U_H * ne * d) / (l * I_H)然后利用反正切函数计算角度：theta = arctan(U_H * ne * d / (l * I_H))3.霍尔计算角度的应用霍尔计算角度在许多领域都有广泛应用，例如：（1）磁头读写：在计算机硬盘驱动器、磁带和磁卡等磁头读写设备中，霍尔计算角度被用于精确控制磁头的位置，实现数据的准确读写。

（2）霍尔效应传感器：霍尔效应传感器广泛应用于汽车、工业自动化和家电等领域，通过测量磁场强度和角度变化，实现对各种物理量的监测和控制。

（3）地球物理勘探：在地球物理勘探中，霍尔计算角度可用于测量地磁场，帮助地质学家研究地壳结构和资源分布。

4.总结霍尔计算角度是一种基于霍尔效应原理的磁场角度测量方法，具有精度高、可靠性好、结构简单等优点，在磁头读写、霍尔效应传感器和地球物理勘探等领域具有广泛的应用前景。

霍尔效应霍尔效应[1]是磁电效应的一种，这一现象是美国物理学家霍尔（A.H.Hall，1855—193 8）于1879年在研究金属的导电机构时发现的。

当电流垂直于外磁场通过导体时，在导体的垂直于磁场和电流方向的两个端面之间会出现电势差，这一现象便是霍尔效应。

这个电势差也被叫做霍尔电势差。

霍尔效应的原理导体中的电荷在电场作用下沿电流方向运动，由于存在垂直于电流方向的磁场，电荷受到洛伦兹力，产生偏转，偏转的方向垂直于电流方向和磁场方向，而且正电荷和负电荷偏转的方向相反，这样就产生了电势差。

补充上面的人：正电荷与负电荷偏转的方向是相同的，只是因为导体中导电的是电子，所以只有电子偏转，才会有在两面有电压。

在半导体中，有两种载流子（空穴与自由电子），而它们的偏转方向是相同的，产生的电压也只是多数载流子与少数载流子之差，即表现了多数载流子的效果。

正是因为这样，所以才能利用霍尔效应来判断N、P型半导体。

霍尔效应的发展霍尔效应此后在测量、自动化、计算机和信息技术等领域得到了广泛的应用，比如测量磁场的高斯计。

在霍尔效应发现约100年后，德国物理学家克利青(Klaus von Klitzing,1943-)等在研究极低温度和强磁场中的半导体时发现了量子霍耳效应（运动电荷受到了磁场的作用力，从而运动方向发生偏转，这个力通常叫做洛伦兹力[1]，它为荷兰物理学家H.A.洛伦兹首先提出，故得名。

），这是当代凝聚态物理学令人惊异的进展之一，克利青为此获得了1985年的诺贝尔物理学奖。

之后，美籍华裔物理学家崔琦(Daniel Chee Tsui,1939-)和美国物理学家劳克林(Robert ughlin，1950-)、施特默(Horst L.St rmer，1949-)在更强磁场下研究量子霍尔效应时发现了分数量子霍尔效应，这个发现使人们对量子现象的认识更进一步，他们为此获得了1998年的诺贝尔物理学奖。

最近，复旦校友、斯坦福教授张首晟与母校合作开展了“量子自旋霍尔效应”的研究。

几种常见的转速传感器的工作原理转速传感器是用于测量物体转速的设备，常见的转速传感器有霍尔效应传感器、磁致伸缩传感器、光敏传感器和电流传感器等。

1. 霍尔效应传感器（Hall Effect Sensor）：霍尔效应是指当通过导体流动的电流受到垂直于电流方向的磁场的作用时，导体两侧会产生一种电势差。

霍尔传感器利用了这种效应来检测磁场的变化，从而测量转速。

传感器内部包含有一个霍尔元件和一个磁场发生器（通常是一个永磁体或一个电磁线圈）。

当被检测的物体上有一个磁场通过时，霍尔元件感受到电平的变化，从而测量转速。

2. 磁致伸缩传感器（Magnetic Inductive Sensor）：磁致伸缩传感器是利用磁致伸缩效应来测量转速的。

该传感器的工作原理是通过一个电磁线圈产生一个变化的磁场，当被检测的物体接近传感器时，物体的磁导率影响了电磁线圈的电压，从而测量转速。

3. 光敏传感器（Optical Sensor）：光敏传感器利用光信号来测量转速。

通常，光敏传感器含有一个光源和一个光敏元件。

光源发出一个光束，当被检测的物体经过传感器时，物体遮挡了光源，光敏元件接收到的光信号发生变化，从而测量转速。

4. 电流传感器（Current Sensor）：电流传感器能够通过测量物体通过的电流来测量转速。

通常，电流传感器内部含有一个电流变压器或者霍尔元件。

当电流通过传感器时，它会引起感应电压或电流的变化，从而测量转速。

这些转速传感器的工作原理各有特点，而选择合适的转速传感器要根据实际应用的要求。

无论是工业自动化领域还是汽车制造领域，转速传感器的准确可靠的测量对于保证设备和系统的正常运行都具有重要意义。

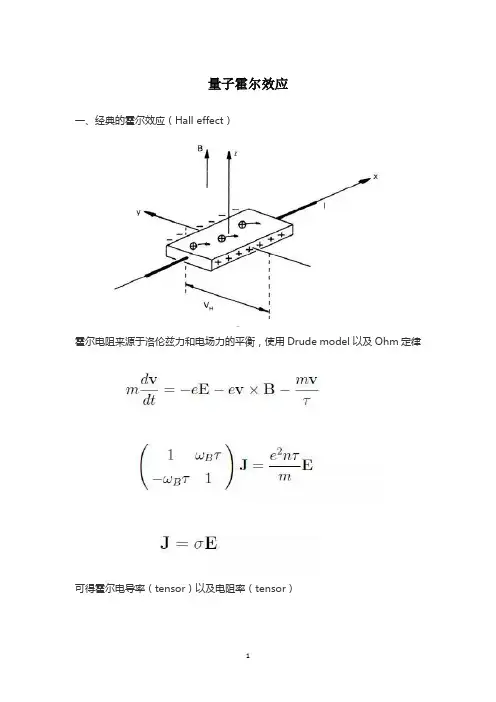
量子霍尔效应一、经典的霍尔效应（Hall effect）霍尔电阻来源于洛伦兹力和电场力的平衡，使用Drude model以及Ohm定律可得霍尔电导率（tensor）以及电阻率（tensor）二、（整数）量子霍尔效应弱磁场的情况下，非对角的霍尔电导和磁场强度满足经典的线性关系，强磁场作用下出现了很多量子化的平台量子化的起源-朗道能级这里使用Landau gauge，Hamiltonian可转化为谐振子模型从而求解其能级波函数代入current operator此时若在y方向加个电场ε，破坏其对称性得到的current依然是不变的（shift Gaussian wave packet center）。

对电流积分可得量子化的霍尔电导率，其中n对应了朗道能级的占据数目Laughlin’s gauge argument将IQHE解释为quantum pump，增加一个量子磁通的test flux的就对应着Gaussian wave packet移动一个单位。

Landauer's approach （Edge modes）Drift velocity 直接由化学电势差决定拓扑的引入（Kubo Formula，Chern number or TKNN number，Berry curvature...）Kubo Formula 是通过linear response得到的电导率上式红色部分是纯虚数，Berry curvature是纯实数所以第n个band的霍尔电导率是上式括号里面的积分是一个整数，即Chern number （first Chern number）=TKNN number。

证明略。

复旦大学物理学系教授修发贤课题组通过对量子霍尔效应的研究，实现了从二维迈向三维的新突破。

他们的科研成果于2018年12月18日在线发表于《自然》期刊上。

早在1879年，美国物理学家霍尔在研究金属的导电机制时发现，如果对通电的导体加上垂直于电流方向的磁场，电子的运动轨迹将发生偏转，在与导体纵向垂直的方向产生电压。

量子霍尔效应原理量子霍尔效应（quantum Hall effect，QHE）是指在强磁场下，二维电子气体中出现整除的基本电荷的离散Hall电导。

该效应于1980年首次被德国物理学家Klaus von Klitzing实验证明，因此他获得了1985年的诺贝尔物理学奖。

该效应在微电子学中具有重要意义，是开发高效的电子元件的基础。

量子霍尔效应原理包括以下几个方面：1. 磁场作用：在一定的强磁场下，电子气体的电子将朝同一方向相互排斥，形成许多正负电荷隔离的小块。

这些块被称为“霍尔细胞”，内部电行为呈凝结态，外部呈电导态，构成量子霍尔效应。

2. 孤立子的存在：霍尔细胞中存在孤立子，即电子跃迁时，其能级发生分裂，形成两个不同的能级。

由于电子的波函数只能在能级之间跃迁，因此孤立子对电子的运动起到了限制作用，导致电子在霍尔细胞内排布呈离散状态，从而形成量子霍尔效应。

3. 费米-狄拉克统计：费米-狄拉克统计是导致量子霍尔效应的关键之一。

在磁场中，电子由于自旋的存在和量子力学的约束，只能呈现离散能级。

这导致在磁场的作用下，电子排列方式具有一些特殊的性质，称为费米-狄拉克统计。

4. 量子霍尔效应中的基本电荷：在量子霍尔效应中，电荷的传输被限制在霍尔细胞内，而不是整个电子气体中。

电子在霍尔细胞中按整数倍的基本电荷q传输，这个基本电荷q是元电荷的N倍，即q = N ×e，其中 e 是电子的电荷，N 是任意整数。

5. 分数量子霍尔效应：分数量子霍尔效应是指在某些分数分子填充状态下，在极低温下，磁场中布洛赫电子发生量子霍尔效应。

这种效应和量子霍尔效应相似，但其中的基本电荷是分数形式的。

总之，量子霍尔效应是自然界中具有重大影响的现象之一，其在电子学领域的发展对未来的技术革新具有深远的影响。

需要不断深入研究，以探索其潜在的应用价值。

霍尔效应科技名词定义中文名称：霍尔效应英文名称：Hall effect定义1：在物质中任何一点产生的感应电场强度与电流密度和磁感应强度之矢量积成正比的现象。

应用学科：电力（一级学科）；通论（二级学科）定义2：通过电流的半导体在垂直电流方向的磁场作用下，在与电流和磁场垂直的方向上形成电荷积累和出现电势差的现象。

应用学科：机械工程（一级学科）；工业自动化仪表与系统（二级学科）；机械量测量仪表-机械量测量仪表一般名词（三级学科）百科名片霍尔效应是磁电效应的一种，这一现象是美国物理学家霍尔（A.H.Hall，1855—1938）于1879年在研究金属的导电机构时发现的。

当电流垂直于外磁场通过导体时，在导体的垂直于磁场和电流方向的两个端面之间会出现电势差，这一现象便是霍尔效应。

这个电势差也被叫做霍尔电势差。

发现霍尔效应在1879年被E.H. 霍尔发现，它定义了磁场和感应电压之间的关系，这种效应和传统的感应效果完全不同。

当电流通过一个位于磁场中的导体的时候，磁场会对导体中的电子产生一个垂直于电子运动方向上的的作用力，从而在导体的两端产生电压差。

虽然这个效应多年前就已经被大家知道并理解，但基于霍尔效应的传感器在材料工艺获得重大进展前并不实用，直到出现了高强度的恒定磁体和工作于小电压输出的信号调节电路。

根据设计和配置的不同，霍尔效应传感器可以作为开/关传感器或者线性传感器。

霍尔效应（图中电场方向应向上）解释在导体上外加与电流方向垂直的磁场，会使得导线中的电子与电洞受到不同方向的洛伦兹力而往不同方向上聚集，在聚集起来的电子与电洞之间会产生电场，此一电场将会使后来的电子电洞受到电力作用而平衡掉磁场造成的洛伦兹力，使得后来的电子电洞能顺利通过不会偏移，此称为霍尔效应。

而产生的内建电压称为霍尔电压。

方便起见，假设导体为一个长方体，长度分别为a,b,d，磁场垂直ab平面。

电流经过ad，电流I = nqv(ad)，n为电荷密度。

霍尔效应的实验研究与解释霍尔效应（Hall Effect）是指当一块导电材料处于垂直于外磁场方向的电流流动时，在材料的宽度方向会产生与电流方向垂直的电场。

这个现象最早由美国物理学家霍尔（Hall）于1879年发现并解释。

霍尔效应不仅在科学研究中有重要的应用，而且在电子器件的设计中也有着广泛的应用。

为了研究霍尔效应，我们可以进行一项简单的实验。

实验所需材料包括一块导电板、一台电源、一块磁铁和一台电压表。

首先，将导电板固定在一块平整的支架上，然后将电源的正极连接到导电板的一侧，负极连接到另一侧，使电流在导电板上产生一定的流动。

接下来，将磁铁放置在导电板下方并靠近导电板。

最后，用电压表测量导电板两侧产生的电势差。

实验结果显示，在材料的宽度方向，电流通过后会产生一个与电流方向垂直的电场。

这样的话，电子在导电板上运动时会受到这个电场的作用，导致电子的运动受到偏折。

由于磁场的存在使电子发生在垂直于磁场方向上的偏折, 偏转直至两个力平衡。

能达到平衡的电子数量受到偏折作用的强度和电子在材料中的浓度的影响。

实验解释霍尔效应的机理。

根据洛伦兹力的原理，电子在磁场作用下会受到一个由以下公式给出的力的作用：F = q * (v x B)其中，F为力，q为电子的电荷，v为电子的速度矢量，B为磁场的磁感应强度矢量。

可以看出，力的方向与速度和磁场的方向垂直。

当电子在导电板上运动时，电场引起的力将与洛伦兹力相抵消，形成一个平衡。

根据霍尔效应的定义，我们可以得到霍尔电压（VH）与电流（I）、磁感应强度（B）和导电板材料特性（例如载流子浓度）之间的关系。

具体来说，霍尔电压由以下公式给出：VH = R * IH * B / d其中，R为导电板的霍尔系数，IH为电流强度，B为磁感应强度，d为导电板的宽度。

从这个公式可以看出，霍尔电压与电流和磁场的乘积成正比，与导电板的宽度成反比。

因此，通过对实验数据的分析，我们可以确定导电板材料的特性。

霍尔系数与样品材料属性
霍尔系数
导体内部的电流是由带有负电荷的粒子（自由电子）之运动所造成。

霍尔效应于1879年由埃德温·赫伯特·霍尔（Edwin Herbert Hall）发现。

除导体外，半导体也能产生霍尔效应，而且半导体的霍尔效应要强于导体。

霍尔元件应用的基本原理是霍尔效应。

霍尔效应是一种磁敏效应，一般在半导体薄片的长度X方向上施加磁感应强度为B的磁场，则在宽度Y方向上会产生电动势UH，这种现象即称为霍尔效应。

UH称为霍尔电势，其大小可表示为：
U H=R H*I C*B/d（1）
式中，R H称为霍尔系数，它的单位是米的三次方每库仑，由半导体材料的性质决定；d为半导体材料的厚度,I C 为电流，B为磁场强度
设R H/d=K,则式（1）可写为：
U H=K*I C*B (2)
可见，霍尔电压与控制电流及磁感应强度的乘积成正比，K称为乘积灵敏度。

K值越大，灵敏度就越高；元件厚度越小，输出电压也越大。

霍尔电推进器原理
霍尔电推进器（Hall Effect Thruster）是一种利用霍尔效应产生的离子推进器，是一种高效、低排放、长寿命的电推进器。

它的原理是利用霍尔效应，在磁场和电场的作用下，将电子和离子分离并加速，产生推力，从而推动航天器。

霍尔电推进器由阴极、阳极和磁场组成。

当电子经过电子枪加速后，进入磁场区域。

磁场使电子发生螺旋运动，并与气态工作介质（如氙气、氩气等）碰撞，将其离子化。

离子在电场的作用下进一步加速，并通过出口喷出，形成推力。

霍尔电推进器的优点在于高效、低排放、长寿命。

由于它采用气态工作介质，因此比传统的固体火箭发动机更加节能和环保。

此外，由于离子的速度非常高，所以霍尔电推进器的推力也非常大。

在航天器的轨道调整和姿态控制方面，霍尔电推进器被广泛应用。

此外，它还可以用于卫星的长期稳定轨道保持和空间站的供电等方面。

霍尔效应中的副效应及其消除方法
低温电子器件中的霍尔效应是指当绕组处于外电磁场影响下时，绕组中回路电流与外部强磁场强度成正比；当绕组施加偶磁场时，磁感线圈行驶在磁场中时，产生偶磁势，偶磁势改变电流变化，称为霍尔效应（Hall-effect）。

霍尔效应中的副效应又称作热效应或热导效应，即当电流变化时，会导致芯片内部的温度升高，把芯片的原有所要检测的信号耦合出来而使检测结果不准确，是令人头疼的问题。

为了消除霍尔效应中的副效应，可以采取如下措施：
一、采用冷却装置：采用冷却装置可以降低绕组中发热元件的工作温度，减少霍尔效应中的副效应。

二、采用模拟电路：为了解决霍尔效应的副效应，可以采用模拟电路，如电流放大环或速度补偿技术，可以实现电流变化量的调节，防止热效应的发生。

三、信号调试：采用灵敏的信号调试技术可以减小霍尔效应中的副效应，以防止热对测试信号的影响，提高测量精度。