2018最新试题资料-2018—2018学年度第一学期钱高、灵二高高三月考联考语文试卷及答案

高2018级高三（上）11月月考（文科）数学参考答案第Ⅰ卷 （选择题 共60分）一、单选题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个是符合题目要求的）1-5:DBBAA; 6-10:ADCCB 11-12:BD第Ⅱ卷 （非选择题 共90分）二、填空题（本大题共4个小题，每小题5分，共20分，请把答案填在答题卷上）13． 5 .14．____120_____.15．____.16.__1(,)2+∞____. 三、解答题（本大题共6小题，共70分。

解答应写出文字说明，证明过程或演算步骤。

） 17、（本小题满分12分）【解析】（1） //，所以()0cos 2cos =--A b c B a ， 由正弦定理得-B A cos sin ()0cos sin sin 2=-A B C ，A C AB B A cos sin 2cos sin cos sin =+∴()A C B A cos sin 2sin =+∴，由π=++C B A ，A C C cos sin 2sin =∴由于π<<C 0，因此0sin >C ，所以21cos =A ，由于π<<A 0，3π=∴A （6分）（2）由余弦定理得A bc c b a cos 2222-+=bc bc bc bc c b =-≥-+=∴21622，因此16≤bc ，当且仅当4==c b 时，等号成立；因此ABC ∆面积34sin 21≤=A bc S ，因此ABC ∆面积的最大值34．（12分） 18．（本小题满分12分）【详解】（1）由频率分布直方图可知，0.010.001520.0010.006m n +=-⨯-=， 由中间三组的人数成等差数列可知0.00152m n +=，可解得0.0035m =，0.0025n =（4分）（2）周平均消费不低于300元的频率为()0.00350.00150.0011000.6++=⨯，因此100人中，周平均消费不低于300元的人数为1000.660⨯=人.（6分） 所以22⨯列联表为（8分）男性 女性 合计消费金额30020 40 60消费金额300< 25 15 40合计 45 55 10022100(20152540)8.249 6.63545556040K ⨯-⨯=≈>⨯⨯⨯所以有99%的把握认为消费金额与性别有关.（12分）19．（本小题满分12分）【解析】()1取AB 的中点N ，连接MN ，PN ，MN //AC ∴，且1MN AC 22==，PQ //AC ，P ∴、Q 、M 、N 确定平面α，QM //平面PAB ，且平面α⋂平面PAB PN =，又QM ⊂平面α，QM //PN ∴，∴四边形PQMN 为平行四边形，PQ MN 2∴==．（6分）()2取AC 的中点H ，连接QH ，PQ //AH ，且PQ=AH=2，∴四边形PQHA 为平行四边形，QH //PA ∴，PA ⊥平面ABC ，QH ∴⊥平面ABC ，AMC11SAC AB 322=⨯⨯=（），QH PA 2==， ∴三棱锥Q AMC -的体积：AMC11V SQH 32233=⋅=⨯⨯=．（12分） 20．（本小题满分12分）解：（Ⅰ）设222a b c -=，则32c a=，设(),P x y ，则1212,3F PF F PF S c y y b S bc ∆∆=≤∴≤=解得21a b =⎧⎨=⎩.所以椭圆C 的方程为2214x y +=.（4分）（Ⅱ）设MN 方程为(),0x ny m n =+≠，1122(x ,),N(x ,)M y y ，联立22440x ny mx y =+⎧⎨+-=⎩， 得()2224240n y nmy m +++-=，212122224,44nm m y y y y n n --∴+==++，（6分） 因为关于x 轴对称的两条不同直线12,l l 的斜率之和为0，即1212044y y x x +=--，即1212044y y ny m ny m +=+-+-，（8分）得()()121212240ny y m y y y y ++-+=，即()2222224280444n m nmnmn n n --+=+++.解得：1m =.直线MN 方程为：1x ny =+，所以直线MN 过定点()1,0B （12分） 21．（本小题满分12分）【详解】（1）由题意得函数()f x 的定义域为(0,)+∞，1()23f x ax x'=+- 由函数()f x 在点()()1,1f 处的切线方程为2y =-，得(1)1230f a '=+-=，解得1a =（2分）此时2()ln 3f x x x x =+-，21231()23x x f x x x x-+'=+-=.令()0f x '=，得1x =或12x =.（3分） 当10,2x ⎛⎫∈ ⎪⎝⎭和(1,)x ∈+∞时，()0f x '>，函数()f x 单调递增，当1,12x ⎛⎫∈ ⎪⎝⎭时，()0f x '<，函数()f x 单调递减，则当1x =时，函数()f x 取得极小值，为(1)ln1132f =+-=-，当12x =时，函数()f x 取得极大值，为11135ln ln 222424f ⎛⎫=+-=-- ⎪⎝⎭.（5分）（2）由1a =得2()ln 3f x x x x =+-.不等式()()()211212m x x f x f x x x -->可变形为()()1212m m f x f x x x ->-， 即()()1212m mf x f x x x ->-因为12,[1,10]x x ∈，且12x x <，所以函数()my f x x=-在[1,10]上单调递减.（8分） 令2()()ln 3,[1,10]m mh x f x x x x x x x=-=+--∈， 则21()230mh x x x x'=+-+≤在[1,10]x ∈上恒成立， 即3223m x x x -+-在[1,10]x ∈上恒成立（10分）设32()23F x x x x =-+-，则2211()661622F x x x x ⎛⎫'=-+-=--+ ⎪⎝⎭.因为当[1,10]x ∈时，()0F x '<，所以函数()F x 在[1,10]上单调递减，所以32min ()(10)210310101710F x F ==-⨯+⨯-=-，所以1710m -，即实数m 的取值范围为(,1710]-∞-.（12分）22．[选修4-4：坐标系与参数方程]（本小题满分10分）【解】（I ）依题曲线22:(2)4C x y -+=，故2240x y x +-=，即24cos 0ρρθ-=，即4cos ρθ=．（2分），由324sin πρθ⎛⎫-= ⎪⎝⎭，可得222sin cos θρθ=，即10sin cos ρθρθ+-=，（3分）将x cos ρθ=，y sin ρθ=代入上式，可得直线l 的直角坐标方程为10x y +-=．（5分）（Ⅱ）将直线l 的参数方程22212x t y ⎧=-⎪⎪⎨⎪=+⎪⎩（6分），代入2240x y x +-=中，化简可得23210t t ++=，设M ，N 所对应的参数分别为1t ，2t ，则1232t t +=-，121t t =，（8分）故121211||||32||||||||t t AM AN AM AN AM AN t t +++===⋅（10分） 23．[选修4-5：不等式选讲]（本小题满分10分）【解析】（1）当3a =时，()|2|3|1|f x x x =++-，不等式()6f x <可化为|2|3|1|6x x ++-<．（1分）①当2x <-时，不等式可化为2336x x --+-<，即45x -<，无解；②当21x -≤≤时，不等式可化为2336x x ++-<，即21x -<，解得112x -<≤；（3分）③当1x >时，不等式可化为2336x x ++-<，即47x <，解得714x <<， 综上，可得1724x -<<，故不等式()6f x <的解集为17(,)24-．（5分） （2）当12x ≥时，不等式2()3f x x x ≤++，即22|3|3x ax x x ++-≤++，整理得2|3|1ax x -≤+，即22131x ax x --≤-≤+，即2224x ax x -+≤≤+，因为12x ≥，所以分离参数可得24a x xa x x ⎧≥-+⎪⎪⎨⎪≤+⎪⎩．（8分） 显然函数2()g x x x =-+在1[,)2+∞上单调递减，所以17()()22g x g ≤=，而函数44()24h x x x x x=+≥⨯=，当且仅当4x x =，即2x =时取等号，所以实数a 的取值范围为7[,4]2．（10分）。

2018届高三理综上册第二次月考检测试题（有答案）5、Na+、N03-、Al2-③加入Al能放出H2的溶液中cl-、S042 -、N03–、g2+④在由水电离出的c（H-）= 10–3的溶液中Na+、Ba2+、cl-、I-⑤在溶液中能大量共存，加入NaH后加热既有气体放出又有沉淀生成的ca2+、Hc03–、NH4+、Al2–⑥能使无色酚酞变红色的溶液Na+、 cl -、S2-、S032-A．①③⑤ B．②④⑤ c．②④⑥ D．④⑤⑥9、下列离子方程式正确的是A．向g( Hc03)2溶液中加入过量的NaH溶液g2+ +2 Hc03- ++ 2H十Al3++ 2 S42-==2BaS04↓+Al02- +2HD．向Fe( N03)2溶液中加入稀盐酸3Fe2+ +4H++N03-==3Fe3++ N↑+2H14 l L-1的溶液中，①NH4+、Al3+、Br-、S42- ② Na+、g2+、cl-、N3-③+、Ba2+、cl-、N3- ④+、Na+、Hc3-、S42-四组离子中，一定可以大量共存的是 (填序号，下同)，可能大量共存的是，一定不能大量共存的是。

（3）在下列反应中，水仅做氧化剂的是 (填字母，下同)，水既不做氧化剂又不做还原剂的是。

A．cl2＋H2＝Hcl＋HclB．2Na22＋2H2＝4NaH＋2↑c．caH2＋2H2＝ca(H)2＋2H2↑ D．3Fe＋4H2（g） Fe34＋4H230、（12分）甲、乙、丙、丁、戊为原子序数依次增大的短周期元素。

甲、丙处于同一主族，丙、丁、戊处于同一周期，戊原子的最外层电子数是甲、乙、丙原子最外层电子数之和。

甲、乙组成的常见气体X能使湿润的红色石蕊试纸变蓝；戊的单质与X反应能生成乙的单质，同时生成两种溶于水均呈酸性的化合物和Z, 01 l/L的溶液。

2018届高三年级第一次月考化学试卷可能用到的相对原子质量：H-1 N-14 O-16 As-75 Zn-65 Cu-64 Fe-56 Na-23 C-12 一、选择题（每小题只有一个正确答案，每小题3分共48分）1．下列关于有机化合物的说法正确的是（）A. C3H6和C4H8互为同系物B. CH2Cl2有2种同分异构体C．苯乙烯分子中的所有原子不可能处于同一个平面D．乙酸与乙醇的酯化反应是可逆反应2．生产生活中的许多现象或应用都与化学知识有关。

下列现象成应用与胶体性质无关的是（）A．将盐卤或石青加人豆浆中，制成豆腐B．冶金厂常用高压电除去烟尘，是因为烟尘微粒带电荷C．泡沫灭火器中将Al2(SO4)3与NaHCO3两溶液混合后，喷出大量泡沫，起到灭火作用D．胶体、溶液和浊液这三种分散系的根本区别是分散质粒子直径的大小3．设N A为阿伏加德罗常数的数值，下列叙述正确的是（）A．1mol/L氯化铜溶液中的Cu2+数小于N AB．标准状况下，22.4LCl2与水反应转移的电子数为N AC．28g聚乙烯含有的碳原子数为2N AD．情性电极电解食盐水．若线路中通过1N A电子电量，则阳极产生气体11.2L4．N A为阿伏加德罗常数的值，下列叙述正确的是（）A.1.0L1.0mol/L的NaAlO2水溶液中含有的氧原子数为2N AB.12g石墨烯（单层石墨）中含有六元环的个数为0.5N AC.25℃时pH=13的NaOH溶液中含有OH-的数目为0.1N AD.1mol的羟基与1mol的氢氧根离子所含电子数均为9N A5．下列关于物质分类的说法正确的是（）①SO2、NO2都能和碱溶液发生反应属子酸性氧化物，Fe203、Al203属于碱性氧化物②碳酸钠、氢氧化钡、氯化铵、过氧化钠都属于离子化合物③蔗糖、硝酸钾和硫酸钡分别属于非电解质、强电解质和弱电解质④醋酸、烧碱、纯碱和生石灰分别属于酸、碱、盐和氧化物⑤NaHCO3是发酵粉主要成分之一，Na2CO3可治疗胃酸过多⑥盐酸属于混合物，而液氯、冰醋酸均属于纯净物A．①③⑤B．④⑤⑥C．②③④D．②④⑥6．1.76克铜镁合金完全溶解于50mL、密度为1.400g/cm3、质量分数为63％的浓硝酸中，得到NO2气体1792ml （标准状况），向反应后的溶液中加入适量的1.0mol/LNaOH溶液，恰使溶液中的金属离子全部沉淀。

2018届高三理综上册11月月考试题（有参考答案）
5 c
桂林中学+4H+
B．过量二氧化碳通入偏铝酸钠溶液中c2+2H2+Al2-=Al（H）3↓+Hc3-
c．等物质的量的亚硫酸氢铵与氢氧化钠溶液混合NH4++HS3-+2H-=S32-+NH3↑+2H2
D．碳酸氢镁溶液中加入过量石灰水
g2++2Hc3-+ca2++2H-=cac3↓+2H2+gc3↓
8．一种从植物中提取的天然化合物，其结构为可用于制作香水。

有关该化合物的下列说法不正确的是
A．1 l该化合物可跟2 lH2 发生加成反应
B．该化合物可使酸性n4溶液褪色
c．1 l该化合物完全燃烧消耗155l 2
D．1 l该化合物可与2l Br2加成
9．已检测出pH=1的某未知溶液中含有Al3+和N3-，检验此溶液中是否大量存在以下6种离子；①cl- ②NH4+ ③Fe2+ ④+ ⑤Hc3- ⑥cl-，其中不必检验就能加以否定的离子是（）
A．①②⑥B．②③④c．①③⑤D．④⑤⑥
10 在氧化还原反应的过程中，氧化反应和还原反应同时发生，有关S2－2e－＋2H2→
S42－＋4H＋反应的说法错误的是
A．该反应为氧化反应
B．上述反应中若产生01 l S42－，则消耗S2的物质的量为01l c．Fe2(S4)3、品红两种溶液都能使上述反应进行
D．通入cl2会降低S2的漂白作用
11．甲、乙、丙、丁、戊五种溶液的溶质分别是Hcl、cH3cH、。

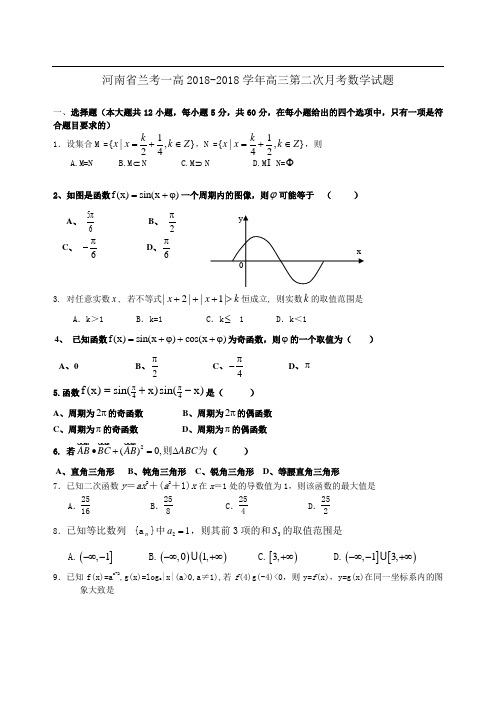
河南省兰考一高2018-2018学年高三第二次月考数学试题一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的） 1．设集合M =},412|{Z k k x x ∈+=，N =},214|{Z k k x x ∈+=，则 A.M=N B.M ⊂N C.M ⊃N D.M N=Φ2、如图是函数f (x)sin(x )=+ϕ一个周期内的图像，则ϕ可能等于 （ ）A 、56π B 、 2πC 、 6π-D 、6π3. 对任意实数x , 若不等式k x x >+++|1||2|恒成立, 则实数k 的取值范围是A ．k ＞1B ．k=1C ．k ≤ 1D ．k ＜14、 已知函数f (x)sin(x )cos(x )=+ϕ++ϕ为奇函数，则ϕ的一个取值为（ ） A 、0 B 、2π C 、4π- D 、π 5.函数44f (x)sin(x)sin(x)ππ=+-是（ ）A 、周期为2π的奇函数B 、周期为2π的偶函数C 、周期为π的奇函数D 、周期为π的偶函数6. 若2()0,AB BC AB ABC ∙+=∆ 则为（ ）A 、直角三角形B 、钝角三角形C 、锐角三角形D 、等腰直角三角形7．已知二次函数y ＝ax 2＋(a 2＋1)x 在x ＝1处的导数值为1，则该函数的最大值是A ．2516B ．258C ．254D ．2528．已知等比数列{a n }中21a =，则其前3项的和3S 的取值范围是A.(],1-∞-B.()(),01,-∞+∞C.[)3,+∞D.(][),13,-∞-+∞9．已知f(x)=a x-2,g(x)=log a |x|(a>0,a ≠1),若f (4)g(-4)<0，则y=f (x)，y=g(x)在同一坐标系内的图象大致是（1） （2） （3） （4）10、在△ABC 中，已知S ABC ⋅===∆则,3,1||,4||的值为（ ）A 、－2B 、2C 、±4D 、±211、△ABC 中，下列结论：①a 2>b 2+c 2 ，则△ABC 为钝角三角形；②a 2=b 2+c 2+bc ，则A 为60°；③a 2+b 2>c 2 ，则△ABC 为锐角三角形；④若A:B:C=1:2:3 ，则a:b:c=1：2：3 ，其中正确的个数为（ ） A. 1 B. 2 C. 3 D. 412．下列所给4个图象中，与所给3件事吻合最好的顺序是：①我离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再上学； ②我骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间； ③我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速．A ．（4）（1）（2）B ．（3）（1）（2）C ．（2）（1）（4）D ．（3）（2）（1）二、填空题（本大题共4小题，每小题5分，共20分）13．函数x y 2log =与函数2log (2)y x =-的图象及2y =-与3y =-所围成的图形面积是__ __． 14．已知函数()y f x =是定义在R 上的奇函数，且(2)0f =，对任意x ∈R ，都有(4)()(4)f x f x f +=+ 成立，则(2008)f =__ __．15、已知113a (,2sin ),b (cos ,a 322=α=α 且∥b ，则锐角α的值为 ；16．已知函数()2xf x =,等差数列{}x a 的公差为2.若246810()4f a a a a a ++++=,则212310log [()()()()]f a f a f a f a ⋅⋅⋅= __ __．三 解答题：本大题共6小题，共70分 解答应写出文字说明，证明过程或演算步骤（17）（本小题满分10分）已知函数21()cos cos 1()2f x x x x x R =⋅+∈ （1）求函数)(x f 的对称中心，最大值及取得最大值的条件; （2）求)(x f 的单调增区间。

2018—2018学年度上学期高三第二学月数学（理）考试题班级_______学号_____ 姓名__________全卷满分150分，用时150分钟。

一、选择题：本大题共10小题，每小题5分，共50分。

1.若点)sin sin (tan ααα，-P 在第三象限，则角α的终边必在（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 2.三个数20.620.6,log 0.6,2a b c ===之间的大小关系是（ ） A ．b c a <<.B ．c b a <<C ．c a b <<D ．a c b << 3.函数x x y 26ln +-=的零点一定位于的区间是( )A ．(3,4)B ．(2,3)C ．(1,2)D ．(0,1) 4．定义在R 上的函数)(x f 既是偶函数又是周期函数，若)(x f 的最小正周期是π，且当]2,0[π∈x 时，x x f sin )(=，则)35(πf 的值为（ ）A ．—21B ．23 C ．—23D ．215．使函数f （x ）=sin （2x+θ）+)2cos(3θ+x 是奇函数，且在[0，]4π上是减函数的θ的一个值（ ） A ． 3πB ．32πC ．34πD ．35π 6．给出四个函数，则同时具有以下两个性质的函数是： ①最小正周期是π；②图象关于点（6π，0）对称（ ）A ．)62cos(π-=x y B ．)62sin(π+=x yC ．)62sin(π+=x yD ．)3tan(π+=x y7. ()f x是定义在(0,)+∞上的非负可导函数，且满足()()0xf x f x'->，对任意的正数a b、，若a b>，则必有（）A．()()af a bf b< B．()()af b bf a<C．()()bf a af b< D．()()bf b af a<8 .二次函数y=ax2+bx与指数函数y=(ab)x的图象只可能是（）BC D9.已知函数()y xf x'=的图象如右图所示(其中'()f x是函数()f x的导函数)，下面四个图象中()y f x=的图象大致是（10. 由曲线2y x=和直线()20,1,,0,1x x y t t===∈所围成的图形（阴影部分）的面积的最小值为A、23B、13C、12D、14二、填空题：本大题共5小题，每小题5分，共25分。

2018—2018学年度第一学期钱高、灵二高月考联考试卷数 学（理科）考试时间：120分钟 满分：150分一、选择题（本大题共10小题，每小题5分，共50分）1. 下列四类函数中，有性质“对任意的x >0，y >0，函数f (x )满足f （xy ）＝f （x ）+f （y ）”的是（ ） （A ）幂函数 （B ）对数函数 （C ）指数函数（D ）余弦函数2.定义{}B x A x x B A ∉∈=-且，若{}5,4,3,2,1=M ，{}6,3,2=N ，则N-M 等于（ ） （A ）M (B)N (C) {}5,4,1 （D) {}63. 若函数x x e e x f -+=)(与x x e e x g --=)(的定义域为R ，则（ ）（A ）()x f 与)(x g 均为偶函数 （B ）()x f 为偶函数，)(x g 均为奇函数 （C ）()x f 与)(x g 均为奇函数 （B ）()x f 为奇函数，)(x g 均为偶函数4. 定义运算⎩⎨⎧>≤=ba b b a a b a ,,*，则函数x x x f 1*)(3=（0≠x ）的最大值是 （ ）（A ）1（B)2 （C)3 （D)无最大值5. 如表定义函数)(x f ：对于数列{}n a ，41=a ，,4,3,2),(1==-n a f a n n ，则2010a 等于 （ ） (A)1(B)2(C)3（D)46. 已知0>a 且1≠a ，则函数x a y =与()x y a -=log 的图象可能是 （ ）7. 方程3log 3+-=x x 的解所在的区间是（ ）（A ）()1,0（B)()2,1（C))3,2(（D)()+∞,3 8. 已知直线1+=x y 与曲线)ln(a x y +=相切，则a 的值为（ ）（A ）1(B)2（C)-1（D)-29. 已知无穷数列{}n a 和{}n b 都是等差数列，其公差分别是k 和h ，若数列{}n n b a 也是等差数列，则（ ）（A ）022=+k h （B ）k h ,可以是任何实数 （C ）0=hk（D ）不存在满足条件的实数h 和k10. 已知函数()21x f x =-，对于满足1202x x <<<的任意12,x x ，给出下列结论：（1）[]2121()()()0x x f x f x --<；（2）2112()()x f x x f x <；（3）2121()()f x f x x x ->-；（4）1212()()()22f x f x x xf ++>，其中正确结论的序号是（ ）（A ）(1)(2) （B ）(1)(3)（C ）(2)(4)（D ）(3)(4)二、填空题（本大题共7小题，每小题4分，共28分）11. 函数()1log 12)(2---=x x x f 的定义域为__________________________。

18-18学年度第一学期高三数学第二次月考试题试卷满分150分,考试时间120分钟 2018.12.10一．填空题：（本题满分48分，每小题4分）1、直线2x －y+1=0的倾钭角为 (用反三角函数表示)2、函数1)24lg(--=x y x 的定义域是3、已知sin α=54,且α是第二象限的角,则tg α=______ 4、函数)0(1)(2>+=x x x f 的反函数是 5、用列举法表示集合{x ︱x=N n ii n n∈+,1}= 6、从6种不同颜色的球中任选4个球,分别放入标有1,2,3,4号的盒内,若红,白两球都不能放入1号盒内, 则不同的放法有 种(结果用数值表示) 7、函数y=sin(x+2π)sinx 的最小正周期T= 8、不等式xx 1>的解集为 9、等差数列{a n }中,a 1=1, a 3+a 5=14.S n 为数列{a n }的前n 项之和,则nn n S n 12lim 2-→=10、(理)已知(1+x )+(1+x )2+……+(1+x )n =a 0+a 1x +a 2x 2+a 2x 2+……+a n x n, 如果a 1+a 2+……+a n=510－n ，则n=_______.005203≥≥≤-+≥-+且y x y x y x ,则Z=y-2x 的最大值是_______.(文)已知,x y 满足约束条件 11、已知函数1lg )1()(+=x xf x f ,则f(100)=___________12、已知函数))(2(log )()1(N n n n f n ∈+=+.若存在k ∈N 满足f(1)f(2)…f(n)=k 那么我们将k 叫做关于n 的“对整数”.当n ∈[1,100]时,则“对整数”k 的个数为 个二．选择题：（本题满分16分，每小题4分） 13、命题p ：a=1;命题q ：关于x 的方程0222=+-a x x 的实数解,别p 是q 的 （ ）Ａ．充分不必要条件； Ｂ．必要不充分条件； Ｃ．充要条件； Ｄ．既不充分又不必要条件14、在⊿ABC 中,cosAcos B －sinAsinB>0,别此三角形一定是 （ ）A ．锐角三角形B ．钝角三角形C ．直角三角形D ．以上都可能15、关于x 的方程1+=kx x 有一个负根,但没有正根,则实数k 满足 ( )A ．k ≥－1B ．k ≤－1C ．k ≤1D ．k ≥1班学16、下列命题正确的是 ( )(1)若函数f(x)既是奇函数,又是偶函数,则f(x)的值域为{0};(2)若函数f(x)是偶函数,则f(x )=f(x);(3)若函数f(x)在其定义域内非单调,则函数f(x)不存在反函数;(4)若函数f(x)与其反函数f －1(x)不完全相同,且有公共点P,则P 点必定在直线y=x 上A ．(1)(2)B ．(1)(2)(3)(4)C ．(1)(3)D ．(2)(4)三．解答题：17、(本题满分10分)已知}2sin ,{cos x x =，}23,{cos x =（11=,求锐角x ； （2）求⋅的取值范围.18、(本题满分12分)已知函数)4)(log 2(log 22xx y =,x ∈[2,4],求函数的最大值与最小值.19、（本小题满分14分）某村2018年底有人口1000人,全年农业总产值多2000万元;该村 从2018年起10年内每年总产值增加60万元,每年人口净增a 人.如果2018年作为第一年,之后的第x 年的该村人均产值为y 万元. (1)写出x 与y 的函数关系式；(2)为保证人均产值年年增加,那么人口净增数a 应控制在什么范围.20、(本题满分16分)定义min{a,b}表示两实数a,b 中的较小者,即当a ≤b 时, min{a,b}=a;当 a>b 时, min{a,b}==b.(1)求f(x)=min{x -3,x －1}的解析式；(2)解方程：f(x)=22-x .21、（本题满分16分）已知函数f(x)=157++x x ,数列{a n }中,2a n+1－2a n +a n+1a n =0 a 1=1,且a n ≠0, 数列{b n }中, b n =f(a n －1)（1）求证：数列{na 1}是等差数列；（2）求数列{b n }的通项公式；(3)求数列{n b }的前n 项和S n .22、（本题满分18分）设函数f(x)=x 2+ax+1,)0(,2)1()2()1()()(<++-++=ab xx f b x f x bxf x g ,且f(x+1)是偶函数.（1）求实数a 的值；（2）讨论函数g(x)的单调性；（3）若函数g(x)在[4,+∞)上的最小值为－6,求实数b 的值.高三数学参考答案及评分标准1. arctg22.(－∞,1)∪(1,2)3. －34 4.),1(,12+∞∈-x x 5. {－2,0,2} 6. 240 7.π 8. (－∞,0)∪(1,+ ∞) 9. 2 10. (理) 8(文)0 11.5312. 513. A 14. B 15. D 16. A17. 解：(1)1=，∴cos 2x+sin 22x=1 ………… …1分sin 22x=sin 2x, sin 2x(4 cos 2x －1)=0 …………… 2分 sin 2x=0(舍去) 3分 cosx=21± 4分 ∴x=3π5分 (2) b a ⋅= cos 2x+23sin2x …………6分=++22cos 1x 23sin2x …………7分 =sin(2x+6π)+21…………9分∴⋅∈[－21,23] ……… …10分18. 解：y=(log 2x －log 22)(log 2x －log 24) ……… …1分=x 22log －3log 2x+2=41)23(log 22--x ……… …3分 ∵x ∈[2,4],令t= log 2x t ∈[21,2] ……… …6分 23∈[21,2],当t=23,即x=22时,y min =41……… …9分 …当t=21,即x=2时,y max =43……… 12分∴函数的最大值为43,最小值为4119. 解：(1)y=),101(,1000602000N x x axx∈≤≤++… 4分(2)设1≤x 1<x 2≤10,(x 1、x 2∈N) 5分 则f(x 1)－f(x 2)=221110006020001000602000ax x ax x ++-++ 6分=)1000)(1000()30)((20002112ax ax a x x ++-- 9分∵人均产值年年增加, ∴f(x 1)－f(x 2)<0 11分 ∴ 当0≤a<30(a ∈N)时,f(x)为增函数,即人均产值年年增加 14分 20.解：（1）当x -3≤x －1时,得 x －1≥0,…(3－x)2≤(x －1)2 2分∴x ≥2… 5分∴当x -3>x －1时, 得 x －1<0 x －1≥0x -3≥0 或 (3－x)2>(x －1)2 8分 … ∴ x<2 10分 x －1(x<2) ∴f(x)=x -3 (x ≥2) 12分 （2）方程f(x)=22-x 的解：x 1=0或x 2=4或3814分 21. 解：（1）2a n+1－2a n +a n+1a n =0 ∵a n ≠0, 两边同除a n+1a n …1分21111=-+n n a a 4分 4分∴数列{na 1}是首项为1,公差为21的等差数列 …5分（2）∵n a 1=21)1(11+=-+n d n a … 7分 ∴a n －1=)(,11N n n n∈+-… 8分 ∵b n =f(a n －1)=f(11+-n n)=－n+6 (n ∈N) … 10分（3） －n+6 (n ≤6, n ∈N )n b = … 12分n －6 (n>6, n ∈N )2)11(2)6(1n n n b n -=-+ (n ≤6, n ∈N ) 14分 ∴S n = 260112))(6(276+-=+-+n n b b n S n (n>6, n ∈N) 16分22. 解：（1）∵f(x+1)是偶函数, ∴f(x)的图象关于直线x=1对称,a =－2 … 3分(2)g(x)=xb+2x+2－2b … 4分 ab<0则b>0,当x b =2x,即x=±22b5分判断：g(x)在(－∞,－22b ],[22b,+∞)上为增函数 7分g(x)在[－22b ,0),(0.22b]上为减函数 9分证明：设0<x 1<x 2, g(x 1)－g(x 2)=221122x x b x x b --+=2121122)(x x x x b x x -- 11分 x 2－x 1>0, x 1x 2>0,当b －2x 1x 2>0即0<b<22b时, g(x 1)－g(x 2)>0 g(x 1)>g(x 2), g(x)在 (0.22b]上为减函数 当b －2x 1x 2<0即b>22b时, g(x 1)－g(x 2)<0 g(x 1)<g(x 2), g(x)在[22b,+∞)上为增函数 13分同理可证g(x)在[－22b,0)上为减函数g(x)在(－∞,－22b]上为增函数 14分(3)若4≤22b ,即b ≥32时,当x=22b,g(x)最小,即2b 2+2－2b=－6无解 16分 若4>22b,即b<32时,当x=4,g(x)最小,即g(x)=－6, ∴b=764 18分。

浙江省杭州高中2018－2018学年度第一学期高三第二次月考数 学注意事项：1．本试卷满分150分.考试时间120分钟. 2．将所有答案填写在答题卷的相应位置.一、选择题（本大题共10小题，每小题5分，共 50分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．a ，b ，c 是常数，则“a >0且b 2－4ac <0”是“对任意x ∈R ，有ax 2＋bx ＋c >0”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．函数344)(23++-=ax ax xx f 的定义域为（－∞，＋∞），则实数a 的取值范围是 A ．（－∞，＋∞） B ．[0，43) C ．（43，＋∞） D ．[0，43] 3．若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“同族函数”，那么函数解析式为y ＝x 2，值域为{1，4}的“同族函数”共有A ．7个B ．8个C ．9个D ．10个4．已知e <x <10，记a ＝ln （ln x ），b ＝lg （lg x ），c ＝ln （lg x ），d ＝lg （ln x ），则a ，b ，c ，d 的大小关系A ．a <b <c <dB ．c <d <a <bC ．c <b <d <aD ．b <d <c <a5．（理）设函数f （x ）＝（x －1）（x －2）（x －3）（x －4），则f ′（x ）＝0有A ．分别位于区间（1，2）（2，3）（3，4）内三个根B ．四个实根x i ＝i （i ＝1，2，3，4）C ．分别位于区间（0，1）（1，2）（2，3）（3，4）内四个根D ．分别位于区间（0，1）（1，2）（2，3）内三个根 （文）函数f （x ）＝x 3－x 2－x ＋1在[－1，1]上的最大值是 A ．2732B ．2726 C ．0 D ．2732-6．已知y ＝f （x ）是定义在R 上的奇函数，当x >0时，f （x ）＝x －1，那么不等式f （x ）<21的解集是A ．{x |0<x <23} B ．{x |－21<x <0} C ．{x |－21<x <0或0<x <23}D ．{x |x <－21或0≤x <23} 7．已知A ＝B ＝{1，2，3，4，5}，从A 到B 的映射f 满足（1）f （1）≤f （2）≤……≤f （5）（2）A 中元素在B 中的象有且只有2个，则适合条件的映射f 的个数是 A ．10B ．20C ．30D ．408．（理）若f （x ）是在（l l ,-）内的可导奇函数，且f ′（x ）不恒为0，则f ′（x ）A ．必为（l l ,-）内的奇函数B ．必为（l l ,-）内的偶函数C ．必为（l l ,-）内的非奇非偶函数D ．可能为奇函数也可能为偶函数（文）下列函数中，不是奇函数的是 A ．)1lg(2++=x x y B ．y ＝ 5－x ＋ 5xC ．55lg-+=x x yD ．2xx e e y --=9．先作函数xy -=11lg的图像关于原点对称的图像，再将所得图像向右平移一个单位得图像C 1，又函数y ＝f （x ）的图像C 2与C 1关于直线y ＝x 对称，则函数y ＝f （x ）的解析式是A ．y ＝10xB ．y ＝10x－1C ．y ＝lg xD ．y ＝lg （x －1）10．若函数f （x ）＝x 3＋ax 2＋bx ＋c ，x ∈[－2，2]表示的曲线过原点，且在x ＝±1处的切线的斜率为－1，有以下命题：（1）f （x ）的解析式为：f （x ）＝x 3－4x ，x ∈[－2，2] （2）f （x ）的极值点有且仅有一个 （3）f （x ）的最大值与最小值之和等于零 其中假命题个数为 A ．0个 B ．1个 C ．2个 D ．3个二、填空题（本大题共4小题，每小题4分，共16分）11．设函数⎪⎩⎪⎨⎧+∞∈-∞∈=-),1(log )1,(2)(81x x x x f x ，则满足f （x ）＝41的x 值是____________12．若函数f （x ）＝211x -的定义域为M ，g （x ）＝)62(log 221x x -+的单调递减区间是开区间N ，设全集U ＝R ，则M ∩C u （N ）＝_______________13．地区的一种特色水果上市时间仅能持续5个月，预测上市初期和后期会因供不应求使价格呈连续上涨态势，而中期又将出现供大于求使价格连续下跌，现有三种价格模拟函数：① f （x ）＝p ·q x ；② f （x ）＝px 2＋qx ＋1；③ f （x ）＝x （x －q ）2＋p .（以上三式中p 、q 均为常数，且q ＞1，x ＝0表示4月1日，x ＝1表示5月1日，依次类推）.（1）为准确研究其价格走势，应选_______种价格模拟函数.（2）若f （0）＝4，f （2）＝6，预测该果品在_________月份内价格下跌. 14．若f （x ）＝a x x +的反函数f －1（x ）满足f －1（x ）＝f （x ），则f （a1）的值为_____________ 三、解答题（本大题共6小题，每题14分，满分84分，解答应写出文字说明，证明过程或演算步骤.）15．已知}19239|{},082|{2+≤-=≥-+=x x x B x x x A ，22{|430}C x x ax a =-+≤，()A B C ⋂⊆若，求实数a 的取值范围．16．32()f x x ax bx c =+++，在1x =与2x =-时，都取得极值。