伍德里奇《计量经济学导论》(第6版)复习笔记和课后习题详解-第二篇(第10~12章)【圣才出品】

伍德里奇计量经济学导论第6版笔记和课后答案
第1章计量经济学的性质与经济数据
1.1 复习笔记
考点一：计量经济学及其应用★
1计量经济学
计量经济学是在一定的经济理论基础之上，采用数学与统计学的工具，通过建立计量经济模型对经济变量之间的关系进行定量分析的学科。

进行计量分析的步骤主要有：①利用经济数据对模型中的未知参数进行估计；②对模型进行检验；③通过检验后，可以利用计量模型来进行相关预测。

2经济分析的步骤
经济分析是指利用所搜集的相关数据检验某个理论是否成立或估计某种关系的方法。

经济分析主要包括以下几步，分别是阐述问题、构建经济模型、经济模型转化为计量模型、搜集相关数据、参数估计和假设检验。

考点二：经济数据★★★
1经济数据的结构（见表1-1）
表1-1 经济数据的结构
2面板数据与混合横截面数据的比较（见表1-2）
表1-2 面板数据与混合横截面数据的比较
考点三：因果关系和其他条件不变★★
1因果关系
因果关系是指一个变量的变动将引起另一个变量的变动，这是经济分析中的重要目标之一。

计量分析虽然能发现变量之间的相关关系，但是如果想要解释因果关系，还要排除模型本身存在因果互逆的可能，
否则很难让人信服。

2其他条件不变
其他条件不变是指在经济分析中，保持所有的其他变量不变。

“其他条件不变”这一假设在因果分析中具有重要作用。

《计量经济学导论》考研伍德里奇考研复习笔记二第1章计量经济学的性质与经济数据1.1 复习笔记一、什么是计量经济学计量经济学是以一定的经济理论为基础，运用数学与统计学的方法，通过建立计量经济模型，定量分析经济变量之间的关系。

在进行计量分析时，首先需要利用经济数据估计出模型中的未知参数，然后对模型进行检验，在模型通过检验后还可以利用计量模型来进行预测。

在进行计量分析时获得的数据有两种形式，实验数据与非实验数据：（1）非实验数据是指并非从对个人、企业或经济系统中的某些部分的控制实验而得来的数据。

非实验数据有时被称为观测数据或回顾数据，以强调研究者只是被动的数据搜集者这一事实。

（2）实验数据通常是通过实验所获得的数据，但社会实验要么行不通要么实验代价高昂，所以在社会科学中要得到这些实验数据则困难得多。

二、经验经济分析的步骤经验分析就是利用数据来检验某个理论或估计某种关系。

1．对所关心问题的详细阐述问题可能涉及到对一个经济理论某特定方面的检验，或者对政府政策效果的检验。

2构造经济模型经济模型是描述各种经济关系的数理方程。

3经济模型变成计量模型先了解一下计量模型和经济模型有何关系。

与经济分析不同，在进行计量经济分析之前，必须明确函数的形式，并且计量经济模型通常都带有不确定的误差项。

通过设定一个特定的计量经济模型，我们就知道经济变量之间具体的数学关系，这样就解决了经济模型中内在的不确定性。

在多数情况下，计量经济分析是从对一个计量经济模型的设定开始的，而没有考虑模型构造的细节。

一旦设定了一个计量模型，所关心的各种假设便可用未知参数来表述。

4搜集相关变量的数据5用计量方法来估计计量模型中的参数，并规范地检验所关心的假设在某些情况下，计量模型还用于对理论的检验或对政策影响的研究。

三、经济数据的结构1横截面数据（1）横截面数据集，是指在给定时点对个人、家庭、企业、城市、州、国家或一系列其他单位采集的样本所构成的数据集。

第12章时间序列回归中的序列相关和异方差性12.1复习笔记考点一：含序列相关误差时OLS 的性质★★★1．无偏性和一致性当时间序列回归的前3个高斯-马尔可夫假定成立时，OLS 的估计值是无偏的。

把严格外生性假定放松到E（u t ｜X t ）＝0，可以证明当数据是弱相关时，∧βj 仍然是一致的，但不一定是无偏的。

2．有效性和推断假定误差存在序列相关，即满足u t ＝ρu t－1＋e t ，t＝1，2，…，n，｜ρ｜＜1。

其中，e t 是均值为0方差为σe 2满足经典假定的误差。

对于简单回归模型：y t ＝β0＋β1x t ＋u t 。

假定x t 的样本均值为零，因此有：1111ˆn x t tt SST x u -==+∑ββ其中：21nx t t SST x ==∑∧β1的方差为：()()122221111ˆ/2/n n n t j xt t x x t t j t t j Var SST Var x u SST SST x x ---+===⎛⎫==+ ⎪⎝⎭∑∑∑βσσρ其中：σ2＝Var（u t ）。

根据∧β1的方差表达式可知，第一项为经典假定条件下的简单回归模型中参数的方差。

因此，当模型中的误差项存在序列相关时，OLS 估计的方差是有偏的，假设检验的统计量也会出现偏差。

3．拟合优度当时间序列回归模型中的误差存在序列相关时，通常的拟合优度指标R 2和调整R 2便会失效；但只要数据是平稳和弱相关的，拟合优度指标就仍然有效。

4．出现滞后因变量时的序列相关（1）在出现滞后因变量和序列相关的误差时，OLS 不一定是不一致的假设E（y t ｜y t－1）＝β0＋β1y t－1。

其中，｜β1｜＜1。

加上误差项把上式写为：y t ＝β0＋β1y t－1＋u t ，E（u t ｜y t－1）＝0。

模型满足零条件均值假定，因此OLS 估计量∧β0和∧β1是一致的。

误差{u t }可能序列相关。

虽然E（u t ｜y t－1）＝0保证了u t 与y t－1不相关，但u t－1＝y t －1－β0－β1y t－2，u t 和y t－2却可能相关。

第1章计量经济学的性质与经济数据1.1复习笔记考点一:计量经济学★1计量经济学的含义计量经济学,又称经济计量学,是由经济理论、统计学和数学结合而成的一门经济学的分支学科,其研究内容是分析经济现象中客观存在的数量关系。

2计量经济学模型(1)模型分类模型是对现实生活现象的描述和模拟。

根据描述和模拟办法的不同,对模型进行分类,如表1-1所示。

(2)数理经济模型和计量经济学模型的区别①研究内容不同数理经济模型的研究内容是经济现象各因素之间的理论关系,计量经济学模型的研究内容是经济现象各因素之间的定量关系。

②描述和模拟办法不同数理经济模型的描述和模拟办法主要是确定性的数学形式,计量经济学模型的描述和模拟办法主要是随机性的数学形式。

③位置和作用不同数理经济模型可用于对研究对象的初步研究,计量经济学模型可用于对研究对象的深入研究。

考点二:经济数据★★★1经济数据的结构(见表1-3)2面板数据与混合横截面数据的比较(见表1-4)考点三:因果关系和其他条件不变★★1因果关系因果关系是指一个变量的变动将引起另一个变量的变动,这是经济分析中的重要目标之计量分析虽然能发现变量之间的相关关系,但是如果想要解释因果关系,还要排除模型本身存在因果互逆的可能,否则很难让人信服。

2其他条件不变其他条件不变是指在经济分析中,保持所有的其他变量不变。

“其他条件不变”这一假设在因果分析中具有重要作用。

1.2课后习题详解一、习题1.假设让你指挥一项研究，以确定较小的班级规模是否会提高四年级学生的成绩。

(i)如果你能指挥你想做的任何实验，你想做些什么?请具体说明。

(ii)更现实地，假设你能搜集到某个州几千名四年级学生的观测数据。

你能得到它们四年级班级规模和四年级末的标准化考试分数。

你为什么预计班级规模与考试成绩成负相关关系?(iii)负相关关系一定意味着较小的班级规模会导致更好的成绩吗?请解释。

答:(i)假定能够随机的分配学生们去不同规模的班级，也就是说，在不考虑学生诸如能力和家庭背景等特征的前提下，每个学生被随机的分配到不同的班级。

伍德里奇《计量经济学导论》（第6版）复习笔记和课后习题详解OLS用于时间序列数据的其他问题第11章OLS用于时间序列数据的其他问题11.1复习笔记考点一：平稳和弱相关时间序列★★★★1．时间序列的相关概念（见表11-1）表11-1时间序列的相关概念2．弱相关时间序列（1）弱相关对于一个平稳时间序列过程{x t：t＝1，2，…}，随着h的无限增大，若x t和x t＋h“近乎独立”，则称为弱相关。

对于协方差平稳序列，如果x t和x t＋h之间的相关系数随h的增大而趋近于0，则协方差平稳随机序列就是弱相关的。

本质上，弱相关时间序列取代了能使大数定律（LLN）和中心极限定理（CLT）成立的随机抽样假定。

（2）弱相关时间序列的例子（见表11-2）表11-2弱相关时间序列的例子考点二：OLS的渐近性质★★★★1．OLS的渐近性假设（见表11-3）表11-3OLS的渐近性假设2．OLS的渐近性质（见表11-4）表11-4OLS的渐进性质考点三：回归分析中使用高度持续性时间序列★★★★1．高度持续性时间序列（1）随机游走（见表11-5）表11-5随机游走（2）带漂移的随机游走带漂移的随机游走的形式为：y t＝α0＋y t－1＋e t，t＝1，2，…。

其中，e t（t＝1，2，…）和y0满足随机游走模型的同样性质；参数α0被称为漂移项。

通过反复迭代，发现y t的期望值具有一种线性时间趋势：y t＝α0t＋e t＋e t－1＋…＋e1＋y0。

当y0＝0时，E（y t）＝α0t。

若α0＞0，y t的期望值随时间而递增；若α0＜0，则随时间而下降。

在t时期，对y t＋h的最佳预测值等于y t加漂移项α0h。

y t的方差与纯粹随机游走情况下的方差完全相同。

带漂移随机游走是单位根过程的另一个例子，因为它是含截距的AR（1）模型中ρ1＝1的特例：y t＝α0＋ρ1y t－1＋e t。

2．高度持续性时间序列的变换（1）差分平稳过程I（1）弱相关过程，也被称为0阶单整或I（0），这种序列的均值已经满足标准的极限定理，在回归分析中使用时无须进行任何处理。

第5章多元回归分析：OLS 的渐近性5.1复习笔记考点一：一致性★★★★1．定理5.1：OLS 的一致性（1）一致性的证明当假定MLR.1～MLR.4成立时，对所有的j＝0，1，2，…，k，OLS 估计量∧βj 是βj 的一致估计。

证明过程如下：将y i ＝β0＋β1x i1＋u i 代入∧β1的表达式中，便可以得到：()()()()11111111122111111ˆnni ii i i i n ni i i i xx y n x x u xxnxx ββ-==-==--==+--∑∑∑∑根据大数定律可知上式等式右边第二项中的分子和分母分别依概率收敛于总体值Cov （x 1，u）和Var（x 1）。

假定Var（x 1）≠0，因为Cov（x 1，u）＝0，利用概率极限的性质可得：plim ∧β1＝β1＋Cov（x 1，u）/Var（x 1）＝β1。

这就说明了OLS 估计量∧βj 具有一致性。

前面的论证表明，如果假定只有零相关，那么OLS 在简单回归情形中就是一致的。

在一般情形中也是这样，可以将这一点表述成一个假定。

即假定MLR.4′（零均值与零相关）：对所有的j＝1，2，…，k，都有E（u）＝0和Cov（x j1，u）＝0。

（2）MLR.4′与MLR.4的比较①MLR.4要求解释变量的任何函数都与u 无关，而MLR.4′仅要求每个x j 与u 无关（且u 在总体中均值为0）。

②在MLR.4假定下，有E（y｜x 1，x 2，…，x k ）＝β0＋β1x 1＋β2x 2＋…＋βk x k ，可以得到解释变量对y 的平均值或期望值的偏效应；而在假定MLR.4′下，β0＋β1x 1＋β2x 2＋…＋βk x k 不一定能够代表总体回归函数，存在x j 的某些非线性函数与误差项相关的可能性。

2．推导OLS 的不一致性当误差项和x 1，x 2，…，x k 中的任何一个相关时，通常会导致所有的OLS 估计量都失去一致性，即使样本量增加也不会改善。

《计量经济学导论》考研伍德里奇版考研复习笔记第1章计量经济学的性质与经济数据1.1 复习笔记一、计量经济学由于计量经济学主要考虑在搜集和分析非实验经济数据时的固有问题，计量经济学已从数理统计分离出来并演化成一门独立学科。

1．非实验数据是指并非从对个人、企业或经济系统中的某些部分的控制实验而得来的数据。

非实验数据有时被称为观测数据或回顾数据，以强调研究者只是被动的数据搜集者这一事实。

2．实验数据通常是在实验环境中获得的，但在社会科学中要得到这些实验数据则困难得多。

二、经验经济分析的步骤经验分析就是利用数据来检验某个理论或估计某种关系。

1．对所关心问题的详细阐述在某些情形下，特别是涉及到对经济理论的检验时，就要构造一个规范的经济模型。

经济模型总是由描述各种关系的数理方程构成。

2．经济模型变成计量模型先了解一下计量模型和经济模型有何关系。

与经济分析不同，在进行计量经济分析之前，必须明确函数的形式。

通过设定一个特定的计量经济模型，就解决了经济模型中内在的不确定性。

在多数情况下，计量经济分析是从对一个计量经济模型的设定开始的，而没有考虑模型构造的细节。

一旦设定了一个计量模型，所关心的各种假设便可用未知参数来表述。

3．搜集相关变量的数据4．用计量方法来估计计量模型中的参数，并规范地检验所关心的假设在某些情况下，计量模型还用于对理论的检验或对政策影响的研究。

三、经济数据的结构1．横截面数据（1）横截面数据集，就是在给定时点对个人、家庭、企业、城市、州、国家或一系列其他单位采集的样本所构成的数据集。

有时，所有单位的数据并非完全对应于同一时间段。

在一个纯粹的横截面分析中，应该忽略数据搜集中细小的时间差别。

（2）横截面数据的重要特征①假定它们是从样本背后的总体中通过随机抽样而得到的。

当抽取的样本（特别是地理上的样本）相对总体而言太大时，可能会导致另一种偏离随机抽样的情况。

这种情形中潜在的问题是，总体不够大，所以不能合理地假定观测值是独立抽取的。

伍德⾥奇《计量经济学导论》（第6版）复习笔记和课后习题详解-多元回归分析：推断【圣才出品】第4章多元回归分析：推断4.1复习笔记考点⼀：OLS估计量的抽样分布★★★1．假定MLR.6（正态性）假定总体误差项u独⽴于所有解释变量，且服从均值为零和⽅差为σ2的正态分布，即：u～Normal（0，σ2）。

对于横截⾯回归中的应⽤来说，假定MLR.1～MLR.6被称为经典线性模型假定。

假定下对应的模型称为经典线性模型（CLM）。

2．⽤中⼼极限定理（CLT）在样本量较⼤时，u近似服从于正态分布。

正态分布的近似效果取决于u中包含多少因素以及因素分布的差异。

但是CLT的前提假定是所有不可观测的因素都以独⽴可加的⽅式影响Y。

当u是关于不可观测因素的⼀个复杂函数时，CLT论证可能并不适⽤。

3．OLS估计量的正态抽样分布定理4.1（正态抽样分布）：在CLM假定MLR.1～MLR.6下，以⾃变量的样本值为条件，有：∧βj～Normal（βj，Var（∧βj））。

将正态分布函数标准化可得：（∧βj－βj）/sd（∧βj）～Normal（0，1）。

注：∧β1，∧β2，…，∧βk的任何线性组合也都符合正态分布，且∧βj的任何⼀个⼦集也都具有⼀个联合正态分布。

考点⼆：单个总体参数检验：t检验★★★★1．总体回归函数总体模型的形式为：y＝β0＋β1x1＋…＋βk x k＋u。

假定该模型满⾜CLM假定，βj的OLS 量是⽆偏的。

2．定理4.2：标准化估计量的t分布在CLM假定MLR.1～MLR.6下，（∧βj－βj）/se（∧βj）～t n－k－1，其中，k＋1是总体模型中未知参数的个数（即k个斜率参数和截距β0）。

t统计量服从t分布⽽不是标准正态分布的原因是se（∧βj）中的常数σ已经被随机变量∧σ所取代。

t统计量的计算公式可写成标准正态随机变量（∧βj－βj）/sd（∧βj）与∧σ2/σ2的平⽅根之⽐，可以证明⼆者是独⽴的；⽽且（n－k－1）∧σ2/σ2～χ2n－k－1。

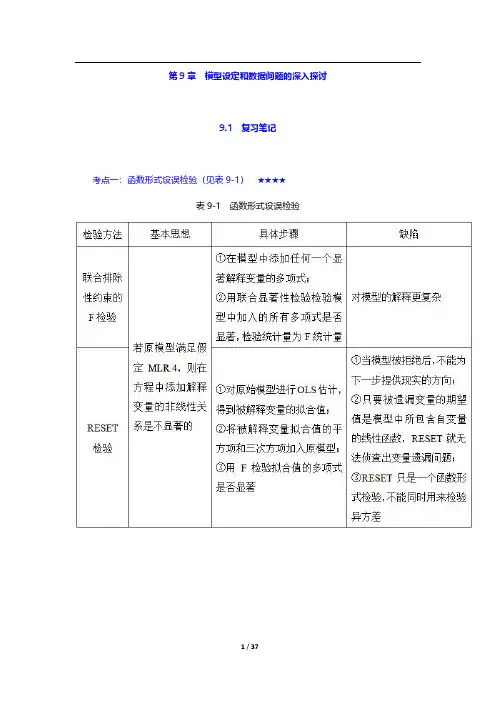
第9章模型设定和数据问题的深入探讨9.1复习笔记考点一：函数形式设误检验（见表9-1）★★★★表9-1函数形式设误检验考点二：对无法观测解释变量使用代理变量★★★1．代理变量代理变量就是某种与分析中试图控制而又无法观测的变量相关的变量。

（1）遗漏变量问题的植入解假设在有3个自变量的模型中，其中有两个自变量是可以观测的，解释变量x3*观测不到：y＝β0＋β1x1＋β2x2＋β3x3*＋u。

但有x3*的一个代理变量，即x3，有x3*＝δ0＋δ3x3＋v3。

其中，x3*和x3正相关，所以δ3＞0；截距δ0容许x3*和x3以不同的尺度来度量。

假设x3就是x3*，做y对x1，x2，x3的回归，从而利用x3得到β1和β2的无偏（或至少是一致）估计量。

在做OLS之前，只是用x3取代了x3*，所以称之为遗漏变量问题的植入解。

代理变量也可以以二值信息的形式出现。

（2）植入解能得到一致估计量所需的假定（见表9-2）表9-2植入解能得到一致估计量所需的假定2．用滞后因变量作为代理变量对于想要控制无法观测的因素，可以选择滞后因变量作为代理变量，这种方法适用于政策分析。

但是现期的差异很难用其他方法解释。

使用滞后被解释变量不是控制遗漏变量的唯一方法，但是这种方法适用于估计政策变量。

考点三：随机斜率模型★★★1．随机斜率模型的定义如果一个变量的偏效应取决于那些随着总体单位的不同而不同的无法观测因素，且只有一个解释变量x，就可以把这个一般模型写成：y i＝a i＋b i x i。

上式中的模型有时被称为随机系数模型或随机斜率模型。

对于上式模型，记a i＝a＋c i和b i＝β＋d i，则有E（c i）＝0和E（d i）＝0，代入模型得y i＝a＋βx i＋u i，其中，u i＝c i＋d i x i。

2．保证OLS无偏（一致性）的条件（1）简单回归当u i＝c i＋d i x i时，无偏的充分条件就是E（c i｜x i）＝E（c i）＝0和E（d i｜x i）＝E（d i）＝0。

CHAPTER 10TEACHING NOTESBecause of its realism and its care in stating assumptions, this chapter puts a somewhat heavier burden on the instructor and student than traditional treatments of time series regression. Nevertheless, I think it is worth it. It is important that students learn that there are potential pitfalls inherent in using regression with time series data that are not present for cross-sectional applications. Trends, seasonality, and high persistence are ubiquitous in time series data. By this time, students should have a firm grasp of multiple regression mechanics and inference, and so you can focus on those features that make time series applications different from cross-sectional ones.I think it is useful to discuss static and finite distributed lag models at the same time, as these at least have a shot at satisfying the Gauss-Markov assumptions. Many interesting examples have distributed lag dynamics. In discussing the time series versions of the CLM assumptions, I rely mostly on intuition. The notion of strict exogeneity is easy to discuss in terms of feedback. It is also pretty apparent that, in many applications, there are likely to be some explanatory variables that are not strictly exogenous. What the student should know is that, to conclude that OLS is unbiased – as opposed to consistent – we need to assume a very strong form of exogeneity of the regressors. Chapter 11 shows that only contemporaneous exogeneity is needed for consistency. Although the text is careful in stating the assumptions, in class, after discussing strict exogeneity, I leave the conditioning on X implicit, especially when I discuss the no serial correlation assumption. As the absence of serial correlation is a new assumption I spend a fair amount of time on it. (I also discuss why we did not need it for random sampling.)Once the unbiasedness of OLS, the Gauss-Markov theorem, and the sampling distributions under the classical linear model assumptions have been covered – which can be done rather quickly – I focus on applications. Fortunately, the students already know about logarithms and dummy variables. I treat index numbers in this chapter because they arise in many time series examples.A novel feature of the text is the discussion of how to compute goodness-of-fit measures with a trending or seasonal dependent variable. While detrending or deseasonalizing y is hardly perfect (and does not work with integrated processes), it is better than simply reporting the very high R-squareds that often come with time series regressions with trending variables.117118SOLUTIONS TO PROBLEMS10.1 (i) Disagree. Most time series processes are correlated over time, and many of themstrongly correlated. This means they cannot be independent across observations, which simply represent different time periods. Even series that do appear to be roughly uncorrelated – such as stock returns – do not appear to be independently distributed, as you will see in Chapter 12 under dynamic forms of heteroskedasticity.(ii) Agree. This follows immediately from Theorem 10.1. In particular, we do not need the homoskedasticity and no serial correlation assumptions.(iii) Disagree. Trending variables are used all the time as dependent variables in a regression model. We do need to be careful in interpreting the results because we may simply find a spurious association between y t and trending explanatory variables. Including a trend in the regression is a good idea with trending dependent or independent variables. As discussed in Section 10.5, the usual R -squared can be misleading when the dependent variable is trending.(iv) Agree. With annual data, each time period represents a year and is not associated with any season.10.2 We follow the hint and writegGDP t -1 = α0 + δ0int t -1 + δ1int t -2 + u t -1,and plug this into the right-hand-side of the int t equation:int t = γ0 + γ1(α0 + δ0int t-1 + δ1int t-2 + u t-1 – 3) + v t= (γ0 + γ1α0 – 3γ1) + γ1δ0int t-1 + γ1δ1int t-2 + γ1u t-1 + v t .Now by assumption, u t -1 has zero mean and is uncorrelated with all right-hand-side variables in the previous equation, except itself of course. SoCov(int ,u t -1) = E(int t ⋅u t-1) = γ1E(21t u -) > 0because γ1 > 0. If 2u σ= E(2t u ) for all t then Cov(int,u t-1) = γ12u σ. This violates the strictexogeneity assumption, TS.2. While u t is uncorrelated with int t , int t-1, and so on, u t is correlated with int t+1.10.3 Writey* = α0 + (δ0 + δ1 + δ2)z* = α0 + LRP ⋅z *,and take the change: ∆y * = LRP ⋅∆z *.11910.4 We use the R -squared form of the F statistic (and ignore the information on 2R ). The 10% critical value with 3 and 124 degrees of freedom is about 2.13 (using 120 denominator df in Table G.3a). The F statistic isF = [(.305 - .281)/(1 - .305)](124/3) ≈ 1.43,which is well below the 10% cv . Therefore, the event indicators are jointly insignificant at the 10% level. This is another example of how the (marginal) significance of one variable (afdec6) can be masked by testing it jointly with two very insignificant variables.10.5 The functional form was not specified, but a reasonable one islog(hsestrts t ) = α0 + α1t + δ1Q2t + δ2Q3t + δ3Q3t + β1int t +β2log(pcinc t ) + u t ,Where Q2t , Q3t , and Q4t are quarterly dummy variables (the omitted quarter is the first) and the other variables are self-explanatory. This inclusion of the linear time trend allows the dependent variable and log(pcinc t ) to trend over time (int t probably does not contain a trend), and the quarterly dummies allow all variables to display seasonality. The parameter β2 is an elasticity and 100⋅β1 is a semi-elasticity.10.6 (i) Given δj = γ0 + γ1 j + γ2 j 2 for j = 0,1, ,4, we can writey t = α0 + γ0z t + (γ0 + γ1 + γ2)z t -1 + (γ0 + 2γ1 + 4γ2)z t -2 + (γ0 + 3γ1 + 9γ2)z t -3+ (γ0 + 4γ1 + 16γ2)z t -4 + u t = α0 + γ0(z t + z t -1 + z t -2 + z t -3 + z t -4) + γ1(z t -1 + 2z t -2 + 3z t -3 + 4z t -4)+ γ2(z t-1 + 4z t -2 + 9z t -3 + 16z t -4) + u t .(ii) This is suggested in part (i). For clarity, define three new variables: z t 0 = (z t + z t -1 + z t -2 + z t -3 + z t -4), z t 1 = (z t -1 + 2z t -2 + 3z t -3 + 4z t -4), and z t 2 = (z t -1 + 4z t -2 + 9z t -3 + 16z t -4). Then, α0, γ0, γ1, and γ2 are obtained from the OLS regression of y t on z t 0, z t 1, and z t 2, t = 1, 2, , n . (Following our convention, we let t = 1 denote the first time period where we have a full set of regressors.) The ˆj δ can be obtained from ˆj δ= 0ˆγ+ 1ˆγj + 2ˆγj 2.(iii) The unrestricted model is the original equation, which has six parameters (α0 and the five δj ). The PDL model has four parameters. Therefore, there are two restrictions imposed in moving from the general model to the PDL model. (Note how we do not have to actually write out what the restrictions are.) The df in the unrestricted model is n – 6. Therefore, we wouldobtain the unrestricted R -squared, 2ur R from the regression of y t on z t , z t -1, , z t -4 and therestricted R -squared from the regression in part (ii), 2r R . The F statistic is120222()(6).(1)2ur r ur R R n F R --=⋅-Under H 0 and the CLM assumptions, F ~ F 2,n -6.10.7 (i) pe t -1 and pe t -2 must be increasing by the same amount as pe t .(ii) The long-run effect, by definition, should be the change in gfr when pe increasespermanently. But a permanent increase means the level of pe increases and stays at the new level, and this is achieved by increasing pe t -2, pe t -1, and pe t by the same amount.10.8 It is easiest to discuss this question in the context of correlations, rather than conditional means. The solution here does both.(i) Strict exogeneity implies that the error at time t , u t , is uncorrelated with the regressors in every time period: current, past, and future. Sequential exogeneity states that u t is uncorrelated with current and past regressors, so it is implied by strict exogeneity. In terms of conditional means, strict exogeneity is 11E(|...,,,,...)0t t t t u -+=x x x , and so u t conditional on any subset of 11(...,,,,...)t t t -+x x x , including 1(,,...)t t -x x , also has a zero conditional mean. But the lattercondition is the definition of sequential exogeneity.(ii) Sequential exogeneity implies that u t is uncorrelated with x t , x t -1, …, which, of course, implies that u t is uncorrelated with x t (which is contemporaneous exogeneity stated in terms of zero correlation). In terms of conditional means, 1E(|,,...)0t t t u -=x x implies that u t has zero mean conditional on any subset of variables in 1(,,...)t t -x x . In particular, E(|)0t t u =x .(iii) No, OLS is not generally unbiased under sequential exogeneity. To show unbiasedness, we need to condition on the entire matrix of explanatory variables, X , and use E(|)0t u =X for all t . But this condition is strict exogeneity, and it is not implied by sequential exogeneity.(iv) The model and assumption imply1E(|,,...)0t t t u pccon pccon -=,which means that pccon t is sequentially exogenous. (One can debate whether three lags isenough to capture the distributed lag dynamics, but the problem asks you to assume this.) But pccon t may very well fail to be strictly exogenous because of feedback effects. For example, a shock to the HIV rate this year – manifested as u t > 0 – could lead to increased condom usage in the future. Such a scenario would result in positive correlation between u t and pccon t +h for h > 0. OLS would still be consistent, but not unbiased.SOLUTIONS TO COMPUTER EXERCISESC10.1 Let post79 be a dummy variable equal to one for years after 1979, and zero otherwise. Adding post79 to equation 10.15) gives3t i= 1.30 + .608 inf t+ .363 def t+ 1.56 post79t(0.43) (.076) (.120) (0.51)n = 56, R2 = .664, 2R = .644.The coefficient on post79 is statistically significant (t statistic≈ 3.06) and economically large: accounting for inflation and deficits, i3 was about 1.56 points higher on average in years after 1979. The coefficient on def falls once post79 is included in the regression.C10.2 (i) Adding a linear time trend to (10.22) giveslog()chnimp= -2.37 -.686 log(chempi) + .466 log(gas) + .078 log(rtwex)(20.78) (1.240) (.876) (.472)+ .090 befile6+ .097 affile6- .351 afdec6+ .013 t(.251) (.257) (.282) (.004) n = 131, R2 = .362, 2R = .325.Only the trend is statistically significant. In fact, in addition to the time trend, which has a t statistic over three, only afdec6 has a t statistic bigger than one in absolute value. Accounting for a linear trend has important effects on the estimates.(ii) The F statistic for joint significance of all variables except the trend and intercept, of course) is about .54. The df in the F distribution are 6 and 123. The p-value is about .78, and so the explanatory variables other than the time trend are jointly very insignificant. We would have to conclude that once a positive linear trend is allowed for, nothing else helps to explainlog(chnimp). This is a problem for the original event study analysis.(iii) Nothing of importance changes. In fact, the p-value for the test of joint significance of all variables except the trend and monthly dummies is about .79. The 11 monthly dummies themselves are not jointly significant: p-value≈ .59.121C10.3 Adding log(prgnp) to equation (10.38) givesprepop= -6.66 - .212 log(mincov t) + .486 log(usgnp t) + .285 log(prgnp t)log()t(1.26) (.040) (.222) (.080)-.027 t(.005)n = 38, R2 = .889, 2R = .876.The coefficient on log(prgnp t) is very statistically significant (t statistic≈ 3.56). Because the dependent and independent variable are in logs, the estimated elasticity of prepop with respect to prgnp is .285. Including log(prgnp) actually increases the size of the minimum wage effect: the estimated elasticity of prepop with respect to mincov is now -.212, as compared with -.169 in equation (10.38).C10.4 If we run the regression of gfr t on pe t, (pe t-1–pe t), (pe t-2–pe t), ww2t, and pill t, the coefficient and standard error on pe t are, rounded to four decimal places, .1007 and .0298, respectively. When rounded to three decimal places we obtain .101 and .030, as reported in the text.C10.5 (i) The coefficient on the time trend in the regression of log(uclms) on a linear time trend and 11 monthly dummy variables is about -.0139 (se≈ .0012), which implies that monthly unemployment claims fell by about 1.4% per month on average. The trend is very significant. There is also very strong seasonality in unemployment claims, with 6 of the 11 monthly dummy variables having absolute t statistics above 2. The F statistic for joint significance of the 11 monthly dummies yields p-value≈ .0009.(ii) When ez is added to the regression, its coefficient is about -.508 (se≈ .146). Because this estimate is so large in magnitude, we use equation (7.10): unemployment claims are estimated to fall 100[1 – exp(-.508)] ≈ 39.8% after enterprise zone designation.(iii) We must assume that around the time of EZ designation there were not other external factors that caused a shift down in the trend of log(uclms). We have controlled for a time trend and seasonality, but this may not be enough.C10.6 (i) The regression of gfr t on a quadratic in time givesˆgfr= 107.06 + .072 t- .0080 t2t(6.05) (.382) (.0051)n = 72, R2 = .314.Although t and t2 are individually insignificant, they are jointly very significant (p-value≈ .0000).122。