和倍问题必背知识点

小学数学必背知识点汇总小数的基本性质：在小数末尾添上零或者去掉零，小数的大小不变。

分数的基本性质：分数的分子和分母都乘以或者除以相同的数（零除外），分数的大小不变。

比的基本性质：比的前项和后项都乘以或者除以相同的数（零除外），比值不变。

比例的基本性质：在比例里，两个外项的积等于两个内项的积。

比例尺=图上距离÷实际距离（单位要相同）商不变的性质：在除法里，被除数和除数都乘以或者除以相同的数（零除外），商的大小不变。

税后利息=本金×存款时间×利率×（1-20%）运算定律及性质加法交换律：a＋b＝b＋a加法结合律：a＋b＋c＝a＋(b＋c)减法的性质：a－b－c＝a－（b＋c）乘法交换律：a×b＝b×a乘法结合律：a×b×c＝a×(b×c)乘法分配律：(a＋b) ×c＝a×c＋b×c连减简便计算：a-b-c=a-(b+c)；连除简便计算：a÷b÷c=a÷(b×c)积不变的性质：a×b＝(a×c)×( b÷c)除法的性质：a÷b÷c＝a÷(b×c)商不变的性质：a÷b＝(a÷c) ÷(b÷c)、a÷b＝(a×c) ÷(b×c)数的整除1．因数和倍数：如果数 a 能被数 b 整除，a就叫做 b 的倍数，b就叫做 a 的因数。

（如：20÷5=4 20是5和4的倍数；5和4是20的因数）2．质数（素数）：一个数除了1和它本身，不再有别的因数，这样的数叫做质数（素数）。

（如：2、3、5、7、11、13……）3．合数：一个数除了1和它本身，还有别的因数，这样的数叫做合数。

（如：4、6、8、9、……）．互质数：公因数只有1的两个数，叫做互质数。

三年级数学上册第五单元的必背知识点一、倍的概念1.定义：“倍”是由两个数量相比较而产生的，表示一个数是另一个数的几份。

例如，A是B的3倍，即A有3个B 那么多。

2.标准量：在比较两个数量时，作为比较基准的数称为“标准量”（或“一倍数”）。

3.比较量：与标准量相比较的数称为 “比较量”（或 “多倍数”）。

二、倍的计算1.求一个数是另一个数的几倍：使用除法计算。

例如，求72是8的几倍，列式为72 ÷8 = 9，即72是8的9倍。

注意：倍数关系不带单位。

2.求一个数的几倍是多少：使用乘法计算。

例如，求5的7倍是多少，列式为5 ×7 = 35。

3.求比一个数的几倍多几或少几的数是多少：使用乘加或乘减计算。

例如，求比4的6倍多10的数是多少，列式为4 ×6 + 10 = 34；求比6的9倍少12的数是多少，列式为6 ×9 - 12 = 32。

三、实际应用1.解决实际问题：通过理解“倍”的概念，能够解决与“倍”相关的实际问题，如比较两个数量的多少、计算某个数量的几倍是多少等。

2.情境理解：在具体情境中理解 “倍”的含义，如通过实物操作、图形展示等方式帮助学生形成直观的认识。

四、其他相关知识点1.钟表知识：钟面上有3根针：时针、分针、秒针。

时针走1大格是1小时；分针走1大格是5分钟，走1圈是60分钟 （即1小时）；秒针走1大格是5秒钟，走1圈是60秒（即1分钟）。

时间的进率：1时=60分，1分=60秒。

2.解决问题策略：从条件想起：明确题目中的已知条件和需要解决的问题。

确定解题步骤：根据已知条件逐步推导未知条件。

列式计算或画图辅助理解：通过列式计算或画图来辅助解题过程。

总结三年级数学上册第五单元的核心知识点是 “倍”的概念及其相关计算和应用。

学生需要掌握倍的定义、计算方法和实际应用技巧，并能够解决与倍相关的实际问题。

五年级下册重要数学知识点五年级下册重要数学知识点第一单元小数乘法1、小数乘整数：@意义——求几个相同加数的和的简便运算。

如：1.5×3表示求3个1.5的和的简便运算(或1.5的3倍是多少)。

@计算方法：先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。

2、小数乘小数：@意义——就是求这个数的几分之几是多少。

如：1.5×0.8就是求1.5的十分之八是多少(或求1.5的1.8倍是多少)。

@计算方法：先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。

注意：按整数算出积后，小数末尾的0要去掉，也就是把小数化简;位数不够时，要用0占位。

3、规律：一个数(0除外)乘大于1的数，积比原来的数大;一个数(0除外)乘小于1的数，积比原来的数小。

4、求近似数的方法一般有三种：⑴四舍五入法; ⑵进一法; ⑶去尾法5、计算钱数，保留两位小数，表示计算到分;保留一位小数，表示计算到角。

6、小数四则运算顺序和运算定律跟整数是一样的。

7、运算定律和性质：@ 加法：加法交换律：a+b=b+a加法结合律:(a+b)+c=a+(b+c)@ 减法：a-b-c=a-(b+c)a-(b+c)=a-b-c@ 乘法：乘法交换律：a×b=b×a乘法结合律：(a×b)×c=a×(b×c)乘法分配律：(a+b)×c=a×c+b×c【(a-b)×c=a×c-b×c】@ 除法：a÷b÷c=a÷(b×c)a÷(b×c) =a÷b÷c第二单元位置1、数对：由两个数组成，中间用逗号隔开，用括号括起来。

括号里面的数由左至右分别为列数和行数，即“先列后行”。

五年级数学下《因数与倍数》知识点总结归纳
一、因数和倍数的概念
1.因数：整数A除以整数B（B≠0）的商正好是整数而没有余数，我们就说B
是A的因数。

2.倍数：整数A除以整数B（B≠0）的商是整数，并且商是C，我们就说A是
B的C倍。

3.找一个数的因数和倍数的方法：一个数的因数是有限的，最小的因数是1，最大
的因数是它本身。

一个数的倍数的个数是无限的，最小的倍数是它本身，没有最大的倍数。

二、2、3、5的倍数的特征
1.2的倍数的特征：个位上是0、2、4、6、8的数都是2的倍数。

2.3的倍数的特征：各位上的数字之和是3的倍数，这个数一定是3的倍数。

3.5的倍数的特征：个位上是0或5的数都是5的倍数。

三、质数和合数
1.质数：一个数如果只有1和它本身两个因数，这样的数叫做质数（或素数）。

例如：2、3、5、7都是质数。

2.合数：一个数如果除了1和它本身还有别的因数，这样的数叫做合数。

例如：
4、6、8都是合数。

3.1不是质数也不是合数。

4.常见的质数有：2、3、5、7。

小学六年级必背公式　1.每份数×份数=总数 总数÷每份数=份数 总数÷份数=每份数 2.1倍数×倍数=几倍数 几倍数÷1倍数=倍数 几倍数÷倍数=1倍数 3.速度×时间=路程 路程÷速度=时间 路程÷时间=速度 4.单价×数量=总价 总价÷单价=数量 总价÷数量=单价 5.工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间 工作总量÷工作时间=工作效率 6加数+加数=和 和-一个加数=另一个加数 7被减数-减数=差 被减数-差=减数 差+减数=被减数 8因数×因数=积 积÷一个因数=另一个因数 9被除数÷除数=商 被除数÷商=除数 商×除数=被除数 小学数学图形计算公式 1.正方形 C周长S面积a边长 周长=边长×4 C=4a 面积=边长×边长 S=a×a 2.正方体 V:体积a:棱长 表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长 V=a×a×a 3.长方形 C周长S面积a边长 周长=(长+宽)×2 C=2(a+b) 面积=长×宽 S=ab 4.长方体 V:体积s:面积a:长b:宽h:高 (1)表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh) (2)体积=长×宽×高 V=abh 5.三角形 s面积a底h高 面积=底×高÷2 s=ah÷2 三角形高=面积×2÷底 三角形底=面积×2÷高 6.平行四边形 s面积a底h高 面积=底×高 s=ah 7.梯形 s面积a上底b下底h高 面积=(上底+下底)×高÷2 s=(a+b)×h÷2 8圆形 S面积C周长∏d=直径r=半径 (1)周长=直径×∏=2×∏×半径 C=∏d=2∏r (2)面积=半径×半径×∏ 9.圆柱体 v:体积h:高s;底面积r:底面半径c:底面周长 (1)侧面积=底面周长×高 (2)表面积=侧面积+底面积×2 (3)体积=底面积×高 (4)体积=侧面积÷2×半径 10.圆锥体 v:体积h:高s;底面积r:底面半径 体积=底面积×高÷3 11.和差问题的公式 总数÷总份数=平均数 (和+差)÷2=大数 (和-差)÷2=小数 12.和倍问题 和÷(倍数-1)=小数 小数×倍数=大数 (或者和-小数=大数) 13.差倍问题 差÷(倍数-1)=小数 小数×倍数=大数 (或小数+差=大数) 14.植树问题： 1)非封闭线路上的植树问题主要可分为以下三种情形: ⑴如果在非封闭线路的两端都要植树,那么: 株数=段数+1=全长÷株距-1 全长=株距×(株数-1) 株距=全长÷(株数-1)#p#副标题#e# ⑵如果在非封闭线路的一端要植树,另一端不要植树,那么: 株数=段数=全长÷株距 全长=株距×株数 株距=全长÷株数 ⑶如果在非封闭线路的两端都不要植树,那么: 株数=段数-1=全长÷株距-1 全长=株距×(株数+1) 株距=全长÷(株数+1) 2)封闭线路上的植树问题的数量关系如下 株数=段数=全长÷株距 全长=株距×株数 株距=全长÷株数 15.盈亏问题： (盈+亏)÷两次分配量之差=参加分配的份数 (大盈-小盈)÷两次分配量之差=参加分配的份数 (大亏-小亏)÷两次分配量之差=参加分配的份数 16.相遇问题： 相遇路程=速度和×相遇时间 相遇时间=相遇路程÷速度和 速度和=相遇路程÷相遇时间 17.追及问题： 追及距离=速度差×追及时间 追及时间=追及距离÷速度差 速度差=追及距离÷追及时间 18.流水问题： 顺流速度=静水速度+水流速度 逆流速度=静水速度-水流速度 静水速度=(顺流速度+逆流速度)÷2 水流速度=(顺流速度-逆流速度)÷2 19.浓度问题： 溶质的重量+溶剂的重量=溶液的重量 溶质的重量÷溶液的重量×100%=浓度 溶液的重量×浓度=溶质的重量 溶质的重量÷浓度=溶液的重量 20.利润与折扣问题： 利润=售出价-成本 利润率=利润÷成本×100%=(售出价÷成本-1)×100% 涨跌金额=本金×涨跌百分比 折扣=实际售价÷原售价×100%(折扣<1) 利息=本金×利率×时间 税后利息=本金×利率×时间×(1-20%)。

求一个数的因数和倍数（教案）一、教学背景分析数学作为一种基础学科，是各学科必不可少的一门学科。

在小学数学教育中，求任意一个数的因数和倍数是一个非常重要的知识点，它是基础知识的重要组成部分，也是学习数学的必备知识。

作为老师，教师需要对本学科的知识点进行细致的剖析，了解学生能够掌握的能力，将它们基本有机合理地组织在教学中。

接下来，我将结合“求一个数的因数和倍数”的知识点进行分析。

二、教学目标与内容1. 教学目标：通过本节课的学习，学生能够：(1) 理解“因数”和“倍数”的概念。

(2) 了解如何找到一个数的所有因数和倍数。

(3)掌握如何用公式求出一个数的因数和倍数。

(4) 认识因数和倍数在实际生活中的应用。

2. 教学内容：(1) 概念的讲解：因数和倍数分别是什么？(2)方法的讲解：如何求一个数的因数和倍数？(3)公式的介绍：如何用公式求一个数的因数和倍数？(4)实例操作的演示：通过实例来巩固所学知识。

(5)应用实例的分析：将因数和倍数的知识点与实际生活中的应用结合起来。

三、教学重点与难点1.教学重点：(1) 理解因数和倍数的概念。

(2) 通过公式巩固和深化对因数和倍数的理解。

(3) 运用因数和倍数的知识点解决实际问题。

2.教学难点：(1) 让学生理解因数和倍数的概念。

(2) 让学生掌握用公式求一个数的因数和倍数的方法。

(3) 让学生能够运用因数和倍数的知识点解决实际问题。

四、教学方法1. 综合运用教学方法课堂教学采用综合运用教学的方法，以板书讲解、练习题操作和案例分析等方式相结合，有助于深入学生的理解和巩固知识。

2. 案例分析法案例分析法是在实际生活中提取和总结出来的一系列典型问题，主要是为了解决某个特定问题而建立的。

本课程中，将以解决一些实际问题的例子来演示如何用因数和倍数的知识解决实际问题。

五、教学过程1.前言首先，介绍本节课的教学目标和目的，让学生知道本节课要学习的知识点和教师的教学重点。

2.导入通过一些问题提出学习本节课的主题：“求一个数的因数和倍数”。

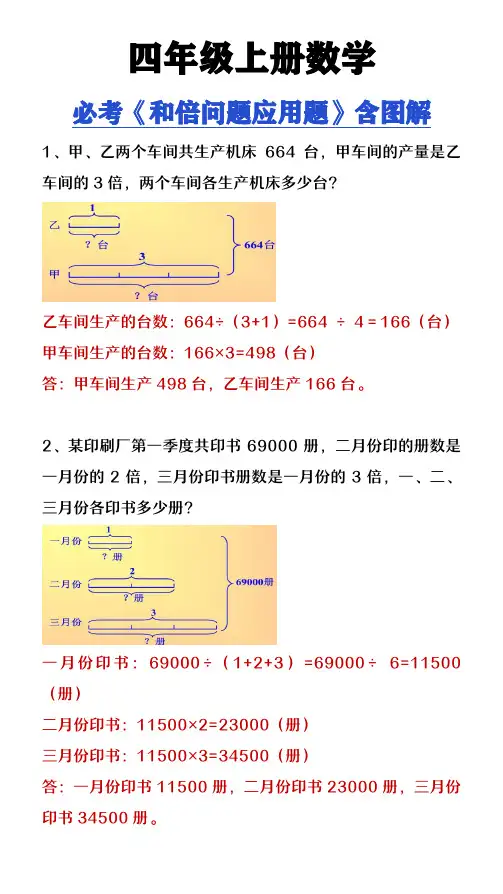
四年级上册数学必考《和倍问题应用题》含图解1、甲、乙两个车间共生产机床664台，甲车间的产量是乙车间的3倍，两个车间各生产机床多少台？乙车间生产的台数：664÷（3+1）=664 ÷4＝166（台）甲车间生产的台数：166×3=498（台）答：甲车间生产498台，乙车间生产166台。

2、某印刷厂第一季度共印书69000册，二月份印的册数是一月份的2倍，三月份印书册数是一月份的3倍，一、二、三月份各印书多少册？一月份印书：69000÷（1+2+3）=69000÷6=11500（册）二月份印书：11500×2=23000（册）三月份印书：11500×3=34500（册）答：一月份印书11500册，二月份印书23000册，三月份印书34500册。

3、饲养场公鸡、母鸡共4150只，其中母鸡只数是公鸡只数的4倍，求公鸡、母鸡各养了多少只?公鸡只数：4150÷（1+4）=4150÷5＝830（只）母鸡只数：830×4=3320（只）答：养公鸡830只，养母鸡3320只。

4、一辆汽车运进大米和面粉共3200千克，其中大米的重量是面粉的3倍，运进大米和面粉各多少千克?面粉重量：3200÷（1+3）=3200 ÷4=800（千克）大米重量：800×3=2400（千克）答：运进大米2400千克，运进面粉800千克。

5、甲、乙二人共存款3510元，甲的存款是乙的2倍，甲、乙各存款多少元?乙存款钱数：3510÷（1+2）=3510÷3＝1170（元）甲存款钱数：1170×2=2340（元）答：甲存款2340元，乙存款1170元。

三年级数学必背知识点打印三年级数学上册数学必背知识点第一单元时、分、秒计量很短的时间，常用比分更小的单位——秒。

时间单位：1时=60分 1分=60秒 1时=3600秒开始时刻+时间=结束时刻结束时刻-开始时刻=时间结束时刻-时间=开始时刻1、钟面上有（12）个大格，每个大格分成（5 ）小格。

钟面上一共有（60 ）个小格。

2、时针走1大格是（1小时），分针正好走（一圈），是（60分）。

时针走一圈是（12时），走两圈是（24时），正好是（一日）。

3、分针走1小格是（1分），分针走1大格是（5分）。

分针走一圈是（60分），也是（1小时）。

4、秒针走1小格是（1秒），秒针走1大格是（5秒）。

秒针走一圈是（60秒），也是（1分钟）。

第二、四单元万以内的加法和减法笔算多位数加法法则：1、相同数位要对齐；2、从个位加起；3、哪一位上相加满十，就向前一位进一。

笔算多位数减法法则：1、相同数位要对齐；2、从个位减起；3、哪一位上不够减，就向前一位退一，在本位上加十再减。

加法的验算方法：加数+加数=和（1）和－加数=另一个加数（2）交换加数的位置和不变。

减法的验算方法：被减数－减数=差（1）差+减数=被减数（2）被减数－差=减数0加任何数都等于任何数。

第三单元测量（一）我们学过的长度单位有：千米（km）、米（m）、分米（dm）、厘米（cm）、毫米（mm）。

1千米=1000米1米=10分米1分米=10厘米 1厘米=-10毫米1米=100厘米 1分米=100毫米1米=-1000毫米量比较短的物体长度或者要求量得比较精确时，可以用“毫米”作单位。

量物体的长度有时也用“分米”作单位。

计量比较长的路程，通常用“千米”作单位。

一拃（zha）长大约是1分米，一个手指的宽大约是1厘米，一枚硬币的厚度大约是1毫米。

千米（也叫公里）是比米大的长度单位，运动场的跑道通常1圈是400米，2圈半正好是1千米。

（二）我们学过的质量单位有吨（t）、千克（kg）、克（g）。

数学三年级上册【必背知识点】第1单元时分秒1、钟面上有3根针，它们是（时针）、（分针）、（秒针），其中走得最快的是（秒针），走得最慢的是（时针）。

2、钟面上有(12)个数字，(12)个大格，(60)个小格；每两个数间是(1)个大格，也就是(5)个小格。

3、时针走1大格是(1)小时；分针走1大格是(5)分钟，走1小格是( 1)分钟；秒针走1大格是(5)秒钟，走1小格是(1)秒钟。

4、时针走1大格，分针正好走(1)圈，分针走1圈是(60)分，也就是(1)小时。

时针走1圈，分针要走(12)圈。

5、分针走1小格，秒针正好走(1)圈，秒针走1圈是(60)秒，也就是(1)分钟。

6、时针从一个数走到下一个数是(1小时)。

分针从一个数走到下一个数是(5分钟)。

秒针从一个数走到下一个数是(5秒钟)。

7、钟面上时针和分针正好成直角的时间有：（3点整）、（9点整）。

8、公式。

（每两个相邻的时间单位之间的进率是60）1时=60分 1分=60秒半时=30分 60分=1时 60秒=1分 30分=半时第2、4单元万以内的加法和减法1、认识整千数（记忆： 10个一千是一万）2、读数和写数（读数时写汉字写数时写阿拉伯数字）①一个数的末尾不管有一个0或几个0，这个0都不读。

②一个数的中间有一个0或连续的两个0，都只读一个0。

3、数的大小比较：①位数不同的数比较大小，位数多的数大。

②位数相同的数比较大小，先比较这两个数的最高位上的数，如果最高位上的数相同，就比较下一位，以此类推。

4、三位数的连续进位加法的运算步骤：①列竖式时相同数位一定要对齐；②从个位加起③哪一位上的数相加满10，则向前一位进1。

5、三位数的连续退位减法的运算步骤：①列竖式时相同数位一定要对齐；②从个位减起③哪一位上的数不够减，从前一位退1；如果前一位是0，则再从前一位退1。

6、在做题时，我们要注意中间的0，因为是连续退位的，所以从百位退1到十位当10后，还要从十位退1当10，借给个位，那么十位只剩下9，而不是10。

公式1.和差问题是指知道两个数的“和”与“差”，要求这两个数，基本公式有：大数=（和+差）÷2，小数=（和-差）÷2；2.和倍问题是指知道两个数的“和”与“倍”，要求这两个数，基本公式有：小数=和÷（倍数+1），大数=和-小数或大数=小数×倍数；3.差倍问题是指知道两个数的“差”与“倍”，要求这两个数，基本公式有：小数=差÷（倍数-1），大数=小数+差或大数=小数×倍数。

我们先普及一个知识点：一个数是另一个数的a倍，也就说一个数比另一个数多（a-1）倍（现在有些读六年级的学生都不知道这个知识点）。

一、和倍问题1、商店运来苹果和梨共185千克，如果苹果再运15千克就相当于梨的3倍，这个商店运来苹果和梨各多少千克？2、汽车运输队第一运输队有20部汽车，第二运输队有10部汽车。

要使第一队的汽车是第二队的4倍，第二队应当调几部汽车给第一队？3、两数相除商和余数都是5，被除数、除数、商和余数的和是129，求被除数、除数分别是多少？4、兄弟俩各有一些钱，哥哥的钱比弟弟多4500元，国庆那天，他们都拿出2000元去合买了一台彩电。

这时，哥哥的钱恰好是弟弟的4倍，哥弟俩原来各有多少钱？5、四（3）班有学生50人，若女生增加14人，男生增加2人，女生的人数就是男生的2倍。

求四（3）班男、女学生各有多少人？6、三，四年级共有学生165人，三年级学生比四年级学生人数的2倍少6人，三，四年级学生各有多少人？7、三年级一班有学生48人，如果再转来3名男生，那么男生的人数就正好是女生的2倍，三年级一班有男生多少人？8、两筐鸭梨共重154千克，其中第一筐比第二筐的2倍少14千克，求两筐鸭梨各有多少千克？9、姐姐和妹妹共有人民币264元，姐姐的钱数的个位是0，如果姐姐把自己的钱数的个位上的0去掉，恰好和妹妹的钱数相等，姐姐妹妹各有人民币多少元？10、把一个减法算式里的被减数，减数与差相加，得数是990，已知减数是差的2倍，减数是多少？二、差倍问题1、南街村种花生公顷数是玉米的8倍，花生比玉米多种63公顷。

34个奥数解题公式34个小学奥数“必考”公式，打印贴墙背，6年数学“不慌张”！数学是一门十分重视根底的学科，小学数学正是孩子打根底的最好阶段，而小学数学中，应用题一直是考试中的重难点。

1．和差倍问题和差问题和倍问题差倍问题已知条件几个数的和与差几个数的和与倍数几个数的差与倍数公式适用范围已知两个数的和，差，倍数关系公式①(和－差)÷2=较小数较小数＋差=较大数和－较小数=较大数②(和＋差)÷2=较大数较大数－差=较小数和－较大数=较小数和÷(倍数＋1)=小数小数×倍数=大数和－小数=大数差÷(倍数-1)=小数小数×倍数=大数小数＋差=大数关键问题求出同一条件下的和与差和与倍数差与倍数2．年龄问题的三个基本特征：①两个人的年龄差是不变的；②两个人的年龄是同时增加或者同时减少的；③两个人的年龄的倍数是发生变化的；3．归一问题的基本特点：问题中有一个不变的量，一般是那个“单一量”，题目一般用“照这样的速度”……等词语来表示。

关键问题：根据题目中的条件确定并求出单一量；4．植树问题基本类型在直线或者不封闭的曲线上植树，两端都植树在直线或者不封闭的曲线上植树，两端都不植树在直线或者不封闭的曲线上植树，只有一端植树封闭曲线上植树基本公式棵数=段数＋1棵距×段数=总长棵数=段数－1棵距×段数=总长棵数=段数棵距×段数=总长关键问题：确定所属类型，从而确定棵数与段数的关系5．鸡兔同笼问题基本概念：鸡兔同笼问题又称为置换问题、假设问题，就是把假设错的那部分置换出来；基本思路：①假设，即假设某种现象存在（甲和乙一样或者乙和甲一样）：②假设后，发生了和题目条件不同的差，找出这个差是多少；③每个事物造成的差是固定的，从而找出出现这个差的原因；④再根据这两个差作适当的调整，消去出现的差。

基本公式：①把所有鸡假设成兔子：鸡数＝（兔脚数×总头数－总脚数）÷（兔脚数－鸡脚数）②把所有兔子假设成鸡：兔数＝（总脚数一鸡脚数×总头数）÷（兔脚数一鸡脚数）关键问题：找出总量的差与单位量的差。

小学六年级必背公式1.每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2.1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3.速度×时间=路程路程÷速度=时间路程÷时间=速度4.单价×数量=总价总价÷单价=数量总价÷数量=单价5.工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6加数+加数=和和-一个加数=另一个加数7被减数-减数=差被减数-差=减数差+减数=被减数8因数×因数=积积÷一个因数=另一个因数9被除数÷除数=商被除数÷商=除数商×除数=被除数小学数学图形计算公式1.正方形C周长S面积a边长周长=边长×4C=4a面积=边长×边长S=a×a2.正方体V:体积a:棱长表面积=棱长×棱长×6S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3.长方形C周长S面积a边长周长=(长+宽)×2C=2(a+b)面积=长×宽S=ab4.长方体V:体积s:面积a:长b:宽h:高(1)表面积=(长×宽+长×高+宽×高)×2S=2(ab+ah+bh)(2)体积=长×宽×高V=abh5.三角形s面积a底h高面积=底×高÷2s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6.平行四边形s面积a底h高面积=底×高s=ah7.梯形s面积a上底b下底h高面积=(上底+下底)×高÷2s=(a+b)×h÷28圆形S面积C周长∏d=直径r=半径(1)周长=直径×∏=2×∏×半径C=∏d=2∏r(2)面积=半径×半径×∏9.圆柱体v:体积h:高s;底面积r:底面半径c:底面周长(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高(4)体积=侧面积÷2×半径10.圆锥体v:体积h:高s;底面积r:底面半径体积=底面积×高÷311.和差问题的公式总数÷总份数=平均数(和+差)÷2=大数(和-差)÷2=小数12.和倍问题和÷(倍数-1)=小数小数×倍数=大数(或者和-小数=大数)13.差倍问题差÷(倍数-1)=小数小数×倍数=大数(或小数+差=大数)14.植树问题：1)非封闭线路上的植树问题主要可分为以下三种情形:⑴如果在非封闭线路的两端都要植树,那么:株数=段数+1=全长÷株距-1全长=株距×(株数-1)株距=全长÷(株数-1)#p#副标题#e#⑵如果在非封闭线路的一端要植树,另一端不要植树,那么:株数=段数=全长÷株距全长=株距×株数株距=全长÷株数⑶如果在非封闭线路的两端都不要植树,那么:株数=段数-1=全长÷株距-1全长=株距×(株数+1)株距=全长÷(株数+1)2)封闭线路上的植树问题的数量关系如下株数=段数=全长÷株距全长=株距×株数株距=全长÷株数15.盈亏问题：(盈+亏)÷两次分配量之差=参加分配的份数(大盈-小盈)÷两次分配量之差=参加分配的份数(大亏-小亏)÷两次分配量之差=参加分配的份数16.相遇问题：相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间17.追及问题：追及距离=速度差×追及时间追及时间=追及距离÷速度差速度差=追及距离÷追及时间18.流水问题：顺流速度=静水速度+水流速度逆流速度=静水速度-水流速度静水速度=(顺流速度+逆流速度)÷2水流速度=(顺流速度-逆流速度)÷219.浓度问题：溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量20.利润与折扣问题：利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成本-1)×100%涨跌金额=本金×涨跌百分比折扣=实际售价÷原售价×100%(折扣<1)利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%)。

公务员考试必背公式大全第一章 数量关系一、计算问题1.等差数列：记第一项为a 1，第n 项为a n ，公差为d ，则有 通项公式：a n =a 1+（n-1）×d ，a n =a m +（n-m ）×d ； 等差数列求和公式：S n =a 1n+⨯−d n n 2(1)=⨯+n a a n 21=n 中a 。

2.等比数列：记第一项为a 1，第n 项为a n ，公比为q ，则有 通项公式：a n =a 1−q n 1，a n =a m −q n m ；等比数列求和公式：S n =−qa q n 1-(1)1=−q a a qn 1-1（q ≠1）。

3.分式的裂项公式：+n n (1)1=n 1-+n 11+n n d (1)=(n 1-+n 11)×d+=−+n n d d n n d1()1(11)4.基础计算公式：平方差公式：−=+−a b a b a b 22()() 完全平方公式：±=±+a b a ab b ()2222立方和与立方差公式： ±=±+a b a b a ab b 3322()()5.正约数的个数公式：设将自然数n 进行质因数分解得n=n n p p p ααα1212，则n 的正约数个数为(1)(1)(1)n ααα+++12。

二、利润问题1.利润=售价-成本当售价大于成本时，赢利，反之，亏损，此时商品利润用负数表示。

2.利润率利润成本售价成本成本（售价成本）=⨯=⨯=⨯100%-100%-1100% 推出公式：①售价=成本×（1+利润率） ②成本=1+售价利润率3.折扣=打折后的售价原来的售价=11⨯+⨯+成本（后来的利润率）成本（原来的利润率）=11++后来的利润率原来的利润率三、行程问题设路程为S ，速度为v ，时间为t ，则S=vt 。

1.平均速度公式：=平均速度总路程总时间等距离平均速度公式：平均速度=+v v v v 212122.普通行程：S 一定，v 与t 成反比；v 一定，S 与t 成正比；t 一定，S 与v 成正比。

数量关系—数学运算 必背 资料整理（一） 数的整除特性 一、数的整除检定被被被被被二、数的整除性质1．如果两个整数a 、b 都能被c 整除，那么a+b ／a-b 也能被c 整除2．如果两个整数a 、b 都不能被c 整除．那么a 与b 的和（或差）能或不能被c 整除．这是一个不肯定的结论。

3．如果整数a 能被c 整除，ｍ为任意整数，那么am 也能被c 整除4．如果a 、b 、c 这三个数中，a 能被b 整除，b 又能被c 整除，那么a 一定能被c 整除（这是整除的传递性）．5. 如果a 能被b 整除，a 又能被c 整除，且b 和c 互质，那么a 能被bc 整除 （二）数的约数和倍数（对于求大数之间的最大公约数问题，一般采用辗转相除法） EG ：6731÷2809＝2……1113；2809÷1113＝2……583； 1113÷583＝1……530 ； 583÷530＝1……53 ； 530÷53＝10所以6731和2809的最大公因数是53（三）同余与剩余问题一、余数性质：1．基本公式：被除数=除数³商+余数2．余数总是小于除数，即0≤d＜b二、同余问题：1．两个整数a、b,若他们除以m所得的余数相同，则称a与b对于m同余，或称a与b同余。

EG：23÷5余3；18÷5余3；则23与15同余。

2．对于同一个除数m,两个数和（差、积）的余数与余数的和同余。

EG:15÷7余1；18÷7余4；则：18+15=33,1+4=5,33÷7的余数与5同余。

18-15=3, 4-1=3,3÷7的余数与3同余。

18³15=270,1³4=4,270÷7的余数与4同余。

三、剩余问题：1．同时满足被A整除余X，被B整除余Y……的数可以表示为nk+m，其中k为A、B的最小公倍数，m为同时满足被A整除余X，被B整除余Y……的最小的整数。

小学奥数必背公式和相关知识点题型一：归一问题【含义】在解题时先求出一份是多少（即单一量），然后以单一量为标准，求出所要求的数量。

【数量关系】总量÷份数=单一量单一量×所占份数=所求几份的数量或总量A÷（总量B÷份数B）=份数A【解题思路】先求出单一量，以单一量为标准，求出所要求的数量。

【例】买5支铅笔需要0.6元钱，买同样的铅笔16支，需要多少钱？解：先求出一支铅笔多少钱——0.6÷5=0.12（元）再求买16支铅笔需要多少钱——0.12×16=1.92（元）综合算式：0.6÷5×16=0.12×16=1.92（元）题型二：归总问题【含义】解题时先找出“总数量”，再根据已知条件解决问题的题型。

所谓“总数量”可以指货物总价、几天的工作量、几亩地的总产量、几小时的总路程等。

【数量关系】1份数量×份数=总量总量÷一份数量=份数【解题思路】先求出总数量，再解决问题。

【例】服装厂原来做一套衣服用布3.2米，改进剪裁方法后，每套衣服用布2.8米。

问原来做791套衣服的布，现在可以做多少套衣服？解：先求这批布总共多少米——3.2×791=2531.2（米）再求现在可以做多少套——2531.2÷2.8=904（套）综合算式：3.2×791÷2.8=904（套）题型三：和差问题【含义】已知两个数量的和与差，求这两个数量各是多少。

【数量关系】大数=（和+差）÷2小数=（和－差）÷2【解题思路】简单题目直接套用上述公式，复杂题目变通后再套用公式。

【例1】某机床厂第一、二两个车间共有车床96部，如果第一车间拨给第二车间8部，那么两个车间车床数相等。

两个车间各有车床多少部？解：已知第一、二两个车间共有车床96部，又根据“如果第一车间拨给第二车间8部，两个车间车床数相等”，从线段图上我们可以看出第一车间原来比第二车间多8×2=16部车床。

小学数学公式大全总结必背公式以下是小学数学公式汇总（人教版）：1.每份数×份数＝总数；总数÷每份数＝份数；总数÷份数＝每份数。

2.倍数×倍数＝几倍数；几倍数÷1倍数＝倍数；几倍数÷倍数＝1倍数。

3.速度×时间＝路程；路程÷速度＝时间；路程÷时间＝速度。

4.单价×数量＝总价；总价÷单价＝数量；总价÷数量＝单价。

5.工作效率×工作时间＝工作总量；工作总量÷工作效率＝工作时间；工作总量÷工作时间＝工作效率。

6.加数＋加数＝和；和－一个加数＝另一个加数。

7.被减数－减数＝差；被减数－差＝减数；差＋减数＝被减数。

8.因数×因数＝积；积÷一个因数＝另一个因数。

9.被除数÷除数＝商；被除数÷商＝除数；商×除数＝被除数。

以下是小学数学图形计算公式：1.正方形：C周长，S面积，a边长；周长＝边长×4，C=4a；面积=边长×边长，S=a×a。

2.正方体：V体积，a棱长；表面积=棱长×棱长×6，S表=a×a×6；体积=棱长×棱长×棱长，V=a×a×a。

3.长方形：C周长，S面积，a边长；周长=(长+宽)×2，C=2(a+b)；面积=长×宽，S=ab。

4.长方体：V体积，s面积，a长，b宽，h高；表面积=(长×宽+长×高+宽×高)×2，S=2(ab+ah+bh)；体积=长×宽×高，V=abh。

5.三角形：s面积，a底，h高；面积=底×高÷2，s=ah÷2；三角形高=面积×2÷底，三角形底=面积×2÷高。

小学数学公式大全1、长方形的周长=（长+宽）×2 C=(a+b)×22、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽 S=ab4、正方形的面积=边长×边长 S=a×a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高 S=ah7、梯形的面积=（上底+下底）×高÷2 S=（a＋b）h÷28、直径=半径×2 d=2r 半径=直径÷2 r= d÷29、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr10、圆的面积=圆周率×半径×半径 s=πr211、长方体的表面积=（长×宽+长×高＋宽×高）×212、长方体的体积 =长×宽×高 V =abh13、正方体的表面积=棱长×棱长×6 S =6a×a14、正方体的体积=棱长×棱长×棱长 V=a.a.a= a15、圆柱的侧面积=底面圆的周长×高 S=ch16、圆柱的表面积=上下底面面积+侧面积S=2πr +2πrh=2π(d÷2) +2π(d÷2)h=2π(C÷2÷π) +Ch 17、圆柱的体积=底面积×高 V=ShV=πr h=π(d÷2) h=π(C÷2÷π) h18、圆锥的体积=底面积×高÷3V=Sh÷3=πr h÷3=π(d÷2) h÷3=π(C÷2÷π) h÷3小学数学图形计算公式1 、正方形 C周长 S面积 a边长周长＝边长×4 C=4a 面积=边长×边长 S=a×a2 、正方体 V:体积 a:棱长表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长 V=a×a×a3 、长方形C周长 S面积 a边长周长=(长+宽)×2C=2(a+b)面积=长×宽S=ab4 、长方体V:体积 s:面积 a:长 b: 宽 h:高(1)表面积(长×宽+长×高+宽×高)×2S=2(ab+ah+bh)(2)体积=长×宽×高V=abh5 三角形s面积 a底 h高面积=底×高÷2s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6 平行四边形s面积 a底 h高面积=底×高s=ah7 梯形s面积 a上底 b下底 h高面积=(上底+下底)×高÷2s=(a+b)× h÷28 圆形S面积 C周长 d=直径 r=半径(1)周长=直径×π=2×π×半径C=πd=2πr(2)面积=半径×半径×π9 圆柱体v:体积 h:高 s;底面积 r:底面半径 c:底面周长(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高（4）体积＝侧面积÷2×半径10 圆锥体v:体积 h:高 s;底面积 r:底面半径体积=底面积×高÷3总数÷总份数＝平均数概念1、加法交换律：两数相加交换加数的位置，和不变。