统计学实验报告4.Excel 在抽样推断中的应用

统计学excel实验报告《经济统计学》实验报告【试验目的】通过实验教学，使学生验证并加深理解和巩固课堂教学内容，掌握常用统计分析方法在Excel中的实现，更好的理解和掌握统计分析方法的应用原理、基本条件、实现步骤、结果的内涵等问题。

通过实验，使学生能够结合具体任务和条件对社会经济问题进行初步的调查研究，结合自己的专业，在定性分析基础上做好定量分析，提高学生的科研能力和解决实际问题的能力，以适应社会主义市场经济中各类问题的实证研究、科学决策和经济管理的需要。

【试验内容】Excel中的统计分析功能，包括制作频数分布表和统计图、计算描述统计量、计算置信区间、相关与回归分析、时间序列分析。

试验一: 某百货公司连续40天的商品销售额如图1-1所示，根据图中的数据进行适当的分组，编制频数分布表，并绘制直方图。

图1-1操作步骤:1、根据上表将数据输入2、划分区间范围，如图1-2图1-23、单击“工具”?“数据分析”，弹出对话框，如图1-3图1-34、选择“直方图”，并单击“确定”，弹出对话框，如图1-4图1-4 4、单击“输入区域”的标志，并选定输入区域;单击“接受区域”标志，并选定接受区域。

在“标志”前打对勾，选定“新工作表组”并输入“p60图表输出”，选定“柏拉图”、“累积百分率”、“图表输出”，效果如图1-5图1-55，单击图1-5界面中的“确定”按钮，输出统计结果，如图1-6图1-6在图中显示的统计结果中，可以看见输出的内容分为两部分，一部分是数据表示形式，一部分是直方图形式。

在数据表部分，显示每个区间中的天数及累计百分率数值。

通过该统计结果，我们可以知道，在这40天中有1天的销售额在25万元以下，5天在25~30之间，6天在30~35之间，14天在35~40之间，10天在40~45之间，4天在45~50之间。

试验二: 某大学为了了解学生每天上网的时间，在全校7500名学生中采取不重复抽样方法随即抽取36人，调查他们每天上网的时间，得到以下数据(单位:小时)，求该校大学生平均上网时间的置信区间，置信水平分别为90%、95%和99%。

一．实验目的与要求（一）目的实验一: EXCEL的数据整理与显示1. 了解EXCEL的基本命令与操作、熟悉EXCEL数据输入、输出与编辑方法；2. 熟悉EXCEL用于预处理的基本菜单操作与命令；3. 熟悉EXCEL用于整理与显示的基本菜单操作与命令。

实验二: EXCEL的数据特征描述、抽样推断熟悉EXCEL用于数据描述统计、抽样推断实验三: 时间序列分析掌握EXCEL用于移动平均、线性趋势分析的基本菜单操作与命令。

实验四: 一元线性回归分析掌握EXCEL用于相关与回归分析的基本操作与命令。

（二）要求1.按要求认真完成实验任务中规定的所有练习；2.实验结束后要撰写格式规范的实验报告, 正文统一用小四号字, 必须有页码；3、实验报告中的图表制作要规范, 图表必须有名称和序号；4、实验结果分析既要简明扼要, 又要能说明问题。

二、实验任务实验一根据下面的数据。

1.1用Excel制作一张组距式次数分布表, 并绘制一张条形图(或柱状图), 反映工人加工零件的人数分布情况。

从某企业中按随即抽样的原则抽出50名工人, 以了解该企业工人生产状况（日加工零件数）：117 108 110 112 137 122 131 118 134 114 124 125 123127 120 129 117 126 123 128 139 122 133 119 124 107133 134 113 115 117 126 127 120 139 130 122 123 123128 122 118 118 127 124 125 108 112 135 5091.2整理成频数分布表, 并绘制直方图。

1.3 假设日加工零件数大于等于130为优秀。

实验二百货公司6月份各天的销售额数据如下(单位:万元)257 276 297 252 238 310 240 236 265 278271 292 261 281 301 274 267 280 291 258272 284 268 303 273 263 322 249 269295（1）计算该百货公司日销售额的均值、众数、中位数;（2）计算该百货公司日销售额的极差、标准差;（3）计算日销售额分布的偏态系数和峰度系数。

ｓ ｐ ｏ ｉｉｎ ｘ ｍ ｉ ａｉ ｎ ｃ ｎｅ ｔ ｕ ｐ ｓｔｏ ｅ ａ ｎ ｔ ｏ ｔｎ ． ｏ
Ｋｅ ｒ ｙ ｗｏ ｄ：Ｅ ＸＣ Ｌ ａ ｌ ｇ ｄ ｓｒ ｕ ｉｎ Ｅ ；ｓ ｍｐ ｉ ｉｔ ｂ ｔ ｎ ｉ ｏ
统 计 学 的教 学 中 ， 生 一 般 感 到难 学 ， 学 因这 门
Ａｂ ｔ ａ ｔ Ｓ ｍｐ ｉｇ ｄ ｓｒ ｕ ｉｎ ｉ ａ ｄ ｆ ｃ ｌ ａ ｅ ｌ ａ ｅ ｏｎ ｎ ｔ ｅ ｔａ ｈ ｎ ｆ Ｓａ ｉｔ ｓ ＸＣ Ｌ ｓ ｒ ｃ ： ａ ｌ ｉｔ ｂ ｔ ｓ ｉ ｕ ｔ ｓ ｗ ｌ ｓ ａ ｋ ｙ ｐ ｉ ｔ ｉ ｈ ｅ ｃ ｉ ｇ ｏ ｔｔ ｉ ．Ｅ ｎ ｉ ｏ ｉ ｓｃ Ｅ
ｐ ｉ ｇ ｄ ｓｒ ｕ ｉｎ ｏ ｎ ｔｔ ｎ Ｅ ｉ ｉｔ ｂ ｔ ｃ ｎ ｏ ｉ ． ＸＣＥ ｓ ｈ ｌ ｆ ｌ ｏ ｇ ａ ｐ ａ ｌ ｇ ｉｔ ｂ ｔ ｎ ｐ ｒ ｍｅ ｅ ｓ ｍａ ｉｎ ｎ ｎ ｉ ｏ ａ ｏ Ｌ ｉ ｅｐ ｕ ｔ ｒ ｓ ｍｐ ｉ ｄ ｓｒ ｕ ｉ ， ａ ａ ｔｒ ｅ ｔ ｔ ａ ｄ ｓ ｎ ｉ ｏ ｉ ｏ
22保山师专学报第27卷如果我们感兴趣的是总体的均值可以用一个样本统计量进行估计可以用样本均值样本中位数或样本众数来估计因样本均值具有很好的数学性质无妨用样本均值来进行估计我们知道因样本是随机变量作第一次抽样得样本值x10抛1第二次抽样得到样本值并圆髫2圆
２０ ０ ８年 ９月
保 山师专学报
Ｊ ｕｎ ｌ ｆ ａ ｓ ａ ｅ ｃ ｅ ｏ ｒ ａ ｏ ｈ ｎＴ ａ ｈ ￣ Ｃ ｌ ｇ ｏ Ｂ ｏ ｅｅ ｌ
Ｓ ｐ． ０ ８ ｅｔ ，２ ０
第２ ７卷 第 ５期
Ｖ０ ．７ １ Ｎｏ５ ２ ．
Ｅ ＣＥ 在 抽样分布教 学 中的应用 Ｘ Ｌ

一Байду номын сангаас
赠送礼品，并对抽 出的号码 进行排序。 我们采 用 随机 函数 Ｒ Ｎ Ｂ Ｔ Ｅ Ａ Ｄ Ｅ ＷＥ Ｎ来 实现这
个 随机抽样 ，具体步骤如下： １ 建一个 工作表 “ １ ” ． 新 例 ． ，并命 名表头 “ １ 采 用 随机函数实现简单 随机抽样” 。 ２ ． 设置抽样 区域 的显示格式 ，选择 Ｂ ：１ ３ ２单元 Ｂ 格 区域，作为要 显示抽样 结果 的 １ 单元格 ，右 Ｏ个 击选 中单元格区域，在菜单栏中选择 【 设置单元格 格 式】 ，在 【 单元格格 式】 对话框 的【 数字】 选项卡中 选 择【 自定义】 ，在 【 型】 类 文本 框 中输入 “ ００ ” ０ ００ ， 表 示 ５位数字 ，不足部分 以 “ ”补齐 ，完成后单 ０
（ １ ） 例 ．。 ３
作为样本 ，并根据其数量特征对整体进行推断 。下 面主要介绍随机抽样 ，说明如何确定随机抽样并应 用 Ｅ ｃｌ ｘｅ来进行 随机抽样 ，并在 此基础上确 定随机 样本的大小。
一
例 １ ：某 商场举 行 幸运顾客 抽奖 ，需要从编 ． １
、
随机 抽 样
号 ０ ０ １ ９ ９ ９的顾客中随机抽取 ｌ ００ 到 ９９ Ｏ位幸运顾客
常采用随机数函数产生随机数来实现。
收 稿 日期 ：２ １— ６ １ ０００—２
３ ． 采用 Ｒ Ｎ Ｂ Ｔ Ｅ Ａ Ｄ Ｅ ＷＥ Ｎ函数 抽样，单击 Ｂ ３单 元 格 ， 在 编 辑 栏 中 输 入 “＝ Ａ Ｄ Ｅ ＷＥ Ｎ Ｒ ＮＢＴ Ｅ
ｆ，９９９” ０ ９９），再单击 Ｂ ，运用 自动填充单元格拖动 ３ 鼠标至 Ｂ ２单元格 ，完成 Ｂ ：１ 单元格 自动填充 ， ２ ３ ２ Ｂ
般并不是对 总体 中的所有样本进行逐一测试 ，而

实验三EXCEL在推断统计中的应用一．实验目的：1．掌握Excel的常用函数的使用；2．学会运用Excel进行统计分析。

二．实验要求：1．掌握样本推断总体方法。

2．通过练习，能够构造一张能够实现在总体方差已知情况下进行总体均值假设检验的Excel工作表。

三．实验内容：1．熟练运用Excel的常用函数。

2．了解Excel的图表功能：创建图表、增强图表；3．掌握样本推断总体的方法；4．掌握利用Excel进行假设检验的方法；5、掌握线性回归分析方法。

四．实验步骤：1、样本推断总体⑴构造工作表如附图所示，首先在各个单元格输入以下的内容，左边是变量名，右边是相应的计算公式。

⑵将A列的名称定义成为B列各个公式计算结果的变量名。

选定A4:B6,A8:B8和A10：B15单元格（先用鼠标选择第一部分，再按住CTRL键选取另外两个部分），选择“插入”菜单的“名称”子菜单的“指定”选项，用鼠标点击“最左列”选项，然后点击“确定”按钮即可。

⑶结果说明：以上例子说明如何交叉组合使用Excel的公式和函数，以构造一个能实现样本推断总体有关计算的Excel工作表。

2、假设检验⑴构造工作表。

如图所示，首先在各个单元格输入以下内容，其中左边是变量名，右边是相应的计算公式。

⑵将A列的名称定义成为B列各个公式计算结果的变量名。

选定A3:B4,A6:B8,A10:B11,A13:B15和A17:B19单元格，选择“插入”菜单的“名称”子菜单的“指定”选项，用鼠标点击“确定”按钮即可。

⑶输入样本数据，以及总体标准差、总体均值假设、置信水平数据。

⑷为样本数据指定名称。

选定C1:C11单元格，选择“插入”菜单的“指定”选项，用鼠标点击“首行”选项，然后点击“确定”按钮，得到如下图计算结果。

⑸结果说明：如上图所示，该例子的检验结果不论是单侧还是双侧均为拒绝H0假设。

所以，根据样本的计算结果，在5%的显著水平之下，拒绝总体均值为35的假设。

同时由单侧显著水平的计算结果还可以看出：在总体均值是35的假设之下，样本均值小于等于31.4的概率仅为0.020303562<0.05，小概率事件居然发生，所以，同样得出5%的显著水平下，拒绝总体均值为35的假设的结论。

excel在统计学实验报告Excel在统计学实验报告中的应用统计学实验报告是统计学课程中常见的一种学术写作形式，它旨在通过实验数据的收集和分析，得出科学的结论并进行推断。

在这个过程中，Excel作为一种强大的数据处理工具，可以发挥重要的作用。

本文将探讨Excel在统计学实验报告中的应用，并介绍一些常用的功能和技巧。

一、数据收集与整理在统计学实验中，数据的收集和整理是非常重要的一步。

Excel提供了丰富的数据输入和整理功能，可以帮助我们高效地处理实验数据。

首先，我们可以使用Excel的数据输入工具，将实验数据逐个输入到表格中，确保数据的准确性和完整性。

其次，Excel的筛选和排序功能可以帮助我们快速地对数据进行整理和分类，便于后续的分析和统计。

二、数据可视化数据可视化是统计学实验报告中不可或缺的一部分。

通过图表的形式展示数据，可以更直观地观察和分析实验结果。

Excel提供了多种图表类型，如柱状图、折线图、饼图等，可以根据实验数据的特点选择合适的图表类型。

在创建图表时，我们可以根据需要调整图表的样式、颜色和字体等，使其更加美观和易读。

此外，Excel还支持多个图表的组合，可以将不同类型的图表放在同一个图表中进行对比和分析。

三、数据分析与统计数据分析和统计是统计学实验报告的核心内容。

Excel提供了丰富的数据分析和统计函数，可以帮助我们进行各种统计计算和推断。

例如，我们可以使用Excel的平均值函数、标准差函数和相关系数函数等，对实验数据进行描述性统计分析。

此外，Excel还支持各种假设检验和回归分析等高级统计方法，可以根据实验的需要进行相应的分析。

四、结果解释与讨论在统计学实验报告中，我们需要对实验结果进行解释和讨论，得出科学的结论并进行推断。

Excel可以帮助我们将分析结果直观地呈现出来，并提供相应的统计指标和图表。

通过对实验结果的解释和讨论，我们可以深入分析实验数据的意义和潜在的影响因素。

此外，Excel还支持数据的导出和共享，方便与他人进行交流和合作。

ｎ
３
罐
≥囊 Ｓ
～
醴
魏
嚣
４
圣
１ ５
１ ６
ｏ
ｐ
擎
ｉ
ｉ
４
＂ ；
ｑ ｓ
２
ｌ
黪
５
ｌ ８
３
ｉ
＿
ｊ
５
５
２ ｏ
§
ｔ
ｓ
三、 分层抽样 ， 指先将总体 的单位按某种 特征 分为若
干次级总体（ ）然 后再从每一层 内进 行单纯随机抽样 ， 层 ，
随机化 。然后按照事前确 定的样本数量 ， 按照连续的顺序 从中截 取。这里需要 注意 的是 ， 由于 ｒｎ （ 函数每次计算 ａｄ ）
样， 因此使用起来不够灵活 。
工作表时都 将返回一个新 的随机实数 ，因此应 当在 编辑
其 实 ， 抽样过程 中 ， 完全可 以采 用 Ｅｃｌ 在 我们 ｘｅ 函数 栏 中输入 “Ｒ Ｎ （” ， ＝ Ａ Ｄ ）后 保持编辑状 态 ， 然后按 Ｆ 或者 ９
３
５
３。
驺
ｌ
２
ｆ
霉 ２
巷 ａ
ｉ
霉
２
２
８
９
Ｉ ｌ
ｈ
ｉ
ｋ
３
唾
ｊ 童
８ｉ
翻 密
巍
毽
瓤
２
Ｓ
一 ｌ ２ ｌ ２ ＿源自薹 ｉｉ １ ２ｉ ￣ ｉ
魏 ３
ｌ ３
１ ４
Ｉ ｔ
与其他 内置功能的结合来 实现多种抽样方法 。
一

《统计学》实验指导书【试验目的】通过实验教学，使学生验证并加深理解和巩固课堂教学内容，掌握常用统计分析方法在Excel、SPSS 的应用，理解和掌握统计分析方法的应用原理、基本条件、实现步骤、结果的内涵等问题。

通过实验，使学生能够结合具体任务和条件对社会经济问题进行初步的调查研究，结合自己的专业，在定性分析基础上做好定量分析，提高学生的科研能力和解决实际问题的能力，以适应社会主义市场经济中各类问题的实证研究、科学决策和经济管理的需要。

【试验内容】一、Excel中的统计分析功能包括：1、数据的整理与显示，包括数据的排序与筛选、数据透视表与分类汇总、制作频数分布表和绘制各种统计图。

2、计算描述统计量，选择适合的描述统计量反映统计数据的集中和离中趋势。

3、利用Excel进行推断统计。

4、利用Excel进行相关回归分析。

试验一：数据的整理与显示（一）数据的筛选和排序1、数据的筛选在对统计数据进行整理时，首先需要进行审核，以保证数据的质量。

对审核中发现的错误应尽可能予以纠正。

如果对发现的错误无法纠正，或者有些数据不符合调查的要求而又无法弥补时，就要对数据进行筛选。

数据筛选有两方面内容：一是将某些不符合要求的数据或有明显错误的数据予以剔除；二是将符合某种特定条件的数据筛选出来，不符合特定条件的数据予以剔除。

数据筛选可借助于计算机自动完成。

下面通过一个实例说明用Excel进行数据筛选的过程。

【例】下表是8名学生4门课程的考试成绩数据（单位：分）。

试找出统计学成绩等于75分的学生，英语成绩最高的前三名学生，4门课程都高于70分的学生。

8名学生的考试成绩数据首先，选择“工具”菜单，并选择“筛选”命令。

如果要筛选出满足给定条件的数据，可使用自动筛选命令。

如图所示。

自动筛选(1)这时会在第一行出现下拉箭头，用鼠标点击箭头会出现下面的结果，如图自动筛选(2)要筛选出统计学成绩为75分的学生，选择75，得到结果：自动筛选(3)要筛选出英语成绩最高的前三名学生，可选择“前10个”，并在对话框中输入数据3，得到的结果如图所示。

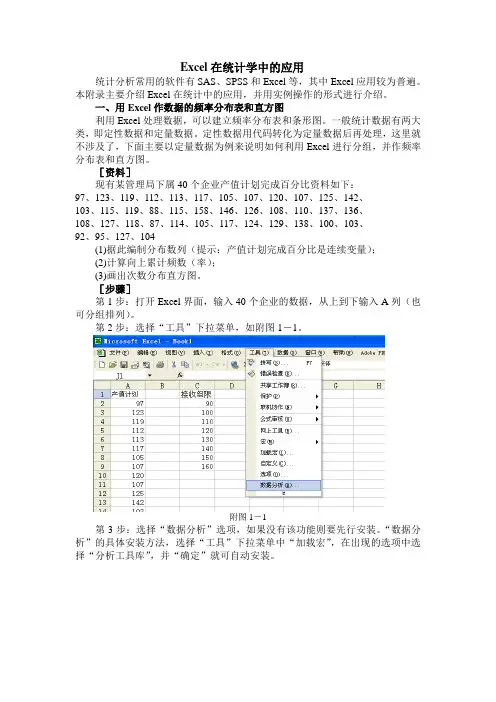
Excel在统计学中的应用统计分析常用的软件有SAS、SPSS和Excel等，其中Excel应用较为普遍。

本附录主要介绍Excel在统计中的应用，并用实例操作的形式进行介绍。

一、用Excel作数据的频率分布表和直方图利用Excel处理数据，可以建立频率分布表和条形图。

一般统计数据有两大类，即定性数据和定量数据。

定性数据用代码转化为定量数据后再处理，这里就不涉及了，下面主要以定量数据为例来说明如何利用Excel进行分组，并作频率分布表和直方图。

［资料］现有某管理局下属40个企业产值计划完成百分比资料如下：97、123、119、112、113、117、105、107、120、107、125、142、103、115、119、88、115、158、146、126、108、110、137、136、108、127、118、87、114、105、117、124、129、138、100、103、92、95、127、104(1)据此编制分布数列（提示：产值计划完成百分比是连续变量）；(2)计算向上累计频数（率）；(3)画出次数分布直方图。

［步骤］第1步：打开Excel界面，输入40个企业的数据，从上到下输入A列（也可分组排列）。

第2步：选择“工具”下拉菜单，如附图1－1。

附图1－1第3步：选择“数据分析”选项，如果没有该功能则要先行安装。

“数据分析”的具体安装方法，选择“工具”下拉菜单中“加载宏”，在出现的选项中选择“分析工具库”，并“确定”就可自动安装。

附图1－2第4步：在分析工具中选择“直方图”，如附图1－2。

附图1－3第5步：当出现“直方图”对话框时，在“输入区域”方框内键入A2:A41或$A$2：$A$41（“$”符号起到固定单元格坐标的作用，表示的是绝对地址），40个数据已输入该区域内，如果是分组排列的，就应选择整个分组区域。

在“接收区域”方框内键入C2：C9或$C$2：$C$9，所有数据分成8组（主要根据资料的特点，决定组数、组距和组限），把各组的上限输入该区域内。

统计学excel实训报告一、引言统计学是研究收集、整理、分析和诠释数据的学科。

而Excel作为一种功能强大的电子表格软件，具有丰富的数据分析功能，可以帮助我们进行统计学实验和数据处理。

本文将介绍我在统计学Excel实训中的实际操作和结果。

二、实验目的通过这次实训，我们的目的是掌握在Excel中进行基本统计学实验的方法和技巧，了解数据的描述性统计分析以及相关图表的绘制，提高对数据的分析能力和数据处理能力。

三、实验过程1. 数据收集与整理在实训开始之前，我们首先需要收集相关数据并进行整理。

以某商品销售数据为例，我们收集了该商品在一周内的销售数据，包括日期、销售量和价格等信息。

然后，我们将数据整理成Excel表格的形式，方便后续的统计分析。

2. 描述性统计分析接下来，我们利用Excel提供的函数和工具进行描述性统计分析。

通过计算均值、中位数、众数、标准差等指标，我们可以更好地了解数据的分布情况和特征。

此外，我们还可以利用Excel绘制直方图、箱线图等图表，直观地展示数据的分布情况。

3. 假设检验与回归分析在统计学中，假设检验和回归分析是两个重要的内容。

通过Excel中的函数和工具，我们可以进行各种假设检验，如t检验、方差分析等，以检验数据之间是否存在显著差异。

同时，我们还可以利用回归分析来建立数据之间的关系模型，并进行相关系数、拟合优度等指标的计算。

四、实验结果与讨论在实验过程中，我们得到了一系列的实验结果。

通过描述性统计分析，我们可以看出商品销售量的均值为XX，标准差为XX，表明销售量的分布相对稳定。

通过绘制直方图，我们可以看出销售量主要集中在一个范围内，这对于制定合理的销售策略有很大的指导意义。

对于假设检验部分，我们进行了一项t检验，结果显示两组数据之间的差异是显著的（P值小于0.05），说明两组数据来自不同的总体。

此外，通过回归分析，我们建立了销售量与价格之间的线性关系模型，R平方值为0.8，表明价格对销售量的影响较大。

（二）随机抽样工具
任务
11
Excel在抽样推断中的应用
二、推断统计
1．BINOMDIST函数 BINOMDIST函数用于计算二项分布的概率值或累积概率。 语法格式：BINOMDIST(number_s ，trials ，probability_s ，cumlative) 。
这四个参数分别表示实验成功的次数、实验的总次数、每次实 验中成功的概率、是否计算累积概率。参数 是逻辑值，0或FALSE 表示计算概率密度函数概率值，1或TRUE表示计算累积分布函数 概率值。
（一）样本单位的选取
6
任务
Excel在抽样推断中的应用
一、抽样
Excel中的RAND( )函数产生的是0～1之间均匀分布的随机数，
RAND( )不带任何参数运行，每次运算时都将产生一个新的随机数。
如果将RAND( )函数从一个单元格 复制或移动到另外一个单元格，也会重 新产生一个随机数。RAND( )函数可以 被用来作为不重复抽样调查的工具。
例如，从10个象征性的样本数据中随机抽取5个数据，其步骤如上。
步骤 03
（二）随机抽样工具
10
任务
Excel在抽样推断中的应用
一、抽样
上述例子进行的是不重复随机抽样，若要进行重复随 机抽样，可利用Excel的 函数实现。 函数可随机产生介于 bottom（最低）与top（最高）之间的随机整数，抽取 此整数对应编号的样本可作为总体重复随机抽样的结果。
步骤 01
（二）随机抽样工具
8
任务
Excel在抽样推断中的应用
一、抽样
步骤 02
例如，从10个象征性的样本数据中随机抽取5个数据，其步骤如下。
对于B2:B11单元格的随机数，要先变成稳定的随机数，才能正确进行排序。 ① 选取单元格B2:B11，右击选中的区域选择“复制”选项。 ② 再次右击选中的区域，选择“选择性粘贴”选项，单击“数值”选项。 ③ 点击“确定”按钮，此时B2:B11中的数据就是稳定的随机数了。 （二）随机抽样工具

统计学实验报告姓名：学号：班级：成绩：一、实验步骤总结成绩：实验一：数据的搜集与整理一、数据的搜集统计数据主要来源于两种渠道：一种是来源于别人的调查或实验数据，称为间接数据；另一种是来源于科学实验或者直接的调查数据，称为直接数据。

1.间接数据的搜集间接统计数据主要是公开出版或报道的数据，可以通过年鉴、期刊、报纸、广播、电视等途径搜集获取。

在网络广泛普及的今天，通过网络搜集间接数据已经成为了一种主流手段。

一般，在网络上搜集数据可以采用两种方式。

一种方式是直接进入网站查询数据。

2.直接数据的搜集直接统计数据可以通过两种途径获得：一是统计调查或观察，二是实验。

统计调查是取得社会经济数据的最主要来源，它主要包括普查、重点调查、典型调查、抽样调查、统计报表等调查方式。

本实验主要介绍抽样调查取得直接数据的方法。

二、数据的整理1.Excel的数据整理及数据文件的建立首先，大家应该熟悉Excel的操作界面。

（1）数据的编码编码是对数据进行初步分组和确定数字代码的过程。

它可以把复杂的文字用简单的代码代替，有利于简化数据输入和处理。

一般直接数据如果是由封闭式问题获取，那么涉及问题的时候就已经对答案进行了预编码。

如果数据是由开放式的问题来获取的，那么，需要对答案进行罗列、合并、设码三个过程来完成编码工作。

（2）数据的录入数据的录入是将搜集到的数据直接输入到数据库文件中。

数据录入既要讲究效率，又要保证质量。

Excel的数据录入操作比较简单，一般只要在工作表中，单击激活一个单元格就可以录入数据了。

单元格的切换可以使用鼠标，也可以在激活一个单元格以后用Enter键（或者Tab）键，向下（或者向右）切换单元格。

在单元格内部的换行可以使用“Alt+Enter”。

当然，数据录入中最重要的还是要保证数据形式完整和性质正确。

这就需要通过“格式-单元格格式”（Ctrl+1）菜单来实现。

对于录入重复数据，大家一般都习惯使用复制功能（Ctrl+C），但是Excel在简单复制数据时不能保证格式的完整性，这个时候，就需要单击鼠标右键，使用“选择性粘贴”，进行设置来实现复制的格式要求。

实验目的：学会计算机上利用Excel进行单因素方差分析和有交互作用的双因素方差分析以及无交互作用的双因素方差分析。
实验步骤：在Excel中，进行方差分析可以使用公式和函数的方法。
一:单因素方差分析
例：根据学生调查的结果，试用方差分析的方法比较在5%的显著性水平下能否认为学生的学习兴趣对他们的统计成绩有显著影响。
全部选中，再选择插入，插入图表，饼图，得到下图：
实验二描述统计分析过程（用Excel计算描述统计量）
实验目的：用Excel计算描述统计量
实验步骤：Excel中用于描述统计量的方法有两种，函数方法和描述统计工具的方法。
一：用函数计量描述统计量
了解实习生的工资情况，随机抽取了30人。并输入单元格，如图：
实验三用Excel进行参数估计与假设检验
实验目的：用Excel进行参数估计与假设检验
实验步骤：在Excel中，进行参数估计只能使用公式和函数的方法，而假设检验除以上两种方法外，还可以使用假设检验工具。
一．使用Excel进行区间估计
抽查40位顾客的消费额，求在概率90%的保证下，顾客平均消费额的估计区间。
实验一Excel基本操作（用Excel搜集与整理数据）
实验目的：掌握用Excel进行数据的搜集整理与显示
实验步骤：
一：用Excel搜集数据
使用Excel进行抽样，先对各个总体单位进行编号，编号后，可以输入工作表。
例如：有60个总体单位，每个总体单位一个编
选择数据分析选项，打开数据分析对话框，从中选择抽样。如下图。
三：用Excel进行有重复双因素方差分析
与无重复的双因素方差分析不同，有重复双因素方差分析可以分为有交互作用和无交互作用两种情况。
例子：
在Excel表格中输入相应数据，从“数据分析”中选择“方差分析”

一、实验目的1. 了解医学统计学抽样的基本原理和方法；2. 掌握随机抽样的操作技巧；3. 学会运用统计学方法对抽样数据进行统计分析；4. 提高对医学研究数据的处理和分析能力。

二、实验原理1. 随机抽样：随机抽样是指从总体中随机选取一定数量的样本，使得每个个体被抽中的概率相等。

随机抽样可以保证样本的代表性，使样本数据能够反映总体特征。

2. 统计分析：通过对抽样数据进行分析，可以了解总体特征，为医学研究提供依据。

三、实验材料1. 实验数据：选取某地区某医院1000例患者的临床资料，包括年龄、性别、疾病类型、治疗方案、疗效等。

2. 统计软件：SPSS、Excel等。

四、实验步骤1. 数据整理：将1000例患者的临床资料整理成电子表格，确保数据完整、准确。

2. 随机抽样：采用随机抽样的方法，从1000例患者中随机抽取100例作为样本。

3. 数据录入：将随机抽取的100例患者的临床资料录入SPSS软件。

4. 数据分析：运用SPSS软件对抽样数据进行统计分析，包括描述性统计、推断性统计等。

5. 结果解读：根据统计分析结果，对样本数据进行分析，了解总体特征。

五、实验结果与分析1. 描述性统计（1）样本患者年龄分布：20-30岁、31-40岁、41-50岁、51-60岁、61岁以上，分别占总体的10%、20%、30%、20%、20%。

（2）样本患者性别分布：男、女，分别占总体的50%、50%。

（3）样本患者疾病类型分布：A型、B型、C型，分别占总体的20%、30%、50%。

2. 推断性统计（1）假设检验：对样本数据中的疾病类型与治疗方案进行卡方检验，以检验两种因素是否存在关联。

（2）相关性分析：对样本数据中的年龄与疗效进行Spearman秩相关分析，以了解年龄与疗效之间的关系。

六、讨论与分析1. 随机抽样方法在本实验中得到了有效运用，保证了样本的代表性。

2. 描述性统计结果显示，样本患者的年龄、性别、疾病类型等特征与总体特征基本一致，说明随机抽样方法在本实验中具有较高的可靠性。

统计学excel实训报告一、引言统计学是一门研究数据收集、整理、分析和解释的学科，而Excel 是一款功能强大的电子表格软件。

本报告旨在通过对Excel实训的详细描述和分析，展示统计学在实际应用中的重要性和效果。

二、实训目的本次实训的目的是通过运用Excel软件进行数据处理和分析，增进对统计学的理解，并提高数据分析能力。

实训内容包括Excel的基本操作、数据的导入与清洗、数据的统计描述与可视化，以及简单的假设检验等。

三、实训步骤1. Excel基本操作我们首先学习了Excel的基本操作，包括新建工作簿、数据输入、单元格格式化、公式计算等。

这为后续实训内容的顺利进行提供了基础。

2. 数据的导入与清洗在实际数据处理过程中，往往需要将数据导入Excel中进行进一步的操作。

我们学习了如何从外部文件导入数据，并对数据进行清洗和处理，例如删除重复值、填充空白单元格等。

这样可以保证数据的准确性和有效性。

3. 数据的统计描述与可视化统计描述是对数据进行概括和总结的过程，而数据可视化则能通过图表等形式更直观地展现数据的特征与规律。

我们在实训过程中学习了如何计算数据的平均值、中位数、标准差等统计量，并利用Excel的图表功能绘制直方图、折线图、饼图等，以便更直观地了解数据特征。

4. 假设检验假设检验是统计学的重要内容之一，在实际应用中常用于判断两组样本间是否存在显著差异。

我们在实训中学习了如何进行均值差异的t检验，以及两组样本间相关性的相关分析。

这样可以帮助我们更准确地判断和解释数据间的差异。

四、实训成果通过本次实训，我们不仅提高了Excel的操作技能，还深入了解了统计学在实际应用中的重要性和效果。

以下是我们的实训成果：1. 数据清洗与处理我们成功导入了实际数据，并对数据进行了去重和填充空白单元格的操作，确保了数据的准确性和可靠性。

2. 数据统计描述与可视化我们运用Excel的函数和工具，计算了数据的平均值、中位数、标准差等统计量，并使用直方图、折线图、饼图等图表进行了数据可视化，使数据更加直观易懂。

统计应用实验报告excel实验概述本次实验旨在使用Excel 进行统计应用，探索Excel 在数据处理和分析中的功能和应用。

通过对实验数据的输入、处理和输出，我们能够熟悉Excel 的基本操作和常用函数，掌握使用Excel 进行数据分析的方法。

实验步骤1. 数据输入首先，打开Excel 软件，新建一个工作簿。

然后，在表格中输入实验数据。

本次实验数据为一份学生成绩单，包含学生姓名、科目以及对应的成绩。

我们将这些数据按照指定格式输入到Excel 的不同列和行中。

2. 数据处理在输入数据完成后，我们需要对数据进行处理，以便进行后续的分析。

常见的数据处理操作包括数据排序、数据筛选和数据求和等。

通过在Excel 中使用相应的功能和公式，我们可以轻松地完成这些操作。

* 数据排序：我们可以选择对成绩列进行升序或降序排序，以确定学生的成绩排名情况。

通过Excel 的排序功能，我们可以迅速对数据进行排序，并得到排序后的结果。

* 数据筛选：我们可以按照特定的条件筛选数据。

比如，我们可以选择只显示某个科目及对应的成绩，或者只显示成绩超过某个分数的学生。

通过Excel 的筛选功能，我们可以很方便地对数据进行筛选，并得到我们想要的结果。

* 数据求和：我们可以使用Excel 的求和函数，对成绩进行求和，得到总分、平均分等数据。

通过这些统计数据，我们可以更好地了解学生的成绩状况。

3. 数据分析在数据处理完成后，我们可以进行进一步的数据分析，以了解更多有关实验数据的信息。

* 数据可视化：通过使用Excel 的图表功能，我们可以将数据用图表的形式展示出来，从而更直观地观察数据的分布和变化趋势。

比如，我们可以使用柱状图表示各科成绩的对比关系，或者使用折线图表示不同学生的成绩随时间的变化情况。

这些图表可以帮助我们更好地理解数据，并进行更深入的分析。

* 数据摘要：通过使用Excel 的统计函数，我们可以对数据进行进一步的摘要分析。

常见的统计函数包括计数、最大值、最小值、平均值和标准差等。

学习excel的抽样与抽样分布工具的使用心得学习 excel 的抽样与抽样分布工具的使用心得，当然也就离不开抽样这个功能。

很多人都在追求高效率，却忽视了自己本身已经有一定水平上的问题，盲目的“崇拜”速度。

反而忘记了慢工出细活的道理。

从数据处理角度来看，一般地抽样方法所适合的总体是无限可分的、非零总体。

它可以在比较短时间内迅速找到对象，但是缺点明显：样本太小、信息不完整或不确切；统计误差很大（由于所研究对象数值范围相同引起），即推断过程中随机性和系统性都受影响。

所以最好采取适当方式选择样本。

这里介绍了简单的抽样原则——重复原则。

今天，如果你能站在一个高度审视抽样这件事情，那么我想你应该会清楚地知道，什么才是真正符合时代需要的智慧行为。

从大量的实践操作中我们不难发现，抽样的基础是样本容量。

如何设置样本容量呢？很简单，就是将数据按照一定规律进行排列，形成一组样本。

例如，将一组成绩按照从低到高的顺序排列，便可以形成一个标准化样本。

假若，再加入考试成绩的年级等因素，还可以进一步提升其精确度。

我们必须意识到，无论采用哪种样本容量设置方案，关键之处只有两点：第一，每次调查结束后，根据结果及时更新样本；第二，做好样本的维护管理工作。

这两者缺一不可！
- 1 -。