应用统计学第九章分类数据分析-学生版
- 格式:pdf
- 大小:3.35 MB
- 文档页数:31



第9章 分类数据分析一、思考题1.简述列联表的构造与列联表的分布。
答:列联表是由两个以上的变量进行交叉分类的频数分布表。
列联表的分布可以从两个方面看,一个是观察值的分布,又称为条件分布,每个具体的观察值就是条件频数;一个是期望值的分布。
2.用一张报纸、一份杂志或你周围的例子构造一个列联表,说明这个调查中两个分类变量的关系,并提出进行检验的问题。
答:对三个生产厂甲、乙、丙提供的学习机的A、B、C三种性能进行质量检验,欲了解生产厂家同学习机性能的质量差异是否有关系。
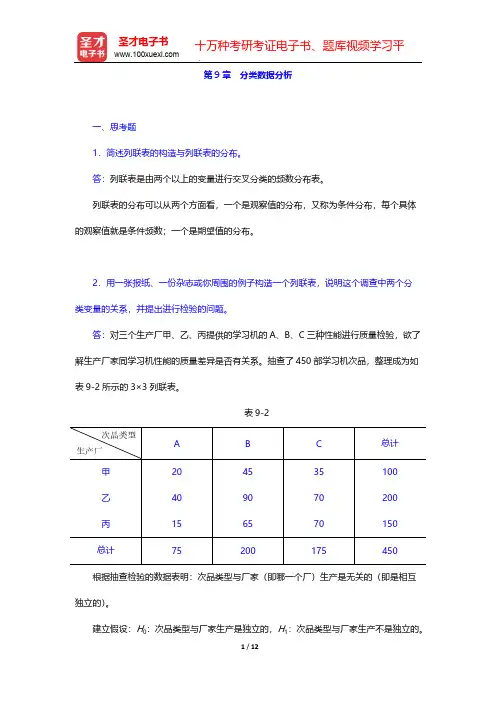
抽查了450部学习机次品,整理成为如表9-2所示的3×3列联表。
表9-2根据抽查检验的数据表明:次品类型与厂家(即哪一个厂)生产是无关的(即是相互独立的)。
建立假设:H0:次品类型与厂家生产是独立的,H1:次品类型与厂家生产不是独立的。
可以计算各组的期望值,如表9-3所示(表中括号内的数值为期望值)。
表9-3 各组的期望值计算表所以2222(2017)(4033)(7058)9.821173358χ---=+++=…。
而自由度等于(R -1)(C -1)=(3-1)×(3-1)=4,若以0.01的显著性水平进行检验,查χ2分布表得20.01(4)13.277χ=。
由于220.019.821(4)13.277χχ=<=,故接受原假设H 0,即次品类型与厂家生产是独立的。
3.说明计算2χ统计量的步骤。
答:计算2χ统计量的步骤:(1)用观察值o f 减去期望值e f ;(2)将(o f -e f )之差平方;(3)将平方结果2)(e o f f -除以e f ;(4)将步骤(3)的结果加总,即得:22()o e ef f f χ-=∑。
4.简述ϕ系数、c 系数、V 系数的各自特点。
答:(1)ϕ相关系数是描述2×2列联表数据相关程度最常用的一种相关系数。
它的计算公式为:ϕ,式中,∑-=ee of f f 22)(χ;n 为列联表中的总频数,也即样本量。

第一章导论1.什么是统计学?统计学是搜集、处理、分析、解释数据并从中得出结论的科学。
2.解释描述统计与推断统计。
描述统计研究的是数据搜集、处理、汇总、图表描述、概括与分析等统计方法。
推断统计研究的是如何利用样本数据来推断总体特征的统计方法。
3.统计数据可分为哪几种类型?不同类型的数据各有什么特点?按照计量尺度可分为分类数据、顺序数据和数值型数据;按照数据的搜集方法,可以分为观测数据和试验数据;按照被描述的现象与实践的关系,可以分为截面数据和时间序列数据。
4.解释分类数据、顺序数据和数值型数据的含义。
分类数据是只能归于某一类别的非数字型数据;顺序数据是只能归于某一有序类别的非数字型数据;数值型数据是按照数字尺度测量的观测值,其结果表现为具体的数值。
5.举例说明总体、样本、参数、统计量、变量这几个概念。
总体是包含所研究的全部个体的集合,样本是从总体中抽取的一部分元素的集合,参数是用来描述总体特征的概括性数字度量,统计量是用来描述样本特征的概括性数字度量,变量是用来说明现象某种特征的概念。
6.变量可分为哪几类?变量可分为分类变量、顺序变量和数值型变量。
分类变量是说明书屋类别的一个名称,其取值为分类数据;顺序变量是说明十五有序类别的一个名称,其取值是顺序数据;数值型变量是说明事物数字特征的一个名称,其取值是数值型数据。
7.举例说明离散型变量和连续型变量。
离散型变量是只能去可数值的变量,它只能取有限个值,而且其取值都以整位数断开,如“产品数量”;连续性变量是可以在一个或多个区间中取任何值的变量,它的取值是连续不断的,不能一一列举,如“温度”等。
第二章数据的搜集1.什么是二手资料?使用二手资料需要注意些什么?与研究内容有关、由别人调查和试验而来、已经存在并会被我们所利用的资料为二手资料。
使用时要评估资料的原始搜集人、搜集目的、搜集途径、搜集时间且使用时要注明数据来源。
2.比较概率抽样和非概率抽样的特点。
举例说明什么情况下适合采用概率抽样,什么情况下适合采用非概率抽样。


第9章分类数据分析一、单项选择题1.列联分析是利用列联表来研究()。
A.两个数值型变量的关系B.两个分类变量的关系C.两个数值型变量的分布D.一个分类变量和一个数值型变量的关系【答案】B【解析】列联表是由两个或以上的变量进行交叉分类的频数分布表,列联分析是利用列联表来研究两个分类变量之间的关系。
2.列联表中的每个变量()。
A.只能有一个类别B.只能有两个类别C.对类别没有限制D.可以有两个或两个以上的类别【答案】D3.设列联表的行数为3,列数为4,则χ2检验的自由度为()。
A.3B.4C.6D.12【答案】C【解析】列联分析中,χ2检验的自由度=(行数-1)(列数-1)=(R-1)(C-1)=(3-)×(4-1)=6。
4.一所大学准备采取一项学生对餐厅改革意见的调查,为了解男女学生对这一措施的看法,分别抽取了300名男学生和240名女学生进行调查,得到的结果如表9-1所示。
这个表格是()。
A.4×3列联表B.3×2列联表C.2×3列联表D.3×4列联表【答案】B【解析】表中的行是态度变量,这里划分为三类,即赞成、中立和反对;表中的列是单位变量,这里划分为两类,即男同学和女同学,因此这个表格是3×2列联表。
5.一所大学为了解男女学生对后勤服务质量的评价,分别抽取了300名男学生和240名女学生进行调查,得到的结果如表9-2所示。
这个列联表的最下边一行称为()。
A.总频数B.条件频数C.行边缘频数D.列边缘频数【答案】D6.某中学为了解教师对新课标改革的看法,分别抽取了300名男教师和240名女教师进行调查,得到的结果如表9-3所示。
这个列联表的最右边一列称为()。
A.总频数B.条件频数C.行边缘频数D.列边缘频数【答案】C7.某大学为了解学生对研究生奖学金制度改革的看法,分别抽取了300名男研究生和240名女研究生进行调查,得到的结果如表9-4所示。



《应用统计学》教学大纲一、课程简介统计学是农林经济管理本科专业的一门学科基础必修课。
本课程采取理论讲授与实验操作交替进行的方式,理论讲授部分主要包括统计数据的收集、整理、分析及预测,重点讲授各种统计方法,如参数估计、假设检验、方差分析、时间序列分析、统计指数、相关与回归分析等;实验操作部分包括统计工作过程的实验、Excel等电子表格在统计分析中的应用、统计学知识的综合应用三个实验。
二、教学大纲1.教学目的开设此课旨在培养学生数据收集、处理和分析能力。
通过本课程的学习,学生掌握统计学基本理论、方法及在Excel等统计软件中的运用,达到能应用统计方法分析问题和解决问题的目的。
2.教学要求(1)对教师的要求教师要积极备课,认真准备实验,对课程内容要融会贯通,切忌照本宣科。
授课在多媒体教室,结合典型实用案例和相关统计软件,理论讲授与上机操作交替进行。
做到授课内容与大纲相符,注重全程考核,最终成绩由考勤、调查方案设计、实验报告撰写、调查报告撰写、上机测试及期末考试构成,成绩评价体系标准真实、严谨、公平、公正、公开,提升学生学习积极性。
(2)对学生的要求学生能系统地掌握各种统计方法,并理解各种统计方法中所包含的统计思想;能运用统计方法分析和解决实际问题的能力;能够熟练应用Excel等统计软件进行数据分析。
3.预备知识或先修课程要求先修课程包括《概论论与数理统计》、《微观经济学》、《宏观经济学》、《管理学原理》等。
4.教学方式课程包括理论讲授和实验操作两部分。
理论授课32学时,教师讲授与课堂讨论相结合;实验操作24学时,包括统计工作过程实验、Excel等统计软件的运用及统计学知识的综合运用,以学生上机操作为主,教师引导、实地调查为辅。
5.实验环境和设备1)硬件环境:每个学生一台微型计算机。
2)软件环境:Windows 7、Office 2007(或以上版本)(Excel需安装数据分析及规划求解功能)软件包、卓越班学生还需SPSS、DPS软件包。
可编辑修改精选全文完整版应用统计学第9章分类数据分析9.1 欲研究不同收入群体对某种特定上坡是否有相同的购买习惯,市场研究人员调查了四个不同收入组的消费者共527人,购买习惯分为:经常购买,不购买,有时购买。
调查结果如下表所示。
要求:(1)提出假设。
χ值。
(2)计算2(3)以α=0.1的显著水平进行检验。
解:(1):提出假设:oH:不同收入群体对某种特定商品的购买习惯相同H不同收入群体对某种特定商品的购买习惯不全相同1:(2):χ计算结果3⨯4列联表期望值及22()2fo fe feχ=-÷=∑17.63所以2χ的值为17.63.(3):α=0.1 自由度(31)(41)6df=-⨯-=临界值χ0.1²(6)=10.64 2χ=17.63>χ0.1²(6)=10.64∴拒绝原假设,接受备择假设。
结论:不同收入群体对某种特定商品的购买习惯不全相同9.4 教学改革后学生有了更多的选课自由,但学院领导在安排课程上也面临新的问题。
例如MBA研究生班的学生选课学年之间的变化常常很大,去年的学生很多人选会计课,而今年的学生很多人选市场营销课。
由于事先无法确定究竟有多少学生选各门课程,所以无法有效地进行教学资源的准备。
由于有人提出学生所选课程与其本科所学的专业有关。
为此学院(1)以0.05的显著性水平检验学生本科所学专业是否影响其读MBA期间所选的课程。
(2)计算P值。
解:4⨯3列联表期望值及2χ计算结果2()2fo fe feχ=-÷=∑14.93提出假设:oH:本科学生所学专业受其读MBA期间所选的课程影响1:H本科学生所学专业不受其读MBA期间所选的课程影响α=0.05 自由度(41)(31)6df=-⨯-=临界值χ0.05²(6)=12.59 2χ=14.93>χ0.05²(6)=12.59∴拒绝原假设,接受备择假设。
结论:本科学生所学专业不受其读MBA期间所选的课程影响(2):利用Excel计算得出P=0.1856。
新人教版九年级数学上册教案:数据的分类整理和统计分析随着现代社会的高速发展,数据已经成为了我们工作中必不可少的一部分,数据的分类整理和统计分析也成为了我们必须具备的一项能力。
在新人教版九年级数学上册的教学中,数据的分类整理和统计分析也是非常重要的一环,下面我们就来详细介绍一下这一部分的内容。
一、教学目标1、掌握数据的搜集和整理方法,能够进行分类整理。
2、理解数据的分布规律,并能够用图形展示数据分布。
3、掌握统计学常用的统计量,并能够应用统计量进行数据分析。
4、能够进行简单的推断统计学,从而对问题进行分析和解决。
5、培养学生严谨的逻辑思维能力和数据分析能力。
二、教学内容1、数据的搜集和整理数据的搜集和整理是进行数据分析的第一步,正确地进行数据搜集和整理对统计数据的精准性有着非常大的影响。
学生需要学会如何通过调查问卷、抽样等方式进行数据的搜集,并学会如何对数据进行分类,整理。
2、图形展示数据分布图形展示数据分布是为了更好地理解数据的分布规律,仅仅用统计量是很难从数据中发现规律的。
在教学中,我们会介绍常见的图形如:条形图、饼状图、折线图等,让学生学会用图形展示数据分布。
3、统计学常用的统计量统计学常用的统计量有很多,如:平均数、中位数、众数、方差、标准差等。
在教学中,我们会详细介绍这些统计量的概念和计算方法,并让学生学会如何应用这些统计量进行数据分析。
4、推断统计学推断统计学是基于样本数据对总体数据进行推断的一种方法。
在教学中,我们将介绍常见的假设检验、置信区间等推断统计学方法,让学生学会如何应用这些方法对问题进行分析和解决。
5、综合应用在教学中,我们会安排一些综合性的应用题,让学生将学到的知识应用到实际问题中,并培养学生的思维能力和解决问题的能力。
三、教学方法1、案例分析法我们将提供一些实际案例,让学生对数据的搜集、整理、分析、解决问题等方面有更好的理解。
2、互动教学法互动教学法是指让学生在课堂上积极参与,与老师和同学互动,让学生能够更好地掌握知识。