二次函数动点面积最值问题

二次函数最大面积例1如图所示，等边△ ABC中，BC=10cm，点R, P?分别从B,A同时岀发，以1cm/s的速度沿线段BA,AC 移动，当移动时间练习1如图，在矩形ABCD中，AB=6cm , BC=12cm,点P从点A岀发沿AB边向点B以1cm/s的速度移动，同时点Q从点B岀发沿BC边向C以2cm/s的速度移动，如果P,Q同时岀发，分别到达B、C两点就停止移动。

_ ___________________________________________ 2(1 )设运动开始后第t秒，五边形APQCD的面积是Scm ，写岀S与t函数关系式，并指岀t的取值范围。

(2) t为何值时，S最小？并求岀这个最小值。

A开始沿QBB边向点B以A2 如图，在△ ABC 中，/ B=9 0°, AB=22CM,BC=20CM ，点P 从点2cm/S的速度移动，点Q从点B开始沿着BC边向点C以1cm/S的速度移动,P,Q分别从A,B 同时岀发。

2求四边形APQC的面积y ( cm )与PQ移动时间x (s)的函数关系式, 以及自变量x的取值范围。

C3如图正方形ABCD的边长为4cm，点P是BC边上不与B,C重合的任意一点点P作PQ丄AP交DC于点Q,设BP的长为x cm，CQ的长为y cm。

(1)求点P在BC上的运动的过程中y的最大值。

1(2 )当y= cm时，求x的值。

44如图所示，边长为在线段记CD(1)过ADPBB1的正方形OABC的顶点O为坐标原点，点A在x轴的正半轴上，动点点E,连接O BC上移动(不与B,C重合)，连接OD，过点D作DE丄OD, 的长为t o1当t=丄时，求线段DE3如果梯形CDEB的面积为所在直线的函数表达式S,那么S是否以及此时(2) 存在最大值？若存在，请求出最大值，t的值；若不存在，请说明理由。

2 2(3)当OD DE的算术平方根取最小值时,(4)求点E的坐标。

二次函数最大面积交ABD BE能力提高例题如图所示，在梯形ABCD中，AD// BC,AB=AD=DC=2CM,BC=4C在等腰△ PQR中，/ QPR=120 ,底边QR=6CM点B,C,Q，R在同一直线1cm/s的速度沿直线I向左匀速移动，(1)(2) t秒时梯形I上，且C,Q两点重合，如果等腰△ PQR以2 ABCD与等腰△ PQF重合部分的面积记为Scm当t=4时，求S的值。

是由同一个三角形ABC平移得到的,请计 算三角形ABC的面积.
(-3,3)
图2 O
(0,2.5)
(0,2) (4,2) X轴
图1：铅垂高CD为：6-2.5=3.5
图2：铅垂高CD为：2-（-1.5）=3.5
(-3,-1)
(0,-1.5) (0,-2)
(4,-2) 图3：铅垂高CD为：-2-（-5.5）=3.5
2
三、自我检测
4.抛物线
y 4 2 24 x x 4 在平面直角坐标系中的位置如图，直线 5 5
4 y x4 5
与y轴交于点B.在抛物线上是否 与x轴交于点A(-5,0)，
存在一点P， 使得△PAB的面积最小？若存在， 求△PAB面积的最小值；
若不存在，请说明理由.
则△ ， ABC的面积为
1 3 x 与x轴交于A、B两点，顶点为C， 2 2
.
则△ABC的面积为
三、自我检测
3. 已知抛物线 y x 2 x 3 与x轴交于A(-3,0)，B(1,0)两点， 与y轴交于点C，直线y=x+1与抛物线交于E，F两点．点Ｐ是直线EF 下方抛物线上的动点，求△PEF 面积的最大值及点P的坐标.
变式3 如图，抛物线中的点A、B、C与例题中的点A、B、C一样， 点P是直线AC上方抛物线上的动点，是否存在点P，使 S PAC 2S ABC ，若存在，求出点P的坐标.
二、试题解析
变式4 若B、C是抛物线与x轴的交点，A是抛物线与y轴的交 点，点D是线段AC上的动点，过点D作x轴的垂线与抛 物线相交于点E，当点D运动到什么位置时，四边形 ABCE的面积最大？求四边形ABCD面积的最大值及此 时点D的坐标.
图3 (-3,-5)

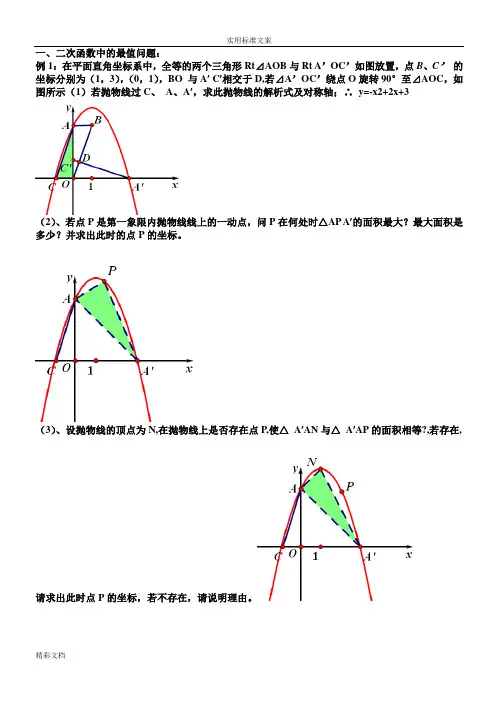
一、二次函数中的最值问题：例1：在平面直角坐标系中，全等的两个三角形Rt⊿AOB与Rt A’OC’如图放置，点B、C’的坐标分别为（1，3），（0，1），BO 与A’ C’相交于D,若⊿A’OC’绕点O旋转90°至⊿AOC，如图所示（1）若抛物线过C、A、A’，求此抛物线的解析式及对称轴；∴y=-x2+2x+3（2）、若点P是第一象限内抛物线线上的一动点，问P在何处时△AP A’的面积最大？最大面积是多少？并求出此时的点P的坐标。

（3）、设抛物线的顶点为N,在抛物线上是否存在点P,使△A’AN与△A’AP的面积相等?,若存在,请求出此时点P的坐标，若不存在，请说明理由。

例2、（2012攀枝花）如图，在平面直角坐标系xOy中，四边形ABCD是菱形，顶点A．C．D均在坐标轴上，且AB=5，sinB=．（1）求过A．C．D三点的抛物线的解析式；（2）记直线AB的解析式为y1=mx+n，（1）中抛物线的解析式为y2=ax2+bx+c，求当y1＜y2时，自变量x的取值范围；（3）设直线AB与（1）中抛物线的另一个交点为E，P点为抛物线上A．E两点之间的一个动点，当P点在何处时，△PAE的面积最大？并求出面积的最大值．解答：解：（1）∵四边形ABCD是菱形，∴AB=AD=CD=BC=5，sinB=sinD=；Rt△OCD中，OC=CD•sinD=4，OD=3；OA=AD﹣OD=2，即：A（﹣2，0）、B（﹣5，4）、C（0，4）、D（3，0）；设抛物线的解析式为：y=a（x+2）（x﹣3），得：2×（﹣3）a=4，a=﹣；∴抛物线：y=﹣x2+x+4．（2）由A（﹣2，0）、B（﹣5，4）得直线AB：y1=﹣x﹣；由（1）得：y2=﹣x2+x+4，则：，解得：，；由图可知：当y1＜y2时，﹣2＜x＜5．（3）∵S△APE=AE•h，∴当P到直线AB的距离最远时，S△ABC最大；若设直线L∥AB，则直线L与抛物线有且只有一个交点时，该交点为点P；设直线L：y=﹣x+b，当直线L与抛物线有且只有一个交点时，﹣x+b=﹣x2+x+4，且△=0；求得：b=，即直线L：y=﹣x+；可得点P（，）．由（2）得：E（5，﹣），则直线PE：y=﹣x+9；新课标第一网则点F（，0），AF=OA+OF=；∴△PAE的最大值：S△PAE=S△PAF+S△AEF=××（+）=．综上所述，当P（，）时，△PAE的面积最大，为．针对训练：1、（2013宜宾）如图，抛物线y1=x2﹣1交x轴的正半轴于点A，交y轴于点B，将此抛物线向右平移4个单位得抛物线y2，两条抛物线相交于点C．（1）请直接写出抛物线y2的解析式；（2）若点P是x轴上一动点，且满足∠CPA=∠OBA，求出所有满足条件的P点坐标；（3）在第四象限内抛物线y2上，是否存在点Q，使得△QOC中OC边上的高h有最大值？若存在，请求出点Q的坐标及h的最大值；若不存在，请说明理由．解答：解：（1）抛物线y1=x﹣1向右平移4个单位的顶点坐标为（4，﹣1），所以，抛物线y2的解析式为y2=（x﹣4）2﹣1；（2）x=0时，y=﹣1，y=0时，x2﹣1=0，解得x1=1，x2=﹣1，所以，点A（1，0），B（0，﹣1），∴∠OBA=45°，联立，解得，∴点C的坐标为（2，3），∵∠CPA=∠OBA，∴点P在点A的左边时，坐标为（﹣1，0），在点A的右边时，坐标为（5，0），所以，点P的坐标为（﹣1，0）或（5，0）；（3）存在．∵点C（2，3），∴直线OC的解析式为y=x，设与OC平行的直线y=x+b，联立，消掉y得，2x2﹣19x+30﹣2b=0，当△=0，方程有两个相等的实数根时，△QOC中OC边上的高h有最大值，此时x1=x2=×（﹣）=，此时y=（﹣4）2﹣1=﹣，∴存在第四象限的点Q（，﹣），使得△QOC中OC边上的高h有最大值，此时△=192﹣4×2×（30﹣2b）=0，解得b=﹣，∴过点Q与OC平行的直线解析式为y=x﹣，令y=0，则x﹣=0，解得x=，设直线与x轴的交点为E，则E（，0），过点C作CD⊥x轴于D，根据勾股定理，OC==，则sin ∠COD==， 解得h 最大=×=．2、如图，抛物线)0(2232≠--=a x ax y 的图象与x 轴交于A 、B 两点，与y 轴交于C 点，已知B 点坐标为()0,4.（1）求抛物线的解析式；（2）试探究ABC ∆的外接圆的圆心位置，并求出圆心坐标；（3）若点M 是线段BC 下方的抛物线上一点，求MBC ∆的面积的最大值，并类型一、最值问题：类型一、最值问题：（2013•泸州）如图，在直角坐标系中，点A 的坐标为（﹣2，0），点B 的坐标为（1，﹣），已知抛物线y=ax 2+bx+c （a ≠0）经过三点A 、B 、O （O 为原点）．（1）求抛物线的解析式；（2）在该抛物线的对称轴上，是否存在点C ，使△BOC 的周长最小？若存在，求出点C 的坐标；若不存在，请说明理由；（3）如果点P 是该抛物线上x 轴上方的一个动点，那么△PAB 是否有最大面积？若有，求出此时P 点的坐标及△PAB 的最大面积；若没有，请说明理由．（注意：本题中的结果均保留根号）），﹣﹣（+，解得：﹣，﹣，﹣﹣x（PE（+y）﹣y）﹣（（y+（﹣x+x x+（）﹣的面积最大，最大值为××，，类型二、探索三角形的存在性。

个分支的理解和掌握。
02
掌握解题方法
解决二次函数动点面积最值问题需要掌握一定的解题技巧和方法，包括
数形结合、参数分离、极值法等。通过对这些方法的运用，可以有效地
解决各种复杂的问题。
03
理解问题本质
二次函数动点面积最值问题的本质是寻找函数在某个区间上的最大值或
最小值，以及对应的自变量取值。通过对问题本质的深入理解，可以更
矩形面积的最值
在矩形中找一点，使得该点与矩形顶点的连线将矩形划分为四个面积相等的部分 ，也可以利用二次函数动点面积最值问题求解。
在实际生活中的应用
土地规划
在土地规划中，经常需要确定土地的 分割方式以及各部分的面积，利用二 次函数动点面积最值问题可以找到最 优的分割方案，使得土地的利用率达 到最高。
局。
城市绿化
在城市绿化规划中，通过求解二 次函数动点面积最值问题，可以 确定最佳的绿化区域和分布方式 ，提高城市绿化覆盖率和环境质
量。
06
总结和展望
对二次函数动点面积最值问题的理解和总结
01
理解问题背景
二次函数动点面积最值问题是一个经典的数学问题，涉及到几何、代数
和微积分等多个领域的知识。通过对该问题的研究，可以加深对数学各
要点二
代数解法
通过几何方法（如相似三角形、勾股定理等）来求解动点 面积的最值。
利用代数公式和不等式，通过代数运算求解动点面积的最 值。
二次函数动点面积最值问题的实际应用案例
建筑规划
在建筑规划中，需要考虑土地利 用效率与美观性，动点面积最值 问题可以帮助规划者找到最佳的
建筑布局方案。
农业种植
农业种植中，为了最大化土地利 用率和产量，可以利用二次函数 动点面积最值问题来优化种植布

二次函数双动点面积最值引言二次函数是高中数学中的一个重要内容，涉及到很多有趣的性质和应用。

本文将讨论二次函数中的一个特殊问题：如何确定二次函数的两个动点，使得其面积最值。

我们将从理论和实际问题两个方面进行探讨。

二次函数的基本性质在讨论如何确定二次函数的两个动点面积最值之前，我们先来回顾一下二次函数的基本性质。

1. 二次函数的一般形式二次函数的一般形式可以表示为：y=ax2+bx+c，其中a、b、c为常系数。

2. 二次函数的图像二次函数的图像通常为抛物线，其开口的方向由a的正负决定。

当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

3. 二次函数的顶点二次函数的顶点对应着抛物线的最值点。

对于一般形式的二次函数y=ax2+bx+c，顶点的横坐标为x=−b2a ，纵坐标为y=−b2−4ac4a。

利用动点确定二次函数在确定二次函数的两个动点面积最值之前，我们需要先明确什么是动点。

在二次函数中，动点指的是抛物线上的一点，其坐标可以随着抛物线的变化而变化。

1. 动点的坐标表示假设我们的二次函数为y=ax2+bx+c，动点的坐标为(x1,y1)和(x2,y2)，其中x1、x2为动点的横坐标，y1、y2为动点的纵坐标。

2. 动点的面积表示由于动点位于抛物线上，我们可以通过计算动点形成的三角形的面积来表示动点的面积。

假设动点为(x1,y1)和(x2,y2)，则动点形成的三角形的面积为S=12(x1−x2)(y1+y2)。

寻找面积最值的方法接下来，我们将讨论如何确定二次函数的两个动点，使得其面积最大或最小。

1. 面积最大值的情况要确定二次函数的两个动点，使得其面积最大，我们需要寻找抛物线的顶点。

由于顶点对应着抛物线的最值点，我们可以利用二次函数的顶点公式来确定动点的横坐标。

设顶点的横坐标为x v，则可知x1=x v和x2=x v。

将这些坐标代入动点面积的公式中，可以得到动点面积的表达式S=12(x v−x v)(y1+y2)。

教学过程一、课堂导入在平面直角坐标系中，四边形ABCD的顶点坐标分别为A（1，0），B（5，0），C（3，3），D（2，4），问题：这是在平面直角坐标系那章我们经常遇到的求四边形面积的题目，这类问题相信大家都有不同的解题方法，在二次函数这一章，我们依然要研究四边形的面积，如果我们将二次函数容纳其中，在抛物线(直线、坐标轴等)上求作一点，使得四边形面积最大并求出该点坐标时,又该如何解答呢？二、复习预习（一）二次函数y=ax2+bx+c的图像和性质：（二）相似三角形的性质：(1)相似三角形的对应角相等。

(2)相似三角形的对应边成比例。

(3)相似三角形的对应高线的比，对应中线的比和对应角平分线的比都等于相似比。

(4)相似三角形的周长比等于相似比。

(5)相似三角形的面积比等于相似比的平方。

（三）相似三角形模型探究与解题技巧：1、课堂导入题解如图，在平面直角坐标系中有两点A（4，0）、B（0，2），如果点C在x轴上（C与A不重合），当点C的坐标为_________________时，使得由点B、O、C组成的三角形与△AOB相似（至少找出两个满足条件的点的坐标）．解：∵点C在x轴上，∴点C的纵坐标是0，且当∠BOC=90°时，由点B、O、C组成的三角形与△AOB 相似，即∠BOC应该与∠BOA=90°对应，①当△AOB∽△COB，即OC与OA相对应时，则OC=OA=4，C（-4，0）；②当△AOB∽△BOC，即OC与OB对应，则OC=1，C（-1，0）或者（1，0）．故答案可以是：（-1，0）；（1，0）．解析：分类讨论：①当△AOB∽△COB时，求点C的坐标；②当△AOB∽△BOC时，求点C的坐标；如果非直角三角形也要分类讨论，对应边不一样就得到不同的结果。

2、几种常见的相似三角形模型①直角三角形相似的几种常见模型②非直角三角形相似的几种常见模型3、解题技巧函数中因动点产生的相似三角形问题一般有三个解题途径。

求解动点图形面积最值的步骤
1
步骤1
确定最值问题的区间。
2
步骤2
通过求导或综合判断确定极值点或临界点。
3
ቤተ መጻሕፍቲ ባይዱ
步骤3
计算极值点或临界点对应的面积。
案例分析：计算动点图形面积 最大值和最小值
假设二次函数为y = -x^2 + 3x + 2，动点轨迹为一条垂直于x轴的直线，探索动 点图形的面积变化。通过计算可以得到动点图形的最大面积和最小面积。
二次函数中动点图形的面 积最值
二次函数是数学中的一个重要概念，它描述了一种用抛物线表示的函数关系。 本节将探讨如何通过动点图形的面积来寻找二次函数中的最值。
二次函数简介
二次函数是一种具有二次项的代数函数，它的一般形式为y = ax^2 + bx + c。二次函数在数学和物理学中有广泛 的应用，可以用来描述各种实际问题。
问题讨论与思考
除了计算动点图形面积的最值，我们还可以思考以下问题：如何改变函数的系数以改变图形的面积范围？是否 存在其他方法来求解动点图形的最值？这些问题可以帮助我们深入理解二次函数和面积最值概念的应用。
结论和总结
通过寻找二次函数中动点图形的面积最值，我们可以进一步理解函数的性质 和图像的变化规律。这一概念在数学和实际问题中都具有重要的应用价值。
最值的概念和意义
最值是指函数在给定区间内取得的最大值或最小值。在二次函数中，最值的 位置和数值可以提供关于函数图像的重要信息，帮助我们解决实际问题。
动点图形面积的计算方法
步骤1
确定二次函数的表达式，并 绘制函数图像。
步骤2
确定动点的轨迹，通常是垂 直于x轴的直线或水平于y轴 的直线。
步骤3
计算动点图形的面积。

“二次函数”面积最值问题的几种解法以微课堂公益课堂，奥数国家级教练与四位特级教师联手执教。

二次函数是初中数学的一个重点、难点，也是中考数学必考的一个知识点。

特别是在压轴题中，二次函数和几何综合出现的题型，才是最大的区分度。

而求三角形面积的最值问题，更是常见。

今天介绍二次函数考试题型种，面积最值问题的4种常用解法。

同学们只要熟练运用一两种解法，炉火纯青，在考试答题的时候，能够轻松答题，就好。

原题：在（1）中的抛物线上的第二象限是否存在一点P，使△PBC的面积最大？若存在，求出P点的坐标及△PBC的面积最大值，若没有，请说明理由。

考试题型，大多类似于此。

求面积最大值的动点坐标，并求出面积最大值。

一般解题思路和步骤是，设动点P的坐标，然后用代数式表达各线段的长。

通过公式计算，得出二次函数顶点式，则坐标和最值，即出。

解法一：补形，割形法。

方法要点是，把所求图像的面积适当的割补，转化成有利于面积表达的常规几何图形。

请看解题步骤。

解法二：铅锤定理，面积=铅锤高度×水平宽度÷2。

这是三角形面积表达方法的一种非常重要的定理。

铅锤定理，在教材上没有，但是大多数数学老师都会作为重点，在课堂上讲解。

因为，铅锤定理，在很多地方都用的到。

这里，也有铅锤定理的简单推导，建议大家认真体会。

解法二：铅锤定理，在求二次函数三角形面积最值问题，运用非常多。

设动点P的坐标，然后用代数式分别表达出铅锤高度和水平宽度，然后利用铅锤定理的计算公式，得出二次函数，必有最大值。

解法三：切线法。

这其实属于高中内容。

但是，基础好的同学也很容易理解，可以看看，提前了解一下。

解法四：三角函数法。

请大家认真看上面的解题步骤。

总之，从以上的四种解法可以得出一个规律。

过点P做辅助线，然后利用相关性质，找出各元素之间的关系。

设动点P的坐标，然后找出各线段的代数式，再通过面积计算公式，得出二次函数顶点式，求出三角形面积的最大值。

对于同学们中考数学来说，只要你熟练掌握解法一和解法二，那么二次函数几何综合题中，求三角形面积最大值问题，就非常简单了。

二次函数双动点面积最值一、问题描述在平面直角坐标系内，给定二次函数 $y=ax^2+bx+c$，且 $a<0$。

定义该二次函数的双动点为其图像上两个不同的点 $(x_1,y_1)$ 和$(x_2,y_2)$，满足 $y=ax^2+bx+c$ 在区间 $(x_1,x_2)$ 内单调递减或单调递增。

现在要求求出所有可能的双动点，并计算出其对应的面积最大值。

二、解题思路本题需要分别考虑二次函数的凸性和双动点的性质。

具体来说，我们可以通过求导数来判断二次函数的凸性，并通过判别式来计算二次方程的根以确定双动点。

然后，我们可以利用双动点的性质，结合微积分知识求出面积最大值。

三、解题步骤1. 求解二次函数的凸性由于$a<0$，因此该二次函数开口向下。

此时，当且仅当$a>0$ 时，该二次函数在整个定义域内为凸函数；当且仅当 $a<0$ 时，该二次函数在整个定义域内为下凸函数。

因此，在本题中，我们可以通过判断 $a$ 的符号来确定该二次函数的凸性。

2. 计算二次方程的根由于$a<0$，因此该二次函数的图像是一个开口向下的抛物线。

此时，该二次函数的双动点必然是两个不同的零点，即 $ax^2+bx+c=0$ 的两个根。

根据二次方程求根公式可得：$$x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$由于 $a<0$，因此 $\sqrt{b^2-4ac}$ 为实数。

因此，当 $b^2-4ac>0$ 时，该二次方程有两个不同的实根；当 $b^2-4ac=0$ 时，该二次方程有一个重根；当$b^2-4ac<0$ 时，该二次方程无实数解。

在本题中，我们需要计算出所有可能的双动点。

因此，在计算完根之后，我们需要对其进行判断：若两个根均在定义域内，则它们为一个双动点；若其中一个根在定义域内而另一个不在，则不存在双动点；若两个根均不在定义域内，则也不存在双动点。

二次函数最大面积例1 如图所示，等边△ABC 中，BC=10cm ，点1P ,2P 分别从B,A 同时出发，以1cm/s 的速度沿线段BA,AC 移动，当移动时间t 为何值时，△21P AP 的面积最大？并求出最大面积。

A1P 2PB C练习1如图，在矩形ABCD 中，AB=6cm ，BC=12cm,点P 从点A 出发沿AB 边向点B 以1cm/s 的速度移动，同时点Q 从点B 出发沿BC 边向C 以2cm/s 的速度移动，如果P,Q 同时出发，分别到达B 、C 两点就停止移动。

（1）设运动开始后第t 秒，五边形APQCD 的面积是2Scm ，写出S 与t 函数关系式，并指出t 的取值范围。

（2）t 为何值时，S 最小？并求出这个最小值。

D CQA P B2 如图，在△ABC 中，∠B=90°，AB=22CM,BC=20CM ，点P 从点A 开始沿AB 边向点B 以2cm/S 的速度移动，点Q 从点B 开始沿着BC 边向点C 以1cm/S 的速度移动，P,Q 分别从A,B 同时出发。

求四边形APQC 的面积y （2cm ）与PQ 移动时间x （s ）的函数关系式， A 以及自变量x 的取值范围。

PB Q C3 如图 正方形ABCD 的边长为4cm ，点P 是BC 边上不与B,C 重合的任意一点，连接AP ，过点P 作PQ ⊥AP 交DC 于点Q,设BP 的长为x cm ，CQ 的长为y cm 。

（1）求点P 在BC 上的运动的过程中y 的最大值。

（2）当y=41cm 时，求x 的值。

A DB P C4如图所示，边长为1的正方形OABC 的顶点O 为坐标原点，点A 在x 轴的正半轴上，动点D 在线段BC 上移动（不与B,C 重合），连接OD ，过点D 作DE ⊥OD,交AB 于点E ，连接OE ，记CD 的长为t 。

y （1） 当t=31时 ，求线段DE 所在直线的函数表达式。

二次函数动点问题中面积最值的解法策略摘要：我国正在实施新的基础教育课程改革，《义务教育数学课程标准（２０22年版）》指出要培养学生的数学核心素养，而二次函数和几何图形的综合应用题，能充分的考查学生的数学抽象，逻辑推理，数学运算以及数学建模等综合能力。

这种类型的综合题，通常出现在中考的压轴题中，综合性强，计算强度大，具有较大的难度，在二次函数与几何图形的综合题中，求二次函数面积的最值问题比较常见，本文就此问题解法进行探讨。

关键词：二次函数与几何图形；函数动点问题；二次函数面积最值二次函数动点问题就是通过点的运动生成一种函数关系及函数图象，抛物线上点的运动与直线相结合而产生的三角形面积问题，就是将几何图形与函数图象有机地融合在一起，解决的关键是结合图形通过点坐标衔接函数、方程找到函数关系。

本文就求解二次函数面积最值的问题，浅谈几种解决此类问题的方法策略。

一、割补法在解决二次函数面积最值问题时，不规则多边形的面积往往可以通过割补法把多边形分为几个三角形或者是规则的四边形的面积来求解，当三角形中有一边是在坐标轴上，或者在以坐标轴平行的直线上，那么就可以把这一条边当作三角形的底边，第三个点到这一条边的距离，作为三角形的高，直接利用三角形的面积公式求解，或者过图形的各端点作两坐标轴的平行线，构造与轴平行的最小矩形对所要求面积的图形进行覆盖，然后所求图形的面积即为矩形面积减去多余的几个直角三角形的面积。

最终把多边形面积的最值问题，转化为求三角形面积的最值问题，这也体现了一种“化归”的思想方法。

题目1、(2019枣庄)已知抛物线y＝ax2＋x＋4的对称轴是直线x＝3，与x轴相交于A，B两点(点B在点A右侧)，与y轴交于点C.(1)求抛物线的解析式和A，B两点的坐标；(2)如图①，若点P是抛物线上B、C两点之间的一个动点(不与B、C重合)，是否存在点P，使四边形PBOC的面积最大？若存在，求点P的坐标及四边形PBOC面积的最大值；若不存在，请说明理由.[思路分析]（1）由抛物线的对称轴是直线x=3，解出a的值，即可求得抛物线的表达式，再令其y值为0，解一元二次方程即可求出A和B的坐标。

（A在B的左边），与y轴交于点C.
y
（4）若点P是抛物线的顶点,
求四边形ACPB的面积.
y
y
A
B
O
x
O
A
B
C
P
O
y
xA
B
CQ
x
C
PO
P
HA
B
x
C
P
7
问题5：抛物线上的面积问题
已知二次函数 y=x2-2x-3 与x轴交于A、B两点 （A在B的左边），与y轴交于点C.
y
（5）设M（a，b）（其中0<a<3）是
2020/4/4
3
如图1，抛物线y＝－x2＋bx＋c与x轴交于A(1，0)， B(－3，0)两点．
(1)求该抛物线的解析式；
• (2)如图2，在(1)中的抛物线上的第二象限上是否存在 一点P，使△PBC的面积最大？若存在，求出点P的坐 标及△PBC的面积最大值；若没有，请说明理由。
2020/4/4
二次函数中的动点面积问题
教学目标：1.会用代数法表示几何 图形的面积最值问题。 2.能用函数图象的性质解决相关问题。
教学重点：二次最值问题的解决。
2020/4/4
1
2020/4/4
2
22．（12分）（2016•安徽）如图，二次函数 y=ax2+bx的图象经过点A（2，4）与B（6，0）． （1）求a，b的值； （2）点C是该二次函数图象上A，B两点之间的一动 点，横坐标为x（2＜x＜6），写出四边形OACB的面 积S关于点C的横坐标x的函数表达式，并求S的最大 值．
4
知识总结
“二次函数中动点图形的面积最值”试题 解析一般规律： 这类问题的特征是要以静代动解题，首先 找面积关系的函数解析式，关键是用含未 知数的代数式表示出相关的线段的长度， 若是规则图形则套用公式，若为不规则图 形则用割补法.

二次函数与面积最值定值问题(六大类型)1.考向分析题型一:二次函数与三角形面积最值问题1如图，已知抛物线y =12x 2+bx 过点A (-4，0)、顶点为B ，一次函数y =12x +2的图象交y 轴于M ，对称轴与x 轴交于点H ．(1)求抛物线的表达式；(2)已知P 是抛物线上一动点，点M 关于AP 的对称点为N ．①若点N 恰好落在抛物线的对称轴上，求点N 的坐标；②请直接写出△MHN 面积的最大值．【解析】解：(1)∵抛物线y =12x 2+bx 过点A (-4，0)，∴12×(-4)2-4b =0，解得：b =2，∴该抛物线的表达式为y =12x 2+2x ；(2)①∵y =12x 2+2x ，∴抛物线对称轴为直线x =-22×12=-2，∵对称轴与x 轴交于点H ，∴H (-2，0)，∵A (-4，0)，∴AH =2，∵直线y =12x +2交y 轴于M ，∴M (0，2)，∴AM 2=OA 2+OM 2=42+22=20，设N (-2，n )，则NH =|n |，如图1、图2，∵M 、N 关于直线AP 对称，∴AN =AM ，即AN 2=AM 2，∴22+n 2=20，∴n =±4，∴点N 的坐标为(-2，-4)或(-2，4)；②如图，连接MH ，以点A 为圆心，AM 为半径作⊙A ，过点A 作AN ⊥MH 于点F ，交⊙A 于点N ，则AN =AM ，在Rt △AMO 中，OM =2，OA =4，∴AM =OA 2+OM 2=42+22=25，∴AN =25，∵OH =OM =2，∠HOM =90°，∴△HOM 是等腰直角三角形，∠MHO =45°，MH =22，∴∠AHF =∠MHO =45°，在Rt △AFH 中，AH =OA -OH =4-2=2，∴AF =AH ×sin45°=2×22=2，∴NF =AN +AF =25+2，∴S △MHN =12MH •NF =12×22×(25+2)=210+2，故△MHN 面积的最大值为210+2．题型二:二次函数与三角形面积等积问题2如图，等腰直角三角形OAB 的直角顶点O 在坐标原点，直角边OA ，OB 分别在y 轴和x 轴上，点C 的坐标为(3，4)，且AC 平行于x 轴．(1)求直线AB 的解析式；(2)求过B ，C 两点的抛物线y =-x 2+bx +c 的解析式；(3)抛物线y =-x 2+bx +c 与x 轴的另一个交点为D ，试判定OC 与BD 的大小关系；(4)若点M 是抛物线上的动点，当△ABM 的面积与△ABC 的面积相等时，求点M 的坐标．【解析】解：(1)∵点C 的坐标为(3，4)，且AC 平行于x 轴，∴点A 的坐标为(0，4)且OA =4，∵△OAB 是等腰直角三角形，∠AOB =90°，∴OB =OA =4，∵点B 的坐标为(4，0)，设直线AB的解析式为：y=mx+n，由题意得4m+n=0n=4，解得：m=-1n=4，∴直线AB的解析式为：y=-x+4；(2)∵抛物线y=-x2+bx+c过B，C两点，∴-16+4b+c=0-9+3b+c=4，解得：b=3c=4，∴抛物线的解析式为：y=-x2+3x+4；(3)BD=OC；理由：∵抛物线的解析式为y=-x2+3x+4=-x-322+52，∴抛物线的对称轴直线为x=32，∵点B的坐标为(4，0)，点B与点D关于对称轴对称，∴点D的坐标为(-1，0)，∴BD=4-(-1)=5，∵点C的坐标为(3，4)，∴OC=32+42=5，∴BD=OC；(4)∵点C的坐标为(3，4)，且AC平行于x轴，∴AC=3，∴S△ABC=12AC•y C=12×3×4=6，当点M在直线AB的上方时，如图所示，过点M作MN∥y轴，交直线AB于点N，设M的坐标为(t，-t2+3t+4)，则N的坐标为(t，-t+4)，∴MN=-t2+3t+4-(-t+4)=-t2+4t，∴S△AMB=12MN•x B=12×(-t2+4t)×4=-2t2+8t，∵△ABM的面积与△ABC的面积相等，∴-2t2+8t=6，解得：t=1或t=3(舍，该点为点C)，此时M的坐标为(1，6)或(3，4)；当点M在直线AB的下方时，如图所示，过点M作MN∥x轴，交直线AB于点N，设M的坐标为(t，-t2+3t+4)，则N的坐标为(t2-3t，-t2+3t+4)，∴MN=t2-3t-t=t2-4t，∴S△ABM=12MN•y A=12×(t2-4t)×4=2t2-8t，∵△ABM的面积与△ABC的面积相等，∴2t2-8t=6，解得：t=2±7，此时M的坐标为(2+7，-1-7)或(2-7，7-1)；综上可得，M的坐标为(2+7，-1-7)或(2-7，7-1)或(1，6)．题型三:二次函数与四边形面积最值问题3如图，在平面直角坐标系中，抛物线y=-x2+bx+c与x轴交于A、B两点，与y轴交于点C．已知A(3，0)，该抛物线的对称轴为直线x=1．(1)求该抛物线的函数表达式；(2)求点B、C的坐标；(3)将线段BC平移，使得平移后线段的一个端点在这条抛物线上，另一个端点在x轴上，若将点B、C平移后的对应点分别记为点D、E，求以B、C、D、E为顶点的四边形面积的最大值．【解析】解：(1)∵抛物线对称轴为直线x=-b-2=1，∴b=2，∴y=-x2+2x+c，将(3，0)代入y=-x2+2x+c得0=-9+6+c，解得c=3，∴y=-x2+2x+3．(2)∵抛物线对称轴为直线x=1，点A坐标为(3，0)，∴由抛物线对称性可得点B坐标为(-1，0)，将x=0代入y=-x2+2x+3得y=3，∴点C坐标为(0，3)．(3)如图，可得图2中四边形面积最大，∵BC∥DE且BC=DE，图1图2图3∵y C-y B=y E-y D，∴y D=-3，将y=-3代入y=-x2+2x+3得-3=-x2+2x+3，解得x1=1-7(舍)，x2=1+7，∴点E横坐标为1+7+1=2+7，∴BE=2+7+1=3+7，∴S四边形BDEC =12BE•y C+12BE•|y D|=12×(3+7)×3+12×(3+7)×3=9+37．题型四:二次函数与面积分割问题4已知抛物线y=x2+4mx+4m2-4m-3的顶点C在定直线l上．(1)求C点的坐标(用含m的式子表示)；(2)求证：不论m为何值，抛物线与定直线l的两交点间的距离d恒为定值；(3)当抛物线的顶点C在y轴上，且与x轴交于A，B两点(点A在点B的左侧)时，是否存在直线n满足以下三个条件：①n与抛物线相交于点M，N(点M在点N的左侧)，且与线段AC交于点P；②∠APN=2∠ACO；③n将△ABC的面积分成1：2的两部分．若存在，求出直线n的解析式；若不存在，请说明理由．【解析】(1)解：∵y=x2+4mx+4m2-4m-3=(x+2m)2-4m-3，∴顶点C(-2m，-4m-3)；(2)证明：∵C(-2m，-4m-3)，∴C点在直线y=2x-3上，∴定直线l为y=2x-3，联立方程组y=2x-3y=x2+4mx+4m2-4m-3 ，解得x=-2my=-4m-3或x=2-2my=-4m+1，∴两个交点分别为(-2m，-4m-3)，(2-2m，-4m+1)，∴d=(2-2m+2m)2+(-4m+1+4m+3)2=25，∴抛物线与定直线l的两交点间的距离d恒为定值；(3)解：存在直线n，理由如下：∵顶点C在y轴上，∴m=0，∴y=x2-3，令y=0，则x2-3=0，解得x=3或x=-3，∴A(-3，0)，B(3，0)，∴AB=23，∵抛物线关于y轴对称，∴∠ACO=∠BCO，∵∠APN=2∠ACO，∴∠APN=∠ACB，∴MN ∥BC ，设直线BC 的解析式为y =kx +b ，∴b =-33k +b =0 ，解得k =3b =-3 ，∴y =3x -3，设直线MN 的解析式为y =3x +t ，直线MN 与x 轴的交点为H ，∵直线MN 将△ABC 的面积分成1：2，∴S △PAH =13S △ACB 或S △PAH =23S △ACB ，∴AH AB2=13或AH AB 2=23，∴AH 23=33或AH 23=63，解得AH =2或AH =22，∴H (2-3，0)或(22-3，0)，∴直线MN 的解析式为y =3x +3-23或y =3x +3-26．题型五:二次函数与面积比问题5如图，在平面直角坐标系xOy 中，二次函数y =23x 2+bx -2的图象与x 轴交于点A (3，0)，B (点B 在点A 左侧)，与y 轴交于点C ，点D 与点C 关于x 轴对称，作直线AD ．(1)填空：b =　-43　；(2)将△AOC 平移到△EFG (点E ，F ，G 依次与A ，O ，C 对应)，若点E 落在抛物线上且点G 落在直线AD 上，求点E 的坐标；(3)设点P 是第四象限抛物线上一点，过点P 作x 轴的垂线，垂足为H ，交AC 于点T ．若∠CPT +∠DAC =180°，求△AHT 与△CPT 的面积之比．【解析】解：(1)把A (3，0)代入y =23x 2+bx -2，得23×9+3b -2=0，解得b =-43；故答案为：-43；(2)如图所示：由(1)得y =23x 2-43x -2，令x =0，y =-2，∴C (0，-2)，∵点D 与点C 关于x 轴对称，∴D (0，2)，设直线AD ：y =kx +2，把A (3，0)代入y =kx +2，得3k +2=0，解得k =-23，∴直线AD 解析式：y =-23x +2，∵将△AOC 平移到△EFG ，∴OA =EF =3，FG =OC =2，设E m ，23m 2-43m -2 ，则G m -3，-23(m -3)+2 ，F m -3，-23(m -3)+4 ，∵EF ∥x 轴，∴23m 2-43m -2=-23(m -3)2+4，解得m =-3或m =4，∴E (-3，8)或4，103；(3)如图所示：过C 作CK ⊥AD ，CQ ⊥HP ，∵OD =2，OA =3∴AD =13，∵CK ⊥AD∴CD •AO =AD •CK ，∴CK =121313，DK =81313，AK =51313，∴tan ∠CAK =CK AK=125，∵CQ ⊥HP ，∴∠CPQ +∠CPT =180°，∵∠CPT +∠DAC =180°，∴∠CPQ =∠CAK ，∴tan ∠CPQ =tan ∠CAK =125，∴CQ PQ =125，设P n ，23n 2-43n -2 ，∴PQ =23n 2-43n ，CQ =n ，∴n 23n 2-43n =125，解得n =218，∴P 218，-2932，∴CQ =218，AH =3-218=38，∵tan ∠OAC =TH AH =OC OA =23，∴TH =23AH =23×38=14，∴TP =2132，∴S △ATH S △CPT =12×AH ×TH 12×TP ×CQ =8147，即△AHT 与△CPT 的面积之比为8：147．题型六:函数关系与面积问题6平面直角坐标系中，已知抛物线y =-x 2+(1+m )x -m (m 为常数，m ≠±1)与轴交于定点A 及另一点B ，与y 轴交于点C ．(1)当点(2，2)在抛物线上时，求抛物线解析式及点A ，B ，C 的坐标；(2)如图1，在(1)的条件下，D 为抛物线x 轴上方一点，连接BD ，若∠DBA +∠ACB =90°，求点D 的坐标；(3)若点P 是抛物线的顶点，令△ACP 的面积为S ，①直接写出S 关于m 的解析式及m 的取值范围；②当58≤S ≤158时，直接写出m 的取值范围．【解析】(1)将点(2，2)代入y =-x 2+(1+m )x -m ，求出m 即可确定函数的解析式；(2)过D 点作DE ⊥x 轴交于E ，过A 点作AF ⊥BC 交于F ，由题意可知∠ACB =∠BDE ，求出tan ∠ACF =tan ∠BDE =BE DE=35，设D (t ，-t 2+5t -4)(0<t <4)，求出t 的值即可求D 点坐标；(3)①求出P 1+m 2，(1-m )24，C (0，-m )，定点A (1，0)，B (m ，0)，AC 的解析式为y =kx +b ，y =mx -m ，再画出函数图象结合函数图象分类讨即可；②对①中求出的解析式分别进行求解即可．【解答】解：(1)将点(2，2)代入y =-x 2+(1+m )x -m ，∴m =4，∴y =-x 2+5x -4，令x =0，则y =-4，∴C (0，-4)，令y =0，则-x 2+5x -4=0，∴x =1或x =4，∴A (1，0)，B (4，0)；(2)如图1，过D 点作DE ⊥x 轴交于E ，过A 点作AF ⊥BC 交于F ，∵∠DBA +∠ACB =90°，∠DBA +∠BDE =90°，∴∠ACB =∠BDE ，∵B (4，0)，C (0，-4)，∴OB =OC =4，∴∠OBC =45°，∵BA =3，∴AF =322，∵A (1，0)，∴AC =17，∴CF =522，∴tan ∠ACF =AF CF =35，∴tan ∠BDE =BE DE=35，设D (t ，-t 2+5t -4)(0<t <4)，∴4-t -t 2+5t -4=35，解得x =4(舍)或x =83，∴D 83，209；(3)①∵y =-x 2+(1+m )x -m =-x -1+m 2 2+(1-m )24，∴P 1+m 2，(1-m )24，令x =0，则y =-m ，∴C (0，-m )，令y =0，则-x 2+(1+m )x -m =0，解得x =1或x =m ，∴定点A (1，0)，B (m ，0)，设AC 的解析式为y =kx +b ，∴k +b =0b =-m，解得k =m b =-m ，∴y =mx -m ，如图2，当m <-1时，S =S 梯形PNOC +S △OCA -S △PAN =12×(1-m )24-m×1+m 2+12×1×(-m )-12×1-1+m 2 ×(1-m )24=18m 2-18；如图3，当-1<m <0时，S =S 梯形PNOC +S △PNA -S △AOC =12×(1-m )24-m ×1+m 2+12×1-1+m 2 ×(1-m )24-12×1×(-m )=-18m 2+18；如图4，当0≤m <1时，设对称轴与直线AC 交于点M ，∴M 1+m 2，m 2-m 2，∴PM =-14m 2+14，∴S =12×-14m 2+14 ×1=-18m 2+18；如图5，当m >1时，过点C 作CM ⊥PN 交于点M ，∴M 1+m 2，-m ，∴S =S 矩形OCMN +S △APN -S △OCA -S △CMP =1+m 2×m +12×1+m 2-1 ×(1-m )24-12×1×m -12×1+m 2×(1-m )24+m =18m 2-18；综上所述：当m <-1时，S =18m 2-18；当-1<m <1，S =-18m 2+18；当m >1时，S =18m 2-18；②当m <-1时，58≤18m 2-18≤158，解得-4≤m ≤-6；当-1<m <0，58≤-18m 2+18≤158，此时m 无解；当0≤m <1时，58≤-18m 2+18≤158，此时m 无解；当m >1时，58≤18m 2-18≤158，解得6≤m ≤4；综上所述：当58≤S ≤158时，-4≤m ≤-6或6≤m ≤4．2.压轴题速练1一、解答题1(2023春·全国·九年级专题练习)已知：如图，抛物线y =ax 2+bx +c (a ≠0)与坐标轴分别交于点A (0,6)，B (6,0)，C (-2,0)，点P 是线段AB上方抛物线上的一个动点．(1)求抛物线的解析式；(2)当点P 运动到什么位置时，△PAB 的面积有最大值，面积最大值是多少？【答案】(1)y =-12x 2+2x +6(2)当P 3,152 时，△PAB 的面积有最大值，最大值是272．【解析】(1)由题意得：36a +6b +c =04a -2b +c =0c =6，解得：a =-12b =2c =6，∴抛物线的表达式为：y =-12x 2+2x +6；(2)∵A (0,6)∴直线AB 的表达式为：y =kx +6，将点B 的坐标代入上式得：0=6k +6，解得：k =-1，∴直线AB 的表达式为：y =-x +6，点P 的横坐标为m ，则P m ,-12m 2+2m +6 ，过点P 作x 轴的垂线，交线段AB 于点D ，则D (m ,-m +6)，∴S =12×OB ×PD =12×6×-12m 2+2m +6+m -6 =-32(m -3)2+272，∴当m =3时，S 的值取最大，此时P 3,152；2(2023春·全国·九年级专题练习)如图，抛物线y =ax 2+bx +6(a ≠0)与x 轴交于A (-1，0)，B (6，0)，与y 轴交于点C ，点P 为第一象限内抛物线上一动点，过点P 作x 轴的垂线，交直线BC 于点D ，交x 轴于点E ，连接 PB ．(1)求该抛物线的解析式；(2)当△PBD 与△BDE 的面积之比为1：2时，求点P 的坐标；【答案】【答案】(1)y =-x 2+5x +6(2)P 12,334【解析】(1)∵抛物线y =ax 2+bx +6(a ≠0)与x 轴交于A -1,0 ,B 6,0∴a -b +6=036a +6b +6=0，∴a =-1b =5 ，∴抛物线的解析式为y =-x 2+5x +6；(2)∵抛物线y =-x 2+5x +6过点C ，∴C (0，6)，设直线BC 的解析式为 y =kx +n ，∴6k +n =0n =6，∴k =-1n =6 ，∴直线BC 的解析式为y =-x +6，设P m ,-m 2+5m +6 ，则D m ,-m +6 ，∴PE =-m 2+5m +6，DE =-m +6，∵△PBD 与△BDE 的面积之比为1：2，∴PD ：DE =1：2，∴PE ：DE =3：2，∴3-m +6 =2-m 2+5m +6 ，解得m 1=12，m 2=6(舍去)，∴P 12,334；3(2023春·全国·九年级专题练习)如图，抛物线y =-x 2+bx +c 过点A 、B ，抛物线的对称轴交x 轴于点D ，直线y =-x +3与x 轴交于点B ，与y 轴交于点C ，且OA =13OB ．(1)求抛物线的解析式；(2)点M t ,0 是x 轴上的一个动点，点N 是抛物线对称轴上的一个动点，当DN =2t ，△MNB 的面积为154时，求出点M 与点N 的坐标；【答案】【答案】(1)y =-x 2+2x +3(2)3+262,0 ,1,3+26 【解析】(1)解：对于直线y =-x +3，令y =0，即-x +3=0，解得：x =3，令x =0，得y =3，∴B 3,0 ,C 0,3 ，∵A 为x 轴负半轴上一点，且OA =13OB ，∴A -1,0 ．将点A 、B 的坐标分别代入y =-x 2+bx +c 中，得-1-b +c =0-9+3b +c =0 ，解得b =2c =3 ，∴抛物线的解析式为y =-x 2+2x +3；(2)解：由(1)知：A -1,0 ，B 3,0 ，抛物线解析式为y =-x 2+2x +3，∴对称轴x =-b 2a =-22×-1=1，∴D 点坐标为D 1,0 ，∵M t ,0∴BM =3-t ，∵S △MNB =12×BM ×DN =154，即12×3-t ×2t =154，当t <3时，12×3-t ×2t =154，化简得：4t 2-12t +15=0，∵Δ=b 2-4ac <0，∴方程无解；当t >3时，12×t -3 ×2t =154，解得t1=3+262,t2=3-262(舍)，∴DN=2t=3+26，∴点M的坐标为3+262,0，点N的坐标为1,3+262；4(2023·广西贵港·统考一模)在平面直角坐标系中，已知抛物线y=ax2+bx经过A(4，0)，B(1，3)两点．P是抛物线上一点，且在直线AB的上方．(1)求抛物线的表达式；(2)若△OAB面积是△PAB面积的2倍，求点P的坐标；(3)如图，OP交AB于点C，PD∥BO交AB于点D．记△CPB，△BCO的面积分别为S1，S2，判断S1S2是否存在最大值．若存在，求出最大值；若不存在，请说明理由．【答案】【答案】(1)y=-x2+4x(2)P(2，4)或(3,3)(3)见解析【解析】(1)解：将A(4，0)，B(1，3)代入y=ax2+bx得16a+4b=0a+b=3，解得：a=-1b=4，∴抛物线的解析式为：y=-x2+4x；(2)解：设直线AB的解析式为：y=kx+t，将A4，0，B1，3代入y=kx+t得4k+t=0 k+t=3 ，解得：k=-1 t=4，∴直线AB的解析式为：y=-x+4，∵A4，0，B1，3，∴S△OAB=12×4×3=6，∴S△OAB=2S△PAB=6，即S△PAB=3，过点P作PM⊥x轴于点M，PM与AB交于点N，过点B作BE⊥PM于点E，如图，∴S△PAB=S△PNB+S△PNA=12PN×BE+12PN×AM=32PN=3，∴PN=2，设点P 的横坐标为m ，∴P (m ,-m 2+4m )(1<m <4)，N (m ,-m +4)，∴PN =-m 2+4m -(-m +4)=2，解得：m =2或m =3；∴P (2,4)或(3，3)；(3)解：S 1S 2存在最大值．理由如下：∵PD ∥OB ，∴∠DPC =∠BOC ，∠PDC =∠OBC ，∴△DPC ∽△BOC ，∴CP :CO =CD :CB =PD :OB ，∵S 1S 2=CD CB =PD OB，设直线AB 交y 轴于点F ，则F (0，4)，过点P 作PH ⊥x 轴，垂足为H ，PH 交AB 于点G ，如图，∵∠PDC =∠OBC ，∴∠PDG =∠OBF ，∵PG ∥OF ，∴∠PGD =∠OFB ，∴PD ：OB =PG ：OF ，∴△PDG ∽△OBF ，∴PD ：OB =PG ：OF ，设P (n ,-n 2+4n )1<n <4 由(2)可知，PG =-n 2+4n --n +4 =-n 2+5n -4，∴S 1S 2=PD BO =PG OF=14PG =-14n -52 2+916，∵1<n <4，∴当n =52时，S 1S 2的最大值为916．5(2023·新疆克孜勒苏·统考一模)如图所示，抛物线y =-x 2+2x +3的图像与x 轴交于A ，B 两点，与y 轴交于点C ，连结BC ．(1)求抛物线顶点D 的坐标；(2)在直线BC 上方的抛物线上有一点M ，使得四边形ABMC 的面积最大，求点M 的坐标及四边形ABMC 面积的最大值；(3)点E 在抛物线上，当∠EBC =∠ACO 时，直接写出点E 的坐标．【答案】【答案】(1)(1,4)(2)当点M 32,154 时，四边形ABMC 面积最大，最大值为758(3)(1,4)或-12,74【解析】(1)∵y =-x 2+2x +3=-x -1 2+4．∴抛物线顶点D 的坐标为(1,4)；(2)令y =0，则x 2-2x -3=0，解得x 1=-1,x 2=3，∴点A -1,0 ,B 3,0 ，令x =0，则y =-3，∴点C 的坐标为(0,3)∴AB =3--1 =4,OC =3，∴S ΔABC =12AB ⋅OC =6∴△BCM 的面积最大时四边形ABMC 面积最大．设直线BC 的解析式为y =kx +b ，则3k +b =0b =3，∴b =3k =-1 ，∴y =-x +3．设过点M 与y 轴平行的直线交BC 于点N ，M x ,-x 2+2x +3 ，N x ,-x +3 ，则MN =-x 2+2x +3 --x +3 =-x 2+3x ，S △BCM =12-x 2+3x ×3=-12x -32 2+278，∴当x =32时，△BCM 的面积最大，最大值为278，此时，y =-32 2+2×32+3=154，所以，当点M 32,154 时，四边形ABMC 面积最大，最大值为6+278=758(3)①连接CD ,BD ，作DM ⊥OC 于点M ．∵C (0,3),D (1,4)，∴CM =DM =1，∴△CDM 是等腰直角三角形，∴∠DCE =45°．∵B (3,0),C (0,3)，∴△BOC 是等腰直角三角形，∴∠BCO =45°，∴∠BCD =90°，∵BC =32+32=32，CD =12+(-3+4)2=2，∴.tan ∠CBD =232=13，∴∠DBC =∠ACO ，∴点E 与点D 重合，∴点E 的坐标为(1,-4)，②作点D 关于BC 的对称点D ，作DN ⊥OC 于点N ，∵∠DMC =∠D NC =90°，∠DCM =D CN ，DC =D C ，∴△DCM ≌△D CN ，∴D N =DM =1,CM =CN =1，∴ON =3-1=2，∴D (-1,2)，设直线BD 的解析式为y =mx +n ,，则3m +n =0-m +n =2，解得m =-12n =32，所以，直线BD ′的解析式为y =-12x +32，联立y =-x 2+2x +3y =-12x +32，解得x 1=3y 1=0 (为点B 坐标，舍去)，x 2=-12y 2=74，所以，点H 的坐标为-12,74 ，综上所述，点E 的坐标为1,4 或-12,74时，∠EBC =∠ACO ．6(2023·广东珠海·统考一模)如图，抛物线与x 轴交于点A -1,0 、B 4,0 ，与y 轴交于点C 0,2 ．点D 为抛物线第四象限一动点，连接AC 、BC 、BD 、AD ．(1)求抛物线的解析式；(2)当S △BCD =S △ABC 时，求此时点D 的坐标；(3)在第(2)问的条件下，延长线段AC 、DB 交于点E ．请判断△ADE 的形状，并说明理由．【答案】(1)y =-x 2+32x +2(2)D 5,-3(3)△ADE 是等腰直角三角形，理由见详解【解析】(1)设抛物线的解析式为y =ax 2+bx +c ，∵抛物线与x 轴交于点A -1,0 、B 4,0 ，与y 轴交于点C 0,2 ，∴a -b +c =016a +4b +c =0c =2，解得：a =-12b =32c =2 ，∴抛物线的解析式为y =-x 2+32x +2；(2)连接OD ，，∵A -1,0 ，B 4,0 ，C 0,2 ，∴AB =5，OC =2，∴S △ABC =12AB ⋅OC =5，设D m ,-12m 2+32m +2 m >4 ，∵S △BCD =S △OBD +S △OBC -S △OCD =S △ABC ，∴12×4×12m 2-32m -2 +12×4×2-12×2×m =5，整理，得m 2-4m -5=0，解得：m 1=5，m 2=-1(舍去)，∴D 5,-3 ；(3)△ADE 是等腰直角三角形，理由如下：设直线AC 的解析式为y =k 1x +b 1，把A -1,0 ，C 0,2 代入，得-k 1+b 1=0b 1=2 ，解得：k 1=2b 1=2∴y =2x +2，设直线BD 的解析式为y =k 2x +b 2，把B 4,0 ，D 5,-3 代入，得4k 2+b 2=05k 2+b 2=-3 ，解得：k 2=-3b 2=12∴y =-3x +12，联立y =2x +2和y =-3x +12得，y =2x +2y =-3x +12 ，解得：x =2y =6 ，∴E 2,6 ，又∵A -1,0 ，D 5,-3 ，∴AE =-1-2 2+0-6 2=35，AD =-1-5 2+0+3 2=35，DE =5-2 2+-3-6 2=310，∴AE =AD ，AE 2+AD 2=DE 2，∴△ADE 是等腰直角三角形．7(2023春·上海·八年级专题练习)在边长为4的正方形ABCD 中，点O 是对角线AC 的中点，P 是对角线AC 上一动点，过点P 作PF ⊥CD 于点F ，作PE ⊥PB 交直线CD 于点E ，设PA =x ，S △PCE =y ．(1)求证：DF =EF ；(2)当点P 在线段AO 上时，求y 关于x 的函数关系式及自变量x 的取值范围；(3)点P 在运动过程中能否使△PEC 为等腰三角形？如果能，请直接写出PA 的长；如果不能，请简单说明理由．【答案】(1)证明见解析(2)y =12x 2-32x +8，0≤x ≤22 (3)能使△PEC 为等腰三角形，PA =0或PA =4【解析】(1)证明：延长FP 交AB 于点G ，∵正方形ABCD 中，PF ⊥CD 于点F ，∴四边形AGFD 是矩形，∴DF =AG ，∠AGF =90°，∵正方形ABCD ，∴∠BAC =45°，∵∠AGF =90°，∴AG =GP ，∴DF =GP ，同理可得：CF =PF =BG ，∵PE ⊥PB ，∠AGF =90°，∴∠GBP +∠GPB =∠FPE +∠GPB =90°,∴∠GBP =∠FPE ，在△GBP 和△FPE 中，∵∠GBP =∠FPEPF =BG ∠BGP =∠PFE，∴△GBP ≌△FPE (ASA )，∴GP =EF ，∵DF =GP ，∴DF =EF ；(2)∵PA =x ，∴AG =GP =22x ，DF =EF =22x ，则DE =2x ，∴CE =4-2x ，∵PF =4-22x ，∴y =124-2x 4-22x =12x 2-32x +80≤x ≤22 ；(3)点P 在运动过程中能使△PEC 为等腰三角形；当点E 在CD 边上时，∵∠CEP ≥90°，若△PEC 为等腰三角形，只能是∠CPE =∠ECP =45°，则PE ⊥CE ，∵PE ⊥PB ，∴PB ∥CD ，∴PB ∥AB ，于是点P 在AB 上，又∵点P 在AC 上，∴A 与P 重合，此时PA =0；当点E 在DC 延长线上时，如图，若△PEC 为等腰三角形，只能是PC =CE ，设PA =x ，则PC =42-x ，EF =DF =AG =GP =22x ，PF =CF =BG =4-22x ，∴CE =EF -CF =22x -4-22x=2x -4，∵PC =CE ，∴42-x =2x -4，∴x =4，∴即PA =4；综上所述，当PA =0或PA =4时，△PEC 为等腰三角形．【点睛】本题主要考查正方形的性质的综合运用，等腰三角形的性质和判定，全等三角形的判定和性质，三角形的面积等知识，综合运用这些性质进行推理，同时注意对等腰的分类讨论是解题的关键．8(2023春·江苏无锡·九年级统考期中)在平面直角坐标系中xOy 中，二次函数y =ax 2+bx +2a <0 的图像与x 轴交于点A (-1,0)、B (2,0)，与y 轴交于点C ．(1)求二次函数的表达式；(2)若点P 是二次函数图像上位于线段BC 上方的一个动点．①如图，连接AC ，CP ，AP ，AP 交BC 于点E ，过点P 作AC 的平行线交BC 于点Q ，将△PEQ 与△PCE的面积比S △PEQ S △PCE 记为a ，将△PCE 与△ACE 的面积比S △PCE S △ACE记为b ，当a +22b 有最大值时，求点P 的坐标；②已知点N 是y 轴上一点，若点N 、P 关于直线AC 对称，求CN 的长．【答案】(1)y =-x 2+x +2(2)①当点P 的坐标为1,1 时，a +22b 有最大值；②CN =516【解析】(1)解：将A (-1,0)、B (2,0)，代入y =ax 2+bx +2中可得：a -b +2=04a +2b +2=0 ，解得：a =-1b =1 ，∴二次函数的表达式为：y =-x 2+x +2；(2)①当x =0时，y =2，则C 0,2 ，设BC 的解析式为：y =kx +b ，将B (2,0)，C 0,2 ，代入可得：2k +b =0b =2 ，解得：k =-1b =2 ，∴BC 的解析式为：y =-x +2，由题意可知，OB =OC =2，则△BOC 是等腰直角三角形，∴∠BCO =45°，∵A (-1,0)，则OA =1，∴AC =OA 2+OC 2=5，∴sin ∠ACO =55，cos ∠ACO =255，过点P 作PN ∥y 轴，QM ⊥PN ，设AP 与y 轴交于点D ，则∠ADO =∠APN ，∠QNM =∠BCO =45°，即：△MQN 为等腰直角三角形，∴QM =MN ，∵AC ∥PQ ，∴∠CAP =∠APQ ，△AEC ∽△PEQ ，则EQ CE =EP AE =PQ AC，又∵∠ADO =∠ACP +∠ACO ，∠APN =∠APQ +∠QPM ，∴∠ACO =∠QPM ，则：PM =PQ ⋅cos ∠QPN =PQ ⋅cos ∠ACO =255PQ ，QM =MN =PQ ⋅sin ∠QPN =PQ ⋅sin ∠ACO =55PQ ，则PN =PM +MN =355PQ ，即：PQ =53PN ，∵S △PEQ S △PCE =EQ CE ，S △PCE S △ACE =EP AE ，EQ CE =EP AE =PQ AC，∴a =b =EQ CE =EP AE =PQ AC =PQ 5=13PN ，∴a +22b =1+22 ×13PN ，则当PN 取最大值时，a +22b 有最大值，设P t ,-t 2+t +2 ，0<t <2，则N t ,-t +2 ，∴PN =-t 2+t +2 --t +2 =-t 2+2t =-t -1 2+1，即：当t =1时，PN 取最大值，此时点P 的纵坐标为1，即：当点P 的坐标为1,1 时，a +22b 有最大值；②由题意可知，点N 在点C 下方时，点N 关于直线AC 的对称点在AC 的左侧，不符合题意，点N 在点C 上方时，连接PN ，交AC 于H ，作PF ⊥y 轴，由对称可知，NH =PH =12PN ，CH ⊥PN ，则∠NHC =∠PFN =90°，∴∠NCH +∠CNP =∠CNP +∠FPN ，∴∠NCH =∠FPN∵∠ACO =∠NCH ，sin ∠ACO =55，cos ∠ACO =255，∴∠ACO =∠NCH =∠FPN ，设CN =m ，则NH =CN ⋅sin ∠NCH =55m ，∴PN =2NH =255m ，则PF =PN ⋅cos ∠FPN =45m ，NF =PN ⋅sin ∠FPN =25m ∴CF =CN -NF =35m ，则OF =OC +CF =2+35m ，∴点P 的坐标为：45m ,2+35m ，0<45m <2，即0<m <52，∵点P 在二次函数图象上，∴-45m 2+45m +2=2+35m ，解得：m 1=0(舍去)，m 2=516，∴CN =516．9(2023·黑龙江哈尔滨·统考一模)如图，在平面直角坐标系中，直线BC 的解析式为y =-x +6，直线BC 交x 轴和y 轴分别于点B 和点C ，抛物线y =-29x 2+bx +c 交x 轴于点A 和点B ，交y 轴于点C ．(1)求抛物线的解析式；(2)点P 是第二象限抛物线上的点，连接PB 、PC ，设点P 的横坐标为t ，△PBC 的面积为S ．求S 与t 的函数关系式(不要求写出t 的取值范围)；(3)在(2)的条件下，点D 在线段OB 上，连接PD 、CD ，∠PDC =45°，点F 在线段BC 上，EF ⊥BC ，FE 的延长线交x 轴于点G ，交PD 于点E ，连接CE ，若∠GED +∠DCE =180°，DC >DE ，S △CDE =15，求点P 的横出标．【答案】(1)y =-29x 2+13x +6(2)S =23t 2-4t (3)3-3112【解析】(1)解：直线y=-x+6交x轴和y轴于点B和点C 令x=0时，y=6，即C0,6，令y=0时，x=6，即B6,0，∵点B、C在抛物线上，∴代入解析式可得：c=6-29×62+13×6+6=0，解得：c=6b=-13，∴解析式为y=-29x2+13x+6；(2)过点P作x轴的垂线交BC延长线于点M，交x轴于点N，过点C作CR⊥MN于R ∵P在抛物线上，P横坐标为t∴P t,-29t2+13t+6，∵M在直线BC上，∴M t,-t+6，∴MP=-t+6--29t2+13t+6=29t2-43t，S△PBC=S△MPB-S△MPC=12MP⋅OB=1229t2-43t×6=23t2-4t，即S=23t2-4t；(3)由(1)得，OB=OC=6，∴∠OBC=∠OCB=45°又EF⊥BC交x轴于点G，∴∠GFB=90°∴∠FGB=90°-∠FBG=45°即∠FGB=∠FBG=45°∴FG=FB又∠PDC=45°设∠PDA=α，∴∠CDA=45°+α=∠CBD+∠BCD=45°+∠BCD∴∠BCD=α=∠PDA又∠GED+∠DCE=180°(已知)∠GED+∠FED=180°(平角定义)∴∠DCE=∠FED，又∠FED=∠FGE+∠PDG=45°+a∴∠FED=∠CDA，∴∠DCE=∠CDA，过点D作DR⊥CE于R，如图所示∴在Rt△CRD中，∠CDR=90°-∠RCD=45°-α，∴∠RDE=∠CDE-∠CDR=α，，∴∠RDE=∠EDA=α，∵∠CRD=∠DOC=90°，∠DCE=∠CDA，CD=CD，∴△RCD≌△ODC(AAS)，∴RD=CO=6，CR=OD，∠CDR=∠DCO，又∵S△DCE=15，∴12CE×DR=15∴CE=5作EM⊥x轴于M，CN⊥EM于N，DT⊥CN于T，如图所示∵∠RDE=∠EDA，∠ERD=∠EMD=90°，DE=DE，∴△RED ≌△MED (AAS )，∴RE =EM ，RD =MD ，∵EM ⊥x ，CN ⊥EM ，DT ⊥CN ，∴四边形NTDM 为矩形，∴∠MDT =90°，∴∠CDT =∠MDT -∠CDE -∠EDA =45°-α=∠CDR ，∴△DCR ≌△DCT (AAS )，∴DR =DT ，∴DM =DT ，∴四边形NMDT 是正方形∴DM =MN =NT =DT =OC =6，设EM =ER =m ，则CR =5-m =CT ，如图所示：∴NE =6-m ，NC =NT -TC =m +1在Rt △NEC 中，6-m 2+m +1 2=52解得：m 1=2，m 2=3，∵CD >DE ，∴m <5-m ，即m <2.5，∴m =3不符合题意，应舍去；当m =2时，CT =OD =3=MO ，∴E -3,2 ，又点D 3,0 ，设直线ED 的解析式为y =kx +b ，则-3k +b =23k +b =0 ，解得：k =-13b =1 ，∴直线ED 的解析式为：y =-13x +1，y =-13x +1y =-29x 2+13x +6 ，∴x =3-3112或3+3112(舍)，∴P 的横坐标是3-311210(2023春·江苏宿迁·九年级统考阶段练习)如图，在平面直角坐标系中，抛物线y =ax 2+bx +c a <0 与x 轴交于A -2,0 、B 4,0 两点，与y 轴交于点C ，且OC =2OA ．(1)试求抛物线的解析式；(2)直线y =kx +1k >0 与y 轴交于点D ，与抛物线在第一象限交于点P ，与直线BC 交于点M ，记m =S △CPM S △CDM，试求m 的最大值及此时点P 的坐标；(3)在(2)的条件下，m 取最大值时，点Q 是x 轴上的一个动点，点N 是坐标平面内的一点，是否存在这样的点Q 、N ，使得以P 、D 、Q 、N 四点组成的四边形是矩形？请直接写出满足条件的N 点的坐标．【答案】(1)y =-12x 2+x +4(2)m 取得最大值23，此时点P 的坐标为2,4 (3)存在，满足条件的N 的坐标为72,3 或6,-3 【解析】(1)解：∵A -2,0 ，∴OA =2，∵OC =2OA ，∴OC =4，∴C 0,4 ，∵抛物线y =ax 2+bx +c 经过点A -2,0 ，B 4,0 ，C 0,4 ，∴4a -2b +c =016a +4b +c =0c =4，解得：a =-12b =1c =4，∴该抛物线的解析式为y =-12x 2+x +4；(2)解：如图1，过点P 作PE ∥y 轴交直线BC 于E ，连接CP ，设直线BC 的解析式为y =kx +d ，∵B 4,0 ，C 0,4 ，∴4k +d =0d =4 ，解得：k =-1d =4 ，∴直线BC 的解析式为y =-x +4，设P t ,-12t 2+t +4 ，则E t ,-t +4 ，∴PE =-12t 2+t +4-(-t +4)=-12t 2+2t ，∵直线y =kx +1k >0 与y 轴交于点D ，∴D 0,1 ，∴CD =4-1=3，∵PE ∥y 轴，即PE ∥CD ，∴△EMP ∽△CMD ，∴PM DM =PE CD =-12t 2+2t 3=-16t 2+23t ，∵m =S △CPM S △CDM =PM DM，∴m =-16t 2+23t =-16t -2 2+23，∵-16<0，∴当t =2时，m 取得最大值23，此时点P 的坐标为2,4 ；(3)解：存在这样的点Q 、N ，使得以P 、D 、Q 、N 四点组成的四边形是矩形．①当DP 是矩形的边时，有两种情形，a 、如图2-1中，四边形DQNP 是矩形时，由(2)可知P 2，4 ，代入y =kx +1中，得到k =32，∴直线DP 的解析式为y =32x +1，可得D 0,1 ，E -23,0 ，由△DOE ∽△QOD 可得OD OQ =OE OD，∴OD 2=OE ⋅OQ ,∴1=23⋅OQ ，∴OQ =32，∴Q 32,0 ．根据矩形的性质，将点P 向右平移32个单位，向下平移1个单位得到点N ，∴N 2+32,4-1 ，即N 72,3 ，b 、如图2-2中，四边形PDNQ 是矩形时，∵直线PD 的解析式为y =32x +1，PQ ⊥PD ，∴直线PQ 的解析式为y =-23x +163，∴Q 8,0 ，根据矩形的性质可知，将点D 向右平移6个单位，向下平移4个单位得到点N ，∴N 0+6,1-4 ，即N 6,-3 ．②当DP 是对角线时，设Q x ,0 ，则QD 2=x 2+1，QP 2=x -2 2+42，PD 2=13，∵Q 是直角顶点，∴QD 2+QP 2=PD 2，∴x 2+1+x -2 2+42=13，整理得x 2-2x +4=0，方程无解，此种情形不存在，综上所述，满足条件的N 的坐标为72,3 或6,-3 ．11(2023·山东济宁·统考一模)如图，抛物线y =ax 2+bx +3与坐标轴分别交于A ，B ，C 三点，其中A (-4,0)、B (1，0)，M 是第二象限内抛物线上的一动点且横坐标为m ，(1)求抛物线的解析式；(2)连接BM ，交线段AC 于点D ，求S ΔADM S ΔADB的最大值(其中符号S 表示面积)；(3)连接CM ，是否存在点M ，使得∠ACO +2∠ACM =90°，若存在，求m 的值，若不存在，请说明理由．【答案】(1)y =-34x 2-94x +3(2)S ΔADM S ΔADB 的最大值为45(3)存在，m =-319【解析】(1)解：(1)分别代入A (-4，0)、B (1，0)到抛物线解析式，解得：y =-34x 2-94x +3；故答案为：y =-34x 2-94x +3．(2)设直线AC 的解析式为y =kx +b ，将点A (-4，0)和点C (0，3)代入y =kx +b 中，-4k +b =0b =3 ，解得：k =34b =3，∴直线AC 的解析式为y =34x +3，如图所示，过点M 作MG ∥x 轴交于AC 于点G ，过点A 作AF ⊥MB 交MB 与点F ，∴G 点的纵坐标与M 点的纵坐标相同，∵M 为抛物线y =-34x 2-94x +3上的一点，设M m ，-34m 2-94m +3 ，又∵G 点在直线AC 上，直线AC 的解析式为y =34x +3，∴G -m 2-3m ,-34m 2-94m +3 ，∴MG =-m 2-4m ，又∵MG ∥AB ，∴MD DB =MG AB =-m 2-4m 5，∵S ΔADM =12MD ⋅AF ,S ΔADB =12DB ⋅AF ，∴S ΔADM S ΔADB =DM DB，∴S ΔADB S ΔADB =DM DB =MG AB=-m 2-4m 5=-m 2+4m 5=-15m +2 2+45，∴S ΔADM S ΔADB 的最大值为45．故答案为：45．(3)过点C 作CP ∥x 轴，延长CM 交x 轴于点T ．∴∠MCO =90°,∠MCP =∠MTA ，∵∠ACO +2∠ACM =90°∠ACO +∠PCM +∠MCA =90°，∴∠MCP =∠MCA ，∴∠MCA =∠MTA ，∴△ACT 为等腰三角形，∴AC =AT ．在Rt △ACO 中，AC =AO 2+OC 2=42+32=5，∴AC =AT =5，∴OT =AT +OA =5+4=9，∴T (-9，0)，设直线CT 的解析式为y =kx +b ，将点T (-9，0)和点C (0，3)代入y =kx +b 中，解得：k =13b =3 ，∴直线CT 的解析式为y =13x +3，∵M 是直线CT 和抛物线y =-34x 2-94x +3的交点，-4<m <0，∴令-34m 2-94m +3=13m +3，∴9m 2+27m +4m =0，∴9m 2+31m =0，∴m 9m +31 =0，解得m =0(舍去)或m =-319故答案为：m =-319．12(2023·海南海口·海口市第九中学校考二模)如图①，已知抛物线L :y =x 2+bx +c 的图象经过点A 0,3 ，B 1,0 ．过点A 作AC ∥x 轴交抛物线于点C ，∠AOB 的平分线交线段AC 于点E ，连结OE ．(1)求抛物线的关系式并写出点E的坐标；(2)若动点P在x轴下方的抛物线上，连结PE、PO，当△OPE面积最大时，求出此时P点横坐标；(3)若将抛物线向上平移h个单位，且其顶点始终落在△OAE的内部或边上，写出h的取值范围；(4)如图②，F是抛物线的对称轴上l的一点，在抛物线上是否存在点P，使△POF成为以点P为直角顶点的等腰直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．【答案】(1)y=x2-4x+3；E(3,3)(2)P的横坐标为52；(3)3≤h≤4；(4)存在，点P的坐标是：5-52,1-52或3-52,5+12或3+52,1-52或5+5 2,5+12【解析】(1)解：∵抛物线L：y=x2+bx+c的图象经过点A(0,3)，B(1,0)，∴1+b+c=0c=3，解得b=-4c=3，∴抛物线的解析式为：y=x2-4x+3；∵OE平分∠AOB，∠AOB=90°，∴∠AOE=45°，∴△AOE是等腰直角三角形，∴AE=OA=3，∴E(3,3)，(2)如图1，过P作PG∥y轴，交OE于点G，设P(m，m2-4m+3)，设直线OE的解析式为y=kx，把点E(3，3)代入得，3=3k，解得k=1，∴直线OE的解析式为：y=x，∴G(m，m)，∴PG=m-(m2-4m+3)=-m2+5m-3，∴S△OPE=S△OPG+S△EPG=12PG×AE=12×3×(-m 2+5m -3)=-32(m 2-5m +3)=-32m -52 2+398，∵-32<0，∴当m =52时，△OPE 面积最大，∴P 的横坐标为52(3)由y =x 2-4x +3=(x -2)2-1，得抛物线l 的对称轴为直线x =2，顶点为(2，-1)，抛物线L 向上平移h 个单位长度后顶点为F (2，-1+h )．设直线x =2交OE 于点M ，交AE 于点N ，则N (2，3)，如图2，∵直线OE 的解析式为：y =x ，∴M (2，2)，∵点F 在△OAE 内(包括△OAE 的边界)，∴2≤-1+h ≤3，解得3≤h ≤4；(4)设P (m ，m 2-4m +3)，分四种情况：①当P 在对称轴的左边，且在x 轴下方时，如图3，过P 作MN ⊥y 轴，交y轴于M ，交l 于N ，∴∠OMP =∠PNF =90°，∵△OPF 是等腰直角三角形，∴OP =PF ，∠OPF =90°，∴∠OPM +∠NPF =∠PFN +∠NPF =90°，∴∠OPM =∠PFN ，∴△OMP ≌△PNF (AAS )，∴OM =PN ，∵P (m ，m 2-4m +3)，则-m 2+4m -3=2-m ，解得：m =5+52或5-52，∵m =5+52>2，不合题意，舍去，∴m =5-52，此时m 2-4m +3=1-52，∴P 的坐标为5-52,1-52；②当P 在对称轴的左边，且在x 轴上方时，同理得：2-m =m 2-4m +3，解得：m 1=3+52或m 2=3-52，∵3+52>2，不合题意，舍去，∴m =3-52，此时m 2-4m +3=5+12，∴P 的坐标为3-52,5+12；③当P 在对称轴的右边，且在x 轴下方时，如图4，过P 作MN ⊥x 轴于N ，过F 作FM ⊥MN 于M ，同理得△ONP ≌△PMF ，∴PN =FM ，则-m 2+4m -3=m -2，解得：m 1=3+52或m 2=3-52，∵3-52<2，不合题意，舍去，∴m =3+52，此时m 2-4m +3=1-52，P 的坐标为3+52,1-52；④当P 在对称轴的右边，且在x 轴上方时，如图5，同理得m 2-4m +3=m -2，解得：m =5+52或5-52(舍)，P 的坐标为：5+52,5+12；综上所述，点P 的坐标是：5-52,1-52 或3-52,5+12或3+52,1-52 或5+52,5+12．13(2023·广东珠海·校考一模)如图，在平面直角坐标系中，抛物线y =-12x 2+bx +c 与x 轴交于点A ，B ，其中点B 的坐标为(4,0)，与y 轴交于点C (0,2)．(1)求抛物线y =-12x 2+bx +c 和直线BC 的函数表达式；(2)点P 是直线BC 上方的抛物线上一个动点，当△PBC 面积最大时，求点P 的坐标；(3)连接B 和(2)中求出点P ，点Q 为抛物线上的一点，直线BP 下方是否存在点Q 使得∠PBQ =45°？若存在，求出点Q 的坐标．【答案】(1)y =-12x 2+32x +2，y =-12x +2(2)(2,3)(3)存在，-35，2325【解析】(1)把B (4,0)，C (0,2)代入y =-12x 2+bx +c 得：-8+4b +c =0c =2 ，解得b =32c =2，∴抛物线的函数表达式为y =-12x 2+32x +2；设直线BC 的函数表达式为y =mx +2，把B (4,0)代入得：4m +2=0，解得m =-12，∴直线BC 的函数表达式为y =-12x +2；(2)过P 作PH ∥y 轴交BC 于H ，如图：设P t ,-12t 2+32t +2 ，则H t ,-12t +2 ，∴PH =-12t 2+32t +2--12t +2 =-12t 2+2t ，∴S ΔPBC =12PH ⋅OB =12×-12t 2+2t ×4=-t 2+4t =-(t -2)2+4，∵-1<0，∴当t =2时，S ΔPBC 取最大值4，此时P 的坐标为(2,3)；(3)直线BP 下方存在点Q ，使得∠PBQ =45°，理由如下：过P 作PM ⊥PB 交BQ 的延长线于M ，过P 作TK ∥x 轴，过B 作BK ⊥TK 于K ，过M 作MT ⊥TK 于T ，如图：由(2)知P (2,3)，∵B (4,0)，∴PK =2，BK =3，∵∠PBQ =45°，∴ΔPBM 是等腰直角三角形，∴∠MPB =90°，PB =PM ，∴∠KPB =90°-∠TPM =∠TMP ，∵∠K =∠T =90°，∴ΔBPK ≅ΔPMT (AAS )，∴PK =MT =2，BK =PT =3，∴M (-1,1)，由M (-1,1)，B (4,0)得直线BM 函数表达式为y =-15x +45，联立y =-15x +45y =-12x 2+32x +2 ，解得x =4y =0 或x =-35y =2325，∴Q 的坐标为-35，2325 ．14(2023·广西梧州·统考一模)如图1，在平面直角坐标系中，△ABC 的顶点A -6，0 ，B 0，8 ，C 8，0，点P 为线段AC 上的一动点(点P 与点A ，C 不重合)，过点P 作PQ ∥BC 交AB 于点Q ，将△APQ 沿PQ 翻折，点A 的对应点为点D ，连接PD ，QD ，BD ．设点P 的坐标为t ，0(1)当点D 恰好落在BC 上时，求点P 的坐标；(2)若△PDQ 与△ABC 重叠部分面积S 与点P 横坐标t 之间的函数解析式为S =a (t +6)2(-6<t ≤1)-67t 2+bt +647(1<t <8) ，其图象如图2所示，求a 、b 的值；(3)是否存在点P ，使得∠BDQ 为直角？若存在，请求出点P 的坐标；若不存在，请说明理由．【答案】(1)1，0(2)a =27，b =247(3)67，0【解析】(1)解：∵A -6，0 ，B 0，8 ，C 8，0 ，∴OB =OC =8，∴∠C =45°．∵PQ ∥BC ，∴∠APQ =∠C =45°．由折叠的性质可得AP =PD ，∠APQ =∠DPQ =45°，∴∠DPA =90°．∵B 0，8 ，C 8，0 ，∴直线BC 的解析式为y =-x +8，∵P t ，0 ，∴PA =t --6 =t +6．∵点D 恰好落在BC 上，∴D (t ，-t +8)，∴PD =-t +8，∴t +6=-t +8，解得：t =1，∴点P 的坐标为1，0 ；(2)解：∵PQ ∥BC ，∴可设直线PQ 的解析式为y =-x +m ，∴0=-t +m ，解得：t =m ，直线PQ 的解析式为y =-x +t ．∵A -6，0 ，B 0，8 ，∴直线AB 的解析式为：y =43x +8．　联立y =-x +t y =43x +8 ，解得：x =3t -247y =4t +247，∴Q 3t -247，4t +247．当-6<t ≤1时，点D 在△ABC 内部，此时重叠部分面积为△PDQ 的面积，由折叠可知S △PDQ =S △APQ =12AP ⋅y Q =12×t +6 ×4t +247=27t +6 2，∴a =27；当1<t <8时，点D 在△ABC 外部，由图象可得当t =4时，S =1287，∴-67×42+4b +647=1287，解得：b =247；(3)解：如图，过点Q 和点B 分别作PD 的垂线，交PD 于点M 和PD 延长线于点N ，∵∠BDQ 为直角，∴∠BDN +∠MDQ =90°∵∠BDN +∠DBN =90°，∴∠MDQ =∠DBN ，∴tan ∠MDQ =tan ∠DBN ，即QM DM =DN BN ．∵Q 3t -247，4t +247 ，M t ，4t +247，D t ，t +6 ，N t ，8 ，B 0，8 ，∴QM =t -3t -247=4t +247，DM =t +6-4t +247=3t +187，DN =8-(t +6)=2-t ，BN =t ，∴4t +2473t +187=2-t t，解得：t 1=67，t 2=-6(舍)．∴存在，点P 的坐标为67，0 ．15(2023·吉林长春·统考一模)在平面直角坐标系中，抛物线y =-x 2+ax +1(a 为常数)，经过点P 2,-7 ，点Q 在抛物线上，其横坐标为m ，将此抛物线上P 、Q 两点间的部分(包括P 、Q 两点)记为图像G ．。

二次函数几何动点问题（含解析）一、面积最大值问题1.（2020九上·休宁月考）如图，已知二次函数的图象经过点、和原点O．P为二次函数图象上的一个动点，过点P作x轴的垂线，垂足为，并与直线OA交于点C．（1）求出二次函数的解析式；（2）当点P在直线OA的上方时，求线段PC的最大值；（3）当点P在直线OA的上方时，求的最大面积．2.（2021·芜湖模拟）如图，抛物线与直线相交于点，，且这条抛物线的对称轴为．（1）若将该抛物线平移使其经过原点，且对称轴不变，求平移后的抛物线的表达式及k的值：（2）设P为直线下方的抛物线上一点，求面积的最大值及此时P点的坐标．3.（2020九上·寻乌期末）已知二次函数的图象的对称轴是直线，它与x轴交于A、B两点，与y轴交于点C，点A的坐标是．（1）请在平面直角坐标系内画出示意图，并根据图象直接写出时x的取值范围；（2）求此图象所对应的函数关系式；（3）若点P是此二次函数图象上位于x轴上方的一个动点，求面积的最大值．4.（2020九上·瑶海月考）如图，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，已知点A（-1，0），且对称轴为直线x=1（1）求该抛物线的解析式；（2）点M是第四象限内抛物线上的一点，当△BCM的面积最大时，求点M的坐标；5.（2020·洞头模拟）如图，在平面直角坐标系中，二次函数的图象交坐标轴于A（﹣1，0），B（4，0），C（0，﹣4）三点，点P是直线BC下方抛物线上一动点．（1）求这个二次函数的解析式；（2）动点P运动到什么位置时，△PBC面积最大，求出此时P点坐标和△PBC的最大面积．6.（2020九上·山亭期末）己知:如图，抛物线与坐标轴分别交于点，点是线段上方抛物线上的一个动点，（1）求抛物线解析式:（2）当点运动到什么位置时，的面积最大?7.（2020九上·旬阳期末）已知抛物线经过点，，与y轴交于点C.（1）求这条抛物线的解析式；（2）如图，点P是第三象限内抛物线上的一个动点，求四边形面积的最大值.8.（2020九上·永年期末）如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（）和B（4，6），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．（1）求抛物线的解析式；（2）当C为抛物线顶点的时候，求的面积.（3）是否存在这样的点P，使的面积有最大值，若存在，求出这个最大值，若不存在，请说明理由.二、等腰三角形问题9.（2020九上·呼和浩特期中）如图，抛物线y= +bx+c的对称轴为x=﹣1，该抛物线与x轴交于A、B 两点，且A点坐标为（1，0），交y轴于C（0，3），设抛物线的顶点为D．（1）求该抛物线的解析式与顶点D的坐标．（2）试判断△BCD的形状，并予证明．（3）在对称轴上是否存在一点P，使得△ACP为等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．10.（2020·肇东模拟）如图，抛物线与y轴交于点A（0，3），与x轴交于点B（4，0）．（1）求抛物线的解析式；（2）连接AB，点C为线段AB上的一个动点，过点C作y轴的平行线交抛物线于点D，设C点的横坐标为m，线段CD长度为d（d≠0）．求d与m的函数关系式（不要求写出自变量m的取值范围）；（3）在（2）的条件下，连接AD，是否存在m值，使△ACD是等腰三角形？若存在，求出m的值；若不存在，请说明理由．三、直角三角形问题11.（2020九下·扎鲁特旗月考）如图，二次函数的图象经过点，直线与y轴交于点为二次函数图象上任一点．（1）求这个二次函数的解析式；（2）若点E是直线上方抛物线上一点，过E分别作和y轴的垂线，交直线于不同的两点在G的左侧)，求周长的最大值；（3）是否存在点E，使得是以为直角边的直角三角形？如果存在，求点E的坐标；如果不存在，请说明理由．12.（2020九上·芦淞期末）如图，已知抛物线与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C，直线经过点C，与x轴交于点D．（1）求该抛物线的函数关系式；（2）点P是（1）中的抛物线上的一个动点，设点P的横坐标为t（0＜t＜3）．①求△PCD的面积的最大值；②是否存在点P，使得△PCD是以CD为直角边的直角三角形？若存在，求点P的坐标；若不存在，请说明理由．13.（2020九上·泉州期中）如图，直线交轴于点，交轴于点B，抛物线的顶点为，且经过点．（1）求该抛物线所对应的函数表达式；（2）点是抛物线上的点，是以为直角边的直角三角形，请直接写出点的坐标．四、平行四边形问题14.（2019九上·武威期中）如图，抛物线y＝x2+bx+c与直线y＝x﹣3交于，B两点，其中点A在y轴上，点B坐标为（﹣4，﹣5），点P为y轴左侧的抛物线上一动点，过点P作PC⊥x轴于点C，交AB于点D.（1）求抛物线对应的函数解析式；（2）以O，A，P，D为顶点的平行四边形是否存在若存在，求点P的坐标；若不存在，说明理由.15.（2020九上·广丰期末）如图二次函数的图像交轴于、，交轴于，直线平行于周，与抛物线另一个交点为.（1）求函数的解析式；（2）若是轴上的动点，是抛物线上的动点，求使以、、、为顶点的四边形是平行四边形的的横坐标.16.（2020九上·桐城期末）已知直线y＝kx＋b（k≠0）过点F（0，1），与抛物线y＝x2相交于B、C两点．（1）如图，当点C的横坐标为1时，求直线BC的表达式；（2）在（1）的条件下，点M是直线BC上一动点，过点M作y轴的平行线，与抛物线交于点D，是否存在这样的点M，使得以M、D、O、F为顶点的四边形为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．答案解析部分一、综合题1.【答案】（1）设，把A点坐标代入得：，∴二次函数的解析式是（2），轴，P在上，∴，∵点，∴直线OA的解析式为y=x，又点C在直线OA上，∴点C（m，m）当点P在直线OA的上方时，，，，，开口向下，当m= 时，PC有最大值，即当点P在直线OA的上方时，线段PC的最大值是．（3）∵A点坐标，且PC有最大值，∴．【解析】【分析】（1）利用待定系数法求解即可；（2）由题意可知，易求得直线OA 的解析式，可得点，由= ，利用二次函数最值求法求解即可；（3）根据点A坐标和PC的最大值即可求解．2.【答案】（1）解：抛物线过点，，且这条抛物线的对称轴为．代入得，解得．∴抛物线为．∵该抛物线平移使得其经过原点，且对称轴不变，∴平移后的抛物线为．将代入得．（2）解：如图，过P作轴，交于Q．设，则，则．∴．∵∴当时，的面积最大，，当t=2时，∴．【解析】【分析】利用待定系数法求一次函数的解析式和二次函数式的解析式。

当点CC在何处时SS△AAAAAA有最大值?1.铅垂高法做CCCC⊥ xx轴且交直线AABB于点D,设点CC坐标为(mm, aamm2+ bbmm+ cc),直线AB的解析式为gg(xx) = kkxx + qq,∴点D坐标为(mm, kkmm + qq),∴CC CC的长度为f(m) − g(m) = aamm2 + bbmm + cc−kkmm−qq, ∴SS△AA AAAA= SS△AAAAAA+ SS△AA AAAA= AAAA×(xx BB−xx AA),将CC CC为aamm2 + bbmm + cc−kkmm−qq代入，令(xx−xx) = ss,可2 AA AA得SS= (aamm2+bbmm+cc−kk mm−qq)×ss= aa ss mm2+(bb−kk)ss mm+ss(cc−qq),当aassmm2+ (bb−△AAAAAA 2 2kk)ssmm + ss(cc−qq)有最大值时，SS△AA AAAA有最大值.当m = −bb= −(bb−kk)ss= −bb−kk时, aassmm2 + (bb−kk)ssmm + ss(cc−qq)有最2aa2aass2aa大值, SS△AAAAAA有最大值.A A � A A A � A作直线l l 平行于直线AABB 且与f(x)只有一个交点C （即直线l 与ff (xx ) = aaxx 2 + bbxx + cc 相切）,此时SS △AAAAAA 为最大值.∴ ff ′(xx ) =ff (xx AA ) − ff (xx A A ) = 2aaxx + bb xx AA − xx AA (aaxx 2 + bbxx AA + cc ) − (aaxx 2 + bbxx A A + cc ) ⇒= 2aaxx + bb xx AA − xx AA aa (xx 2 − xx 2) + bb (xx AA − xx A A ) ⇒= 2aaxx + bb xx AA − xx AA aa (xx AA + xx A A )(xx AA − xx A A ) + bb (xx AA − xx A A )⇒ xx AA − xx AA= 2aaxx + bb ⇒ aa (xx AA + x x AA ) + bb = 2aaxx + bb ⇒ xx = xx AA + xx AA 2 ∴当xx = xx BB +xx AA时, SS 有最大值. 2 △AAAAAA。

微信公众号
从小学数学-------------------------------------------------
解法二：铅锤定理，在求二次函数三角形面积最值问题，运用非常多。 设动点 P 的坐标，然后用代数式分别表达出铅锤高度和水平宽度，然后利用铅锤定理的 计算公式，得出二次函数，必有最大值。
微信公众号
从小学数学-------------------------------------------------
原 题 ：在（ 1）中 的 抛 物 线 上 的 第 二 象 限 是 否 存 在 一 点 P，使 △PBC 的 面 积 最 大 ？ 若 存 在 ， 求出 P 点的坐标及△PBC 的面积最大值，若没有，请说明理由。 考试题型，大多类似于此。求面积最大值的动点坐标，并求出面积最大值。 一般解题思路和步骤是，设动点 P 的坐标，然后用代数式表达各线段的长。通过公式计 算，得出二次函数顶点式，则坐标和最值，即出。
解法一：补形，割形法。方法要点是，把所求图像的面积适当的割补，转化成有利于面 积表达的常规几何图形。请看解题步骤。
微信众号
从小学数学-------------------------------------------------
解 法 二 ： 铅 锤 定 理 ， 面 积 =铅 锤 高 度 ×水 平 宽 度 ÷2。 这 是 三 角 形 面 积 表 达 方 法 的 一 种 非 常 重要的定理。 铅锤定理，在教材上没有，但是大多数数学老师都会作为重点，在课堂上讲解。因为， 铅 锤 定 理 ，在 很 多 地 方 都 用 的 到 。这 里 ，也 有 铅 锤 定 理 的 简 单 推 导 ，建 议 大 家 认 真 体 会 。
解法四：三角函数法。请大家认真看上面的解题步骤。 总之，从以上的四种解法可以得出一个规律。过点 P 做辅助线，然后利用相关性质，找 出各元素之间的关系。 设动点 P 的坐标，然后找出各线段的代数式，再通过面积计算公式，得出二次函数顶点 式，求出三角形面积的最大值。 对于同学们中考数学来说，只要你熟练掌握解法一和解法二，那么二次函数几何综合题 中，求三角形面积最大值问题，就非常简单了。