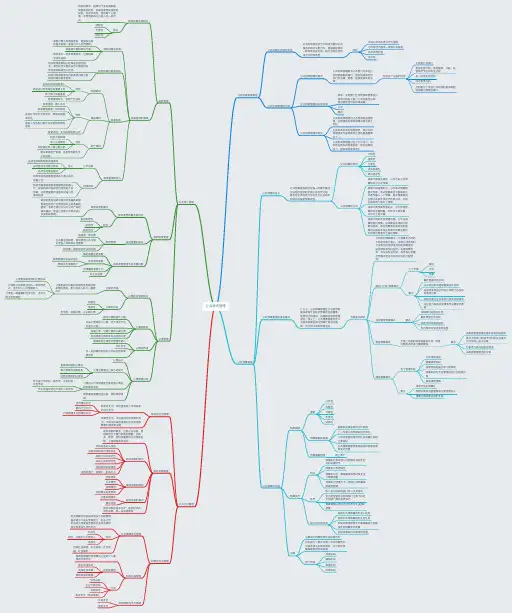
第八章力（复习思维导图）
J
静摩擦力
力的作用效果
力的作用是相互的
弹力(F)
重力(G)
摩擦力（f）
形变
概念：
弹簧形变量与外力的关系
弹性势能：
概念：
大小
方向
作用点
重力势能
滑动摩擦力
滚动摩擦力
大小
方向
作用点
力的表示
力的示意图：用一根带箭头的线段
将力的三要素都表示出来的方法。
由于地球吸引
G=mg
不同地方g不同，通常g=9.8N/kg.
竖直向下区别于垂直向下
重心
取决于物体的形状、质
量分布情况。
被举的高度
物体的质量
符号：F
单位：N
测量：弹簧测力计
接触面粗糙程度
压力大小
思维导图的优势与作用 一、思维导图的优势 您是否经常遇到过这样的情况： 1、您买了很多书，可惜很多都没有读？就是有幸读过也掌握不了多少？ 2、走进书店发现新书、想买的书层出不穷，可是总担心买回去也没有时间消化？ 3、如果在图书馆的书海中遨游，您是不是望书兴叹，游不了多久见没有时间了？ 4、作为学生您是不是感觉学习教材都比较吃力，只有刻苦才能通过考试？ 5、已经工作的您是不是感觉学习能力不如学生时代，在激烈的竞争面前感觉知识更新缓慢？
6、当您面对的无限丰富的知识、智慧和技能您是不是感到力不从心？ 是我们的能力不够吗？是我们的大脑不好使？NO！！！ 您的大脑是一个沉睡的巨人，心理学家告诉我们普通人终其一生才用了4-6%的大脑潜能。我们大脑的潜能绝大部分还在沉睡！我们的一生可能花费90%以上的学习时间学习各种各样的业务知识，也许只花了10%不到的时间学习训练学习的方法。 现在有一种方法可以全面解决这些问题，这就是思维导图！有没有听说过？我们都有体会，形象的、具体的、直观的事物要比抽象的语言容易记得多。美国图论学者哈里有一句名言：“千言万语不及一图。”说的就是这种道理。俗话说：“百闻不如一见。”也是这个意思。 思维导图和传统的学习记忆方法相比有较大的优势。 1、使用思维导图进行学习，可以成倍提高学习效率，增进了理解和记忆能力。如通过使用关键字强迫我们在做笔记的时候就要思考句子的要点到底是什么，这使我们可以积极地倾听讲课者。而且思维导图还激发我们的右脑，因为我们在创作导图的时候还使用颜色、形状和想象力。根据科学研究发现人的大脑是由两部分组成的。左大脑负责逻辑、
词汇、数字，而右大脑负责抽象思维、直觉、创造力和想象力。巴赞说：“传统的记笔记方法是使用了大脑的一小部分，因为它主要使用的是逻辑和直线型的模式。”所以，图像的使用加深了我们的记忆，因为使用者可以把关键字和颜色、图案联系起来，这样就使用了我们的视觉感官。 2、把学习者的主要精力集中在关键的知识点上。您不需要浪费时间在那些无关紧要的容上。节省了宝贵的学习时间。 通过使用关键字强迫我们在开展业务或做笔记的时候就要思考句子的要点到底是什么，这使我们可以积极地倾听讲课者。关键知识点之间的连接线会引导您进行积极主动思考。快速系统的整合知识，可以为您的知识融会贯通创造了极其有利的条件。发展创造性思维和创新能力。发散思维是创新思维的核心。画思维导图的方法恰恰是发散思维的具体化、形象化。 3、思维导图具有极大的可伸缩性，它顺应了我们大脑的自然思维模式。从而，可以使我们的主观意图自然地在图上表达出来。它能够将新旧知识结合起来。学习的过程是一个由浅入深的过程，在这个过程中，将新旧知识结合起来是一件很重要的事情，因为人总是在已有知识的基础上学习新的知识，在学习新知识时，要把新知识与原有认知结构相结合，改变原有认知结构，把新知识同化到自己的知识结构中，能否具有建立新旧知识之间的联系是学习的关键。
紧扣核心问题，妙用思维导图 ——三年级上册第三单元教后记 本单元的人文主题是“童话世界”，单元导语即点明了童话最本质的特点——想象。“乘着想象的翅膀，游历奇妙的童话王国，看花儿跳舞，听星星歌唱。”童话最大的特点就是充满了丰富而奇特的想象，在作者笔下，花草树木、鸟兽虫鱼都具有了人的情感、人的语言、人的动作、人的心理，想象来源于生活但又高于生活。故事往往趣味十足、引人入胜又发人深思。本单元的语文要素是“感受童话丰富的想象”“试着自己编童话，写童话”。也就是说本单元主要任务就是 要学习读童话、编童话、写童话。 通过一、二年级的学习，学生对童话这一体裁已有一定的感性认识，《蜘蛛开店》《青蛙卖泥塘》《小毛虫》等等，课后也都有思维导图。教学时可以充分利用这一点。本单元选编了中外不同作家、不同风格的四篇童话。《卖火柴的小女孩》中的小女孩擦燃火柴后看到了奇异的幻象，折射她内心的愿望；《那一定会很好》的主人公不断产生愿望，不断实现愿望；《在牛肚子里旅行》中，小蟋蟀红头经历了一场惊险的旅行；《一块奶酪》中，蚂蚁队长因为小小的奶酪渣， 进行了激烈的思想斗争。 这一单元课文较长，应该怎么教？在教学《卖火柴的小女孩》时，我就在思考这个问题。我觉得可以借助于课后习题设计核心问题，妙用思维导图。课后习题往往就是课文的核心问题，就是引导学生把握语文要素的关键点。既要关注到 文本的内容，又要关注到文本的表达。 一、《卖火柴的小女孩》 这篇课文习题2：“小女孩一共擦燃了几次火柴？每次擦燃后看到了什么，表达了她怎样的愿望？”将之分解到两课时的教学中去。 第一课时揭示课题，简介安徒生，初读课文后让学生思考小女孩一共擦燃了几次火柴？再读课文，到文章中划出相关语句。①她终于抽出了一根。②她又擦了一根。③她又擦着了一根火柴。④她以墙上又擦着了一根火柴。⑤她赶紧擦着了一大把火柴，要把奶奶留住。抓住重点段指导分段，5－9这几个自然段可以归并为一段，擦火柴。剩下的1－4为一段，写卖火柴；10－11写小女孩冻死街头。借助于这样一个核心问题帮助学生理清脉络。然后品读第一段，这个卖火柴的小女孩给你留下了什么印象？（可怜、悲惨）你从哪些语句感受到的？事实上第1－4自然段每一句话都能让我们感受到小女孩的可怜。 第二课时则解决“每次擦燃后看到了什么，表达了她怎样的愿望？”根据学生的回答指导朗读，体会小女孩的心情变化和神奇的想象。小女孩最渴望什么，什么就会出现。希望一次次落空，而她擦燃火柴的愿望却越来越强烈，从一开始下了好大决心的“终于”，到最后“赶紧擦着了一大把火柴”，她多想和慈爱的奶奶在一起，多想过上幸福的生活啊！最终形成思维导图 小女孩最后的结局抓住两个幸福，前一个幸福是在幻想中的美好生活，后一个幸福则是指永远地离开了这个悲惨的世界。至于以乐衬哀的写法，反复出现的大年夜，包括文中多处出现的对比，也可以适当讲一讲。最后可以交流印象深刻
八年级下数学思维导图 一.知识框架 二知识概念 1.勾股定理：如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2+b2=c2。 勾股定理逆定理：如果三角形三边长a,b,c满足a2+b2=c2。，那么这个三角形是直角三角形。 2.定理：经过证明被确认正确的命题叫做定理。 3.我们把题设、结论正好相反的两个命题叫做互逆命题。如果把其中一个叫做原命题，那么另一个叫做它的逆命题。(例：勾股定理与勾股定理逆定理) 勾股定理是直角三角形具备的重要性质。本章要求学生在理解勾股定理的前提下，学会利用这个定理解决实际问题。可以通过自主学习的发展体验获取数学知识的感受 一、树形思维导图 因为在最初指导学生认识思维导图的时候，我给学生展示的就是树形图。所以学生运用树形图对数学知识进行梳理比较熟练。学生在生活中早已认识了树的形状，对树干、树枝、树叶及分枝的感知非常清晰，也就很容易的联想到树干、树枝与主题、分主题的逻辑关系。所以学生运用树形图的时候比较多，也绘制的比较好。如图1是苏科版数学八年级下册第10章分式的树形思维导图. 树形图的优点是主干分支非常明确，但画起来比较麻烦。为了更简单的运用思维导图，后来我们发动学生研究更简单的思维导图形式，大家确认就把树干简化为一个圆、椭圆或正方形等简单易画的图形，如图2：学生把树干简化成一个圆环，涂上不同颜色，画上
一个指针，这是苏科版数学八年级下册第8章第二节数学实验室中 的转盘模型变形图，学生的这一构想即贴近课本又有一定的创造性。 二、箭头或框架式思维导图 箭头或框架样式的思维导图，老师在日常备课或给学生做知识梳理的时候会经常使用，非常简洁明了，而且容易绘制。只是以前我 们没有把它作为一种学习方法并上升到理论高度去重视。这种结构 图实际上就是一种很简单好用的思维导图，特别适合在课堂中应用。在具体的运用中我们要先总结出本节课的主题，用一个关键词表示。然后直接用箭头往下分支出二级、三级等主题，也是常见的框架结 构图，学生运用起来非常简单容易上手。有好多学生把框架结构变 形为椭圆形箭头图、鱼骨头型箭头图。如图3是学生梳理二次根式 的箭头式思维导图。 三、实物型思维导图 学生的思维被打开以后，他们的想象力非常丰富，画出了许多实物型思维导图，如风筝、蝴蝶、花篮、风车等等。如图4：花篮即 是主干，也就是主体部分。学生冠上各个关键词后，就能对学过的 知识进行清晰的梳理和记忆。学生也非常喜欢进行这样的勾画。 三、表格式思维导图 我们在数学教学中经常会运用表格来进行知识的梳理和比较，能让学生一目了然的了解知识的区别与联系。这实际上也可以看作是 一种思维导图，利用表格来绘制思维导图，学生比较容易接受和理解，所以，表格式思维导图也是学生比较喜欢的的一种形式。如图 5是学生在学习完苏科版数学八年级下册第11章反比例函数后绘制 的表格式思维导图，总结比较了一次函数与反比例函数的知识。 以上是我在指导学生运用思维导图梳理数学知识时最常用的几种方法，在具体指导的过程中，笔者首先给学生逐渐展示一些不同类 型的思维导图，让学生先获得一些感性认识，在头脑中有思维导图 的概念和形象，然后引导学生勾画。慢慢学生就学会了，而且非常 有兴趣。学生在绘制思维导图时学到了思维的方法，找到了学习的 方法。思维导图让学生真正的学会了学习，提高了学习的效率。教
[思维导图的运用心得体会]在您所教学科中，思维导图可以用在哪些地方？ 但是在教学的过程中也出现了各种各样的问题和困惑： 1、在效率和时间上： 2、在协作和研究上： 在主题研究性学习的过程中，经常会发现一个小组只有个别学生在参与，而其他学生都是观看的份，无法真正的参与进来，小组缺乏合作性。面对一个主题，学生在研究的过程中，由于没有规划好，经常无法达到教学任务，这样的结果是不仅无法提高教学技能，更加不要说培养其他的能力了。 虽然主题研究性教学模式可以培养学生的信息素养，培养学生分组合作、协作学习的能力，可是在实施的过程中存在着这样那样的难度，比如：遇事一窝蜂，个人为主，缺乏团队意识；活动没有组织和策略，得不到实质的提高等等。如何让主题研究性学习不流于形式，成为真正的研究学习，这时让我想到了思维导图，它能够很好的对我们的信息进行高度的组织，能够让我们的活动在思维导图的引导下进行合理的操作，它可以培养学生科学的、逻辑的思维习惯，能够让学生条理清晰的解决问题。 1、通过思维导图，理清思路 面对一个问题，如果只是口头的回答，没有进行及时的整理，那么即使老师总结的很好，那么学生的印象还是模糊的没有一个整体的概念，利用思维导图，可以发散我们的思维，让我们的大脑行动起来，在小组讨论的过程中，全体小组成员都参与进来，然后在思维导图中进行增增减减，不断的讨论，不断的进行修改，来进行学习，一张思维导图制作完成了，那么一个学习也算告一个段落了，心得体会《思维导图的运用心得体会》。 2、应用思维导图，进行创作 1）增减随意，快乐的创作 研究性学习中，一个重要的环节是对收集的资料进行筛选和创作，进而制作出一个作品。而大多数学生在计划安排环节总是无法很明确的知道自己到底要查找哪些资料，制作出怎样的作品？经常对小组作品进行再创作，可是由于种种原因，总是无法在规定的时间内完成任务。在平时的教学过程中经常会出现下面这样几种情况： （1）查找资料与制作不同步，等资料查找好再进行创作的时候，才发现自己查找的资料不够理想，于是重新再查找一次，浪费了很多的时间。 （2）由于一节课时间的有限性，等资料查找好，再到第二节课进行创作时发现自己查找的资料已经完全陌生，重新浏览自己查找到的资料，浪费了很多的时间。
八年级数学的思维导图 ：全等三角形 ：二次根式 ：实数 ：相似图形 因式分解 1. 因式分把一个多项式化为几个整式的积的形式,叫做把 这个多项式因式分解;注意：因式分解与乘法是相反的两个转 化. 2.因式分解的方法：常用提取公因式法、公式法、分组分 解法、十字相乘法. 3.公因式的确定：系数的最大公约数相同因式的最低次幂. 注意公式：a+b=b+a; a-b=-(b-a); (a-b)2=(b-a)2; (a- b)3=-(b-a)3. 4.因式分解的公式： (1)平方差公式： a2-b2=(a+ b)(a- b); (2)完全平方公式： a2+2ab+b2=(a+b)2, a2-2ab+b2=(a- b)2. 5.因式分解的注意事项：
(1)选择因式分解方法的一般次序是：一提取、二公 式、三分组、四十字; (2)使用因式分解公式时要特别注意公式中的字母都具有 整体性; (3)因式分解的最后结果要求分解到每一个因式都不能分 解为止; (4)因式分解的最后结果要求每一个因式的首项符号为正; (5)因式分解的最后结果要求加以整理; (6)因式分解的最后结果要求相同因式写成乘方的形式. 6.因式分解的解题技巧：(1)换位整理,加括号或去括号整 理;(2)提负号;(3)全变号;(4)换元;(5)配方;(6)把相同的式子 看作整体;(7)灵活分组;(8)提取分数系数;(9)展开部分括号或 全部括号;(10)拆项或补项. 7.完全平方式：能化为(m+n)2的多项式叫完全平方式;对 于二次三项式x2+px+q, 有 x2+px+q是完全平方式 . 分式 1.分式：一般地,用A、B表示两个整式,AB就可以表示为 的形式,如果B中含有字母,式子叫做分式. 2.有理式：整式与分式统称有理式;即 . 3.对于分式的两个重要判断：(1)若分式的分母为零,则分 式无意义,反之有意义;(2)若分式的分子为零,而分母不为零,
玩转小学数学 女儿开始上小学了，为了女儿，我特地花了一些时间，将小学数学课程研究了一遍，并用我最最喜欢的思维导图转化的，清晰度有限，只能看个大概。 经过这样整理，关于小学数学，我对教学内容、课程结构、编排顺序等有了清晰地了解。并有了几点看法 1、20以内的加减法是基础，一旦20以内加减掌握了，多位数进退位加减、小数加减、乘、除、四则运算规律可是象大纲这样拖沓，小数的加减要拖到四年级下册才教。 我的女儿刚刚上小学一年级，按照我的方法，她已经能做小数的竖式加减了，而我并没有花太多的时间教 2、统计：分布在不同的学期，过来过去教，当然了，有所不同，感觉太拖沓。个人觉得柱状图、饼状图、折线何用制作。计算机是工具，让孩子从小就学习运用它，而不是将计算机当成游戏机。 关键是让孩子理解统计的意义：统计是将死数据变成活数据的途径，让数据说话的方式。 3、分数、最小公倍数、最大公约数是小学的难点，也是重点。以后的因式分解、集合、加减转化为乘除，这都 4、图形变换、面积、体积可以对比学习、集中学习。 5、方程、代数直到五年级才开始接触，感觉有点晚。在小学四年级的时候有不少题目，如果用方程会很简单， 我常和一年级的女儿玩一种扑克牌游戏，我就尝试用大小王代替任何数，渐渐让她领悟"王”可以代替任何"X"。而她已经娴熟运用了。 6、做好应用题的关键是将文字信息用数学语言表达出来：画图、列式子、列方程 7、个人觉得小数数学课本的亮点是"“数学广角”，它让数学与生活紧密相连，让数学变得亲切可人。 经过上述剖析，我想到一些很有趣的游戏。通过轻松快乐的方式，就可以让孩子在比较短的时间内轻松玩时，孩子会感到轻松很多。
序 中国记忆力训练网（海马教育记忆培训公司）是目前国内最大型、最权威、最受欢迎的记忆力，思维导图，速读，早教及脑潜力研究网站，是国内首屈一指的记忆技术专业研究和学术交流平台，提供大量的学习资料免费下载，致力于帮助所有的爱好者提高记忆力、思维方式，速读及激发脑潜能。 中国记忆力训练网（https://www.doczj.com/doc/1716924872.html,）曾培养出多位获得大奖的记忆大师,其中包括： CCTV记忆挑战英雄：张海洋、陈明月、孙盒凇、王仙妮 CCTV状元360记忆大赛冠军：李桂荣，吴天胜 北京电视台记忆挑战冠军：方然、黄伟 拥有多位出色的资深版主：牛头、闲云、大猫、随风、水木清华、马其顿方阵、大奔、太圆、阿峰、纳闷王、李详齐、落叶梧桐等。 另外还有：著名早教专家冯德全，儿童记忆训练专家李振泉，首席速读专家巧克力，思维导图训练专家慧瑶，右脑开发专家曾冠茗等。 中国记忆力训练网培养出无数的学员，包括中小学生、大学生、白领等人群，并曾经为通信行业、美容化妆品行业、教育培训业以及国内众多的企业和团体提供图像记忆，思维导图等培训，服务过的客户包括：广东移动公司、广东电信、广州安植公司、上海莎谷娜公司、大连爱梦公司、香港超妍美容集团、济南天佑公司、南京圣莎拉公司、广东众行顾问公司、郑州诺言、天津中兴美容美发公司、江苏丽源公司、武汉嘉丽公司、杭州宝琳公司、广州成功教育咨询公司……
值中国记忆力训练网站建立5周年之际，为了感谢大家长久以来对我们网站的支持，我把我们网站的思维导图精华资料按一定的格式进行整理归类，并加上必要的介绍和点评，让以后有志于思维导图学习和推广的朋友更容易入门，更方便地学习，请大家多多支持！ 1、《思维导图的入门制作与作用》 文章简介：思维导图制作它不需要什幺高深的专业知识，而且它是我们大脑思维的自然的表达方式。思维导图的使用也没有任何年龄、学历或专业的限制，可以这样说上至９０多岁的老人下至５岁的孩童都可以学习和使用思维导图作为自己提高学习和思维技巧的工具。看了这篇文章，你将会发现：绘制思维导图并不像你想象的那样复杂，正如成功并不像你想象的那样困难一样……（来源：海马思维导图）。详情请点击： https://www.doczj.com/doc/1716924872.html,/viewthread.php?tid=1034&fromuid=262190 2、《思维导图的三招十八式》 文章简介：如何利用思维导图这个终极思维工具把大脑的潜力充分的发挥？又怎样把思维导图的快速记忆与创新思维功能发挥出来？请看思维导图的三招十八式……（来源：海马思维导图）。详情请点击： https://www.doczj.com/doc/1716924872.html,/viewthread.php?tid=667&fromuid=262190 3、《成为思维导图高手的24个习惯》 文章简介：想要成为思维导图的高手？好习惯是成功之母！请看《成为思维导图学习高手的24个习惯》，每个习惯都价值连城，只要养成其中的几个好习惯，你一定会取得学习的胜利！（来源：海马思维导图）详情请点击：。 https://www.doczj.com/doc/1716924872.html,/viewthread.php?tid=31683&fromuid=262190 4、《如何对一本书做思维导图》 文章简介：一天内分析几本书并牢记重点？2周内阅读速度提高5-10倍？可能么？看了这篇《如何对一本书做思维导图》你将明白这些都不是神话，完全可以变成现实，正所谓君子善借于物也，有了好工具，一切都不难……（来源：海马
作为现代办公的一员，大家可能对思维导图有一定的了解，在我们办公中的很多地方都是可以用的到的。今天小编就带领大家了解一下思维导图的用途有哪些？又是怎样在线绘制思维导图的，有兴趣的小伙伴可以跟着小编学习一下哟。 用途说明： （1）阅读总结 俗话说“活到老，学到老。”我们在学习的过程中要学会掌握方法，这样才可以更加高效的学习，在读书时，如果大家理不清思路的话，可以绘制思维导图来帮助我们提高我们的阅读和理解能力。 （2）生活垃圾分类 在我们日常的生活中也是可以用到思维导图，很多人对垃圾分类一直存在困惑，
具体的垃圾是哪一类的总是分不清，使用思维导图可以帮助我们记住多种类别的垃圾。 （3）办公技巧 生活和学习中需要用到思维导图的帮助，工作中也是可以用到的，比如说知乎推广思维导图，可以具体到人群属性，用户流量。 具体绘制操作步骤：
方法一：在线绘制 思维导图的绘制可以是在线绘制，也可以是使用模板，当我们对绘制思维导图的迅捷画图在线网站有所熟悉之后，自己进行绘制也是可以的，进入到浏览器并搜索到对应网站后，在思维导图网页点击“立即体验”即可进入新建思维导图页面了。
进入网页后，我们需要进行的是主题选取，根据我们要绘制思维导图风格选择一个合适的主题即可。点击页面左上角的主题图标就行啦。 接下来就是对内容的填充了，选中页面内的中心节点，在布局中选择一个样式即可。然后再将下级主题或是同级主题添加进去，简单进行一下内容的修改即可。 方法二：套用模板 除了在线绘制的方法，还可以直接套用网站中的模板。当我们进入思维导图在线网站后，在搜索框中搜索我们需要思维导图的模板关键词，在多个思维导图的模板中找到我们需要的模板后，就可以点击在线绘制按钮了。
怎样用思维导图做好知识管理？如何用思维导图做好读书笔记 思维导图是一款可以提高我们思考和学习效率的工具，它被广泛应用于策划方案，计划安排，笔记整理，知识管理等等各个方面。 一为什么要用思维导图？ 很多人思考问题的时候，思维混乱，没有条理。记笔记的时候，主次凌乱，没有重点，复习起来非常麻烦，也不方便记忆。 思维导图可以有效地辅助我们思考。大脑能够更好地适应发散性的思维方式，而思维导图本身恰恰也是发散型的结构，它可以让我们的思维条理化，清晰化。 1 思维导图对细节的更新迭代方便，只需要在后面添加分支就行了。 2 思维导图有助于我们提炼书籍中，课程中的关键点和框架，理清大纲。 3 通过某个领域的思维导图，我们可以对该领域的知识大体框架有整体性的理解。 4 理清工作，梳理思路，不丢细节。 二普通人使用思维导图的常见误区 1 总想把所有的东西都放在思维导图上，纠结于细节。 思维导图的目的是让我们把握整体的框架，而不是细枝末叶，不要妄想把所有的内容都放在一张导图上，密密麻麻一片，结果就跟笔记一样，没有什么区别，没有重点，这样，也就失去了导图的意义。 2 做思维导图的时候，没有深入理解和思考，只是照抄原文。 有些人读了很多书，整理了很多的思维导图，却发现自己并没有什么实质性的成长，原因之一就在于，没有自己的思考和总结，仅仅是把书上的知识搬运到了思维导图中，之后也就再也没有花时间去查看整理过的导图了。而所得到的收获感也仅仅是在做完思维导图的那一刻。 做图的时候，我们需要加入自己的一些思考和理解，归纳和总结出重点。并且时常定期地查看整理过的导图。 3 不是所有内容都适合做成思维导图 有些没有明显的分层，或者说逻辑关系的文章和书籍，就不太适合做成思维导图。比如散文，一些情感类的文章和书籍。
思维导图在阅读教学中的运用 □文/重庆市武隆县职业教育中心李小琴 思维导图是英国心理学家、教育学家东尼·博赞发明的一种先进的思维工具。它运用图文并茂的技巧，把各级主题关系用相互隶属的相关层级图表现出来，把主题关键词与图像、颜色等建立起记忆链接，利用记忆、阅读、思维的规律，协助人们在科学与艺术、逻辑与想象之间平衡发展，从而开启人类大脑的无限潜能[1][2]。 在阅读教学中使用思维导图，不仅可以克服学生记忆方面的问题，还能调动学生学习的积极性，更多地激发学生思考与课文内容相关的信息，从而拓宽文本的深度和广度。 那么在阅读教学中如何运用思维导图呢？ 首先，让学生学会画思维导图。(1)找到一张足够大的纸和颜色尽量多的笔。(2)在纸的中央画出(或写出)你所要记忆的内容的核心部分，如思维导图模板一“解读文本”。然后，从中心部分分出很多曲线，再在线上写下你要记忆的内容。(3)认真看图，你会不会联想到以下的事物：大树的枝干，人的神经，或是飞鸟的轮廓……(4)在某些内容的旁边画上可表示其内容的图 画。总之，“写”与“画”双管齐下，使你的画既美观又实用。 其次，在阅读教学中，让学生从不同的角度和层面绘制思维导图[3]。 力求用思维导图将阅读思考的过程反映出来，笔者认为应从四个不同层面将思维导图运用于阅读教学中。 第一层面：解读文本 即跨越读者与文本的距离，全面理解文本的思想内容和表达形式。要咬文嚼字，读出字里行间所含的深意。通过重点句段来解读文本，体会作者的思想感情。这一思维过程见思维导图模板一。
在教学中，教师利用思维导图帮助学生建构解读文本时的知识结构，以简洁明了的方式呈现主要知识框架，对学习的课程进行有效的资源整合[4]。学生整体掌握解读文本的知识框架后，让他们选择“思维导图模板一”中的一两个方面来作深入思考，并鼓励他们将思维的过程用思维导图表现出来。通过整理和绘制思维导图，可以更好地帮助学生领悟文本，并将所学内容进一步加以深化。 第二层面：理解作者 即对作者旨意的反思阅读[ 5 ]。对作品的解读要考察作者的世界观和方法论，才能由表及里、由浅入深，接近文本的真谛，了解文中主人公，把握作者的主旨，才能让学生（读者）与作者产生共鸣，生发联想，进而影响学生的人生观、价值观。这一思维过程见思维导图模板二。
第八章东半球其他的地区和国家 第一节中东 1.中东位于亚洲西南部和非洲东北部。包括西亚的大部分和非洲的埃及。 2.中东之所以会成为全世界一直关注的热点地区主要是由于其处于“三洲五海”之地的重要地理位置、丰富的石油资源、匮乏的水资源和文化方面的差异。 3.三洲五海两洋一湾：1、亚洲、欧洲、非洲；2、地中海、红海、黑海、里海、阿拉伯海； 3、太平洋、大西洋； 4、波斯湾 4.中东是目前世界上石油储量最大、生产和输出石油最多的地区。 5.中东石油主要分布在波斯湾及其沿岸地区生产的石油主要运往西欧、美国、日本等发达国家和地区。 6.中东石油路线： A波斯湾－霍尔木兹海峡－阿拉伯海－红海－苏伊士运河－地中海-直布罗陀海峡-大西洋B:波斯湾－霍尔木兹海峡－印度洋－好望角－大西洋 C波斯湾－霍尔木兹海峡－阿拉伯海－孟加拉湾－马六甲海峡－南海-太平洋（输油最大）7.中东人种主要是白色人种大多数居民信仰伊斯兰教少数居民信仰基督教、犹太教和其他宗教。 8.世界最大半岛：阿拉伯半岛；主要地形区：伊朗高原；主要的气候：热带沙漠气候 9伊斯兰教、基督教和犹太教都把耶路撒冷看作是圣城。 10沙特阿拉伯的麦加是伊斯兰教创始人，穆罕默德的诞生地被伊斯兰教尊为圣城。 11中东多数国家和地区的居民是阿拉伯人信仰伊斯兰教这些国家被叫做“阿拉伯国家”。12波斯人主要分布在伊朗主要信仰伊斯兰教犹太人集中分布在以色列主要信仰犹太教。阿拉伯人喜爱白色。
第二节欧洲西部 1位于欧洲的西半部面积约500万平方千米，人口稠密国家重多绝大部分是发达国家。 2北临北冰洋，南临地中海，西北和东北部依次有北海和波罗的海。 3这里是工业革命的发源地，目前也是世界上工业发达的地区之一，这里工业工艺精，技术水平和生产效率高，是世界上著名的工业密集地带。 4.欧洲西部的农业在国民经济中所占比重较小，但生产水平高，多用机械、自动化程度高，耗用劳动力少。 5.欧洲西部的服务业体系完善，服务质量优，产值大，成为国民经济的支柱。 6欧洲西部形成了一个区域性国际组织叫做欧洲联盟简称欧盟，欧盟内部人们可以使用统一的货币——欧元。 欧盟加强了欧洲国与国之间的政治和经济联系并在世界经济领域和国际政治舞台上发挥着重要作用。 7欧洲西部的工业以制造业为主，制造业是把原料进行加工制造成各种各样产品的工业部门。 8欧洲人酷爱乳产品和牛羊肉他们的餐桌上常见牛排、奶油、奶酪等食品。 9欧洲西部的人们称牧草为“绿色金子”在英国畜牧业产值占全部农业产值的70以上。欧洲畜牧业发达的原因是：气候——地处中纬度大陆西岸，属温带海洋性气候（特点：全年温和多雨）形成多汁的牧草；地形——地势低平，以平原为主．致使草场广布。因此欧洲西部的畜牧业发达。 10欧洲大陆西岸温带海洋性气候分布广泛，该气候的特点是全年温暖湿润。地中海沿岸为地中海气候，夏季炎热少雨，冬季温和多雨。 11欧洲西部航运价值最高的河流是莱茵河流经国家最多的河流是多瑙河。 12欧洲西部最高峰是属于阿尔卑斯山脉的勃朗峰欧洲最高峰为属于大高加索山脉的厄尔布鲁士山。 13位于欧洲西部的北端的大半岛是斯堪的纳维亚半岛，南端的三大半岛自西向东依次为伊比利亚半岛、亚平宁半岛和巴尔干半岛。 14 欧洲西部地形以平原为主，主要的地形区有西欧平原，波德平原 15 欧洲西部主要的岛屿海峡：大不列颠岛、爱尔兰岛、英吉利海峡、直布罗陀海峡 16.旅游资源：挪威峡湾风光；英国白金汉宫；荷兰风车；波兰华沙肖邦雕像；法国卢浮宫博物馆、埃菲尔铁塔；意大利罗马古斗兽场；希腊奥林匹克公园；瑞士阿尔卑斯滑雪场。繁荣的旅游业：欧洲西部的自然和人文旅游资源异常丰富。南欧阳光灿烂的地中海海边风景区和沙滩浴场，北欧曲折、幽深的峡湾，引人入胜；中部高耸的阿尔卑斯山，是登山和滑雪运动的好场所；独特的风土人情，古老的城堡，庄严的教堂、为数众多的博物馆，使欧洲西部成为世界旅游业发达的地区。法国、西班牙和意大利成为欧洲著名的三大旅游国。 17、欧洲西部的地形特点是：地势低平，以平原为主，南北多山地，中部平原广大。平原分布在中部，以莱茵河为界，以西为西欧平原，以东为波德平原。山地主要分布在南部和北部半岛上。北部有斯堪的纳维亚山脉，南部有阿尔卑斯山脉。阿尔卑斯山脉呈东西走向，有利于大西洋暖湿流深入内陆。
关于“思维导图”应用的总结 “思维导图”作为一种可视化的思维工具，在教师教学和学生学习中起到重要作用。利用可视化思维工具，学生的思维就可以展示出来，从这种公开的展示中，学生既能分享个人思维、学习他人思维方式，也能对思维过程、内容以及思维的演化历程进行自我反省。 本学期，学校在教师课堂教学和学生的学习过程中，特别强调教师在课堂上自觉运用“思维导图”，并引导学生在学习中正确使用，争取教育教学效益的最大化。 一、教研学习，认识“思维导图”的教学工具 在3.20的教研活动会议上，校长就“思维导图”特点和使用作了专题讲座。强调它是**县教体局2019年大力推介和实施的一个重点项目，以引起参训教师的高度重视，并在教学和指导学生学习中积极使用。通过讲解，教师们厘清了“思维教学”、“思维发展型课堂”和“思维训练”三个核心概念，加深教师对概念的认知和理解。初步知道了几类可视化思维工具——八大思维图示，以及每种图示特点和作用。启发教师：八种图示各具特点，可以依据自身学科特点、教学目标和课时内容加以选择和灵活使用。 二、专题培训，为教师提供优质的教学工具 3月21日下午，**九年制学校在物理功能室，举行了“思维导图”在教学中的应用培训活动。培训内容用PPT展示，直观形象，便于教师理解。
在介绍使用图示时，用语文、历史、政治等学科教师教学和学生学习的案例加以生动注解。培训指导了教师思维导图的绘制方法，老师明白了思维导图的定义、绘制步骤和纸张、中心图、关键词、线条以及颜色的使用规则。 培训还列举了思维导图使用的注意事项，希望教师认真领会思维导图的要义。帮助教师从会使用到用的好，最后达到高效使用，让思维导图在教学中起到良好的作用。 思维导图培训结束前，老师当堂练习，绘制一份本学科的思维导图。老师迫不及待开始绘制思维导图，完成的图形各具特色。 三、在教学中，要求教师大胆实践 学校要求3—8年级老师和学生，在教学中大胆使用“思维导图”。教师们从不懂到明白，从不会使用到尝试运用，变化明显，收效显著。从教案、课堂教学中可以发现，老师都已不同程度的运用思维导图，使知识更加层次化、系统化，教学更加形象化，更具吸引力。 四、学生学习主动，创新素养提高 学生对思维导图从好奇到使用，学习从被动变主动。思维导图使学生学习过程变得有趣，思维过程变得形象，学生能够主动完成作业，增强了学习的积极性，作业质量明显提升。有的学生还可以对图示的中心词和图表、图像进行改造和加工，使之更形象，更能准确地反映学生的思维过程和思维表述。 学生利用思维导图进行课前预习、课堂总结、课后复习，自主参与了学习，积极的思考，认真的总结，从中发现问题，并探寻解决问
思维导图应用领域汇总 关于MindManager思维导图，小无论是文章写作、读书笔记和课程学习，还是项目管理、分析问题等各方面，思维导图都发挥着很重要的作用，除此之外，它还有更多的应用领域 1、笔记：（阅读、课堂学习、面试、演讲、研讨会、会议记录等，需记录要点时） 接收讯息时，用思维导图作记录，将要点以词语形式记下，把相关的想法用线连上加以组织，方便记忆。使用思维导图的好处是无论信息表达的次序如何，都能放在适当的位置
上，在画思维导图的过程中，还可以帮助了解和总结信息及想法。 2、复习：（预备考试、预备演说……需加深记忆时） 将已知的资料或想法从记忆中以思维导图画出来，或将以往画的思维导图重复再画出，能加深记忆，思维导图也能帮助组织想法，令想法更清楚。 3、小组学习：（头脑风暴、小组讨论、家庭或小组计划……需共同思考时） 小组共同创作思维导图。首先由各人自己画出自己的想法，然后将各人的思维导图合并并讨论，决定哪些较为重要，再加入新想法，最后重组成为一个共同的思维导图。在这个过程中，每个组员的意见都被考虑，提升了团队归属感及合作。共同思考时，也可产生更多创意和有用的想法，最后的思维导图是小组共同的结晶，各组员有共同的方向和结论。
4、创作：（写作、学科研习、水平思维、新计划……需创新时） 首先将所有环绕主题的想法都写下来，包括新的、不可能发生的，不用理会对或错。然后再将想法组织合并，重新画出思维导图，不要将不可能的划去，让大脑放松，这时候创意可能产生，然后将思维导图改写。在这个过程中，思维导图帮助我们将大量的想法联系起来，产生新的想法，而且中心目标十分清楚。
“思维导图”在高三物理实验复习中的妙用 矿院附中夏红胜 在有关“友善用脑”的理论中，“思维导图”是学生进行复习整合知识的有力工具，而高三物理教学复习课，该如何利用“思维导图”使复习课取得“举一反三”的理想效果呢？下面就以实验复习课为例，简述在这方面的尝试。 高三实验复习总共两周十课时，却要复习十四个实验，而且还要兼顾实验原理和实际操作两方面，时间非常紧，如何做到省时、高效呢？的确需要教师开动脑筋，用科学的复习方法引领学生进行有效的知识整合。我在上实验复习课之初确定的思路就是找出某些实验的共同点，分成几块进行复习。 首先拿出的第一块是“与纸带相关的实验”。这部分实验考查的知识点涉及“加速度计算”和“机械能守恒”，而且计算量大，一直是学生的一个难点。为了能够使这节复习课更有实效性，上课之前，我留给了学生几个问题： 1.高中阶段，我们在哪几个实验中用到了纸带？ 2.从纸带我们能直接得到的信息有哪些？ 3.总结近几年的高考题，你能发现什么？请把你的总结画成“思维导图”。 提出这几个问题的目的在于：①学生事先复习整理好已学知识可以节省课堂时间；②提醒学生总结纸带的功能；③引领学生通读高考题后能发现高考考查的重点是知识迁移能力，提醒学生要在这方面多下功夫，才能“举一反三”。 在上课时，学生带着这些问题来到课堂，也就使课堂教学更有针对性了。学生自己总结画出的“思维导图”各式各样的都有。我在此只选一个较好的展示（见下文所示框架图），并以此来说明上课时“思维导图”的用途。
上面的“思维导图”是通过学生讨论，教师引导等过程不断整理、完善得到的。整个思维导图分为三部分。每画出一部分，我便要求学生在自己已复习整理的相关习题中挑出与之对应的习题，这样就使上课不再只是教师为主体的讲题过程，而是学生为主体的整理、提高整合知识能力的过程，学生的积极性也很高。下面就举几个学生选取的相关例题来说明整个的教学过程。 教学过程一：学生一致认为基本实验部分不必占用课堂时间复习，自己看书、整理就可以了。这部分只进行了实验名称，纸带信息用途，相关知识点的回顾就一带而过了，耗时约5分钟； 教学过程二：重点落实纸带能反映出的信息整理。教师结合学生的观点引导学生把信息寻找方向落在“看、量、算”三个方面，并给出下面相关例题进行落实：例1：在研究匀变速直线运动规律的实验中，小车拖动纸带运动，每秒50次打点的打点计时器，打出的纸带如图1所示，选出A、B、C、D、E五个计数点，每相邻两个计数点间，还有4个数据点未在图中标出，求： ①AE间平均速度V＝ m/s; ②C点的瞬时速度V C= m/s; ③小车运动的加速度a= m/s2; ④A点的瞬时速度V A= m/s 图1 学生从“看、量、算”三个方面落实纸带信息的获取方法，为下一步知识运用和迁移做好准备，此过程耗时约十分钟。 教学过程三：知识运用与迁移能力的培养―――教学重点 例2：（1997，上海）如图2中甲表示用打点计时器记录小车的运动情况，开始时小车在光滑水平玻璃板上运动，后来在薄布面上作匀减速运动，所打出的纸带如图乙所示，纸带上相邻两点对应的时间间隔为0.02秒，从纸带上可以确定小车作匀减速运动的初速度是，小车在布上运动的加速度是
运用思维导图梳理语 文知识 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
运用思维导图梳理语文知识的研究 一、本课题选题的目的和意义： 1、目的： 思维导图(Mind Mapping)是英国著名脑思维学者Tony Buzan 在上世纪70年代所创造，它能提供一种运用图文并重的技巧，开启人类大脑的无限潜能的有效工具。 本课题研究旨在将思维导图技术引入语文教学中，望能更快更有效的进行语文知识的梳理，提高学生主动学习的能力，帮助学生建立完整的知识框架体系，对学习的课程进行有效的资源整合，使得学生掌握新型的思维方法，利用新型的思维工具，达到高质量学习的目的。 2、选题意义： 践行《新课标》的育人理念：在实施建议中，特别强调教师要“帮助学生形成自主学习能力”，培养和提高学生的自主能力。通过思维导图的学习及应用，学生对于知识结构之间的密切联系会有更深刻的理解，避免知识的孤立，片面化。 有效地预习能帮助学生明确学习目的，对于所学内容条理清晰，在学习过程中思维积极活跃，注重知识的梳理与积累。思维导图的使用强化重点脉络，帮助学生清晰了解所学。思维导图提高学生复习高效：学生将零散的知识用结构图示展示，能够更加形象生动地串接所学知识，能够梳理好所有知识点，建立知识空间感，提高学习的深度和广度，是复杂的课文篇章简单明了化，增强清晰度。 思维导图是提高自主学习能力最有效的方式之一：导图给学生提供了一幅思维“全景图”，学生能够帮助学生突破思维定势，在不同知识间构建桥梁，系统有条理的思考学习内容，使学生会学、乐学，形成较强的自主学习乃至终身学习的能力。 二、本课题的研究目标、研究内容 1、研究目标： 使学生了解思维导图的起源、思维方法、应用制作方法；掌握绘制思维导图的手段；应用思维导图梳理语文学科知识以改善学习方式、激发学生的学习兴趣、培养学生的放射性思维能力，实现与新课程标准的接轨。提高记忆能力和建构生成知识网络，改变过去学生单线思维的状态，增强学生的思维能力，启发学生的联想力和创造力，从而提高学生的学习能力和学习的效率。 使教师在教学过程中借助思维导图这一思维技术，利用思维导图的有关软件，通过对众多知识点的自由组合或建构多种方案，培养和训练学生的创新思维，树立全局的观念，提高教学效率以及深化教学方法的改革提供最有力的工具；在教学过程中，通过运用思维导图技术，从而提高教学能力和教学效率。 2、研究内容 教学过程中运用思维导图梳理语文学科知识的研究。 三、研究方法与实施步骤
图解思维导图（黄娟） 思维导图以图解的形式和网状结构，用来存储、组织、优化和输出信息。是一种思维工具，被称为——大脑的瑞士军刀。思维导图和发散性思维相关，它反映了脑细胞的形状，类似大自然的创造和连接方式，如叶脉、树枝等。心理学、脑科学研究表明，大脑是非线性的，而且是非常复杂地相互关联着的。大脑是多维度的，因此要结合左右大脑皮层的功能，创造全脑思维。关键词和关键图像会刺激大脑的2个半球，会调动各种感官。因此要学会选择关键图像和关键词。 思维导图的创始人是东尼·巴赞。 思维导图，是一种用图画展示自己思维的一种方法，一种革命性的思考方法，结合右脑的思维，将逻辑抽象的文字表达方式通过画画的方式展现出来。思维导图已经在全球范围得到广泛应用，包括大量的500强企业。 一、思维导图的特点 思维导图作为一种学习的工具，思维导图跟有哪些不一样的地方呢？接下来说说思维导图的一些特点。 1.遵循大脑规律
这是左脑和右脑负责处理不同进程的思维导图。 大家目前都比较清楚，创意部分都在右脑，所以现在社会上都在高呼——发展孩子的右脑。 2.帮助记忆效果好 大家怎样看待记忆力和想象力？世界上有记忆协会，还有很多培训，都在训练人们的记忆力。 事实上，记忆力和想象力是相关的。想象和联想是记忆的基石。通过关键性的记忆工具，例如词语、数字和图像，可以将记忆运用得很有效，思维能力和记忆能力也可以得到加强。 利用上述12种方法，可以使得记忆加强。 1.感官； 2.运动； 3.联想；4；性；5.幽默；6.想象；7.编号；8.符号；9.颜色； 10.顺序/次序；11.积极形象；12.夸张。 东尼博赞把这些做成了思维导图。 达芬奇说，要想真正地有创造力，需要： 1）培养感觉； 2）学习科学的艺术； 3）学习艺术的科学； 4）认识到万物之间都存在某种程度上的联系。 而创造性的要素包括： 想象；联想；思维敏捷；求新；灵活；批量生产。 还有一个促使创意产生的工具——头脑风暴法。
八年级历史下册中国现代史思维导图
最可爱的人完成反帝反封建的任务, 改变半半社会性质 爱国主义、革命 英雄主义糟神 毛泽东主席-届政协 中国人民从此站起来开国大典 结束百年屈辱历史（新中国成立） 祖国大陆统一 _西藏和平解放 '?,,^≡ ≡jt外：抗美援朝 邱少牙 ＜中华人民共和国土地改革法》.,ω, . 废除対建土地制度内：土地革命 基本国策基本政治制度5个省级民 族自治区1997年7月!.日1999 年12 月20 B 两岸关系历史性的一 步 中华人民共和国大陆社会主义制度港澳 台资本主义制度 一国 两制 规模最大 规格最高 八年级历史下册中国现代史思维导图 成立 巩固 民族区域自治 香港回归 澳门回归 汪辜会谈 定义（邓小平） 国两制 人民空军人民海军战略导弹 部队和平共处五项原则求同 存异万1?会议联合国合注席 位的恢H 尼克松访华 华东军区海军 上海举办APEC会议 IR子弹、导弹 东方红一号 两弹一星 科技 琏隆平杂交水稻 863计划 九年义务教育 教育 优先发展教育科教兴国 第一个奥运冠军许海峰 亚运会体育 奥运会 一、新中国成立与巩固 !■、民族 2、统一 3、国防 4、外交 （周恩来） 5、科教文化 二、社会主义道路的探索丿3、十年建设 （1956-1966年） 1＞一五计划乂且业. （1953-1957年）| 一届人大|第一部《中华人民共租醮迭Ll 2、三大改造益私有船公有制?初级阶段 （1953 195；资本主审业」公私合营I 厘好开端★!中共八大I / _人民公社化运动 帙人。王进喜/ 两弹元肋。邓?＞先/ .覚的好干部.為裕標 / 结束:江靑反草命集团被粉碎 4、十年文革（~ （19664976年2」彩叫氏治被践踏 4、十年文革 中国现代史解放思想） 实事求是） 新吋期的事会议（WI郭不平） 建国以来 四、社会主义成就 珠海、汕头 三、改革开放KrJ 1988年。海南 小他邓小平理追 深圳国际化的经济中心和金融中心 福建 开端A十届三中全会 垫遁史上具有深远盘义的历史賢折 对外开放 内地 确立为党的指导思?a∕中共十五大I 科找是复一 电严力一 ~ 对内改审 u?.m IlhiI 经济建设） 改革开放） 农村家庭联产承包制 国有迤业改革 沿海开放城市沿海 縉济开放区 1980年 经济待区&