圆与圆之间的位置关系

圆与圆的位置关系的判断方法一、圆与圆的位置关系的判断方法有两种，一种是~d r 法，另一种是判别式法.以下详解这两种方法. 1、~d r 法根据两圆心距与两圆径的大小关系来判断：①外离d R r ； ②外切d R r ； ③相交R r dR r ；④内切dR r ； ⑤内含dR r .其中，R 是大圆的半径，r 是小圆的半径，12||d C C .如果是等圆，那么两圆就没有内切和内含这种位置关系，而有个重合的情况.如果两圆是等圆，那么两圆的位置关系只有外离，外切，相交和重合四种. 2、判别式法已知22111:0C xy D x E y F 1⊙，半径为r 和222222:0C xy D x E y F ⊙，半径为R ，且R r 判断两圆的位置关系：两圆的方程相减，得 121212()()()0D D x E E y F F简记为 0AxBy C其中220A B （1）将（1）式代入其中一个圆的方程中，消去x 或y ，可得一个关于y 或x 一元二次方程，记为20ay by c 或20ax bx c，其中0a①0两圆有两个公共点（相交）； ②0两圆有一个公共点（内切或外切）； ③0两圆无公共点（内含或外离）； 以上②③中，如何区分内切和外切，内含和外离呢？请看以下数学思想方法： 将问题转化为小圆的圆心与大圆的位置关系（亦即点圆位置关系）来判断！ 如果圆心1C 在圆2C 的外面，即dR ，那么两圆外切或外离；如果圆心1C 在圆2C 的内部，即d R ，那么两圆内切或内含. 二、两圆方程作差的意义 两圆作差后得到的方程：121212()()()0D D x E E y F F简记为 0AxBy C其中220A B （1）其意义为①当两圆相交时，方程（1）是相交弦所在的直线方程； ②当两圆相切时，方程（1）是过切点的公切线的方程； ③当两圆没有公共点时，方程（1）没有特别的含义. 三、应用举例 例题1 已知22:2440C xy x y 1⊙和222:1090C x y x ⊙，判断两圆的位置关系，若两圆相交，则求出相交弦所在直线的方程.【解析】方法一：~d r 法 圆心1(1,2)C ，半径3r ，圆心2(5,0)C ，半径4R ，则1,7R r R r两圆圆心距为22(15)(20)210(1,7)d所以，两圆相交，将两圆的方程相减可得 124130x y 即为相交弦的方程.方法二：判别式法将两圆的方程相减，得 124130x y 即 1334y x（2） 将（2）式代入222:1090C xy x ⊙得21604723130x x 24724160313224640所以，两圆相交，相交弦所在直线的方程是124130x y .【变式训练】 已知22:650C xy y 1⊙和222:870C x y x ⊙，判断两圆的位置关系，若两圆相交，则求出相交弦所在直线的方程；若两圆相切，则求出过切点的公切线的方程.例题2 已知22:4210C xy x y 1⊙和222:142410C x y x y ⊙，判断两圆的位置关系，若两圆相交，则求出相交弦所在直线的方程；若两圆相切，则求出过切点的公切线的方程.【解析】方法一：~d r 法 圆心1(2,1)C ，半径2r ，圆心2(7,1)C ，半径3R ，则1,5R r R r两圆圆心距为 22(72)(11)5dR r所以，两圆外切，将两圆的方程相减可得 4x 即为所求公切线的方程.方法二：判别式法将两圆的方程相减，得 4x （3）将（3）式代入222:142410C xy x y ⊙得2210y y 2(2)4110所以，两圆相切.小圆圆心1(2,1)C ，坐标代入222:142410C xy x y ⊙中，有222214241211422141170x y x y所以，两圆是外切关系，所求公切线的方程4x .【变式训练】 1.已知22:1C xy 1⊙和222:6890C x y x y ⊙，判断两圆的位置关系，若两圆相交，则求出相交弦所在直线的方程；若两圆相切，则求出过切点的公切线的方程. 2.已知22:46120C x y x y 1⊙和222:680C x y x y⊙，判断两圆的位置关系.。

圆与圆位置关系知识点
在几何学中，圆与圆之间的位置关系涉及到它们的相对位置和相交情况。

以下
是一些关于圆与圆位置关系的重要知识点。

1. 内切：当一个圆完全位于另一个圆内部，并且两个圆的边界相切于一个点时，我们称这两个圆为内切圆。

内切圆的半径小于外切圆的半径。

2. 外切：当一个圆完全位于另一个圆外部，并且两个圆的边界相切于一个点时，我们称这两个圆为外切圆。

外切圆的半径大于内切圆的半径。

3. 相离：当两个圆没有任何交点且没有相切点时，我们称这两个圆为相离圆。

4. 相交：当两个圆有交点时，我们称这两个圆为相交圆。

a. 两个圆相交于两个不同的点时，我们称这种相交为普通相交。

b. 当两个圆的圆心重合且半径相等时，这两个圆相交于一条直径线，我们称
这种相交为重合相交。

5. 同心圆：当两个圆的圆心重合但半径不相等时，我们称这两个圆为同心圆。

这些是圆与圆位置关系的基本知识点，它们帮助我们理解圆的排列方式并解决
与圆相关的几何问题。

了解这些知识点可以为我们进一步学习和应用几何学提供基础。

图1扇形、圆与圆的位置关系一、圆和圆的位置关系.1、外离、外切、相交、内切、内含(包括同心圆)这五种位置关系的定义.(1)外离: 两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离.(2)外切: 两个圆有惟一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时, 叫做这两个圆外切.这个惟一的公共点叫做切点.(3)相交: 两个圆有两个公共点,此时叫做这个两个圆相交.(4)内切: 两个圆有惟一的公共点,并且除了这个公共点以外,一个圆上的都在另一个圆的内部时,叫做这两个圆内切.这个惟一的公共点叫做切点.(5)内含: 两个圆没有公共点, 并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含.两圆同心是两圆内的一个特例. 2、相切两圆的性质:如果两个圆相切,那么切点一定在连心线上. 3、 相交两圆的性质:相交两圆的连心线垂直平分公共弦. 二、弧长及扇形的面积1、圆周长公式: 圆周长C=2πR (R 表示圆的半径)2. 弧长公式: 弧长180R n l π= (R 表示圆的半径, n 表示弧所对的圆心角的度数)3、扇形定义:一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.4、弓形定义:由弦及其所对的弧组成的图形叫做弓形. 弓形弧的中点到弦的距离叫做弓形高. 5、圆的面积公式.2R S π= (R 表示圆的半径) 6、扇形的面积公式:扇形的面积3602R n S π=扇形 (R 表示圆的半径, n 表示弧所对的圆心角的度数)※弓形的面积公式:(如图5) (1)当弓形所含的弧是劣弧时, 三角形扇形弓形S S S -= (2)当弓形所含的弧是优弧时, 三角形扇形弓形S S S += (3)当弓形所含的弧是半圆时, 扇形弓形S R S ==221π提高试题1、如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm 2,则该半圆的半径为（ ）A. (4+cm B. 9 cmC. D.cm第1题 第2题2、如图，MN 是半径为1的⊙O 的直径，点A 在⊙O 上，∠AMN =30°，B 为AN 弧的中点，点P 是直径MN 上一个动点，则PA+PB 的最小值为（ ）A ．22B ．2C ．1D ．23、已知两圆的半径为Ｒ，r 分别是方程X 2-5X+6=0两根，两圆的圆心距为1，两圆的位置关系是（ ） A.外离 B.外切 C.内切 D.相交4、已知圆锥的母线长为4，底面半径为2，则圆锥的侧面积等于 （ ）A ．8πB ．9πC ．10πD ．11π 5、一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是 （ ）．A ．1B ．34C ．12D ．136、 现有一个圆心角为，半径为的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计）.该圆锥底面圆的半径为（ ）A ．B ．C ．D ．7、如图，正方形ABCD 内接于⊙O ，点P 在劣弧AB 上，连接DP ，DP 交AC 于点Q ．若QO=PQ ，则QA QC的值为（ ） （A ）132-（B ）32（C ）23+（D ）23+8、已知锐角△ABC 的顶点A 到垂心H 的距离等于它的外接圆的半径，则∠A 的度数是（ ） （A ）30° （B ）45° （C ）60° （D ）75°9、如图，已知平行四边形ABCD ，过A 、B 、C 三点的圆交AD 于E ，且与CD 相切。

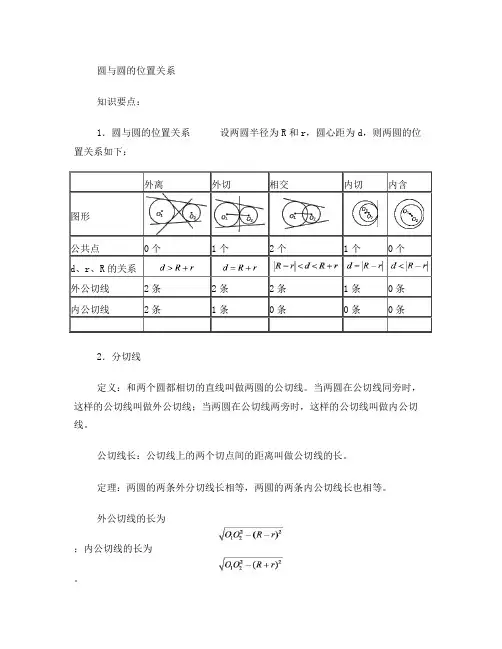
圆与圆的位置关系知识要点：1．圆与圆的位置关系设两圆半径为R和r，圆心距为d，则两圆的位置关系如下：2．分切线定义：和两个圆都相切的直线叫做两圆的公切线。

当两圆在公切线同旁时，这样的公切线叫做外公切线；当两圆在公切线两旁时，这样的公切线叫做内公切线。

公切线长：公切线上的两个切点间的距离叫做公切线的长。

定理：两圆的两条外分切线长相等，两圆的两条内公切线长也相等。

外公切线的长为；内公切线的长为。

3．相交两圆的性质定理：相交两圆的连心线垂直平分两圆的公共弦。

4．相切两圆的性质定理：相切两圆的连心线经过切点。

1．圆和圆的位置关系（设两圆半径分别为R和r，同心距为d）（1）两圆外离d＞R+r；（2）两圆外切d=R+r；（3）两圆相交R－r＜d＜R+r；（4）两圆内切d=R－r；（5）两圆内含d＜R－r。

（同心圆（6）是一种内含的特例）2．有关性质：（1）连心线：通过两圆圆心的直线。

如果两个圆相切，那么切点一定在连心线上。

（2）公共弦：相交两圆的连心线垂直平分两圆的公共弦。

（3）公切线：和两个圆都相切的直线，叫做两圆的公切线。

两个圆在公切线同旁两个圆在公切线两旁3．已知两圆半径分别为R、r，同心距为d，填定下表：名称公共点数圆心距半径关系公切线条数内外外离d=R+r相交d=R－r内含一星级题：1．如果两圆有且只有两条公切线，那么这两圆的位置关系是（）A．外离 B．外切 C．相交 D．内含2．如果两圆半径分别为3㎝和5㎝，圆心距为2㎝，则两个圆的位置关系为（）。

A．外离 B．外切 C．相交 D．内切3．已知⊙O1和⊙O2内切，它们的半径分别为2㎝和3㎝，则两圆圆心距O1O2= ㎝。

4．半径分别为3㎝和4㎝的两圆外切，那么这两圆的圆心距为㎝。

5．已知半径为R的两个等圆的圆心距为d，那么当两圆外切时，d与R满足的关系式是。

6．已知两圆半径分别为5㎝和2㎝，它们的圆心距为7㎝，则两圆位置关系为。

7．已知：两圆⊙O1与⊙O2的圆心距O1O2=5㎝，两圆的半径分别为㎝和㎝，则这两圆的位置关系是。

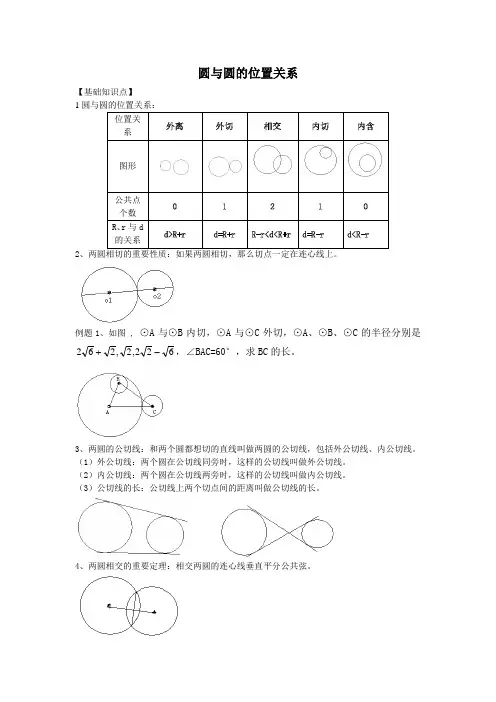
圆与圆的位置关系【基础知识点】12例题1、如图 ,⊙A与⊙B内切，⊙A与⊙C外切，⊙A、⊙B、⊙C的半径分别是,2+，∠BAC=60°，求BC的长。

2-62,2623、两圆的公切线：和两个圆都想切的直线叫做两圆的公切线，包括外公切线、内公切线。

（1）外公切线：两个圆在公切线同旁时，这样的公切线叫做外公切线。

（2）内公切线：两个圆在公切线两旁时，这样的公切线叫做内公切线。

（3）公切线的长：公切线上两个切点间的距离叫做公切线的长。

4、两圆相交的重要定理：相交两圆的连心线垂直平分公共弦。

例题2、已知⊙1和⊙2的半径分别为8cm和5cm，它们相交于A、B，且AB=6cm，求圆心距O1O2.(自己作图，考虑两种情况，分类讨论：圆心在AB同侧或者异侧)例题3、如图，已知直角三角形ABC的斜边AB为4，内切圆半径为26 ，求三角形ABC的面积。

例题4、（2011•南京）如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．P为BC的中点，动点Q从点P出发，沿射线PC方向以2cm/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t s．（1）当t=1.2时，判断直线AB与⊙P的位置关系，并说明理由；（2）已知⊙O为△ABC的外接圆．若⊙P与⊙O相切，求t的值．例题5、（2008•威海）如图，点A，B在直线MN上，AB=11厘米，⊙A，⊙B的半径均为1厘米．⊙A 以每秒2厘米的速度自左向右运动，与此同时，⊙B的半径也不断增大，其半径r（厘米）与时间t（秒）之间的关系式为r=1+t（t≥0）．（1）试写出点A，B之间的距离d（厘米）与时间t（秒）之间的函数表达式；（2）问点A出发后多少秒两圆相切？例题6、（2011•绵阳）如图，在梯形ABCD中，AB∥CD，∠BAD=90°，以AD为直径的半圆O与BC 相切．（1）求证：OB⊥OC；（2）若AD=12，∠BCD=60°，⊙O1与半⊙O外切，并与BC、CD相切，求⊙O1的面积．例题7、（2007•南充）如图是某城市一个主题雕塑的平面示意图，它由置放于地面l上两个半径均为2米的半圆与半径为4米的⊙A构成．点B、C分别是两个半圆的圆心，⊙A分别与两个半圆相切于点E、F，BC长为8米．求EF的长．例题8（2011•黄石）已知⊙O1与⊙O2相交于A、B两点，点O1在⊙O2上，C为⊙O2上一点（不与A，B，O1重合），直线CB与⊙O1交于另一点D．（1）如图（1），若AD是⊙O1的直径，AC是⊙O2的直径，求证：AC=CD；（2）如图（2），若C是⊙O1外一点，求证：O1C丄AD；（3）如图（3），若C是⊙O1内的一点，判断（2）中的结论足否成立．例题9、（2006•成都）已知：如图，⊙O与⊙A相交于C，D两点，A，O分别是两圆的圆心，△ABC内接于⊙O，弦CD交AB于点G，交⊙O的直径AE于点△CDE，连接BD．（1）求证：△ACG∽△DBG；（2）求证：AC2=AG•AB；6，15，且CG：CD=1：4，求AB和BD的长（3）若⊙A，⊙O的直径分别为5【课堂练习】一、填空与选择1、（2010•宁夏）如图是三根外径均为1米的圆形钢管堆积图和主视图，则其最高点与地面的距离是__米．2、（2010•菏泽）如图，在正方形ABCD中，O是CD边上的一点，以O为圆心，OD为半径的半圆恰好与以B为圆心，BC为半径的扇形的弧外切，则∠OBC的正弦值为________3、（2008•绍兴）如图中的圆均为等圆，且相邻两圆外切，圆心连线构成正三角形，记各阴影部分面积从左到右依次为S1，Ss，S3，…，Sn，则S12：S4的值等于__________。

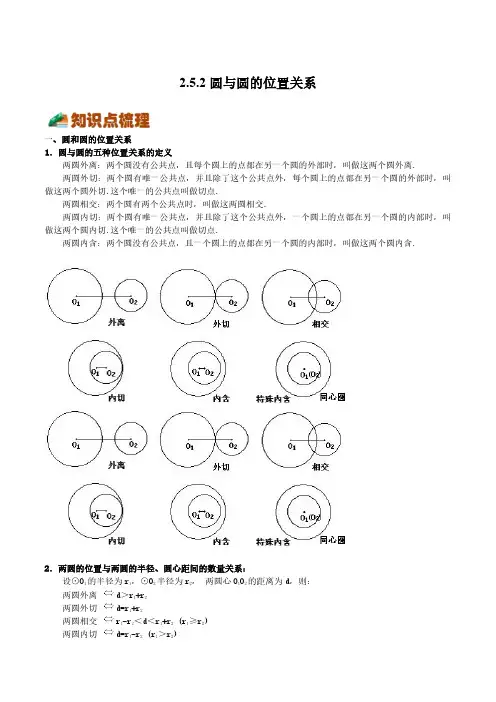
2.5.2圆与圆的位置关系一、圆和圆的位置关系1．圆与圆的五种位置关系的定义 两圆外离：两个圆没有公共点，且每个圆上的点都在另一个圆的外部时，叫做这两个圆外离. 两圆外切：两个圆有唯一公共点，并且除了这个公共点外，每个圆上的点都在另一个圆的外部时，叫做这两个圆外切.这个唯一的公共点叫做切点. 两圆相交：两个圆有两个公共点时，叫做这两圆相交. 两圆内切：两个圆有唯一公共点，并且除了这个公共点外，一个圆上的点都在另一个圆的内部时，叫做这两个圆内切.这个唯一的公共点叫做切点. 两圆内含：两个圆没有公共点，且一个圆上的点都在另一个圆的内部时，叫做这两个圆内含.2．两圆的位置与两圆的半径、圆心距间的数量关系： 设⊙O1的半径为r1，⊙O2半径为r2，两圆心O1O2的距离为d，则： 两圆外离d＞r1+r2 两圆外切d=r1+r2 两圆相交r1-r2＜d＜r1+r2(r1≥r2) 两圆内切d=r1-r2(r1＞r2) 两圆内含d＜r1-r2(r1＞r2)要点： (1) 圆与圆的位置关系，既考虑它们公共点的个数，又注意到位置的不同，若以两圆的公共点个数分类，又可以分为：相离(含外离、内含)、相切(含内切、外切)、相交； (2) 内切、外切统称为相切，唯一的公共点叫作切点； (3) 具有内切或内含关系的两个圆的半径不可能相等，否则两圆重合.A ．2种B ．3种C ．4种D ．5种【答案】A 【解析】由图形可以看出，有两种位置关系，相交和内切．故选A.题型2：根据圆与圆的位置关系求半径4．已知1O e 与2O e 相切，若1O e 的半径为3cm ，127cm O O =，，则2O e 的半径为（ ）A ．4cm 或12cmB ．10cm 或6cmC ．4cm 或10cmD ．6cm 或12cm【答案】C【分析】根据圆与圆的位置关系，内切时()2121d r r r r =->，外切时12d r r =+，计算即可．【解析】解：两圆内切时，2O e 的半径7310=+=(cm)，外切时，2O e 的半径734=-=(cm)，∴2O e 的半径为4cm 或10cm ．故选：C ．【点睛】本题考查了圆与圆的位置关系，熟练掌握知识点是解题的关键．5．如果两圆有两个交点，且圆心距为13，那么此两圆的半径可能为（ ）A ．1、10B ．5、8C ．25、40D ．20、30【答案】D【分析】先由两圆有两个交点得到两圆相交，然后根据半径与圆心距之间的关系求解即可．【解析】∵两圆有两个交点，∴两圆相交，∵圆心距为13∴两圆的半径之差小于13，半径之和大于13．A ．1101113+=<，故不符合题意；B ．5813+=，故不符合题意；【点睛】此题重点考查圆与圆的位置关系、线段的垂直平分线的性质、勾股定理以及数形结合与分类讨论数学思想的运用等知识与方法，正确地作出所需要的辅助线是解题的关键．9．已知两圆的半径分别为2和5，如果这两圆内含，那么圆心距A．0＜d＜3B．0＜d＜7C．3＜d＜7A．45°B．30°【答案】B【分析】连接O1O2，AO2，O1B，可得【解析】解：连接O1O2，AO2，O∵O 1B = O 1A∴112112O AB O BA AO O Ð=Ð=Ð ∵⊙O 1和⊙O 2是等圆，∴AO 1=O 1O 2=AO 2，∴△AO O 是等边三角形，【点睛】本题考查了相交两圆的性质以及等边三角形的判定与性质，得出21AO O D 是等边三角形是解题的关键．题型5：分类讨论13．已知圆1O 、圆2O 的半径不相等，圆1O 的半径长为5，若圆2O 上的点A 满足15AO =，则圆1O 与圆2O 的位置关系是（ ）A ．相交或相切B ．相切或相离C ．相交或内含D ．相切或内含【答案】A【分析】根据圆与圆的位置关系，分类讨论．【解析】解：如图所示：当两圆外切时，切点A 能满足15AO =，当两圆相交时，交点A 能满足15AO =，当两圆内切时，切点A 能满足15AO =，当两圆相离时，圆2O 上的点A 不能满足15AO =，所以，两圆相交或相切，故选：A ．【点睛】本题考查了由数量关系来判断两圆位置关系的方法．14．如图，长方形ABCD 中，4AB =，2AD =，圆B 半径为1，圆A 与圆B 外切，则点C 、D 与圆A 的位置关系是（ ）A ．点C 在圆A 外，点D 在圆C ．点C 在圆A 上，点D 在圆【答案】A 【分析】先根据两圆外切求出圆A 的半径，连接【解析】解：∵4AB =，圆B 半径为【点睛】本题考查了点与圆的位置关系、圆与圆的位置关系、勾股定理，熟练掌握点与圆的位置关系是关键，还利用了数形结合的思想，通过图形确定圆的位置．15．如图，1O e ，2O e 的圆心 1O ，128cm O O =．1O e 以 1cm /s 的速度沿直线A ．外切B ．相交C ．内切D ．内含【答案】D 【分析】先求出7s 后，两圆的圆心距为1cm ，结合两圆的半径差即可得到答案．【解析】解：∵1O e 的半径为 2cm ，2O e 的半径为 3cm ，128cm O O =．1O e 以 1cm /s 的速度沿直线 l 向右运动，7s 后停止运动．∴7s 后，两圆的圆心距为1cm ，此时两圆的半径差为321cm -=，∴此时两圆内切，∴在此过程中，1O e 与 2O e 没有出现的位置关系是：内含，故选D ．【点睛】本题主要考查圆与圆的位置关系，掌握d R r =+，则两圆外切，d R r =-，则两圆外切，是关键．题型6：圆的位置关系综合16．如图，∠MON =30°，p 是∠MON 的角平分线，PQ 平行ON 交OM 于点Q ，以P 为圆心半径为4的圆ON 相切，如果以Q 为圆心半径为r 的圆与P Q 相交，那么r 的取值范围是（ ）A ．4<r <12B ．2<r <12C ．4<r <8D ．r >4【答案】A 【分析】过点Q 作QA ⊥AN 于A ，过点P 作PB ⊥ON 于B ，得到四边形ABPQ 是矩形，QA=PB=4，根据∠MON =30°求出OQ=2QA=8，根据平行线的性质及角平分线的性质得到PQ=8，再分内切与外切两种求出半径r ，即可得到两圆相交时的半径r 的取值范围.【解析】过点Q 作QA ⊥AN 于A ，过点P 作PB ⊥ON 于B ，∵PQ ∥ON ，∴PQ ⊥PB ，∴∠QAB=∠QPB=∠PBA=90°，∴四边形ABPQ 是矩形，∴QA=PB=4，∵∠MON =30°，∴OQ=2QA=8，∵OP 平分∠MON ，PQ ∥ON ，∴∠QOP=∠PON=∠QPO ，∴PQ=OQ=8，当以Q 为圆心半径为r 的圆与P Q 相外切时，r=8-4=4，当以Q 为圆心半径为r 的圆与P Q 相内切时，r=8+4=12，∴以Q 为圆心半径为r 的圆与P Q 相交，4<r<12，故选：A.【点睛】此题考查角平分线的性质，平行线的性质，矩形的判定及性质，两圆相切的性质.17．如图，在Rt ABC V 中，90C Ð=°，4AC =，7BC =，点D 在边BC 上，3CD =，A e 的半径长为3，D e 与A e 相交，且点B 在D e 外，那么D e 的半径长r 可能是（ ）A ．1r =B ．3r =C ．=5r D ．7r =【答案】B 【分析】连接AD 交A e 于E ，根据勾股定理求出AD 的长，从而求出DE DB 、的长，再根据相交两圆的位置关系得出r 的范围即可．【解析】解：连接AD 交A e 于E ，如图1，在Rt ACD V 中，由勾股定理得：则532DE AD AE =-=-=，73BC CD ==Q ，，734BD \=-=，\D e A eA ．142r <<B ．52r <<【答案】C【分析】过点O 作OE AD ^，勾股定理求得11,OE AB OF AD ==，根据题意，画出相应的图形，即可求解．当圆O 与CD 相切时，过点O 作OF CD ^于点F ，如图所示，则162OF AD ==则1325622r =+=∴O e 与直线AD 相交、与直线CD 相离，且D e 与O e 内切时，作AD⊥BC，以A为圆心，以AD为半径画圆一、单选题1．如果两圆的半径长分别为5和3，圆心距为8，那么这两个圆的位置关系是（）A．内切B．外离C．相交D．外切【答案】D【分析】根据两圆半径的和与圆心距，即可确定两圆位置关系．【解析】解：∵两圆的半径长分别为5和3，圆心距为8，538+=，∴两圆外切，故选：D ．【点睛】本题考查了圆与圆的位置关系，解题的关键是掌握：外离，则d R r >+；外切，则d R r =+；相交，则R r d R r -<<+；内切，则d R r =-；内含，则d R r <-．2．两圆的半径分别为2和3，圆心距为7，则这两个圆的位置关系为（ ）A ．外离B ．外切C ．相交D ．内切【答案】A【分析】本题直接告诉了两圆的半径及圆心距，根据它们数量关系与两圆位置关系的对应情况便可直接得出答案．【解析】解：∵两圆的半径分别为2和3，圆心距为7，又∵7＞3+2，∴两圆的位置关系是：外离．故选A ．【点睛】本题主要考查了圆与圆的位置关系，解题的关键在于能够准确掌握相关知识进行求解.3．已知直径分别为6和10的两圆没有公共点，那么这两个圆的圆心距的取值范围是（ ）A ．d ＞2B ．d ＞8C ．d ＞8或0≤d ＜2D ．2≤d ＜8【答案】C【分析】分两种情况讨论：当两圆外离时，两圆没有公共点时，当两圆内含时，两圆没有公共点时，从而可得答案.【解析】解：Q 直径分别为6和10的两圆没有公共点，\ 两圆的半径分别为3和5，当两圆外离时，两圆没有公共点时，8,d >当两圆内含时，两圆没有公共点时，02,d £<综上：所以两圆没有公共点时，8d >或0 2.d £<故选C【点睛】本题考查的是两圆的位置关系，熟练的运用两圆外离与内含的定义解题是解本题的关键.4．已知点()4,0A ，()0,3B ，如果⊙A 的半径为2，⊙B 的半径为7，那么⊙A 与⊙B 的位置关系（ ）【点睛】本题考查了两圆外切的条件，两圆相交的条件，等腰直角三角形的性质和对称性，熟练掌握两圆D ．当⊙1O 与⊙2O 没有公共点时，1202O O <≤．【答案】D【分析】根据圆与圆位置关系的性质，对各个选项逐个分析，即可得到答案．【解析】当1224O O <<时，⊙1O 与⊙2O 相交，有两个公共点，故选项A 描述正确；当⊙1O 与⊙2O 有两个公共点时，1224O O <<，故选项B 描述正确；当1202O O <≤时，⊙1O 与⊙2O 没有公共点，故选项C 描述正确；当⊙1O 与⊙2O 没有公共点时，1202O O <≤或124O O >，故选项D 描述错误；故选：D ．【点睛】本题考查了圆与圆位置关系的知识；解题的关键是熟练掌握圆与圆位置关系的性质，从而完成求解．9．如图，矩形ABCD 中，AB=4，BC=6，以A 、D 为圆心，半径分别为2和1画圆，E 、F 分别是⊙A 、⊙D 上的一动点，P 是BC 上的一动点，则PE+PF 的最小值是( )A ．5B ．6C ．7D ．8【答案】C 【分析】以BC 为轴作矩形ABCD 的对称图形A′BCD′以及对称圆D′，连接AD′交BC 于P ，交⊙A 、⊙D′于E 、F′，连接PD ，交⊙D 于F ，EF′就是PE+PF 最小值；根据勾股定理求得AD′的长，即可求得PE+PF 最小值．【解析】解：如图，以BC 为轴作矩形ABCD 的对称图形A′BCD′以及对称圆D′，连接AD’交BC 于P ，则EF′就是PE+PF最小值；∵矩形ABCD中，AB=4，BC=6，圆A的半径为2，圆D的半径为1，∴A′D′=BC=6，AA′=2AB=8，AE=2,D′F′=DF=1，∴AD′=10，EF′=10-2-1=7∴PE+PF=PF′+PE=EF′=7，故选C．【点睛】本题考查了轴对称-最短路线问题，勾股定理的应用等，作出对称图形是解答本题的关键．10．如图，在⊙O中，弦AD等于半径，B为优弧AD上的一动点，等腰△ABC的底边BC所在直线经过点D．若⊙O的半径等于1，则OC的长不可能为（）A．2﹣B．﹣1C．2D．+1【答案】A【解析】试题分析：利用圆周角定理确定点C的运动轨迹，进而利用点与圆的位置关系求得OC长度的取值范围．解：如图，连接OA、OD，则△OAD为等边三角形，边长为半径1．作点O关于AD的对称点O′，连接O′A、O′D，则△O′AD也是等边三角形，边长为半径1，∴OO′=×2=．由题意可知，∠ACB=∠ABC=∠AOD=30°，∴∠ACB=∠AO′D，∴点C在半径为1的⊙O′上运动．由图可知，OC长度的取值范围是：﹣1≤OC≤+1．故选A．考点：相交两圆的性质；轴对称的性质．二、填空题当1O e 位于2O e 外部，且P ，1O ，2O 位于同一条直线上时，如图所示，min 121523r O O PO =-=-=．故答案为：37r ££．【点睛】本题主要考查圆与圆的位置关系，能采用数形结合的方法和分类讨论的思想分析问题是解题的关键．16．在矩形ABCD 中，5AB =，8AD =，点E 在边AD 上，3AE =图)，点F 在边BC 上，以点F 为圆心、CF 为半径作F e ．如果F e【答案】4116【分析】连接EF ，作FH 股定理得到()(235r r +=-【解析】解：连接EF ，作BQe过点A，且7AB=，由函数图象可知，当即不等式①的解集为同理可得：不等式②【点睛】此题主要考查了相交两圆的性质以及勾股定理，熟练利用正三角形以及正方形的性质是解题关键．20．已知A e ，B e ，C e 【答案】A e 的半径为2厘米，(1)设AP ＝x ，求两个圆的面积之和S ；(2)当AP 分别为13a 和12a 时，比较S 【答案】(1)22111422a ax x p p p -+11求：(1)弦AC的长度；(2)四边形ACO1O2的面积．【答案】(1)8(2)21（2）解：在2Rt AO E △中，由勾股定理得：∴1212426O O O E O E =+=+=∴1111831222O AC S AC O D ==´´=g △，S ∴四边形ACO 1O 2的面积为：S S +(1)如图1所示，已知，点()02A ，，点()32B ，．①在点()()()123011141P P P -，，，，，中，是线段AB 的“对称平衡点”的是___________②线段AB 上是否存在线段AB 的“对称平衡点”？若存在，请求出符合要求的 “对称平衡点若不存在，请说明理由；(2)如图2，以点()02A ，为圆心，1为半径作A e ．坐标系内的点C 满足2AC =，再以点作C e ，若C e 上存在A e 的“对称平衡点”，直接写出C 点纵坐标C y 的取值范围．【答案】(1)①1P ，3P ；②不存在，理由见解析(2)02c y ££∴线段AB的“对称平衡点”的是1P，故答案为：1P，3P；②不存在设P为线段AB上任意一点，则它与线段££，PA PB33点P关于x轴的对称点为P¢，它到线段，是线段AB上的任意两点，即若M N∵()()0,2,0,0A O ∴02c y ££【点睛】本题考查了对称平衡点．两圆的位置关系，点与圆的位置关系等知识，解题的关键是理解题意，学会取特殊点特殊位置解决问题．。

圆与圆的位置关系的判断方法李吉文一、圆与圆的位置关系的判断方法有两种，一种是~d r 法，另一种是判别式法D .以下详解这两种方法. 1、~d r 法根据两圆心距与两圆径的大小关系来判断： ①外离Ûd R r >+； ②外切Ûd R r =+；③相交ÛR r d R r -<<+； ④内切Ûd R r =-； ⑤内含Ûd R r <-.其中，R 是大圆的半径，r 是小圆的半径，如果是等圆，那么两圆就没有内含这种位置关系了.2、判别式法D已知22111:0C x y D x E y F ++++=1⊙，半径为r 和222222:0C x y D x E y F ++++=⊙，半径为R ，且R r >判断两圆的位置关系：两圆的方程相减，得 121212()()()0D D x E E y F F -+-+-=简记为 0A x B yC ++= 其中220A B +? （1） 将（1）式代入其中一个圆的方程中，消去x 或y ，可得一个关于y 或x 一元二次方程，记为20ay by c ++=或20ax bx c ++=，其中0a >①0D >?两圆有两个公共点（相交）；②0D =?两圆有一个公共点（内切或外切）； ③0D <?两圆无公共点（内含或外离）；以上②③中，如何区分内切和外切，内含和外离呢？请看以下数学思想方法： 将问题转化为小圆的圆心与大圆的位置关系（亦即点圆位置关系）来判断！如果圆心1C 在圆2C 的外面，即d R >，那么两圆外切或外离；如果圆心1C 在圆2C 的内部，即d R <，那么两圆内切或内含.二、两圆方程作差的意义两圆作差后得到的方程：121212()()()0D D x E E y F F -+-+-=简记为 0A x B yC ++= 其中220A B +? （1） 其意义为①当两圆相交时，方程（1）是相交弦所在的直线方程； ②当两圆相切时，方程（1）是过切点的公切线的方程； ③当两圆没有公共点时，方程（1）没有特别的含义.三、应用举例例题1 已知22:2440C x y x y ++--=1⊙和222:1090C x y x +-+=⊙，判断两圆的位置关系，若两圆相交，则求出相交弦所在直线的方程.【解析】方法一：~d r 法圆心1(1,2)C -，半径3r =，圆心2(5,0)C ，半径4R =，则1,7R r R r -=+= 两圆圆心距为(1,7)d =所以，两圆相交，将两圆的方程相减可得 124130x y --= 即为相交弦的方程. 方法二：判别式法D将两圆的方程相减，得 124130x y --= 即 1334y x =-（2） 将（2）式代入222:1090C x y x +-+=⊙得 21604723130x x -+=24724160313224640D =-创=>所以，两圆相交，相交弦所在直线的方程是124130x y --=.【变式训练】 已知22:650C x y y +-+=1⊙和222:870C x y x +-+=⊙，判断两圆的位置关系，若两圆相交，则求出相交弦所在直线的方程；若两圆相切，则求出过切点的公切线的方程.例题2 已知22:4210C x y x y +--+=1⊙和222:142410C x y x y +--+=⊙，判断两圆的位置关系，若两圆相交，则求出相交弦所在直线的方程；若两圆相切，则求出过切点的公切线的方程. 【解析】方法一：~d r 法圆心1(2,1)C ，半径2r =，圆心2(7,1)C ，半径3R =，则1,5R r R r -=+= 两圆圆心距为5d R r ===+所以，两圆外切，将两圆的方程相减可得 4x = 即为所求公切线的方程. 方法二：判别式法D将两圆的方程相减，得 4x = （3） 将（3）式代入222:142410C x y x y +--+=⊙得2210y y -+= 2(2)4110D =--创=所以，两圆相切.小圆圆心1(2,1)C ，坐标代入222:142410C x y x y +--+=⊙中，有222214241211422141170x y x y +--+=+-??=>所以，两圆是外切关系，所求公切线的方程4x =.【变式训练】1.已知22:1C x y +=1⊙和222:6890C x y x y +--+=⊙，判断两圆的位置关系，若两圆相交，则求出相交弦所在直线的方程；若两圆相切，则求出过切点的公切线的方程. 2.已知22:46120C x y x y +--+=1⊙和222:680C x y x y +--=⊙，判断两圆的位置关系.。