下载文档原格式
数理方程练习题（1）一、填空题1．二阶线性偏微分方程xx xy yy x y Au Bu C u D u Eu Fu G +++++=（其中各系数均为x 和y 的函数）在某一区域的性质由式子：24B AC -的取值情况决定，取值为正对应的是（双曲）型，取值为负对应的是（椭圆）型，取值为零对应的是（抛物）型。
2．在实际中广泛应用的三个典型的数学物理方程：第一个叫（弦自由横振动），表达式为（2tt xx u a B u =），属于（双曲）型；第二个叫（热传导），表达式为（ 2t xx u a B u =），属于（椭圆）型；第三个叫（拉普拉斯方程和泊松方程），表达式为（0x x y yu u+=，(,)xx yy u u x y ρ+=-），属于（椭圆）型；二、选择题1．下列泛定方程中，属于非线性方程的是［ B ］(A) 260t xx u u xt u ++=；(B) sin i t tt xx u u u e ω-+=； (C) ()220y xxxxy u x yuu +++=； (D) 340t x xx u u u ++=；2. 下列泛定方程中，肯定属于椭圆型的是［ D ］(A)0xx yy u xyu +=； (B) 22x xx xy yy x u xyu y u e -+=；(C)0xx xy yy u u xu +-=； (D)()()()22sin sin 2cos xx xy yy x u x u x u x ++=； 3. 定解问题()()()()()()2,0,00,,0,0,,0tt xx x x t u a u t x lu t u l t u x x u x xφ?=><<?==??==?的形式解可写成［ D ］(A) ()01,coscos2n n a n at n x u x t a ll ππ∞==+∑(B) ()001,coscosn n n at n x u x t a b t a llππ∞==++∑(C) ()0,cos sin cos n nn n at n at n x u x t a b l l l πππ∞=?=+∑(D) ()001,cos sin cos n n n n at n at n x u x t a b t a b l llπππ∞=??=+++??∑ 4. 若非齐次边界条件为12(0,)(),(,)()x u t t u l t t μμ==，则辅助函数可取［C ］(A) ()()12(,)W x t t x t μμ=+； (B) ()()21(,)W x t t x t μμ=+；(C) ()()()12(,)W x t x l t t μμ=-+； (D) ()()()21(,)W x t x l t t μμ=-+；三、求解下列问题（1）2,0,tt xx u a u t x =>-∞<<∞ ，其中a 为常数。
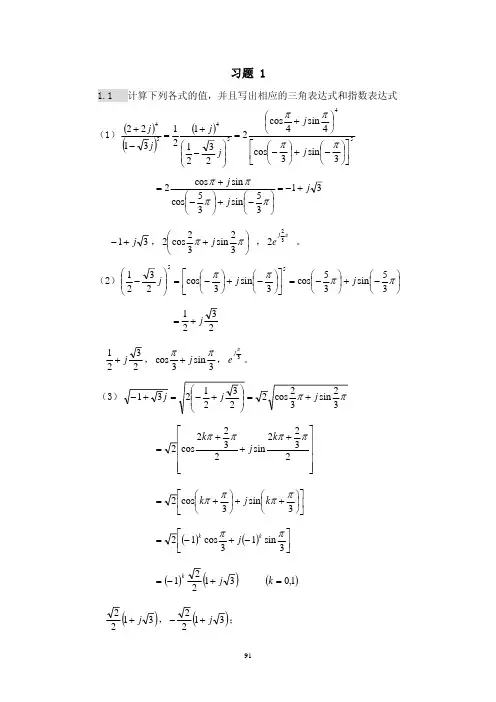
数理方程练习题第二章定解问题与偏微分方程理论习题2.11. 密度为ρ均匀柔软的细弦线x =0端固定，垂直悬挂，在重力作用下，于横向拉它一下，使之作微小的横振动。
试导出振动方程。
2. 长为L ，均匀细杆，x = 0端固定，另一端沿杆的轴线方向被拉长b 静止后（在弹性限度内）突然放手，细杆作自由振动。
试写出振动方程的定解条件。
3. 长为L 、密度为ρ的底半径为R 的均匀圆锥杆（轴线水平）作纵振动，锥的顶点固定在x =0处。
导出此杆的振动方程。
4. 一根长为L 、截面面积为1的均匀细杆，其x =0端固定，以槌水平击其x =L 端，使之获得冲量I 。
试写出定解问题。
习题2.21. 一半径为r ，密度为ρ，比热为c ，热传导系数为k 的匀质圆杆，如同截面上的温度相同，其侧面与温度为u 1的介质发生热交换，且热交换的系数为k 1。
试导出杆上温度u 满足的方程。
4. 设有一根具有绝热的侧表面的均匀细杆，它的初始温度为)(x ?，两端满足下列边界条件之一：（1）一端（x =0）绝热，另一端（x = L ）保持常温u 0；（2）两端分别有热流密度q 1和q 2进入；（3）一端（x =0）温度为u 1(t )，另一端（x = L ）与温度为)(t θ的介质有热交换。
试分别写出上述三种热传导过程的定解问题。
习题2.41. 判断下列方程的类型：（1）04=+++++u cu bu au au au y x yy xy xx ；（2）02=+++++u cu bu au au au y x yy xy xx ；（3）02222=+++++u au bu au au au y x yy xy xx ；（4）0=+yy xx xu u 。
2. 求下列方程的通解（1）0910=++yy xy xx u u u ；（3）0384=++yy xy xx u u u 。
第三章分离变量法习题3.12. 求解下列定解问题（1）-====><<=====)(,00)0,0(,0002x L x u u u u t L x u a u t t t L x x xx tt3. 求下列边值问题的固有值和固有函数：（1）===+''==0,000L x x X X X X λ （3）0,0012===+'+''==e x x y y y y x y x λ 习题3.21.求定解问题：-===><<====)(0,0)0,0(,002x L x u u u t L x u a u t L x x xx t 习题3.52. 求解定解问题：===><<=+-===-00020,0)0,0(,0T u u u t L x Ae u a u t L x x x t xx α 0T 是常数。
第一章曲线论§ 1 向量函数1.证明本节命题3、命题5 中未加证明的结论略2.求证常向量的微商等于零向量。
证：设，为常向量，因为所以。
证毕3.证明证：证毕4.利用向量函数的泰勒公式证明：如果向量在某一区间所有的点其微商为零，则此向量在该区间上是常向量。
证：设，为定义在区间上的向量函数，因为在区间上可导当且仅当数量函数，和在区间上可导。
所以，，根据数量函数的Lagrange 中值定理，有其中，，介于与之间。
从而上式为向量函数的0 阶Taylor 公式，其中。
如果在区间上处处有，则在区间上处处有，从而，于是。
证毕5.证明具有固定方向的充要条件是证：必要性：设具有固定方向，则可表示为，其中为某个数量函数，为单位常向量，于是。
充分性：如果，可设，令，其中为某个数量函数，为单位向量，因为，于是为常向量，于是，，即具有固定方向证毕因为，故，从而6.证明平行于固定平面的充要条件是。
证：必要性：设平行于固定平面，则存在一个常向量，使得，对此式连续求导，依次可得和，从而，，和共面，因此充分性：设，即，其中，如果，根据第5 题的结论知， 具有固定方向， 则某个数量函数， 为单位常向量，任取一个与 垂直的单位常向量 ，于是作以 为法向量过原点的平面 ，则 平行于 。
如果 ，则 与 不共线， 又由 可知， ， ，和 共面，于是 ，，那么 ，这说明 与共线，从而，根据第 5 题的结论知， 具有固定方向，则 可表 示为，其中 为某个数量函数， 为单位常向量，作以为法向 量，过原点的平面 ，则 平行于 §2 曲线的概念1. 求圆柱螺线 在点 的切线与法平面的方程。
解： ，点 对应于参数 ，于是当 时， ，，于是切线的方程为：法平面的方程为2. 求三次曲线 在点 处的切线和法平面的方程。
解： ，当 时， ， ， 于是切线的方程为：法平面的方程为3. 证明圆柱螺线 的切线和 轴成固定角 证：可表示为 ，其中 为其中 ， 为数量函数， 令 证毕令为切线与轴之间的夹角，因为切线的方向向量为，轴的方向向量为，则证毕4.求悬链线从起计算的弧长解：5.求抛物线对应于的一段的弧长解：6. 求星形线，的全弧长。
第一章定义和方程类型1、34233(,,)v v v xyv g x y z x x y z∂∂∂+++=∂∂∂∂ 是( D )偏微分方程 A 、 一阶 B 、二阶 C 、 三阶 D 、 四阶 1、22(,,)vxy v g x y z z∂+=∂ 是( A )偏微分方程 A 、 一阶 B 、二阶 C 、 三阶 D 、 四阶1、33232(,,)v v vv xyv g x y z x x y z ∂∂∂+++=∂∂∂∂ 是( C )偏微分方程A 、 一阶B 、二阶C 、 三阶D 、 四阶 2、2(,)txx u a u f x t -= (其中0>a ) 属于( A )型偏微分方程A 、 抛物B 、双曲C 、 椭圆D 、 混合 2、2(,)ttxx u a u x t ϕ-= (其中0>a ) 属于( B )型偏微分方程A 、 抛物B 、双曲C 、 椭圆D 、 混合2、22(,,)tt xx u a u x y t ϕ+= (其中0>a ) 属于( C )型偏微分方程 A 、 抛物 B 、双曲 C 、 椭圆 D 、 混合 2、(,)xx yy u u f x y += (其中(,)u u x y =) 属于( C )型偏微分方程A 、 抛物B 、双曲C 、 椭圆D 、 混合 4、下列方程是非线性偏微分方程的是（ A ）A 22()()sin u u x x y 抖+=抖 B (,)u uf x y x y抖+=抖 C 22(,)(,)cos u ua x tb x t x x t抖+=抖 D 3433(,,)v v v g x y z x x y z ∂∂∂++=∂∂∂∂ 7、下列方程是非齐次方程的是（ A ）A(,)(,)0u uxy f x y f x y x y 抖+=?抖， B 2,0t xx u a u a =?C 22(,)(,)0u u a x t b x t x t 抖+=抖 D 34330v v v x x y z ∂∂∂++=∂∂∂∂3、在用分离变量法求解定解问题200,0,0|0,|0|()t xx x x x l t u a u x l t u u u x ϕ===⎧=<<>⎪==⎨⎪=⎩时，得到的固有函数系为( D ) A 、,...2,1,sin=⎭⎬⎫⎩⎨⎧n x ln π B 、,...2,1,0,cos=⎭⎬⎫⎩⎨⎧n x l n π C 、{},...2,1,sin =n x n π D 、 ,...2,1,2)12(sin =⎭⎬⎫⎩⎨⎧-n x ln π 3、在用分离变量法求解定解问题⎪⎩⎪⎨⎧====><<=====)(|),(|0|,0|0,0,0002x u x u u u t l x u a u t t t l x x x x xx tt ψϕ时，得到的固有函数系为( B )A 、,...2,1,sin=⎭⎬⎫⎩⎨⎧n x l n πB 、,...2,1,0,cos=⎭⎬⎫⎩⎨⎧n x l n πC 、(21)cos ,1,2,...2n x n l π-⎧⎫=⎨⎬⎩⎭ D 、 ,...2,1,2)12(sin =⎭⎬⎫⎩⎨⎧-n x l n π3、在用分离变量法求解定解问题⎪⎩⎪⎨⎧===><<====)(|0|,0|0,0,002x u u u t l x u a u t l x x xx t ϕ时，得到的固有函数系为( A )A 、,...2,1,sin=⎭⎬⎫⎩⎨⎧n x l n π B 、,...2,1,0,cos=⎭⎬⎫⎩⎨⎧n x l n πC 、(21)cos,1,2,...2n x n l π-⎧⎫=⎨⎬⎩⎭ D 、,...2,1,2)12(sin=⎭⎬⎫⎩⎨⎧-n x l n π7、给出未知函数 u 在区域Ω的边界Γ上的值0,),,(|≥Γ∈=Γt M t M u μ 的边界条件，称为第( A )类边界条件。
例 1.1.1 设v=v(线x,y),二阶性偏微分方程v xy =xy 的通解。
解 原方程可以写成 ð／ðx（ðv／ðy） =xy 两边对x 积分，得v y =¢（y ）+1/2 x 2Y,其中¢（y ）是任意一阶可微函数。
进一步地，两边对y 积分，得方程得通解为v （x,y ）=∫v y dy+f （x ）=∫¢（y ）dy+f （x ）+1/4 x 2y 2=f （x ）+g （y ）+1/4 x 2y 2其中f （x ）,g （y ）是任意两个二阶可微函数。
例1.1.2即 u(ξ,η) = F(ξ) + G(η),其中F(ξ),G(η)是任意两个可微函数。
例1.2.1设有一根长为L 的均匀柔软富有弹性的细弦，平衡时沿直线拉紧，在受到初始小扰动下，作微小横振动。
试确定该弦的运动方程。
取定弦的运动平面坐标系是O XU ,弦的平衡位置为x 轴，弦的长度为L ，两端固定在O,L 两点。
用u(x,t)表示弦上横坐标为x 点在时刻t 的位移。
由于弦做微小横振动，故u x ≈0.因此α≈0，cos α≈1,sin α≈tan α=u x ≈0,其中α表示在x 处切线方向同x 轴的夹角。
下面用微元法建立u 所满足的偏微分方程。
在弦上任取一段弧'MM ,考虑作用在这段弧上的力。
作用在这段弧上的力有力和外力。
可以证明，力T 是一个常数，即T 与位置x 和时间t 的变化无关。
事实上，因为弧振动微小，则弧段'MM 的弧长dx u xx xx ⎰∆++=∆21s ≈x ∆。
这说明该段弧在整个振动过程中始终未发生伸长变化。
于是由Hooke 定律，力T 与时间t 无关。
因为弦只作横振动，在x 轴方向没有位移，故合力在x 方向上的分量为零，即T(x+x ∆)cos α’-T(x)cos α=0.由于co's α’≈1，cos α≈1,所以T(X+∆x)=T(x),故力T 与x 无关。
例 1.1.1 设v=v(线x,y),二阶性偏微分方程v xy =xy 的通解。
解 原方程可以写成 ð／ðx（ðv／ðy） =xy 两边对x 积分，得v y =¢（y ）+1/2 x 2Y,其中¢（y ）是任意一阶可微函数。
进一步地，两边对y 积分，得方程得通解为v （x,y ）=∫v y dy+f （x ）=∫¢（y ）dy+f （x ）+1/4 x 2y 2=f （x ）+g （y ）+1/4 x 2y 2其中f （x ）,g （y ）是任意两个二阶可微函数。
例1.1.2即 u(ξ,η) = F(ξ) + G(η),其中F(ξ),G(η)是任意两个可微函数。
例1.2.1设有一根长为L 的均匀柔软富有弹性的细弦，平衡时沿直线拉紧，在受到初始小扰动下，作微小横振动。
试确定该弦的运动方程。
取定弦的运动平面坐标系是O XU ,弦的平衡位置为x 轴，弦的长度为L ，两端固定在O,L 两点。
用u(x,t)表示弦上横坐标为x 点在时刻t 的位移。
由于弦做微小横振动，故u x ≈0.因此α≈0，cos α≈1,sin α≈tan α=u x ≈0,其中α表示在x 处切线方向同x 轴的夹角。
下面用微元法建立u 所满足的偏微分方程。
在弦上任取一段弧'MM ,考虑作用在这段弧上的力。
作用在这段弧上的力有力和外力。
可以证明，力T 是一个常数，即T 与位置x 和时间t 的变化无关。
事实上，因为弧振动微小，则弧段'MM 的弧长dx u xx xx ⎰∆++=∆21s ≈x ∆。
这说明该段弧在整个振动过程中始终未发生伸长变化。
于是由Hooke 定律，力T 与时间t 无关。
因为弦只作横振动，在x 轴方向没有位移，故合力在x 方向上的分量为零，即T(x+x ∆)cos α’-T(x)cos α=0.由于co's α’≈1，cos α≈1,所以T(X+∆x)=T(x),故力T 与x 无关。
于是，力是一个与位置x 和时间t 无关的常数，仍记为T.作用于小弧段'MM 的力沿u 轴方向的分量为 Tsin α’-Tsin α≈T(u x (x+x ∆,t)-u x (x,t)).设作用在该段弧上的外力密度函数为F （x,t ）那么弧段'MM 在时刻t 所受沿u 轴方向的外力近似的等于F(x,t)x ∆.由牛顿第二定律得T （u x (x+x ∆,t)-u x (x,t)+F(x,t)x ∆=ρx ∆tt u ,其中ρ是线密度，由于弦是均匀的，故ρ为常数。
这里tt u 是加速度tt u 在弧段'MM 上的平均值。
设u=u(x,t)二次连续可微。
由微分中值定理得Tu zz （x+θx ∆，t)x ∆+F(x,t)x ∆=ρtt u x ∆, 0<θ<1. 消去x ∆，并取极限x ∆→0得 Tu xx （x,t ）+F(x,t)=ρu tt , 即u tt =ɑ2u xx +ƒ(x,t), 0<x<L,t>0,其中常数ɑ2=T/ρ，函数ƒ（x,t ）=F(x,t)/ρ表示在x 处单位质量上所受的外力。
上式表示在外力作用下弦的振动规律，称为弦的强迫横振动方程，又称一维非齐次波动方程。
当外力作用为零时，即ƒ=0时，方程称为弦的自由横振动方程。
类似地，有二维波动方程u tt =ɑ2（u xx +u y y ）+ƒ（x.y.t ）, (x,y)Ω∈,t>0, 电场E 和磁场H 满足三维波动方程E c E 2222t ∇=∂∂和H c H 2222t∇=∂∂, 其中c 是光速和2222222x zy ∂∂+∂∂+∂∂=∆=∇⋅∇=∇。
例1.2.2设物体Ω在无热源。
在Ω中任取一闭曲面S （图1.2）。
以函数u(x,y,z,t)表示物体在t 时刻，M=M(x,y,z)处的温度。
根据Fourier 热传导定律，在无穷小时段dt 流过物体的一个无穷小面积dS 的热量dQ 与时间dt ，曲面面积dS 以及物体温度u 沿曲面的外法线n 的方向导数三者成正比，即,其中k=k(x,y,z)是在物体M(x,y,z)处的热传导系数，取正值。
我们规定外法线n 方向所指的那一侧为正侧。
上式中负号的出现是由于热量由温度高的地方流向温度低得地方。
故当0nu>∂∂时，热量实际上是向-n 方向流去。
对于Ω任一封闭曲面S ，设其所包围的空间区域为V ，那从时刻t 1到时刻t2经曲面流出的热量为1Q =dSdt nukS⎰⎰⎰∂∂21t t - 设物体的比热容为c(x,y,z)，密度为ρ(x,y,z)，则在区域V ，温度由u(x,y,z,1t )到u(x,y,z)所需的热量为[]dvdt tuc dv t z y x u t z y x u c t t VV∂∂=-=⎰⎰⎰⎰⎰⎰⎰21),,,(),,,(Q 122ρρ. 根据热量守恒定律，有12Q Q -=即[]dSst nukdv t z y x u t z y x t t S⎰⎰⎰⎰⎰⎰∂∂=-21),,,(),,,u c 12V（ρ 假设函数u(x,y,z,t)关于x,y,z 具有二阶连续偏导数，关于t 具有一阶连续偏导数，那么由高斯公式得0][21t =⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎪⎭⎫ ⎝⎛∂∂∂∂-∂∂⎰⎰⎰⎰dvdt z u k z y u k y y u k x t u c t Vρ. 由于时间间隔[]21t ,t 及区域V 是任意的，且被积函数是连续的，因此在任何时刻t ，在Ω任意一点都有⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂=∂∂z u k z y u k y y u k y x u ρc(1.2.6)方程称为非均匀的各向同性体的热传导方程。
如果物体是均匀的，此时k,c 及ρ均为常数，令2a =ρc k，则方程(1.2.6)化为 u a z u y u xu ∆=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂=∂∂22222222a t u ,(1.2.7)它称为三维热传导方程若物体有热源，其热源密度函数为，则有热源的热传导方程为),,,(a u 2t t z y x f u +∆= (1.2.8)其中ρc F f =类似地，当考虑的物体是一根均匀细杆时如果它的侧面绝热且在同一截面上的温度分布相同，那么温度只与有关，方程变成一维热传导方程xx u 2t a u = （1.2.9）同样，如果考虑一块薄板的热传导，并且薄板的侧面绝热，则可得二维热传导方程 ）yy 2t u (u +=xx u a （1.2.10）（P16)例1.3.1一长为L 的弹性杆，一端固定，另一端被拉离平衡位置b 而静止，放手任其振动。
试写出杆振动的定解问题。
解 取如图1.3所示的坐标系。
O L L+b x泛定方程就是一维波动方程（杆的纵振动方程） u tt =a 2u xx , 0<x<L.在初始时刻（即放手之时），杆振动的速度为零，即u t (x,0)=0,0≤x ≤L.而在x=L 端拉离平衡位置，使整个弹性杆伸长了b 。
这个b 是来自整个杆各部分伸长后的贡献，而不是x=L 一端伸长的贡献，故整个弹性杆的初始位移为u|0=t =Lbx, 0≤x ≤L. 再看边界条件。
一端x=0固定，即该端位移为零，故有u(0,t)=0,0≤x ≤L.另一端由于放手任其振动时未受外力，故有u x (L,t)=0,t ≥0.所以，所求杆振动的定解问题为u tt =a 2u xx , 0<x<L,t>0, u(x,0)=Lbx, u t （x,0)=0, 0≤x ≤L, u(0,t)=0, u x (L,t)=0, t ≥0.（P17）例1.3.2 ：长为L 的均匀弦，两端x=0和x=L 固定，弦中力为T ，在x=x0处以横向力F 拉弦，达到稳定后放手任其振动。
试写出初始条件。
解：建立如图坐标系。
的两端绝热；（3）杆的一端为恒温零度，另一端绝热。
试写出该绝热传导问题在以上三种情况下的边界条件。
解：设杆的温度为u(x,t),则（1） u （x,t ）=0，u(L,t)=0. （2） 当沿杆长方向有热量流动时，由Fourier 实验定律得Lx x xu kq xukq ==∂∂-=∂∂=201,'其中q1,q2分别为x=0和x=L 处的热流强度。
而杆的两端绝热，这就意味着杆的两端与外界没有热交换，亦没有热量的流动，故有q1=q2=0和,0),0(=t x u 0),(=t L u x .(3)显然，此时有 0),(,0),0(==t L u t u x .例1.5.1求Poisson 方程Uxx +Uyy =X^2 +XY+Y^2的通解 解:先求出方程的一个特解V=V （x ，y),使其满足 Vxx +Vyy=X^2 +XY+Y^2 由于方程右端是一个二元二次齐次多项式，可设V （x ，y) 具有形式V(x,y)=aX^4 +bX^3 Y+cY^4,其中a,b,c 是待定常数 Vx=4aX^3+3bX^2 Y Vy=bX^3+4cY^3 Vxx=12aX^2+6bXY Vyy=12cY^2 得Vxx+Vyy=12aX^2 +6bXY+12cY^2=X^2 +XY+Y^2 比较两边系数，可得 a=1/12,b=1/6,c=1/12于是V （x,y)=1/12(X^4 +2X^3 Y+Y^4）下面求函数W=W(x,y),使其满足Wxx+Wyy=0.作变量代换e=x,n=iy(为d)Ue=du/de=du/dx=Ux Un=du/dn=du/dy *dy/dn=-iy Uee=dUe/de=Uxx Unn=-Uyy 可得Wee-Wnn=0 再作变量代换s=e+n,t=e-nUe=du/de(s,t)=Us+Ut Un=du/dn=Us-Ut Uee=dUe/de=d(Us+Ut)/de=Uss+Utt+2Ust Unn=dUn/dn=d(Us-Ut)/dn=Uss+Utt-2Ust 那么方程进一步化为Wst=0其通解为W=f(s)+g(t)=f(e+n)+g(e-n)=f(x+iy)+g(x-iy),其中f,g 是任意两个二阶可微函数。
那么根据叠加原理，方程的通解为u(x,y)=V+W=f(x+iy)+g(x-iy)+1/12(X^4+2X^3 Y+Y^4)(P32)例2.1.1 判断方程U xx +2U xy -3U yy +2U x +6U y =0（2.1.22）的类型，并化简。
解： 因为a 11= 1,a 12= 1,a 22= -3,所以 =a 212-a 11a 22=4>0,故方程为双曲型方程。
