大学物理仿真实验报告牛顿环分析

牛顿环物理实验报告【篇一：用牛顿环测量透镜的曲率半径实验报告】一、实验名称：用牛顿环测量透镜的曲率半径二、实验目的：1、观察光的等厚干涉现象，了解干涉条纹特点。

2、利用干涉原理测透镜曲率半径。

3、学习用逐差法处理实验数据的方法。

三、实验仪器：牛顿环装置（其中透镜的曲率未知）、钠光灯（波长为589.3nm）、读数显微镜（附有反射镜）。

四、实验原理：将一块曲率半径r较大的平凸透镜的凸面放在一个光学平板玻璃上，使平凸透镜的球面aob和平面玻璃cd面相切于o点，组成牛顿环装置，如图所示，则在平凸透镜球面和平板玻璃之间形成一个以接触点o为中心向四周逐渐增厚的空气劈尖。

当单色平行光束近乎垂直地向ab面入射时，一部分光束在aob面上反射，一部分继续前进，到cod面上反射。

这两束反射光在aob面相遇，互相干涉，形成明暗条纹。

由于aob面是球面，和o点等距的各点对o点是对称的，因而上述明暗条纹排成如图所示的明暗相间的圆环图样，在中心有一暗点（实际观察是一个圆斑），这些环纹称为牛顿环。

图（4）牛顿环装置图（5）牛顿环根据理论计算可知，和k级条纹对应的两束相干光的光程差为? 2?式中e为第k级条纹对应的空气膜的厚度，为半波损失。

2?由干涉条件可知，当??(2k?1)(k?0,1,2,3,?)时，干涉条纹为暗条纹。

即2解得??2e?e?k(2) 2设透镜的曲率半径为r，和接触点o相距为r处空气层的厚度为e，由图4所示几何关系可得r2??r?e??r2?r2?2re?e2?r2 由于r??e，则e2可以略去。

则r2e?(3)2r2?由式（2）和式（3）可得第k级暗环的半径为rk2?2re?kr? (4)由式（4）可知，如果单色光源的波长?已知，只需测出第k级暗环的半径rk，即可算出平凸透镜的曲率半径r；反之，如果r已知，测出rk后，就可计算出入射单色光波的波长?。

但是由于平凸透镜的凸面和光学平玻璃平面不可能是理想的点接触；接触压力会引起局部弹性形变，使接触处成为一个圆形平面，干涉环中心为一暗斑；或者空气间隙层中有了尘埃等因素的存在使得在光程差公式中附加了一项。

大学物理牛顿环实验报告大学物理牛顿环实验报告引言在大学物理实验中，我们学习了许多经典的实验，其中之一就是牛顿环实验。

这个实验是由英国科学家艾萨克·牛顿于17世纪末提出的，通过光的干涉现象，帮助我们理解光的波动性质。

在这篇报告中，我将详细介绍牛顿环实验的原理、实验装置和实验结果。

实验原理牛顿环实验是基于光的干涉现象。

当平行光垂直照射到一个透明介质上时，光线会发生反射和折射。

在牛顿环实验中，我们使用一个凸透镜和一块平板玻璃来观察干涉现象。

当光线从凸透镜的平面表面射入玻璃平板时，一部分光线会被反射，一部分光线会被折射。

在玻璃平板和凸透镜之间形成了一层薄空气膜。

这层薄空气膜会引起光的干涉现象，形成一系列明暗相间的环状条纹，即牛顿环。

实验装置牛顿环实验的装置相对简单。

我们需要准备一个凸透镜、一块平板玻璃、一束平行光源以及一个显微镜。

首先，将凸透镜放置在光源上方，使得光线垂直照射到凸透镜的平面表面上。

然后，在凸透镜上方放置一块平板玻璃，使其与凸透镜保持平行。

最后，将显微镜放置在玻璃平板上方，以便观察牛顿环的形成。

实验过程在实验过程中，我们首先调整光源的位置，使得光线垂直入射到凸透镜的平面表面上。

然后，通过调整显微镜的焦距，使其能够清晰地观察到牛顿环。

当我们通过显微镜观察牛顿环时，会看到一系列明暗相间的环状条纹。

这些条纹的亮暗程度取决于光线在薄空气膜中的相位差。

相位差的大小与光线在薄空气膜中的路径差有关。

实验结果通过实验观察，我们可以得出以下结论：1. 牛顿环的中心是暗的，而环状条纹向外逐渐变亮。

这是因为在中心位置，光线的路径差为零，相位差也为零，因此不会发生干涉现象。

而随着距离中心越远，路径差增大，相位差也逐渐增大，导致干涉现象的发生。

2. 牛顿环的亮暗程度与光的波长有关。

当使用不同波长的光源进行实验时，我们会观察到不同的牛顿环。

这是因为不同波长的光在薄空气膜中的路径差不同，导致相位差的变化。

3. 牛顿环的半径与凸透镜的曲率半径有关。

大学物理牛顿环实验一、实验目的1、观察牛顿环的干涉现象2、研究干涉现象与光波的波动性质3、学习使用分光仪、读数显微镜的方法二、实验原理牛顿环是一种典型的干涉现象，它是由一束光分成两束相干光，在空间叠加而成。

当一束光照射在玻璃表面时，会产生反射和透射两种现象。

反射光会在玻璃表面形成亮斑，而透射光则会继续传播。

当透射光再次照射到玻璃表面时，会再次产生反射和透射，形成一系列的反射和透射光。

这些反射和透射光会相互干涉，形成明暗相间的条纹，这就是牛顿环。

三、实验步骤1、调整分光仪，使一束光通过玻璃棱镜，分成两束相干光，并在空间叠加。

2、调整分光仪的望远镜，观察到清晰的牛顿环。

3、使用读数显微镜测量牛顿环的直径，并记录下来。

4、改变分光仪的棱镜角度，观察干涉条纹的变化，并记录下来。

5、分析实验数据，得出结论。

四、实验结果与分析1、实验结果在实验中，我们观察到了清晰的牛顿环干涉现象，并且使用读数显微镜测量了牛顿环的直径。

随着分光仪棱镜角度的变化，干涉条纹也会发生变化。

2、结果分析通过实验数据，我们可以得出以下（1）牛顿环是由两束相干光在空间叠加而形成的干涉现象。

（2）干涉条纹的明暗交替是由于两束光的相位差引起的。

（3）通过测量牛顿环的直径，我们可以计算出光波的波长。

（4）随着分光仪棱镜角度的变化，干涉条纹会发生变化，这是因为光的波长和入射角发生了变化。

五、结论通过本次实验，我们深入了解了干涉现象与光波的波动性质，学习了使用分光仪、读数显微镜的方法。

这对于我们今后在光学领域的研究具有重要意义。

大学物理牛顿环实验一、实验目的1、观察牛顿环的干涉现象2、研究干涉现象与光波的波动性质3、学习使用分光仪、读数显微镜的方法二、实验原理牛顿环是一种典型的干涉现象，它是由一束光分成两束相干光，在空间叠加而成。

当一束光照射在玻璃表面时，会产生反射和透射两种现象。

反射光会在玻璃表面形成亮斑，而透射光则会继续传播。

当透射光再次照射到玻璃表面时，会再次产生反射和透射，形成一系列的反射和透射光。

牛顿环物理实验报告【篇一：用牛顿环测量透镜的曲率半径实验报告】一、实验名称：用牛顿环测量透镜的曲率半径二、实验目的：1、观察光的等厚干涉现象，了解干涉条纹特点。

2、利用干涉原理测透镜曲率半径。

3、学习用逐差法处理实验数据的方法。

三、实验仪器：牛顿环装置（其中透镜的曲率未知）、钠光灯（波长为589.3nm）、读数显微镜（附有反射镜）。

四、实验原理：将一块曲率半径r较大的平凸透镜的凸面放在一个光学平板玻璃上，使平凸透镜的球面aob和平面玻璃cd面相切于o点，组成牛顿环装置，如图所示，则在平凸透镜球面和平板玻璃之间形成一个以接触点o为中心向四周逐渐增厚的空气劈尖。

当单色平行光束近乎垂直地向ab面入射时，一部分光束在aob面上反射，一部分继续前进，到cod面上反射。

这两束反射光在aob面相遇，互相干涉，形成明暗条纹。

由于aob面是球面，和o点等距的各点对o点是对称的，因而上述明暗条纹排成如图所示的明暗相间的圆环图样，在中心有一暗点（实际观察是一个圆斑），这些环纹称为牛顿环。

图（4）牛顿环装置图（5）牛顿环根据理论计算可知，和k级条纹对应的两束相干光的光程差为? 2?式中e为第k级条纹对应的空气膜的厚度，为半波损失。

2?由干涉条件可知，当??(2k?1)(k?0,1,2,3,?)时，干涉条纹为暗条纹。

即2解得??2e?e?k(2) 2设透镜的曲率半径为r，和接触点o相距为r处空气层的厚度为e，由图4所示几何关系可得r2??r?e??r2?r2?2re?e2?r2 由于r??e，则e2可以略去。

则r2e?(3)2r2?由式（2）和式（3）可得第k级暗环的半径为rk2?2re?kr? (4)由式（4）可知，如果单色光源的波长?已知，只需测出第k级暗环的半径rk，即可算出平凸透镜的曲率半径r；反之，如果r已知，测出rk后，就可计算出入射单色光波的波长?。

但是由于平凸透镜的凸面和光学平玻璃平面不可能是理想的点接触；接触压力会引起局部弹性形变，使接触处成为一个圆形平面，干涉环中心为一暗斑；或者空气间隙层中有了尘埃等因素的存在使得在光程差公式中附加了一项。

西安交通大学大学物理仿真实验报告实验名称：牛顿环法测曲率半径实验日期：专业班级：姓名：学号：教师签字： ________________一、实验目的1.学会用牛定透曲率半径。

2.正确使用微，学用逐差法理数据。

二、实验仪器牛，数微，光灯，入射光架。

三、实验原理如所示，在平板玻璃面 DCF上放一个曲率半径很大的平凸透ACB，C 点接触点，在 ACB和 DCF之，形成一厚度不均匀的空气薄膜，色光从上方垂直入射到透上，透透，近似垂直地入射于空气膜。

分从膜的上下表面反射的两条光来自同一条入射光，它足相干条件并在膜的上表面相遇而生干涉，干涉后的度由相遇的两条光的光程差决定，由可，二者的光程差等于膜厚度 e 的两倍，即此外，当光在空气膜的上表面反射，是从光密媒射向光疏媒，反射光不生相位突，而在下表面反射，会生相位突，即在反射点，反射光的相位与入射光的相位之相差，与之的光程差/2，所以相干的两条光具有/2 的附加光程差，的光程差（1）当足条件（2），生相干涉，出第K 亮，而当（k = 0,1,2⋯）（3），生相消干涉，出第k 暗。

因1同一级条纹对应着相同的膜厚，所以干涉条纹是一组等厚度线。

可以想见，干涉条纹是一组以 C 点为中心的同心圆，这就是所谓的牛顿环。

如图所示，设第k 级条纹的半径为，对应的膜厚度为，则（4）在实验中， R 的大小为几米到十几米，而的数量级为毫米，所以 R >> e，e2相对于k k2Re k是一个小量，可以忽略，所以上式可以简化为（ 5）如果 r k是第k级暗条纹的半径，由式（1）和（ 3）可得（ 6）代入式（ 5）得透镜曲率半径的计算公式（7）对给定的装置，R 为常数，暗纹半径（ 8）和级数 k 的平方根成正比，即随着k 的增大，条纹越来越细。

同理，如果r k是第k级明纹，则由式（1）和（ 2）得（9）代入式（ 5），可以算出（ 10）2由式（ 8）和（ 10）可见，只要测出暗纹半径（或明纹半径），数出对应的级数k，即可算出 R。

大学物理仿真实验报告--牛顿环法测曲率半径大学物理仿真实验报告实验名称:牛顿环法测曲率半径共 6 页系别: 实验日期专业班级: 组别____ 实验报告日期姓名学号报告退发 ( 订正、重做 ) 一实验目的1.学会用牛顿环测定透镜曲率半径。

2.正确使用读书显微镜，学习用逐差法处理数据。

二实验仪器牛顿环装置，读数显微镜，钠光灯。

三实验原理如下图所示，在平板玻璃面DCF上放一个曲率半径很大的平凸透镜ACB，C点为接触点，这样在ACB和DCF之间，形成一层厚度不均匀的空气薄膜，单色光从上方垂直入射到透镜上，透过透镜，近似垂直地入射于空气膜。

分别从膜的上下表面反射的两条光线来自同一条入射光线，它们满足相干条件并在膜的上表面相遇而产生干涉，干涉后的强度由相遇的两条光线的光程差决定，由图可见，二者的光程差等于膜厚度e的两倍，即此外，当光在空气膜的上表面反射时，是从光密媒质射向光疏媒质，反射光不发生相位突变，而在下表面反射时，则会发生相位突变，即在反射点处，反射光的相位与入射光的相位之间相差? ，与之对应的光程差为?/2 ，所以相干的两条光线还具有?/2的附加光程差，总的光程差为(1)当?满足条件 (2)时，发生相长干涉，出现第K级亮纹，而当(k = 0,1,2…) (3)时，发生相消干涉，出现第k级暗纹。

因为同一级条纹对应着相同的膜厚，所以干涉条纹是一组等厚度线。

可以想见，干涉条纹是一组以C点为中心的同心圆，这就是所谓的牛顿环。

如图所示，设第k级条纹的半径为，对应的膜厚度为，则(4)在实验中，R的大小为几米到十几米，而的数量级为毫米，所以R >> ek，ek相对于22Rek是一个小量，可以忽略，所以上式可以简化为(5)如果rk是第k级暗条纹的半径，由式(1)和(3)可得(6)代入式(5)得透镜曲率半径的计算公式(7)对给定的装置，R为常数，暗纹半径(8)和级数k的平方根成正比，即随着k的增大，条纹越来越细。

中南大学牛顿环实验报告篇一：牛顿环实验报告等厚干涉——牛顿环【实验目的】(1)用牛顿环观察和分析等厚干涉现象；(2)学习利用干涉现象测量透镜的曲率半径；(3)学会使用读数显微镜测距。

【实验原理】在一块平面玻璃上安放上一焦距很大的平凸透镜，使其凸面与平面相接触，在接触点附近就形成一层空气膜。

当用一平行的准单色光垂直照射时，在空气膜上表面反射的光束和下表面反射的光束在膜上表面相遇相干，形成以接触点为圆心的明暗相间的环状干涉图样，称为牛顿环，其光路示意图如图。

如果已知入射光波长，并测得第k级暗环的半径rk，则可求得透镜的曲率半径R。

但实际测量时，由于透镜和平面玻璃接触时，接触点有压力产生形变或有微尘产生附加光程差，使得干涉条纹的圆心和环级确定困难。

用直径Dm、Dn，有22Dm?DnR?4(m?n)?此为计算R用的公式，它与附加厚光程差、圆心位置、绝对级次无DD关，克服了由这些因素带来的系统误差，并且m、n可以是弦长。

【实验仪器】JCD3型读数显微镜，牛顿环，钠光灯，凸透镜(包括三爪式透镜夹和固定滑座)。

【实验内容】1、调整测量装置按光学实验常用仪器的读数显微镜使用说明进行调整。

调整时注意：(1)调节45玻片，使显微镜视场中亮度最大，这时，基本上满足入射光垂直于透镜的要求(下部反光镜不要让反射光到上面去)。

(2)因反射光干涉条纹产生在空气薄膜的上表面，显微镜应对上表面调焦才能找到清晰的干涉图像。

(3)调焦时，显微镜筒应自下而上缓慢地上升，直到看清楚干涉条纹时为止，往下移动显微镜筒时，眼睛一定要离开目镜侧视，防止镜筒压坏牛顿环。

(4)牛顿环三个压紧螺丝不能压得很紧，两个表面要用擦镜纸擦拭干净。

2、观察牛顿环的干涉图样（1）调整牛顿环仪的三个调节螺丝，在自然光照射下能观察到牛顿环的干涉图样，并将干涉条纹的中心移到牛顿环仪的中心附近。

调节螺丝不能太紧，以免中心暗斑太大，甚至损坏牛顿环仪。

（2）把牛顿环仪置于显微镜的正下方，使单色光源与读数显微镜上45?角的反射透明玻璃片等高，旋转反射透明玻璃，直至从目镜中能看到明亮均匀的光照。

牛顿环和劈尖干涉实验【实验目的】1、观察光的等厚干涉现象，熟悉光的等厚干涉的特点；2、用牛顿环干涉测定平凸透镜的曲率半径；3、用劈尖干涉法测定细丝直径或微小薄片厚度。

【实验仪器及装置】牛顿环仪、读数显微镜、钠光灯、劈尖、数显游标卡尺。

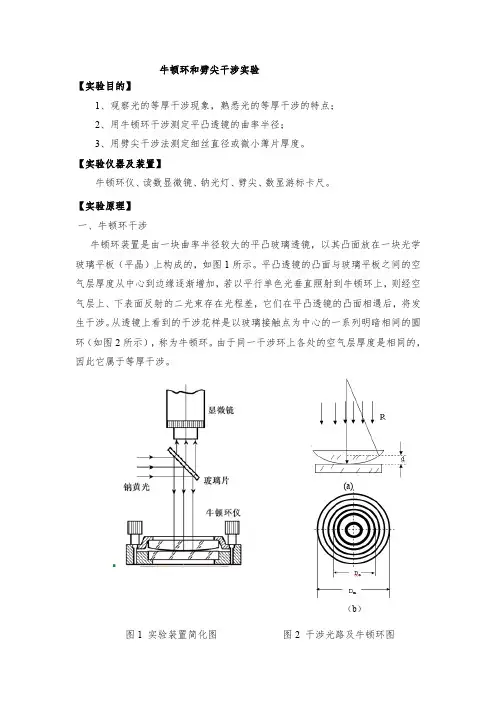
【实验原理】 一、牛顿环干涉牛顿环装置是由一块曲率半径较大的平凸玻璃透镜，以其凸面放在一块光学玻璃平板（平晶）上构成的，如图1所示。

平凸透镜的凸面与玻璃平板之间的空气层厚度从中心到边缘逐渐增加，若以平行单色光垂直照射到牛顿环上，则经空气层上、下表面反射的二光束存在光程差，它们在平凸透镜的凸面相遇后，将发生干涉。

从透镜上看到的干涉花样是以玻璃接触点为中心的一系列明暗相间的圆环（如图2所示），称为牛顿环。

由于同一干涉环上各处的空气层厚度是相同的，因此它属于等厚干涉。

图1 实验装置简化图 图2 干涉光路及牛顿环图(a)（b ）由图2 (a)可见，如设透镜的曲率半径为R ，与接触点Ｏ相距为r 处空气层的厚度为d ，其几何关系式为：()2222222r d Rd R r d R R ++-=+-=由于R>>d ，可以略去d 2得22r d R= (1)光线应是垂直入射的，计算光程差时还要考虑光波在平玻璃板上反射会有半波损失，从而带来/2λ的附加程差，所以光程差δ为：22λδ+=d (2)产生暗环的条件是：(21)2k λδ=+ (3)其中k ＝0，1，2，3，...为干涉暗条纹的级数。

综合(1)、(2)和(3)式可得第ｋ级暗环的半径为：2r kR λ= (4)由(4)式可知，如果单色光源的波长λ已知，测出第m 级的暗环半径m r ，即可得出平凸透镜的曲率半径R ；反之，如果R 已知，测出m r 后，就可计算出入射单色光波的波长λ。

但是用此测量关系式往往误差很大，原因在于凸面和平面不可能是理想的点接触；接触压力会引起局部形变，使接触处成为一个圆形平面，干涉环中心为一暗斑。

牛顿环实验报告一.实验目的1.观察等厚干涉现象，并利用等厚干涉测量凸透镜表面的曲率半径2.了解读书显微镜的使用方法二.实验原理当曲率半径为R的平凸透镜放置在一平板玻璃上时，在透镜和平板玻璃之间形成一个厚度变化的空气间隙。

当光线垂直照射到其上，从空气间隙的上下表面反射的两束光线 1.2将在空气间隙的上边面附近实现干涉叠加，两束光之间的光程差随空气间隙的厚度变化而变化，空气间隙厚度相同处的两束光具有相同的光程差Δ，所以干涉条纹是以接触点为圆心的一组明暗相间的同心圆环，称为牛顿环。

R为待测透镜凹面的曲率半径，r k是第k级干涉环的半径，d k是第k级干涉环所对应的空气间隙的厚度。

如果入射光的波长为ƛ，则第k级干涉环所对应的光程差为Δk=2dk+ƛ/2 (1)其中，ƛ/2为光由光疏介质入射到光密介质时，反射光的半波损失。

因此，在接触点出（d0=0）的光程差为Δ0= ƛ/2（2）在k级干涉暗环处的光程差为Δk=2d k+ ƛ/2 =(k+1/2)k (3)所对应的空气间隙的厚度为d k==kƛ/2 (4)第k级干涉暗环的半径为r k=√kƛR (5)在实验中用给定波长的光进行照明时，只要测得第k级次干涉暗环的半径r k，就可以测得曲率半径R。

但在实际测量中，由于无法准确确定干涉环圆心所在位置，这样就不可能准确的测量干涉环的半径。

因此，直接利用式（5）作为测量公式将对测量结果带来很大的误差。

事实上，在测量过程中可以准确地获得各个级次干涉环的弦长。

假设这个弦到圆心的距离是s，可得以下几何关系L k2=4(r k2-s2) (6)L k2=4k ƛR-4s2 (7)利用式（7）作为测量公式时，所遇到的问题是如何确定s或排除它对测量结果的影响。

有如下两种解决方法:（1）在式（7）中弦长的平方与干涉环的级次间是一个线性关系，在测量中，可以测量一组不同级次干涉环在某一直线上的弦长，利用最小二乘法或作图法求得该直线的斜率，再利用已知的波长得到凸透镜的曲率半径。

大学物理实验牛顿环实验报告含数据一、实验目的1、观察等厚干涉现象——牛顿环。

2、学习用干涉法测量透镜的曲率半径。

3、掌握读数显微镜的使用方法。

二、实验原理牛顿环是一种等厚干涉现象。

将一块曲率半径较大的平凸透镜放在一块平面玻璃上，在透镜的凸面与平面玻璃之间就会形成一个上表面是球面，下表面是平面的空气薄层，其厚度从中心接触点到边缘逐渐增加。

当一束单色平行光垂直照射到牛顿环装置上时，在空气薄层的上、下表面反射的两束光将产生干涉。

在反射光中观察会看到以接触点为中心的一系列明暗相间的同心圆环，即牛顿环。

设透镜的曲率半径为 R，形成的第 m 级暗环的半径为 rm，对应的空气薄层厚度为 em。

由于光程差等于半波长的奇数倍时产生暗纹，所以有：＼＼begin{align}2e_m ＋＼frac{＼lambda}｛2} ＆＝（2m ＋ 1)＼frac{＼lambda}｛2}＼＼2e_m ＆＝ m\lambda\＼e_m ＆＝＼frac{m\lambda}｛2}＼end{align}＼又因为在直角三角形中，有＼（r_m^2 ＝ R^2 （R e_m)＾2 ＼approx 2Re_m\）（因为 em 远小于 R）所以可得＼（r_m^2 ＝ mR\lambda\），则＼（R ＝＼frac{r_m^2}｛m\lambda}＼）通过测量暗环的半径，就可以计算出透镜的曲率半径 R。

三、实验仪器读数显微镜、钠光灯、牛顿环装置。

四、实验步骤1、调节读数显微镜调节目镜，使十字叉丝清晰。

转动调焦手轮，使镜筒自下而上缓慢移动，直至从目镜中看到清晰的牛顿环图像。

移动牛顿环装置，使十字叉丝交点与牛顿环中心大致重合。

2、测量牛顿环直径转动测微鼓轮，使十字叉丝从牛顿环中心向左移动，依次对准第30 到第 15 暗环，记录读数。

继续转动鼓轮，使叉丝越过中心向右移动，依次对准第 15 到第 30 暗环，记录读数。

3、重复测量重复上述步骤，共测量 5 组数据。

大学物理实验牛顿环实验报告(含数据)牛顿环实验报告引言：牛顿环实验是物理实验中经典的干涉实验之一，通过测量光的干涉色条纹来研究光的波动性质。

本实验旨在探究牛顿环的特点及其与透明介质的厚度之间的关系。

通过对实验数据的收集和分析，我们得到了关于牛顿环的一些有趣的结论。

实验装置与方法：1. 实验装置：我们使用了一台平行板构成的牛顿环实验装置。

装置包括一个透明玻璃平板、一束白光源、一台显微镜及光屏等。

2. 实验方法：(1) 首先，我们在实验室中搭建牛顿环实验装置。

(2) 将光源打开，使其照射在透明玻璃平板上。

(3) 调节显微镜位置，使其焦距与透明玻璃平板接近，并将显微镜对准光源的光斑。

(4) 通过调节透明玻璃平板的厚度，观察和记录不同厚度下的牛顿环干涉色条纹。

(5) 使用光屏记录实验数据，包括透明玻璃平板的厚度和对应的干涉色条纹。

实验数据与结果分析：实验中，我们记录了不同透明玻璃平板厚度下的牛顿环干涉色条纹的数据。

根据我们的观察和记录，我们进行了以下主要分析：1. 牛顿环的特点：我们观察到牛顿环是由一系列同心圆环组成的，且颜色从中心向外渐变。

颜色的变化是由于光的干涉效应引起的。

2. 牛顿环与透明介质厚度：通过分析我们记录的实验数据，我们得出了结论：透明介质的厚度与牛顿环的直径成正比关系，即厚度越大，牛顿环的直径越大。

3. 干涉色的原因：牛顿环的干涉色是由于光的干涉效应引起的。

当光线通过透明玻璃平板和空气之间的边界时，光线会发生折射和反射。

不同波长的光在折射和反射过程中会产生不同的相位差，从而导致干涉色的形成。

结论：通过本实验，我们验证了牛顿环实验的重要性，并获得了有关牛顿环的实验数据，并分析了数据的结果。

我们得出的结论是：牛顿环的直径与透明介质的厚度成正比关系。

这一实验结果对于进一步理解光的干涉效应和光的波动性质具有重要意义。

致谢：在此，我们要特别感谢实验中的指导老师及实验室助理们的帮助和支持。

没有他们的指导和帮助，我们无法顺利完成这一实验报告。

大学物理牛顿环干涉实验报告一、实验目的1、观察等厚干涉现象——牛顿环。

2、掌握用牛顿环测量平凸透镜曲率半径的方法。

3、加深对光的波动性的理解。

二、实验原理将一块曲率半径较大的平凸透镜放在一块平面玻璃上，在透镜的凸面和平面玻璃之间就形成了一个从中心向四周逐渐增厚的空气薄层，其等厚点的轨迹是以接触点为圆心的一系列同心圆，这些同心圆的干涉条纹就是牛顿环。

当一束平行单色光垂直照射到牛顿环装置上时，在空气薄层的上、下表面反射的两束光会发生干涉。

设入射光的波长为λ，在空气薄层厚度为 d 处，两束反射光的光程差为：＼（＼Delta ＝ 2d ＋＼frac{＼lambda}｛2}＼）当光程差为波长的整数倍时，两束光相互加强，形成亮条纹；当光程差为半波长的奇数倍时，两束光相互削弱，形成暗条纹。

对于暗条纹，有：＼（2d ＋＼frac{＼lambda}｛2} ＝（2k ＋ 1)＼frac{＼lambda}｛2}＼）（k ＝ 0, 1, 2,）解得：＼（d ＝＼frac{k\lambda}｛2}＼）由于平凸透镜的曲率半径 R 远大于空气薄层的厚度 d，所以可以近似认为：＼（d ＝ r^2 ／（2R)＼）（其中 r 为条纹半径）将上式代入＼（d ＝＼frac{k\lambda}｛2}＼）可得：＼（r^2 ＝ k\lambda R\）所以，只要测量出第 k 级暗条纹的半径 r 和波长λ，就可以计算出平凸透镜的曲率半径 R。

三、实验仪器牛顿环装置、钠光灯、读数显微镜、移测显微镜。

四、实验步骤1、调节牛顿环装置将牛顿环装置放置在显微镜的载物台上，调节目镜，使十字叉丝清晰。

调节显微镜的焦距，使清晰地看到牛顿环的图像。

调节牛顿环装置的位置，使十字叉丝与牛顿环的中心大致重合。

2、测量牛顿环的直径转动显微镜的鼓轮，使十字叉丝从牛顿环的中心向一侧移动，依次测量第 10 到 20 级暗条纹的位置。

测量时，要注意十字叉丝要与暗条纹相切，且要在不同的位置测量多次，取平均值。

牛顿环等厚干涉的实验仿真与智能分析
牛顿环，又称多层牛顿环，是一种重要的光学元件，大量应用于光学系统中。

牛顿环的优越性能实现了广泛的应用，特别是厚度全变的厚度牛顿环，它能够实现幅宽和频率可调。

有许多研究发现，牛顿环可以用于实验仿真和智能分析，这些研究对提升系统性能和设计高性能光学系统有着重要的意义。

本文就是牛顿环等厚度牛顿环的实验仿真及其智能分析进行深入分析。

首先，本文介绍了牛顿环的历史、结构和性能特点。

牛顿环是由英国天文学家牛顿于1672年发明的，它是一种光学元件，用于检测和分析光线波动，它可以实现两个完全独立的光线路径：衍射路径和反射路径，可以方便地调节和检测这两条路径的变化情况。

牛顿环的现代变体是多层环，其中最重要的特性是可调厚度，使其在噪声抑制、全变化频带等方面取得良好的控制效果。

接着，本文讨论了牛顿环的实验仿真，实验仿真通过使用正交分离方法，模拟线性和非线性光学系统，能够有效分离真实情况下物理量的虚拟体系，更好地模拟光学系统性能，从而提高光学系统的性能。

此外，实验仿真还可以用于精准调节系统的参数，从而实现系统的优化。

最后，本文对牛顿环的智能分析进行了讨论。

智能分析是一种针对物理量的算法，可以分析和估计光学系统特性，从而提高系统性能。

智能分析通过提取物理量之间的联系和特征，判断出物理量的变化规律，提供物理量参数的估计结果，可以调节系统参数来改善系统性能。

综上所述，牛顿环等厚度牛顿环可以用于实验仿真和智能分析，这大大提高了光学系统的性能，也有助于提高光学系统的可靠性。

因此，这些研究对于提升光学系统性能来说具有重要意义。

⼤学物理仿真实验报告--⽜顿环法测曲率半径⼤学物理仿真实验报告实验名称：⽜顿环法测曲率半径共 6 页系别：实验⽇期专业班级：组别____ 实验报告⽇期姓名学号报告退发 ( 订正、重做 )教师审批签字⼀实验⽬的1.学会⽤⽜顿环测定透镜曲率半径。

2.正确使⽤读书显微镜，学习⽤逐差法处理数据。

⼆实验仪器⽜顿环装置，读数显微镜，钠光灯。

三实验原理如下图所⽰，在平板玻璃⾯DCF上放⼀个曲率半径很⼤的平凸透镜ACB，C点为接触点，这样在ACB和DCF之间，形成⼀层厚度不均匀的空⽓薄膜，单⾊光从上⽅垂直⼊射到透镜上，透过透镜，近似垂直地⼊射于空⽓膜。

分别从膜的上下表⾯反射的两条光线来⾃同⼀条⼊射光线，它们满⾜相⼲条件并在膜的上表⾯相遇⽽产⽣⼲涉，⼲涉后的强度由相遇的两条光线的光程差决定，由图可见，⼆者的光程差等于膜厚度e的两倍，即此外，当光在空⽓膜的上表⾯反射时，是从光密媒质射向光疏媒质，反射光不发⽣相位突变，⽽在下表⾯反射时，则会发⽣相位突变，即在反射点处，反射光的相位与⼊射光的相位之间相差π，与之对应的光程差为λ/2 ，所以相⼲的两条光线还具有λ/2的附加光程差，总的光程差为（1）当?满⾜条件（2）时，发⽣相长⼲涉，出现第K级亮纹，⽽当（k = 0,1,2…）（3）时，发⽣相消⼲涉，出现第k级暗纹。

因为同⼀级条纹对应着相同的膜厚，所以⼲涉条纹是⼀组等厚度线。

可以想见，⼲涉条纹是⼀组以C点为中⼼的同⼼圆，这就是所谓的⽜顿环。

如图所⽰，设第k级条纹的半径为，对应的膜厚度为，则（4）在实验中，R的⼤⼩为⼏⽶到⼗⼏⽶，⽽的数量级为毫⽶，所以R >> e k，e k2相对于2Re k是⼀个⼩量，可以忽略，所以上式可以简化为（5）如果r k是第k级暗条纹的半径，由式（1）和（3）可得（6）代⼊式（5）得透镜曲率半径的计算公式（7）对给定的装置，R为常数，暗纹半径（8）和级数k的平⽅根成正⽐，即随着k的增⼤，条纹越来越细。

光的⼲涉—⽜顿环-⼤学物理实验-海南⼤学光的⼲涉—⽜顿环【实验⽬的】1、了解⽜顿环等厚⼲涉的原理和观察⽅法2、利⽤⼲涉⽅法测量平/凸透镜的曲率半径3、掌握读数显微镜的调节和使⽤4、学习⽤逐差法和图解法处理数据，并⽐较两种处理结果【实验原理】通常将同⼀光源发出的光分成两束光，在空间经过不同的路程后合在⼀起产⽣⼲涉。

⽜顿环是典型的等厚⼲涉现象⽜顿环实验装置通常是由光学玻璃制成的⼀个平⾯和⼀个曲率半径较⼤的球⾯组成，在两个表⾯之间形成⼀劈尖状空⽓薄层。

以凸⾯为例，当单⾊光垂直⼊射时，在透镜表⾯相遇时就会发⽣⼲涉现象，空⽓膜厚度相同的地⽅形成相同的⼲涉条纹，这种⼲涉称作等厚⼲涉。

在⼲涉条纹是以接触点为中⼼的⼀系列明暗相间的同⼼圆环，称⽜顿环。

⽜顿环的形成：由于透镜表⾯B点处的反射光1和玻璃板表⾯C点的反射光2在B点出发⽣⼲涉，在该处产⽣等厚⼲涉条纹。

按照波动理论，设形成⽜顿环处空⽓薄层厚度为d，两束相⼲光的光程差为：△=2d + λ/ 2 = kλ当适合下列条件时有△ =2d + λ/ 2 = kλ　---------（1） ( K = 1，2，3，... 明△ =2d + λ/ 2 = (2k+1)λ/2---------（2）　( K = 1，2，3，... 暗式中λ为⼊射光的波长，λ/2 是附加光程差，他是由于光在光密介质⾯上反射时产⽣的半波损失⽽引起的）表明，当 K=0 时（零级），d=0，即平⾯玻璃和平凸透镜接触处的条纹为暗纹。

光程差Δ仅与d 有关，即厚度相同的地⽅⼲涉条纹相同。

平凸透镜曲率半径的测量：由⼏何关系，在B点可得：r2=R2-(R2-d2)=2Rd-d2因为 R>>d 所以得上式表明d 与　成正⽐，说明离中⼼越远，光程差增加越快，⼲涉条纹越来越密。

由公式：... (暗环)可知若测出第K级暗环的半径，且单⾊光的波长已知时，就能算出球⾯的曲率半径R 。

但在实验中由于机械压⼒引起的形变以及球⾯上可能存在的微⼩尘埃，使得凸⾯和平⾯接触处不可能是⼀个理想的点，⽽是⼀个不很规则的圆斑，因此很难准确测出⽐较简单的⽅法是测量距中⼼较远处的⽜顿环直径。