基于SAS软件的时间序列实验的代码

结果分析：上图是数据对应的时序图，从图上曲线分析来看，数据并没有周期性或者趋向性规律，因而可以初步判断这是平稳数列。

proc arima data=ex3_1;结果分析：本过程中，我们建立了8阶自回归分析模型，图上依次是变量的描述性统计量、样本自相关图、样本逆相关图和样本偏自相关图。

由于本次实验探究的是平稳序列，因而样本逆相关图先不作分析。

结果分析：从上图可以看出，在众多模型中，MA（4）模型的BIC信息量是最小的，因而我们接下来会采用结果分析：结果分析: 结果分析：结果分析：该图为预测的图像，其中，红色线段表示预测出来的数列，绿色的两条线段分别表示95%的置信下限和95%的置信上限，而黑色的星号标识则是对应的样本数据值。

从图来分析，我们可以看出，黑色的样本数据值跟我们预测出来的线段非常的吻合，因而模型建立得很不错。

再结合上一步骤的参数结果，二、课后习题（老师布置的习题部分）17.data lianxi3_17;input x@@;time=_n_;cards;126.4 82.4 78.1 51.1 90.9 76.2 104.5 87.4110.5 25 69.3 53.5 39.8 63.6 46.7 72.979.6 83.6 80.7 60.3 79 74.4 49.6 54.771.8 49.1 103.9 51.6 82.4 83.6 77.8 79.389.6 85.5 58 120.7 110.5 65.4 39.9 40.188.7 71.4 83 55.9 89.9 84.8 105.2 113.7124.7 114.5 115.6 102.4 101.4 89.8 71.5 70.998.3 55.5 66.1 78.4 120.5 97 110;proc gplot data=lianxi3_17;plot x*time=1;symbol1c=red I=join v=star;run;结果分析：上图是数据对应的时序图，从图上曲线分析来看，数据并没有周期性或者趋向性规律，因而可以初结果分析：本过程中，我们建立了8阶自回归分析模型，图上依次是变量的描述性统计量、样本自相关图、样本逆相关图和样本偏自相关图。

SAS软件绘制时序图—平稳性的检验方法之一PROC GPLOT过程proc gplot过程用于作出高分辨率的散点图或曲线图。

其主要语句形式为：proc gplot options;plot yvariable*xvariable/ options;symbol options;命令说明：（1）proc gplot options;此语句中的options主要指定SAS数据集的名称。

（2）plot y variable*x variable/options;此语句画出y变量与x变量的（y,x）图,options主要选项有：Cframe:给定图的底色，如黄色（yellow）、红色（red）、蓝色（blue）、灰色（gray）、浅灰色（ligr）等。

默认的颜色为白色。

Overlay:若要将两个以上的图形画在同一坐标系中，可用”overlay”选项。

（3）symbol options;此语句定义绘图的符号、颜色、是否连线以及线条的粗细等等。

Options主要选项有：c为点或线的颜色；v为定义点的表示符号，可以取dot(大点)，point(小点)，plus(加号)，star（星号），circle（圆圈），square（方形），triangle（三角），diamond（菱形）等；i为确定散点之间连线的形状，可以取join(直线)，spline（光滑线），needle（向水平轴的垂线）；w=n确定线的粗细。

n为线的粗细的号。

n越大，线条越粗。

默认时为1。

L=n，n为线型的序号。

1表示实线，2表示虚线，等等。

例如：下列数据为y1与y2变量的取值，绘制其时序图（time=intnx('month','01jul2004'd,_n_-1);）。

12.85 15.2113.56 14.2315.36 17.3614.53 18.2513.50 15.33解答：data example1;input y1 y2;time=intnx('month','01jul2004'd,_n_-1);format time date.;cards;12.85 15.2113.56 14.2315.36 17.3614.53 18.2513.50 15.33;proc gplot data=example1;plot y1*time=1 y2*time=2/overlay;symbol1c=black v=star i=join;symbol2c=red v=circle i=spline;run;y1191817161514131201JU L0401A U G0401S E P0401O C T0401N O V0401D E C04t i m eplot y1*time y2*time/overlay;symbol1c=black v=star i=join w=2;symbol2c=red v=circle i=spline w=3;run;y1191817161514131201JU L0401A U G0401S E P0401O C T0401N O V0401D E C04t i m eproc gplot data=example1;plot y1*time y2*time/overlay cframe=yellow;symbol1c=black v=star i=join w=2;symbol2c=red v=circle i=spline w=3;run;y1191817161514131201JU L0401A U G0401S E P0401O C T0401N O V0401D E C04t i m eplot y1*time y2*time/overlay cframe=yellow;symbol1c=black v=star i=join l=1w=2;symbol2c=red v=circle i=spline l=2w=3;run;y1191817161514131201JU L0401A U G0401S E P0401O C T0401N O V0401D E C04t i m e。

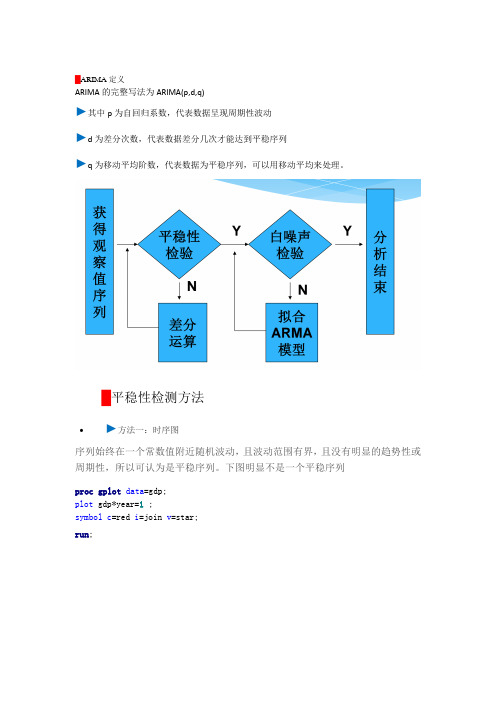
█ARIMA定义ARIMA的完整写法为ARIMA(p,d,q)►其中p为自回归系数，代表数据呈现周期性波动►d为差分次数，代表数据差分几次才能达到平稳序列►q为移动平均阶数，代表数据为平稳序列，可以用移动平均来处理。

█平稳性检测方法•►方法一：时序图序列始终在一个常数值附近随机波动，且波动范围有界，且没有明显的趋势性或周期性，所以可认为是平稳序列。

下图明显不是一个平稳序列proc gplot data=gdp;plot gdp*year=1 ;symbol c=red i=join v=star;run;•►方法二：自相关图自相关系数会很快衰减向0，所以可认为是平稳序列。

proc arima data= gdp;identify var=gdp stationarity =(adf=3) nlag=12;run;•►ADF单位根检验（精确判断）三个检验中只要有一个Pr<Rho小于0.05即可认定为平稳序列，主要是stationarity=(adf=3) 起作用proc arima data= gdp;identify var=gdp stationarity =(adf=3) nlag=12; run;█白噪声检验Pr>卡方<0.05即可认定为通过白噪声检验。

proc arima data= gdp;identify var=gdp stationarity =(adf=3) nlag=12; run;█非平稳序列转换为平稳序列方法一：将数据取对数。

方法二：对数据取差分dif函数data gdp_log;set gdp;loggdp=log(gdp);cfloggdp=dif(loggdp);run;/**对数数据散点图**/proc gplot;plot loggdp*year=1 ;symbol c=black i=join v=star; run;/* 一阶差分对数数据散点图*/ proc gplot;plot cfloggdp*year=1;symbol c=green v=dot i=join;run;从上图中可以看出，一阶差分后序列已经变成平稳的了，因此，数列需要做一阶差分█转换完毕后再验证下面代码中的（1）就代表1阶差分，adf=3则代表平稳性检验0-3，/* 一阶差分对数数据的自相关图、偏自相关图、纯随机性检验、单位根检验 */ proc arima data=gdp_log;identify var=loggdp(1) stationarity =(adf=3) nlag=12;run;用Q LB统计量作的 2检验结果表明：对数差分后的GDP序列的Q LB统计量的P值为0.0045（<0.05），故序列为非白噪声序列。

sas常用代码1、导入数据2、提取年份（在年份不为4位数时，需要这一步）Data 某表1；set某表；Year=year（date）;Run;注：如果需要提取一般数据，则采用如下数据：Data 某表1，set某表；Year=year(date,2,4);表示从第二个字符起，取4个字符Run3、排序（按照代码和年对ROA里的数据进行排序）【这一步是在合并具有相同变量的表时必须要做的。

】PROCSORT DATA=ROA;BY CODE YEAR;RUN;4、合并Datahebing;Merge ROA1 ASSEST1;by code year;run;注：hebing中包含了所有的ROA1和ASSEST1数据（无if）有取舍合并Datahebing;mergeROA1 (in=a) ASSEST1 (in=b);by code year;if a=1 and b=1;Run;5、删除不需要的数据Data hebing1;sethebing;ifROA<0 then delete;run;Data hebing1;sethebing;if roa=.or roa=" " then delete;(删除缺失值)（if ros+roa+roe=. then delete;同时删除rosroa roe中的缺失值）run;6、取自然对数和删除变量Data hebing2;set hebing1;Inassest=log(assest);InROA=log(1+roa);Run；7、对连续变量的缩尾处理winsorize(消除极端值影响)只有连续变量才能消除极端值影响Data temp1;set hebing2; d=1;run;procmeansnoprint;varinassestinroa; by d;output out=tmp2(drop=_freq_ _type_) p1=x1-x2 p99=y1-y2;Data hebing3;merge temp1 tmp2; by d;array z{1:2} inassestinroa;array x{1:2} x1-x2; array y{1:2} y1-y2;do i=1 to 2;if z[i]if z[i]>y[i] then z[i]=y[i];end; drop i d x1-x2 y1-y2;run;8、年份和行业的控制data hebing3; set hebing2;if year=2001then year01=1; else year01=0;if year=2002then year02=1; else year02=0;if year=2003then year03=1; else year03=0;if year=2004then year04=1; else year04=0;if year=2005then year05=1; else year05=0;if year=2006then year06=1; else year06=0;if year=2007then year07=1; else year07=0;if year=2008then year08=1; else year08=0;if year=2009then year09=1; else year09=0;if year=2010then year10=1; else year10=0;if year=2011then year11=1; else year11=0;if year=2012then year12=1; else year12=0;if year=2013then year13=1; else year13=0;if indus="B"then induB=1; else induB=0;if indus="C"then induC=1; else induC=0;if indus="D"then induD=1; else induD=0;if indus="E"then induE=1; else induE=0;if indus="F"then induF=1; else induF=0;if indus="G"then induG=1; else induG=0;if indus="H"then induH=1; else induH=0;if indus="J"then induJ=1; else induJ=0;if indus="K"then induK=1; else induK=0;if indus="L"then induL=1; else induL=0;if indus="M"then induM=1; else induM=0;run;9、描述性统计（针对所有变量）procmeans data=hebing3 n（数量）mean（均值）std（标准偏差）minq1medianq3maxmaxdec=4（最多保留4位小数）;var lnfeelnnum ;run;9、变量之间的相关性分析proccorr data=hebing3pearsonspearman; var lnfeelnnum ;run;10、回归procreg data=hebing3;model lnfee=lnnum;run;1、以e为底的自然对数是LOG(x)；2、以2为底的对数是LOG2(x)；3、以10为底的对数是LOG10(x)。

基于SAS软件的时间序列实验的代码实验指南目录实验一分析太阳黑子数序列 (3)实验二模拟AR模型 (4)实验三模拟MA模型和ARMA模型 (6)实验四分析化工生产量数据 (8)实验五模拟ARIMA模型和季节ARIMA模型 (10)实验六分析美国国民生产总值的季度数据 (13)实验七分析国际航线月度旅客总数数据 (16)实验八干预模型的建模 (19)实验九传递函数模型的建模 (22)实验十回来与时序相结合的建模 (25)太阳黑子年度数据 (28)美国国民收入数据 (29)化工生产过程的产量数据 (30)国际航线月度旅客数据 (30)洛杉矶臭氧每小时读数的月平均值数据 (31)煤气炉数据 (35)芝加哥某食品公司大众食品周销售数据 (37)牙膏市场占有率周数据 (39)某公司汽车生产数据 (44)加拿大山猫数据 (44)实验一分析太阳黑子数序列实验目的：了解时刻序列分析的差不多步骤，熟悉SAS/ETS软件使用方法。

二、实验内容：分析太阳黑子数序列。

三、实验要求：了解时刻序列分析的差不多步骤，注意各种语句的输出结果。

四、实验时刻：2小时。

五、实验软件：SAS系统。

六、实验步骤1、开机进入SAS系统。

创建名为exp1的SAS数据集，即在窗中输入下列语句：data exp1;input a1 @@;year=intnx(‘year’,’1jan1742’d,_n_-1);format year year4.;cards;输入太阳黑子数序列(见附表)run;储存此步骤中的程序，供以后分析使用（只需按工具条上的储存按钮然后填写完提咨询后就能够把这段程序储存下来即可）。

绘数据与时刻的关系图，初步识别序列，输入下列程序：proc gplot data=exp1;symbol i=spline v=star h=2 c=green;plot a1*year;run;提交程序，在graph窗口中观看序列，能够看出此序列是均值平稳序列。

1、导入数据2、提取年份（在年份不为4位数时，需要这一步）Data 某表1；set某表；Year=year（date）;Run;注：如果需要提取一般数据，则采用如下数据：Data 某表1，set某表；Year=year(date,2,4);表示从第二个字符起，取4个字符Run3、排序（按照代码和年对ROA里的数据进行排序）【这一步是在合并具有相同变量的表时必须要做的。

】PROC SORT DATA=ROA;BY CODE YEAR;RUN;4、合并Data hebing;Merge ROA1 ASSEST1;by code year;run;注：hebing中包含了所有的ROA1和 ASSEST1数据（无if）有取舍合并Data hebing;merge ROA1 (in=a) ASSEST1 (in=b);by code year;if a=1 and b=1;Run;5、删除不需要的数据Data hebing1;set hebing;if ROA<0 then delete;run;Data hebing1;set hebing;if roa=.or roa=" " then delete;(删除缺失值)（if ros+roa+roe=. then delete;同时删除ros roa roe 中的缺失值）run;6、取自然对数和删除变量Data hebing2;set hebing1;Inassest=log(assest);InROA=log(1+roa);Run；7、对连续变量的缩尾处理winsorize(消除极端值影响)只有连续变量才能消除极端值影响Data temp1;set hebing2; d=1;run;proc means noprint;var inassest inroa; by d;output out=tmp2(drop=_freq_ _type_) p1=x1-x2 p99=y1-y2;Data hebing3;merge temp1 tmp2; by d;array z{1:2} inassest inroa;array x{1:2} x1-x2; array y{1:2} y1-y2;do i=1 to 2;if z[i]<x[i] and z[i]~=. then z[i]=x[i];if z[i]>y[i] then z[i]=y[i];end; drop i d x1-x2 y1-y2;run;8、年份和行业的控制data hebing3; set hebing2;if year=2001then year01=1; else year01=0;if year=2002then year02=1; else year02=0;if year=2003then year03=1; else year03=0;if year=2004then year04=1; else year04=0;if year=2005then year05=1; else year05=0;if year=2006then year06=1; else year06=0;if year=2007then year07=1; else year07=0;if year=2008then year08=1; else year08=0;if year=2009then year09=1; else year09=0;if year=2010then year10=1; else year10=0;if year=2011then year11=1; else year11=0;if year=2012then year12=1; else year12=0;if year=2013then year13=1; else year13=0;if indus="B"then induB=1; else induB=0;if indus="C"then induC=1; else induC=0;if indus="D"then induD=1; else induD=0;if indus="E"then induE=1; else induE=0;if indus="F"then induF=1; else induF=0;if indus="G"then induG=1; else induG=0;if indus="H"then induH=1; else induH=0;if indus="J"then induJ=1; else induJ=0;if indus="K"then induK=1; else induK=0;if indus="L"then induL=1; else induL=0;if indus="M"then induM=1; else induM=0;run;9、描述性统计（针对所有变量）proc means data=hebing3 n（数量）mean（均值）std（标准偏差）min q1median q3max maxdec=4（最多保留4位小数）;var lnfee lnnum ;run;9、变量之间的相关性分析proc corr data=hebing3 pearson spearman;var lnfee lnnum ;run;10、回归proc reg data=hebing3;model lnfee=lnnum;run;1、以e为底的自然对数是LOG(x)；2、以2为底的对数是LOG2(x)；3、以10为底的对数是LOG10(x)。

SAS时间序列分析上机报告得到的结果如图⼀所⽰：图⼀时间序列editor窗中输⼊如下程序：(1) t t t X X ε+=-11.1data a; x1=0.5;n=-50;do i=-50 to 1000;a=rannor(32565);*随机正态，32565是种⼦; x=a+1.1*x1; x1=x; n=n+1;if i>0 then output ; end ; run ;proc print data =a; var x;proc gplot data =a;symbol i =spline c =red; plot x*n; run ;得到的结果如下图⼆所⽰：图⼆时间序列data a; x1=0.5;n=-50;do i=-50 to 1000;a=rannor(32565);*随机正态，32565是种⼦; x=a-1.1*x1; x1=x;n=n+1;if i>0 then output ; end ; run ;proc print data =a; var x;proc gplot data =a;symbol i =spline c =red; plot x*n; run ;(2) t t t X X ε+-=-11.1图三时间序列从上⾯的图形我们可以看到图⼀的所有值均在0左右波动，整个时间序列是平稳的，⽽图⼆和图三都是随着时间的推迟，越发偏离初始值，是不平稳的。

根据t t t X X εφ+=-11，只有11<φ，模型才是平稳的，显然后⾯两个模型不符合条件。

．模拟⾃回归模型t t t t X X X ε++=--213.05.0的程序如下：data a;x1=x;n=n+1;if i>0then output;end;run;proc print data=a;var x;proc gplot data=a;symbol i=spline c=red;plot x*n;run;得到的结果如下图四所⽰：图四A R(2)模拟图形8．针对第⼋题，我们利⽤⽤第七题的程序产⽣数据，在根据第⼋题的相关程序观察⾃相关函数和偏⾃相关函数的图像。

sas中时间格式在SAS（Statistical Analysis System）软件中，处理时间数据是一个常见的任务。

正确使用时间格式能够帮助我们更好地分析数据，进行时间序列分析、时间模式识别等工作。

本文将介绍SAS中常见的时间格式，以及如何使用它们对时间数据进行处理和分析。

1. 日期格式日期格式是用于表示年月日的格式，常见的日期格式包括YYYY-MM-DD、YYMMDD和MM/DD/YYYY等。

在SAS中，我们可以使用日期格式将字符型的日期数据转换为日期型数据，以便进行日期的计算和比较。

例如，可以使用以下语句将字符型日期数据转换为日期型数据：```sasdata work.example;input date $10.;date_num = input(date, yymmdd10.);format date_num yymmdd10.;datalines;2022-01-012022-02-012022-03-012022-04-012. 时间格式时间格式是用于表示时分秒的格式，常见的时间格式包括HH:MM:SS和HHMMSS等。

在SAS中，我们可以使用时间格式将字符型的时间数据转换为时间型数据，以便进行时间的计算和比较。

例如，可以使用以下语句将字符型时间数据转换为时间型数据：```sasdata work.example;input time $8.;time_num = input(time, time8.);format time_num time8.;datalines;10:00:0012:30:0015:45:0020:15:003. 日期时间格式日期时间格式是将日期和时间结合起来表示的格式，常见的日期时间格式包括YYYY-MM-DDTHH:MM:SS、YYMMDDHHMMSS和MM/DD/YYYY HH:MM:SS等。

在SAS中，我们可以使用日期时间格式将字符型的日期时间数据转换为日期时间型数据，以便进行日期时间的计算和比较。