通信原理 第三章 信道

通信原理第三章答案在通信原理的学习中，第三章是非常重要的一部分，它涉及到了很多与通信相关的基础知识和原理。

在这一章节中，我们将学习到很多关于信号传输、调制解调、数字通信等方面的知识。

下面，我将对第三章的一些重要问题进行解答，希望能够帮助大家更好地理解这一部分内容。

1. 什么是信号传输？它的作用是什么？信号传输是指将信息从一个地方传送到另一个地方的过程。

在通信系统中，信号传输是非常重要的，它可以帮助我们实现信息的传递和交流。

通过信号传输，我们可以将声音、图像、数据等信息传送到远方，实现远程通信。

2. 什么是调制解调？它的作用是什么？调制解调是指将原始信号转换成适合在信道上传输的信号，以及将接收到的信号转换成原始信号的过程。

调制是为了适应信道的特性，使信号能够有效地在信道上传输；解调则是为了将接收到的信号转换成原始信号，以便我们能够正确地接收和理解信息。

3. 数字通信和模拟通信有什么区别？数字通信和模拟通信是两种不同的通信方式。

在模拟通信中，信号是连续变化的，它可以表示成无限个可能的数值；而在数字通信中，信号是离散的，它只能表示成有限个可能的数值。

数字通信具有抗干扰能力强、传输质量稳定等优点，而模拟通信则更适合传输连续变化的信号。

4. 为什么要进行信号调制？信号调制是为了适应不同信道的特性，使信号能够有效地在信道上传输。

不同的信道具有不同的传输特性，通过调制可以使信号更好地适应这些特性，提高信号的传输质量和可靠性。

5. 什么是码元和波特？码元是数字通信中的基本单位，它是表示数字信号的最小时间间隔。

波特是衡量数据传输速率的单位，它表示每秒传输的码元数。

在数字通信中，码元和波特是非常重要的概念，它们直接影响着数据传输的速率和效率。

通过以上问题的解答，我们对通信原理第三章的内容有了更深入的理解。

希望大家能够通过学习，掌握这些重要的知识点，为以后的通信技术应用打下坚实的基础。

同时，也希望大家能够在学习过程中多加思考，多进行实践，进一步提高自己的理论水平和实践能力。

习题解答3-1．填空题（1） 在模拟通信系统中，有效性与已调信号带宽的定性关系是（ 已调信号带宽越小，有效性越好），可靠性与解调器输出信噪比的定性关系是（解调器输出信噪比越大，可靠性越好）。

（2） 鉴频器输出噪声的功率谱密度与频率的定性关系是（功率谱密度与频率的平方成正比），采用预加重和去加重技术的目的是（提高解调器输出信噪比）。

（3） 在AM 、DSB 、SSB 、FM 等4个通信系统中，可靠性最好的是（FM ），有效性最好的是（SSB ），有效性相同的是（AM 和DSB ），可靠性相同的是（DSB 、SSB ）。

（4） 在VSB 系统中，无失真传输信息的两个条件是：（相干解调）、（系统的频率特性在载频两边互补对称）。

（5） 某调频信号的时域表达式为6310cos(2105sin10)t t ，此信号的载频是（106）Hz ，最大频偏是（2500）Hz ，信号带宽是（6000）Hz ，当调频灵敏度为5kHz/V 时，基带信号的时域表达式为（30.5cos10t ）。

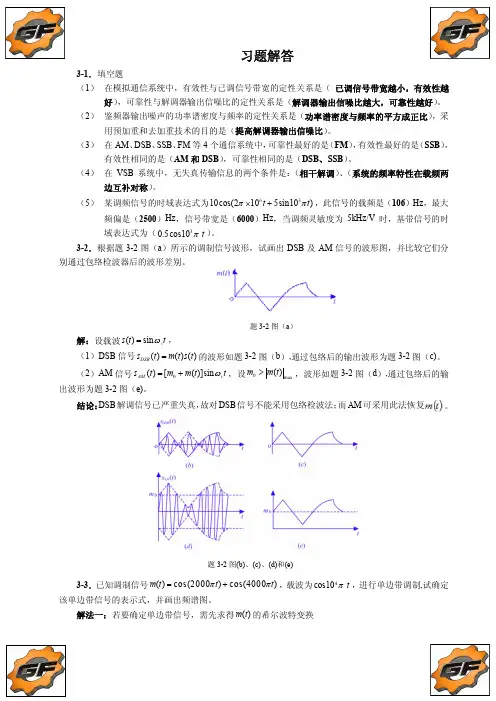
3-2．根据题3-2图（a ）所示的调制信号波形，试画出DSB 及AM 信号的波形图，并比较它们分别通过包络检波器后的波形差别。

解：设载波()sin c s t t ，（1）DSB 信号()()()DSB s t m t s t 的波形如题3-2图（b ）,通过包络后的输出波形为题3-2图（c)。

（2）AM 信号0()[()]sin AM c s t m m t t ，设0max ()m m t ，波形如题3-2图（d ）,通过包络后的输出波形为题3-2图（e)。

结论：DSB 解调信号已严重失真，故对DSB 信号不能采用包络检波法；而AM 可采用此法恢复。

3-3．已知调制信号()cos(2000)cos(4000)m t t t ，载波为4cos10t ，进行单边带调制,试确定该单边带信号的表示式，并画出频谱图。

解法一：若要确定单边带信号，需先求得()m t 的希尔波特变换题3-2图（a ）题3-2图(b)、(c)、(d)和(e)ˆ()cos(2000)cos(4000)22sin(2000)sin(4000)mt t t t t故上边带信号11ˆ()()cos ()sin 2211cos(12000)cos(14000)22USB c c s t m t t mt t t t下边带信号为11ˆ()()cos ()sin 2211cos(8000)cos(6000)22LSB c c s t m t t mt t t t其频谱图如题2-3图所示。

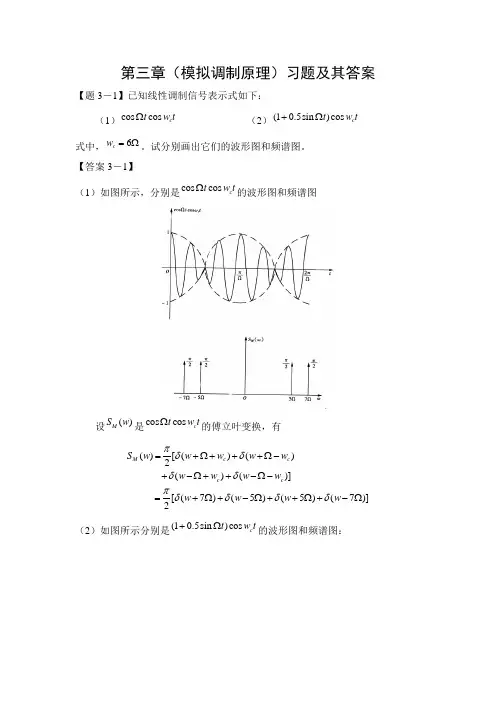
第三章（模拟调制原理）习题及其答案【题3－1】已知线性调制信号表示式如下：（1）cos cos c t w t Ω （2）(10.5sin )cos c t w t +Ω 式中，6c w =Ω。

试分别画出它们的波形图和频谱图。

【答案3－1】（1）如图所示，分别是cos cos c t w t Ω的波形图和频谱图设()M S w 是cos cos c t w t Ω的傅立叶变换，有()[()()2()()] [(7)(5)(5)(7)]2M c c c c S w w w w w w w w w w w w w πδδδδπδδδδ=+Ω+++Ω-+-Ω++-Ω-=+Ω+-Ω++Ω+-Ω（2）如图所示分别是(10.5sin )cos c t w t +Ω的波形图和频谱图：设()M S w 是(10.5sin )cos c t w t +Ω的傅立叶变换，有()[()()] [()()2()()] [(6)(6)] [(7)(5)2(7)(5)]M c c c c c c S w w w w w j w w w w w w w w w w j w w w w πδδπδδδδπδδπδδδδ=++-++Ω+++Ω---Ω+--Ω-=+Ω+-Ω++Ω+-Ω--Ω-+Ω【题3－2】根据下图所示的调制信号波形，试画出DSB 及AM 信号的波形图，并比较它们分别通过包络检波器后的波形差别。

【答案3－2】AM 波形如下：通过低通滤波器后，AM 解调波形如下：DSB 波形如下：通过低通滤波器后，DSB 解调波形如下：由图形可知,DSB 采用包络检波法时产生了失真。

【题3－3】已知调制信号()cos(2000)cos(4000)m t t t ππ=+载波为4cos10t π，进行单边带调制，试确定单边带信号的表达式，并画出频谱图。

【答案3－3】可写出上边带的时域表示式4411ˆ()()cos ()sin 221 [cos(2000)cos(4000)]cos1021 [sin(2000)sin(4000)]sin 1021 [cos12000cos 8000cos14000cos 6000]41 [cos 8000co 4m c c s t m t w t mt w t t t t t t tt t t t t πππππππππππ=-=+-+=+++--s12000cos 6000cos14000]11 cos12000cos1400022t t t t tπππππ+-=+其傅立叶变换对()[(14000)(12000)2+(14000)(12000)]M S w w w w w πδπδπδπδπ=+++-+-可写出下边带的时域表示式'4411ˆ()()cos ()cos 221 [cos(2000)cos(4000)]cos1021 [sin(2000)sin(4000)]sin 1021 [cos12000cos 8000cos14000cos 6000]41 +[cos 8000c 4m c c s t m t w t mt w t t t t t t tt t t t t πππππππππππ=+=+++=+++-os12000cos 6000cos14000]11 cos 8000cos1600022t t t t tπππππ+-=+其傅立叶变换对'()[(8000)(6000)2(8000)(6000)]M S w w w w w πδπδπδπδπ=++++-+-两种单边带信号的频谱图分别如下图。

3-1设理想信道的传输函数为()d j 0e t H K ωω-=式中，K 0和t d 都是常数。

试分析信号s (t )通过该理想信道后的输出信号的时域和频域表示式，并对结果进行讨论。

解 设输入()s t 的频谱用()S ω表示，则通过上述信道后，输出信号的频谱可表示为0()()()()d j t o S S H K S e ωωωωω-==则输出信号为0()()o d s t K s t t =-可见该信道满足无失真条件，对信号的任何频率分量的衰减倍数及延迟相同，故信号在传输过程中无失真。

3-2设某恒参信道的传输函数具有升余弦特性()221cos ,2220,sT js s ssT T e T H T ωωπωωπω-⎧⎛⎫+≤⎪⎪⎪⎝⎭=⎨⎪>⎪⎩式中， T s 为常数。

试求信号s (t )通过该信道后的输出表示式，并对结果进行讨论。

解 设()s t 的频谱用()S ω表示，则通过上述恒参信道后，输出信号的频谱可表示为()222()1cos ()1cos ,2222()()()20,s s T T j jss ss s o sT T TT S e S e T S S H T ωωϕωωωπωωωωωωπω⎛⎫-- ⎪⎝⎭⎧⎛⎫⎛⎫+=+≤⎪⎪⎪⎪⎝⎭⎝⎭==⎨⎪>⎪⎩输出信号为0()()()()4224s s s s s T T T Ts t s t s t s t T =+-+- 分析可见，若信号频率1s s f f T >=，则信道对信号产生截止。

若信号频率1s sf f T ≤=，则信道对输入信号的幅度有函数加权，即信号中不同频率的分量分别受到信道不同的衰减，产生了幅频失真。

()2sT τω=-为常数即没有产生相频失真。

3-3假设某随参信道有两条路径，路径时差为τ =1ms ，试求该信道在哪些频率上传输衰耗最大？哪些频率范围传输信号最有利？解 假设该随参信道两条路径的衰减系数均为K ，该信道的幅频特性为()2cos 2H K ωτω⎛⎫=⎪⎝⎭当cos 12ωτ⎛⎫=⎪⎝⎭（即2n ωτπ=）时，对传输信号最有利，此时出现传输极点 2n πωτ=或 nf τ=当cos 02ωτ⎛⎫=⎪⎝⎭（即122n ωτπ⎛⎫=+ ⎪⎝⎭）时，传输损耗最大，此时出现传输零点 (21)n πωτ+=或 1/2n f τ+=3-4 在移动信道中，市区的最大时延差为5μs ，室内的最大时延差为0.04μs 。

第三章 总结节1 信道的概念一、信道定义：狭义信道、广义信道二、信道模型：1、调制信道共性：①一对（或多对）信道输入，必对应有一对（或多对）信道输出。

②绝大多数信道是线性的，满足叠加定理。

③信道对信号有延时，还有衰耗（固定或时变）④无信号输入，信道也有输出。

调制信道可用时变线性网络表示恒参信道、随参信道2、编码信道编码信道模型用码序列的转移概率描述3、信道分类节2 调制信道特性及对信号传输的影响一、恒参信道1、幅频特性：2、相频特性：若Φ(ω) = - ω t d （ t d 是常数，为线性函数），无失真。

Φ(ω) 非线性，有失真。

二、随参信道1、随参信道传输媒质三个特点：①传输衰耗随时间而变；()()则有幅频失真则无幅频失真const H const H ≠=ωω②传输时延随时间而变；③多径传播。

2、随参信道对信号传输的影响分析：影响结果：①等幅信号变为有包络变化的信号，即存在幅度快衰落影响；②单一频率信号变为窄带频谱信号，即存在频率弥散影响。

相关带宽△f节3 加性噪声节4 信道容量概念信道传输信息的最大速率 R 称为信道容量， C 为差错任意小的最高信息速率。

待传送的信源信息速率 R 源>C ，则信道肯定不能正确传送该信息；而R 源≤C ，采用适当的方法，该信道能正确无误的传送该信息。

加性高斯白噪声作用下的调制信道（白高斯信道）可由Shannon 公式计算信道的容量：B ：信道带宽（Hz ） S ：信号功率( W )N = n 0 B ：白噪声功率s bit B n S B N S B C /1log 1log 022⎪⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=。

第三章（模拟调制原理）习题及其答案【题3－1】已知线性调制信号表示式如下：（1）cos cos c t w t Ω （2）(10.5sin )cos c t w t +Ω 式中，6c w =Ω。

试分别画出它们的波形图和频谱图。

【答案3－1】（1）如图所示，分别是cos cos c t w t Ω的波形图和频谱图设()M S w 是cos cos c t w t Ω的傅立叶变换，有()[()()2()()] [(7)(5)(5)(7)]2M c c c c S w w w w w w w w w w w w w πδδδδπδδδδ=+Ω+++Ω-+-Ω++-Ω-=+Ω+-Ω++Ω+-Ω（2）如图所示分别是(10.5sin )cos c t w t +Ω的波形图和频谱图：设()M S w 是(10.5sin )cos c t w t +Ω的傅立叶变换，有()[()()][()()2()()] [(6)(6)][(7)(5)2(7)(5)]M c c c c c c S w w w w w j w w w w w w w w w w j w w w w πδδπδδδδπδδπδδδδ=++-++Ω+++Ω---Ω+--Ω-=+Ω+-Ω++Ω+-Ω--Ω-+Ω【题3－2】根据下图所示的调制信号波形，试画出DSB 及AM 信号的波形图，并比较它们分别通过包络检波器后的波形差别。

【答案3－2】AM波形如下：通过低通滤波器后，AM解调波形如下：DSB波形如下：通过低通滤波器后，DSB解调波形如下：由图形可知,DSB 采用包络检波法时产生了失真。

【题3－3】已知调制信号()cos(2000)cos(4000)m t t t ππ=+载波为4cos10t π，进行单边带调制，试确定单边带信号的表达式，并画出频谱图。

【答案3－3】可写出上边带的时域表示式4411ˆ()()cos ()sin 221[cos(2000)cos(4000)]cos1021[sin(2000)sin(4000)]sin1021[cos12000cos8000cos14000cos 6000]41[cos8000co 4m c c s t m t w t mt w t t t tt t tt t t t t πππππππππππ=-=+-+=+++--s12000cos 6000cos14000]11cos12000cos1400022t t t t tπππππ+-=+ 其傅立叶变换对()[(14000)(12000)2+(14000)(12000)]M S w w w w w πδπδπδπδπ=+++-+-可写出下边带的时域表示式'4411ˆ()()cos ()cos 221[cos(2000)cos(4000)]cos1021[sin(2000)sin(4000)]sin1021[cos12000cos8000cos14000cos 6000]41+[cos8000c 4m c c s t m t w t mt w t t t tt t tt t t t t πππππππππππ=+=+++=+++-os12000cos 6000cos14000]11cos8000cos1600022t t t t tπππππ+-=+其傅立叶变换对'()[(8000)(6000)2(8000)(6000)]M S w w w w w πδπδπδπδπ=++++-+-两种单边带信号的频谱图分别如下图。